Research Paper:
Research on Evaluation of College-Classroom Teaching Quality Based on Pentapartitioned Neutrosophic Cubic Sets and Machine Vision
Huan Ni*1, Fangwei Zhang*2,†
 , Jun Ye*3
, Jun Ye*3
 , Bing Han*4, and Yuanhong Liu*1
, Bing Han*4, and Yuanhong Liu*1
*1School of Navigation and Shipping, Shandong Jiaotong University
1508 Hexing Road, Chucun Town, Huancui District, Weihai City, Shandong Province 246210, China
*2School of International Business, Shandong Jiaotong University
1508 Hexing Road, Chucun Town, Huancui District, Weihai City, Shandong Province 246210, China
†Corresponding author
*3School of Civil and Environmental Engineering, Ningbo University
818 Fenghua Road, Jiangbei District, Ningbo City, Zhejiang Province 315211, China
*4Warwick Manufacturing Group, University of Warwick
Coventry CV 7, United Kingdom
University-teaching quality evaluations are crucial for assessing teachers’ effectiveness and enhancing students’ learning in classrooms. To improve the evaluation efficiency, this study suggests a creative classroom evaluation approach by using machine vision and pentapartitioned neutrosophic cubic set (PNCS). First, this study uses machine vision technology to establish a PNCS to capture the students’ states in classrooms. Second, it proposes four entropy functions to determine the attribute weights. Third, it combines the improved entropy weight functions with the PNCS to evaluate the teaching effectiveness. This study’s practical price is to introduce big data theories into teaching evaluation fields. Last, an example is provided to confirm the efficacy and applicability of the evaluation approach suggested in this study.
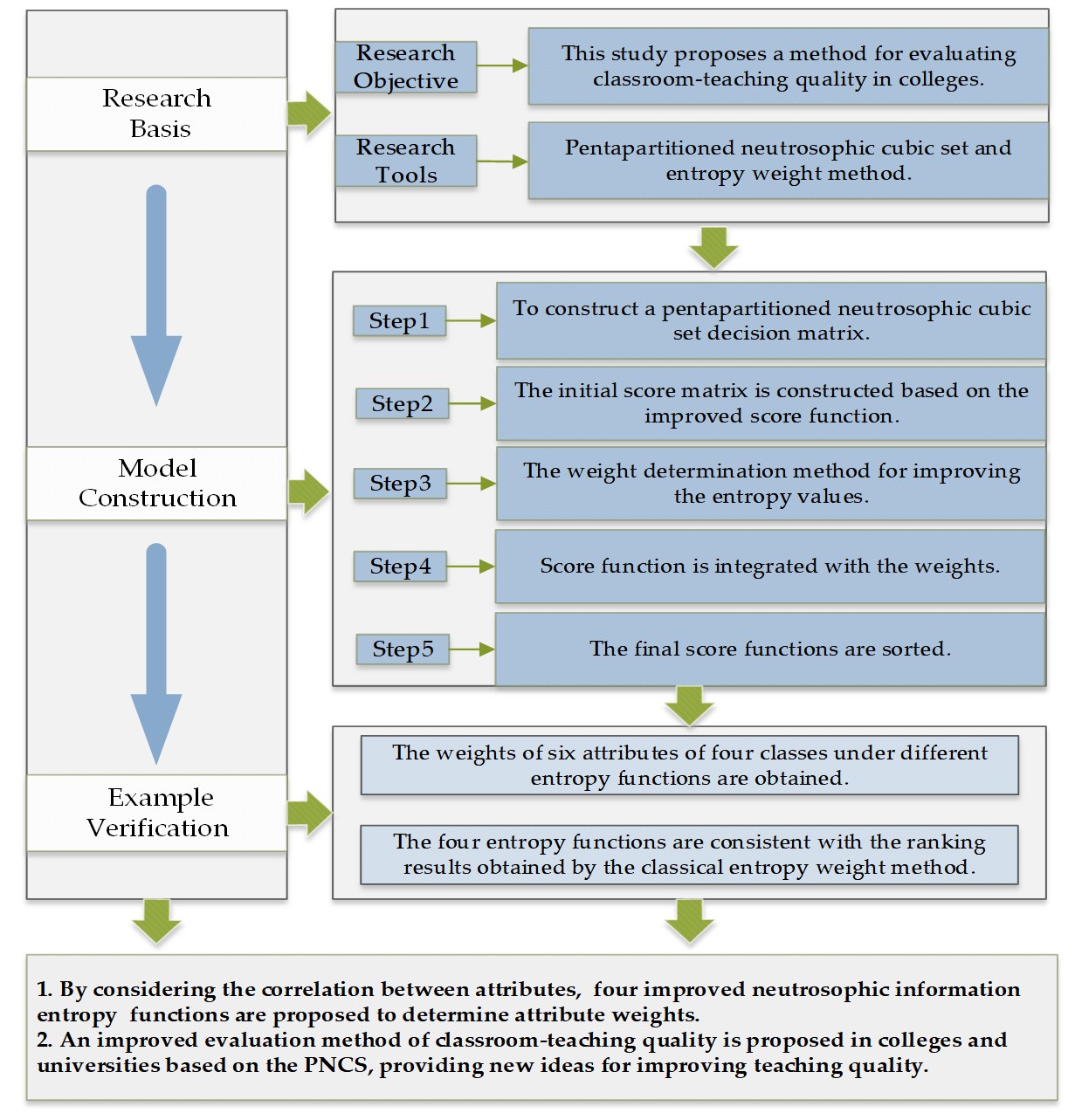
Research framework
- [1] T. Falkowski et al., “Ethicalisation of higher education reform: The strategic integration of academic discourse on scholarly ethos,” Educational Philosophy and Theory, Vol.53, No.5, pp. 479-491, 2021. https://doi.org/10.1080/00131857.2020.1740684
- [2] J. T. Cheng et al., “The quality evaluation of classroom teaching based on FOA-GRNN,” Procedia Computer Science, Vol.107, pp. 355-360, 2017. https://doi.org/10.1016/j.procs.2017.03.117
- [3] C. Pabba et al., “An intelligent system for monitoring students’ engagement in large classroom teaching through facial expression recognition,” Expert Systems, Vol.39, No.1, Article No.e12839, 2022. https://doi.org/10.1111/exsy.12839
- [4] H. Y. Zhang et al., “An improved genetic algorithm and neural network-based evaluation model of classroom teaching quality in colleges and universities,” Wireless Communication & Mobile Computing, Vol.2021, 2021. https://doi.org/10.1155/2021/2602385
- [5] W. T. Ma, “Study on the evaluation method of students’ English classroom performance based on big data analysis,” Int. J. Cont. Engineering Education and Life-Long Learning, Vol.32, No.1, pp. 19-34, 2022. https://doi.org/10.1504/IJCEELL.2021.10033053
- [6] J. W. Hou, “Online teaching quality evaluation model based on support vector machine and decision tree,” J. of Intelligent & Fuzzy Systems, Vol.40, No.2, pp. 2193-2203, 2021. https://doi.org/10.3233/JIFS-189218
- [7] X. Sun, “Method for fuzzy number intuitionistic fuzzy multiple attribute decision making and its application to blended classroom teaching reform effect evaluation,” Mathematical Problems in Engineering, Vol.2022, pp. 1-14, 2022. https://doi.org/10.1155/2022/3907871
- [8] F. Smarandache, “A unifying field in logics: Neutrosophic logic,” Multiple-Valued Logic, Vol.8, No.3, 1999.
- [9] P. D. Liu et al., “Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean,” Neural Computing and Applications, Vol.25, pp. 2001-2010, 2014. https://doi.org/10.1007/s00521-014-1688-8
- [10] J. Ye, “A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets,” Int. J. of Fuzzy Systems, Vol.26, pp. 2459-2466, 2014. https://doi.org/10.1007/s00521-014-1688-8
- [11] J. Ye, “Vector similarity measures of simplified neutrosophic sets and their application in multicriteria decision making,” Int. J. of Fuzzy Systems, Vol.16, No.2, pp. 204-211, 2014. https://doi.org/10.2478/amcs-2014-0033
- [12] J. J. Peng et al., “Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems,” Int. J. of Systems Science, Vol.47, pp. 2342-2358, 2016. https://doi.org/10.1080/00207721.2014.994050
- [13] H. Y. Zhang et al., “Interval neutrosophic sets and their application in multicriteria decision making problems,” The Scientific World J., Vol.2014, 2014. https://doi.org/10.1155/2014/645953
- [14] C. X. Fan, “Correlation coefficients of refined-single valued neutrosophic sets and their applications in multiple attribute decision-making,” J. Adv. Comput. Intell. Intell. Inform., Vol.23, No.3, pp. 421-426, 2019. https://doi.org/10.20965/jaciii.2019.p0421
- [15] S. S. Hussain et al., “New concepts on quadripartitioned single-valued neutrosophic graph with real-life application,” Int. J. of Fuzzy Systems, Vol.24, pp. 1515-1529, 2022. https://doi.org/10.1007/s40815-021-01205-8
- [16] P. Qin et al., “The evaluation model of fuzzy analytic hierarchy process in water project of Xiasha district Based on entroy weight,” Applied Mechanics & Materials, Vols.477-478, pp. 836-839, 2013. https://doi.org/10.4028/www.scientific.net/AMM.477-478.836
- [17] J. Ye et al., “Mult-period medical diagnosis method using a single-valued neutrosophic similarity measure based on tangent function,” Computer Methods and Programs in Biomedicine, Vol.123, pp. 142-149, 2016. https://doi.org/10.1016/j.cmpb.2015.10.002
- [18] J. Ye, “Single-valued neutrosophic similarity measures based on cotangent function and their application in the fault diagnosis of steam turbine,” Soft Computing, Vol.21, pp. 817-825, 2017. https://doi.org/10.1007/s00500-015-1818-y
- [19] F. F. Jin et al., “Single-valued neutrosophic entropy and similarity measures to solve supplier selection problems,” J. of Intelligent & Fuzzy Systems, Vol.35, No.6, pp. 6513-6523, 2018. https://doi.org/10.3233/JIFS-18854
- [20] H. Tian, “Entropy analysis on intuitionistic fuzzy sets and interval-valued intuitionistic fuzzy sets and its applications in mode assessment on open communities,” J. Adv. Comput. Intell. Intell. Inform., Vol.22, No.1, pp. 147-155, 2018. https://doi.org/10.20965/jaciii.2018.p0147
- [21] Y. Uemura et al., “Effective Action Learning Method Using Information Entropy for a Single Robot Under Multi-Agent Control,” J. Adv. Comput. Intell. Intell. Inform., Vol.28, No.2, pp. 273-283, 2024. https://doi.org/10.20965/jaciii.2024.p0273
- [22] G. Lu et al., “Real-Time Dynamic Gesture Recognition Algorithm Based on Adaptive Information Fusion and Multi-Scale Optimization Transformer,” J. Adv. Comput. Intell. Intell. Inform., Vol.27, No.6, pp. 1096-1107, 2023. https://doi.org/10.20965/jaciii.2023.p1096
- [23] R. Alfanz et al., “Predicting Student Performance Through Data Mining: A Case Study in Sultan Ageng Tirtayasa University,” J. Adv. Comput. Intell. Intell. Inform., Vol.27, No.6, pp. 1159-1167, 2023. https://doi.org/10.20965/jaciii.2023.p1159
- [24] L. Zhou et al., “Reclining Public Chair Behavior Detection Based on Improved YOLOv5,” J. Adv. Comput. Intell. Intell. Inform., Vol.27, No.6, pp. 1175-1182, 2023. https://doi.org/10.20965/jaciii.2023.p1175
- [25] C. Udeh et al., “Multimodal Facial Emotion Recognition Using Improved Convolution Neural Networks Model,” J. Adv. Comput. Intell. Intell. Inform., Vol.27, No.4, pp. 710-719, 2023. https://doi.org/10.20965/jaciii.2023.p0710
- [26] H. B. Wang et al., “Interval neutrosophic sets and logic: theory and applications in computing,” Computer Science, Vol.65, No.4, 2012. https://doi.org/10.5281/zenodo.8818
- [27] Y. B. Jun et al., “Neutrosophic Cubic Sets,” New Mathematics and Natural Computation, Vol.13, No.1, pp. 41-54, 2017. https://doi.org/10.1142/S1793005717500041
- [28] R. Mallick et al., “Pentapartitioned neutrosophic set and its properties,” Neutrosophic Sets and Systems, Vol.36, No.1, pp. 184-192, 2020. https://digitalrepository.unm.edu/nss_journal/vol36/iss1/
- [29] Y. M. Li et al., “Designing pentapartitioned neutrosophic cubic set aggregation operator-based air pollution decision-making model,” Complex & Intelligent Systems, 2023. https://doi.org/10.1007/s40747-023-00971-2
- [30] J. Ye, “Linguistic neutrosophic cubic numbers and their multiple attribute decision-making method,” Information, Vol.8, No.3, Article No.110, 2017. https://doi.org/10.3390/info8030110
- [31] H. L. Xue et al., “Possibility neutrosophic cubic sets and their application to multiple attribute decision making,” Symmetry, Vol.12, No.2, Article No.269, 2020. https://doi.org/10.3390/sym12020269
- [32] X. G. Chen et al., “A new geometric construction method of single-valued neutrosophic entropy,” J. of Science of Teachers’ College and University, Vol.42, No.8, pp. 6-9,40, 2022. https://doi.org/10.3969/j.issn.1007-9831.2022.08.002
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.