Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation.

Warfield SK; Zou KH; Wells WM

doi:10.1109/tmi.2004.828354

Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation.

Warfield SK ¹,

Zou KH ,

Wells WM

Affiliations

1. Harvard Medical School and the Department of Radiology of Brigham and Women's Hospital, 75 Francis St, Boston, MA 02115, USA.
Authors
Warfield SK¹
(1 author)

ORCIDs linked to this article

Warfield SK | 0000-0002-7659-3880

IEEE Transactions on Medical Imaging, 01 Jul 2004, 23(7):903-921
https://doi.org/10.1109/tmi.2004.828354 PMID: 15250643 PMCID: PMC1283110

Free full text in Europe PMC

Abstract

Characterizing the performance of image segmentation approaches has been a persistent challenge. Performance analysis is important since segmentation algorithms often have limited accuracy and precision. Interactive drawing of the desired segmentation by human raters has often been the only acceptable approach, and yet suffers from intra-rater and inter-rater variability. Automated algorithms have been sought in order to remove the variability introduced by raters, but such algorithms must be assessed to ensure they are suitable for the task. The performance of raters (human or algorithmic) generating segmentations of medical images has been difficult to quantify because of the difficulty of obtaining or estimating a known true segmentation for clinical data. Although physical and digital phantoms can be constructed for which ground truth is known or readily estimated, such phantoms do not fully reflect clinical images due to the difficulty of constructing phantoms which reproduce the full range of imaging characteristics and normal and pathological anatomical variability observed in clinical data. Comparison to a collection of segmentations by raters is an attractive alternative since it can be carried out directly on the relevant clinical imaging data. However, the most appropriate measure or set of measures with which to compare such segmentations has not been clarified and several measures are used in practice. We present here an expectation-maximization algorithm for simultaneous truth and performance level estimation (STAPLE). The algorithm considers a collection of segmentations and computes a probabilistic estimate of the true segmentation and a measure of the performance level represented by each segmentation. The source of each segmentation in the collection may be an appropriately trained human rater or raters, or may be an automated segmentation algorithm. The probabilistic estimate of the true segmentation is formed by estimating an optimal combination of the segmentations, weighting each segmentation depending upon the estimated performance level, and incorporating a prior model for the spatial distribution of structures being segmented as well as spatial homogeneity constraints. STAPLE is straightforward to apply to clinical imaging data, it readily enables assessment of the performance of an automated image segmentation algorithm, and enables direct comparison of human rater and algorithm performance.

Free full text

IEEE Trans Med Imaging. Author manuscript; available in PMC 2005 Nov 14.

Published in final edited form as:

IEEE Trans Med Imaging. 2004 Jul; 23(7): 903–921.

https://doi.org/10.1109/TMI.2004.828354

PMCID: PMC1283110

NIHMSID: NIHMS2330

PMID: 15250643

Simultaneous Truth and Performance Level Estimation (STAPLE): An Algorithm for the Validation of Image Segmentation

Simon K. Warfield, Member, IEEE,^* Kelly H. Zou, and William M. Wells, Member, IEEE

Author information Copyright and License information Disclaimer

The publisher's final edited version of this article is available at IEEE Trans Med Imaging

See other articles in PMC that cite the published article.

Go to:

Abstract

The performance of raters (human or algorithmic) generating segmentations of medical images has been difficult to quantify because of the difficulty of obtaining or estimating a known true segmentation for clinical data. Although physical and digital phantoms can be constructed for which ground truth is known or readily estimated, such phantoms do not fully reflect clinical images due to the difficulty of constructing phantoms which reproduce the full range of imaging characteristics and normal and pathological anatomical variability observed in clinical data. Comparison to a collection of segmentations by raters is an attractive alternative since it can be carried out directly on the relevant clinical imaging data. However, the most appropriate measure or set of measures with which to compare such segmentations has not been clarified and several measures are used in practice.

We present here an expectation-maximization algorithm for simultaneous truth and performance level estimation (STAPLE). The algorithm considers a collection of segmentations and computes a probabilistic estimate of the true segmentation and a measure of the performance level represented by each segmentation. The source of each segmentation in the collection may be an appropriately trained human rater or raters, or may be an automated segmentation algorithm. The probabilistic estimate of the true segmentation is formed by estimating an optimal combination of the segmentations, weighting each segmentation depending upon the estimated performance level, and incorporating a prior model for the spatial distribution of structures being segmented as well as spatial homogeneity constraints. STAPLE is straightforward to apply to clinical imaging data, it readily enables assessment of the performance of an automated image segmentation algorithm, and enables direct comparison of human rater and algorithm performance.

Index Terms: Accuracy, classifier fusion, expectation-maximization, gold standard, ground truth, Markov random field, precision, segmentation, sensitivity, specificity, STAPLE, validation

Go to:

I. Introduction

MEDICAL image segmentation has long been recognized as a difficult problem. Many interactive and automated algorithms have been proposed, and in practice approaches specifically tuned to the important characteristics of the application are often successful. When selecting, designing, or optimizing particular algorithms for a segmentation task, the performance characteristics of the algorithms must be assessed.

Characterizing the performance of image segmentation approaches has also been a persistent challenge. Quantitative performance analysis is important since segmentation algorithms often have limited accuracy and precision. Interactive drawing of the desired segmentation by domain experts has often been the only acceptable approach, and yet suffers from intraexpert and inter-expert variability and is time consuming and expensive to carry out. Automated algorithms have been sought in order to remove the variability introduced by experts, but automated algorithms must be assessed to ensure they are suitable for the task.

Measurement tools are often characterized by assessment of their accuracy and precision. The accuracy of a human or an algorithm in creating a segmentation is the degree to which the segmentation corresponds to the true segmentation, and so the assessment of accuracy of a segmentation requires a reference standard, representing the true segmentation, against which it may be compared. Precision is determined by the reproducibility of the segmentations obtained repeatedly from the same image [1]. The precision may be assessed without comparison to a reference standard. High accuracy and high precision are both desirable properties.

An ideal reference standard for image segmentation would be known to high accuracy and would reflect the characteristics of segmentation problems encountered in practice. There is a tradeoff between the accuracy and realism of the reference standard. As the accuracy of the reference standard segmentation increases, the degree to which the reference standard reflects segmentation problems encountered in practice tends to decrease. The accuracy of segmentations of medical images has been difficult to quantify in the absence of an accepted reference standard for clinical imaging data.

Synthetic images can be constructed with known true segmentation (high accuracy) but typically lack characteristics encountered in practice. Phantoms can be built and imaged, which increases the realism of the model by incorporating the imaging system characteristics, but also reduces the fidelity with which the true segmentation is known. Although such physical and digital phantoms [2], [3] have an important role to play in quantifying algorithm performance, such phantoms do not fully reflect clinical images due to the difficulty of constructing phantoms that reproduce the full range of imaging characteristics (such as partial volume artifact, intensity in-homogeneity artifact and noise). In addition, such phantoms typically cannot reproduce both the normal and pathological anatomical variability observed in clinical data. Therefore, alternative approaches have an important role, as it is not necessarily possible to generalize performance measurements on a phantom to the results expected in practice.

Cadavers provide a more realistic model of anatomy, but the true segmentation can only be estimated, and such models differ from in vivo data [4], [5]. Patient data provides the most realistic model for a given application task, but is the most difficult for which to identify a reference standard.

A common alternative to phantom studies has been to carry out behavioral comparisons: an automated algorithm is compared to the segmentations generated by a group of experts, and if the algorithm generates segmentations sufficiently similar to the experts, it is considered to be an acceptable substitute for the experts. In addition to acceptable accuracy, good automated segmentation algorithms also typically require less time to apply and have better precision than interactive segmentation by an expert.

The most appropriate way to carry out the comparison of a segmentation to a group of expert segmentations is so far unclear. A number of metrics have been proposed to compare segmentations. Simply measuring the volume of segmented structures has often been used [6], [7]. Two segmentation methods may be compared by assessing the limits of agreement [8] of volume estimates derived from the segmentations. However, volume estimates may be quite similar when the segmented structures are located differently, have different shapes or have different boundaries [9] and so alternative measures have been sought [10].

Other measures used in practice include measures of spatial overlap, such as the Dice and Jaccard Similarity Coefficients [11], [12]. For example, spatial overlap has been used to compare manual segmentations with segmentations obtained through nonrigid registration [13]. Furthermore, measures inspired by information theory have been applied [14], [15]. In many applications, assessment of boundary differences is useful and the Hausdorff measure and modifications have been used for this [16]. Agreement measures for comparing different experts, such as the kappa statistic, have also been explored [17].

A reference standard has sometimes been formed by taking a combination of expert segmentations. For example, a voting rule as often used in practice selects all voxels where some majority of experts agree the structure to be segmented is present [18], [19]. This simple approach unfortunately does not provide guidance as to how many experts should agree before the structure is considered to be present. Furthermore vote counting strategies treat each voter equally without regard to potential variability in quality or performance amongst the voters, and does not allow for a priori information regarding the structure being segmented to be incorporated. In the case of binary segmentations, a majority vote is at least unique in the case of an odd number of voters. However, in the case of multicategory segmentations, the category with the most votes may not be unique and may not reflect the overall preferred choice of the voters. Preferential voting strategies, operating on votes or class probabilities, have been examined in the context of classifier fusion [20]. Examples include the Borda count [21] for preferential vote ordering, class probability combining strategies (the Product Rule and the Sum Rule which can be used to express the Min Rule, the Max Rule, the Median Rule and the Majority Vote Rule as described by [22]), and strategies which assume each classifier has expertise in a subset of the decision domain [23]–[25]. Similar issues in combining decisions from multiple raters or studies arise in content-based collaborative filtering [26] and in meta-analysis of diagnostic tests [27], [28]. Estimating performance in the presence of an imperfect or limited reference standard has also been explored [29], [30]. The most appropriate vote ordering or decision combining strategy remains unclear.

We present here a new algorithm, simultaneous truth and performance level estimation (STAPLE), which takes a collection of segmentations of an image, and computes simultaneously a probabilistic estimate of the true segmentation and a measure of the performance level represented by each segmentation. The source of each segmentation in the collection may be an appropriately trained human rater or raters, or it may be an automated segmentation algorithm. Our algorithm is formulated as an instance of the expectation-maximization (EM) algorithm [31], [32] and builds upon our earlier work [33], [34]. In the formulation of our algorithm described here, the expert segmentation decision at each voxel is directly observable, the hidden true segmentation is a binary variable for each voxel, and the performance level, or quality, achieved by each segmentation is represented by sensitivity and specificity parameters. We also describe a generalization of the algorithm to unordered multicategory labels, suitable for when the hidden true segmentation at each voxel is one of an unordered finite set of labels.

The complete data consists of the segmentation decisions at each voxel, which are known, and the true segmentation, which is not known. If we did know the true segmentation, it would be straightforward to estimate the performance parameters by maximum-likelihood (ML) estimation. Since the complete data is not available, the complete data log likelihood cannot be constructed and instead must be estimated. Doing so requires evaluating the conditional probability density of the hidden true segmentation given the segmentation decisions and a previous estimate of the performance level of each segmentation generator. The expectation of the complete data log likelihood with respect to this density is then calculated, and from this estimate of the complete data log likehood, the performance parameters are found by ML estimation (or maximum a posteriori (MAP) estimation when a prior distribution for the parameters is considered). We iterate this sequence of estimation of the conditional probability of the true segmentation and performance parameters until convergence is reached. Convergence to a local maximum is guaranteed. Since we obtain both an estimate of the true segmentation and performance parameters from a collection of segmentations and a prior model, the algorithm is straightforward to apply to clinical imaging data. The algorithm enables the assessment of the performance of an automated image segmentation algorithm, and provides a simple method for direct comparison of human and algorithm performance.

This paper is organized as follows. In Section II, we describe the STAPLE algorithm. We describe how STAPLE can be appropriately initialized both when there is no or limited prior information and when rich prior information is available. We describe how convergence of the estimation scheme is detected. In Section III, we describe the application of the STAPLE algorithm to digital phantoms where the true segmentation is known by construction and investigate the characterization of segmentations by synthetic raters with predefined sensitivities and specificities. We demonstrate that STAPLE accurately estimates the performance level parameters and the true segmentation. We demonstrate the use of STAPLE with data from several clinical applications in order to compare with previously reported validation measures and to illustrate how the algorithm may be used in practice. The computational complexity and the run time of the algorithm are reported, and indicate the algorithm converges rapidly in practical applications.

Go to:

II. Method

We describe in this section an EM algorithm for estimating the hidden true segmentation and performance level parameters from a collection of segmentations and a prior model.

A. Description of STAPLE Algorithm

Consider an image of N voxels, and the task of segmenting a structure in that image by indicating the presence or absence of the structure at each voxel. Let p = (p₁, p₂,…p_R)^T be a column vector of R elements, with each element a sensitivity parameter characterising one of R segmentations, and q = (q₁, q₂,…q_R)^T be a column vector of R elements, with each element a specificity parameter characterising the performance of one of R segmentations. Let D be an N × R matrix describing the binary decisions made for each segmentation at each voxel of the image. Let T be an indicator vector of N elements, representing the hidden binary true segmentation, where for each voxel the structure of interest is recorded as present (1) or absent (0). Let the complete data be (D, T) and let the probability mass function of the complete data be f (D, T|p, q).

Our goal is to estimate the performance level parameters of the experts characterized by parameters (p, q) which maximize the complete data log likelihood function

(\hat{p}, \hat{q}) = arg max_{p, q} ln f (D, T | p, q) .

(1)

If we knew the true segmentation, we could construct a 2 × 2 conditional probability table, by comparing the decision D_ij of segmentation j (for j = 1,…, R) as to the presence or absence of a structure at voxel i with the true segmentation. Recall the definition of sensitivity and specificity, where p_j represent the “true positive fraction” or sensitivity (relative frequency of D_ij = 1 when T_i = 1),

p_{j} = Pr (D_{i j} = 1 | T_{i} = 1)

(2)

and q_j represent the “true negative fraction” or specificity (relative frequency of D_ij = 0 when T_i = 0)

q_{j} = Pr (D_{i j} = 0 | T_{i} = 0) .

(3)

The parameters p_j, q_j [set membership] [0,1] are assumed to be characteristic of the rater, and may be equal for different raters but in general are not. We assume that the segmentation decisions are all conditionally independent given the true segmentation and the performance level parameters, that is (D_ij|T_i, p_j, q_j) [perpendicular] (D_ij′|T_i, p_j′, q_j′), ∀j ≠ j′. This model expresses the assumption that the raters derive their segmentations of the same image independently from one another and that the quality of the result of the segmentation is captured by the sensitivity and specificity parameters.

Implicit in this model is the notion that the experts have been trained to interpret the images in a similar way, the segmentation decisions may differ due to random or systematic rater differences, and that a probabilistic estimate of the true segmentation can be formulated as an optimal combination of the observed decisions and a prior model.

We now present the version of the EM algorithm that we have developed for this problem which enables us to estimate the solution of (1). Detailed descriptions of the EM algorithm and generalizations are available [31], [32] and our exposition closely follows those sources. The essence of the EM algorithm is the observation that certain ML estimation problems would be considerably simplified if some missing data were available, and this is the case for our problem. The observable data, the segmentation decisions at each voxel, is regarded as being incomplete and is regarded as an observable function of the complete data. Here, the complete data is the segmentation decisions D augmented with the true segmentation of each voxel T. This true segmentation T is called the missing or hidden data, and is unobservable. Let

θ_{j} = {(p_{j}, q_{j})}^{T}, \forall j \in 1, \dots, R

(4)

be the unknown parameters characterizing performance of segmentation j and

θ = [θ_{1} θ_{2}, \dots, θ_{R}]

(5)

the complete set of unknown parameters for the R segmentations that we wish to identify. Let f (D, T | θ) denote the probability mass function of the random vector corresponding to the complete data. We write the complete data log likelihood function as

ln L_{c} {θ} = ln f (D, T | θ) .

(6)

The EM algorithm approaches the problem of maximizing the incomplete data log likelihood equation

ln L {θ} = ln f (D | θ)

(7)

by proceeding iteratively with estimation and maximization of the complete data log likelihood function. As the complete data log likelihood function is not observable, it is replaced by its conditional expectation given the observable data D using the current estimate of θ. Computing the conditional expectation of the complete data log likelihood function is referred to as the E-step, and identifying the parameters that maximize this function is referred to as the M-step.

In more detail, let θ⁽⁰⁾ be some initial value for θ. Then, on the first iteration, the E-step requires the calculation of

\begin{array}{l} Q (θ | θ^{(0)}) \equiv E [ln f (D, T | θ) | D, θ^{(0)}] \\ = \sum_{T} ln f (D, T | θ) f (T | D, θ^{(0)}) . \end{array}

(8)

The M-step requires the maximization of Q(θ|θ⁽⁰⁾) over the parameter space of θ. That is, we choose θ⁽¹⁾ such that

Q (θ^{(1)} | θ^{(0)}) \geq Q (θ | θ^{(0)})

(9)

for all θ. The E-step and M-step are then repeated as above where at each iteration k, the current estimate θ⁽^k⁾ and the observed segmentation decisions D are used to calculate the conditional expectation of the complete data log likelihood function, and then the estimate of θ⁽^k⁺¹⁾ is found by maximization of Q(θ|θ⁽^k⁾). The E- and M-steps are iterated until convergence. It has been shown [31] that the incomplete data log likelihood function is not decreased after an EM iteration, and so local convergence is guaranteed when the likelihood function has an upper bound.

The key requirements necessary to carry out the EM algorithm are to have a specification of the complete data, and to have the conditional probability density of the complete data given the observed data. We describe below how the E-step and M-step are formulated for our estimation problem.

The performance parameters at iteration k that maximize the conditional expectation of the log likelihood function are given by

\begin{matrix} θ^{(k)} = arg max_{θ} E [ln f (D, T | θ) | D, θ^{(k - 1)}] \\ = arg max_{θ} E [ln \frac{f (D, T | θ)}{f (θ)} | D, θ^{(k - 1)}] . \end{matrix}

(10)

Hence, on expressing θ⁽^k⁾ as (p⁽^k⁾, q⁽^k⁾)

\begin{array}{l} (p^{(k)}, q^{(k)}) = arg max_{p, q} E [ \\ ln \frac{f (D, Τ, p, q) f (T, p, q)}{f (T, p, q) f (p, q)} | \\ D, p^{(k - 1)}, q^{(k - 1)}] \end{array}

(11)

and so we have

\begin{array}{l} (p^{(k)}, q^{(k)}) = arg max_{p, q} E [ln (f (D | Τ, p, q) f (T)) | \\ D, p^{(k - 1)}, q^{(k - 1)}] \end{array}

(12)

where (p⁽^k⁾, q⁽^k⁾) is the estimate of the expert performance level parameters at iteration k, and the last follows under the assumption that T is independent of the performance level parameters so that f (T, p, q) = f (T) f (p, q).

B. E-Step: Estimation of the Conditional Expectation of the Complete Data Log Likelihood Function

In this section, the estimator for the unobserved true segmentation is derived. We first derive an expression for the conditional probability density function of the true segmentation given the expert decisions (observed segmentations) and the previous estimate of the performance parameters

\begin{array}{l} f (T | D, θ^{(k)}) \\ = \frac{f (D | T, θ^{(k - 1)}) f (T)}{\sum_{T^{'}} f (D | T^{'}, θ^{(k - 1)}) f (T^{'})} \\ = \frac{\prod_{i} [\prod_{j} f (D_{i j} | T_{i}, θ_{j}^{(k - 1)})] f (T_{i})}{\sum_{{T^{'}}_{1}} \dots \sum_{{T^{'}}_{N}} \prod_{i} [\prod_{j} f (D_{i j} | {T^{'}}_{i}, θ_{j}^{(k - 1)})] f ({T^{'}}_{i})} \\ = \frac{\prod_{i} [\prod_{j} f (D_{i j} | T_{i}, p_{j}^{(k - 1)}, q_{j}^{(k - 1)})] f (T_{i})}{\prod_{i} [\sum_{{T^{'}}_{i}} \prod_{j} f (D_{i j} | {T^{'}}_{i}, p_{j}^{(k - 1)}, q_{j}^{(k - 1)})] f ({T^{'}}_{i})} \end{array}

such that at each voxel i we have

\begin{array}{l} f (T_{i} | D_{i}, p^{(k - 1)}, q^{(k - 1)}) \\ = \frac{\prod_{j} f (D_{i j} | T_{i}, p_{j}^{(k - 1)}, q_{j}^{(k - 1)}) f (T_{i})}{\sum_{{T^{'}}_{i}} \prod_{j} f (D_{i j} | {T^{'}}_{i}, p_{j}^{(k - 1)}, q_{j}^{(k - 1)}) f ({T^{'}}_{i})} \end{array}

(13)

Where f (T_i) is the prior probability of T_i, and the conditional independence of the segmentations allows us to write the joint probability as a product of rater-specific probabilities. A voxelwise independence assumption has been made here, and in Section II-E it is shown how voxelwise dependence can be efficiently modeled.

Since the true segmentation is treated as a binary random variable, the conditional probability f (T_i = 0|Di, p⁽^k⁻¹⁾, q⁽^k⁻¹⁾) is simply 1 − f (T_i = 1|Di, p⁽^k⁻¹⁾, q⁽^k⁻¹⁾). We store for each voxel the estimate of the probability that the true segmentation at each voxel is T_i = 1. Section II-D describes a generalization to segmentations with unordered multicategory labels.

Now consider (13) for T_i = 1 and T_i = 0, respectively. Factoring over the raters and using the definition of p_j and q_j, we can write

\begin{array}{l} a_{i}^{(k)} \equiv f (T_{i} = 1) \prod_{j} f (D_{i j} | T_{i} = 1, p_{j}^{(k)}, q_{j}^{(k)}) \\ = f (T_{i} = 1) \prod_{j : D_{i j} = 1} p_{j}^{(k)} \prod_{j : D_{i j} = 0} (1 - p_{j}^{(k)}) \end{array}

(14)

and

\begin{array}{l} b_{i}^{(k)} \equiv f (T_{i} = 0) \prod_{j} f (D_{i j} | T_{i} = 0, p_{j}^{(k)}, q_{j}^{(k)}) \\ = f (T_{i} = 0) \prod_{j : D_{i j} = 0} q_{j}^{(k)} \prod_{j : D_{i j} = 1} (1 - q_{j}^{(k)}) \end{array}

(15)

where j:D_ij = 1 denotes the set of indexes for which the decision of rater j at voxel i (i.e., D_ij) has the value 1.

With these expressions, we can now write a compact expression for the conditional probability of the true segmentation at each voxel. Using the notation common for EM algorithms, we refer to this as the weight variable $W_{i}^{(k - 1)}$

\begin{array}{l} W_{i}^{(k - 1)} \equiv f (T_{i} = 1 | D_{i}, p^{(k - 1)}, q^{(k - 1)}) \\ = \frac{a_{i}^{(k - 1)}}{a_{i}^{(k - 1)} + b_{i}^{(k - 1)}} . \end{array}

(16)

The weight $W_{i}^{(k - 1)}$ indicates the probability of the true segmentation at voxel i being equal to one. It is a normalized product of the prior probability of T_i = 1, the sensitivity of each of the experts that decided the true segmentation was one and (1—sensitivity) of each of the experts that decided the true segmentation was zero.

In order to complete the E-step, we require an expression for the conditional expectation of the complete data log likelihood function. This is dramatically simplified when we consider only the terms necessary for finding the parameters that maximize the function, and this is derived in the next section.

C. M-Step: Estimation of the Performance Parameters by Maximization

Given the estimated weight variables $W_{i}^{(k - 1)}$ , which represent the conditional probabilities of the true segmentation, we can find the values of the expert performance level parameters that maximize the conditional expectation of the complete data log likelihood function.

Considering (12), and noting that since In $\prod_{i} f (T_{i})$ is free of (p, q) it follows that

\begin{array}{l} (p^{(k)}, q^{(k)}) = arg max_{p, q} \sum_{j} \sum_{i} E [ \\ ln f (D_{i j} | T_{i}, p_{j}, q_{j}) | D, p^{(k - 1)}, q^{(k - 1)}] \end{array}

(17)

so for each expert j

\begin{array}{l} (p_{j}^{(k)}, q_{j}^{(k)}) \\ = arg max_{p_{j}, q_{j}} \sum_{i} E [ln f (D_{i j} | T_{i}, p_{j}, q_{j}) | D, p^{(k - 1)}, q^{(k - 1)}] \\ = arg max_{p_{j}, q_{j}} \sum_{i} [W_{i}^{(k - 1)} ln f (D_{i j} | T_{i} = 1, p_{j}, q_{j}) \\ + (1 - W_{i}^{(k - 1)}) ln f (D_{i j} | T_{i} = 0, p_{j}, q_{j})] \\ = arg max_{p_{j}, q_{j}} \sum_{i : D_{i j} = 1} W_{i}^{(k - 1)} ln p_{j} \\ + \sum_{i : D_{i j} = 1} (1 - W_{i}^{(k - 1)}) ln (1 - q_{j}) \\ + \sum_{i : D_{i j} = 0} W_{i}^{(k - 1)} ln (1 - p_{j}) \\ + \sum_{i : D_{i j} = 0} (1 - W_{i}^{(k - 1)}) ln q_{j} . \end{array}

A necessary condition at a maximum of the above with respect to parameter p_j is that the first derivative equal zero. Differentiating Q (θ|θ⁽^k⁾) with respect to parameter p_j and equating to 0, yields (similarly for q_j)

p_{j}^{(k)} = \frac{\sum_{i : D_{i j} = 1} W_{i}^{(k - 1)}}{\sum_{i} W_{i}^{(k - 1)}}

(18)

q_{j}^{(k)} = \frac{\sum_{i : D_{i j} = 0} (1 - W_{i}^{(k - 1)})}{\sum_{i} (1 - W_{i}^{(k - 1)})} .

(19)

We can interpret the weight estimate $W_{i}^{(k - 1)}$ as the strength of belief in the underlying true segmentation being equal to 1. In the case of perfect knowledge about the true segmentation, i.e., $W_{i}^{(k - 1)} \in {0.0, 1.0},$ the estimator of sensitivity given by (18) corresponds to the usual definition of sensitivity as the true positive fraction. When the true segmentation estimate is a continuous parameter, i.e., $W_{i}^{(k - 1)} \in [0, 1]$ as here, the estimator can be interpreted as the ratio of the jth expert true positive detections to the total amount of structure T_i = 1 voxels believed to be in the data, with each voxel detection weighted by the strength of belief in T_i = 1. Similarly, the specificity estimator of (19) is a natural formulation of an estimator for the specificity given a degree of belief in the underlying T_i = 0 state.

Summary: STAPLE estimates the performance parameters, and a probabilistic estimate of the true segmentation, by iterated estimation. The first step of each iteration is estimation of the conditional probability of the true segmentation given the expert decisions and previous performance parameter estimates as given by (16), and the second step is updated estimation of the performance parameters given by (18) and (19).

D. An Extension to Unordered Multicategory Labels

In this section, we provide a generalization of the estimation strategy to the case when the truth is a label from a finite set of unordered categories. For example, consider a brain magnetic resonance image (MRI) tissue segmentation application where we are interested to identify the true label as one of white matter, gray matter, or cerebrospinal fluid. Rather than being restricted to two labels only, here we allow T to take on one of L labels where Ti [set membership] {0,1,…, L − 1} and similarly the segmentation decisions may also be one of these L labels, D_ij {0,1,…, L − 1}, and D is an N × R matrix describing the decisions made for each segmentation at each voxel of the image. In this case, we characterize each rater performance by θ_j, an L × L matrix of parameters where the element of the matrix characterizes the probability rater j will decide label s′ is present when the true label is s. The perfect rater would have a performance matrix with 1 on the diagonal and 0 in each off-diagonal element, that is the rater performance matrix would be an identity matrix.

In order to evaluate the conditional expectation of the complete data log likelihood for this case, we need to compute the conditional probability that the true label at voxel i is s given the set of segmentations and the previous estimate of the performance characteristics. Similarly to the binary case, we find that

\begin{array}{l} W_{s i}^{(k)} \equiv f (T_{i} = s | D_{i}, θ^{(k)}) \\ = \frac{f (T_{i} = s) \prod_{j} f (D_{i j} | T_{i} = s, θ_{j}^{(k)})}{\sum_{s^{'}} f (T_{i} = s^{'}) \prod_{j} f (D_{i j} | T_{i} = s^{'}, θ_{j}^{(k)})} . \end{array}

(20)

With this conditional probability, we can evaluate the expectation of the complete data log likelihood function, with the goal of identifying the performance parameters by ML estimation. Considering each rater separately, we find the new parameter estimates $θ_{j}^{(k + 1)}$ by

\begin{array}{l} θ_{j}^{(k + 1)} \\ = arg max_{θ_{j}} \sum_{i} E [ln f (D_{i j} | T_{i}, θ_{j}) | D, θ_{j}^{(k)}] \\ = arg max_{θ_{j}} \sum_{i} \sum_{s} W_{s i}^{(k)} ln f (D_{i j} | T_{i} = s, θ_{j}) \\ = arg max_{θ_{j}} \sum_{s^{'}} \sum_{i : D_{i j} = s^{'}} \sum_{s} W_{s i}^{(k)} \\ \times ln f (D_{i j} = s^{'} | T_{i} = s, θ_{j}) \\ = arg max_{θ_{j}} \sum_{s^{'}} \sum_{i : D_{i j} = s^{'}} \sum_{s} W_{s i}^{(k)} ln θ_{j s^{'} s} . \end{array}

(21)

Noting the constraint that each row of the rater parameter matrix must sum to one to be a probability mass function

\sum_{s^{'}} θ_{j s^{'} s} = 1

(22)

we can find the parameters that maximize the above expression by formulating the constrained optimization problem

\begin{array}{l} 0 = \frac{\partial}{\partial θ_{j n^{'} n}} [\sum_{s^{'}} \sum_{i : D_{i j} = s^{'}} \sum_{s} W_{s i}^{(k)} ln θ_{j s^{'} s} \\ + λ \sum_{s^{'}} θ_{j s^{'} s}] \\ = \sum_{i : D_{i j} = n^{'}} W_{n i}^{(k)} \frac{1}{θ_{j n^{'} n}} + λ . \end{array}

Therefore, we find

θ_{j s^{'} s}^{(k + 1)} = \frac{\sum_{i : D_{i j} = s^{'}} W_{s i}^{(k)}}{- λ}

(23)

and on substituting the constraint from (22) we have

θ_{j s^{'} s}^{(k + 1)} = \frac{\sum_{i : D_{i j} = s^{'}} W_{s i}^{(k)}}{\sum_{i} W_{s i}^{(k)}} .

(24)

Note that when the number of possible labels is two (L = 2), this estimator for unordered multicategory labels simplifies to the same expression as was derived above for the binary case.

E. A Model for Estimation of Spatially Correlated Structures

One mechanism to capture the spatial variation of a structure of interest is to provide a spatially varying probability for f (T_i = 1) to reflect prior information about the spatial distribution of the T_i. For example, when assessing brain segmentations of white matter, a probabilistic atlas of the distribution of white matter derived from a large group of subjects can provide the prior true segmentation probabilities at each voxel [35]–[37]. However, a probabilistic atlas is not available for all structures of interest. An alternative is to model the local spatial correlation and homogeneity of the structure.

The estimate of the posterior probability of T_i obtained from (13) is correct under the assumption that the true segmentation has no spatial correlation—that is, at any given voxel the probability of the true segmentation is independent of the true segmentation of the neighboring or adjacent voxels. In practical applications it is often the case that the true segmentation has an underlying spatial homogeneity.

A second mechanism for incorporating spatial homogeneity is to introduce a Markov random field (MRF) model. This allows milder assumptions than the strong voxelwise independence assumption used above. Constructing a fully general probability model on random fields such as T is a daunting prospect due to the huge size of such a model—just representing full covariation statistics would be difficult. A useful compromise that partially relaxes the independence assumption is the MRF model, in which the conditional dependence of a given voxel on all of the others is equal to its conditional dependence on the voxels in a local neighborhood.

Beginning with the Ising [38] models of ferromagnetism, these models have frequently been used to model phenomena that exhibit spatial coherence, including medical image segmentation problems [39]–[41].

While the estimators which use MRF models are usually more complex to implement, exact estimates may be obtained in reasonable (polynomial) time [42], [43] and efficient approximation schemes are also available [44], [45].

The Hammersley-Clifford theorem [46] establishes a one to one correspondence between MRFs and probability models written in Gibbs form, as follows:

\begin{array}{l} f (T) = \frac{1}{Z} exp (\frac{- E (T)}{τ}) \\ Z = \sum_{T} exp (\frac{- E (T)}{τ}) \\ - E (T) = \sum_{i} U (T_{i}) + \sum_{i} \sum_{j} V (T_{i}, T_{j}) . \end{array}

(25)

This is the stationary Gibbs form, where Z and τ are constants and E is called the energy function. Selecting E(T) as above, we can factor this standard form into a term depending solely on the single site voxel prior and a term depending on pairwise interactions

\begin{array}{l} f (T) = \frac{1}{Z} exp (\frac{\sum_{i} U (T_{i})}{τ}) \\ \times exp (\frac{\sum_{i} \sum_{j} V (T_{i}, T_{j})}{τ}) \\ = \frac{1}{Z_{1}} exp (\frac{\sum_{i} U (T_{i})}{τ}) \frac{Z_{1}}{Z} \\ \times exp (\frac{\sum_{i} \sum_{j} V (T_{i}, T_{j})}{τ}) \\ = \prod_{i} f (T_{i}) \frac{Z_{1}}{Z} exp (\frac{\sum_{i} \sum_{j} V (T_{i}, T_{j})}{τ}) \\ ln f (T) = \sum_{i} ln f (T_{i}) + ln Z_{1} - ln Z \\ + \frac{1}{τ} \sum_{i} \sum_{j} V (T_{i}, T_{j}) . \end{array}

(26)

The above natural model allows us to incorporate a model for spatial homogeneity of the true segmentation in our estimation scheme. One approach to MRF estimation that has low computational complexity and which is applicable here, is the mean field approximation. An extensive investigation of this has been reported by Elfadel [44] and it has been used to impose a spatial homogeneity constraint for image segmentation [39], [47] and for motion estimation from images [48]. The mean field approximation has been used for constrained surface reconstruction, and its use has been motivated by the fact that it is the minimum variance Bayes estimator of the true field [49].

The mean value of the estimated true segmentation at iteration k (that is, the mean of $W_{s i}^{(k)}$ ), can be found by an embedded iteration process. It is found by initializing with the voxelwise independent estimate, and then iterating the following relation to convergence [47, page 52]

\begin{array}{l} {\bar{W}}_{s i}^{(k)} \leftarrow \frac{1}{Z} exp (ln f (T_{i} = s) \\ + ln \prod_{j} f (D_{i j} | T_{i} = s, θ_{j}^{(k - 1)}) \\ + \sum_{m} \sum_{n} J_{s n} {\bar{W}}_{n m}^{(k)}) \end{array}

with

\sum_{s} {\bar{W}}_{s i}^{(k)} = 1

where ${\bar{W}}_{s i}^{(k)}$ is the mean field estimate of the conditional probability that spatial site i has label, s, J_sn describes the degree of spatial compatibility between label s and label n, m indexes the spatial sites in the neighborhood of site i and Z is a normalizing constant. This MRF approximation is easily computed and is suitable for any number of labels, and allows a model of spatial homogeneity to be incorporated into the iterative estimation scheme of (16), (18), and (19).

In our experiments with binary true segmentations, we have investigated an alternative MRF representation which has twin virtues. First, it computes an exact solution to the MAP estimate of the true segmentation, and second, it is very computationally efficient. With this method a single estimate of the true segmentation incorporating the MRF is obtained following convergence of the EM iteration scheme described above.

We can express the prior probability of the field T by taking (26), omitting the constants, and letting V(T_i, T_j) = β_mn(T_mT_n + (1 − T_m)(1 − T_n)), so that we have

\begin{array}{l} ln f (T) \propto \sum_{i} ln f (T_{i}) \\ + \sum_{m} \sum_{n} β_{m n} (T_{m} T_{n} + (1 - T_{m}) (1 - T_{n})) \end{array}

(28)

where β_mn = 0 for voxels that are not neighbors.

Let the voxels in the neighborhood of voxel i be denoted by ∂i, note as above the neighborhood dependence of the true segmentation is independent of the single site prior probability and recall T_i [set membership] {0, 1}.

The true segmentation T_i, ∀i will be estimated by maximizing the posterior probability

\begin{array}{l} f (T | D, p^{(k)}, q^{(k)}) \\ \propto f (D | T, p^{(k)}, q^{(k)}) f (T) \\ \propto \prod_{i} \prod_{j} f (D_{i j} | T_{i}, p_{j}^{(k)}, q_{j}^{(k)}) f (T_{i}) f (T_{\partial i}) \\ \propto \prod_{i} f (T_{\partial i}) f {(T_{i} = 1)}^{T_{i}} f {(T_{i} = 0)}^{1 - T_{i}} \\ \cdot {(\prod_{j} f (D_{i j} | T_{i} = 1, p_{j}^{(k)}, q_{j}^{(k)}))}^{T_{i}} \\ \cdot {(\prod_{j} f (D_{i j} | T_{i} = 0, p_{j}^{(k)}, q_{j}^{(k)}))}^{1 - T_{i}} \\ \propto \prod_{i} f (T_{\partial i}) {(a_{i}^{(k)})}^{T_{i}} {(b_{i}^{(k)})}^{1 - T_{i}} . \end{array}

(29)

Taking the logarithm of this expression for the posterior probability and assuming a pairwise interaction neighborhood structure leads to

\begin{array}{l} ln f (T | D, p^{(k)}, q^{(k)}) \\ \propto \sum_{m = 1}^{N} \sum_{n = 1}^{N} β_{m n} (T_{m} T_{n} + (1 - T_{m}) (1 - T_{n})) \\ + \sum_{i = 1}^{N} ln (\frac{a_{i}^{(k)}}{b_{i}^{(k)}}) T_{i} \end{array}

(30)

where a term in (29) not depending on T_i has been ignored in (30) as it does not alter the estimate of the true segmentation, and β_mn is an interaction weight between voxels m and n that encodes the strength of the prior probability of true segmentations. If β_mn > 0 then voxels m and n are neighbors, and β_mm = 0 ∀m. If β_mn = 0, ∀m, n, then we have the first model presented above with no neighborhood interaction prior probability. The nonzero interaction weight is often chosen as β_mn = β, ∀ m, n, in a given neighborhood, or an appropriately scaled modification of this depending on the distance between voxels along each coordinate axis, and acts such that as β grows larger, the estimated true segmentation is smoother and more spatially homogeneous.

This particular MRF model is attractive because it enables us to capture the intuitive notion of a spatially correlated true segmentation, and also because it has been shown by Greig et al. [42] that it can be solved exactly with an efficient network flow algorithm. Greig et al. demonstrated the equivalence between exact MAP estimation with the above binary MRF model and a maximum flow-minimum cut network flow problem. Since efficient (polynomial in number of edges and vertices) algorithms for the minimum cut problem are known, this equivalence enables a rapid estimation of the true segmentation T_i ∀i to be found by solving

\sum_{i} λ_{i} T_{i} + \sum_{m} \sum_{n} β_{m n} (T_{m} T_{n} + (1 - T_{m}) (1 - T_{n}))

(31)

where

\begin{array}{l} λ_{i} = ln (\frac{a_{i}^{(k)}}{b_{i}^{(k)}}) \\ = ln (\frac{W_{i}^{(k)}}{1 - W_{i}^{(k)}}) . \end{array}

(32)

The equivalent network flow problem consists of N + 2 vertices, with a source s and a sink t and the N voxels of the image. For each voxel with λ_i > 0 there is a directed edge (s, i) from source s to voxel i with capacity c_si = λ_i, and for each voxel with λ_i < 0 there is a directed edge (i, t) from voxel i to sink t with capacity c_it = −λ_i. There is an undirected edge between pairs of voxels m, n with capacity c_mn =β_mn. A cut of this network is a partitioning of the vertices into two groups, B = s [union or logical sum] i:T_i = 1 and W = t i: T_i = 0 consisting of edges with a vertex in B and a vertex in W. The capacity of the cut is C(T), the sum of the capacities of the edges of the cut. A minimum cut is a cut of smallest capacity. Greig et al. [42] showed that the minimum cut of this network is equivalent to the exact MAP solution of the binary MRF problem, since

\begin{array}{l} C (T) = \sum_{i = 1}^{N} T_{i} max (0, - λ_{i}) \\ + \sum_{i = 1}^{N} (1 - T_{i}) max (0, λ_{i}) \\ + \sum_{i = 1}^{N} \sum_{j = 1}^{N} β_{i j} {(T_{i} - T_{j})}^{2} \end{array}

(33)

differs from (31) only by the sign and a term that does not depend upon T. Therefore, the minimum cut network is also the MAP MRF solution.

When the minimum cut of this network is found all the voxels for which T_i = 0 are on the sink side of the minimum cut and all the voxels for which T_i = 1 are on the other side. Our implementation uses the Edmonds-Karp maximum flow-minimum cut algorithm [50] with the multiresolution solution strategy suggested by Greig et al. [42].

This model allows us to proscribe a spatially correlated true segmentation in our estimation framework, and creates a more locally homogeneous true segmentation estimate. A recent extension of this maximum flow-minimum cut strategy removing the restriction to binary labels has been described [43]. Thus, to model local spatial homogeneity of the true segmentation for multicategory data, a MRF model can be used and both the mean field approximation [44] and maximum flow-minimum cut exact solver are suitable [43].

F. Initialization Strategy and Detection of Convergence

The STAPLE algorithm requires specification of some model parameters, and may be initialized with either performance level parameters or a probabilistic true segmentation. We describe suitable strategies for initialization and for detection of convergence of the estimation process below.

1) Initialization: STAPLE is most conveniently initialized by providing starting estimates for the sensitivity and specificity parameters. In the absence of other information regarding the relative quality of the experts or the true segmentation, initializing the sensitivity and specificity parameters to the same value and equal across all raters is recommended. This is equivalent up to a scaling factor to forming an initial estimate through a voting rule (such as assigning initial probabilities of voxels based on the frequency of selection by experts). In our experience with synthetic data and clinical experiments, successful estimation results were obtained by initializing all of the sensitivity and specificity parameters to the same values, with values close to but not equal to 1: for example, selecting $p_{j}^{(0)} = q_{j}^{(0)} = 0.999 99 \forall j .$

An alternative strategy for initialization, useful when such information is available, is to provide an initial true segmentation estimate. An interesting strategy for certain problems is to use a probabilistic atlas to provide an initial true segmentation. For example, one may use a probabilistic atlas of the brain [37], [51] to provide an initial true segmentation estimate for the tissues of the brain.

We have used the estimated true segmentation from the voxel-wise independent STAPLE to initialize the STAPLE algorithm when incorporating an MRF prior.

2) Convergence: The EM algorithm is guaranteed to converge to a local optimum. Detecting convergence of EM algorithms has been a topic of study, as have strategies for accelerating convergence [32]. STAPLE estimates both performance parameters and the true segmentation, and convergence may be detected by monitoring these. A simple and good measure of convergence is the rate of change of the sum of the true segmentation probability, obtained by summing the estimated weight at each voxel $S_{k} = \sum_{i = 1}^{N} W_{i}$ evaluated at each iteration k. We have found that iterating until S_k − S_k₋₁ = 0 using double precision IEEE arithmetic is both accurate and fast. In the case of L unordered multicategory labels and large three-dimensional (3-D) volumes, we have found it convenient to use a relative convergence based on the change in the normalized trace of the estimated expert performance parameters. We iterate until the normalized trace changes by less than some small amount, for example ε = 1 × 10⁻⁷, where the normalized trace is given by

\frac{1}{LR} \sum_{j = 1}^{R} tr (θ_{j}) .

(34)

Our experience has been that STAPLE convergence generally occurred in less than 20 iterations in several clinical segmentation validation problems.

3) Model Parameters: Selection of different global or spatially varying prior probability f (T_i = 1) may alter the local maxima to which the algorithm converges. This is illustrated below in experiments with synthetic data.

A spatially varying prior f (T_i = 1) is suitable for those structures for which a probabilistic atlas is available. In addition, we are interested in structures for which such an atlas is not available, and we have used a single global prior γ = f (T_i = 1) ∀ i. The prior γ encodes information we have before seeing the segmentation decisions, regarding the relative probability of the structure we wish to segment in the data. In practice, this information may not be readily available, and we have found it convenient to estimate γ from the segmentations themselves as the sample mean of the relative proportion of the label in the segmentations

γ = \frac{1}{R N} \sum_{j = 1}^{R} \sum_{i = 1}^{N} D_{i j} .

(35)

In the case of multicategory labels, we have

γ_{s} = \frac{1}{R N} \sum_{j = 1}^{R} \sum_{i = 1}^{N} δ (D_{i j}, s) \forall s .

(36)

where δ(.,.) is the Kronecker delta which takes the value 1 when D_ij and s are equal and 0 otherwise.

Similarly, when modeling a spatially homogeneous true segmentation with our MRF model, an interaction strength β_mn and neighborhood structure must be specified. This may depend strongly upon the nature of the structure, segmentations and noise pattern of the segmentations under consideration. In our experiments with synthetic data and strong uncorrelated random noise in the segmentations and a strongly homogeneous true segmentation, we found β_mn = β = 2.5 gave satisfactory results.

Go to:

III. Results

We carried out experiments applying STAPLE to digital phantoms where the true segmentation is known by construction and investigated the characterization of segmentations by synthetic experts with predefined sensitivities and specificities. As described below, we found that STAPLE accurately estimates the performance level parameters and the true segmentation. We applied STAPLE to segmentations from several clinical applications to demonstrate the value of the approach in practice, and to compare to a previously reported validation measure. We assessed repeated segmentations by a single expert for the task of identifying the prostate peripheral zone from magnetic resonance images. We compared the STAPLE assessment of the segmentations to a measure of spatial overlap. A brain phantom was used to compare STAPLE to a voting rule. Synthetic segmentations and segmentations by medical students were evaluated.

The capacity of STAPLE to accurately estimate the true segmentation, even in the presence of a majority of raters generating correlated errors, was demonstrated. The quantitative assessment of segmentations of tissues from MRI of a newborn infant was carried out in order to demonstrate the use of STAPLE with 3-D volumetric unordered multicategory data. Empirical timing experiments were also carried out to demonstrate the practicality of the estimation scheme. In all of our experiments, the hardware platform for the assessment of execution time was a Dell Precision 650n workstation running Red Hat Linux 8.0, with the implementation executing on a 3-GHz Intel Xeon CPU.

A. Digital Phantom Experiments

1) Estimation From Noisy Segmentations With Specified Segmentation and Performance Parameters: Fig. 1 illustrates STAPLE estimation from digital phantoms drawn from randomly generated segmentations with specified sensitivity and specificity rates and specified true segmentation. The true segmentation was set to be a square image, 256 × 256 voxels, with the leftmost 128 columns having value 0 and the rightmost 128 columns having value 1. The prior probability of the foreground class is f (T_i = 1) = 0.5. R = 10 segmentations were generated by randomly sampling the specified true segmentation with (p_j, q_j) = (0.95, 0.90). This generated ten random segmentations simulating experts with identical sensitivity and specificity rates. STAPLE required 0.18 s wallclock time to estimate the true segmentation and expert parameters, and the estimates closely matched those specified. Estimated sensitivity over the experts was $\hat{p}$ = 0.950 104 ± 0.001 201 (mean ± standard deviation) and sensitivity q = 0.900 035 ± 0.001685. The estimated true segmentation closely matched the specified true segmentation, with the foreground structure being exactly estimated from raters with a detection error rate of 5% and with (7/32 768) false positives in a region with a detection error rate of 10%. The incorporation of an MRF prior model with four-connected neighborhood structure and an interaction strength β = 2.5 resulted in a STAPLE estimate converging exactly to the known true segmentation. The MRF model was applied to estimate the true segmentation by solving (33) once only, using the estimated true segmentation probabilities obtained from iterating STAPLE without an MRF model to convergence, and required 3.5 s to compute the exact MAP solution. The false positives that occur without the MRF prior are indicated with circles in Fig. l(e) to enhance their visibility, as they are single isolated pixels which are difficult to see in the reproduction of the figure, and to illustrate that there are no false positives in Fig. l(f).

An external file that holds a picture, illustration, etc.
Object name is nihms2330f1.jpg

Fig. 1

A specified true segmentation was randomly sampled to generate R = 10 segmentations with (p_j, q_j) = (0.95, 0.90) ∀j [set membership] 1,…, 10. STAPLE converged in less than 20 iterations. The estimated performance parameters were $\hat{p}$ = 0.950104 ± 0.001201 (mean ± standard deviation) and $\hat{q}$ = 0.900035 ± 0.001685, which closely matches the specified parameters, (a) Example of synthetic segmentation, (b) Example of synthetic segmentation, (c) Example of synthetic segmentation, (d) Example of synthetic segmentation, (e) STAPLE estimated true segmentation. The estimate contains seven isolated single pixel errors which are circled to enable clearer visualization, (f) Estimated true segmentation from STAPLE incorporating an MRF prior. The estimate exactly matches the known true segmentation.

Fig. 2 examines the application of STAPLE to noisy segmentations from unequal quality experts. Segmentations were generated from R = 3 synthetic experts with parameters specified as (p₁, q₁) = (0.95, 0.95), (p₂, q₂) = (0.95, 0.90), and (p₃, q₃) = (0.90, 0.90). Only three observations of segmentations by these experts were generated, leading to a small and noisy set of data from which STAPLE was used to estimate the performance parameters and the true segmentation. STAPLE was executed to convergence, requiring 0.22 s wallclock time. Comparisons were made with and without a spatial homogeneity prior modeled with an MRF prior assuming four-nearest-neighbor pairwise interaction cliques and a homogeneous interaction strength β = 2.5. The MRF model was applied to estimate the true segmentation by solving (33) once only, using the estimated true segmentation probabilities obtained from iterating STAPLE without an MRF model to convergence and required 53 s to compute the exact MAP solution. The increased run time is due to the greater amount of heterogeneity in the initial STAPLE estimate.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f2.jpg

Fig. 2

Segmentations generated from R = 3 synthetic experts with parameters specified as (p₁, q₁) = (0.95, 0.95),(p₂, q₂) = (0.95, 0.90), and (p₃, q₃) = (0.90, 0.90). Only three observations of segmentations by these experts were generated, leading to a small and noisy set of data from which STAPLE was used to estimate the performance parameters and the true segmentation. STAPLE was executed to convergence, initialized with f (T_i = 1) = 0.5 and $(p_{j}^{(0)}, q_{j}^{(0)})$ = (0.99999, 0.99999), ∀j. Comparisons were made with and without a spatial homogeneity prior modeled with an MRF prior assuming four-nearest-neighbor pairwise interaction cliques and homogeneous interaction strength β = 2.5. The results indicate the estimated T found by STAPLE with the MRF prior exactly matches the specified true segmentation used for the simulations, whereas without this constraint the estimated T is somewhat noisier. In both cases, the estimated performance level parameters were very close to the parameters specified for the random segmentations, (a) Expert 1 segmentation, (b) Expert 2 segmentation, (c) Expert 3 segmentation, (d) STAPLE true segmentation estimate under voxelwise independence assumption, (e) STAPLE true segmentation estimate assuming spatially homogeneous true segmentation.

The results indicate the estimated T found by STAPLE with the MRF prior exactly matches the specified true segmentation used for the simulations, whereas without this constraint the estimated T is somewhat noisier. In both cases, the estimated performance level parameters were almost identical to the specified values of the parameters.

2) Influence of Prior Probability: Fig. 3 illustrates synthetic segmentations which differ by structural errors rather than random noise. The true segmentation was specified, as were synthetic expert segmentations, each having equal volume but different spatial location. STAPLE was initialized with $p_{j}^{0} = q_{j}^{0} = 0.99, \forall j$ and required 0.38 s to converge. The STAPLE true segmentation estimate is shown for different prior assumptions. The prior models information available before the data is seen. Three prior models are shown, first assuming global/(T_i = 1) = 0.12 which closely matches the segmentations, with f (T_i = 1) = 0.5 which corresponds to a prior belief that half of the field of view should be the foreground class, and with automatic estimation of the global prior using (35). As can be seen, the estimated true segmentation can be influenced by the global prior probability.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f3.jpg

Fig. 3

R = 3 synthetic true segmentations with equal volume but different spatial locations. STAPLE was initialized with $(p_{j}^{(0)}, q_{j}^{(0)})$ = (0.99, 0.99), ∀j. The STAPLE true segmentation estimate is shown for the different prior probability assumptions: f (T_i = 1) = 0.12 which closely matches the segmentations, f (T_i = 1) = 0.5 which corresponds to a prior belief that half of the field of view should be the foreground class, and with automatic estimation of the prior via (35). (a) First synthetic segmentation, (b) Second synthetic segmentation, equal in size to the first but shifted to the left 10 voxels, (c) Third synthetic segmentation, equal in size to the first but shifted to the right ten voxels, (d) STAPLE true segmentation estimate for f (T_i = 1) = 0.12 ∀i. The estimated performance parameters were $(\hat{p_{1}}, \hat{q_{1}}) = (1.0, 1.0), (\hat{p_{2}}, \hat{q_{2}}) = (\hat{p_{3}}, \hat{q_{3}}) = (0.88, 0.99) .$ (e) STAPLE true segmentation estimate for f (T_i = 1) = 0.5 ∀ i. The estimated performance parameters were $(\hat{p_{j}}, \hat{q_{j}}) = (0.66, 1.0) \forall j .$ (f) STAPLE true segmentation estimate with automatic prior estimation. The estimated performance parameters were $(\hat{p_{1}}, \hat{q_{1}}) = (1.0, 1.0), (\hat{p_{2}}, \hat{q_{2}}) = (\hat{p_{3}}, \hat{q_{3}}) = (0.88, 0.99) .$

In the case of assuming f (T_i = 1) = 0.12, the estimated true segmentation exactly matches the specified true segmentation and one of the experts was identified as generating exactly the true segmentation (p = q = 1.0), and the other two were estimated to have a sensitivity of 0.88 and a specificity of 0.99 reflecting the erroneous shift in these two segmentations. This result was also obtained with automatic estimation of the prior.

In the case of assuming f (T_i = 1) = 0.5, the estimated true segmentation equals the union of each of the three segmentations (which still does not occupy 50% of the image) and each of the experts was identified as having (p_j, q_j) = (0.66, 1.0), j = 1,2,3. This reflects the fact that the segmentations are not in agreement with the assumed global prior. If this was discovered in the application of STAPLE to a clinical validation problem it would indicate either the need to re-evaluate the global prior assumption or the need for improved training of the experts generating the segmentations.

B. Brain Phantom Experiments

Consider estimation of a true segmentation and performance parameters from segmentations generated by two groups of raters, M of whom have significant expertise, and N of whom have limited expertise. We can consider two important cases: where M > N and where M < N. If we have M > N then the errors of the inexperienced raters do not exert significant influence and are overcome by the correct information from the more experienced raters, whereas by comparison, if M < N then there is the possibility that the inexperienced raters may influence the estimation scheme to overcome the more experienced raters.

In the case, M < N, if the inexperienced raters make random errors, then as indicated by Fig. 2, accurate estimation can still be achieved. Similarly, if they make uncorrelated structural errors then, as for random errors, accurate estimation is possible. However, if they make correlated structural errors the impact of the errors could be significant. Without further external information, it is not possible to discriminate between the two groups, and to decide which constitutes the expert raters and which the inexperienced raters. For example, in a majority voting scheme, the inexperienced raters would collect the most votes for the regions with correlated errors and hence a wrong segmentation estimate would result. External information is incorporated in the STAPLE estimate through the prior probability for the structure being segmented, and through the initialization. It is also straightforward to introduce a prior probability density for the rater parameters, enabling expert raters to be distinguished from inexperienced raters via parameters of such a prior distribution.

We carried out an experiment to investigate the performance of the STAPLE algorithm when presented with M = 1 and N = 3 raters, where the task is brain cortical gray matter segmentation. We used a brain phantom created from a high-resolution high signal-to-noise ratio brain MRI scan, for which a consensus segmentation of the cortical gray matter was available. The segmentation was made by automatic segmentation and consensus correction of errors by experts [3]. We used the consensus segmentation to represent an exact ideal “expert” segmentation that we want STAPLE to identify, and we deleted all cortex labels from half of the rows of the exact segmentation and triplicated this in order to represent poor raters generating approximately half of the correct labeling of the cortex, and incorrectly labeling the other half of the cortex as background. Triplicating this data ensures that the inexperienced rater segmentations have correlated errors.

We ran the STAPLE algorithm on these four segmentations, to convergence, stopping when the change in normalized trace was less than 1 × 10⁻⁶, and evaluated the effect of different initialization. We provided a range of different initial values for the sensitivity and specificity of each of the four input segmentations, setting the “expert” segmentation to have high initial sensitivity and specificity $(p_{0}^{(0)} = q_{0}^{(0)} = 0.999 999 999 9),$ and then varying the initial parameter assignments of the other three raters (all equal) over the range of 0.05 to 0.95 in steps of 0.05, and automatic estimation of all other parameters with a uniform spatial prior for the cortex and background.

We found STAPLE identified one of two different estimated true segmentations, depending on the initialization. The first closely matched the exact segmentation, and the second closely matched the inexperienced rater segmentations. If the initialization indicated the “expert” segmentation was superior to the three inexperienced raters $(p_{j}^{(0)} = q_{j}^{(0)} \in [0.1, 0.9], j = 1, 2, 3)$ it converged to match the experienced rater, and if the inexperienced raters were initialized outside this range (for example, close in performance to the “expert”), it converged to the estimate close to that of the inexperienced raters. The phantom, consensus segmentation, STAPLE estimate of the true segmentation and voting rule estimate are illustrated in Fig. 4.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f4.jpg

Fig. 4

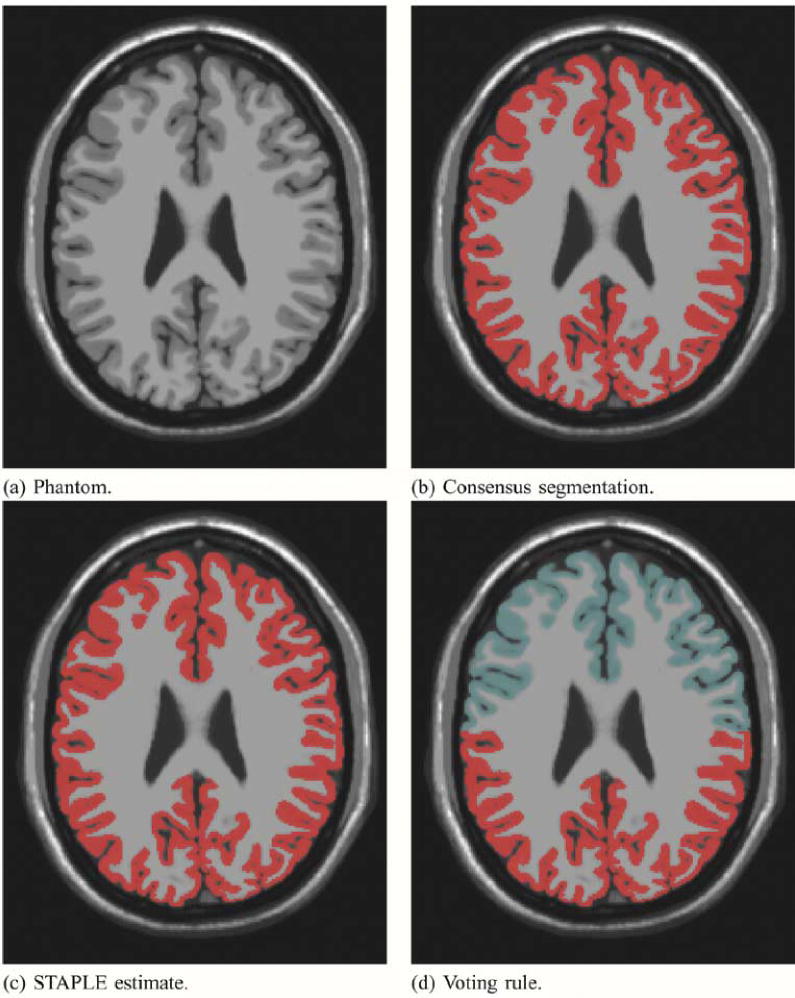
Brain phantom and STAPLE estimated true segmentation with one expert and 3 inexperienced rater segmentations. Different initialization leads to different estimates. Exact estimation of the true segmentation is possible with STAPLE but not with a majority vote rule. The image that was segmented is shown in (a). The red color indicates the segmentation of the cortex from the consensus segmentation in (b), and from the STAPLE estimate in (c). In (d), the area of most frequent selection by the raters and expert is shown in red, and the light blue color represents the region selected only by the expert.

Since the parameter estimates are obtained by maximizing the conditional expectation of the complete data log likelihood function, Q(θ|θ⁽^k⁾) some insight into the convergence behavior of STAPLE in this setting can be drawn by comparing the estimate of Q(θ|θ⁽^k⁾) to the true complete data log likelihood function that can be calculated when the exact true segmentation is known. The estimate Q(θ|θ⁽^k⁾) evolves until the iteration converges, and so in Fig. 5 the estimated function is shown as estimated at each of the two points where the algorithm converges. Shown in this figure is only the part of the estimated function that is necessary to find the sensitivity or the specificity parameters for one of the input segmentations at a time, as this depends on only one variable and is, therefore, simple to graphically represent. Such estimated functions are shown for both for the experienced rater and the inexperienced raters, together with the corresponding function from the exact complete data log likelihood. Fig. 5 shows that when the initialization indicates the experienced rater is superior to the inexperienced raters, the estimated complete data log likelihood exactly matches the true complete data log likelihood at convergence, and that if the initialization indicates all raters are equal then the estimated complete data log likelihood indicates all raters have equal sensitivity and that the experienced rater segmentation corresponds to an oversegmentation, with worse specificity, as compared to the estimated true segmentation. Hence, in the presence of a majority of raters generating repeated structural errors, appropriate initialization or further external information through prior distributions on rater parameters or the spatial distribution of the true segmentation may be used to ensure STAPLE converges to the correct true segmentation estimate. Straightforward vote counting cannot overcome the presence of a majority of raters generating repeated structural errors. It is expected that this situation is atypical, and represents a worst case for estimation of the true segmentation, and can be corrected by improved training or algorithmic modifications to alter the behavior of the raters.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f5.jpg

Fig. 5

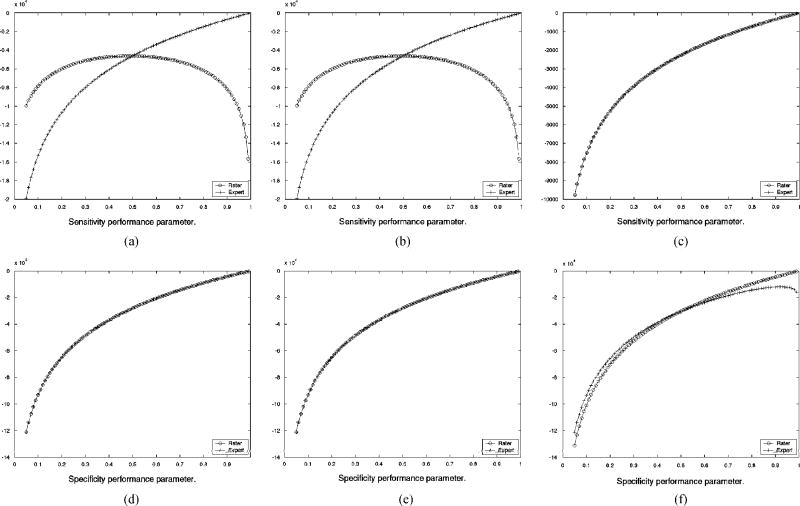
Comparison of exact and estimated complete data log likelihood function for estimation of rater sensitivity and specificity, derived from the brain phantom with one expert and 3 inexperienced rater segmentations, (a) Exact ln f (D, T|θ) dependence on sensitivity for inexperienced rater and expert, (b) Estimated function of sensitivity from Q(θ|θ⁽^k⁾ after convergence from unequal rater initialization, (c) Estimated function of sensitivity from Q(θ|θ⁽^k⁾) after convergence from equal rater initialization, (d) Exact In f (D, T|θ) dependence on specificity for inexperienced rater and expert, (e) Estimated function of specificity from Q(θ|θ⁽^k⁾) after convergence from unequal rater initialization, (f) Estimated function of specificity from Q(θ|θ⁽^k⁾) after convergence from equal rater initialization.

C. Illustration of Clinical Validation Applications

1) Comparison of STAPLE With Voting: Three medical students carried out interactive segmentation of the cortical gray matter of a single slice of a brain phantom [3]. Upon review and visual comparison of the segmentations, it was found that over most of the cortex the segmentations were quite similar to the exact segmentation but in one region the students had all made a misjudgement and incorrectly labeled one region as cortical gray matter when it should be labeled white matter. We know that this is a misinterpretation on the part of the students since the region has signal intensity characteristics different from cortical gray matter and our prior knowledge of anatomy indicates the cortex does not extend through this region. The consensus segmentation correctly labels this region and we used this consensus segmentation to represent a perfect expert. We estimated the true segmentation from the expert and three medical student segmentations, by both vote counting and by STAPLE. Table I quantifies the difference in performance estimates for this region between a vote counting estimate and the STAPLE algorithm. The region is shown in Fig. 6 together with the exact segmentation, an image showing the frequency of selection of each voxel as cortex by the medical students, an image showing the frequency of selection of each voxel when combining the medical students and exact segmentation and the STAPLE estimate of the true segmentation. The figure illustrates that the students incorrectly label some of the white matter as cortical gray matter, and that when vote counting is used to estimate the true segmentation the frequent wrong selection overrules the expert. This does not occur with the STAPLE estimate. The color coding of the frequency of selection is as shown in Fig. 7.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f6.jpg

Fig. 6

Comparison of STAPLE and voting rule estimates of the true segmentation from segmentations of the cortex generated by one expert and three medical students. The color coding of the frequency of selection is as shown in Fig. 7.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f7.jpg

Fig. 7

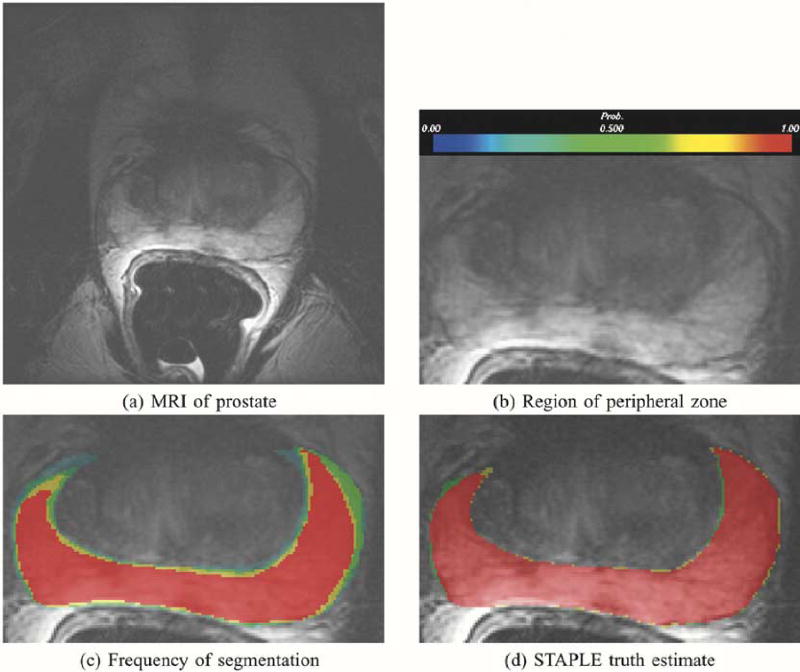
This figure illustrates in (a), MRI of the prostate, in (b) the prostate peripheral zone, in (c) the frequency of assignment of voxels to the prostate peripheral zone in five repeated segmentations by the same rater, and in (d), the probabilistic true segmentation as estimated by STAPLE.

TABLE I

Comparison of STAPLE and Voting Rule Estimates of Rater Performance. the STAPLE Estimate Correctly Identifies the Expert as Having Superior Performance to That of the Three Medical Students

	Students
Segmentations	1	2	3	expert
Estimate of rater performance from a voting rule.
$\hat{p}$	0.88660	0.91366	0.86856	0.79768
$\hat{q}$	0.99940	0.99922	0.99946	0.99972
STAPLE estimate of rater performance.
$\hat{p}$	0.88095	0.91667	0.88690	1.0
$\hat{q}$	0.99890	0.99872	0.99904	1.0
Exact rater performance from conesnsus segmentation.
p	0.88095	0.91667	0.88690	1.0
q	0.99890	0.99872	0.99904	1.0

2) Segmentation of Prostate Peripheral Zone: Fig. 7 illustrates STAPLE applied to the analysis of five segmentations by one expert of the peripheral zone of a prostate as seen in a conventional MRI scan (T2w acquisition, 0.468750 × 0.468750 × 3.0 mm³). The goal of the operator was to segment the prostate peripheral zone to enable radiation dose planning in support of brachytherapy [52]. The STAPLE algorithm ran to convergence in 0.48 s of wallclock time.

For comparison with the STAPLE estimate of the true segmentation, an image color coded by probability of selection of each voxel is also presented. The colors range from blue to red corresponding to probability of selection ranging from 0 to 1 as indicated by the color bar in Fig. 7(b). It is interesting to consider a voting rule scheme and to compare that with the STAPLE result. One voting rule is to estimate the true segmentation by taking all voxels where a majority of the segmentations indicated the foreground was present. We achieved a similar binarization of the STAPLE probabilistic true segmentation estimate, by thresholding at W_i = 0.5, which gives a ML estimate of the binary true segmentation. An alternative is to apply the MAP estimation using the binary MRF model of (33) which also provides a binary estimate of the true segmentation. We found that the binarized STAPLE true segmentation estimate cannot be obtained with a simple voting rule estimate from the segmentations. In order to obtain the binarized STAPLE result directly from the manual segmentation, it would be necessary to identify all the voxels indicated as prostate peripheral zone by at least three of the five segmentations, and then all the voxels indicated by two of the high-quality segmentations but not those voxels indicated by only two of the lower quality segmentations. Without knowledge of the relative quality of the segmentations such a weighted combination cannot be constructed. Thus, the true segmentation estimate depends crucially upon the relative quality of the segmentations that is discovered by the STAPLE algorithm. The STAPLE result cannot be generated by a simple voting rule such as selecting voxels indicated by three out of five segmentations.

3) Comparison of STAPLE With Dice Similarity Coefficient: The performance level estimates for segmentation of the prostate peripheral zone are recorded in Table II. In order to enable comparison of these estimates with the Dice Similarity Coefficient (DSC) [11], a popular measure of spatial overlap defined as DSC ≡ (2|A ∩ B|/|A| + |B|) where |A| is the area of region A, |B| is the area of region B, we formed a binary estimate of the true segmentation by thresholding at W_i = 0.5. We then computed the DSC between each of the individual segmentations and the binarized STAPLE true segmentation. Comparing segmentations 2 and 4, we observe the DSC is similar, approximately 0.95 in each case. However, the STAPLE performance parameter estimates indicate the two segmentations achieve this DSC differently—for example, segmentation 2 has higher sensitivity than segmentation 4, but lower specificity. This indicates that despite the similar DSC values, segmentation 2 is an over-estimate of the peripheral zone, and segmentation 4 is an under-estimate of the peripheral zone.

TABLE II

Quality Estimates for the Five Prostate Segmentations Generated by One Expert, and Dice Similarity Coefficient (DSC), DSC ≡ (2/A ∩B|/|A| + |B|) With |A| the Area of Region A, Comparing the Expert Segmentation With the True Segmentation Estimate Thresholded With W_i ≥ 0.5. Results Are Shown for Two Different Assumptions of the Prior Probability of Prostate Peripheral Zone and Demonstrate That the Parameter Estimates Obtained Do Not Depend Strongly on the Prior Probability Assumption

Expert segmentations	1	2	3	4	5
f (T_i = 1) = 0.10
$\hat{p}$	0.875090	0.987198	0.921549	0.907344	0.880789
$\hat{q}$	0.999163	0.994918	0.999435	0.999739	0.999446
DSC	0.927660	0.957527	0.954471	0.949058	0.932096
f (T_i = 1) = 0.02
$\hat{p}$	0.878533	0.991261	0.936831	0.918336	0.894861
$\hat{q}$	0.998328	0.993993	0.999320	0.999359	0.999301
DSC	0.913083	0.951027	0.967157	0.954827	0.944756

Open in a separate window

4) Assessment of an Automated Segmentation Algorithm: Fig. 8 illustrates STAPLE applied to the analysis of expert segmentations of a brain tumor [53], [54]. The hidden true segmentation was estimated from three expert segmentations, requiring 0.15 s to compute. The segmentation generated by the program was then assessed by evaluating the sensitivity and specificity estimators of (18) and (19) with regard to this estimated true segmentation. The predictive value for tumor segmentation was also calculated. It is defined as PV(s) = Pr(T_i = s|D_ij = s), ∀s [set membership] 0, 1, …, L − 1, the posterior probability that the structure s is present when the rater says it is present, and is easily computed with the STAPLE estimate of the rater performance parameters. This assessment indicates the program is generating segmentations similar to that of the raters, with higher sensitivity and predictive value than one of the raters, but with lower sensitivity and lower predictive value than the two other raters. This provides feedback indicating in what way the algorithm or algorithm parameters need to be modified to improve the performance of the algorithm.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f8.jpg

Fig. 8

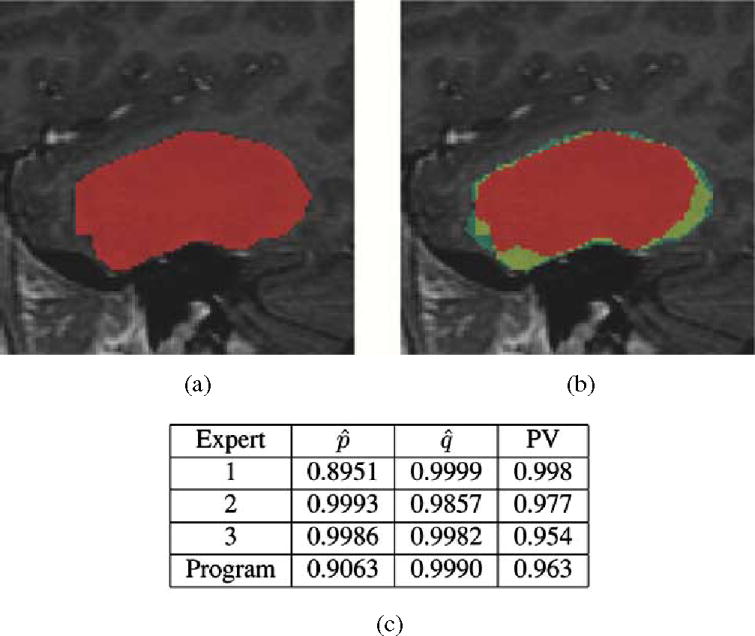
This illustrates the segmentation of a brain tumor from MRI. Three experts carried out segmentation of the brain tumor, and STAPLE was used to estimate the true segmentation of the tumor. The performance level assessment of each of three raters and a semi-automatic algorithm for tumor segmentation program based upon the estimated true segmentation is shown in (c). The estimated sensitivity, specificity, and tumor predictive value are reported. The performance assessment indicates that the program is performing with higher sensitivity than one rater but with lower sensitivity than the other raters, while exhibiting higher specificity than two of the raters and lower specificity than one of the raters. This illustrates that STAPLE can be used to evaluate the performance of segmentation algorithms through comparison to rater segmentations, (a) Estimated true segmentation, (b) Frequency of manual segmentation, (c) Performance level assessment.

D. Assessment of Supervised Tissue Classification of the Neonate Brain

The assessment of tissue types, including cortical gray matter, subcortical gray matter, myelinated white matter, unmyelinated white matter, and cerebrospinal fluid, from volumetric MRI of newborn infants [54]–[56] has been useful in understanding and characterising normal brain development and the processes of maturation [56], and the impact of injury upon brain development [57], [58].

We evaluated the impact of repeated selection of tissue type prototypes upon the classification of an MRI of a newborn infant at term equivalent age. A single operator repeatedly selected sample voxels from the image in order to carry out nonparametric estimation of the class-conditional probability density functions, which are then used to carry out segmentation as previously described [54]. We selected a 3-D volumetric MRI scan of the brain of a newborn infant which contained significant signal intensity artifact. We evaluated the amount of variability due to operator selection of training points in this particularly challenging scan, as the operator repeated the segmentation attempting to best identify each of background, extracranial tissue (such as skin, muscle, etc.), cortical gray matter, subcortical gray matter, myelinated white matter, unmyelinated white matter and cerebrospinal fluid as in [54], [56], [57]. These different tissues are distinguished by subtle signal intensity changes apparent from joint analysis of Tlw, PDw, and T2w MRI. They also appear with unequal proportions and some are more difficult to identify than others (for example, myelinated white matter is more difficult to identify than cerebrospinal fluid).

Table III illustrates the assessment of neonate tissue classification, assessing the identification of each type of tissue using predictive value (posterior probability). The mean predictive value is a simple measure with which to rank the segmentations based on overall quality.

TABLE III

Assessment of Variability of Tissue Classification From Neonate MRI. The Predictive value for Each Type of Tissue as Determined From the STAPLE Estimates, and the Mean Predictive Value, Are Reported for Each of Eight Segmentations. The Mean Predictive Value May Be Used to Rank the Quality of the Segmentations. Tissue Types Are Background (B), Extra-Cranial Tissue (ECT), Cortical Gray Matter (CGM), Cerebrospinal Fluid (CSF), Myelinated White Matter (MWM), Unmyelinated White Matter (UWM), and Subcortical Gray Matter (SCG)

Segmentation	B	ECT	COM	CSF	MWM	UWM	SCO	mean PV
1	0.9999	0.6219	0.8013	0.7035	0.3648	0.9403	0.9097	0.7631
2	1.000	1.000	0.9990	1.000	0.6336	0.9456	0.9990	0.9396
3	1.000	1.000	0.9990	0.9870	0.6339	0.9888	0.9967	0.9436
4	1.000	0.8250	0.6493	0.8853	0.4974	0.9998	0.8076	0.8092
5	1.000	0.9586	0.9816	1000	1.000	0.9967	0.9440	0.9830
6	1.000	1.000	0.9997	1.000	0.9997	0.9846	0.9692	0.9933
7	1.000	1.000	0.9186	1.000	0.9997	0.9977	0.5000	0.9166
8	1.000	1.000	0.7913	1.000	0.9930	0.9863	0.9889	0.9656

Open in a separate window

We also assessed the computational requirements of the STAPLE algorithm. The E-step of (20) is linear in the number of voxels N, linear in the number of raters R and linear in the number of labels L. The M-step of (24) is linear in the number of voxels TV, linear in the number of raters R and quadratic in the number of labels L. The total number of iterations to convergence depends on the degree of agreement between the input segmentations. Fig. 9 illustrates the average computation time per iteration as a function of the number of raters.

An external file that holds a picture, illustration, etc.
Object name is nihms2330f9.jpg

Fig. 9

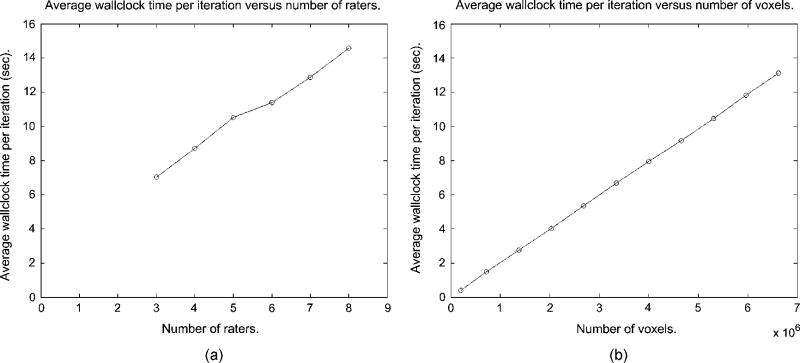
STAPLE average wallclock time per iteration as a function of the number of raters, and average wallclock time per iteration as a function of the number of voxels, (a) Average time per iteration versus number of raters, (b) Average time per iteration versus number of voxels.

This analysis illustrates the application of STAPLE to the assessment of 3-D unordered multicategory segmentations. The STAPLE algorithm ran to convergence in 300 s, computing on the eight segmentations of the dataset of 256 × 256 × 110 voxels, with each voxel assigned one of seven labels. The algorithm is computationally efficient and provides valuable information that enables the ranking of the different segmentations. This may be used for selecting between different segmentations, or for adjusting objectively the parameters of enhancement or segmentation algorithms.

Go to:

IV. Discussion and Conclusion

We have presented an algorithm for taking a collection of both binary and unordered multicategory segmentations and simultaneously constructing an estimate of the hidden true segmentation and an estimate of the performance level of each segmentation generator. This can be used to characterize any type of segmentation generator, including new segmentation algorithms or human operators, by direct comparison to the estimated true segmentation. When prior information regarding the expected anatomy is available, such as from a statistical anatomical atlas, STAPLE provides estimates of performance parameters accounting for this external standard reference. This enables the assessment of the accuracy of the segmentation generators. When such information is not available, STAPLE provides estimates of performance parameters with respect to a weighted combination of the input segmentations and the appropriate weighting is computed automatically. This enables the assessment of the precision of the segmentation generators. STAPLE adds new information regarding the difference between human and algorithm performance beyond what is available from previously reported spatial overlap measures such as the DSC, and generates a plausible “true” segmentation estimate from clinical data where alternative methods of obtaining ground truth estimates are often extremely difficult or unattractive to use.

We carried out experiments with a known true segmentation and raters of prespecified sensitivity and specificity, and demonstrated that STAPLE is able to correctly estimate the true segmentation and the performance parameters from observations of the segmentations. Sensitivity and specificity parameters depend on the relative proportion of the structure being segmented in the image, and it is useful to report the positive predictive value and negative predictive value as these account for the relative proportion of the foreground and background. The predictive values (posterior probabilities) can be derived from the sensitivity and specificity parameters and the proportion of foreground and background in each image. We compared a brain phantom for which the true segmentation is known to the STAPLE estimate of the true segmentation, derived from both synthetic segmentations with specified performance characteristics, and segmentations carried out by medical students. We demonstrated that STAPLE can identify the correct segmentation even when a majority of segmentations contain repeated errors, unlike a majority vote rule. We also demonstrated how to estimate performance parameters when the segmentations consist of unordered multicategory labels. We empirically verified the runtime performance of the algorithm and found it is rapid and easily applied in practice.

We applied STAPLE to illustrative clinically motivated segmentation problems, including the assessment of repeated segmentations of the prostate peripheral zone for brachytherapy radiation dose planning, the assessment of an algorithm for brain tumor segmentation and the analysis of 3-D multicategory unordered labeling of tissue type from MRI of a newborn infant. We compared the STAPLE analysis to commonly used alternative measures. We found the method computationally efficient and straightforward to apply in practice. We found the STAPLE estimated true segmentation cannot be replicated with simple voting rules, and that the performance parameters are important indicators of how segmentations differ, which aid in the interpretation of segmentation quality compared to standard measures such as the DSC.

We have described the STAPLE algorithm with several types of spatial constraints, including none at all, a statistical atlas of prior probabilities for the distribution of the structure of interest, and with MRF models for spatial homogeneity.

Recently the application of the STAPLE algorithm [34] to the evaluation of tumor segmentations was described [59]. The mean and standard deviation of sensitivity and specificity parameters, as estimated by STAPLE, were used to compare a rapid interactive level-set based segmentation algorithm to hand contouring by raters for tumor segmentation. Another application of the STAPLE algorithm [34] has been to identify an optimal combination of image processing algorithms for intracranial cavity segmentation of brain MRI [60].

The STAPLE algorithm [34] and generalizations have also been applied to the evaluation of segmentations derived from nonrigid registration [61], [62]. In that work, comparisons were made between a majority vote rule, pairwise binary and unordered multicategory label estimates of the hidden true segmentation and performance. The advantage of the STAPLE estimation scheme over a majority vote rule was again demonstrated.

A. Future Work

The representation we have chosen for our segmentations involves individual labeling of each voxel. This is particularly flexible and well suited to segmentations of structures of unknown topology, as is often the case when dealing with abnormal tissues. It may be interesting to consider a generalization of this to segmentations represented by enclosed surfaces, such as is often found in segmentations achieved by deformable models or by level set methods. In segmentations obtained with such surface-oriented techniques, the region of the surface boundary typically has the highest variability and is of most interest for the performance assessment. If it is the case that the interior of a region is easy to segment and the boundary is most variable, the STAPLE estimated true segmentation will reflect this and the performance level estimates will reflect the variability of the algorithms or raters in the region of the boundary.

Our algorithm estimates performance parameters and true segmentation probabilities, from which the posterior probability of the correct label being present when a segmentation indicates that label is present can be computed. Techniques for estimating bounds upon parameters estimated in the EM algorithm have been developed ([32, Chapter 4]] and it would be valuable to apply those techniques here also.

We have considered estimation of the true segmentation and performance parameters for an entire scene, and in specified regions of interest. In some applications it may be desirable to assess performance in subregions, for example, when high accuracy is required in some regions and lower accuracy may be tolerated in other regions. Analysis of this can be achieved by defining a region of interest and executing STAPLE only on this region of interest. Note also that the estimated sensitivity and specificity will depend upon the size of the region of interest, whereas the posterior probabilities (predictive values) will not.

Our model assumes the expert segmentations are conditionally independent. The notion is that the segmentations are achieved independently but with each rater having the same true segmentation goal in mind. If different raters differ in their conception of the ideal true segmentation which they are attempting to express in their decisions D_ij, this bias can be discovered and quantified with the STAPLE algorithm. Running STAPLE on repeated observations of a single raters’ segmentations enables the estimation of the rater-specific true segmentation with the random variation of the rater removed. However, rater specific bias, such as structural errors, may remain. This could potentially be addressed by calibrating the rater through segmentation of a phantom, by standardizing the segmentation protocol or by supervised training of the rater. Alternatively, repeating this process for several raters, each with a potentially different bias, allows a spatial model for how raters differ to be constructed. Running STAPLE with the per-rater estimated true segmentations as input would then allow the estimation of the overall “true” segmentation—this effectively treats the bias of each rater as a perturbation away from the true segmentation that is to be recovered. Further investigation of this would be valuable.

Go to:

Acknowledgments

The authors gratefully acknowledge the contributions of the experts and students who generated the segmentations of the clinical data.

Go to:

Footnotes

This work was supported in part by the Whitaker Foundation, in part by the National Institutes of Health (NIH) under Grant R21 MH67054, Grant R01 LM007861, Grant P41 RR13218, Grant P01 CA67165, Grant R01 AG19513, Grant R01 CA86879, Grant R01 NS35142, Grant R33 CA99015, and Grant R21 CA89449, and in part by an award from the Center for Integration of Medicine and Innovative Technology. The Associate Editor responsible for coordinating the review of this paper and recommending its publication was M. A. Viergever.

Go to:

References

1. D. Nicoll and W. Detmer, Basic Principles of Diagnostic Test Use and Interpretation. New York: McGraw-Hill, 2001, ch. 1, pp. 1–16.

2. Styner M, Brechbühler C, Székely G, Gerig G. “Parametric estimate of intensity inhomogeneities applied to MRI,” IEEE Trans Med Imag. 2000 Mar;19(3):153–165. [Abstract] [Google Scholar]

3. Collins D, Zijdenbos A, Kollokian V, Sled J, Kabani N, Holmes C, Evans A. “Design and construction of a realistic digital brain phantom,” IEEE Trans Med Imag. 1998 June;17(3):463–468. [Abstract] [Google Scholar]

4. Spitzer V, Ackerman MJ, Scherzinger AL, Whitlock D. “The visible human male: A technical report,” J Amer Med Inform Assoc. 1996;3(2):118–130. [Europe PMC free article] [Abstract] [Google Scholar]

5. T. S. Yoo, M. J. Ackerman, and M. Vannier, “Toward a common validation methodology for segmentation and registration algorithms,” in Proc. 3rd Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2000), A. M. DiGioia and S. Delp, Eds., 2000, pp. 422–431.

6. Iosifescu DV, Shenton ME, Warfield SK, Kikinis R, Dengler J, Jolesz FA, McCarley RW. “An automated registration algorithm for measuring MRI subcortical brain structures,” NeuroImage. 1997;6:12–25. [Abstract] [Google Scholar]

7. Warfield SK, Mulkern RV, Winalski CS, Jolesz FA, Kikinis R. “An image processing strategy for the quantification and visualization of exercise induced muscle MRI signal enhancement,” J Magn Reson Imag. 2000 May;11(5):525–531. [Abstract] [Google Scholar]

8. Bland JM, Altman DG. “Applying the right statistics: Analyses of measurement studies,” Ultrasound Obstet Gynecol. 2003;22:85–93. [Abstract] [Google Scholar]

9. Levin DN, Hu X, Tan KK, Galhotra S. “Surface of the brain: Three-dimensional MR images created with volume rendering,” Radiology. 1989;171:277–280. [Abstract] [Google Scholar]

10. M. Everingham, H. Muller, and B. Thomas, “Evaluating image segmentation algorithms using the pareto front,” in Lecture Notes in Computer Science. Berlin, Germany: Springer-Verlag, 2002, vol. 2353, ECCV, pp. 34–48.

11. Dice LR. “Measures of the amount of ecologic association between species,” Ecology. 1945;26(3):297–302. [Google Scholar]

12. Jaccard P. “The distribution of flora in the alpine zone,” New Phytologist. 1912;11:37–50. [Google Scholar]

13. Hogan RE, Mark KE, Wang L, Joshi S, Miller MI, Bucholz RD. “Mesial temporal sclerosis and temporal lobe epilepsy: MR imaging deformation-based segmentatino of the hippocampus in five patients,” Radiology. 2000;216:291–297. [Abstract] [Google Scholar]

14. F. Bello and A. C. F. Colchester, “Measuring global and local spatial correspondence using information theory,” in Proc. 1st Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 98), 1998, pp. 964–973.

15. Zou KH, Wells WM, Kikinis R, Warfield SK. “Three validation metrics for automated probabilistic image segmentation in brain tumors,” Statist Med. 2003;23:1259–1282. [Europe PMC free article] [Abstract] [Google Scholar]

16. G. Gerig, M. Jomier, and M. Chakos, “Valmet: A new validation tool for assessing and improving 3D object segmentation,” in Proc. 4th Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2001), M. A. Viergever, Ed., Utrecht, The Netherlands, 2001, pp. 516–523.

17. Zijdenbos AP, Dawant BM, Margolin RA, Palmer AC. “Morphometric analysis of white matter lesions in MR images: Method and validation,” IEEE Trans Med Imag. 1994 Dec;13:716–724. [Abstract] [Google Scholar]

18. Warfield S, Dengler J, Zaers J, Guttmann CR, Wells WM, III, Ettinger GJ, Hiller J, Kikinis R. “Automatic identification of grey matter structures from MRI to improve the segmentation of white matter lesions,” J Image Guid Surg. 1995;1(6):326–338. [Abstract] [Google Scholar]

19. Kikinis R, Shenton ME, Gerig G, Martin J, Anderson M, Metcalf D, Guttmann CRG, McCarley RW, Lorenson WE, Cline H, Jolesz F. “Routine quantitative analysis of brain and cerebrospinal fluid spaces with MR imaging,” J Magn Reson Imag. 1992;2:619–629. [Abstract] [Google Scholar]

20. Cordella LP, Foggia P, Sansone C, Tortorella F, Vento M. “Reliability parameters to improve combination strategies in multi-expert systems,” Pattern Anal Applicat. 1999;2:205–214. [Google Scholar]

21. Ho TK, Hull JH, Srihari SN. “Decision combination in multiple classifier systems,” IEEE Trans Pattern Anal Machine Intell. 1994 Jan;16:66–75. [Google Scholar]

22. Kittler J, Hatef M, Duin RPW, Matas J. “On combining classifiers,” IEEE Trans Pattern Anal Machine Intell. 1998 Mar;20:226–239. [Google Scholar]

23. Windridge D, Kittler J. “A morphologically optimal strategy for classifier combination: Multiple expert fusion as a tomographic process,” IEEE Trans Pattern Anal Machine Intell. 2003 Mar;25:343–353. [Google Scholar]

24. Jacobs RA, Jordan MI, Nowlan SJ, Hinton GE. “Adaptive mixtures of local experts,” Neural Computation. 1991;3:79–87. [Abstract] [Google Scholar]

25. M. I. Jordan and R. A. Jacobs, “Hierarchical Mixtures of Experts and the EM Algorithm,”, Tech. Rep. AIM-1440, 1993.

26. P. Melville, R. J. Mooney, and R. Nagarajan, “Content-boosted collaborative filtering for improved recommendations,” in Proc. 18th Nat. Conf. Artificial Intelligence, vol. AAAI-2002, 2002, pp. 187–192.

27. Irwig L, Macaskill P, Glasziou P, Fahey M. “Meta-analytic methods for diagnostic test accuracy,” J Clin Epidemiol. 1995;48(1):119–130. [Abstract] [Google Scholar]

28. Normand SL. “Tutorial in biostatistics meta-analysis: Formulating, evaluating, combining, and reporting,” Statist Med. 1999;18:321–359. [Abstract] [Google Scholar]

29. Alonzo TA, Pepe MS. “Using a combination of reference tests to assess the accuracy of a new diagnostic test,” Statist Med. 1999;18:2987–3003. [Abstract] [Google Scholar]

30. SV SVB, Campbell G, Meier KL, Wagner RF. “On the problem of ROC analysis without truth: The EM algorithm and the information matrix,” Proc SPIE. 2000;3981:126–134. [Google Scholar]

31. Dempster A, Laird N, Rubin D. “Maximum-likelihood from incomplete data via the EM algorithm,” J Roy Statist Soc Ser B. 1977;39:34–37. [Google Scholar]

32. G. J. McLachlan and T. Krishnan, The EM Algorithm and Extensions. New York: Wiley-Interscience, 1996.

33. S. K. Warfield, K. H. Zou, M. R. Kaus, and W. M. Wells, “Simultaneous validation of image segmentation and assessment of expert quality,” in Proc. Int. Symp. Biomedical Imaging: Macro to Nano, J. Fessler and M. Vannier, Eds., Washington, DC, 2002, pp. 1494:1–1494:4.

34. S. K. Warfield, K. H. Zou, and W. M. Wells, “Validation of image segmentation and expert quality with an expectation-maximization algorithm,” in Proc. 5th Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2002), , Tokyo, Japan, 2002, pp. 298–306.

35. J. Rexilius, “Physics-Based Nonrigid Registration for Medical Image Analysis,” masters thesis, Med. Univ. Luebeck, Luebeck, Germany, 2001.

36. Friston K, Ashburner J, Poline J, Frith C, Heather J, Frackowiak R. “Spatial registration and normalization of images,” Human Brain Mapping. 1995;2:165–189. [Google Scholar]

37. D. L. Collins, “3D Model-based segmentation of individual brain structures from magnetic resonance imaging data,” Ph.D. dissertation, McGill Univ., Montréal, Canada, 1994.

38. Ising E. “Beitrag zur Theorie des Ferromagnetismus,” Zeitschrift f Physik. 1925;31:253–258. [Google Scholar]

39. T. Kapur, W. Grimson, R. Kikinis, and W. W. III, “Enhanced spatial priors for segmentation of magnetic resonance imagery,” in Proc. 1st Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 98), 1998, pp. 457–468.

40. Van Leemput K, Maes F, Vanermeulen D, Suetens P. “Automated model-based bias field correction of MR images of the brain,” IEEE Trans Med Imag. 1999 Oct;18:885–895. [Abstract] [Google Scholar]

41. Zhang Y, Brady M, Smith S. “Segmentation of brain mr images through a hidden Markov random field model and the expectation-maximization algorithm,” IEEE Trans Med Imag. 2001 Jan;20:45–57. [Abstract] [Google Scholar]

42. Greig DM, Porteous BT, Seheult AH. “Exact maximum a posteriori estimation for binary images,” J Roy Statist Soc B. 1989;51(2):271–279. [Google Scholar]

43. Ishikawa H. “Exact optimization for Markov random fields with convex priors,” IEEE Trans Pattern Anal Machine Intell. 2003 Oct;25:1333–1336. [Google Scholar]

44. I. M. Elfadel, “From fields to networks,” Ph.D. dissertation, Massachussetts Inst. Technol., Cambridge, MA, 1993.

45. Besag J. “On the statistical analysis of dirty pictures,” J Roy Statist Soc B. 1986;48(3):259–302. [Google Scholar]

46. ———, “Spatial interaction and the statistical analysis of lattice systems,” J Roy Statist Soc Ser B 36192–235.1974 [Google Scholar]

47. T. Kapur, “Model-based three-dimensional medical image segmentation,” Ph.D. dissertation, Massachussetts Inst. Technol., Cambridge, MA, 1999.

48. J. Zhang and G. G. Hanauer, “The application of mean field theory to image motion estimation,” IEEE Trans. Imag. Processing, pp. 19–33, Jan. 1995. [Abstract]

49. Geieger D, Girosi F. “Parallel and deterministic algorithms from MRF’s: Surface reconstruction,” IEEE Pattern Anal Machine Intell. 1991 May;13:401–412. [Google Scholar]

50. Edmonds J, Karp RM. “Theoretical improvements in algorithmic efficiency for network flow problems,” J Assoc Comput Mach. 1972;19:248–264. [Google Scholar]

51. J. Rexilius, S. K. Warfield, C. R. G. Guttmann, X. Wei, R. Benson, L. Wolfson, M. Shenton, H. Handels, and R. Kikinis, “A novel nonrigid registration algorithm and applications,” in Proc. 4th Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2001), W. J. Niessen and M. A. Viergever, Eds., Utrecht,, The Netherlands, 2001, pp. 923–931.

52. Bharatha A, Hirose M, Hata N, Warfield SK, Ferrant M, Zou KH, Suarez-Santana E, Ruiz-Alzola J, D’Amico A, Cormack RA, Kikinis R, Jolesz FA, Tempany CM. “Evaluation of three-dimensional finite element-based deformable registration of pre- and intra-operative prostate imaging,” Med Phys. 2001 Dec;28:2551–2560. [Abstract] [Google Scholar]

53. Kaus M, Warfield SK, Nabavi A, Black PM, Jolesz FA, Kikinis R. “Automated segmentation of MRI of brain tumors,” Radiology. 2001 Feb;218:586–591. [Abstract] [Google Scholar]

54. Warfield SK, Kaus M, Jolesz FA, Kikinis R. “Adaptive, template moderated, spatially varying statistical classification,” Med Image Anal. 2000 Mar;4(1):43–55. [Abstract] [Google Scholar]

55. ———, “Adaptive template moderated spatially varying statistical classification,” in Proc. 1st Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 98), W. M. Wells, A. Colchester, and S. Delp, Eds., MA, 1998, pp. 231–238.

56. Hüppi P, Warfield S, Kikinis R, Barnes PD, Zientara GP, Jolesz FA, Tsuji MK, Volpe JJ. “Quantitative magnetic resonance imaging of brain development in premature and mature newboms,” Ann Neurol. 1998 Feb;43(2):224–235. [Abstract] [Google Scholar]

57. Inder TE, Huppi PS, Warfield SK, Kikinis R, Zientara GP, Barnes PD, Jolesz FA, Volpe JJ. “Periventricular white matter injury in the premature infant is followed by reduced cerebral cortical gray matter volume at term,” Ann Neurol. 1999;46(5):755–760. [Abstract] [Google Scholar]

58. Murphy BP, Inder TE, Huppi PS, Warfield S, Zientara GP, Kikinis R, Jolesz FA, Volpe JJ. “Impaired cerebral cortical gray matter growth after treatment with dexamethasone for neonatal chronic lung disease,” Pediatrics. 2001 Feb;107(2):217–221. [Abstract] [Google Scholar]

59. A. Lefohn, J. Cates, and R. Whitaker, “Interactive, GPU-Based Level Sets for 3D Segmentation,” in Proc. 6th Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2003), 2003, pp. 564–572.

60. C. Fennema-Notestine, I. B. Ozyurt, G. G. Brown, C. P. Clark, S. Morris, A. Bischoff-Grethe, M. W. Bondi, and T. L. Jernigan, (2003) Bias correction, pulse sequence, and neurodegeneration influence performance of automated skull-stripping methods. Program 863.23. 2003 Abstract Viewer/Itinerary Planner. Washington, CD: Soc. Neurosci, 2003. [Online].

61. T. Rohlfing, D. B. Russakoff, and C. R. Maurer, “Expectation maximization strategies for multi-atlas multi-label segmentation,” in Proc. Int. Conf. Information Processing in Medical Imaging, 2003, pp. 210–221. [Abstract]

62. ———, “Extraction and application of expert priors to combine multiple segmentations of human brain tissue,” in Proc. 6th Int. Conf. Medical Image Computing and Computer-Assisted Intervention (MICCAI 2003), 2003, pp. 578–585.

Full text links

Read article at publisher's site: https://doi.org/10.1109/tmi.2004.828354

Read article for free, from open access legal sources, via Unpaywall: https://europepmc.org/articles/pmc1283110?pdf=render

Citations & impact

Impact metrics

739

Citations

Jump to Citations

Citations of article over time

Alternative metrics

Altmetric item for https://www.altmetric.com/details/35310275

Altmetric
Discover the attention surrounding your research
https://www.altmetric.com/details/35310275

Article citations

Deep learning-based segmentation of kidneys and renal cysts on T2-weighted MRI from patients with autosomal dominant polycystic kidney disease.
Sore R, Cathier P, Vlachomitrou AS, Bailleux J, Arnaud K, Juillard L, Lemoine S, Rouvière O
Eur Radiol Exp, 8(1):122, 30 Oct 2024
Cited by: 0 articles | PMID: 39477840 | PMCID: PMC11525362
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
3D whole body preclinical micro-CT database of subcutaneous tumors in mice with annotations from 3 annotators.
Jensen M, Clemmensen A, Hansen JG, van Krimpen Mortensen J, Christensen EN, Kjaer A, Ripa RS
Sci Data, 11(1):1021, 19 Sep 2024
Cited by: 1 article | PMID: 39300127 | PMCID: PMC11412993
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
Consensus of algorithms for lesion segmentation in brain MRI studies of multiple sclerosis.
De Rosa AP, Benedetto M, Tagliaferri S, Bardozzo F, D'Ambrosio A, Bisecco A, Gallo A, Cirillo M, Tagliaferri R, Esposito F
Sci Rep, 14(1):21348, 12 Sep 2024
Cited by: 1 article | PMID: 39266642 | PMCID: PMC11393062
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
Deep network and multi-atlas segmentation fusion for delineation of thigh muscle groups in three-dimensional water-fat separated MRI.
Annasamudram NV, Okorie AM, Spencer RG, Kalyani RR, Yang Q, Landman BA, Ferrucci L, Makrogiannis S
J Med Imaging (Bellingham), 11(5):054003, 03 Sep 2024
Cited by: 0 articles | PMID: 39234425
BrainSegFounder: Towards 3D foundation models for neuroimage segmentation.
Cox J, Liu P, Stolte SE, Yang Y, Liu K, See KB, Ju H, Fang R
Med Image Anal, 97:103301, 08 Aug 2024
Cited by: 1 article | PMID: 39146701

Go to all (739) article citations

Funding

Funders who supported this work.

NCI NIH HHS (6)

Grant ID: R33 CA99015
3 publications
Grant ID: P01 CA067165
116 publications
Grant ID: P01 CA67165
33 publications
Grant ID: R01 CA086879
7 publications
Grant ID: R01 CA86879
4 publications
Grant ID: R21 CA89449
1 publication

NCRR NIH HHS (2)

Grant ID: P41 RR013218
499 publications
Grant ID: P41 RR13218
73 publications

NIA NIH HHS (2)

Grant ID: R01 AG019513
14 publications
Grant ID: R01 AG19513
3 publications

NIMH NIH HHS (2)

Grant ID: R21 MH067054
18 publications
Grant ID: R21 MH67054
27 publications

NINDS NIH HHS (2)

Grant ID: R01 NS035142
6 publications
Grant ID: R01 NS35142
15 publications

NLM NIH HHS (3)

Grant ID: R01 LM007861
36 publications
Grant ID: R01 LM007861-01A1
6 publications
Grant ID: R01 LM007861-02
7 publications

Search life-sciences literature (45,103,589 articles, preprints and more)

Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation.

Author information

Affiliations

Authors

ORCIDs linked to this article

Abstract

Free full text

Simultaneous Truth and Performance Level Estimation (STAPLE): An Algorithm for the Validation of Image Segmentation

Simon K. Warfield

Kelly H. Zou

William M. Wells

Abstract

I. Introduction

II. Method

A. Description of STAPLE Algorithm

B. E-Step: Estimation of the Conditional Expectation of the Complete Data Log Likelihood Function

C. M-Step: Estimation of the Performance Parameters by Maximization

D. An Extension to Unordered Multicategory Labels

E. A Model for Estimation of Spatially Correlated Structures

F. Initialization Strategy and Detection of Convergence

III. Results

A. Digital Phantom Experiments

B. Brain Phantom Experiments

C. Illustration of Clinical Validation Applications

TABLE I

TABLE II

D. Assessment of Supervised Tissue Classification of the Neonate Brain

TABLE III

IV. Discussion and Conclusion

A. Future Work

Acknowledgments

Footnotes

References

Full text links

Citations & impact

Impact metrics

Citations of article over time

Alternative metrics

Article citations

Similar Articles

Funding

NCI NIH HHS (6)﻿

NCRR NIH HHS (2)﻿

NIA NIH HHS (2)﻿

NIMH NIH HHS (2)﻿

NINDS NIH HHS (2)﻿

NLM NIH HHS (3)﻿

Partnerships & funding

NCI NIH HHS (6)

NCRR NIH HHS (2)

NIA NIH HHS (2)

NIMH NIH HHS (2)

NINDS NIH HHS (2)

NLM NIH HHS (3)