Abstract

Results

Our overall goal is to employ surfactants dissolved in the membrane to perturb the vesicular fusion mechanisms. The first problem, then, is to control and measure the concentration of surfactant in the surface membrane of the cell. We made use of the fact that the lipophilic dyes used to study vesicle cycling (4–7) are surfactants (they have a hydrophobic tail that enters the outer leaflet of the surface membrane and a hydrophilic head that make them soluble in water and keeps them from penetrating to the hydrophobic core of the membrane) and that they fluoresce strongly only in the membrane environment. By measuring fluorescence as a function of bulk solution concentration of the dye, we can determine the relative surfactant concentration in the surface membrane of the cell.

We have examined the membrane solubility of 4 dyes (FM2–10, FM1–43, FM1–84, and FM4–64). The paired hydrophobic tails of these dyes vary in length from one type of dye to the next (see Fig. 1), and this length variation is known to control the rate at which dye dissolved in the membrane exits to the aqueous phase (8, 9). Fig. 1 shows dye concentration in the membrane, measured by fluorescence relative to the maximum, as a function of dye concentration in the bathing solution, and shows that all of the dyes bind to the membrane in a saturating manner.

Open in a separate window

Fig. 1.

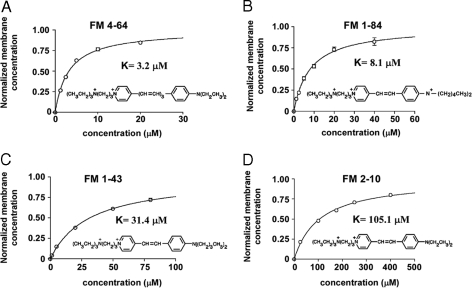
Binding of FM dyes to neuronal surface membranes. In each graph, the abscissa is the bath concentration of the indicated dye and the ordinate is the occupancy of the surface membrane by dye, with an occupancy of 1 for saturation. For each figure, the dye dissociation constant and chemical structure is shown. The surfactants used are the following: FM4–64 (A); FM 1–84 (B); FM1–43 (C); and FM2–10 (D).

The standard theory for the association of surfactant molecules with a lipid bilayer (or monolayer) provides an equation, known as the Langmuir adsorption isotherm,

that describes this process. Here, c is the surfactant concentration (units, μM) in the bathing medium, K is the adsorption constant (units, μM; when c = K, the membrane is half saturated with surfactant), and f(c) is the number of surfactant molecules dissolved in the membrane relative to the maximum number the membrane will hold. When f(c) = 1, the membrane is fully saturated and can hold no more dye. The data in Fig. 1 have been fitted to Eq. 1 and clearly this standard description is an accurate one for our situation. For the normalized data (normalized so that the maximum dye concentration in the membrane is 1), the equation has a single constant, K, the concentration of dye in the solution that gives half saturation of the membrane, and the value of this constant varies >30-fold, from 3.2 μM for FM4–64 to 105.1 μM for FM2–10, for the 4 dyes we have studied.

Having characterized the partitioning of these lipophilic dyes between the bathing solution and the surface membrane of the cell, our second problem is to detect fusion pore opening at individual synapses that have various concentrations of surfactant in their surface membrane. Vesicles normally maintain their lumen at low pH (10), and the intraluminal pH increases rapidly when the fusion pore opens. Because H⁺ ions have such a high mobility in water and can pass through a fusion pore that might impede the flow of larger species, we used a fluorescent reporter to measure the intravesicular pH and thereby detect fusion pore opening (11, 12). To increase the sensitivity for detecting fusion pore opening, we have developed a new sensor, SypHluorin, with 4 copies of pHluorin inserted into the loop of synaptophysin that is exposed to the lumen of synaptic vesicles. Because SypHluorin emits green fluorescence, we selected as our surfactant FM4–64, a dye with red fluroescence, to alter properties of the surface membrane.

To determine the effect of surfactant dissolved in the membrane on vesicle fusion, we activated a population of synapses in cultured hippocampal neurons with field stimulation (5 stimuli in 200 ms) and imaged the SypHluorin response to estimate the average number of fusion pore openings at individual synapses (Fig. 2 A and B). This procedure was carried out with different membrane concentrations of surfactant and the amplitude of the SypHluorin fluorescence response was normalized to the control value (no surfactant in the membrane). Fig. 2C shows the amplitude of fluorescence response (in arbitrary fluorescence units) to 5 stimuli at 20 Hz as a function of time with FM4–64 concentration of 0 (filled circles) and dye concentration of 15 μM (open circles; this concentration gives a relative membrane dye concentration of 0.82). As is evident, a little more than half as many vesicles opened their fusion pores when dye was present as compared with control. Based on data like those shown in Fig. 2C from 125 synapses, we find that 15 μM FM4–64 reduces the number of vesicles that open their fusion pore to 59% of control. We conclude that surfactant dissolved in the membrane decreases the number of vesicle fusion events.

Open in a separate window

Fig. 2.

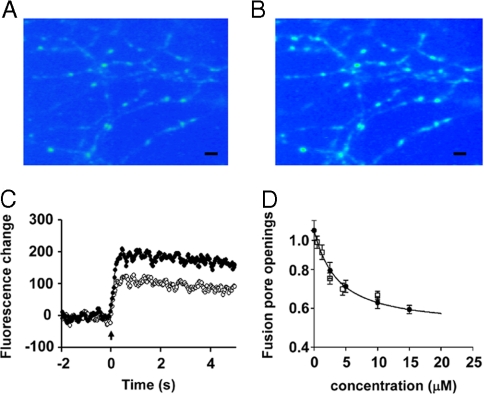
Effect of detergent concentration in the bathing medium on the number of vesicles that fuse for a standard stimulus. (A) Fluorescence image of hippocampal neurons that express the pH sensor SypHluorin. The spots are individual boutons that are resting (have not been stimulated). (Scale bar, 5 μm.) (B) Image of the same field of view as in A obtained after a stimulus (5 stimuli and 20 Hz). (Scale bar, 5 μm.) (C) Fluorescence intensity as a function of time for a single bouton. The standard stimulus was applied at time 0. The upper trace (filled circles) is the response in the absence of surfactant, and the lower trace (open circles) is the response in the presence of 15 μM FM4–64 in the bath. (D) Relative number of vesicular fusion pore openings, in response to a standard stimulus (5 action potentials at 20 Hz), as a function of the concentration of FM4–64 in the bathing medium. Filled circles show fusion pore openings detected with the pH sensor SypHluorin. Open squares give estimates of fusion efficiency measured by loading of the FM4–64 into vesicles. Error bars represent SEM.

Does this effect vary in an orderly way as a function of dye concentration? By making plots like the one shown in Fig. 2C for 586 synapses in 36 experiments at 5 dye concentrations and fitting regression lines, we constructed the plot in Fig. 2D (filled circles) that shows the number of fusion pore openings relative to the control number (no surfactant present) of as a function of FM4–64 concentration in the bath: as the dye concentration increases, there is an orderly decrease in the number of fusion pore openings compared with the control situation (dye concentration is zero).

In the experiments just described, we used a change in vesicular pH to detect fusion pore opening. But the lipophilic dye FM4–64 we used is known (13, 14) to enter the vesicle and dissolve in the inner leaflet of the vesicular membrane when a vesicle releases its contents, and we should also be able to detect fusion pore opening by the staining of vesicles with the FM dye as a check on our pH reporter method. Thus, we measured the number of vesicles stained as a function of dye concentration. The open boxes in Fig. 2D give the number of fusion pore openings in the presence of surfactant relative to the number when surfactant is absent (actually, when the concentration of FM4–64 is 0.5 μM, a value that produces a negligible reduction in fusion pore opening). We conclude that the estimated number of vesicles that open their fusion pores is the same whether measured with the vesicular pH reporter or by FM dye loading.

To this point, we have shown that the presence of dye clearly decreases the number of vesicles that open their fusion pores, but this decrease could simply reflect a change in the calcium concentration transient that triggers vesicle fusion. For example, perhaps the high dye concentrations block sodium or calcium channels and thereby decrease release by causing fewer synapses to be activated or by decreasing the calcium influx at the synapses that are activated. To examine this possibility, we imaged axon terminals loaded with a calcium indicator to measure the effect of dye at the highest concentrations used in Fig. 2 (15 μM) on the influx of calcium through calcium channels. We measured the calcium signal in axon terminals by loading the axons with the calcium indicator Fluo-5F AM (K_d = 2.3 μM) at a concentration of 100 μM, and found the peak value of fluorescence intensity change that resulted from stimulation (5 impulses at a rate of 20 Hz). An example of the fluorescence signal from a single synapse is shown in Fig. 3A. After adding 15 μM FM4–64 to the bathing solution, we repeated the measurement of the calcium signal. Fig. 3B shows a plot of the fluorescence intensity changes measured in the presence of dye as a function of the intensity changes measured in the absence of dye for 226 presynaptic terminals in 6 experiments. The line fitted with the least squares method has a slope of 0.99 (95% confidence limits of 0.96 to 1.0), whereas this concentration of dye reduced vesicle openings to 59% of control. Because dye is limited to the outer leaflet of the surface membrane, we conclude that the effect shown in Fig. 2 is on the vesicle fusion process rather than reflecting a decrease in the calcium concentration transient that triggers the fusion.

Open in a separate window

Fig. 3.

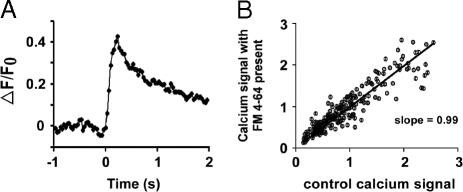
Effect of surfactant dissolved in the surface membrane on influx of calcium into boutons in response to a standard stimulus. (A) Fluorescence signal (arbitrary fluorescence units) from calcium indicator Fluo-5F AM at a single synapse (identified by loading with FM4–64 after calcium imaging experiment was completed) as a function of time (seconds) in response to the standard stimulus used for obtaining Fig. 2 data (5 action potentials at 20 Hz). The stimulus was presented at time 0. (B) Amplitude of calcium signal (as measured in A) with 15 μM FM4–64 present in the bath for 226 synapses as a function of the response of the same synapses when the bathing solution contains no dye.

The results we have described in Fig. 2 are qualitatively what one might expect: pushing surfactant molecules in the outer membrane leaflet closer together takes work and, thus, makes it harder for the fusion pore to open. But standard ideas from surface physics and chemistry can also make quantitative predictions to compare with our experimental observations. Two equations (derived in Materials and Methods) that are needed are: (i) the adsorption curve describing binding of surfactants in the membrane (the Langmuir adsorption isotherm), and (ii) an equation that specifies the number of fusion pores that open when surfactant is present relative to the number that open in the absence of surfactant; this is the quantity on the ordinate in Fig. 2D. The first of these equations (Eq. 1) has already been validated for our experimental situation by the results presented above. The second equation, specifying the relative number of fusion pores that open, is

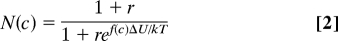
where c is again the surfactant concentration in the bathing medium, f(c) is the relative surfactant concentration in the membrane (f(c) is given by the Langmuir adsorption isotherm), r is a constant, ΔU is the work that must be done to compress the dye in the membrane (at saturating dye concentration) when the fusion pore opens, k is Boltzmann's constant, T is the absolute temperature, and N(c) is the number of fusion pores that open when surfactant is in the membrane relative to the number that open in the absence of surfactant. The smooth curve in Fig. 2D with r = 0.313 and ΔU/kT = 1.64 is a best fit to the data (see Materials and Methods); ΔU = 1.64 kT units corresponds to extra work of ΔU = .99 kcal/mole at room temperature to open the fusion pore in the presence of saturating concentrations of surfactant. The constant r is the ratio of the rate for dissociating calcium from the sensor to the rate of fusion pore opening; once the vesicle enters the activated state, the fusion pore opening is 3.2 times more likely than deactivation (with no surfactant present).

We have formalized the idea that the surface pressure resulting from surfactants dissolved in the membrane (this pressure arises from the work necessary to force the surfactant molecules closer together) should raise the energy barrier for fusion pore opening (see Materials and Methods), and have found that the predictions of this theory are in quantitative agreement with our observations. These same ideas predict that dye dissolved in the vesicle membrane rather than in the surface membrane should have the opposite effect: the increased surface pressure in the vesicle membrane should lower the energy barrier for vesicle fusion, increase the number of vesicles that open their fusion pores, and produce a larger fluorescence signal from our vesicular pH reporter. To test this prediction, we loaded most (we estimate 80%) of the recycling pool of synaptic vesicles with 10 μM FM4–64 by stimulating 600 times (20 Hz) in the presence dye, and then washed the dye out of the surface membrane. Control synapses were stimulated in the same way without dye in the bathing solution to control for the effects of the loading stimulation itself. The synapses with the dye-loaded vesicles (161 synapses in 6 experiments) and their control synapses without dye (166 synapses in 6 experiments) were then stimulated 20 times (20 Hz), and the amplitude of the fluorescence signal from the vesicular pH reporter was measured. The average release probability of synapses varies a little from preparation to preparation, and to control for this, we used the same 1-s long stimulation at 20 Hz and measured the signal from the pH reporter before dye loading; the average release probability of the synapses that were later dye loaded was 94.9% of that of the control preparations, and our data were normalized for this difference.

The results of these experiments are displayed in Fig. 4, where it can be seen that, as predicted, the presence of 10 μM FM4–64 dissolved in the vesicular membrane inner (luminal) leaflet increases the probability of fusion pore opening (by 21%; see Materials and Methods). Because 3 out of 4 activated vesicles normally choose the open-pore state, comparable changes in opening rates have less effect when the rates are increased (as here), rather than decreased (as in the experiments with surfactant in the surface membrane). The quantitative prediction from the earlier data (see Materials and Methods) is that the number of dye loaded vesicles that open fusion pores should be 1.20 times the control number and this is close to the value we observed.

Open in a separate window

Fig. 4.

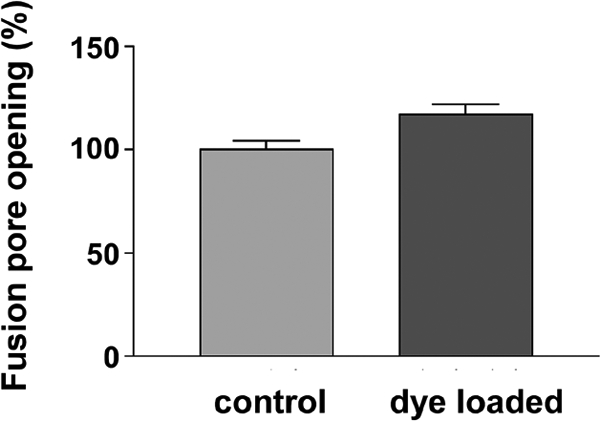
Relative average number of vesicular fusion pore openings in response to a stimulus (20 action potentials at 20 Hz) with 0 μM (control; 166 synapses) or 10 μM FM4–64 (dye loaded; 161 synapses) loaded into ≈80% of the recycling pool vesicles. The dye loaded vesicles release 21.3% ± 6.6% more frequently, and the difference is significant by at test (P = 0.0015). Error bars represent SEM.

According to the fit of Eq. 2 to our data, the extra work ΔU that must be done to open the fusion pore when the membrane is saturated with dye is ≈1 kcal/mole. This extra work is what is necessary to compress the “gas” of dye molecules when the fusion pore expands to open, and we can calculate the change in area needed for the pore to open. Surfactants dissolved in 1 leaflet of a lipid bilayer act like a 2D gas for which the ideal gas law is

where π is the surface pressure (units, kT units per nm²), n is the number of dye molecules per nm², and kT has the meaning given above and is equivalent to an energy of ≈0.6 kcal/mole. From the fits of the Langmuir adsorption isotherm equations, together with the time constant with which FM4–64 leaves the membrane (5.3 sec), we can, as described in Materials and Methods, calculate π. At saturating dye concentrations, the membrane contains 0.39 dye molecules per nm², and this gives a surface pressure of 0.39 kT units per nm².

The work to compress the 2D dye gas by an area ΔA is ΔU = πΔA, and we know both π and ΔU, so ΔA can be calculated. The change in area associated with fusion pore opening is found to 4.2 nm², and this provides an estimate for the area of the fusion pore opening. Note that this area is the one associated with the initial opening of the pore and is not necessarily the area the pore reaches when it finally fully relaxes. Our estimates for the fusion pore area agrees closely with one (2–2.5 nm diameter) inferred from electrophysiologic measurements on mast cell secretory granules (15). However, they are approximately an order of magnitude greater than estimates for the synaptic vesicle fusion pore size based of electrophysiology (16, 17), but the methods used in these studies allowed an estimate only when fusion pores were unusually small.

Discussion

We estimated the number of fusion pore openings that result from a particular stimulus in 2 different ways (by amount of FM4–64 dye loading and with our vesicular pH sensor), and found that both ways agree within measurement error. But this agreement need not have occurred. It has been reported that vesicles can open and release neurotransmitter without dye entry or exit (18), but this apparently does not happen under the conditions of our experiments. More interestingly, it might have been possible for dye to diffuse into the vesicle even if the fusion pore did not open enough for hydrogen ions to escape. Dye loading without fusion pore opening would have occurred if the outer surface membrane leaflet were continuous with the vesicle inner membrane leaflet for vesicles that were poised to open their fusion pore. This situation could have arisen if the fusion pore is lipidic. Because we estimate that 1 activated vesicle fails to open its fusion pore for every 3 vesicles that do, we should have detected lateral diffusion of FM dye if the inner leaflet of the vesicle membrane were continuous with the outer leaflet of the surface membrane. Then, we conclude that we have, in a vesicle poised to fuse, no evidence for membrane continuity between the inner leaflet of the vesicle membrane and the outer leaflet of the cell surface membrane.

Our laboratory has previously used FM dyes to estimate release probability for individual synapses (6, 19), but our new data indicate that these estimates were likely 10% to 17% too low (estimated from the 10 μM or 20 μM FM1–43 concentrations used in those experiments that give dye occupancies f(c) of 0.24 or 0.39). Other laboratories also may need to reevaluate some of their conclusions, because of perturbing effects of the surfactant dyes on the vesicular fusion that causes release of neurotransmitter. Such a perturbing effect could be particularly serious when 2 different dyes at different relative concentrations were used (9).

Materials and Methods

Langmuir Adsorption Isotherm.

Eq. 1 in the text is derived from

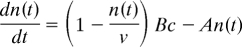
where n(t) (units, nm⁻²) is the number of dye molecules in a nm² of membrane at time t, c is the bath dye concentration (units, μM), A is the dissociation rate of dye from the membrane (units, sec⁻¹), B is the diffusion limited binding rate of dye to the membrane (units, nm⁻²μM⁻¹sec⁻¹), and ν is the maximum number of dye molecules that can be accommodated in a membrane area of 1 nm² (units, nm⁻²). The binding rate constant B has a value of 0.023 nm⁻²μM⁻¹sec⁻¹ [Davies and Rideal (22)], and the dissociation rate constant A has a value measured for FM4–64 of 0.192 sec⁻¹ (data not shown). When the equation above is solved for the value of n(c) at long times, the steady state number of dye molecules bound per nm² of membrane, the result is

where k is defined to be k = A/B = 8.2 nm²μM for FM4–64. Last, define the fractional occupancy of the membrane f(c) = n(c)/ν (units, 1) and the apparent dissociation constant K = νk (units, μM), and Eq. 1 in the text results. The constant K is measured to be 3.2 μM for FM4–64 (see Fig. 1A), and so ν = K/k = 0.39 nm⁻² is the maximum number of dye FM4–64 dye molecules that 1 nm² of membrane can accommodate.

Fusion Pore Opening.

A vesicle is pictured as having 3 states, activated with calcium bound to the vesicular sensor (C), resting with no calcium bound (R), and pore-open with a fusion pore that has opened (O). An activated vesicle has 2 choices for transitions: it can dissociate calcium from its sensor and return to the resting state or it can open its fusion pore. If a(c) is the rate for the C → O transition (units, sec⁻¹) when the dye concentration is c and b(c) is the rate for the C → R transition (units, sec⁻¹) when the dye concentration is c, then the probability p(c) (units, 1) of an activated vesicle entering the pore-open state when it leaves the activated state is

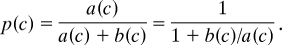
When dye is in the membrane, it acts like a 2D gas that must be compressed when the fusion pore opens and, according to absolute rate theory, the ratio b/a of rates should depend exponentially on the additional work ΔU/kT (units, 1) necessary for this gas compression; this extra work necessary for pore opening depends on the concentration of dye in the membrane. If, in the absence of dye, we define the ratio of rate constants as r = b (0)/a(0) (units, 1), the probability of making a transition to the pore-open state with dye present is given by

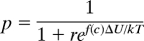
where f(c) is the fractional occupancy by dye as given above. What we measure in experiments is the ratio N(c) = p(c)/p(0) and this is Eq. 2 in the text. For FM4–64, the fit of Eq. 2 to the data gives r = 0.313 and ΔU/kT = 1.64. In the absence of dye, the probability that an activated vesicle chooses the pore-open state is p (0) = 1/(1+r) = 1(1.313) = 0.762; this means that an activated vesicle normally opens its fusion pore 3 times out of 4.

For 15 μM FM4–64 in the surface membrane, N (15) = (1 + r)/(1 + exp(f (15)ΔU/kt)) = 1.313/(1 + exp(0.824(1.64))) = 0.59. With 15 μM FM4–64 in the vesicular rather than surface membrane, the number of vesicles that open their fusion pores is denoted by N_i(c). N_i(c) should follow the same equation as N(c) the sign of the energy is reversed because the dye in the vesicle membrane is trying to expand rather than dye in the surface membrane that must be compressed. The predicted number of vesicles that open their fusion pores, then, is N_i (10) = (1 + r)/(1 + exp(−f (10)ΔU/kt)) = 1.313/(1 + exp(−0.758(1.64))) = 1.20.

Acknowledgments.

Footnotes

References