Abstract
Free full text

Quality of evidence for perceptual decision making is indexed by trial-to-trial variability of the EEG
Abstract
A fundamental feature of how we make decisions is that our responses are variable in the choices we make and the time it takes to make them. This makes it impossible to determine, for a single trial of an experiment, the quality of the evidence on which a decision is based. Even for stimuli from a single experimental condition, it is likely that stimulus and encoding differences lead to differences in the quality of evidence. In the research reported here, with a simple “face”/“car” perceptual discrimination task, we obtained late (decision-related) and early (stimulus-related) single-trial EEG component amplitudes that discriminated between faces and cars within and across conditions. We used the values of these amplitudes to sort the response time and choice within each experimental condition into more-face-like and less-face-like groups and then fit the diffusion model for simple decision making (a well-established model in cognitive psychology) to the data in each group separately. The results show that dividing the data on a trial-by-trial basis by using the late-component amplitude produces differences in the estimates of evidence used in the decision process. However, dividing the data on the basis of the early EEG component amplitude or the times of the peak amplitudes of either component did not index the information used in the decision process. The results we present show that a single-trial EEG neurophysiological measure for nominally identical stimuli can be used to sort behavioral response times and choices into those that index the quality of decision-relevant evidence.
Understanding the behavioral significance of trial-to-trial variability in neural activity is central to systems neuroscience in general, and the neural bases of decision making in particular. Distinguishing between variability that is functionally significant and variability that is simply noise is a key challenge. In this article, we show how sources of variability can be distinguished from each other by combining neurophysiological data with behavioral data and a diffusion model of simple decision making (1–5). This model identifies 4 different sources of variability in processing: within-trial variability, trial-to-trial variability in the evidence accumulated from nominally identical stimuli, trial-to-trial variability in the starting point of the decision process, and trial-to-trial variability in the duration of nondecision components of processing. Distinguishing these sources of variability is necessary to accurately model behavioral data, but there has been no independent way to measure their neurophysiological correlates. Here, we use single-trial analyses of EEG data and map behavior directly to EEG signals.
We present new analyses of data from a face/car perceptual discrimination experiment (Fig. 1A). Previously, research has shown that 2 single-trial EEG components discriminate between face and car stimuli (6, 7, 8). In ref. 6, stimuli were presented for 30 ms, and difficulty was manipulated by varying the spatial-phase coherence of the stimuli from 20% to 45% in 6 steps so that accuracy spanned the range from near 50% to near 100% correct. The EEG data were collected from multiple sensors as subjects performed the face/car task. Logistic regression with linear weighting of the electrode signals was applied to the data from all of the experimental trials to identify 2 component (amplitude) measures in 2 different time windows that discriminated well among the stimulus conditions (see Materials and Methods for details). The analyses identified an early component that occurred around 170 ms after stimulus presentation and a late component that occurred around 300 ms after stimulus presentation (Fig. 1B). This analysis applied to an individual trial produces a measurement of the component amplitude (Fig. 1C). Both components can be thought of as indexing stimulus quality, in that a high positive amplitude reflects an easy face stimulus, an amplitude near zero reflects a difficult stimulus, and a high negative amplitude reflects an easy car stimulus. However, the early-component amplitude is unaffected when the same stimuli are colored red or green and the task is switched to color discrimination. This indicates that this component represents the quality of the incoming sensory evidence (7). In contrast, the late-component amplitude is reduced almost to zero when the task is switched, indicating that it indexes decision-relevant evidence in a later stage of the face-vs.-car decision process.

Behavioral design and single-trial analysis of the EEG. (A) A depiction of the behavioral paradigm (Left) and sample face stimuli at different levels of coherence (Right). (B) An example of discriminant component maps for 1 subject for the 40% phase coherence condition. The 4 panels represent the face-vs.-car discriminator amplitude (y) for the early and late components for face and car trials using the training windows shown by the vertical white bars. Trials are ordered from top to bottom on the basis of the RT for the trial, and RTs are shown by the black sigmoidal curves. Face-like trials were mapped to positive amplitudes (red), and car-like trials were mapped to negative amplitudes (blue). (C) Mean amplitudes (y bar) for the early and late components for each trial for faces and cars at 40% phase coherence. The x axis shows the position of a trial among all of the 40% coherence trials for 1 subject. The late-component amplitudes from the Left are shown as a histogram in the Right panel, with a cutoff (the thick black line) to separate trials into more positive amplitudes, or “better” faces, vs. less positive amplitudes, or “worse” faces. These single-trial amplitudes were used to sort the data from each stimulus condition into 2 groups: those with a more positive amplitude vs. those with a less positive amplitude. The diffusion model was then used to fit the behavioral data from these 2 groups for each condition for each subject.
To provide an explanation of the behavioral data for face/car decisions (7), the diffusion model (1–5), which was developed to account for processing in simple, 2-choice decision making, was fit to the behavioral data. The model is dynamic; evidence is accumulated over time from a starting point to 1 of 2 decision criteria corresponding to the 2 choices. The process is noisy, and replications with exactly the same parameters will produce error responses, correct responses, and response time (RT) distributions (Fig. 2A). The model decomposes RTs and accuracy into components of processing that reflect the quality of evidence driving the decision process (drift rate), the amount of evidence required to make a decision (decision criteria), and the duration of nondecision processes, such as encoding and response production. For the diffusion model to fit accuracy and RT data, especially error RTs, there must be variability across trials in each of the components of processing. Monte Carlo studies (9) have shown that when fitting the model to simulated data, the sources of variability are identified appropriately; for example, across-trial variability in the starting point of the process (equivalent to across-trial variability in the decision criteria) is not misidentified as across-trial variability in drift rate. Our focus here is on drift rate, which varies from trial to trial (1), as in signal detection theory (Fig. 2B).
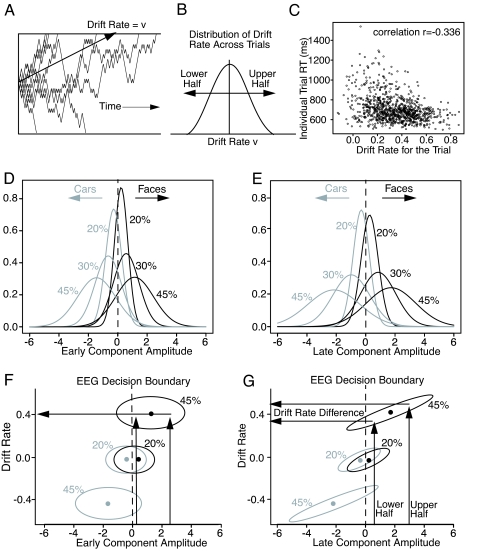
Relationship between drift rate and RT and EEG component activity. (A) Nine simulated diffusion processes with the same mean drift rate v, illustrating the degree of variability in the process. (B) The distribution of drift rates across trials. For the Monte Carlo simulations, the RTs and choices are divided into 2 groups based on the drift rate used for that trial (the drift rate randomly selected from the distribution of drift rates across trials). (C) A plot of RTs as a function of the individual drift rate for the trial. The parameters of the diffusion model were: drift rate v = 0.3, criteria separation a = 0.107, starting point z = 0.048, duration of processes other than the decision process Ter = 0.48 s, standard deviation in drift rate across trial η = 0.20, range in starting points across trials sz = 0.02, and range in Ter across trials st = 0.18 s. (D and E) Normal distributions for each coherence condition plotted from the means and standard deviations in the amplitudes averaged over subjects for the early and late components (compare the histograms in Fig. 1C). (F and G) Bivariate distributions of drift rate versus amplitude. These represent contours in the amplitude by drift rate bivariate distribution with the amplitudes taken from the distributions in D and E. The EEG amplitudes are projected down from D and E for the 20% and 45% coherence stimuli as examples. The ellipses in G are diagonal, showing a positive association between drift rate and the late-component amplitude, whereas the ellipses in E show no association. The arrows illustrate projections from late-component amplitudes to drift rates for each half of the data, showing how differences in component amplitude lead to differences in drift rate.
In ref. 7, the diffusion model was fit to the behavioral data from the face/car discrimination task under the assumption that although a stimulus is presented briefly, drift rate is constant over the time course of evidence accumulation, reflecting output from a stable representation in visual short-term memory (7, 10, 11). This assumption is required by the behavioral data. If the drift rate rose and fell with the brief stimulus presentation, then the starting point would effectively move toward the criterion for a correct response, thus increasing the distance to the criterion for an incorrect response, and hence producing errors that are much slower than correct responses and much slower than the observed error RTs (see ref. 10 for details). In ref. 7, the model fit accuracy and RT distributions well for all levels of phase coherence. For the late-EEG component, drift rate was correlated with the discriminability index, Az, across conditions and subjects (r = 0.86). Az for a component is the area under a receiver-operating characteristic curve (ROC) constructed from the distributions of the component amplitudes for correct and error responses. Az is derived from all of the trials in a condition, and so it cannot be used for single-trial analyses (however, it is linearly related to the mean component amplitude, so conclusions about mean amplitude also apply to Az).
In ref. 7, no analysis was presented that examined the relationship between the single-trial amplitudes for the test items within each experimental condition to the model or to the behavioral data. Moreover, as demonstrated below, the correlation between mean component amplitude and drift rate across trials can remain high even when single-trial correlations are absent. Fig. 1C illustrates substantial trial-to-trial variability in both early and late components. Below, by sorting data based on single-trial component amplitudes, we establish a direct relationship between the late-component amplitude and drift rate at the single-trial level.
Results
Using the data from ref. 6, for each subject we calculated the correlation between drift rate and mean component amplitude across conditions and the correlation between the mean early- and late-component amplitudes. The correlations were averaged over subjects for the early component and drift rate (r = 0.86), for the late component and drift rate (r = 0.86), and for the early and late components (r = 0.93).
If, instead of computing the correlation across the early- and late-component mean amplitudes across conditions, we compute the correlation between the early- and late-component amplitudes within each condition and then average over subjects and conditions, the correlation drops to r = 0.17. The 0.93 correlation shows that the means of the component amplitudes change systematically over conditions in the same way, but the 0.17 correlation shows that within a single condition, the component amplitudes do not line up in the same way.
To illustrate the distributions of component amplitudes, we chose 6 of the 12 conditions for which they are well separated. Fig. 2 D and E shows schematic distributions of the early and late components for these 6 conditions. The distributions of component amplitudes are symmetric (2 sample histograms are shown in Fig. 1C), so we computed means and standard deviations for each condition and subject, averaged over subjects, and then used these means and standard deviations to generate the normal distributions that are shown in Fig. 2 D and E.
We examined whether the trial-to-trial amplitudes of either of the 2 components can be related to the behavioral data. We sorted the trials within each condition of the experiment into 2 groups: those with more positive amplitudes and those with less positive amplitudes (conceptually dividing the distribution up as in Fig. 2B). We then applied the diffusion model to the behavioral data (RTs and accuracies) for each group separately (and for each subject separately). We also sorted the data into halves based on the latency of the peak amplitude for each of the 2 components. For the more accurate conditions (35%, 40%, and 45% coherence), there were too few errors to sufficiently constrain the model, so these 3 conditions were combined after sorting. Combining the 3 conditions was reasonable because there was little difference in their accuracy or their RT distributions. In fitting the diffusion model, all of the model's parameters were free to vary between the more positive amplitude and less positive amplitude groups for each condition. Note that based on behavioral data alone, sorting trials within a stimulus condition is impossible because there is no independent measure of trial-to-trial stimulus quality. The EEG components provide just this measure.
We first fit the model to the more positive and less positive amplitude groups. The model fit the data well, so we can examine whether there are systematic relationships between the components of processing identified by the model and the EEG amplitudes. We expected that drift rate would be more negative for the lower-amplitude trials than the higher-amplitude trials. But before presenting the results, we need to consider how large the drift rate differences recovered from fits of the model might be if, on each trial, the EEG component accurately indexed drift rate. Two simulations were carried out: one with mean drift rate 0.3 and the other with mean drift rate 0.1 (typical of easy and more difficult conditions, respectively). The standard deviation in drift rate across trials (set at 0.20) and the other parameters of the model were fixed at their values from fitting the behavioral data (7). The simulated data were sorted into halves based on the actual drift rate on each trial. Then, accuracy and RTs for correct and error responses for each half were obtained. The diffusion model was fit (9) to the 2 halves of the simulated data separately. The average drift rate difference between the 2 halves for the 0.1 and for the 0.3 drift rates was 0.30. The average standard deviation in drift rate across trials for the 2 halves was 0.12 (see Materials and Methods for more details). Therefore, if the EEG component provided a direct measure of drift rate, the upper limit on the difference that could be obtained between the drift rates for the more positive vs. less positive EEG amplitudes would be 0.30, and the standard deviation in drift rate across trials would be reduced from 0.20 to 0.12.
The hypothesis was that more positive drift rates would be obtained for the data corresponding to the more positive EEG amplitudes, and less positive drift rates would be obtained for the data corresponding to the less positive EEG amplitudes. Fig. 3 A and B plots drift rates for the more positive EEG amplitudes vs. drift rates for the less positive EEG amplitudes for the 8 conditions for each of the 6 subjects. For the early component, there was little difference between the drift rates for the higher and lower EEG amplitudes (F1,5 = 0.99). But for the late component, the drift rates were significantly larger for the more positive EEG amplitudes than the less positive amplitudes (F1,5 = 54.22; P < 0.05). This difference in drift rates (0.151) is about half the difference (0.30) that would be obtained if the late-component amplitude was an exact measure of drift rate as in the simulations above. Thus, the single-trial amplitudes of the late EEG component capture much but not all of the trial-to-trial variability in decision-related evidence.
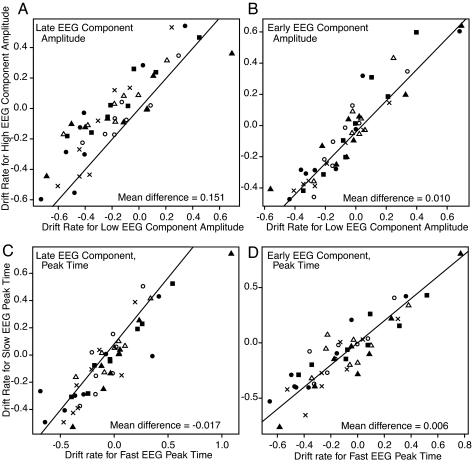
Plots of the drift rates for the 2 halves of the data against each other: the lower-amplitude, or faster peak time, half on the x axis, and the higher-amplitude, or slower peak time, half on the y axis. (A) A plot based on the late-component amplitude. (B) A plot based on the early-component amplitude. (C) A plot based on the late-component peak time. (D) A plot based on the early-component peak time. The different symbols refer to different subjects, 8 conditions per subject. In the experiment, there were 12 conditions, but the easier conditions were similar in amplitude, accuracy, and RT (35%, 40%, and 45% phase coherence conditions), and so were combined together. The positive drift rates are generally for the face stimuli, and negative drift rates are generally for the car stimuli. The diagonal lines, for reference, have slopes one and intercepts zero.
The same analyses as in Fig. 3 A and B were carried out with the data divided into halves based on the peak times of the early and late components, respectively. The results showed no differences in drift rate for either component (Fig. 3C for the early-component peak time, F1,5 = 0.04; Fig. 3D for the late-component peak time, F1,5 = 0.58).
The explanation for these results is illustrated in Fig. 2 F and G. The distributions for the 45% and 20% conditions from Fig. 2 D and E are projected down onto the component–amplitude axis. The ellipses represent horizontal cuts through the 2D bivariate distribution of drift rate vs. component amplitude. For the late component, drift rate maps to amplitude, shown by the diagonally oriented ellipses in Fig. 2G. Dividing the data into halves based on the late-component amplitude and projecting through the ellipse to the drift rate axis (arrows) gives drift rate differences. But there is no relationship for the early component; projections from the 2 early-component halves produce no difference in drift rates (Fig. 2F).
The second prediction from the simulations above was that the standard deviation in drift rate across trials (η) is reduced if component amplitude is related to drift rate. For the fits based on dividing the data according to the late component, the average value of η was estimated at 0.15. This was significantly different from the value of the standard deviation (0.20) for the fit in ref. 7 of the model to all of the data [t(10) = 1.90; P < 0.05]. None of the other parameter values differed significantly between the fits to the more positive and less positive amplitude sets of data. The average χ2 goodness of fit value averaged over subjects was χ2 = 84.2, df = 74, critical value 95.1. The visual quality of the fits was about the same as in figure 10A in ref. 7.
Discussion
In our analyses, the data within each experimental condition from the face/car discrimination experiment were sorted into 2 groups based on the mean amplitudes and peak times of the early and late EEG components. The diffusion model was fit separately to the data from the 2 groups of trials. For the late component, the estimates of drift rate were more positive for the group with the more positive component amplitudes than for the group with the less positive amplitudes. There were no such differences in drift rate when the data were sorted based on the amplitude of the early EEG component or when the data were sorted on the peak time of either component.
We conclude that single-trial analysis of the late EEG component amplitude can track trial-to-trial differences in discriminating activity in the decision process. Across-trial variability in postsensory stimulus quality is required in the diffusion model for behavioral decision making, and this analysis provides evidence for such variability. Our conclusion is supported by the results from ref. 7: switching the task from face/car discrimination to red/green discrimination (with colored versions of the same face and car stimuli) reduced the late EEG component amplitude almost to zero, but it left the early EEG component amplitude unchanged. These results converge to show that the information used to drive the decision process—that is, reflected in the late EEG component—is not the same as that which produces the early EEG response. Thus, our results distinguish between neural responses to early perceptual encoding and, later, to postsensory processing that ultimately provides the decision-relevant evidence entering the diffusion decision process.
Our results highlight the importance of trial-to-trial variability in nominally identical stimuli and its behavioral consequences. Understanding the behavioral significance of trial-to-trial variability in neural activity is central to systems neuroscience. Our results clearly demonstrate that distinguishing between variability that is functionally significant and variability that is simply noise should be a major objective of future research.
Materials and Methods
Subjects.
Six subjects (3 women and 3 men, mean age 25.6 years) participated in the experiment reported in ref. 6. All had normal or corrected-to-normal vision and reported no history of neurological problems. Informed consent was obtained from all subjects in accordance with the guidelines and approval of the Columbia University Institutional Review Board.
Stimuli.
We used a set of 18 face grayscale images (Max-Planck Institute for Biological Cybernetics, Tuebingen, Germany) and 18 car grayscale images (image size 512 × 512 pixels, 8 bits per pixel). All images were equated for spatial frequency, luminance, and contrast. They all had identical magnitude spectra, and their phase spectra were manipulated by using the weighted mean phase (12) technique to generate a set of images characterized by their percent of phase coherence. We processed each image to have 6 different phase coherence values (20%, 25%, 30%, 35%, 40%, and 45%). The range of phase coherence levels was chosen so that subjects performed nearly perfectly at the highest phase coherence but were near chance for the lowest one. Each image subtended 22° × 22° of visual angle.
Behavioral Paradigm.
Subjects performed a simple face-vs.-car discrimination task (6). Within a block of trials, face and car images for the different phase coherences were presented in random order. Each image was presented for 30 ms, followed by an interstimulus interval that was randomized between 1,500 and 2,000 ms, in increments of 100 ms. Subjects were instructed to respond as soon as they formed a decision and before the next image was presented. A total of 54 trials per behavioral condition were presented over 3 blocks (i.e., a total of 648 trials, with each stimulus repeated 3 times). We excluded trials for which subjects failed to respond on time.
Data Acquisition.
EEG data from 60 scalp electrodes were acquired in an electrostatically shielded room (ETS-Lindgren) by using a Sensorium EPA-6 Electrophysiological Amplifier. Three periocular electrodes placed below the left eye and at the left and right outer canthi recorded eye movement data. Data were sampled at 1,000 Hz, and they were referenced to the left mastoid with chin ground. The main data preprocessing steps included a software-based, 0.5-Hz highpass filter to remove DC drifts, and 60- and 120-Hz notch filters to minimize line noise artifacts. Motor response and stimulus events recorded on separate channels were delayed to match latencies introduced by digitally filtering the EEG data. Eye blink and eye movement artifacts were removed by using a principal component analysis-based approach (13).
Single-Trial EEG Data Analysis.
In ref. 6, we used a single-trial analysis of the EEG to discriminate between the experimental conditions (i.e., face vs. car). A linear classifier based on logistic regression was used to find an optimal projection in the sensor space for discriminating between the 2 conditions over a specific temporal window (14, 15). Specifically, we defined a training window starting at a poststimulus onset time τ, with a duration of δ, and used logistic regression to estimate a spatial weighting vector wτ,δ, which maximally discriminates between sensor array signals X for the 2 conditions:

where X is an N × T matrix (N sensors and T time samples). The linear discriminator, through application of w on the N sensors, collapses the N-dimensional EEG space to a 1-dimensional EEG discriminating component space. The result is a “discriminating component” y (indexed by trial), which is specific to activity correlated to the task conditions/labels. For a given trial i, the ith element yi, is a signed quantity, with faces mapped to positive values and cars to negative values. We use the term “component” instead of “source” to make it clear that this is a projection of all of the activity correlated with the underlying source. For our experiments, the duration of the training window (δ) was 60 ms, and the window onset time (τ) was varied across time. We used the reweighted least-squares algorithm to learn the optimal discriminating spatial weighting vector wτ,δ (16). The discrimination vector wτ,δ can be seen as the orientation (or direction) in the space of the EEG sensors that maximally discriminates between the 2 experimental conditions. Thus, the time dimension defines the time of a window (relative to the either the stimulus or response) used to compute this discrimination vector. Given a fixed window width (60 ms in this case), sweeping the training window from the onset of visual stimulation to the earliest RT represents the evolution of the discrimination vector across time. Within a window, at a fixed time, all samples are treated as independent and identically distributed to train the discriminator. Once the discriminator is trained, it is applied across all time so as to visualize the projection of the trials onto that specific orientation in EEG sensor space. A “discriminating component” is defined as one such discrimination vector. To visualize the profile of these components (stimulus or response locked) across all trials, we constructed discriminant component maps. We aligned all trials of an experimental condition of interest to the onset of visual stimulation and sorted them by their corresponding reaction times. Therefore, each row of one such discriminant component map represents a single trial across time [i.e., yi(t)]. Example discriminant component maps are shown in Fig. 1B.
We quantified the performance of the linear discriminator by the area under ROC, referred to as Az, with a leave-one-out approach (17). We used the ROC Az metric to characterize the discrimination performance while sliding our training window from stimulus onset to RT (varying τ). Finally, to assess the significance of the resultant discriminating component, we used a bootstrapping technique to compute an Az value leading to a significance level of P = 0.01. Specifically, we computed a significance level for Az by performing the leave-one-out test after randomizing the truth labels of our face and car trials. We repeated this randomization process 100 times to produce an Az randomization distribution and compute the Az leading to a significance level of P = 0.01.
Fitting the Diffusion Model.
The diffusion model was fit to the data separately for each subject. Accuracy and RT distributions were fit by using a χ2 method. Specifically, the proportions of responses between the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles for correct and error responses were computed from the data and the model, and a SIMPLEX minimization routine was used to adjust parameter values until the proportions best matched each other (see ref. 9 for more details).
The values of the parameters averaged over subjects for the fit to all of the data (and averages for the fits to the 2 halves of the data for the late EEG component in parentheses) were: boundary separation, 0.107 (0.105); starting point, 0.048 (0.44); nondecision component, 0.480 (0.482) s; range in across-trial variability in starting point, 0.019 (0.014); and range in across-trial variability in the nondecision component, 0.189 (0.183) s.
Diffusion Model Simulation and Analysis Details.
Fig. 2C shows the relationship between drift rate and individual simulated RTs for mean drift rate 0.3 and standard deviation in drift rate across trials 0.2. The shortest RTs are approximately the same across all drift rates, whereas the longest RTs increase as drift rate decreases. This occurs because of the high degree of variability in processing (illustrated in Fig. 2A). Thus, a short RT (e.g., 600 ms) is not predictive of the actual drift rate on that trial, but a longer RT will be somewhat more predictive so long as there are no outlier RTs (9). The amount of variability shows that individual RTs cannot be used to index drift rate for individual trials.
To indicate the degree of variability in individual trials in the diffusion model, we generated 100,000 simulated trials from the model by using parameter values from fits to the experiments in ref. 7 with 2 typical drift rates: 0.1 and 0.3. The simulated data were generated, the actual value of drift rate was recorded, and choice and RT were recorded. From these, accuracy values and quantile RTs for the largest half of the drift rates and the smallest half of the drift rates were obtained. The diffusion model was fit to these 2 halves of the simulated data separately. Results showed that the drift rates estimated from fits to the high and low groups of data were 0.491 and 0.143 for drift rate 0.30, and 0.253 and −0.056 for drift rate 0.10. The standard deviation in drift rate across trials (η) used to generate the simulated data was 0.2, and the values recovered from fitting the high and low halves of the data were 0.120 and 0.119 for drift 0.30, and 0.158 and 0.099 for drift 0.10. This shows that if the EEG component was a direct measure of drift rate, we would expect to see an upper limit on the difference in drift rates for the 2 halves of about 0.30, and a reduction in η to about 0.12. These simulations use large numbers of observations to examine what happens theoretically; however, to determine what happens if the number of observations is the same as in the experiment, we ran similar simulations using typical numbers of observations. Results showed a large difference in drift rates (0.371) and a smaller reduction in η (0.16).
Acknowledgments.
This work was supported by National Institute of Mental Health Grant R37-MH4466640 (to R.R.), National Institutes of Health Grant EB004730 (to M.G.P. and P.S.), and by funding from Defense Advanced Research Projects Agency (P.S.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences
Full text links
Read article at publisher's site: https://doi.org/10.1073/pnas.0812589106
Read article for free, from open access legal sources, via Unpaywall:
http://www.pnas.org/content/106/16/6539.full.pdf
Free after 6 months at www.pnas.org
http://www.pnas.org/cgi/content/abstract/106/16/6539
Free after 6 months at www.pnas.org
http://www.pnas.org/cgi/reprint/106/16/6539.pdf
Free after 6 months at www.pnas.org
http://www.pnas.org/cgi/content/full/106/16/6539
Citations & impact
Impact metrics
Article citations
A comparative analysis of face and object perception in 2D laboratory and virtual reality settings: insights from induced oscillatory responses.
Exp Brain Res, 242(12):2765-2783, 12 Oct 2024
Cited by: 1 article | PMID: 39395060 | PMCID: PMC11568981
Confidence control for efficient behaviour in dynamic environments.
Nat Commun, 15(1):9089, 22 Oct 2024
Cited by: 0 articles | PMID: 39433579 | PMCID: PMC11493976
Flexible adaptation of task-positive brain networks predicts efficiency of evidence accumulation.
Commun Biol, 7(1):801, 02 Jul 2024
Cited by: 0 articles | PMID: 38956310 | PMCID: PMC11220037
Modality-specific impacts of distractors on visual and auditory categorical decision-making: an evidence accumulation perspective.
Front Psychol, 15:1380196, 03 May 2024
Cited by: 0 articles | PMID: 38765839 | PMCID: PMC11099231
SHAP value-based ERP analysis (SHERPA): Increasing the sensitivity of EEG signals with explainable AI methods.
Behav Res Methods, 56(6):6067-6081, 07 Mar 2024
Cited by: 2 articles | PMID: 38453828 | PMCID: PMC11335964
Go to all (130) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Neural representation of task difficulty and decision making during perceptual categorization: a timing diagram.
J Neurosci, 26(35):8965-8975, 01 Aug 2006
Cited by: 213 articles | PMID: 16943552 | PMCID: PMC6675324
The Role of Meaning in Visual Memory: Face-Selective Brain Activity Predicts Memory for Ambiguous Face Stimuli.
J Neurosci, 39(6):1100-1108, 12 Dec 2018
Cited by: 7 articles | PMID: 30541914 | PMCID: PMC6363929
Prestimulus alpha power predicts fidelity of sensory encoding in perceptual decision making.
Neuroimage, 87:242-251, 01 Nov 2013
Cited by: 27 articles | PMID: 24185020 | PMCID: PMC3946902
Neurocomputational mechanisms underlying cross-modal associations and their influence on perceptual decisions.
Neuroimage, 247:118841, 21 Dec 2021
Cited by: 0 articles | PMID: 34952232 | PMCID: PMC9127393
Funding
Funders who supported this work.
NIBIB NIH HHS (3)
Grant ID: EB004730
Grant ID: R33 EB004730
Grant ID: R21 EB004730
NIMH NIH HHS (1)
Grant ID: R37-MH4466640





