Abstract
Free full text

A matter of life or death: How microsatellites emerge in and vanish from the human genome
Abstract
Microsatellites—tandem repeats of short DNA motifs—are abundant in the human genome and have high mutation rates. While microsatellite instability is implicated in numerous genetic diseases, the molecular processes involved in their emergence and disappearance are still not well understood. Microsatellites are hypothesized to follow a life cycle, wherein they are born and expand into adulthood, until their degradation and death. Here we identified microsatellite births/deaths in human, chimpanzee, and orangutan genomes, using macaque and marmoset as outgroups. We inferred mutations causing births/deaths based on parsimony, and investigated local genomic environments affecting them. We also studied birth/death patterns within transposable elements (Alus and L1s), coding regions, and disease-associated loci. We observed that substitutions were the predominant cause for births of short microsatellites, while insertions and deletions were important for births of longer microsatellites. Substitutions were the cause for deaths of microsatellites of virtually all lengths. AT-rich L1 sequences exhibited elevated frequency of births/deaths over their entire length, while GC-rich Alus only in their 3′ poly(A) tails and middle A-stretches, with differences depending on transposable element integration timing. Births/deaths were strongly selected against in coding regions. Births/deaths occurred in genomic regions with high substitution rates, protomicrosatellite content, and L1 density, but low GC content and Alu density. The majority of the 17 disease-associated microsatellites examined are evolutionarily ancient (were acquired by the common ancestor of simians). Our genome-wide investigation of microsatellite life cycle has fundamental applications for predicting the susceptibility of birth/death of microsatellites, including many disease-causing loci.
Microsatellites constitute ~3% of the human genome (Lander et al. 2001) and have high mutation rates (Ellegren 2004). Most mutations in microsatellites are insertions/deletions (indels) of their repeated motif due to strand slippage during DNA synthesis (Ellegren 2004). Because of their multi-allelic nature, microsatellites have been widely utilized in population genetic, forensic, and association studies (Ellegren 2004). While many microsatellites have no disease/phenotype association, some of their mutations have crucial phenotypic consequences; e.g., they are associated with over 40 genetic diseases (Pearson et al. 2005).
The evolution of a microsatellite can be represented as a “life cycle” (Amos 1999; Buschiazzo and Gemmell 2006), comprised of (a) birth, when a locus acquires the number of repeats (a threshold) required for high rates of strand slippage; (b) adulthood, characterized by rapid repeat number alterations due to slippage; and (c) death, when a locus degrades to a repeat number below threshold, ceasing to sustain high slippage rates. Elucidating this cycle would expand our understanding of microsatellite mutagenesis and facilitate the development of realistic models of microsatellite evolution (Buschiazzo and Gemmell 2006). Most previous studies have focused on microsatellite adulthood (Buschiazzo and Gemmell 2006; Leclercq et al. 2007; Kelkar et al. 2008; Seyfert et al. 2008), while inquiries into birth and death have been limited (e.g., Messier et al. 1996; Zhu et al. 2000; Wilder and Hollocher 2001).
Microsatellite births can occur because of changes in a generic genomic sequence, e.g., via substitutions or indels at protomicrosatellites (non-repeated sequences that are a few mutations away from becoming microsatellites [Zhu et al. 2000]), slippage-driven expansions of existing repeats with sub-threshold lengths, and/or removals of interruptions from repeated sequences (Messier et al. 1996; Wilder and Hollocher 2001). Births can also occur within transposable elements (TEs)—in particular Short and Long INterspersed Elements (SINEs and LINEs [Arcot et al. 1995; Nadir et al. 1996])—either by the mechanisms listed above, or at arrival. The 3′ poly(A) tail of these TEs and the middle A-stretch of Alus might favor births (Batzer and Deininger 2002). Notably, an [AAG]n microsatellite within the middle A-stretch of an Alu is responsible for Friedrich's ataxia (Saveliev et al. 2003).
The proposed microsatellite death pathways are an interruption of a pure microsatellite via substitutions or insertions, and a decrease in repeat number via deletions (Taylor et al. 1999). The relative frequency of these two mechanisms occurring genome-wide is presently unknown; the latter route has received greater attention, as interruptions of disease-causing microsatellite alleles can decrease severity or prevent disease manifestation (Weisman-Shomer et al. 2000; Matsuura et al. 2006). Experimentally, interruptions have been shown to affect microsatellite mutational behavior in a manner consistent with microsatellite death. Interruptions can reduce DNA polymerase slippage-mediated errors in vitro (Kroutil and Kunkel 1999). Moreover, interruptions reduce the rate of microsatellite mutagenesis in vivo from two- to 90-fold, depending on the type and position of the interruption (Petes 1997; Rolfsmeier and Lahue 2000; Boyer 2008). Thus, in this study, we assume microsatellite interruptions that result in an allele length below the threshold are equivalent to a microsatellite death.
Microsatellites have an uneven distribution across the genome, presumably reflecting regional variation in their birth/death densities (Ellegren 2004). While the lack of microsatellites in coding regions is likely due to selection against frameshift mutations (Li et al. 2004), the heterogeneity in microsatellite density among non-coding regions might be influenced by base composition (Bachtrog et al. 1999), distance to the telomere (Waterston et al. 2002), and recombination rates (Majewski and Ott 2000). For instance, microsatellites form more easily in AT-rich sequences, which have higher substitution and slippage rates (Bacolla and Wells 2004).
Establishing a microsatellite threshold, i.e., the minimal number of repeats required to constitute a microsatellite, is critical for studies of births/deaths. Different approaches (Rose and Falush 1998; Lai and Sun 2003; Kelkar et al. 2010) led to thresholds of seven to nine units and four to eight units for mononucleotide and di- through tetranucleotide microsatellites, respectively. Thus, while most studies concur on the existence of a threshold (but see Pupko and Graur 1999; Leclercq et al. 2010), its exact value is uncertain. Therefore, in the analyses presented below, we used a range of threshold values whenever possible. Moreover, several authors used the term “threshold” to indicate the minimal number of repeats required for slippage to occur (Rose and Falush 1998; Lai and Sun 2003), but recent studies have shown that slippage occurs even at very short repeats (e.g., containing a motif plus its part [Leclercq et al. 2010]). Here, we opt to use the term “threshold” to refer to the transition in mutational behavior of a tandem repeat. We have demonstrated that repeats of a certain length undergo a marked transition in strand slippage rates from background to highly elevated levels, and such acquisition of dynamic mutational activity can be used to define them as microsatellites (Kelkar et al. 2010).
We identified microsatellite births and deaths in three primate genomes and placed such events on a phylogenetic tree using parsimony. With these data in hand, we tackled three previously unresolved questions on a genome-wide scale: (a) What are the relative frequencies of different mutations causing births and deaths? (b) What is the role of transposable elements in these events? (c) Which regional genomic features influence their occurrence? As a result, we comprehensively characterized the birth and death stages of the microsatellite life cycle.
Results
Identification of microsatellite births/deaths
We identified mono-, di-, tri-, and tetranucleotide microsatellites in each of the human, chimpanzee, orangutan, macaque, and marmoset genomes separately, and inferred orthology of microsatellites based on multiple alignments of these genomes (Methods). After filtering for quality and low complexity regions (Methods; Supplemental Table S1), we restricted attention to simple (one repeated motif) and uninterrupted microsatellites, as the mutational dynamics of compound (more than one repeated motif) and interrupted microsatellites is more complex.
Our analyses were carried out separately for a range of repeat numbers (5–10, 3–8, 2–6, and 2–5 repeats for mono-, di-, tri-, and tetranucleotide microsatellites, respectively; Supplemental Table S2) that exceed the range of threshold values proposed previously (Rose and Falush 1998; Lai and Sun 2003; Kelkar et al. 2010). Investigating several thresholds provided us with information about mutational mechanisms operating at sequences with different repeat numbers, focusing on the critical middle range—when repeats acquire their dynamic mutational activity and become mature microsatellites. Thus, in contrast to studies focusing on the mutational pathways from unique to repeated sequence (Zhu et al. 2000), we asked how sequences already possessing a small number of repeats achieve a greater number of repeats, which allows them to undergo high rates of slippage mutations characteristic of mature microsatellites (Kelkar et al. 2010). Hereafter, the threshold values (corresponding to repeat numbers) used for mono- through tetranucleotide microsatellites are indicated as an array (e.g., [9,5,4,3]).
Prior to conducting our analyses, we verified that repeat numbers observed at individual loci in reference genomes were representative of the underlying population variation within the species. To accomplish this, we examined agreement in repeat number between alleles in the reference human genome and modal alleles in 48 humans re-sequenced for ten 0.5-Mb regions as part of the HapMap-ENCODE project (International HapMap Consortium 2003; Kelkar et al. 2010). Within the range of repeat numbers investigated in the present study, the vast majority of mono- and dinucleotide repeat alleles in the human reference sequence were found to coincide with modal alleles in the human populations (Supplemental Fig. S1) (an analogous check could not be performed for tri- and tetranucleotide repeat loci because of their paucity in the re-sequencing data).
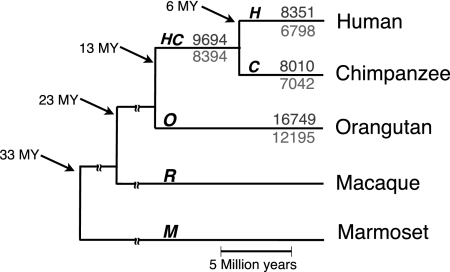
We studied microsatellite births/deaths in the genomes of three focal species—human, chimpanzee, and orangutan—examining orthologous loci where at least one of these species possessed a microsatellite, and at least one of the other two did not. The ancestral state at each such locus was inferred according to microsatellite presence/absence in the outgroup species, macaque and marmoset (loci at which presence/absence differed between macaque and marmoset were discarded; we avoided inferring births/deaths in these genomes due to their relatively high divergence from the focal species). Parsimony on microsatellite presence/absence was used to allocate births/deaths along the human (H), chimpanzee (C), human-chimpanzee common ancestor (HC), and orangutan (O) branches (Fig. 1).
Birth-/death-causing mutations
To attribute “causal mutations” to each birth/death (i.e., mutations required for a repeat to cross the microsatellite threshold), we also utilized parsimony, i.e., we selected mutational pathways requiring the smallest number of steps. We identified births caused by (a) substitutions removing interruptions in phase with the repeat (Fig. 2A); (b) deletions of interruptions out of phase with the repeat (Fig. 2B); and (c) insertions of multiples of a repeated motif (either complete or partial) (Fig. 2C; Supplemental Fig. S1C). We also identified deaths caused by (a) substitutions leading to interruptions in phase with the repeat (Fig. 2E); (b) insertions of interruptions out of phase with the repeat (Fig. 2F); and (c) deletions of multiples of a repeated motif (Fig. 2G). For mononucleotide microsatellites, we could not differentiate between a and b mechanisms for either birth (Fig. 2D) or death (Fig. 2H). More complex scenarios (e.g., Supplemental Fig. S2) usually could be assigned to the mutational types above. Multiple mutations causing a birth/death in the same lineage or in multiple lineages (Supplemental Fig. S2B) were counted independently. Following these rules, we attributed causal mutations to the vast majority of loci (e.g., ~90% for thresholds [9,5,4,3]) (Supplemental Table S2) with a low number of mutations (on average 1.03 per birth/death). Loci for which causal mutations could not be deciphered (Supplemental Fig. 2SD; Supplemental Table S2) were excluded from further analysis.
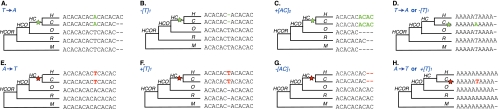
Inference of causal mutation mechanisms for microsatellite birth and death (with thresholds of 5 and 10 repeats for di- and mononucleotide microsatellites, respectively). The lineage experiencing a birth (death) is marked with a green (red) star. (A) Birth by substitution (see Mechanisms of birth/death in Supplementary Information). (B) Birth by non-motif deletion. (C) Birth by motif-insertion. (D) Births resulting from either substitutions or non-motif deletions cannot be distinguished for mononucleotides microsatellites. (E) Death by substitution. (F) Death by non-motif insertion. (G) Death by motif-deletion. (H) Deaths resulting from either substitutions or non-motif insertions cannot be distinguished for mononucleotide microsatellites.
Births were more abundant than deaths at most threshold values examined (Fig. 1; Supplemental Table S2). When the threshold was set to low repeat numbers [≤7,≤5,≤4,≤3], births and deaths along the branches of the phylogeny were proportional to the respective divergence times (Glazko and Nei 2003), suggesting that, at least at the studied loci, these events did not reach saturation (Supplemental Tables S3,S4). For instance, the number of dinucleotide births (with threshold 5) along the H, C, HC, and O branches were 218, 201, 267, and 427, respectively—proportional to the divergence times of 6, 6, 7, and 13 million years (MY).
For each microsatellite motif size and repeat number examined, we computed proportions of different types of causal mutations for births occurring along any of the H, C, O, and HC branches (Fig. 3A–D). We found that the proportion of births due to substitutions (and/or non-motif deletions for mononucleotide microsatellites) consistently decreased as the threshold value used for the analysis increased. In contrast, births due to motif insertions consistently increased with increasing threshold. A marked transition in the relative proportions of birth by substitution versus birth by motif insertion occurred at distinct repeat numbers [7–8 mono; 6–7 di; 4–5 tri; 3–4 tetra]. At all repeat numbers examined, the transition-to-transversion ratios for birth- and death-causing substitutions (Supplemental Table S5) were close to the genome-wide ratio of 2:1 (Zhang and Zhao 2005), attesting to the credibility of our inference. At the thresholds corresponding to the lowest repeat numbers, motif-containing insertions and non-motif deletions contributed to births equally, suggesting low slippage rates. The proportion of non-motif deletions remained constant over all threshold values examined, potentially indicating a mechanism independent from slippage.

Proportion of various causal mutations as a function of the microsatellite threshold for (A) mono-, (B) di-, (C) tri-, and (D) tetranucleotide births; and (E) mono-, (F) di-, (G) tri-, and (H) tetranucleotide deaths. Dashed lines indicate 95% bootstrap confidence intervals that were computed for each threshold by re-sampling the genome-wide set of microsatellite loci with replacement.
Similarly to births, the proportion of deaths (Fig. 3E–H) due to motif deletions consistently increased as the threshold value increased, while that due to substitutions (and/or non-motif insertions for mononucleotide microsatellites) consistently decreased with increasing threshold values. Again, the contributions of motif deletions and non-motif insertions to deaths were comparable at low repeat numbers, while that of non-motif insertions remained approximately constant over all threshold values. However, in contrast to births, deaths were primarily caused by substitutions even at high repeat numbers. Only at the highest repeat numbers examined for mononucleotide microsatellites were motif-containing deletions the dominant mechanism for deaths. Interestingly, 53 of the 8351 human-specific births and 40 of the 8010 chimpanzee-specific births (for thresholds [9,5,4,3]) constituted microsatellite “resurrection” (Harr et al. 2000), i.e., births at loci that formerly experienced death (Supplemental Fig. S2A).
Births/deaths in interspersed repeats
Next, we examined births/deaths within Alu and L1 elements, the most numerous and recently active interspersed repeats in primates. We identified elements present at orthologous locations in (1) all five primate species studied (members of the L1PA7–17, L1PB, AluS, AluJ, and occasionally AluY subfamilies), and (2) human, chimpanzee, and orangutan, but absent from macaque and marmoset (members of the L1PA3–6 subfamilies, and additional recent AluYs). Using the thresholds of [9,5,4,3] and modifying filtering criteria (Methods), we then mapped births/deaths to these elements (Supplemental Table S1) thus restricting the analysis to events that took place after their integration. Here and below we use these thresholds because for these repeat numbers we could decipher the greatest number of causal birth-death mutations (Supplemental Table S2), and at approximately similar repeat numbers we observed a shift in the mutational behavior of repetitive sequences (Fig. 3), as described above, again suggesting the proximity of the real thresholds. We also considered “stationary microsatellites” (born prior to the human-orangutan split, and not experiencing deaths since then). Gene conversion was not the dominant factor in our data set (Supplemental Fig. S3).
Births/deaths in Alus
Alu elements had similar overall numbers of births (2409) and deaths (2390). Interestingly, they were depleted in births and deaths (Alus cover 9% of the aligned human genome but possess only 4% of births and 5% of deaths; Fig. 4A, P < 0.05, χ2-tests) but enriched in stationary microsatellites (6521 loci, 18% of the genome-wide total; Fig. 4A, P < 0.05, χ2-test). These observations held when restricting the comparison to the non-coding non-repetitive (NCNR) part of aligned human genome (Supplemental Fig. S4A).
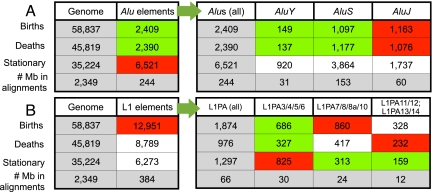
Number of microsatellite births, deaths, and stationary loci mapping to (A) all Alus and different Alu subfamilies, and (B) all L1s and different L1PA subfamilies (thresholds [9,5,4,3]). Gray cells were used to derive expected counts in χ2 tests for over- or under-representation of birth/death/stationary loci in all Alus and L1s (left panels), and in different Alu and L1 subfamilies (right panels). Loci corresponding to green and red colored cells have, respectively, significant under- and over-representation (P-values provided in Supplemental Fig. S10).
First, we investigated the births, deaths, and stationary microsatellites content of the three Alu subfamilies (AluY, AluS, and AluJ, inserted 13–35, 35–55, and 50–65 MYA, respectively [Batzer and Deininger 2002]) in comparison to expectations based on the relative abundance of these subfamilies in the alignments and on the total number of microsatellites belonging to each of the three life cycle stages in all Alus. Older Alus (AluJ elements) were enriched and younger Alus (AluSs and AluYs) depleted in births and deaths (Fig. 4A, P < 0.05, χ2-test), while the distribution of stationary microsatellites reflected expectations (Fig. 4A, P benchmarked at 0.05, χ2-test).
Second, we asked how births, deaths, and stationary microsatellites were distributed along the length of Alu consensus sequence (Fig. 5A–C). Births/deaths of AT-rich microsatellites were concentrated at the 3′ poly(A) tail and the middle A-stretch. Stationary AT-rich microsatellites were located at the poly(A) tails of younger (AluY and AluS) elements but were more evenly distributed between the two A-rich regions of older (AluJ) elements. Births/deaths of GC-rich microsatellites occurred at the protomicrosatellite “5′-GGGAGGCGGAGG-3′” (positions 207–218 bp) in AluS elements (Fig. 5A); AluYs have the same protomicrosatellite, but probably need additional time to accumulate the mutations. AluJ elements exhibited few births/deaths here, as their protomicrosatellite (“AGGAGTTCGAGG”) requires more mutations to become a microsatellite.
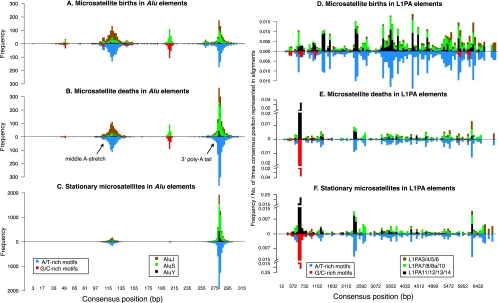
Frequencies of microsatellite births (A), deaths (B), and stationary loci (C) in different Alu subfamilies along the Alu consensus sequence divided into 20-bp bins, and “frequency per alignment count” (see Methods) of microsatellite births (D), deaths (E), and stationary loci (F) in L1PA subfamilies along the L1PA consensus sequence divided into 60-bp bins (and corrected for L1PA sequence representation in alignments). In each plot, bars are decomposed and color-coded by different Alu/L1 subfamilies and by GC richness of the corresponding microsatellites (above and below horizontal midline, respectively).
Births/deaths in L1s
Whereas Alus had similar numbers of births and deaths, the more AT-rich L1 elements (Szak et al. 2002) had more births (12,951) than deaths (8789). L1s were enriched in births, but similar to the overall genome (or to its NCNR portion) in deaths and stationary microsatellites (L1s covered 16% of the aligned human genome and harbored 22% of births, 19% of deaths, and 17% of stationary loci; Fig. 4B; Supplemental Fig. S4B, χ2-tests benchmarked at P = 0.05).
To investigate births/deaths across L1PA elements of different ages, we created three groups with integration times similar to those of Alu subfamilies: (a) L1PA3–L1PA6 (13–26 MY); (b) L1PA7–L1PA10 (31–46 MY); and (c) L1PA11–L1PA14 (53–60 MY) (Khan et al. 2006). Younger L1PAs were depleted in births (P < 0.05, χ2-tests) and older ones (not always significantly) enriched in deaths (Fig. 4B). Unlike in Alu elements, stationary microsatellites were overrepresented in younger and underrepresented in older L1PAs (Fig. 4B, P < 0.05, χ2-test). Similar trends were observed for the comparisons using only the 3′ terminal 300 bp of L1PAs (Supplemental Fig. S5).
After normalizing for the 5′ truncation of L1s (Boissinot et al. 2001) in the genome (Methods), we observed that AT-rich microsatellite births, deaths, and stationary loci in L1PAs of different ages were evenly distributed along the consensus sequence, with a moderate increase from 5′ to 3′ end (Fig. 5D–F). An enrichment in stationary loci and deaths for GC-rich microsatellites occurred near L1PA consensus position 525, which harbors a microsatellite [GCCT]3—suggesting ancient microsatellite birth-death activity at this position. Similar trends were observed for older L1s (Supplemental Fig. S6).
Microsatellite births/deaths in coding regions
Using thresholds [9,5,4,3], a total of 157 births, 174 deaths, and 636 stationary microsatellites were identified within coding exons of the three focal primate genomes (Supplemental Table S6). Protein-coding exons were depleted in births/deaths and enriched in stationary loci compared to either the whole aligned human genome or its NCNR portion (Supplemental Fig. S3C; P < 0.05, χ2-tests). Several deaths (37 instances) took place at regions encoding polypeptide runs, and in particular in poly-Glu (10 instances) and poly-Pro (5 instances) tracts. Most births (135) and deaths (157) were caused by substitutions; 50% of birth- and 75% of death-causing substitutions were synonymous (Supplemental Table S6). Nonsynonymous birth/death-causing substitutions usually led to conservative amino acid replacements (e.g., Glu-Asp and Ala-Val) (Supplemental Table S7). Most birth/death-causing indels were within trinucleotide microsatellites; frameshifting indels leading to births/deaths of mono-, di-, and tetranucleotide microsatellites were extremely rare (Supplemental Table S6).
Microsatellite births/deaths at disease-associated loci
We aimed to determine whether the microsatellite loci associated with human diseases were recent evolutionary acquisitions or were present in the ancestors of the primate species we examined. Among the 40 microsatellite loci known to be associated with (or to be candidate loci for) human genetic diseases (Pearson et al. 2005), we could only examine 17 loci located within single alignment blocks and surrounded by unique flanking sequences (see Methods). The majority (15 out of 17) of these loci had mature alleles (i.e., above the range of threshold values) in all primate species we considered (Supplemental Fig. S7). At the folate-sensitive fragile site FRA10A locus, we found a gradual expansion of a [GCC]n repeat to lengths above the threshold: from two in marmoset to five in orangutan to seven and eight repeats in chimpanzee and humans, respectively. This was the only case of a microsatellite birth at a disease-associated locus in our data set. For the ATXN8 opposite strand (spino-cerebellar ataxia 8) locus (ATXN8OS), all five primates (including human) possessed just two copies of the [CTG] motif, which is below the threshold to be considered a microsatellite (however, this locus expands above the threshold in patients with the disease [Pearson et al. 2005]).
Of the 15 mature microsatellite loci identified, for eight loci (PABPN1 [OPMD], COMP, FXN [FRDA], ATXN8OS [SCA8], PPP2R2B [SCA12], HOXD13, RUNX2 [CBFA1], and FRA11B) similar allele lengths were present in all species. In contrast, seven loci (JPH3 [HDL2], ATN1 [DRPLA], MAB21L1, ATXN7, ATXN1 [SCA1], ATXN2 [SCA2], and TBP [SCA17]) displayed species-specific differences in both allele length and repeat purity (Supplemental Fig. S7). Intriguingly, the human alleles were usually the longest alleles in this set of loci. For example, the MAB21L1 allele is 19 repeat units in humans but 10 units or less in other primates, while the ATN1 (DRPLA) locus in humans is 15 units in humans but 11 units (with an interruption) in orangutan.
Influence of regional genomic features on microsatellite births/deaths
We observed substantial genome-wide variation and co-variation in birth and death densities (Supplemental Fig. S8). To study the effect of regional genomic features on this variation, we contrasted “event windows” (with one or more birth and/or death) and “control windows” (devoid of such events) using multiple logistic regression (Supplemental Fig. S9; Supplemental Table S8) (few windows contained only births or only deaths, as their densities covary, and thus such windows could not have been reliably contrasted). Several genomic predictors and 0.1-, 1-, 10-, 50-, and 100-kb windows were considered (see Methods). The best fit was obtained for 0.1-kb windows, but explained only 7% of the variation in birth/death activity. We also considered regressions contrasting control windows with windows containing a large number (≥4) of births/deaths. Here, the best fit (obtained for 100-kb windows) explained ~13% of the variation.
GC and Alu content were negative predictors, whereas L1 content, substitution rates, and protomicrosatellites were positive predictors of microsatellite births/deaths (Supplemental Fig. S9). The magnitude of the positive contribution of substitution rate was similar across all window sizes. Protomicrosatellites and GC content were more important at small windows. In contrast, Alus' negative contribution increased with window size and was largely driven by younger subfamilies (Supplemental Fig. S10). L1 content was significant only at 1- and 10-kb windows.
Discussion
In this study we unveiled the intricacies of microsatellite birth and death in three primate genomes. These events have been previously understudied due to the lack of a framework for identifying underlying mutations (Buschiazzo and Gemmell 2006), and to the error-proneness of alignments in their proximity. We circumvented these issues by considering (1) parts of the genomes with high sequence complexity and quality; (2) loci with properly aligned flanks; and (3) births/deaths over a relatively short evolutionary time. The proportionality between birth/death numbers and species divergence times suggests that saturation did not significantly affect our inference.
Birth-/death-causing mutations
We found that at thresholds with small repeat numbers the majority of births took place via interruption removal by substitution. However, the dominant mechanism of births at thresholds with high repeat numbers was insertion of the repeated motif, in line with a known positive relationship between repeat number and slippage rate (Ellegren 2004). The observed transition in the relative frequency of substitution vs. slippage mutations is in agreement with a small-scale study of disease-causing mutations (Zhu et al. 2000) and a recent human-chimpanzee analysis (Pumpernik et al. 2008). We observed similar trends in the mutational dynamics of di-, tri-, and tetranucleotide microsatellites when considering overall repeat length, as opposed to repeat number. For instance, the transition in the relative importance of substitutions vs. motif insertions for births occurs at ~10–16 bp (Fig. 3). Mononucleotides differ, as the shift in birth mechanisms occurs at a smaller length for mononucleotide microsatellites, in agreement with higher rates of slippage for these repeats (Schlötterer and Tautz 1992). The similarity among di-, tri-, and tetranucleotide repeats in mutational dynamics and the transition at a specific length might be a reflection of a functional microsatellite threshold, defined as alterations in the mutational spectrum. Thus, the increased proportion of “births” by motif insertion that we detected at repeat lengths above the transition point may actually reflect mutations within mature (early adulthood) microsatellites. This interpretation is consistent with the importance of repeat length in defining a microsatellite threshold (Kelkar et al. 2010), as well as in specifying divergence (Kelkar et al. 2008) and diversity (Payseur et al. 2011) levels for mature microsatellites.
In contrast to births, microsatellite deaths at thresholds of all repeat numbers were predominantly caused by substitutions. (Mononucleotides are an exception, as motif deletions dominated at thresholds of 10 repeats or longer.) Importantly, experimental studies have demonstrated that microsatellite interruptions result in lower mutation rates in vivo (Petes 1997; Rolfsmeier and Lahue 2000; Boyer 2008), and in decreased strand-slippage errors in vitro (Kroutil and Kunkel 1999). The differential mechanisms observed for births and deaths may be explained by differences in size of the substitution target. For microsatellite birth via interruption removal, the target is a single nucleotide, which needs to be replaced by the correct nucleotide, while for microsatellite death via interruption, the target is the whole repeat, with no restriction on the substituting nucleotide. These results corroborate the few previously studied cases of microsatellite deaths (e.g., Taylor et al. 1999), wherein nucleotide substitutions played a key role in repeat degradation.
The inference of individual indel events in distant evolutionary lineages using parsimony is potentially complicated by high indel rates that may increase the chances of homoplasy. However, the effect of homoplasy on our inferences concerning mutational pathways that lead to microsatellite births/deaths is unlikely to be substantial because (1) most of the loci we considered are relatively short (Estoup et al. 2002); (2) we did not observe a saturation in the number of microsatellite births/deaths, again arguing against sizeable homoplasy; and (3) for most births/deaths, a homoplastic scenario would require identical substitutions or non-motif-containing indels (Fig. 3) occurring simultaneously at orthologous loci in multiple lineages, which is highly unlikely given the low rates of these mutations.
Transposable elements' contribution
The previously proposed importance of TEs in microsatellite genesis (Arcot et al. 1995; Nadir et al. 1996; Batzer and Deininger 2002; Buschiazzo and Gemmell 2006) was evaluated here on a genome-wide basis for the two most copious and recently active TE groups—Alus and L1s. Microsatellites can be born in TEs either concurrent to or following their integration. While we focused on the latter, our analysis of stationary microsatellites also provides information about the former.
Indeed, our results indicate that TEs play a pivotal role in the microsatellite life cycle. Remarkably, 36.3% of microsatellites (with thresholds [9,5,4,3]) present at orthologous positions in human, chimpanzee, and orangutan were likely acquired due to insertion of TEs “upon arrival” (12,794 out of 35,224 loci) (Fig. 4), with approximately equal contribution of Alus and L1s (6521 and 6273 loci, respectively). Additionally, among microsatellite births and deaths occurring in the human, chimpanzee, orangutan, or human-chimpanzee common ancestor lineages, 26.3% of births (15,360 out of 58,837) (Fig. 4) and 24.3% of deaths (11,179 out of 45,819) (Fig. 4) occurred within TEs following their integration. While interrupted microsatellites were not considered in the present study, our preliminary results indicate that such microsatellites are enriched in TEs. In fact, although Alus and L1s together cover ~25% of the aligned human genome, they harbor as many as 41% of interrupted microsatellites (126,297 of the total of 293,972 identified; P < 0.05, χ2-test), implying that TEs are important players at all stages of the microsatellite life cycle.
Based on the distribution of births, deaths, and stationary loci along the length of Alu elements in younger and older subfamilies, we propose the following model: Alus give birth to AT-rich microsatellites at 3′ ends upon integration because their 3′ poly(A) tails, essential for transposition (Arcot et al. 1995; Nadir et al. 1996; Roy-Engel et al. 2002), frequently possess long, uninterrupted [A]n stretches. As mutations accumulate in older Alus, 3′ poly(A) tail microsatellites die due to interruptions and/or deletions, while the middle A-stretch becomes the hotbed for births and, subsequently, deaths. As a result, while most stationary microsatellites in young Alus are found in the 3′ poly(A) tails, the corresponding region in older Alus has fewer microsatellites. Integrated Alus remain an important source of microsatellites [in particular at their 3′ poly(A) tails and middle A-stretches], but are depleted in births in comparison to the genome overall, likely due to their overall GC richness. Remarkably, our results indicate that in Alus microsatellite births and deaths tend to balance out, keeping the overall number of microsatellites constant over time.
A different model emerges for L1s. They frequently give birth to microsatellites upon and after their integration; however, unlike Alus, L1s do so evenly throughout their length, potentially because their whole sequence [and not just their 3′-poly(A) tails (Boeke 1997)] is AT-rich (Szak et al. 2002). Relatedly, compared with the genome overall, L1s are enriched in births. Since L1s are on average older than Alus, they may have experienced a substantially greater number of substitutions and indels, generating more protomicrosatellites. Interestingly, we have some evidence that microsatellites in L1PAs are being eroded, likely by an excess of deaths over births; older L1PA subfamilies are depleted in stationary microsatellites and enriched in deaths.
The regional genomic context of births/deaths
The role of TEs in the microsatellite life cycle is further confirmed by our regressions. Consistent with their AT richness (Szak et al. 2002), L1s show a positive association with births/deaths, but only at 1- and 10-kb windows, likely due to their size (average ~1 kb, with some reaching 6–7 kb [Jurka et al. 2005]). Alus have a negative association with births/deaths, congruous with their GC richness. Since composition is proxied by other predictors in our fits, the observed contributions of L1s and Alus may capture additional effects. For instance, TEs are hotspots for non-allelic homologous recombination (Roy-Engel et al. 2002), potentially affecting microsatellite birth/death rates at adjacent loci (Jakupciak and Wells 2000).
Our regressions indicate a dependence of microsatellite birth/death activity on sequence composition, as captured by GC and protomicrosatellite content. Low GC content and an abundance of protomicrosatellites facilitate births/deaths, likely because such sequences have high rates of slippage (Bacolla and Wells 2004) and substitution (Arndt et al. 2005), and in agreement with a recent analysis of microsatellite abundance in protist genomes (Tian et al. 2011). We also observe a positive relationship between births/deaths and substitution rate. High local substitution rate facilitates “tinkering” with AT-rich and/or protomicrosatellites; this might result in microsatellite births, and increase the chances of interruptions in existing microsatellites, leading to their deaths (Santibanez-Koref et al. 2001).
Notwithstanding these results, the low explanatory power of our regressions suggests a limited dependence of births/deaths on regional genomic features, echoing a previous finding for mature microsatellites (Kelkar et al. 2008). However, birth/death activity might associate with other genomic features (e.g., differential efficiency of the repair), which need to be considered in future studies.
Births/deaths in coding regions and at disease-associated loci
We observed an overall deficiency of births/deaths in protein-coding exons, suggesting selective resistance to such changes within these evolutionarily constrained regions. Births/deaths by motif indels, which may involve frameshift mutations at mono-, di-, and tetranucleotide microsatellites, were particularly rare. In line with previous observations (Li et al. 2004), we found a significant enrichment of stationary microsatellites in coding exons compared with the rest of the genome. Thus, microsatellites play a critical role in encoding proteins, particularly their amino acid repeats. Note that most such repeats are encoded by interrupted microsatellites (Mularoni et al. 2010), which were not studied here.
Interestingly, the majority of the disease-associated microsatellite loci we analyzed, many of which lie within or in close proximity of coding regions, were found to be mature microsatellites (above the threshold length) in all primate species examined. This suggests that such loci are ancient, i.e., were born in a common ancestor of simians. For seven of the disease-associated microsatellite loci we examined, the human allele was longer and/or more pure than the alleles present in other primates. Both of these features, length and purity, directly affect the likelihood that the microsatellites will mutate. Thus, alleles such as ATN1 and MAB21L1 in the human genome are poised to increase in size toward a pathologic length in subsequent generations. Other loci, such as ATXN1 and ATXN2, are longer in humans than other primates, but are present as interrupted alleles in the reference genome. Such interruptions have been shown to decrease the propensity for such alleles to expand (Pearson et al. 1998). However, significant inter-individual variations in the patterns of allele interruption have been described for these loci (Sobczak and Krzyzosiak 2004), suggesting that some human populations may be more predisposed toward allele expansion to pathologic lengths. The future identification of additional microsatellite loci that are longer (and therefore more mutable) in humans than other primate species may assist in the association of new microsatellite loci with disease states.
The time scale of the microsatellite life cycle
The analyses presented here also shed light on the time scale of the microsatellite life cycle. The striking enrichment in the frequency of microsatellite deaths at the central A-rich region of the ~55-MY old AluJ vs. the ~35-MY old AluS subfamily elements indicates that the cycles of microsatellite births and deaths take place over tens of millions of years, although many longer microsatellites may persist for hundreds of millions of years (Buschiazzo and Gemmell 2010). Once born, microsatellites might be sustained for long evolutionary times. However, we observed only a few instances of microsatellite rebirth—suggesting that, once degraded, it might be difficult for sequences to resurrect from their hypo-mutating phase into dynamic microsatellites.
From the number of microsatellite births and deaths taking place along the four branches of interest (Fig. 1), we computed the average birth and death rates of microsatellites to be 1.4 × 10−11 and 1.1 × 10−11 per base per generation, respectively (taking into account the total length of the aligned portion of the human genome, and assuming a generation time of 20 yr). In agreement with a previous prediction (Buschiazzo and Gemmell 2006), microsatellite birth rates are higher than death rates, leading to the enrichment of microsatellites observed in primate genomes. Also, the rates of microsatellite births and deaths are lower than primate substitution or non-microsatellite indel rates (on the order of 10−8 and 10−9 mutations per locus per generation [Nachman and Crowell 2000]). This is not surprising, as de novo births/deaths (apart from births in newly integrating TEs) are restricted only to the existing protomicrosatellite/microsatellite sequences in the genome. Birth and death rates are also several orders of magnitude lower than the rates of indel mutations at mature microsatellites (10−2 to 10−5 mutations per locus per generation [Weber and Wong 1993; Boyer and Farber 1998; Kayser et al. 2000; Ellegren 2004]). Thus, microsatellite births and deaths are indeed long-term alterations in the evolutionary fates of repetitive sequences. Note also that, due to our stringent filtering, the microsatellite birth and death rates reported here are likely to be underestimates.
Implications for the microsatellite life cycle in primate genomes
Our results indicate that microsatellites arise primarily by substitutions of interrupting nucleotides, and secondarily by slippage-induced expansions. With their long 3′ poly(A) tails, and other AT-rich regions, TEs furnish the genome with novel microsatellites upon and after integration. Slippage-driven indel mutations at mature microsatellites largely depend on their intrinsic features (motif size, motif composition, and repeat array number [Kelkar et al. 2008]). Over time, mature microsatellites experience substitutions and (more rarely) large deletions. These changes shorten uninterrupted repeats, hampering slippage and hence a microsatellite's ability to actively expand through motif insertions—eventually leading to death.
Our study identified mutations leading to microsatellite births/deaths and provided information on local genomic environments affecting them. This can assist in locating hotbeds of microsatellite birth/death activity in individual human genomes and in the genomes of other species—which is of paramount significance, as microsatellite births/deaths are expected to influence mutagenesis of the flanking sequences (Webster and Hagberg 2007), to have functional implications when located within coding exons, and to modify expression levels when located in proximity of genes (e.g., Hammock and Young 2005). Moreover, our results are instrumental in assessing the probability of a locus to bear novel, potentially disease-causing microsatellites, and of a microsatellite to acquire interruptions leading to its death and thus to a stabilization of the locus (and thus possibly to reduction of disease manifestation [Weisman-Shomer et al. 2000; Matsuura et al. 2006]).
Methods
Identification of orthologous microsatellites
We used Sputnik (http://espressosoftware.com/sputnik/index.html) and custom Perl scripts to extract orthologous microsatellites from MULTIZ (Blanchette et al. 2004) alignments of human (hg18), chimpanzee (panTro2), orangutan (ponAbe2), macaque (rheMac2), and marmoset (calJac1). The following Sputnik parameters were used for our microsatellite search: (1) ERROR_MATCH_POINTS = −1000; (2) MATCH_MIN_SCORE = 3; (3) EXACT_MATCH_POINTS = 1; (4) MIN_UNIT_LENGTH = 1. These parameters allow Sputnik to identify pure repeats of very small lengths; i.e., with at least 5, 6, 7, and 8 bp of mono-, di-, tri-, and tetranucleotide repeats, respectively. To identify interrupted microsatellites, the extracted pure microsatellite sequences were further extended into flanking sequences to include interruptions whenever possible—the maximum allowed interruption length was equal to the length of the microsatellite motif, and the extension of the microsatellite was required to contain at least one complete repetition of the motif. To identify compound microsatellites, we joined adjacent microsatellites separated by at most one non-microsatellite nucleotide. Interrupted and compound microsatellites thus found were later removed from our analysis (Supplemental Table S1). We tested other microsatellite finding programs, such as IMEx (Mudunuri and Nagarajaram 2007), Tandem Repeat Finder (Benson 1999), and ScoROKO (Kofler et al. 2007) in our previous studies, verifying that they provide largely similar results (Kelkar et al. 2008).
We filtered out loci that, in any species (a) had other microsatellite(s) in their 25 bp up- and downstream neighborhood (the central as well as neighborhood loci were removed, to minimize influences among neighboring loci); (b) possessed nucleotides with phred score <20 within microsatellites or within flanks (10 bp up- and downstream); (c) had 20 bp up-/downstream low-complexity flanks (i.e., flanks completely lacking one of the four nucleotides or harboring a six-repeat-unit long mononucleotide or four-repeat-unit long dinucleotide repeat); (d) had flanks' sequence identity <85% in relation to any other species analyzed (to ensure orthology of microsatellites as well as to remove improperly aligned orthologous loci) (Supplemental Table S1). For the microsatellite-containing loci retained after filtering, in rare cases if an identical nucleotide not belonging to a microsatellite motif was found in more than one species, and its immediately flanking motifs were also identical, we re-aligned the nucleotide to the same alignment positions. In these cases, gaps were introduced as necessary within the motif sequences on one of the sides (upstream or downstream) of the non-native nucleotide, minimizing the number of introduced gaps. This “adjustment” of the original multiZ alignments was necessary to avoid overestimating the number of substitutions and/or non-motif indels per microsatellite locus, but was required only for a small fraction of loci (5%).
Population variation at microsatellite loci
To test whether repeat numbers gathered from the reference sequences represented the variation within the species, we investigated human intra-specific sequence variation at repeat loci, using information obtained from the HapMap-ENCODE re-sequencing project (International HapMap Consortium 2003). Here, 48 unrelated individuals from three different populations—Yorubans (YRI), Europeans (CEU), and Eastern Asians (CHB+JPT)—were re-sequenced at ten 0.5-Mb ENCODE regions. In these ENCODE regions, 165 mono- and 16 dinucleotide repeat loci were found to be stationary or to harbor microsatellite births or deaths in the present analysis. At each of these loci, we identified the modal allele (i.e., the most frequent allele among the re-sequenced individuals) following the protocols in Kelkar et al. (2010) and compared it with the allele present in the reference human sequence (hg18).
Identification of births/deaths and mutations causing them
Using microsatellite presence/absence, their births/deaths and causal mutations along the H, C, HC, and O branches were inferred by parsimony (Fig. 2). For loci at which the presence/absence of information indicated a birth or death event, inference of the mutational pathway was carried out in the following four steps. (1) At each microsatellite locus, we identified nucleotides not native to the microsatellite sequence and alignment gaps in all the species. (2) Using sequence alignments at these positions, we inferred single nucleotide substitutions, insertions, and deletions sequentially from the outer nodes of the phylogenetic tree to the deeper nodes, by the principle of maximum parsimony. This takes into account the phylogenetic position of the events and uses information from the respective outgroup species (macaque and marmoset for the HC–O node and orangutan, macaque, and marmoset for the H–C node; we only considered loci at which both macaque and marmoset either possessed or did not possess a microsatellite). We then used the parsimony-derived ancestral sequences thus inferred at evolutionarily recent nodes for inference on mutations along deeper lineages within the tree. (3) Among all mutations identified, we only considered those that allowed a sequence to cross a particular threshold. For instance, while considering microsatellite birth in Figure 2A, we focused on the interruption removal in the HC lineage, while ignoring repeat number differences between human and chimpanzee. (4) We placed each mutation event into one of the classes illustrated in Figure 2. At each threshold, we obtained the 95% confidence intervals for the observed genome-wide proportions of all these mutation classes by generating 1000 bootstrap samples (re-sampling with replacement) of the genome-wide set of microsatellite loci, and computing the 2.5th and 97.5th percentile proportion values.
Microsatellite births inferred to have taken place by substitution of interrupting nucleotides (for instance, Fig. 2A) may also be caused by a slippage-related deletion involving the interrupting nucleotide and, sometimes, flanking bases (in Fig. 2A, the deletion of “CT”). However, given that slippage-related indels are rare in interrupted microsatellites (Brinkmann et al. 1998; Boyer et al. 2002; Sibly et al. 2003), and that slippage-related insertions were found to be rare at small repeat numbers in our own data (Fig. 3), we concluded that the most likely mechanism involved in interruption removal was substitution.
For the majority of microsatellites, the inferred mutations agreed with microsatellite birth/death inferences based on presence/absence (Supplemental Table S2); in a number of cases (e.g., ~10% for thresholds [≤9, ≤5, ≤4, ≤3]), where the presence/absence-based inference was conflicting with the mutational pathway inference, the birth/death scenario revealed by the mutational pathway was given priority. All such cases involved multiple mutations in the same locus. For instance, if at a particular locus marmoset, rhesus and orangutan had an [AC]i microsatellite with repeat numbers above the threshold (e.g., five repeats), and at the orthologous position, the chimpanzee non-microsatellite sequence was [AC]4TC[AC]2 and the human sequence was [AC]4TC[AC]7, then based on microsatellite presence/absence we would infer a death along the chimpanzee lineage. However, the mutational pathway analysis revealed the existence of two separate birth/death events: an A→T substitution leading to a death in the human-chimpanzee lineage, followed by motif insertions leading to a birth in the human lineage. For loci with multiple birth/deaths along different lineages (0.1% of all loci), each event at a locus was counted independently.
Births/deaths in transposable elements (TEs)
RepeatMasker (http://www.repeatmasker.org/) hg18 SINE, LINE, and coding region (refseq) annotations were obtained from the UCSC Genome Browser (http://genome.ucsc.edu/). Consensus sequences for TE subfamilies were obtained from RepBase (Jurka et al. 2005). Portions of the genome that did not overlap with TEs and coding exons were classified as non-coding non-repetitive (NCNR). Microsatellites whose coordinates intersected with those of the TEs were identified as TE microsatellites loci. The position of each TE microsatellite relative to the consensus sequence of its enclosing TE's subfamily (i.e., the consensus-relative position) was determined. For microsatellite loci within Alus, their position relative to the universal Alu consensus sequence (Fig. 5A) was determined by first aligning (using ClustalW with default options) the enclosing Alu's subfamily consensus sequence to the universal primate Alu consensus sequence obtained from RepBase (Jurka et al. 2005). A similar procedure was implemented for microsatellites identified within L1PA elements. Since the focus here is on the role of Alu's and L1's in microsatellite births/deaths (and not on mutational pathways leading to them), we relaxed our filtering criteria by allowing inter-microsatellite distances >10 bp, and permitting lower sequence identity (down to 80%) of flanking sequences between aligning species (Supplemental Table S1). χ2-tests for motif abundance in TEs of different ages were implemented in R (http://www.r-project.org/). P-values were Bonferroni-corrected. To account for the 3′ biased representation of L1s (Boissinot et al. 2001), birth/death frequencies in 60-bp bins of the consensus L1 sequence were divided by the number of times each such bin occurred in the alignments (Fig. 5B).
Evolutionary history of disease-causing microsatellite loci
We used Galaxy (http://galaxy.psu.edu) to obtain alignments of 40 disease-associated loci (and their 10 bp upstream and 10 bp downstream flanking sequences) using their previously published hg18 coordinates (Pearson et al. 2005). We identified 17 loci that (a) were present in single alignment blocks, (b) were flanked by at least 10 bp of non-microsatellite sequences upstream as well as downstream, and (c) were represented in at least three of the hg18, panTro2, ponAbe2, rheMac2, and calJac1 genomes. The other 23 loci were excluded primarily because they contained very long microsatellites broken between alignment blocks and thus we could not infer their lengths accurately.
Multiple logistic regression analysis
Multiple logistic regressions were conducted in R (http://www.r-project.org/) to contrast births/deaths (event) vs. control windows. For every window size considered, event windows were positioned to maximize the number of events per window (e.g., if two events were <1 kb apart, and the window size used was 1 kb, both events were included into a single event window of 1 kb in size). Control windows were placed randomly, but at least 100 bp away from the boundary of any event window, and were equal in number to the event windows. For each window size and each window, we computed the following predictors: recombination rate, recombination hotspot density, coding region content, CpG islands content, SINE content, LINE content, distance from a telomere, human-orangutan substitution and indel rates, and the fraction of the window covered by protomicrosatellites. Human fine-scale regional recombination rates and hotspot locations (Myers et al. 2005) were used to compute, for each window, average recombination rate, and hotspot density. The hg18 annotations for coding regions, CpG islands, SINEs, and LINEs were obtained from the UCSC Genome Browser and used to compute the corresponding contents per window. Distance from telomeres was computed using the UCSC Genome Browser (Fujita et al. 2010) annotations for hg18. Human-orangutan substitution and indel rates were chosen over human-chimpanzee substitution rates to minimize ancestral polymorphisms' influences on these estimates. An additional predictor calculated in each window was the fraction of the window covered by proto-microsatellite sequences (stretches of sequence at least 10 bp in length, of which at least eight are occupied by the same nucleotide; such sequences may give birth to the most common microsatellites). For each window, the number of nucleotides (used to calculate predictor densities and contents) was measured by subtracting from the window size (either 0.1 Kb, 1 Kb, 10 Kb, 50 Kb or 100 Kb) the number of hg18 nucleotides not covered by alignments, and the number of aligned hg18 nucleotides covered by microsatellite loci that were filtered out during our orthologous microsatellite search (see Results).
Filtering steps were implemented before running the regressions. In particular, only event and control windows with high alignment coverage (>95% of window length) were used. For each regression, we also discarded extreme outliers with high influence (Cook's distance of 1 or greater). After filtering, we selected a satisfactory logistic regression by sequentially eliminating predictors based on their individual contributions to model performance, Akaike Information Criterion scores (with/without each predictor) and predictors' variance inflation factors (which were required to be <10 [Kutner 2005]). The performance of a logistic regression is measured as the share of deviance explained, (Do – Dm)/Do, where Do indicates the null deviance, and Dm the residual deviance carried by the model. Accordingly, the individual contribution of a predictor within a model is measured as ([Do – Dm] − [Do – Dm{−}])/(Do–Dm), where Dm and Dm{−} are, respectively, the residual deviances carried by the model and by the reduced model obtained removing the predictor in question.
Galaxy tools
Our completely reproducible computational pipeline is available in the “Regional variation” toolset of Galaxy test site (usegalaxy.org), and can be used to investigate births/deaths for in genome-wide alignments. The tool “Extract Microsatellite information” generates a summary of orthologous microsatellites, while the tool “Extract Microsatellite births and deaths” identifies births and deaths.
Acknowledgments
We thank Astrid Roy-Engel and three anonymous reviewers for important suggestions, and Guruprasad Ananda for assistance with Galaxy. This project was supported by NIH grant R01-GM087472.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.122937.111.
References
- Amos W 1999. A comparative approach to study the evolution of microsatellites. In Microsatellites: Evolution and applications (ed. Goldstein DB, Schlötterer C), pp. 60–79 Oxford University Press, Oxford [Google Scholar]
- Arcot SS, Wang Z, Weber JL, Deininger PL, Batzer MA 1995. Alu repeats: A source for the genesis of primate microsatellites. Genomics 29: 136–144 [Abstract] [Google Scholar]
- Arndt PF, Hwa T, Petrov DA 2005. Substantial regional variation in substitution rates in the human genome: Importance of GC content, gene density, and telomere-specific effects. J Mol Evol 60: 748–763 [Abstract] [Google Scholar]
- Bachtrog DD, Weiss SS, Zangerl BB, Brem GG, Schlötterer CC 1999. Distribution of dinucleotide microsatellites in the Drosophila melanogaster genome. Mol Biol Evol 16: 602–610 [Abstract] [Google Scholar]
- Bacolla A, Wells RD 2004. Non-B DNA conformations, genomic rearrangements, and human disease. J Biol Chem 279: 47411–47414 [Abstract] [Google Scholar]
- Batzer MA, Deininger PL 2002. Alu repeats and human genomic diversity. Nat Rev Genet 3: 370–379 [Abstract] [Google Scholar]
- Benson G 1999. Tandem repeats finder: A program to analyze DNA sequences. Nucleic Acids Res 27: 573–580 [Europe PMC free article] [Abstract] [Google Scholar]
- Blanchette M, Kent WJ, Riemer C, Elnitski L, Smit AF, Roskin KM, Baertsch R, Rosenbloom K, Clawson H, Green ED, et al. 2004. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res 14: 708–715 [Europe PMC free article] [Abstract] [Google Scholar]
- Boeke JD 1997. LINEs and Alus—the polyA connection. Nat Genet 16: 6–7 [Abstract] [Google Scholar]
- Boissinot S, Entezam A, Furano AV 2001. Selection against deleterious LINE-1-containing loci in the human lineage. Mol Biol Evol 18: 926–935 [Abstract] [Google Scholar]
- Boyer JC, Farber RA 1998. Mutation rate of a microsatellite sequence in normal human fibroblasts. Cancer Res 58: 3946–3949 [Abstract] [Google Scholar]
- Boyer JC, Yamada NA, Roques CN, Hatch SB, Riess K, Farber RA 2002. Sequence dependent instability of mononucleotide microsatellites in cultured mismatch repair proficient and deficient mammalian cells. Hum Mol Genet 11: 707–713 [Abstract] [Google Scholar]
- Boyer JC, Hawk JD, Stefanovic L, Farber RA 2008. Sequence-dependent effect of interruptions on microsatellite mutation rate in mismatch repair-deficient human cells. Mutat Res 640: 89–96 [Abstract] [Google Scholar]
- Brinkmann B, Klintschar M, Neuhuber F, Huhne J, Rolf B 1998. Mutation rate in human microsatellites: Influence of the structure and length of the tandem repeat. Am J Hum Genet 62: 1408–1415 [Europe PMC free article] [Abstract] [Google Scholar]
- Buschiazzo E, Gemmell NJ 2006. The rise, fall and renaissance of microsatellites in eukaryotic genomes. Bioessays 28: 1040–1050 [Abstract] [Google Scholar]
- Buschiazzo E, Gemmell NJ 2010. Conservation of human microsatellites across 450 million years of evolution. Genome Biol Evol 2: 153–165 [Europe PMC free article] [Abstract] [Google Scholar]
- Ellegren H 2004. Microsatellites: Simple sequences with complex evolution. Nat Rev Genet 5: 435–445 [Abstract] [Google Scholar]
- Estoup A, Jarne P, Cornuet JM 2002. Homoplasy and mutation model at microsatellite loci and their consequences for population genetics analysis. Mol Ecol 11: 1591–1604 [Abstract] [Google Scholar]
- Fujita PA, Rhead B, Zweig AS, Hinrichs AS, Karolchik D, Cline MS, Goldman M, Barber GP, Clawson H, Coelho A, et al. 2010. The UCSC Genome Browser database: Update 2011. Nucleic Acids Res 39 (Database issue): D876–D882 [Europe PMC free article] [Abstract] [Google Scholar]
- Glazko GV, Nei M 2003. Estimation of divergence times for major lineages of primate species. Mol Biol Evol 20: 424–434 [Abstract] [Google Scholar]
- Hammock EA, Young LJ 2005. Microsatellite instability generates diversity in brain and sociobehavioral traits. Science 308: 1630–1634 [Abstract] [Google Scholar]
- Harr B, Zangerl B, Schlötterer C 2000. Removal of microsatellite interruptions by DNA replication slippage: Phylogenetic evidence from Drosophila. Mol Biol Evol 17: 1001–1009 [Abstract] [Google Scholar]
- International HapMap Consortium 2003. The International HapMap Project. Nature 426: 789–796 [Abstract] [Google Scholar]
- Jakupciak JP, Wells RD 2000. Genetic instabilities of triplet repeat sequences by recombination. IUBMB Life 50: 355–359 [Abstract] [Google Scholar]
- Jurka J, Kapitonov VV, Pavlicek A, Klonowski P, Kohany O, Walichiewicz J 2005. Repbase Update, a database of eukaryotic repetitive elements. Cytogenet Genome Res 110: 462–467 [Abstract] [Google Scholar]
- Kayser M, Roewer L, Hedman M, Henke L, Henke J, Brauer S, Kruger C, Krawczak M, Nagy M, Dobosz T, et al. 2000. Characteristics and frequency of germline mutations at microsatellite loci from the human Y chromosome, as revealed by direct observation in father/son pairs. Am J Hum Genet 66: 1580–1588 [Europe PMC free article] [Abstract] [Google Scholar]
- Kelkar YD, Tyekucheva S, Chiaromonte F, Makova KD 2008. The genome-wide determinants of human and chimpanzee microsatellite evolution. Genome Res 18: 30–38 [Europe PMC free article] [Abstract] [Google Scholar]
- Kelkar YD, Strubczewski N, Hile SE, Chiaromonte F, Eckert KA, Makova KD 2010. What is a microsatellite: A computational and experimental definition based upon repeat mutational behavior at A/T and GT/AC repeats. Genome Biol Evol 2: 620–635 [Europe PMC free article] [Abstract] [Google Scholar]
- Khan H, Smit A, Boissinot S 2006. Molecular evolution and tempo of amplification of human LINE-1 retrotransposons since the origin of primates. Genome Res 16: 78–87 [Europe PMC free article] [Abstract] [Google Scholar]
- Kofler R, Schlotterer C, Lelley T 2007. SciRoKo: A new tool for whole genome microsatellite search and investigation. Bioinformatics 23: 1683–1685 [Abstract] [Google Scholar]
- Kroutil LC, Kunkel TA 1999. Deletion errors generated during replication of CAG repeats. Nucleic Acids Res 27: 3481–3486 [Europe PMC free article] [Abstract] [Google Scholar]
- Kutner MH 2005. Applied linear statistical models. McGraw-Hill Irwin, Boston [Google Scholar]
- Lai Y, Sun F 2003. The relationship between microsatellite slippage mutation rate and the number of repeat units. Mol Biol Evol 20: 2123–2131 [Abstract] [Google Scholar]
- Lander ES, Linton LM, Birren B, Nusbaum C, Zody MC, Baldwin J, Devon K, Dewar K, Doyle M, FitzHugh W, et al. 2001. Initial sequencing and analysis of the human genome. Nature 409: 860–921 [Abstract] [Google Scholar]
- Leclercq S, Rivals E, Jarne P 2007. Detecting microsatellites within genomes: Significant variation among algorithms. BMC Bioinformatics 8: 125 10.1186/1471-2105-8-125 [Europe PMC free article] [Abstract] [Google Scholar]
- Leclercq S, Rivals E, Jarne P 2010. DNA slippage occurs at microsatellite loci without minimal threshold length in humans: A comparative genomic approach. Genome Biol Evol 2: 325–335 [Europe PMC free article] [Abstract] [Google Scholar]
- Li YC, Korol AB, Fahima T, Nevo E 2004. Microsatellites within genes: Structure, function, and evolution. Mol Biol Evol 21: 991–1007 [Abstract] [Google Scholar]
- Majewski JJ, Ott JJ 2000. GT repeats are associated with recombination on human chromosome 22. Genome Res 10: 1108–1114 [Europe PMC free article] [Abstract] [Google Scholar]
- Matsuura T, Fang P, Pearson CE, Jayakar P, Ashizawa T, Roa BB, Nelson DL 2006. Interruptions in the expanded ATTCT repeat of spinocerebellar ataxia type 10: Repeat purity as a disease modifier? Am J Hum Genet 78: 125–129 [Europe PMC free article] [Abstract] [Google Scholar]
- Messier W, Li SH, Stewart CB 1996. The birth of microsatellites. Nature 381: 483. [Abstract] [Google Scholar]
- Mudunuri SB, Nagarajaram HA 2007. IMEx: Imperfect Microsatellite Extractor. Bioinformatics 23: 1181–1187 [Abstract] [Google Scholar]
- Mularoni L, Ledda A, Toll-Riera M, Alba MM 2010. Natural selection drives the accumulation of amino acid tandem repeats in human proteins. Genome Res 20: 745–754 [Europe PMC free article] [Abstract] [Google Scholar]
- Myers S, Bottolo L, Freeman C, McVean G, Donnelly P 2005. A fine-scale map of recombination rates and hotspots across the human genome. Science 310: 321–324 [Abstract] [Google Scholar]
- Nachman MW, Crowell SL 2000. Estimate of the mutation rate per nucleotide in humans. Genetics 156: 297–304 [Europe PMC free article] [Abstract] [Google Scholar]
- Nadir E, Margalit H, Gallily T, Ben-Sasson SA 1996. Microsatellite spreading in the human genome: Evolutionary mechanisms and structural implications. Proc Natl Acad Sci 93: 6470–6475 [Europe PMC free article] [Abstract] [Google Scholar]
- Payseur BA, Jing P, Haasl RJ 2011. A genomic portrait of human microsatellite variation. Mol Biol Evol 28: 303–312 [Europe PMC free article] [Abstract] [Google Scholar]
- Pearson CE, Sinden RR 1998. Trinucleotide repeat DNA structures: dynamic mutations from dynamic DNA. Curr Opin Struct Biol 8: 321–330 [Abstract] [Google Scholar]
- Pearson CE, Nichol Edamura K, Cleary JD 2005. Repeat instability: Mechanisms of dynamic mutations. Nat Rev Genet 6: 729–742 [Abstract] [Google Scholar]
- Petes TD, Greenwell PW, Dominska M 1997. Stabilization of microsatellite sequences by variant repeats in the yeast Saccharomyces cerevisiae. Genetics 146: 491–498 [Europe PMC free article] [Abstract] [Google Scholar]
- Pumpernik D, Oblak B, Borstnik B 2008. Replication slippage versus point mutation rates in short tandem repeats of the human genome. Mol Genet Genomics 279: 53–61 [Abstract] [Google Scholar]
- Pupko T, Graur D 1999. Evolution of microsatellites in the yeast Saccharomyces cerevisiae: Role of length and number of repeated units. J Mol Evol 48: 313–316 [Abstract] [Google Scholar]
- Rolfsmeier ML, Lahue RS 2000. Stabilizing effects of interruptions on trinucleotide repeat expansions in Saccharomyces cerevisiae. Mol Cell Biol 20: 173–180 [Europe PMC free article] [Abstract] [Google Scholar]
- Rose O, Falush D 1998. A threshold size for microsatellite expansion. Mol Biol Evol 15: 613–615 [Abstract] [Google Scholar]
- Roy-Engel AM, Salem AH, Oyeniran OO, Deininger L, Hedges DJ, Kilroy GE, Batzer MA, Deininger PL 2002. Active Alu element “A-tails”: Size does matter. Genome Res 12: 1333–1344 [Europe PMC free article] [Abstract] [Google Scholar]
- Santibanez-Koref MF, Gangeswaran R, Hancock JM 2001. A relationship between lengths of microsatellites and nearby substitution rates in mammalian genomes. Mol Biol Evol 18: 2119–2123 [Abstract] [Google Scholar]
- Saveliev A, Everett C, Sharpe T, Webster Z, Festenstein R 2003. DNA triplet repeats mediate heterochromatin-protein-1-sensitive variegated gene silencing. Nature 422: 909–913 [Abstract] [Google Scholar]
- Schlötterer C, Tautz D 1992. Slippage synthesis of simple sequence DNA. Nucleic Acids Res 20: 211–215 [Europe PMC free article] [Abstract] [Google Scholar]
- Seyfert AL, Cristescu ME, Frisse L, Schaack S, Thomas WK, Lynch M 2008. The rate and spectrum of microsatellite mutation in Caenorhabditis elegans and Daphnia pulex. Genetics 178: 2113–2121 [Europe PMC free article] [Abstract] [Google Scholar]
- Sibly RM, Meade A, Boxall N, Wilkinson MJ, Corne DW, Whittaker JC 2003. The structure of interrupted human AC microsatellites. Mol Biol Evol 20: 453–459 [Abstract] [Google Scholar]
- Sobczak K, Krzyzosiak WJ 2004. Patterns of CAG repeat interruptions in SCA1 and SCA2 genes in relation to repeat instability. Hum Mutat 24: 236–247 [Abstract] [Google Scholar]
- Szak ST, Pickeral OK, Makalowski W, Boguski MS, Landsman D, Boeke JD 2002. Molecular archeology of L1 insertions in the human genome. Genome Biol 3: research0052 10.1186/gb-2002-3-10-research0052 [Europe PMC free article] [Abstract] [Google Scholar]
- Taylor JS, Durkin JM, Breden F 1999. The death of a microsatellite: A phylogenetic perspective on microsatellite interruptions. Mol Biol Evol 16: 567–572 [Abstract] [Google Scholar]
- Tian X, Strassmann JE, Queller DC 2011. Genome nucleotide composition shapes variation in simple sequence repeats. Mol Biol Evol 28: 899–909 [Abstract] [Google Scholar]
- Waterston RH, Lindblad-Toh K, Birney E, Rogers J, Abril JF, Agarwal P, Agarwala R, Ainscough R, Alexandersson M, An P, et al. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420: 520–562 [Abstract] [Google Scholar]
- Weber JL, Wong C 1993. Mutation of human short tandem repeats. Hum Mol Genet 2: 1123–1128 [Abstract] [Google Scholar]
- Webster MT, Hagberg J 2007. Is there evidence for convergent evolution around human microsatellites? Mol Biol Evol 24: 1097–1100 [Abstract] [Google Scholar]
- Weisman-Shomer P, Cohen E, Fry M 2000. Interruption of the fragile X syndrome expanded sequence d(CGG)n by interspersed d(AGG) trinucleotides diminishes the formation and stability of d(CGG)n tetrahelical structures. Nucleic Acids Res 28: 1535–1541 [Europe PMC free article] [Abstract] [Google Scholar]
- Wilder J, Hollocher H 2001. Mobile elements and the genesis of microsatellites in dipterans. Mol Biol Evol 18: 384–392 [Abstract] [Google Scholar]
- Zhang F, Zhao Z 2005. SNPNB: Analyzing neighboring-nucleotide biases on single nucleotide polymorphisms (SNPs). Bioinformatics 21: 2517–2519 [Abstract] [Google Scholar]
- Zhu Y, Strassmann JE, Queller DC 2000. Insertions, substitutions, and the origin of microsatellites. Genet Res 76: 227–236 [Abstract] [Google Scholar]
Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press
Full text links
Read article at publisher's site: https://doi.org/10.1101/gr.122937.111
Read article for free, from open access legal sources, via Unpaywall:
http://genome.cshlp.org/content/21/12/2038.full.pdf
Citations & impact
Impact metrics
Article citations
Ancient and Modern Genomes Reveal Microsatellites Maintain a Dynamic Equilibrium Through Deep Time.
Genome Biol Evol, 16(3):evae017, 01 Mar 2024
Cited by: 0 articles | PMID: 38412309 | PMCID: PMC10972684
Population genetic differentiation of the ubiquitous brooding coral Pocillopora acuta along Phuket Island reefs in the Andaman Sea, Thailand.
BMC Ecol Evol, 23(1):42, 26 Aug 2023
Cited by: 1 article | PMID: 37626296 | PMCID: PMC10464487
Accurate sequencing of DNA motifs able to form alternative (non-B) structures.
Genome Res, 33(6):907-922, 01 Jun 2023
Cited by: 7 articles | PMID: 37433640 | PMCID: PMC10519405
Transposable Elements as a Source of Novel Repetitive DNA in the Eukaryote Genome.
Cells, 11(21):3373, 26 Oct 2022
Cited by: 14 articles | PMID: 36359770 | PMCID: PMC9659126
Review Free full text in Europe PMC
Comparative analysis of microsatellites in coding regions provides insights into the adaptability of the giant panda, polar bear and brown bear.
Genetica, 150(6):355-366, 26 Oct 2022
Cited by: 0 articles | PMID: 36287311
Go to all (45) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
The genome-wide determinants of human and chimpanzee microsatellite evolution.
Genome Res, 18(1):30-38, 21 Nov 2007
Cited by: 149 articles | PMID: 18032720 | PMCID: PMC2134767
The distribution of L1 and Alu retroelements in relation to GC content on human sex chromosomes is consistent with the ectopic recombination model.
J Mol Evol, 63(4):484-492, 04 Sep 2006
Cited by: 25 articles | PMID: 16955238
Identification of human-specific AluS elements through comparative genomics.
Gene, 555(2):208-216, 07 Nov 2014
Cited by: 2 articles | PMID: 25447892
Alu elements and the human genome.
Genetica, 108(1):57-72, 01 Jan 2000
Cited by: 70 articles | PMID: 11145422
Review
Funding
Funders who supported this work.
NIGMS NIH HHS (2)
Grant ID: R01-GM087472
Grant ID: R01 GM087472