Abstract

Introduction

The use of association studies to detect QTLs is an important component of most strategies for finding the genes for complex traits. Complex traits are generally multifaceted and may, in some cases, be best described by one or more quantitative traits. Although linkage mapping has a long history for quantitative traits, interest in association studies with quantitative traits, especially those studies using family-based designs, is more recent. Family-based association tests (FBATs)—in particular, those based on the transmission/disequilibrium test (TDT), popularized by Spielman et al. (1993)—are attractive because of their simplicity and robustness to spurious association, which can arise with population heterogeneity.

There are two broad categories of methods for FBATs. The first category builds on early work by Allison (1997), who described a test for trios that was based on the comparison of two linear-regression models. A subsequent article (Allison et al. 1999) shows how the model can be modified to allow for sibling controls, by using random effects for sibships. Fulker et al. (1999) and Abecasis et al. (2000, 2001) have generalized the linear-model approach, to test both linkage and association, and have added terms to the regression model that enable them to separate out the within- and the between-association effects. The test statistics (i.e., quantitative transmission/disequilibrium tests [QTDTs]) proposed by Abecasis et al. (2000) are obtained using likelihood-ratio tests, on the basis of the assumption of a normal distribution for the traits. To protect against possible deviations from either normality or selection on the trait, Abecasis et al. (2000) have proposed an empirical P value that is based on the permutation of genotypes. A related regression approach for the testing of association in samples of complex pedigrees has been developed by George et al. (1999) and Zhu et al. (2001), who have used model-based correlation structures, to account for familial correlation.

The second category of approaches builds more directly on the original TDT method. The TDT compares the observed distribution of alleles in affected offspring with that expected on the basis of parental genotype. With quantitative traits, it is natural to contrast between the transmissions among offspring who have high quantitative-trait values and the corresponding transmissions among offspring who have low values. This intuitive approach can be formally derived as a conditional score test (see, e.g., Schaid 1996; Rabinowitz 1997). Monks and Kaplan (2000) generalize this, to allow missing parents and tests of association in the presence of linkage (i.e., pedigree disequilibrium tests [PDTs]). As shown by Laird et al. (2000), the score-test approach leads to a statistic that represents the covariance between genotype transmissions and residual-trait deviations. Both Rabinowitz (1997) and Monks and Kaplan (2000) use residuals from the sample mean of the offspring traits. Lunetta et al. (2000) also use this approach but replace the sample mean by an arbitrary constant or offset, which can be chosen to optimize some aspect of the test, either minimizing the variance under H₀ (i.e., FBAT-O) or maximizing the test statistic. Since FBAT-O is easy to implement and performs well in practice, we use it in our comparisons.

The goals of the present article include deriving a general FBAT statistic for quantitative phenotypes, providing power calculations and efficient sampling schemes, and studying the influence that phenotypic correlation between siblings has on the power of the general FBAT. Using the variance model by Fulker et al. (1999), we generalize the quantitative FBAT approach by Laird et al. (2000), so that it can incorporate complex within-family variance structures. Our approach to power calculations for general FBATs, which is an extension of the approach discussed by Lange and Laird (2002a), is very general. It can be used for virtually any FBAT for which the distribution is determined under H₀ by the conditional distribution of the offspring genotypes, conditional on the traits and the sufficient statistic for the parental genotypes. We show how the offset can be chosen to maximize the power, and we show that the sample mean is a very powerful choice when full-population samples are studied. The theory also illustrates why FBATs using the sample mean as the offset do so badly with highly ascertained samples, such as affected sib pairs. Furthermore, we provide a comparison between the FBAT approach and the QTDT and PDT approaches. The proposed generalizations of FBAT and the original FBAT (Laird et al. 2000) are illustrated by their application to an asthma-genetics study.

Remarkably, QTDT and PDT were both designed to test the null hypothesis of no association when linkage may be present. The distribution of an FBAT with multiple offspring per family will depend on which H₀ is tested—H₀ with no linkage and no association or H₀ with linkage but no association (Rabinowitz and Laird 2000). The methodology described here can handle both situations, but, for simplicity, we focus here on the case for which the null hypothesis is H₀ with no linkage and no association.

Family-Based Tests for Quantitative Traits

To keep the derivations and equations simple, we assume here a biallelic marker with alleles A and B, and we assume that the marker locus is the disease locus. The allele frequency of the disease gene is denoted by p. Furthermore, n independent families are given, and the ith family has m_i offspring. The number of transmitted A alleles for the jth offspring in the ith family is denoted by X_ij, with X_ij=0,1,2, and the corresponding quantitative trait is denoted by Y_ij. The parental information for the ith family is given by P_i1 and P_i2. For biallelic markers, the possible values of P_i1 and P_i2 are also characterized as 0, 1, or 2, for the number of target alleles.

For FBATs, Rabinowitz and Laird (2000) proposed the use of a very general condition for the computation of the conditional marker mean, E₀(X_ij), and covariances, , under the null hypothesis—that is, the minimal sufficient statistic of the available genetic information. Loosely speaking and without loss of generality, the minimal sufficient statistic (Rabinowitz and Laird 2000) can be understood as a function of the set of offspring genotypes and available parental genotypes that is held constant when E₀(X_ij) and are computed. When both parents are observed, the sufficient statistic is given by the parental genotypes, P_i1 and P_i2, and E₀(X_ij) and are computed on the basis of transmission probabilities defined by P_i1 and P_i2 and by Mendel’s law of random segregation. When the parental genotypic information is missing, the computation of the transmission probabilities conditional on the sufficient statistics is as described by Rabinowitz and Laird (2000) and Lange and Laird (2002b). For the ith family, we will denote the minimal sufficient statistic as “S_i.”

Under the assumption that the effect of the underlying QTL is additive, the standard genetic model (Falconer and Mackay 1997) is given by

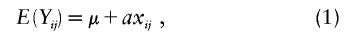
where μ is the overall mean and a is the additive effect size. Denoting the vector of phenotypes for the siblings in the ith family by , Fulker et al. (1999) assumed that the phenotypic variance is given for the ith family by

where V_i is an m_i×m_i variance matrix with components that are attributable to the putative QTL, shared environmental, and polygenic effects. Fulker et al. (1999) decomposed the genotype score into two orthogonal components: the between-family component b_i and the within-family component w_ij=X_ij-b_i. Here, b_i represents the average within-family genotype. Its specification depends on what family data are available (see Abecasis et al. 2000). This decomposition is motivated by the idea that the within-family part w_ij is not sensitive to population structures and is significant only in the presence of linkage disequilibrium. The mean model can be written as follows (Abecasis et al. 2000):

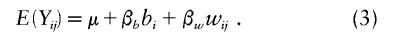
The testing of the null hypothesis of no association, H₀:β_w=0, typically involves one of three test statistics: likelihood-ratio statistic, score statistic, or Wald test statistic. Assuming normality of the phenotypes, Abecasis et al. (2000) derived the QTDT by computing the likelihood-ratio test statistic for β_w in mean model (3).

On the basis of the likelihood model defined by equations (2) and (3), the general FBAT can be obtained as a score test, as follows: First, the normal score for β_w in the model defined by equations (2) and (3) is computed. Then, setting b_i=E₀(X_ij) and β_w=0, we have

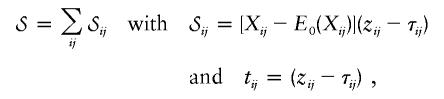
where z_ij and τ_ij are defined by

with an m_i-dimensional offset vector μ_i=(μ_i1,…,μ_imi). The offset values μ_ij may depend on other predictor variables for the phenotype. For the questions discussed here, it is sufficient to look at the case in which all offset values are identical—that is, μ=μ_ij=μ_i^′j^′. Likewise, we consider a relatively simple structure for V_i, where V_i depends on i only through its dimension m_i, the diagonal elements σ²=Var(Y_ij) are all equal, and the off-diagonal elements σ²r=Cov(Y_ij,Y_ij^′) are exchangeable. For the computation of the general quantitative FBAT, the marker score x_ij is the random variable of interest, and t_ij is treated as fixed. The general quantitative FBAT is then given by

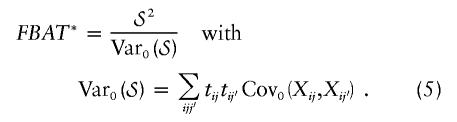
Importantly, a quantitative FBAT disregarding the environmental correlation within families (i.e., assuming that V_i is the identity matrix) can be obtained by setting t_ij=y_ij-μ. We will denote FBATs that ignore environmental correlation by “FBAT” and FBATs that take environmental correlation into account (i.e., eqq. [4] and [5]) by “FBAT*.” The quantitative FBAT-O by Lunetta et al. (2000) then takes the special form wherein t_ij=y_ij-μ and μ is chosen to minimize .

The PDT by Monks and Kaplan (2000) can essentially be interpreted as a Wald test statistic for the covariance between the marker residuals x_ij-E₀(X_ij) and the phenotypic residuals . Under the null hypothesis, the covariance is 0 (Monks and Kaplan 2000) and can be estimated by

where n_info is the number of informative offspring. The variance of the estimate can be computed by the observed empirical variance, so the PDT is given by

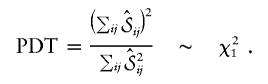
Asymptotic Comparisons of the Quantitative FBAT, PDT, and QTDT

In this section, we discuss the asymptotic properties of the quantitative FBAT, PDT, and QTDT. We provide conditions under which all three tests become equivalent and point out scenarios under which one test might be invalid and permutation testing should be used to obtain valid P values (Abecasis et al. 2000). We focus here exclusively on the asymptotic properties of the tests. Given the large number of tests that are typically done and given the enormous amount of computation time that permutation tests can incur relative to the asymptotic tests, the asymptotic properties of FBAT*/FBAT, PDT, and QTDT are of high practical relevance.

For total population samples (i.e., those with no ascertainment conditions depending on Y_i), we show, in appendix A, that FBAT, PDT, and QTDT are asymptotically equivalent under the null hypothesis when there is no population heterogeneity and no phenotypic correlation within a family—that is, V_i=diag(σ²,…,σ²). In the presence of phenotypic correlation, QTDT and FBAT* remain asymptotically equivalent under the null hypothesis. This holds also for PDT if we replace y_ij with z_ij in equation (6).

However, in the presence of population admixture and/or stratification, the three tests behave differently. For the quantitative FBAT, importantly, since the phenotypic information in FBAT and FBAT* is treated as a fixed/deterministic variable, the validity of the test does not depend on the choice for t_ij or on the correctness of any distributional assumption made in equations (2) and (3). The distribution of any FBAT under H₀ is based solely on the assumption of random Mendelian transmissions and on some weak regularity conditions for the asymptotic distribution, which have been discussed by Lange and Laird (2002b). By treating t_ij as fixed weights in the test statistic, μ, σ², and r become offset and scale parameters that are specified by the user. Although the validity of any FBAT does not depend on the choice of μ, σ², and r, the power of FBAT depends strongly on these parameters. The influence that the offset choice has on the power will be investigated in the “Interaction between Ascertainment Condition and Offset Choice” section, and the influence that a correct specification of the variance matrices has will be investigated in the “Efficient Sampling Designs” section.

Like the score-based FBAT, PDT does not rely on any distributional assumption for the phenotype and uses the assumption of Mendelian transmissions exclusively. PDT and the quantitative FBAT* differ only in two main points. First, they differ in the computation of the phenotypic residuals; whereas PDT assumes the offset to be the phenotypic mean, , and does not use information on phenotypic correlation within families, FBAT* allows any value for the offset and can use phenotypes that are adjusted for within-family correlation. Second, the quantitative FBAT* computes the variances of the marker scores on the basis of Mendelian transmissions, whereas PDT estimates the variance on the basis of the empirical variance; this is also the FBAT approach when linkage is present under the null hypothesis.

Using solely Mendelian transmissions for the computation of the test statistic, FBAT*, FBAT, and PDT are robust against population admixture and/or stratification. The QTDT is based on a full-likelihood model linking the marker information with the phenotypic information, and its validity therefore depends on all model assumptions—for example, the normally distributed phenotypes and the alternative hypothesis. Therefore, permutation tests should be used to assess the statistical significance of the QTDT, especially when the conditions are not met. Thus, conclusions that pertain to the QTDT should be based on its performance under both the permutation and the asymptotic distribution.

We note that, because the distribution of any FBAT statistic depends on discrete random variables (i.e., offspring’s genotypes), exact tests can be statistically implemented with small samples. With larger samples, they are not needed for the validity of the test.

Power Calculations for Continuous Traits

First, assume that the conditional marker means and variances (i.e., E₀ and , respectively), the phenotypes, and the data defining the sufficient statistic are known. Then, the asymptotic distribution of FBAT* as defined in equation (5) can be computed under both hypotheses by using the results of our previous work (Lange and Laird 2002a, 2002b). The distribution under the null hypothesis is χ²₁ conditional on the sufficient statistic and the phenotypes. Under the alternative hypothesis, FBAT* has a scaled, noncentral χ² distribution given by ωFBAT^*~χ²_1,γ with

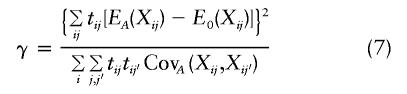
and

where E_A and denote the conditional marker means and covariances under the alternative hypothesis. Note that, since we compute here the power conditional on the phenotypes, the distribution of FBAT* under the alternative is also given by equations (7) and (8) when z_ij^′ is computed on the basis of an estimate for V_i and , for μ based on the null model where β=0.

The conditional power of FBAT* for the significance level α is given by

where Y=(Y₁₁,…,Y_n,mn) and S=(S₁,…,S_n). Since E₀, E_A, , and are computed conditionally on Y and S, the conditional power defined in equation (9) can be computed only when the phenotypes Y and the data defining S are observed. For the computation of the unconditional power, these variables have to be integrated out—that is,

where is the ascertainment condition for the phenotype Y (i.e., Y). We make the assumption that the ascertainment condition depends only on the phenotype Y, but the approach can be extended to allow it to depend on the phenotypes of the parents. The technical details of unconditional power calculation are given in appendix B. The computation of E₀, E_A, , and for dichotomous traits has been discussed by Lange and Laird (2002a) and extends straightforwardly to continuous traits.

The Interaction between Ascertainment Condition and Offset Choice

Assuming a fixed sample size, one has several possibilities to influence the power of FBATs. In this section, we discuss how the offset choice and the ascertainment condition jointly influence the power. Furthermore, we provide rules of thumb for selecting a powerful offset in a given ascertainment condition. We will illustrate the influence that the offset and the ascertainment condition have on the power in two examples. For simplicity, we assume, in this section, that trios are given—that is, m_i=1, which means that FBAT^*=FBAT.

The strength of an additive effect a, relative to the phenotypic variance in model (1), is usually measured by the heritability h² (Falconer and Mackay 1997). Formally, h² is defined as the proportion of phenotypic variation explained by the genetic variation—that is,

Under the assumption of an additive model, equation (11) can be solved for a, to obtain an analytical expression for a, given h² and p, as follows:

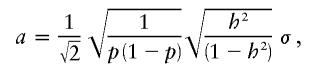
where p denotes the allele frequency of the disease gene in a total population sample.

A common definition of the disease status for a quantitative phenotype is to denote individuals as affected when their phenotypic observation is in some upper or lower β tail of phenotypic distribution. Using the upper β=10% for illustration, we can code the quantitative trait Y as a dichotomous trait Y_d, where Y_d is 1 when the offspring is affected and 0 otherwise. Because of the nonparametric character of FBAT, it is straightforward to modify FBAT so that it can be applied to dichotomous data. Replacing Y by Y_d, in equation (5), and selecting an offset μ between 0 and 1, we obtain the FBAT for dichotomous traits that is identical to the TDT for affected and unaffected offspring that has been proposed by Whittaker and Lewis (1999) and Lange and Laird (2002a).

We will discuss the power of the quantitative FBAT, the dichotomous FBAT, PDT, and QTDT. The power for the quantitative FBAT and the dichotomous FBAT is computed as a function of the offset choice. Whereas the power of the quantitative FBAT is assessed by the approach described above, the power of the dichotomous FBAT is obtained by the approach proposed by Lange and Laird (2002a). The power of PDT and QTDT is obtained by simulation experiments that are based on 100,000 replicates.

The power of these four tests will be compared for two different ascertainment conditions: a total population sample and only affected offspring (i.e., offspring’s phenotypes are in the upper 10% tail of the distribution). For both scenarios, we will assume that the heritability is h²=0.1 and that the allele frequency of the disease gene is 0.3. For marker score x=0, the phenotypic mean is 0, and the phenotypic variance is 1. In the total population sample, the overall phenotypic mean is then 0.31, and the overall phenotypic variance is 1.13. Offspring whose phenotypes are greater than y_min=1.76 (i.e., whose phenotypes are in the upper 10% tail of the distribution) are considered to be affected. When only affected offspring are ascertained, the phenotypic mean is 2.2.

Figure 1a shows the power curves as a function of μ for the quantitative FBAT and for the dichotomous FBAT when a total population sample is analyzed. Figure 1b contains the same information when only affected offspring are ascertained. The power of FBAT-O, PDT, and QTDT is given in the legends of the plots. The power varies substantially for the two ascertainment schemes. When a total population sample is given, the quantitative FBATs, PDT, and QTDT perform much better than the dichotomous FBAT. Abecasis et al. (2001) made the same observation in their simulation experiment. Lange and Laird (2002b) showed that the optimal offset choice for total population samples is the phenotypic mean. This theoretical result is also confirmed by our power calculations. However, the power curve for quantitative FBAT shows a relatively small sensitivity to the offset choice μ in the region of the phenotypic mean (0.39). Thus, the observed sample mean is always a powerful offset choice for total population samples. The offset for FBAT-O is essentially a weighted sample mean, where the weights are determined largely by the number of heterozygous parents. FBAT-O and FBAT with are therefore asymptotically equivalent.

Open in a separate window

Figure 1

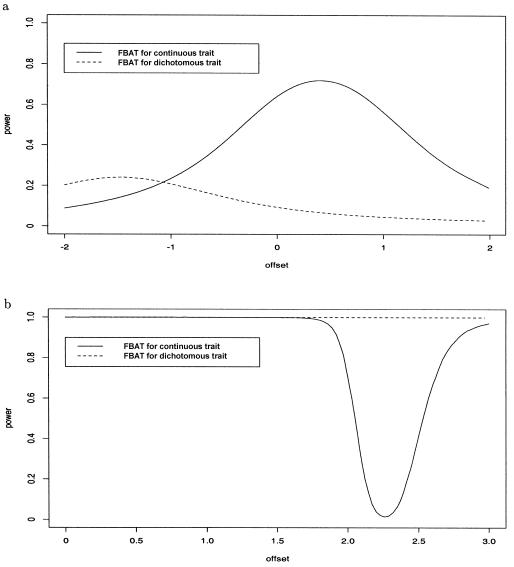
Asymptotic power calculations for a continuous trait. The disease-allele frequency is 0.3, and the heritability, h², is 0.1. The dotted line shows the power of the dichotomous FBAT for offset choices between 0 and 1. Significance level α=0.01 a, Additive model—total population sample with mean , maximal power of FBAT 0.75, power of FBAT-O 0.74, power of PDT 0.73, and power of QTDT 0.74 (n=200). b, Additive model—affected sample with phenotypic mean , maximal power of FBAT 1.00, power of FBAT-O 0.04, power of PDT 0.034, and power of QTDT 0.10 (n=200).

When only affected offspring are ascertained, the situation is reversed. Then, the dichotomous FBAT performs much better than PDT and QTDT. This reversed order has also been observed in Abecasis et al. (2001). The power of FBAT is highly dependent on the offset choice. For offset choices smaller than the ascertainment condition (y_min=1.664), the power of the quantitative FBAT is virtually identical to the power of the dichotomous FBAT. However, for offset choices within the phenotypic range, the power of the quantitative FBAT becomes highly sensitive to the offset choice. For example, for offset choices close to the phenotypic mean (), the power of FBAT is virtually 0. For offset choices outside the phenotypic range (i.e., μ is smaller than y_min=1.664), the power of the quantitative FBAT and the power of the dichotomous FBAT are identical.

This totally different effect that the offset choice has on the quantitative FBAT under the two ascertainment conditions can be explained intuitively. Under the assumption that a total population sample is given, the observed marker distribution does not deviate, on average, from the marker distribution under the null hypothesis—that is, (Lange and Laird 2002b). When we select an offset μ outside the phenotypic range, all phenotypic residuals, y_ij − μ, are either positive or negative. Then, the quantitative FBAT is a weighted average of x_ij-E₀(X_ij), and it holds . FBAT is therefore powerless. However, when the offset μ is approximately identical to the population mean, the correlation between positive and negative phenotypic residuals, y_ij-μ, and genetic residuals, x_ij-E₀(X_ij), is an ideal yardstick for the measurement of the genetic effect on the phenotypes. When only offspring with phenotypes in the upper 10% of the distribution are ascertained, the phenotypic information about the underlying genetic model is restricted by definition. In the presence of association, the sampling of offspring with high phenotypic values will change the observed marker distribution; it will deviate from the marker distribution under the null hypothesis. The actual phenotypes provide little information. Selecting an offset outside the observed phenotypic range will diminish the effect of observed phenotypic values—that is, all y_ij-μ are either positive or negative. Then, the quantitative FBAT is mainly driven by the deviations in the marker distribution—that is, FBAT is a weighted average of x_ij-E₀(X_ij)—and is therefore a powerful test that is asymptotically equivalent to the standard TDT by Spielman et al. (1993).

Because of the similarities between FBAT, FBAT-O, and PDT, the arguments in the present discussion can also be applied toward understanding the behavior of PDT and FBAT-O under both ascertainment conditions. The small power of QTDT for the affected-offspring sample can be explained by the violated model assumption. When only offspring whose phenotypes are in the upper 10% of the distribution are ascertained, the observed phenotypic distribution is heavily skewed. This violation of the normality assumption results in inconsistent parameter estimates that lead to inaccurate test results. When ascertainment conditions are used to obtain the sample, the use of a QTDT that is based on permutations is strongly recommended (Abecasis et al. 2001).

We repeated the power calculations shown in this section for a variety of different allele frequencies and genetic models. Our findings for the powerful offset choices were confirmed in all these calculations. Thus, a rule of thumb might be to use the continuous version of FBAT only for total population samples or for samples with “weak” ascertainment conditions. Because of the potential danger of choosing a power-reducing offset for affected samples or for samples obtained on the basis of a strong ascertainment condition, either the dichotomous FBAT/TDT or the quantitative FBAT with an offset outside the ascertainment condition should be used when such data are analyzed.

Efficient Sampling Designs: Power of FBATs for Continuous Phenotypes When Extremely Discordant Sib Pairs Are Sampled

In this section, we assess the power of sampling designs for quantitative phenotypes when each family has at least two offspring and when phenotypic correlation is present. We will concentrate on the power for quantitative FBATs when extremely discordant sib pairs are sampled (Risch and Zhang 1996; Abecasis et al. 2001). Originally introduced for linkage analysis, the design has been shown to be very powerful also for association studies that are based on family data (Abecasis et al. 2001). We focus here on four aspects of the design that have not yet been investigated for family-based association studies: (i) the influence that the ascertainment condition has on the power, (ii) the influence that environmental/within-family correlation has on the power of the design, (iii) the importance of accounting for environmental/within-family correlation in the test statistic (i.e., using FBAT* or FBAT), and (iv) the influence of missing parental information.

For the power calculations, we assume that n families with two offspring are given and that the parental genotypes are either known or unknown. For each offspring, we observe one continuous phenotype: y_i1 for the first offspring and y_i2 for the second offspring. The marker score of the first offspring is denoted by x_i1, and the marker score of the second offspring is denoted by x_i2. When the marker scores x_i1 and x_i2 are given, the phenotypes y_i1 and y_i2 can be modeled by a multivariate normal distribution—that is,

with additive effect a>0, environmental variance σ², and environmental correlation r. For simplicity of exposition, we assume here the absence of variance components attributable to polygenic effects (Fulker et al. 1999).

Since we want to compare the FBAT approach's power for highly ascertained samples and its power for total population samples, the choice of the nuisance parameters becomes important. Whereas the covariance parameters σ and r will be estimated by moment-based estimators, the offset μ is selected on the basis of the rules f thumb that were derived, in the previous section, for total population samples and ascertained samples.

Risch and Zhang (1996) have proposed the sampling of extremely discordant sib pairs. The ascertainment condition can be written as

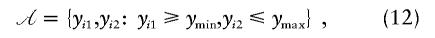
where y_min is the lower threshold for the phenotype of the first offspring and y_max is the upper threshold for the phenotype of the second offspring. A sample obtained on the basis of ascertainment condition is therefore highly discordant, so we select an offset μ that is outside the sampled tails of the phenotypic distribution—that is, between y_min and y_max. So that the contributions of both tails are equally weighted, the offset is set equal to the average of the lower and upper limits—that is, (y_min+y_max)/2. For total population samples, we select as offset μ as the sample mean.

In the computation of the power of FBAT* for total population samples, the variance parameters, σ² and r, are estimated by their empirical estimators—that is, and . For samples ascertained on the basis of condition (12), it is important to note that the phenotypic mean and variance can be different in the upper tail and the lower tail when the ascertainment condition is not symmetric; for example, y_i1 is in the upper 10% of the tail, and y_i2 is in the lower 30% of the tail. For power calculations for ascertained samples, we therefore estimate the phenotypic mean in each tail by . Then, the variance within each tail is computed by = /(n-1),j=1,2, and the covariance is computed by .

Using the approach for power calculations that is outlined in the present article, we computed the sample sizes for FBAT* and FBAT that are required in order to achieve 80% power for a significance level α=10^-7 for a variety of allele frequencies p, heritabilities h, and ascertainment conditions (tables 1 and ​and2).2). Whereas table 1 shows the sample sizes for FBAT* and FBAT that are required in order to achieve 80% power when parental genotypes are known, table 2 gives the required sample size for FBAT under the same scenarios but when the parental information is missing. Since the noncentrality parameter δ and the scaling parameter ω are invariant under linear transformation of the phenotypes when two offspring without parental information are given, the required sample sizes for FBAT* and FBAT are identical under this scenario.

Table 1

Sample Sizes Required in Order to Achieve 80% Power at Significance Level α=1×10^-7 When Two Probands and Both Parents Are Given^[Note]

	Sample Size Required If
	r=.0		r=.4
Ascertainment Condition	h=.05	h=.10	h=.05	h=.10
One sib in top 10% tail, one sib in lower 10% tail:
P=.1:
FBAT*	250	132	110	58
FBAT	…	…	112	61
P=.5:
FBAT*	235	116	108	55
FBAT	…	…	110	57
One sib in top 10% tail, one sib in lower 30% tail:
P=.1:
FBAT*	324	170	158	83
FBAT	…	…	171	92
P=.5:
FBAT*	341	172	165	85
FBAT	…	…	169	92
Total population sample:
P=.1:
FBAT*	854	485	643	356
FBAT	…	…	821	462
P=.5:
FBAT*	841	463	613	352
FBAT	…	…	780	432

Open in a separate window

Note.— r denotes the environmental correlation.

Table 2

Sample Sizes in Order Required to Achieve 80% Power at Significance Level α=1×10^-7 When Two Probands Are Given and No Parental Information Is Available^[Note]

	Sample Size Required If
	r=.0		r=.4
Ascertainment Condition	h=.05	h=.10	h=.05	h=.10
One sib in top 10% tail, one sib in lower 10% tail:
P=.1 (FBAT)	300	177	152	94
P=.5 (FBAT)	265	145	135	81
One sib in top 10% tail, one sib in lower 30% tail:
P=.1 (FBAT)	376	207	200	121
P=.5 (FBAT)	368	193	190	110
Total population sample:
P=.1 (FBAT)	1,657	876	971	570
P=.5 (FBAT)	1,537	779	865	458

Open in a separate window

Note.— FBAT* and FBAT are identical for two sibs and missing parental genotypes. r denotes the environmental correlation.

Tables ​Tables11 and ​and22 clearly demonstrate the importance of all four issues for the study design: ascertainment, environmental correlation, accounting for environmental/within-family correlation in the test statistic, and missing parental information. The ascertainment condition has a very strong effect on the power (table 1). Although the required sample sizes are relatively high for the total population samples, they decrease substantially when discordant sib pairs are ascertained. This effect becomes even stronger in the presence of positive environmental correlation. In general, positive environmental correlation decreases the required sample sizes. When strong ascertainment conditions are applied, there is no advantage in modeling the phenotypic variance matrix V. FBAT and FBAT* have almost the same power. However, for total population samples, inclusion of the phenotypic variance V in the test statistic raises the power of FBAT*, and FBAT* clearly outperforms FBAT.

Table 2 shows the power for the same parameter choices as in table 1, but it is assumed that the parental genotypes are missing. Although the strength of the effect that environmental correlation has on the power remains the same, the effect of the ascertainment condition becomes even stronger. Furthermore, when two sibs are sampled from the extreme tails of the phenotypic distribution, missing parental information has only a minor influence on the required sample size—for example, 58 families with parental information (i.e., 4×58=232 loci to be genotyped) versus 94 families without parental information (i.e., 2×94=188 loci to be genotyped) (tables ​(tables11 and ​and2).2). When only a fixed number of subjects can be genotyped and extremely discordant sib pairs are given, it may be more cost-effective to genotype additional pairs of offspring, rather than the parents. The drawback of this strategy—that is, selecting a phenotype with positive environmental correlation and genotyping only extremely discordant sib pairs without parents—is the additional screening (Risch and Zhang 1996). Since extremely discordant sib pairs are not frequently observed in total population samples, one has to screen many families to find such pairs. The additional screening cost must therefore be weighted versus the additionally achieved power.

Again, we repeated the power calculations shown in this section for a variety of different allele frequencies, environmental correlations, and genetic models (recessive and dominant). All these power calculations suggest that it is a good rule of thumb to choose FBAT* for total population samples and FBAT for highly ascertained samples, where V and μ are estimated as above. FBAT* provides some reduction in sample size with weak ascertainment conditions (e.g., upper 10% and lower 30%) but has only a small effect with stronger ascertainment conditions.

Using simulation experiments, we also assessed the power of FBAT-O, PDT, and QTDT, for the scenarios considered in tables ​tables11 and ​and2.2. When based on y_ij, FBAT, FBAT-O, and PDT showed virtually the same power for all of these scenarios. The same holds for FBAT* and QTDT.

Data Analysis: Childhood Asthma Management Program (CAMP)

We applied the quantitative FBAT approach to a collection of parent/child trios in the CAMP Genetics Ancillary Study. The CAMP study randomized asthmatic children to three different asthma treatments (CAMP Research Group 1999). Blood samples for DNA were collected from 696 complete parent/child trios from 640 nuclear families in the CAMP Ancillary Genetics Study. Baseline phenotype values, before randomization to treatment groups, were used in this analysis. Genotyping was performed at a polymorphism located at the IL13 gene. Asthma is a clinical condition often associated with an atopic predisposition; we have selected one phenotype, total eosinophil count, related to the allergic response. Since the ascertainment condition for CAMP was mild-to-moderate asthma, the total-eosinophil-count data can be considered as a total population sample of children with such disease status.

With 312 informative families and no evidence for population stratification, the regularity conditions for the asymptotic convergence (Lange and Laird 2002b) are certainly met, and one can therefore focus on the asymptotic distributions of the tests. For setting , the test results of FBAT* and FBAT are shown in table 3. Furthermore, the P values for FBAT-O, PDT, and QTDT are given. The advantages of using FBAT* instead of FBAT are clear and are of practical relevance. Note that 56 families (8%) had two offspring, illustrating that using the phenotypic correlation can have a substantial effect even with only a small percentage of siblings in the data set.

Table 3

Testing for Association between Total Eosinophil Count and IL13

	Test Statistic	P Value
FBAT	6.48	.011
FBAT*a	7.84	.006
FBAT-O	6.86	.009
QTDT	6.55	.010
PDT	5.65	.018

Open in a separate window

^aEstimated environmental correlation () .34.

Discussion

We have presented an approach to unconditional power calculations for FBATs that is applicable to almost any scenario. We have illustrated the flexibility of our approach by discussing the optimal FBAT statistic under popular ascertainment conditions and the importance of parental information and environmental correlation when extremely discordant offspring are sampled. We have also illustrated the methodology by an application to an asthma study.

The methodology for power calculations proposed here is fully general—hence, extensions to sampling designs and power calculations for multiallelic loci are straightforward. We have implemented our approach to power calculations in a software package called “PBAT,” which is available at the FBAT Web Page. In addition to the scenarios discussed here, PBAT can also be used in power calculations for binary traits, when parental information is missing and when marker locus and disease locus are not identical.

Using our approach to power calculations and using simulations, we compared the statistics PDT, QTDT, and the general FBAT. All three tests show virtually the same power in the absence of population structures and no ascertainment bias. With extreme ascertainment, they can differ substantially. The score-based statistics (PDT and FBAT) differ largely in how the trait is defined. The phenotype's being model free, the flexibility of modeling or not modeling the phenotypic correlation within a family, and the flexibility of the offset choice are the crucial advantages of the continuous FBAT approach. For example, when multiple offspring per family are available and when neither assumptions about environmental correlation within each family nor assumptions about shared genetic components are made, the quantitative FBAT remains a valid approach; however, when these assumptions are made and are reasonable, a substantial gain in power for FBAT* can be achieved.

The flexibility of the offset choice allows the quantitative FBAT approach to be adapted to the ascertainment condition used in the study. When a strong ascertainment condition is used in the study design, a smart offset choice can make FBAT* more powerful than PDT and QTDT, but a bad offset choice may result in even lower power. We have given rules of thumb that should give FBAT* reasonably good power under common ascertainment settings. Furthermore, the generic character of the FBAT approach allows nonparametric extension to other scenarios—such as FBAT-GEE, for multivariate traits (Lange et al., in press), and FBAT-LOGRANK, for time to onset (C. Lange, D. Blacker, and N. M. Laird, unpublished data).

Acknowledgments

Appendix A : Asymptotic Equivalence of PDT, QTDT, and FBAT* When There Is No Population Admixture

Standard asymptotic theory (Cox and Hinkley 1974) implies that score tests, likelihood-ratio tests, and Wald tests are asymptotically equivalent under the null hypothesis. For the equivalence of FBAT*, PDT, and QTDT under the null hypothesis, it is therefore sufficient to show that all three association tests are asymptotically equivalent to one of these tests when model (3) is true.

For simplicity, we will assume here that trios are observed, and we show the equivalence of FBAT, PDT, and QTDT. The QTDT proposed by Abecasis et al. (2000) is the likelihood-ratio test for β_w and is equivalent to the corresponding score test for β_w, which is defined by

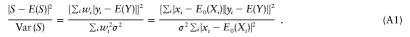
When the offset choice for FBAT is μ=E(Y), the numerator of FBAT and the score test (A1) are identical. The denominator of FBAT can be simplified for n→∞,

Under the null hypothesis, b can be interpreted as a weighted average of (y_i-μ)². Since the weights satisfy the Lindberg condition (Billingsley 1995; Lange and Laird 2002b), b converges to σ² as n→∞. Furthermore, standard asymptotic arguments imply that

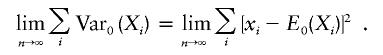
Thus, under the null hypothesis and in the absence of population substructure, the score tests for β_w and FBAT are asymptotically identical. QTDT and FBAT are therefore asymptotically equivalent under the null hypothesis. Because of the similarity between PDT and FBAT, it is straightforward to show that PDT and FBAT also are equivalent under the same conditions.

Appendix B : Unconditional Power Calculations for Quantitative FBATs (Technical Details)

The unconditional power (eq. [10]) is defined as the integral over the conditional power with probability measure —that is, . Since the s_i values are defined by the observed marker scores, they are discrete random variables and (10) can be rewritten as a finite sum of continuous integrals

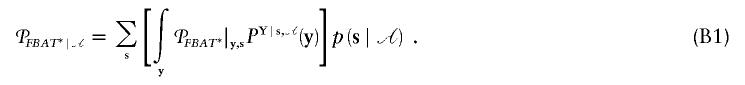
The conditional probabilities and P^Ys, can always be computed under the alternative hypothesis by repeated applications of Bayes-theorem and Mendelian transmissions. By definition of family types on the basis of s_i and the use of a multinomial distribution, the computation of the sum in equation (B1) can be simplified further (Lange and Laird 2002a, appendix B). Nevertheless, when designs with many different family types and sophisticated ascertainment conditions are analyzed, the numerical computation of equation (B1) can become very time-consuming. In such situations, equation (B1) can be computed by Monte Carlo methods or Markov-chain Monte Carlo. Since it is always possible to simulate random samples from and P^Ys,, these techniques can be used for the computation of equation (B1) at all times. Note that this is always computationally faster than a pure simulation study—wherein a dichotomous 0-1 variable (significant/nonsignificant), rather than Monte Carlo integration of the conditional power when the variable of interest is a continuous variable (the conditional power), is performed (Lange and Laird 2002a).

Electronic-Database Information

References