Abstract

Background

As whole genomes are sequenced at increasing rates, using gene-order data^a for phylogenetic analyses and ancestral reconstruction is attracting increasing interest. Comparative genomics, evolutionary biology, and cancer research all require tools to elucidate the history and consequences of the large-scale genomic changes, such as rearrangements, duplications, losses. However, using gene-order data has proved far more challenging than using sequence data and numerous problems plague existing methods: oversimplified models, poor accuracy, poor scaling, lack of robustness, lack of statistical assessment, etc.

Genome rearrangement operations change the ordering of genes on chromosomes. An inversion operation (also called reversal) reverses both the order and orientation of a segment of a chromosome. A transposition is an operation that swaps two adjacent segments of a chromosome. In case of multiple chromosomes, a translocation breaks a chromosome and reattaches a part to another chromosome, while a fusion joins two chromosomes and a fission splits one chromosome into two. Yancopoulos et al. [1] proposed a universal double-cut-and-join (DCJ) operation that accounts for all rearrangements used to date. None of these operations alter the gene content of genomes, whereas deletions (or losses) delete segments of (one or more) contiguous genes from a chromosome, while insertions introduce a segment of (one or more) contiguous genes from external sources into a chromosome. and duplications copies an existing segment within the genome and inserts into a chromosome. Finally, whole genome duplication (WGD) creates an additional copy of the entire genome of a species.

As phylogenies play a central role in biological research, over the past decade many methods were developed to reconstruct phylogenies from gene-order data. The first algorithm for phylogeny inference from gene-order data was BPAnalysis based on breakpoint distances [2]. Moret et al. [3] later extended this approach with GRAPPA by using inversion distances. While these methods were limited to unichromosomal genomes, Bourque and Pevzner [4] developed MGR to handle multichromosomal genomes. These approaches are parsimony-based: they solve the so-called Big Parsimony Problem (BPP) and all suffer from serious scalability issues. In contrast with parsimony-based methods, distance-based methods run in time polynomial in the number and size of genomes. Lin et al. [5] have demonstrated the accuracy and scalability of a distance-based method that uses NJ [6] and FastME [7] with an accurate distance estimator [8]. Instead of working directly with the evolutionary events of the model, one can also transform the problem into the familiar sequence-based reconstruction problem. Wang et al. [9] first proposed a parsimony-based approach, MPBE (Maximum Parsimony on Binary Encoding). Recently Hu et al. [10] developed MLBE, later refined by Lin et al. [11] with MLWD, both of which demonstrate that using maximum-likelihood approaches is the decisive factor in improving the modest accuracy of MPBE.

If the tree is fixed, then computing its parsimony score is known as the Small Parsimony Problem (SPP). Ancestral reconstruction has been studied through several optimization schemes for SPP on gene-order data—using adjacencies [12–15], using conserved intervals (Roci—Reconstruction of Conserved Intervals [16]), using multiple breakpoint graphs (MGRA [17]) and supporting whole-genome duplications [18,19], where continuous regions or complete ancestral genomes have been inferred.

Relatively few of these tools are offered through web servers. Lin et al. [20] had developed a web-server version of MGR with new heuristics to speed up the original MGR algorithm, but the site is no longer accessible. Both Roci and MGRA (for ancestral reconstruction only) are offered through web servers, but none can handle complex events such as gene insertions, deletions and duplications.

We present a new tool MLGO for the reconstruction of phylogeny and/or ancestral genomes from gene-order data. MLGO relies on two methods we have developed: MLWD [11] for phylogenetic reconstruction and PMAG+ [21] for ancestral genome reconstruction. Our tool takes the advantage of binary encoding on gene-order data, supports a fairly general model of genomic evolution (rearrangements plus duplications, insertions, and losses of genomic regions), and successfully accommodates itself into the framework of maximized likelihood. The results of extensive testing on both simulated and real data show that both MLWD and PMAG+ can achieve great performance, scalability and flexibility, suggesting MLGO a suitable tool for large-scale analysis of high-resolution data. Furthermore, MLGO is deployed as a web service, providing the first web tool that is suitable for large scale genomic analysis with a general model of evolution.

Implementation

MLGO preprocesses the gene-order data, configures the transition model, reconstructs a phylogeny, and finally solves the SPP on that phylogeny.

Results and discussion

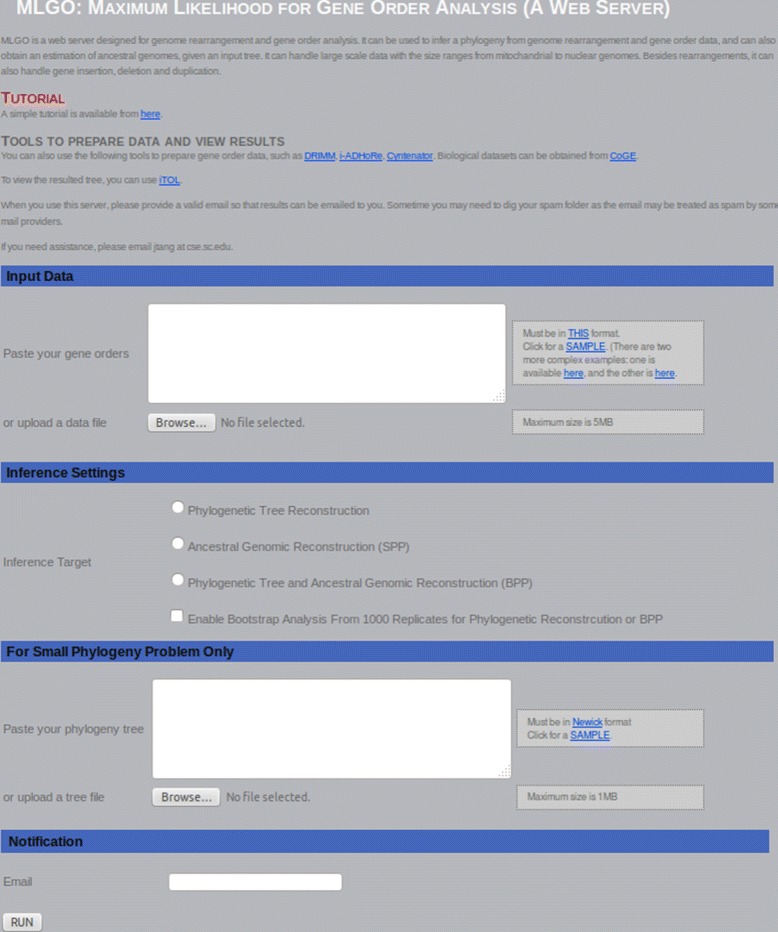
MLGO is written in C++ and Perl as a web tool. Figure ​Figure11 shows the screen shot of the web interface for MLGO. The input format of the dataset is that used by GRAPPA and MGR: FASTA-like headers for the names of the genomes (> followed by an alphanumeric sequence followed by a newline), each chromosome represented by a signed permutation of integers ending with a $ symbol and a newline character. Phylogenies are output as trees in Newick format.

Open in a separate window

Figure 1

The screen shot of the web interface for MLGO .

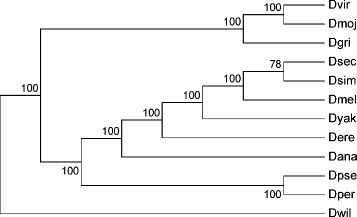
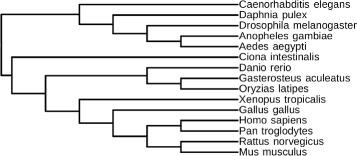
We used the genomes of 12 fully sequenced drosophila species to demonstrate the performance of MLGO. Figure ​Figure22 shows the consensus phylogeny reconstructed by MLGO with the bootstrap support values obtained using 100 replicates. Compared to the study using sequence data published by Clark et al. [28], all major groups in those 12 drosophila genomes were correctly identified with strong support (bootstrap value >90), except for one median support at the bipartition between D. simulans, D. sechellia and the rest. The total running time for reconstructing the phylogeny of 12 drosophila species is less than 1 minute, while ancestral reconstruction adds less than 30 minutes. We also tested the performance of MLGO on 15 Metazoan genomes from the eGOB (Eukaryotic Gene Order Browser) database [29], and the reconstructed phylogeny tree shown in Figure ​Figure33 is perfectly supported from existing studies [30,31].

Open in a separate window

Figure 2

The consensus phylogeny of 12 drosophila genomes with bootstrap support values from 100 replicates.

Open in a separate window

Figure 3

The reconstructed phylogeny of 15 Metazoan genomes.

Conclusion

As whole genomes are sequenced at increasing rates, using gene-order data for phylogenetic analyses and ancestral reconstruction is attracting increasing interest, especially coupled with the recent advances in identifying conserved synteny blocks among multiple species [32–34].

MLGO (Maximum Likelihood for Gene-Order Analysis) is the first web tool for likelihood-based inference of both the phylogeny and ancestral genomes. It provides fast and scalable analyses with bootstrap support of large-scale genomic changes including not only rearrangements but also gene insertions, deletions and duplications.

Availability and requirements

The web tool is available from http://www.geneorder.org/server.php.Project name: MLGOProject home page:http://www.geneorder.org/server.phpOperating system(s): Platform independentProgramming language: PerlOther requirements: NoneLicense: GNURestrictions for use by non-academics: None

Endnote

^a We use the term “gene” as this is in fact a common form of syntenic blocks, but other kinds of markers could be used.

Acknowledgements

Footnotes

Contributor Information

Fei Hu, Email: moc.liamg@cyiefuh.

Yu Lin, Email: ude.dscu@082luy.

Jijun Tang, Email: ude.cs.sec@gnatj.

References