Abstract
Free full text

Viscoelasticity of subcortical gray matter structures
Abstract
Viscoelastic mechanical properties of the brain assessed with magnetic resonance elastography (MRE) are sensitive measures of microstructural tissue health in neurodegenerative conditions. Recent efforts have targeted measurements localized to specific neuroanatomical regions differentially affected in disease. In this work, we present a method for measuring the viscoelasticity in subcortical gray matter (SGM) structures, including the amygdala, hippocampus, caudate, putamen, pallidum, and thalamus. The method is based on incorporating high spatial resolution MRE imaging (1.6 mm isotropic voxels) with a mechanical inversion scheme designed to improve local measures in pre‐defined regions (soft prior regularization [SPR]). We find that in 21 healthy, young volunteers SGM structures differ from each other in viscoelasticity, quantified as the shear stiffness and damping ratio, but also differ from the global viscoelasticity of the cerebrum. Through repeated examinations on a single volunteer, we estimate the uncertainty to be between 3 and 7% for each SGM measure. Furthermore, we demonstrate that the use of specific methodological considerations—higher spatial resolution and SPR—both decrease uncertainty and increase sensitivity of the SGM measures. The proposed method allows for reliable MRE measures of SGM viscoelasticity for future studies of neurodegenerative conditions. Hum Brain Mapp 37:4221–4233, 2016. © 2016 Wiley Periodicals, Inc.
INTRODUCTION
Viscoelastic mechanical properties of the human brain assessed noninvasively with magnetic resonance elastography (MRE) [Muthupillai et al., 1995] have emerged as sensitive measures of neurodegeneration [Sack et al., 2013]. Altered brain tissue viscoelasticity has been observed in aging [Arani et al., 2015; Sack et al., 2011], Alzheimer's disease [Murphy et al., 2011, 2016], and multiple sclerosis [Streitberger et al., 2012; Wuerfel et al., 2010], among other conditions, and these viscoelastic effects have been related to pathology in the tissue microstructure [Riek et al., 2012; Schregel et al., 2012]. The apparent strength of the relationship between mechanics and the structural health of tissue has driven methodological efforts to generate reliable properties that are localized to the neuroanatomical structures which are differentially affected in disease, including lobes [McGarry et al., 2013; Murphy et al., 2013] and white matter (WM) tracts [Guo et al., 2013; Johnson et al., 2013a; Romano et al., 2012].
In contrast, there is a dearth of MRE measurements on subcortical gray matter (SGM) structures. Atrophy of SGM is a hallmark of functional decline in aging [Raz et al., 2005] and neurodegenerative conditions [Braak and Braak, 1998]. Different neurological disorders are associated with volumetric decreases in separable SGM structures; for example, hippocampal volume decreases are a hallmark of Alzheimer's disease [Jack et al., 2010] and thalamic volume atrophy is present in multiple sclerosis [Wylezinska et al., 2003]. Therefore, it follows that MRE measurements on SGM may be particularly sensitive to the structural degradation that underlies atrophic processes. Indeed, Lipp et al. used MRE of the lentiform nucleus (putamen and pallidum) to investigate differences between Parkinson's disease and progressive supranuclear palsy, and found a localized softening effect that was greater than global softening [Lipp et al., 2013]. There remains, however, a strong need for methods that improve the reliability of measurements of SGM viscoelasticity. This is especially critical for potential studies of tissue structure and its role in cognitive performance, as the integrity of specific SGM structures is critical in dissociable cognitive processes such as memory [Cohen and Squire, 1980], executive function [Buckner, 2004], and skill learning [Laforce and Doyon, 2001]. In fact, we have previously reported that hippocampal viscoelasticity is strongly associated with behavioral performance on a relational memory task [Schwarb et al., 2016].
In this work, we introduce and analyze a method for measuring viscoelastic mechanical properties in SGM structures. This method aims to overcome two major limitations in localized brain MRE: insufficient spatial resolution and the nuisance influence of nearby regions. Spatial resolution is critical in MRE as displacement fields captured with poor resolution result in loss of accuracy in small regions [Johnson et al., 2013b, 2014]. However, the smoothing or regularization necessary to stabilize inversion of noisy displacement data suggests that the spatial resolution attainable at clinical MRI field strengths may still be inadequate to isolate regions from surrounding tissues. This is especially critical in examining SGM structures situated near cerebrospinal fluid (CSF) interfaces, as the lack of shear stiffness in CSF will affect the properties in neighboring tissue due to limitations in the achievable resolution of the MRE property maps [Murphy et al., 2013]. To combat this effect in SGM, we adopt an imaging scheme with improved spatial resolution [Johnson et al., 2014] and couple it with an inversion scheme that incorporates prior anatomical information to improve localized property measures and avoid effects from neighboring tissue or CSF [McGarry et al., 2013].
Using the proposed method, we report representative properties in SGM structures from a population of healthy young participants and demonstrate the reliability of these measurements through repeated examinations of a single participant. Given the lack of independent methods to validate MRE observations in the brain, uncertainty analysis using repeated measurements has been the primary method for investigating the reliability of reported properties [Johnson et al., 2013a; McGarry et al., 2013; Murphy et al., 2011, 2013; Sack et al., 2008]. Here, we further explore how different experimental and methodological considerations contribute to parameter measurement and uncertainty. This is the first report of MRE measurements on SGM structures accompanied by a demonstration of measurement reliability.
METHODS
Participants
Twenty‐one healthy volunteers (male; right‐handed; 18–33 yo) provided written informed consent and participated in the study approved by our Institutional Review Board. Each participant completed an imaging session performed with a Siemens 3T Trio MRI scanner and 32‐channel RF receive head coil (Siemens Medical Solutions; Erlangen, Germany). One male participant (30 yo) completed eight separate imaging sessions over 4 days to assess the uncertainty in SGM viscoelasticity measurements. Each imaging session comprised a high‐resolution, T 1‐weighted MPRAGE acquisition, a 3D multishot, multislab spiral MRE acquisition [Johnson et al., 2014], and an auxiliary scan for measuring magnetic field inhomogeneity [Funai et al., 2008]. These scans are used to produce the viscoelastic properties of SGM structures, following the procedure outlined in Figure Figure11 and described in the following section.
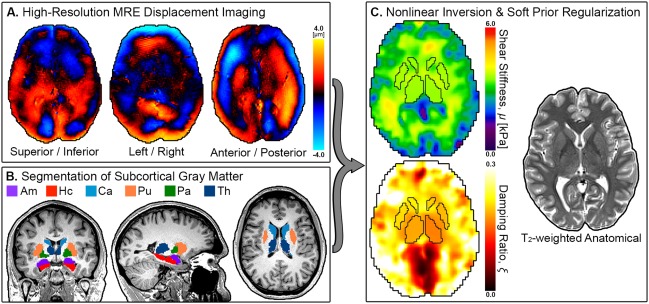
Overview of proposed method for measuring SGM viscoelasticity: (A) high‐resolution MRE imaging of complex, full vector displacement field in the brain; (B) segmentation of SGM structures from T 1‐weighted image (amygdala, Am; hippocampus, Hc; caudate, Ca; putamen, Pu; pallidum, Pa; and thalamus, Th); (C) estimation of viscoelastic shear stiffness, μ, and damping ratio, ξ, from displacement data using NLI with SPR to promote local homogeneity in SGM structures defined by the registered segmentation masks, along with the corresponding high‐resolution, T 2‐weighted anatomical image. [Color figure can be viewed at http://wileyonlinelibrary.com]
SGM Viscoelasticity Measurement
T1‐weighted image segmentation
We segmented the high‐resolution T
1‐weighted images acquired with the MPRAGE sequence (0.9 × 0.9 × 0.9 mm3; TR/TI/TE =
= 1,900/900/2.2 ms) using FreeSurfer [Fischl et al., 2002]. FreeSurfer automatically extracted the SGM structures of interest: amygdala (Am), hippocampus (Hc), caudate (Ca), putamen (Pu), pallidum (Pa), and thalamus (Th).
1,900/900/2.2 ms) using FreeSurfer [Fischl et al., 2002]. FreeSurfer automatically extracted the SGM structures of interest: amygdala (Am), hippocampus (Hc), caudate (Ca), putamen (Pu), pallidum (Pa), and thalamus (Th).
High‐resolution MRE data acquisition
We collected MRE data using a sequence designed to achieve high spatial resolution in the brain through optimal signal‐to‐noise ratio (SNR) efficiency [Johnson et al., 2014]. Imaging parameters included: two in‐plane spiral readouts (parallel imaging R =
= 2); 240 × 240 mm2 field‐of‐view; 150 × 150 matrix; 60, 1.6 mm slices (divided into 10 slabs of 8 slices each, with 25% slab overlap); and TR/TE
2); 240 × 240 mm2 field‐of‐view; 150 × 150 matrix; 60, 1.6 mm slices (divided into 10 slabs of 8 slices each, with 25% slab overlap); and TR/TE =
= 1,800/73 ms. The resulting images had 1.6 × 1.6 × 1.6 mm3 spatial resolution. Iterative image reconstruction included parallel imaging with SENSE [Pruessmann et al., 2001] and correction for field inhomogeneity [Sutton et al., 2003] and motion‐induced phase errors [Van et al., 2011], as described previously [Johnson et al., 2014].
1,800/73 ms. The resulting images had 1.6 × 1.6 × 1.6 mm3 spatial resolution. Iterative image reconstruction included parallel imaging with SENSE [Pruessmann et al., 2001] and correction for field inhomogeneity [Sutton et al., 2003] and motion‐induced phase errors [Van et al., 2011], as described previously [Johnson et al., 2014].
The MRE acquisition imaged brain displacements generated by head vibration with the Resoundant pneumatic actuator (Resoundant; Rochester, MN). Vibrations at 50 Hz were captured with flow‐compensated motion encoding gradients matched to the vibration period. Full vector, complex displacement fields resulted from encoding displacement along three orthogonal directions, with positive and negative gradient polarities, and four time points across one vibration period, followed by unwrapping and standard temporal filtering [Manduca et al., 2001]. The total acquisition time was 12 min.
Nonlinear inversion with soft prior regularization
Both the MRE displacement data and SGM structure masks were input to the nonlinear inversion algorithm (NLI) for optimization‐based estimation of tissue viscoelasticity [McGarry et al., 2012; Van Houten et al., 1999, 2001, 2011]. The masks were formulated in MRE data‐space following registration of the T
1‐weighted image to the MRE magnitude image using FLIRT in FSL [Jenkinson et al., 2002, 2012]. These masks were used as individual regions for soft prior regularization (SPR) in NLI with a weighting of α =
= 10−9 [McGarry et al., 2013]. SPR promotes local homogeneity in pre‐defined regions by penalizing variations in properties across the region during optimization, and was used in this procedure to minimize the influence of tissues and CSF surrounding the SGM structures of interest.
10−9 [McGarry et al., 2013]. SPR promotes local homogeneity in pre‐defined regions by penalizing variations in properties across the region during optimization, and was used in this procedure to minimize the influence of tissues and CSF surrounding the SGM structures of interest.
NLI modeled the tissue as a heterogeneous, nearly incompressible, viscoelastic material and returned property maps corresponding to the complex shear modulus, G =
= G′
G′ +
+ iG″, where G′ is the tissue storage modulus describing elastic behavior and G″ is the tissue loss modulus describing viscous behavior. From G we formulated two composite measures: the viscoelastic shear stiffness, μ
iG″, where G′ is the tissue storage modulus describing elastic behavior and G″ is the tissue loss modulus describing viscous behavior. From G we formulated two composite measures: the viscoelastic shear stiffness, μ =
= 2|G|2/(G′
2|G|2/(G′ +
+ |G|) [Manduca et al., 2001], and damping ratio, ξ
|G|) [Manduca et al., 2001], and damping ratio, ξ =
= G″/2G′ [Cook, 2007]. The shear stiffness describes the resistance of a viscoelastic solid to a harmonic shear stress at the actuation frequency, while the damping ratio governs the attenuation of motion at the actuation frequency (for ξ
G″/2G′ [Cook, 2007]. The shear stiffness describes the resistance of a viscoelastic solid to a harmonic shear stress at the actuation frequency, while the damping ratio governs the attenuation of motion at the actuation frequency (for ξ >
> 1, motion decays rapidly without oscillation). These two composite properties are more closely related to common mechanical parameters reported in MRE of the brain [Murphy et al., 2011; Sack et al., 2013; Schregel et al., 2012].
1, motion decays rapidly without oscillation). These two composite properties are more closely related to common mechanical parameters reported in MRE of the brain [Murphy et al., 2011; Sack et al., 2013; Schregel et al., 2012].
Population measurements
The method described above returned μ and ξ measures for each of the six SGM structures investigated (Am, Hc, Ca, Pu, Pa, and Th) in our population of 21 healthy participants. Here, we report the mean and standard deviation (SD) for each measure in each region. Additionally, inversion of the same data was performed without SPR to calculate global viscoelasticity of the cerebrum. Global cerebral property measures excluded CSF through tissue type segmentation of the T 1‐weighted images using FAST in FSL [Zhang et al., 2001].
To investigate if structures exhibit different μ and ξ, we performed repeated measures analyses of variance (ANOVAs) with subject and region as the independent variables, and tested individual relationships through post hoc paired t‐tests. Significance was determined at P <
< 0.05 following Holm–Bonferroni correction for multiple comparisons [Holm, 1979]. We similarly analyzed whether SGM properties were correlated across subjects by performing post hoc linear correlations and also correcting for multiple comparisons.
0.05 following Holm–Bonferroni correction for multiple comparisons [Holm, 1979]. We similarly analyzed whether SGM properties were correlated across subjects by performing post hoc linear correlations and also correcting for multiple comparisons.
Estimate of Measurement Uncertainty
We estimated the uncertainty in the SGM viscoelasticity measures through the set of repeated examinations on one volunteer. This uncertainty is expressed as the coefficient of variation (CV) equal to the SD across examinations divided by the mean. We report CV for both μ and ξ for each of the six SGM structures investigated.
Sources of uncertainty
As the proposed method combines both MRE displacement fields and SGM masks to generate property measures, it stands to reason that uncertainty in the measurement could derive from either source. To explore the relative contributions from displacement fields and masks to the measurement uncertainty, we registered the masks from each of the eight segmented T
1‐weighted images to each of the eight captured MRE displacement fields for the repeated measures subject. This resulted in a matrix of 64 measures for each of the six SGM structures. For each structure, we performed a two‐way ANOVA with the component displacement field and mask set as the independent variables. From the sum‐of‐squares error (SSE), we computed the effect sizes for displacement field and mask set,
SGM mask evaluation
We further evaluated the differences in SGM masks that were applied to the MRE data. First, the CV in SGM volume for each structure was determined using the eight individual T
1‐weighted segmentations. Then, after registering these masks to the MRE dataset, we compared the amount of overlap between masks to investigate uncertainty in the registration. We calculated the Dice coefficient for all pairs of masks stemming from registration of the different segmentations to a given MRE displacement field. The Dice coefficient for any two masks, A and B, is
Influence of Experimental Parameters
We explored the influence of two methodological considerations on SGM property measures: the use of SPR weighting during inversion and spatial resolution of the imaging acquisition.
To investigate the role of SPR in the proposed method, we also calculated the SGM properties from inversions without SPR, both for the population measurements and repeated examinations. As we expected SPR to result in SGM properties that were more distinct relative to the surrounding tissue represented by a global average, we calculated effect sizes (Cohen's d [Cohen, 1988]) from the t‐statistic of each paired t‐test between SGM structure and the cerebrum, such that
We also calculated material properties using different imaging resolutions. In addition to the acquired 1.6 mm isotropic resolution data, we downsampled the displacement fields to 2.0 mm isotropic resolution by truncation in frequency space. The 2.0 mm resolution had approximately twice the total voxel volume as compared to the 1.6 mm resolution—8.0 mm3 versus 4.1 mm3. For each dataset acquired, SGM viscoelastic properties were calculated at each spatial resolution, and both effect size and uncertainty analyses were performed, as described above.
RESULTS
Figure Figure22 presents the shear stiffness (μ) measures for the different SGM structures across the population, including the first examination from the repeated subject. ANOVA indicated that there is a significant difference in μ among SGM structures (P <
< 0.05), although post hoc comparisons found only a handful of significant differences between structures (Fig. (Fig.2C).2C). The Hc is significantly softer than all other structures, including the neighboring Am, and the Pu is stiffer than the Ca. However, all regions, except the Hc, are stiffer than the cerebrum, suggesting a commonality in the cytoarchitecture of SGM that results in high μ. Figure Figure33 similarly describes SGM damping ratio (ξ). In this case, nearly all relationships between structures are significant, with the Ca having the greatest ξ and the Hc having the smallest. Again, all SGM structures differed from the cerebrum, which has a greater ξ, except for the Ca. There is no relation between either μ or ξ of the SGM structures and their volume.
0.05), although post hoc comparisons found only a handful of significant differences between structures (Fig. (Fig.2C).2C). The Hc is significantly softer than all other structures, including the neighboring Am, and the Pu is stiffer than the Ca. However, all regions, except the Hc, are stiffer than the cerebrum, suggesting a commonality in the cytoarchitecture of SGM that results in high μ. Figure Figure33 similarly describes SGM damping ratio (ξ). In this case, nearly all relationships between structures are significant, with the Ca having the greatest ξ and the Hc having the smallest. Again, all SGM structures differed from the cerebrum, which has a greater ξ, except for the Ca. There is no relation between either μ or ξ of the SGM structures and their volume.
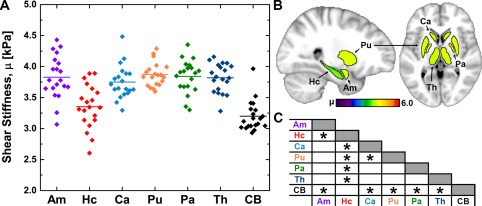
Overview of shear stiffness, μ, measurements at 50 Hz in the population: (A) distribution of properties of each SGM structure and the cerebrum (CB), with line indicating population mean; (B) mean properties of each structure in standard space; (C) chart indicating significant differences between structures found through post hoc paired t‐test (P <
< 0.05 after Holm–Bonferroni correction). [Color figure can be viewed at http://wileyonlinelibrary.com]
0.05 after Holm–Bonferroni correction). [Color figure can be viewed at http://wileyonlinelibrary.com]
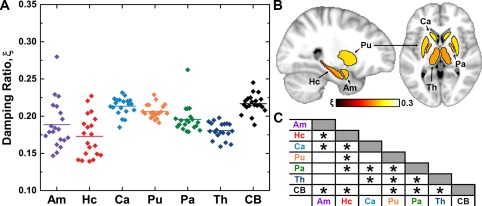
Overview of damping ratio, ξ, measurements at 50 Hz in the population: (A) distribution of properties of each SGM structure and the cerebrum (CB), with line indicating population mean; (B) mean properties of each structure in standard space; (C) chart indicating significant difference between structures found through post hoc paired t‐test (P <
< 0.05 after Holm–Bonferroni correction). [Color figure can be viewed at http://wileyonlinelibrary.com]
0.05 after Holm–Bonferroni correction). [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure Figure44 illustrates how the properties of each structure track together across subjects. Most structures correlated with each other for μ while there is only one pair that is significantly correlated in ξ (Am and Hc). However, if the properties of the cerebrum are used as a control variable, a smaller set of significant relationships remain (Fig. (Fig.44E,F).
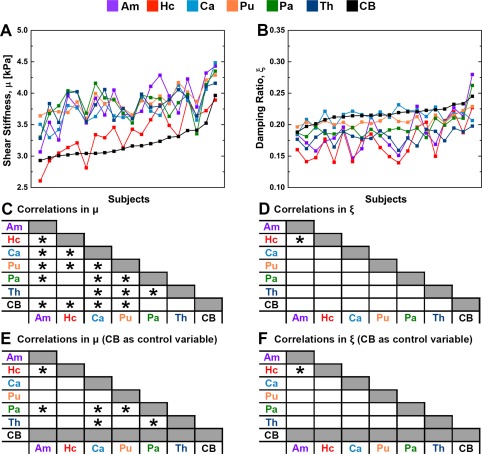
Measured properties of each structure at 50 Hz for all subjects, sorted by the properties of the cerebrum: (A) μ and (B) ξ. Charts indicating significant relationships between structures found through post hoc linear correlations: (C) μ and (D) ξ; and (E‐F) the relationships using cerebrum properties as a control variable. Significance is determined at P <
< 0.05 after Holm–Bonferroni correction. [Color figure can be viewed at http://wileyonlinelibrary.com]
0.05 after Holm–Bonferroni correction. [Color figure can be viewed at http://wileyonlinelibrary.com]
Table Table11 reports the results of the uncertainty analysis from the repeated measurements for both μ and ξ. The CV for each measure is presented as an estimate of the measurement uncertainty, and, in general, most of the CVs fall between 3 and 7%, with Hc μ being slightly higher at 7.1% and Pu μ lower at 2.4%. In contrast, the CVs for global measures are smaller, 1.4% for μ and 2.1% for ξ, which is expected given the much larger volume of the global regions.
Table 1
Analysis of uncertainty for observed shear stiffness, μ, and damping ratio, ξ, from repeated measurements: coefficient of variation and contributions from displacement field and SGM mask
| Shear stiffness, μ (kPa) | Damping ratio, ξ | |||||
|---|---|---|---|---|---|---|
| CV (SPR) |
|
| CV (SPR) |
|
| |
| Amygdala | 5.2% | 0.975 | 0.011 | 6.8% | 0.967 | 0.010 |
| Hippocampus | 7.1% | 0.983 | 0.007 | 5.1% | 0.936 | 0.042 |
| Caudate | 3.4% | 0.979 | 0.003 | 3.7% | 0.976 | 0.005 |
| Putamen | 2.4% | 0.973 | 0.006 | 4.2% | 0.980 | 0.002 |
| Pallidum | 5.7% | 0.979 | 0.006 | 5.7% | 0.976 | 0.002 |
| Thalamus | 6.8% | 0.994 | 0.001 | 3.6% | 0.967 | 0.004 |
| Cerebrum | 1.4% | – | – | 2.1% | – | – |
We also include in Table Table11 the effect sizes used to portion the measurement variance between experimental and computational aspects of the measurement. In all measures, the MRE displacement field used has very large effect sizes, with
Table 2
Description of bilateral SGM volume from FreeSurfer segmentation, reported as mean (standard deviation), and variability in SGM masks: uncertainty in segmentation and Dice overlap after registration to MRE displacement field
| FreeSurfer volume (cm3) | Volume uncertainty (CV) | Registered volume (Dice overlap) | |
|---|---|---|---|
| Amygdala | 3.50 (0.35) | 3.6% | 0.766 |
| Hippocampus | 9.53 (0.83) | 1.6% | 0.801 |
| Caudate | 8.45 (0.89) | 2.5% | 0.825 |
| Putamen | 12.01 (0.99) | 3.1% | 0.850 |
| Pallidum | 3.18 (0.27) | 5.8% | 0.737 |
| Thalamus | 18.52 (1.37) | 3.3% | 0.886 |
Compared to the uncertainty of SGM measures from the proposed method, the CV for each measure calculated without the use of SPR is considerably greater. Figure Figure5A5A presents the CV for each SGM measure, calculated both with and without SPR, and the CVs for measures without SPR are, on average, approximately two times larger. Figure Figure5B5B also contrasts the effect sizes, d, for each measure, both with and without SPR, relative to the cerebrum. In all cases, d for measures with SPR are greater than for those without SPR and the ratio between the two is typically in the range of 1.5 to 4.5, indicating improved ability to separate local and global properties using SPR.
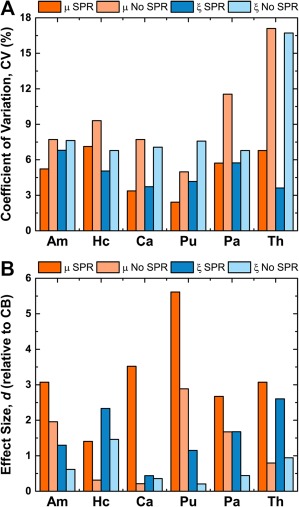
The use of soft prior regularization (SPR) improves the SGM viscoelastic property measures, μ and ξ. (A) Coefficient of variation, CV, for each SGM property measured with and without SPR. Without SPR, the CV for each measure is much larger indicating greater measurement uncertainty. (B) Effect size (Cohen's d) of difference between SGM properties and those of the entire cerebrum (CB) as measured using SPR and without. For all measures, d is greater with SPR, demonstrating the improved measurement sensitivity. [Color figure can be viewed at http://wileyonlinelibrary.com]
Table Table33 presents the population statistics (mean and SD) for both μ and ξ across all SGM structures. Also included are the population measures calculated using the same procedure, but from motion fields that have been downsampled to the poorer 2.0 mm isotropic resolution. Figure Figure66 contrasts the performance of the proposed method using both 1.6 and 2.0 mm spatial resolutions. For each SGM structure, we compare the difference in effect sizes, d, and uncertainty, CV, between the two resolutions. In general, for μ measures, d decreases and CV increases for the 2.0 mm spatial resolution (compared to 1.6 mm) for all structures except Th (Fig. (Fig.6A).6A). Similar differences were found for ξ, again with the 2.0 mm resolution exhibiting poorer effect sizes and uncertainty in each structure (Fig. (Fig.6B).6B). These results demonstrate the greater measurement sensitivity and smaller uncertainty with the improved 1.6 mm spatial resolution.
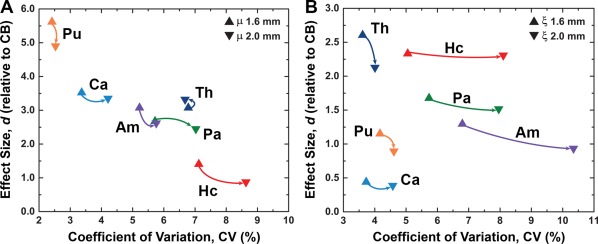
Lower spatial resolution increases measurement uncertainty and reduces sensitivity. Comparison of coefficient of variation, CV, and effect size, d, for (A) μ and (B) ξ measurements from data at 1.6 and 2.0 mm isotropic voxel size (arrows point from 1.6 to 2.0 mm for each structure). For all measures except Th μ, the use of the lower 2.0 mm resolution resulted in both higher CV and lower d, demonstrating the gains from using higher resolution imaging when investigating SGM structures. [Color figure can be viewed at http://wileyonlinelibrary.com]
Table 3
Population statistics for shear stiffness, μ, and damping ratio, ξ, at 50 Hz calculated using different isotropic image resolutions: 1.6 mm (acquired) and 2.0 mm (downsampled)
| Shear stiffness, μ (kPa) | Damping ratio, ξ | |||
|---|---|---|---|---|
| 1.6 mm | 2.0 mm | 1.6 mm | 2.0 mm | |
| Amygdala | 3.83 (0.35) | 3.63 (0.31) | 0.189 (0.032) | 0.198 (0.034) |
| Hippocampus | 3.35 (0.35) | 3.30 (0.35) | 0.173 (0.028) | 0.177 (0.028) |
| Caudate | 3.75 (0.27) | 3.84 (0.29) | 0.213 (0.012) | 0.216 (0.013) |
| Putamen | 3.87 (0.19) | 3.88 (0.17) | 0.206 (0.009) | 0.211 (0.009) |
| Pallidum | 3.84 (0.26) | 3.80 (0.24) | 0.196 (0.018) | 0.199 (0.019) |
| Thalamus | 3.82 (0.23) | 3.89 (0.21) | 0.181 (0.011) | 0.185 (0.014) |
| Cerebrum | 3.20 (0.24) | 3.28 (0.26) | 0.217 (0.013) | 0.220 (0.014) |
Reported as mean (standard deviation).
DISCUSSION
The method for measuring SGM viscoelasticity proposed in this work combines MRE imaging with high spatial resolution and NLI with SPR to improve the material property measures in the small SGM structures. The MRE acquisition used a 1.6 mm isotropic spatial resolution, which we previously demonstrated to improve local property measures [Johnson et al., 2014]. SPR is used to further amplify the benefits of spatial resolution by promoting local homogeneity in the pre‐defined SGM regions. An SPR weighting of α =
= 10−9 was chosen empirically to balance the separation of properties from the background from the homogenization of properties due to over‐regularization (see Supporting Information and Figure S1). Using this procedure, we measured the viscoelasticity of six SGM structures—Am, Hc, Ca, Pu, Pa, and Th—in healthy young adults. We report average bilateral properties of these structures, as our population did not exhibit significant left–right differences in any of the structures (see Supporting Information and Tables S1 and S2).
10−9 was chosen empirically to balance the separation of properties from the background from the homogenization of properties due to over‐regularization (see Supporting Information and Figure S1). Using this procedure, we measured the viscoelasticity of six SGM structures—Am, Hc, Ca, Pu, Pa, and Th—in healthy young adults. We report average bilateral properties of these structures, as our population did not exhibit significant left–right differences in any of the structures (see Supporting Information and Tables S1 and S2).
Each of the SGM μ values reported here are greater than the global μ, primarily comprising WM. The prevailing notion is that cortical GM is softer than WM, which has been reported in several in vivo human brain MRE studies [Braun et al., 2014; Johnson et al., 2013a; Kruse et al., 2008] and is typically consistent with mechanical interrogations of ex vivo animal brains [Feng et al., 2013; van Dommelen et al., 2010; Velardi et al., 2006] despite large variations in testing procedures. However, SGM structures are commonly found to be stiffer relative to WM, consistent with the data reported in this work. In porcine brains, the thalamus was found to be as stiff [van Dommelen et al., 2010] or stiffer [Prange and Margulies, 2002] than WM. Similarly, the hippocampus is stiffer than WM in the adult rat brain [Elkin et al., 2011; Finan et al., 2012].
Comparing the viscoelastic property values for SGM structures reported here with those from previous MRE efforts is more challenging. Guo et al. found the Ca to be softer than the Th, with both being softer than global WM [Guo et al., 2013]. We found no significant difference in μ between the Ca and Th, and our report of higher ξ in the Ca also contradicts their lack of difference in mechanical phase angle, which is a similar measure of relative elastic and viscous contributions.
Despite the apparent incongruity of these results, the MRE approach used by Guo et al. (MDEV; [Hirsch et al., 2014]) required collecting four sets of MRE data at different excitation frequencies (30‐60 Hz) to generate spatially‐resolved composite viscoelastic property measures, and the well‐documented frequency‐dependent behavior of tissue [Klatt et al., 2007; Sinkus et al., 2007] is essentially averaged over the four frequencies, weighted by the relative amplitude of each frequency component. High frequencies have substantially higher stiffness (μ at 62.5 Hz is approximately 1.8 times greater than at 25 Hz [Sack et al., 2009]) and attenuate much faster. Therefore, regions further from the primary motion sources of the skull, falx, and tentorium [Clayton et al., 2012] are weighted toward low frequencies in the MDEV inversion and appear softer. Our method only requires MRE data at a single excitation frequency, thus all regions of the brain are evaluated at a consistent frequency. Additionally, our method includes using higher imaging resolution, SPR, and a heterogeneous material model, which, together, likely account for the higher relative stiffness measures for SGM structures near CSF, as demonstrated by the analysis of SPR and resolution effects.
We also report SGM structures to be much stiffer than in Guo et al., and also have a lower damping ratio. Part of this discrepancy is due to how values are recovered and reported (i.e., shear stiffness, μ, vs. magnitude of shear modulus, |G|; damping ratio, ξ, vs. mechanical phase angle, ϕ). As mentioned above, the multifrequency MRE approach of Guo et al. incorporates a wide range of frequencies in generating a single property value that can be biased toward to lower frequencies and substantially lower shear moduli [Guo et al., 2013]. Additionally, the very high ϕ values reported in that work are likely attributable to noise sensitivity of the inversion scheme used, as demonstrated recently [Dittmann et al., 2016].
The finding that the SGM structures are largely correlated in μ, or that they track together between subjects, is very similar to a previous finding by Murphy et al. [2013] between lobes of the brain. This suggests that SGM structures share some common global stiffness but coupled with subject‐specific variations, which has implications for how the measurements are used on the individual subject or patient level in the future. This concept appears to be much less strong in ξ where the only significant relationship exists between the Am and Hc—both located in the medial temporal lobe—and is unchanged by the consideration of global properties. This may support the sensitivity of ξ that we reported previously for the Hc [Schwarb et al., 2016].
The estimated measurement uncertainties are small—CVs between 3 and 7% for SGM structures—and are comparable to those previously reported in the literature for other brain MRE studies. Sack et al. reported variations in stiffness of 4.5% in a single slice [Sack et al., 2008], while Murphy et al. reported 3.1% stiffness variation in whole‐brain WM [Murphy et al., 2011]. We previously found CVs of approximately 5% for the global complex shear modulus [Johnson et al., 2013a], with variations ranging between 5 and 9% in WM tracts [Johnson et al., 2013a] and between 2‐9% in the frontal lobe [McGarry et al., 2013]. Of particular note is the recent work by Murphy et al., which reported CVs for global stiffness less than 1% and stiffness of individual lobes less than 2% [Murphy et al., 2013] using an inversion technique designed to remove uncertainty stemming from nearby tissues and CSF. This approach is similar in spirit to our proposed method, although over much larger lobe regions.
In almost all measures, the CV is less than the intersubject variation across the young, healthy population examined in this work (see Figs. Figs.22 and and33 and Table Table3),3), and in some cases, the population variation is as much as three times greater (Hc ξ). Given that the CVs reported in the present work are both less than the population variation, and also comparable to CVs reported in other brain MRE studies, we can conclude that properties determined with our proposed method are useful measures of the true mechanical properties of SGM structures.
We suggest that the measurement reliability reported here is a product of the considerations of the proposed method aimed at improving SGM property measures. In particular, the use of SPR is included to reduce the influence of nearby tissues and CSF on the SGM structures that increase measurement uncertainty and reduce sensitivity. This is evidenced by our finding that individual SGM structure CVs from the proposed method incorporating SPR are, on average, two times smaller than measures without SPR. SPR also improves the sensitivity of the SGM measurements by allowing the structure boundary to be better defined relative to the surrounding tissue and CSF, and thus better detect processes that differentially affect SGM. In this work, we use the relationship between SGM properties and those of the cerebrum as a surrogate marker for sensitivity as represented by effect size, d, which is reduced in all measures when not using SPR. Taken together, the improvements in CV and d speak to the critical role of SPR in examining fine SGM structures with MRE.
We further considered the sources of measurement uncertainty in the proposed method, from both the acquired MRE displacement field and the SGM masks used with SPR, and found that the overwhelming majority of the variance can be attributed to the imaged displacements (
Identifying SGM structures from T 1‐weighted images can be performed in several different ways, including automatic segmentation with packages like FreeSurfer [Fischl et al., 2002] and FIRST in FSL [Patenaude et al., 2011], or through manual tracing. While automatic methods differ from each other and from manual tracing in estimating SGM volume, these methods, and FreeSurfer in particular, have been shown to produce reliable volume estimates [Cherbuin et al., 2009; Doring et al., 2011; Morey et al., 2009]. The CVs for each structure volume in this study are consistent with those reported in other works using FreeSurfer [Jovicich et al., 2009; Maclaren et al., 2014].
Further variations in mask creation are potentially introduced through registration with FLIRT in FSL [Jenkinson et al., 2002] to linearly transform the SGM volumes into MRE data space prior to inversion. Our repeatability analysis naturally included the effects of potential misalignment due to registration, and we captured this by comparing the masks from different T 1‐weighted images and segmentations registered to the same MRE displacement field. Through the Dice overlap coefficient for each structure we find that each mask shares on the order of 75–85% of its voxels with any other mask. Given that the variation in mask size from FreeSurfer is on the order of 2–5% prior to registration, it stands to reason that the variations in final mask are not due to segmentation alone but are also due to uncertainty in the registration step.
Despite the uncertainty associated with the SGM volume masks due to segmentation and registration, these variations have minimal downstream effect on our MRE property measures. This indicates that the method presented in this work is robust to the small differences in performance between proven software packages. However, it should be noted that these masks are still realistic representations of the SGM structures in their correct anatomical location, and that large errors in the size, shape, or placement of the mask should not be expected to have a similarly negligible effect.
The observation that the MRE displacement field accounts for almost all of the uncertainty in the SGM viscoelasticity measurements is not surprising, as there are many potential sources of error in the acquisition and inversion of brain MRE data, including imaging artifacts, model/data mismatch, and inadequate spatial resolution.
SGM regions are particularly susceptible to artifacts in the images acquired to capture the MRE motion field, including residual field inhomogeneity distortions and motion‐induced phase errors [Johnson et al., 2014], as well as g‐factor penalties from parallel imaging with SENSE [Pruessmann et al., 2001]. While the image acquisition and reconstruction used in this work is designed to overcome these effects, future strategies may further minimize the residual artifacts and improve SGM property measures.
Errors also arise during inversion when the chosen material model does not appropriately describe the underlying tissue behavior. Viscoelasticity, represented by the complex shear modulus, is the most widely used material model for inversion in brain MRE, although this model for attenuation may be inappropriate in SGM. Alternative material models, including Rayleigh damping [McGarry and Van Houten, 2008; Van Houten et al., 2011] and poroelasticity [McGarry et al., 2015; Pattison et al., 2014], may better explain attenuation in SGM structures and have shown promise in brain MRE [Johnson et al., 2013b; Weaver et al., 2012]. And, while GM is generally considered to be isotropic [Prange and Margulies, 2002; Velardi et al., 2006], the structure of SGM includes axonal pathways and may benefit from a direction‐dependent material model as has been used in WM [Anderson et al., 2016; Romano et al., 2012].
One source of uncertainty not considered in this work is the expected heterogeneity of the SGM structures themselves, particularly the hippocampus [Van Leemput et al., 2009] and thalamus [Wiegell et al., 2003], which comprise several subfields or nuclei that may exhibit unique mechanical properties. By applying SPR to heterogeneous regions, there is the possibility of further introducing modeling errors by attempting to enforce homogeneity where it is not appropriate [McGarry et al., 2013]. However, based on the observation of highly reliable property measures in all investigated SGM structures in this work, we do not feel that their level of heterogeneity is sufficient enough to affect our results. While we could apply a similar technique to subdivide these structures, it is unlikely that the current resolution of MRE would allow for reliable measures to be extracted, as evidenced by performance in regions of the medial temporal lobe cortex [Schwarb et al., 2016]. As the resolution of MRE is pushed further, such as with 7T scanners [Braun et al., 2014], the technique presented here may be adapted to probe subdivisions of these SGM structures.
The parameter most expected to play a significant role in MRE of SGM is the spatial resolution of the imaging acquisition, as we have previously demonstrated how greater resolution helps recover the properties of small structures [Johnson et al., 2013b, 2014]. Thus, we adopted a 1.6 mm isotropic resolution for our MRE acquisition—the highest brain MRE resolution reported at 3T field strength—to best capture the properties of the small SGM structures. Based on the population measures and the analysis of repeated examinations, we concluded that the measures from the proposed method are reliable. Many MRE studies use poorer resolution with 3 mm isotropic voxel size [Murphy et al., 2013; Zhang et al., 2011]; our analysis suggests that these sequences would likely be less effective at resolving small SGM structures with single frequency data.
However, we also explored the effect of resolution on the SGM property measures by downsampling the imaged displacement fields prior to inversion. Compared to the measures from data at the native 1.6 mm resolution, measures from data at 2.0 mm resolution exhibited reduced sensitivity and increased uncertainty (see Fig. Fig.6).6). These differences are modest—average decreases in d and increases in CV of 13% and 23%, respectively—and one measure actually exhibited a small trend in the opposite direction (Th μ). These findings support the idea that the greater 1.6 mm resolution improved our property measures, but also that using the lower 2.0 mm resolution does not preclude SGM measurements using the proposed method, provided that more samples would be needed to achieve the same statistical power. This is further reflected in the recovery of very similar average property values, regardless of resolution, across our sample of 21 subjects (see Table Table3).3). We note that our analysis does not capture other benefits of acquiring data with lower resolution, including reduced scan time or greater SNR, which may improve SGM measurements at 2.0 mm resolution. The data presented in this work have sufficient SNR for stable inversion [McGarry et al., 2011], although the interaction of resolution, SPR regularization, and noise level is a topic for future study and optimization. Our current analysis, however, clearly points to the gains from improved spatial resolution and suggests further resolution advancements as one avenue to maximizing the quality of the SGM property measures in future studies.
CONCLUSIONS
The localization of viscoelastic property measurements to specific neuroanatomical regions has enabled brain MRE investigations of areas that are differentially affected in neurodegenerative conditions and play a significant role in cognitive performance. In this work, we further extend this localization to SGM structures through a method that combines high‐resolution MRE imaging with an inversion scheme designed to improve property measures in pre‐defined regions. In a population of healthy, young adult volunteers, we found that, in general, each SGM structure (amygdala, hippocampus, caudate, putamen, pallidum, and thalamus) exhibited different viscoelasticity, as represented by the shear stiffness and damping ratio, and that these structures also differed from the global viscoelasticity of the cerebrum. Through analyses of repeated examinations we found that these measurements are reliable, and that the specific methodological considerations included—using higher spatial resolution and SPR weighting during inversion—both decreased uncertainty and increased sensitivity. Together, this report of a reliable method for MRE of SGM structures provides a framework for future studies investigating degeneration of SGM and its relationship with function and cognition.
ACKNOWLEDGMENTS
The Biomedical Imaging Center of the Beckman Institute at the University of Illinois supported collection of the MRI data. The Blue Waters sustained‐petascale computing project at the National Center for Supercomputing Applications at the University of Illinois provided computational resources. The authors have no conflicts of interest with regards to this work.
REFERENCES
- Anderson AT, Van Houten EEW, McGarry MDJ, Paulsen KD, Holtrop JL, Sutton BP, Georgiadis JG, Johnson CL (2016): Observation of direction‐dependent mechanical properties in the human brain with multi‐excitation MR elastography. J Mech Behav Biomed 59:538–546. [Europe PMC free article] [Abstract] [Google Scholar]
- Arani A, Murphy MC, Glaser KJ, Manduca A, Lake DS, Kruse SA, Jack CR, Ehman RL, Huston J (2015): Measuring the effects of aging and sex on regional brain stiffness with MR elastography in healthy older adults. NeuroImage 111:59–64. [Europe PMC free article] [Abstract] [Google Scholar]
- Braak H, Braak E (1998): Evolution of neuronal changes in the course of Alzheimer's disease. J Neural Transm Suppl 53:127–140. [Abstract] [Google Scholar]
- Braun J, Guo J, Lutzkendorf R, Papazoglou S, Hirsch S, Sack I, Bernarding J (2014): High‐resolution mechanical imaging of the human brain by three‐dimensional multifrequency magnetic resonance elastography at 7T. NeuroImage 90:308–314. [Abstract] [Google Scholar]
- Buckner RL (2004): Memory and executive function in aging and AD. Neuron 44:195–208. [Abstract] [Google Scholar]
- Cherbuin N, Anstey KJ, Réglade‐Meslin C, Sachdev PS (2009): In vivo hippocampal measurement and memory: A comparison of manual tracing and automated segmentation in a large community‐based sample. PLoS One 4:e5265. [Europe PMC free article] [Abstract] [Google Scholar]
- Clayton EH, Genin GM, Bayly PV (2012): Transmission, attenuation and reflection of shear waves in the human brain. J R Soc Interface 9:2899–2910. [Europe PMC free article] [Abstract] [Google Scholar]
- Cohen J (1988): Statistical Power Analysis for the Behavioral Sciences. Mahwah, NJ: Lawrence Erlbaum Associates. [Google Scholar]
- Cohen NJ, Squire LR (1980): Preserved learning and retention of pattern‐analyzing skill in amnesia: Dissociation of knowing how and knowing that. Science 210:207–210. [Abstract] [Google Scholar]
- Cook RD (2007): Concepts and Applications of Finite Element Analysis. New York: Wiley. [Google Scholar]
- Dittmann F, Hirsch S, Tzschätzsch H, Guo J, Braun J, Sack I (2016): In vivo wideband multifrequency MR elastography of the human brain and liver. Magn Reson Med 76:1116–1126. [Abstract] [Google Scholar]
- Doring TM, Kubo TTA, Cruz LCH Jr, Juruena MF, Fainberg J, Domingues RC, Gasparetto EL (2011): Evaluation of hippocampal volume based on MR imaging in patients with bipolar affective disorder applying manual and automatic segmentation techniques. J Magn Reson Imaging 33:565–572. [Abstract] [Google Scholar]
- Elkin BS, Ilankovan AI, Morrison B III (2011): A detailed viscoelastic characterization of the P17 and adult rat brain. J Neurotraum 28:2235–2244. [Abstract] [Google Scholar]
- Feng Y, Namani R, Okamoto RJ, Genin GM, Bayly PV (2013): Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J Mech Behav Biomed 23:117–132. [Europe PMC free article] [Abstract] [Google Scholar]
- Finan JD, Elkin BS, Pearson EM, Kalbian IL, Morrison BIII (2012): Viscoelastic properties of the rat brain in the sagittal plane: Effects of anatomical structure and age. Ann Biomed Eng 40:70–78. [Abstract] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert MS, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM (2002): Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron 33:341–355. [Abstract] [Google Scholar]
- Funai AK, Fessler JA, Yeo DTB, Olafsson VT, Noll DC (2008): Regularized field map estimation in MRI. IEEE Trans Med Imaging 27:1484–1494. [Europe PMC free article] [Abstract] [Google Scholar]
- Guo J, Hirsch S, Fehlner A, Papazoglou S, Scheel M, Braun J, Sack I (2013): Towards an elastographic atlas of brain anatomy. PLoS One 8:e71807. [Europe PMC free article] [Abstract] [Google Scholar]
- Hirsch S, Guo J, Reiter R, Papazoglou S, Kroencke T, Braun J, Sack I (2014): MR Elastography of the Liver and the Spleen Using a Piezoelectric Driver, Single‐Shot Wave‐Field Acquisition, and Multifrequency Dual Parameter Reconstruction. Magn Reson Med 71:267–277. [Abstract] [Google Scholar]
- Holm S (1979): A simple sequentially rejective multiple test procedure. Scand J Stat 6:65–70. [Google Scholar]
- Jack CR, Knopman DS, Jagust WJ, Shaw LM, Aisen PS, Weiner MW, Petersen RC, Trojanowski JQ (2010): Hypothetical model of dynamic biomarkers of the Alzheimer's pathological cascade. Lancet Neurol 9:119–128. [Europe PMC free article] [Abstract] [Google Scholar]
- Jenkinson M, Bannister PR, Brady M, Smith SM (2002): Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage 17:825–841. [Abstract] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM (2012): FSL. NeuroImage 62:782–790. [Abstract] [Google Scholar]
- Johnson CL, McGarry MDJ, Gharibans AA, Weaver JB, Paulsen KD, Wang H, Olivero WC, Sutton BP, Georgiadis JG (2013a): Local mechanical properties of white matter structures in the human brain. NeuroImage 79:145–152. [Europe PMC free article] [Abstract] [Google Scholar]
- Johnson CL, McGarry MDJ, Van Houten EEW, Weaver JB, Paulsen KD, Sutton BP, Georgiadis JG (2013b): Magnetic resonance elastography of the brain using multishot spiral readouts with self‐navigated motion correction. Magn Reson Med 70:404–412. [Europe PMC free article] [Abstract] [Google Scholar]
- Johnson CL, Holtrop JL, McGarry MDJ, Weaver JB, Paulsen KD, Georgiadis JG, Sutton BP (2014): 3D multislab, multishot acquisition for fast, whole‐brain MR elastography with high signal‐to‐noise efficiency. Magn Reson Med 71:477–485. [Europe PMC free article] [Abstract] [Google Scholar]
- Jovicich J, Czanner S, Han X, Salat D, van der Kouwe A, Quinn B, Pacheco J, Albert MS, Killiany R, Blacker D, Maguire P, Rosas D, Makris N, Gollub R, Dale A, Dickerson BC, Fischl B (2009): MRI‐derived measurements of human subcortical, ventricular and intracranial brain volumes: Reliability effects of scan sessions, acquisition sequences, data analyses, scanner upgrade, scanner vendors and field strengths. NeuroImage 46:177–192. [Europe PMC free article] [Abstract] [Google Scholar]
- Klatt D, Hamhaber U, Asbach P, Braun J, Sack I (2007): Noninvasive assessment of the rheological behavior of human organs using multifrequency MR elastography: A study of brain and liver viscoelasticity. Phys Med Biol 52:7281–7294. [Abstract] [Google Scholar]
- Kruse SA, Rose GH, Glaser KJ, Manduca A, Felmlee JP, Jack CR, Ehman RL (2008): Magnetic resonance elastography of the brain. NeuroImage 39:231–237. [Europe PMC free article] [Abstract] [Google Scholar]
- Laforce R Jr, Doyon J (2001): Distinct contribution of the striatum and cerebellum to motor learning. Brain Cogn 45:189–211. [Abstract] [Google Scholar]
- Lipp A, Trbojevic R, Paul F, Fehlner A, Hirsch S, Scheel M, Noack C, Braun J, Sack I (2013): Cerebral magnetic resonance elastography in supranuclear palsy and idiopathic Parkinson's disease. NeuroImage Clin 3:381–387. [Europe PMC free article] [Abstract] [Google Scholar]
- Maclaren J, Han Z, Vos SB, Fischbein N, Bammer R (2014): Reliability of brain volume measurements: A test‐retest dataset. Sci Data 1:140037–140039. [Europe PMC free article] [Abstract] [Google Scholar]
- Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, Felmlee JP, Greenleaf JF, Ehman RL (2001): Magnetic resonance elastography: Non‐invasive mapping of tissue elasticity. Med Image Anal 5:237–254. [Abstract] [Google Scholar]
- McGarry MDJ, Van Houten EEW (2008): Use of a Rayleigh damping model in elastography. Med Biol Eng Comput 46:759–766. [Abstract] [Google Scholar]
- McGarry MDJ, Van Houten EEW, Perriñez PR, Pattison AJ, Weaver JB, Paulsen KD (2011): An octahedral shear strain‐based measure of SNR for 3D MR elastography. Phys Med Biol 56:N153–N164. [Europe PMC free article] [Abstract] [Google Scholar]
- McGarry MDJ, Van Houten EEW, Johnson CL, Georgiadis JG, Sutton BP, Weaver JB, Paulsen KD (2012): Multiresolution MR elastography using nonlinear inversion. Med Phys 39:6388–6396. [Europe PMC free article] [Abstract] [Google Scholar]
- McGarry MDJ, Johnson CL, Sutton BP, Van Houten EEW, Georgiadis JG, Weaver JB, Paulsen KD (2013): Including spatial information in nonlinear inversion MR elastography using soft prior regularization. IEEE Trans Med Imaging 32:1901–1909. [Europe PMC free article] [Abstract] [Google Scholar]
- McGarry MDJ, Johnson CL, Sutton BP, Georgiadis JG, Van Houten EEW, Pattison AJ, Weaver JB, Paulsen KD (2015): Suitability of poroelastic and viscoelastic mechanical models for high and low frequency MR elastography. Med Phys 42:947–957. [Europe PMC free article] [Abstract] [Google Scholar]
- Morey RA, Petty CM, Xu Y, Hayes JP, Wagner HRII, Lewis DV, LaBar KS, Styner M, McCarthy G (2009): A comparison of automated segmentation and manual tracing for quantifying hippocampal and amygdala volumes. NeuroImage 45:855–866. [Europe PMC free article] [Abstract] [Google Scholar]
- Murphy MC, Huston J, Jack CR, Glaser KJ, Manduca A, Felmlee JP, Ehman RL (2011): Decreased brain stiffness in Alzheimer's Disease determined by magnetic resonance elastography. J Magn Reson Imaging 34:494–498. [Europe PMC free article] [Abstract] [Google Scholar]
- Murphy MC, Huston J, Jack CR, Glaser KJ, Senjem ML, Chen J, Manduca A, Felmlee JP, Ehman RL (2013): Measuring the characteristic topography of brain stiffness with magnetic resonance elastography. PLoS One 8:e81668. [Europe PMC free article] [Abstract] [Google Scholar]
- Murphy MC, Jones DT, Jack CR, Glaser KJ, Senjem ML, Manduca A, Felmlee JP, Carter RE, Ehman RL, Huston J (2016): Regional brain stiffness changes across the Alzheimer's disease spectrum. NeuroImage Clin 10:283–290. [Europe PMC free article] [Abstract] [Google Scholar]
- Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL (1995): Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science 269:1854–1857. [Abstract] [Google Scholar]
- Patenaude B, Smith SM, Kennedy DN, Jenkinson M (2011): A Bayesian model of shape and appearance for subcortical brain segmentation. NeuroImage 56:907–922. [Europe PMC free article] [Abstract] [Google Scholar]
- Pattison AJ, McGarry MDJ, Weaver JB, Paulsen KD (2014): Spatially‐resolved hydraulic conductivity estimation via poroelastic magnetic resonance elastography. IEEE Trans Med Imaging 33:1373–1380. [Europe PMC free article] [Abstract] [Google Scholar]
- Prange MT, Margulies SS (2002): Regional, directional, and age‐dependent properties of the brain undergoing large deformation. J Biomech Eng 124:244–252. [Abstract] [Google Scholar]
- Pruessmann KP, Weiger M, Börnert P, Boesiger P (2001): Advances in sensitivity encoding with arbitrary k‐space trajectories. Magn Reson Med 46:638–651. [Abstract] [Google Scholar]
- Raz N, Lindenberger U, Rodrigue KM, Kennedy KM, Head D, Williamson A, Dahle C, Gerstorf D, Acker JD (2005): Regional brain changes in aging healthy adults: General trends, individual differences and modifiers. Cereb Cortex 15:1676–1689. [Abstract] [Google Scholar]
- Riek K, Millward JM, Hamann I, Mueller S, Pfueller CF, Paul F, Braun J, Infante‐Duarte C, Sack I (2012): Magnetic resonance elastography reveals altered brain viscoelasticity in experimental autoimmune encephalomyelitis. NeuroImage Clin 1:81–90. [Europe PMC free article] [Abstract] [Google Scholar]
- Romano AJ, Scheel M, Hirsch S, Braun J, Sack I (2012): In vivo waveguide elastography of white matter tracts in the human brain. Magn Reson Med 68:1410–1422. [Abstract] [Google Scholar]
- Sack I, Beierbach B, Hamhaber U, Klatt D, Braun J (2008): Non‐invasive measurement of brain viscoelasticity using magnetic resonance elastography. NMR Biomed 21:265–271. [Abstract] [Google Scholar]
- Sack I, Beierbach B, Wuerfel J, Klatt D, Hamhaber U, Papazoglou S, Martus P, Braun J (2009): The impact of aging and gender on brain viscoelasticity. NeuroImage 46:652–657. [Abstract] [Google Scholar]
- Sack I, Streitberger K‐J, Krefting D, Paul F, Braun J (2011): The influence of physiological aging and atrophy on brain viscoelastic properties in humans. PLoS One 6:e23451. [Europe PMC free article] [Abstract] [Google Scholar]
- Sack I, Jöhrens K, Wuerfel J, Braun J (2013): Structure‐sensitive elastography: On the viscoelastic powerlaw behavior of in vivo human tissue in health and disease. Soft Matter 9:5672–5680. [Google Scholar]
- Schregel K, Wuerfel E, Garteiser P, Gemeinhardt I, Prozorovski T, Aktas O, Merz H, Petersen D, Wuerfel J, Sinkus R (2012): Demyelination reduces brain parenchymal stiffness quantified in vivo by magnetic resonance elastography. Proc Natl Acad Sci USA 109:6650–6655. [Europe PMC free article] [Abstract] [Google Scholar]
- Schwarb H, Johnson CL, McGarry MDJ, Cohen NJ (2016): Medial temporal lobe viscoelasticity and relational memory performance. NeuroImage 132:534–541. [Europe PMC free article] [Abstract] [Google Scholar]
- Sinkus R, Siegmann KC, Xydeas T, Tanter M, Claussen CD, Fink M (2007): MR elastography of breast lesions: Understanding the solid/liquid duality can improve the specificity of contrast‐enhanced MR mammography. Magn Reson Med 58:1135–1144. [Abstract] [Google Scholar]
- Streitberger K‐J, Sack I, Krefting D, Pfüller C, Braun J, Paul F, Wuerfel J (2012): Brain viscoelasticity alteration in chronic‐progressive multiple sclerosis. PLoS One 7:e29888. [Europe PMC free article] [Abstract] [Google Scholar]
- Sutton BP, Noll DC, Fessler JA (2003): Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans Med Imaging 22:178–188. [Abstract] [Google Scholar]
- Van AT, Hernando D, Sutton BP (2011): Motion‐induced phase error estimation and correction in 3D diffusion tensor imaging. IEEE Trans Med Imaging 30:1933–1940. [Abstract] [Google Scholar]
- van Dommelen JAW, van der Sande TPJ, Hrapko M, Peters GWM (2010): Mechanical properties of brain tissue by indentation: Interregional variation. J Mech Behav Biomed 3:158–166. [Abstract] [Google Scholar]
- Van Houten EEW, Paulsen KD, Miga MI, Kennedy FE, Weaver JB (1999): An overlapping subzone technique for MR‐based elastic property reconstruction. Magn Reson Med 42:779–786. [Abstract] [Google Scholar]
- Van Houten EEW, Miga MI, Weaver JB, Kennedy FE, Paulsen KD (2001): Three‐dimensional subzone‐based reconstruction algorithm for MR elastography. Magn Reson Med 45:827–837. [Abstract] [Google Scholar]
- Van Houten EEW, Viviers DV, McGarry MDJ, Perriñez PR, Perreard IM, Weaver JB, Paulsen KD (2011): Subzone based magnetic resonance elastography using a Rayleigh damped material model. Med Phys 38:1993–2004. [Europe PMC free article] [Abstract] [Google Scholar]
- Van Leemput K, Bakkour A, Benner T, Wiggins G, Wald LL, Augustinack J, Dickerson BC, Golland P, Fischl B (2009): Automated segmentation of hippocampal subfields from ultra‐high resolution in vivo MRI. Hippocampus 19:549–557. [Europe PMC free article] [Abstract] [Google Scholar]
- Velardi F, Fraternali F, Angelillo M (2006): Anisotropic constitutive equations and experimental tensile behavior of brain tissue. Biomech Model Mech 5:53–61. [Abstract] [Google Scholar]
- Weaver JB, Pattison AJ, McGarry MDJ, Perreard IM, Swienckowski JG, Eskey CJ, Lollis SS, Paulsen KD (2012): Brain mechanical property measurement using MRE with intrinsic activation. Phys Med Biol 57:7275–7287. [Europe PMC free article] [Abstract] [Google Scholar]
- Wiegell MR, Tuch DS, Larsson H, Wedeen VJ (2003): Automatic segmentation of thalamic nuclei from diffusion tensor magnetic resonance imaging. NeuroImage 19:391–401. [Abstract] [Google Scholar]
- Wuerfel J, Paul F, Beierbach B, Hamhaber U, Klatt D, Papazoglou S, Zipp F, Martus P, Braun J, Sack I (2010): MR‐elastography reveals degradation of tissue integrity in multiple sclerosis. NeuroImage 49:2520–2525. [Abstract] [Google Scholar]
- Wylezinska M, Cifelli A, Jezzard P, Palace J, Alecci M, Matthews PM (2003): Thalamic neurodegeneration in relapsing‐remitting multiple sclerosis. Neurology 60:1949–1954. [Abstract] [Google Scholar]
- Zhang Y, Brady M, Smith SM (2001): Segmentation of brain MR images through a hidden Markov random field model and the expectation‐maximization algorithm. IEEE Trans Med Imaging 20:45–57. [Abstract] [Google Scholar]
- Zhang J, Green MA, Sinkus R, Bilston LE (2011): Viscoelastic properties of human cerebellum using magnetic resonance elastography. J Biomech 44:1909–1913. [Abstract] [Google Scholar]
Articles from Human Brain Mapping are provided here courtesy of Wiley
Full text links
Read article at publisher's site: https://doi.org/10.1002/hbm.23314
Read article for free, from open access legal sources, via Unpaywall:
https://rss.onlinelibrary.wiley.com/doi/am-pdf/10.1002/hbm.23314
Citations & impact
Impact metrics
Citations of article over time
Alternative metrics
Smart citations by scite.ai
Explore citation contexts and check if this article has been
supported or disputed.
https://scite.ai/reports/10.1002/hbm.23314
Article citations
Low-frequency MR elastography reveals altered deep gray matter viscoelasticity in multiple sclerosis.
Neuroimage Clin, 42:103606, 16 Apr 2024
Cited by: 0 articles | PMID: 38669859
Viscoelastic polyacrylamide MR elastography phantoms with tunable damping ratio independent of shear stiffness.
J Mech Behav Biomed Mater, 154:106522, 22 Mar 2024
Cited by: 0 articles | PMID: 38537609
Associations between vascular health, brain stiffness and global cognitive function.
Brain Commun, 6(2):fcae073, 29 Feb 2024
Cited by: 1 article | PMID: 38505229 | PMCID: PMC10950054
Association Between Anatomic and Clinical Indicators of Injury Severity After Moderate-Severe Traumatic Brain Injury: A Pilot Study Using Multiparametric Magnetic Resonance Imaging.
Neurotrauma Rep, 5(1):232-242, 13 Mar 2024
Cited by: 0 articles | PMID: 38524727 | PMCID: PMC10960168
Estimating the viscoelastic properties of the human brain at 7 T MRI using intrinsic MRE and nonlinear inversion.
Hum Brain Mapp, 44(18):6575-6591, 01 Nov 2023
Cited by: 3 articles | PMID: 37909395 | PMCID: PMC10681656
Go to all (70) article citations
Data
Data behind the article
This data has been text mined from the article, or deposited into data resources.
BioStudies: supplemental material and supporting data
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
High-resolution magnetic resonance elastography reveals differences in subcortical gray matter viscoelasticity between young and healthy older adults.
Neurobiol Aging, 65:158-167, 06 Feb 2018
Cited by: 61 articles | PMID: 29494862 | PMCID: PMC5883326
Standard-space atlas of the viscoelastic properties of the human brain.
Hum Brain Mapp, 41(18):5282-5300, 15 Sep 2020
Cited by: 27 articles | PMID: 32931076 | PMCID: PMC7670638
Mechanical properties of the in vivo adolescent human brain.
Dev Cogn Neurosci, 34:27-33, 10 Jun 2018
Cited by: 36 articles | PMID: 29906788 | PMCID: PMC6289278
MR elastography of the brain and its application in neurological diseases.
Neuroimage, 187:176-183, 07 Oct 2017
Cited by: 80 articles | PMID: 28993232 | PMCID: PMC5889749
Review Free full text in Europe PMC
Funding
Funders who supported this work.
NIBIB NIH HHS (3)
Grant ID: R01 EB018230
Grant ID: R37 EB001981
Grant ID: R01 EB001981
NIMH NIH HHS (1)
Grant ID: R01 MH062500
National Multiple Sclerosis Society (1)
Grant ID: IL‐1503‐03395
 1
,
2
1
,
2





