Abstract

1 Introduction

Alternative splicing (AS), the process by which segments of pre-mRNA can be arranged in different subsets to yield distinct mature transcripts, is a major contributor to transcriptome complexity. In humans, over 90% of multi-exon genes are alternatively spliced, and most of these exhibit splicing variations which are tissue- or condition-dependent (Pan et al., 2008). This key role of AS in transcriptome complexity, combined with the fact that aberrant splicing is commonly associated with disease state (Wang and Cooper, 2007), has led to various research efforts. These include efforts to accurately map transcriptome complexity and identify splicing variations between different cellular conditions, across developmental stages, or between cohorts of patients and controls.

Detection of splicing variations and the mapping of transcriptome complexity has been greatly facilitated by the development of high-throughput technologies to sequence transcripts, collectively known as RNA-Seq. Briefly, RNA from the cells of interest, typically poly-A selected or ribo-depleted, are sheared to a specific size range, amplified, and sequenced. In most technologies used today, the resulting sequence reads are typically around 100 bp with read number varying greatly, from around 20 to 200 M reads. The shortness of the reads, their sparsity, and various experimental biases make inference about changes in RNA splicing a challenging computational problem (Alamancos et al., 2014). To aid RNA-Seq based analysis, many studies include samples which are biological replicates of the conditions being studied. Replicates are a key component in helping researchers distinguish between the biological variability of interest (e.g. differences between two tissues) and variability associated with experimental or technical factors. However, what constitutes a ‘good’ replicate or an outlier experiment is not always clear. Intuitively, in the context discussed here, an outlier is a sample which exhibits disproportionately large deviations in exon inclusion levels compared with other samples from the same experimental condition (biological replicates). An outlier could be the result of a failed experiment or of some hidden deviation in sample identity (i.e. different tissue source). Remarkably, despite the obvious importance of the question of what constitutes an outlier, this question has been mostly ignored in the literature. Instead, researchers are left to define outliers based on heuristics which may not be accurate or carry unconscious biases. For example, in a recent work focused on good practices for RNA-Seq data analysis, the authors recommend performing PCA analysis to see if samples from the same condition ‘cluster together’ but admit ‘no clear standard exists for biological replicates’ (Conesa et al., 2016). As we demonstrate here, the presence of outliers can have deleterious effects on algorithms that aim to detect differential splicing (DS) between groups of replicates from different conditions. Thus an important contribution of this work is to formalize what constitutes an outlier replicate and suggest a method which researchers could use to detect outliers before applying any DS algorithm.

A second contribution of this work is in assessing the effect of outliers on DS algorithms and, more broadly, producing a general framework with matching datasets for assessing the performance of DS algorithms. Generally, DS algorithms can be divided into two classes. The first, which includes tools such as RSEM (Li and Dewey, 2011) and Cuffdiff (Trapnell et al., 2012), aims to quantify full gene isoforms, typically by assuming a known transcriptome and assigning the observed reads to the various gene isoforms in the given transcriptome database. The second class of algorithms, which includes rMATS (Shen et al., 2014) and DEXSeq (Anders et al., 2012), works at the exon level, detecting differential inclusion of exons or exonic fragments. Some algorithms, such as SUPPA (Entizne et al., 2017), can be considered a hybrid as they collapse isoform abundance estimates from other algorithms such as Salmon (Patro et al., 2017) to compute relative exon inclusion levels. Previous works showed that for the task of DS, quantification algorithms that work at the exon level generally perform better since they solve a simpler task and are less sensitive to isoform definitions or RNA-Seq biases within samples or along full isoforms (Liu et al., 2014). Thus, for the comparative analysis section of this paper, we focus on the second class of algorithms, and specifically the commonly used DEXSeq, rMATS, as well as the recently updated SUPPA, all of which support replicates. Using these algorithms and the one we propose (MAJIQ-lw) we detail here several metrics to assess DS algorithm performance based on biological or technical replicates. We also develop a synthetic dataset where each sample is generated so as to model a matching real sample.

A third contribution of this work is in developing MAJIQ-lw, an adaption of our recently published MAJIQ algorithm (Vaquero-Garcia et al., 2016) to automatically detect and downweight samples and splicing variations suspected to be outliers. MAJIQ offers a combined solution to detect, quantify, and visualize DS between experimental conditions with or without replicates. Besides the details of its statistical model and its visualization capabilities, two key features distinguish MAJIQ from the DS algorithms mentioned above. First, MAJIQ allows users to supplement previous transcriptome annotation with reliably detected de novo junctions, which results in over 30% increase in detection of differential variations and robustness to transcriptome definitions (Vaquero-Garcia et al., 2016). Second, MAJIQ uses a novel formulation for transcript variations. It does not quantify whole gene isoforms as the first class of algorithms described, nor does it use only the previously defined AS ‘types’ (e.g. cassette exons) as the second class of algorithms. Instead, MAJIQ defines a more general concept of ‘local splicing variations’, or LSVs. Briefly, LSVs are defined as splits in a gene splice graph where a reference exon is spliced together with other segments downstream or upstream of it (see Fig. 1a). Importantly, the formulation of LSVs enables MAJIQ to capture all previously defined types of AS but also many other variations which are more complex (see Fig. 1b and c). Similar to classical AS events, LSVs are quantified by the fraction of inclusion of each of the junctions, termed percent spliced in (PSI, $\psi \in [0,1]$), see Fig. 1d). However, despite its novel features and capabilities, the original MAJIQ algorithm was not built to handle outlier replicates. Indeed, we show here that such outliers can significantly affect MAJIQ’s performance. In contrast, the new generalization of MAJIQ, denoted MAJIQ-lw, offers a DS algorithm which is not only robust to outliers but can also salvage useful information from outlier samples. In order to demonstrate this improved performance, we perform extensive comparative analysis of the new MAJIQ to the original algorithm as well as the other algorithms listed earlier.

Open in a separate window

Fig. 1.

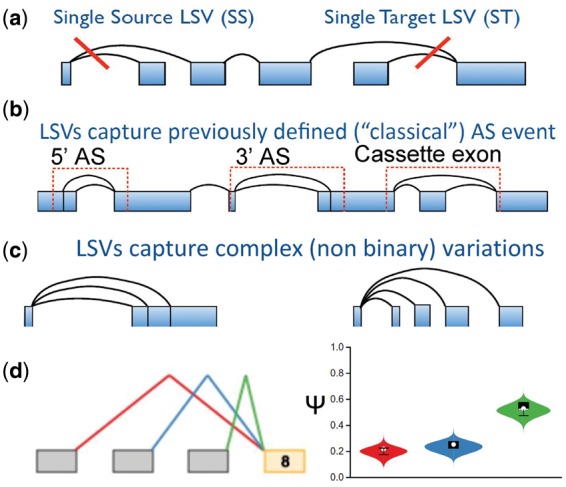
Illustration of LSVs. (a) LSVs are splits in a gene splice graph where multiple edges spawn out from (single-source, 5’ split) or merge into (single-target, 3’ join) a reference exon. (b) The LSV definition captures classical binary splicing event types. (c) The LSV definition can capture complex variations that involve more than two junctions. (d) A sample from MAJIQ’s output for a single-target LSV involving Exon 8 of Clta gene in mouse cerebellum. MAJIQ quantifies the LSV shown on the left by the marginal inclusion level (${\psi }_j\in [0,1]$) of each of the possible junction j, estimating a posterior distribution over those (right, in matching order). Similarly, when comparing two conditions, a distribution over $\Delta {\psi }_j\in [-1,1]$ is derived (not shown)

2 Materials and methods

2.1 Outlier weight model

Let ${\psi }_{i,j}^t$ be the inclusion ratio of junction j of LSV i within experiment t, such that ${\sum }_{j=1}^J{\psi }_{i,j}^t=1$, with $i\in [1\dots L],\hspace{0.17em}t\in \mathbf{T}=[1\dots T]$, and $j\in \mathbf{J}=[1\dots J]$. Notably, we never observe ${\psi }_{i,j}^t$ directly, only junction spanning reads drawn according to it. Consequently, the MAJIQ model does not infer ${\psi }_{i,j}^t$ as a point estimate but rather as a posterior beta distribution, denoted $P({\Psi }_{i,j}^t$) or, with slight abuse of notation, simply ${\Psi }_{i,j}^t$ (Vaquero-Garcia et al., 2016). Importantly for the discussion here, MAJIQ assumes that all the experiments are replicates of the same biological condition denoted $\mathcal{T}$ (e.g. tissue type, treatment, disease state) such that they share an underlying (hidden) junction inclusion levels, denoted ${\psi }_{i,j}^{\mathcal{T}},\hspace{0.17em}\forall i,j,t\in \mathcal{T}$. Under this model, an outlier$s\in [1\dots T]$ is an experiment which significantly deviates from ${\psi }_{i,j}^{\mathcal{T}}$ for a disproportionately large set of LSVs.

In order to make the above definition formal we first need to specify a way to estimate ${\psi }_{i,j}^{\mathcal{T}}$ or at least a distribution over its possible values. We use the median over ${\left\{{\Psi }_{i,j}^t\right\}}_{t=1}^T$, denoted ${\widehat{\Psi }}_{i,j}^{\mathcal{T}}$, as a proxy for ${\Psi }_{i,j}^{\mathcal{T}}$ and quantify the degree to which an experiment’s ${\Psi }_{i,j}^t$ deviates from ${\widehat{\Psi }}_{i,j}^{\mathcal{T}}$ using the L₁ divergence:

$$d_1({\Psi }_{i,j}^t,{\widehat{\Psi }}_{i,j}^{\mathcal{T}})=\frac{1}{2}{\int }_0^{\mathrm{1}}|P({\psi }_{i,j}^t)-P({\widehat{\psi }}_{i,j}^{\mathcal{T}})|d\psi .$$

(1)

This allows us to define the deviation of sample t for LSV i as ${\phi }_{t,i}={\max }_j{d}_1({\Psi }_{i,j}^t,{\widehat{\Psi }}_{i,j}^{\mathcal{T}})$. According to our model, when all experiments are true biological replicates they should all have a similar distribution of ${\phi }_{t,i}$ over $i\in [1\dots L]$. Outliers however, will have a distribution skewed towards higher values, reflecting an accumulation of LSVs for which ${\phi }_{t,i}$ is high. This skew towards high ${\phi }_{t,i}$ values is illustrated in Figure 2 by the blue line (outlier) compared with the red and green lines (true replicates). To capture such skewness, we find $K_t=\left|\right\{i:{\phi }_{t,i}>\tau \left\}\right|$, i.e. the number of highly-disagreeing LSVs for each experiment t, where τ is an arbitrary threshold for strong disagreement. In the experiments described below we used $\tau =0.75$ but we find that results were robust to changes in τ value as long as it was reasonably high (see blue line in Fig. 2). Theoretically, if all experiments are equally ‘well-behaved’, we expect K_t to follow a binomial distribution $K_t\sim \text{Binom}(K_T,p)$, where $p=\frac{1}{T}$ is the equal probability for every sample to ‘misbehave’ and K_T is the union over all LSVs that have a highly disagreeing experiment, $K_T=\left|\right\{i:\exists t,{\phi }_{t,i}>\tau \left\}\right|$. In practice, we find the distribution of K_t to have higher dispersion which we model using a Beta Binomial such that $p\sim \text{Beta}\left(\frac{\alpha }{T},\alpha \left(1-\frac{1}{T}\right)\right)$. We set α = 5 and observe that outlier detection and consequent local weights model described next were robust to α’s setting even when considering GTEx samples from different individuals (see Supplementary Figures). Finally, we set the weight ${\rho }_t\in [0,1]$ representing our belief that sample t belongs to condition $\mathcal{T}$ using the following ratio test: We compute the probability mass for the tail of the beta binomial probability P_BB for the observed number of highly disagreeing LSVs K_t, divided by the tail from the excepted $\frac{K_T}{T}$ under the null-hypothesis:

$${\rho }_t=\min \left(1,\frac{P_{\text{BB}}(X>K_t)}{P_{\text{BB}}\left(X>\frac{K_T}{T}\right)}\right).$$

(2)

Open in a separate window

Fig. 2.

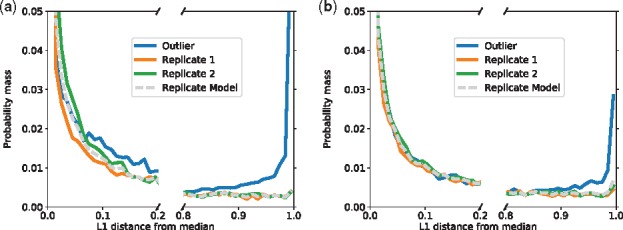
Per-experiment empirical PDF over LSVs L₁ divergences from group median. The L1 divergence (${\phi }_{t,i}$) is defined in Section 2.1. Each solid line represents a different RNA-seq experiment (t). The gray dashed line represents a replicate model as described in Section 2.2. (a) A swap case of three ‘replicates’ from Zhang et al. (2014) with two liver samples (green, red) and an outlier, ‘mislabeled’, muscle sample (blue). (b) Same as in (a) but a less extreme case where less LSVs have extreme divergence from the median. Here the blue outlier was produced by synthetically perturbing 10% of the LSVs by 10% in a cerebellum sample at the same coverage level (see Section 2.5). In both scenarios most LSVs have low divergence (${\phi }_{t,i}<0.2$) but a small fraction of LSVs in the blue outlier have ${\phi }_{t,i}>0.5$

This formulation has the desired characteristic that ρ = 1 for ‘well behaved’ experiments for which K_t is less than the expected $\frac{K_T}{T}$, while other experiments are penalized by their deviation from this expected value in proportion to the tail of the null distribution. In the new MAJIQ implementation users can now invoke the option to compute these weights for groups of replicates to detect possible outliers. We note that since the LSVs in the experiments are expected to be quantified in any case, the computational overhead associated with these weight computations is negligible.

In addition, the above global weight per-experiment ρ_t can be plugged into MAJIQ to produce a generalized version of the previous MAJIQ algorithm:

$$P\left({\Psi }_{i,j}^t\right|{\left\{R_{i,j}^{t,\text{inc}}\right\}}_{t\in \mathbf{T}},{\left\{R_{i,j}^{t,\text{exc}}\right\}}_{t\in \mathbf{T}})=\text{Beta}\left({\sum }_{t\in \mathbf{T}}{\rho }_t{R}_{i,j}^{t,\text{inc}},{\sum }_{t\in \mathbf{T}}{\rho }_t{R}_{i,j}^{t,\text{exc}}\right),$$

(3)

where $R_{i,j}^{t,\text{inc}},R_{i,j}^{t,\text{exc}}$ represent estimated read rates supporting inclusion or exclusion of a specific junction. Details of how these read rates are derived from observed reads are given in (Vaquero-Garcia et al., 2016). Also, we note these weights and above computation is done per condition $\mathcal{T}$ and does not change when two conditions are compared with compute $\Delta \Psi$. In the evaluations that follow, we refer to the resulting MAJIQ model with global weights per experiments as MAJIQ-gw while the previous MAJIQ model with no weighting scheme is denoted MAJIQ-nw.

3 Results

To demonstrate the robustness of both the global (MAJIQ-gw) and local (MAJIQ-lw) weighting algorithms, we applied the synthetic perturbation procedure in Section 2.5 to one experiment in a group of three cerebellum samples from (Zhang et al., 2014), varying each of the three hyperparameters $\theta ,\delta ,\gamma$ while holding the other two fixed. We compared these new generalizations of MAJIQ to both the previous algorithm (MAJIQ-nw) run with the outlier sample and to a case where we assume some heuristic (e.g. PCA) was able to detect and remove the outlier before the old algorithm was run (MAJIQ-rm). Figure 3 shows the effect of varying each hyper-parameter on the global weight associated with that experiment ($\hspace{0.17em}{\text{log}}_{10}{\rho }_t$, left column), the number (N_A, middle column) of LSVs reported as differentially spliced with high confidence ($P(|\Delta \Psi |>0.2)>0.95$), and the RR ($R{R}_A(N_A)$, right column). At $\delta =0.6,\gamma =1$ (a-c, top row), the outlier’s weight ρ_t scales linearly in log scale to the fraction of LSVs perturbed (θ) such that perturbing 10% is sufficient to drop ρ_t below 0.1. Consequently, the original MAJIQ-nw detects ~900 additional events which are likely to be false positives as reproducibility drops down to ~60%, while the N_A and RR for both weighting algorithms (MAJIQ-gw and MAJIQ-lw) remain stable (Fig. 3b and c). Notably, the power of MAJIQ-lw to detect changing LSVs under control conditions of no outliers ($\theta =0.0$) is approximately that of the old MAJIQ-nw and slightly exceeds that of MAJIQ-gw, possibly due to the heterogeneous nature of the replicates (different circadian time points). When outlier LSVs are added ($\theta >0.0$) MAJIQ-gw and even more so MAJIQ-lw maintain robust RR while being able to identify more changing LSVs (N_A) compared with simply removing the sample as in MAJIQ-rm. At $\theta =0.3,\gamma =1$ (Fig. 3d–f, middle row), increasing δ initially causes the weight on the outlier to decrease towards a nonzero infimum. For larger $\delta >0.5$, the original $N_{\text{MAJIQ}-\text{nw}}$ increases over 3-fold with a corresponding 45% drop in RR, indicating these are likely false positives. At $\theta =0.3,\delta =0.6$ (Fig. 3g–i, bottom row), decreasing γ towards 0 causes the outlier weight to shrink below ${10}^{-8}$, suggesting that the algorithm is sensitive to a sample with very low read counts. Indeed, with very few reads the estimated $\Psi$ distribution does not vary significantly from the prior in most cases but the sample has minimal effect on the posterior for the group as it contributes only few reads. This is reflected in the fact that the original MAJIQ-nw is not affected too at such low coverage levels. Unsurprisingly, increasing the read rates to 150% (Fig. 3g–i for x-axis $\delta =1.5$) does not significantly affect the weight, which remains very low. It does, however, increase the unreliability of the original MAJIQ, more than doubling $N_{\text{MAJIQ}-\text{nw}}$ while nearly halving $R{R}_{\text{MAJIQ}-\text{nw}}$, again indicating a high FPR. In summary, we find that in all synthetic perturbation schemes we tested both MAJIQ-gw and MAJIQ-lw where able remain resistant to the perturbations. Both new algorithms and MAJIQ-lw in particular, exhibited improved statistical power and detected more changing LSVs than MAJIQ-rm while maintaining the same level of reproducibility. In contrast, the previous MAJIQ-nw detected many more changing LSVs which were FP, as indicated by a sharp drop in RR.

Open in a separate window

Fig. 3.

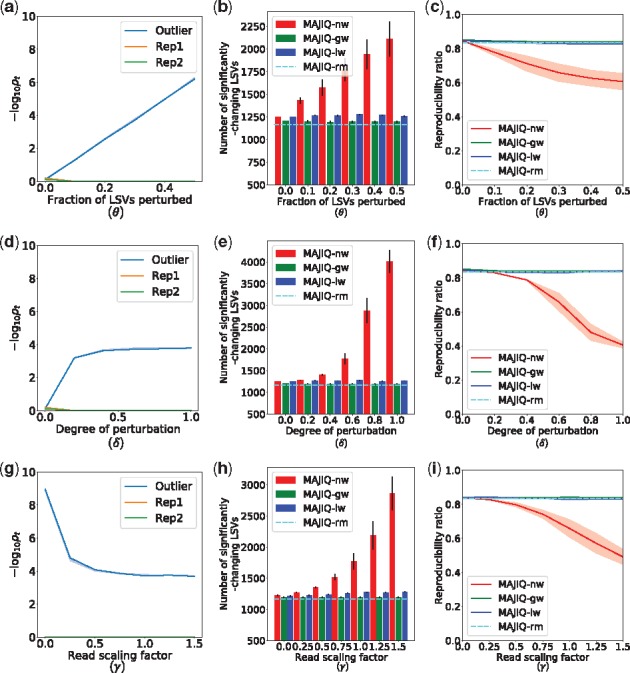
Synthetic perturbation of tissue replicates. In each test, three cerebella were compared against three livers from Zhang et al. (2014), but one of the cerebella was perturbed. Perturbation procedure detailed in Section 2.5. MAJIQ-nw is the previous algorithm equivalent to fixed weights (${\rho }_t=1$). MAJIQ-rm is a control case where we assume some heuristic (e.g. PCA) was able to detect the outlier and remove it before executing the previous fixed-weights MAJIQ. (a, d, g) Effect on ρ_t for the perturbed ‘outlier’ (blue) and unperturbed replicates (Rep1, 2 in green and orange). (b, e, h) Effect on the number N_A of events detected to have $P(\Delta \Psi >0.20)>0.95$ between the cerebellum and liver samples. (c, f, i) Effect on the RR(N), defined in Section 2.3. (a–c) θ, the fraction of LSVs perturbed, is varied between 0 and 0.5. At 0, the effect is the same as having no perturbation at all. (d–f) δ, the maximal amount by which $\Psi$ is perturbed, is varied between 0 and 1. δ = 0 is equivalent to no perturbation. (g–i) γ, the ‘read scaling factor’, is varied between 0 and 1.5. When this factor is 0, it is functionally equivalent to a global weight of 0

Given the above results, we decided to focus subsequent comparative analysis on MAJIQ with local-weights (MAJIQ-lw) and the original algorithm (MAJIQ-nw). Using the procedure described in Section 2.6 we created a synthetic dataset based on real RNA-Seq samples from (Keane et al., 2011), involving mouse liver and hippocampus with 5-6 biological replicates per tissue. Following a common criteria in the RNA splicing field we used $E[|\Delta \Psi |]\ge 20\%$ and $E[|\Delta \Psi |]\le 5\%$ to define the sets of events that are changing (CHG) and not changing (NO_CHG) respectively between conditions. Any events which may be considered borderline ($20\%>E[|\Delta \Psi |]>5\%$, denoted GREY) were removed from this analysis. We also tested another common threshold, $E[|\Delta \Psi |]\ge 10\%$, for defining changing events, with similar results (data not shown). We tested two configurations involving naive or realistic read simulation, and a third configuration where an outlier (swapped sample) was introduced. All tests included three samples in each group (see Supplementary Figures for a test involving the full set of five and six replicates). Each algorithm was evaluated based on its own definition of splicing variation. Figure 4 summarizes the results of this evaluation, with the outlier mostly affecting FNR and sensitivity. In all scenarios MAJIQ compared favorably with MAJIQ-lw capable of detecting more true events with reduced FNR when an outlier was introduced.

Open in a separate window

Fig. 4.

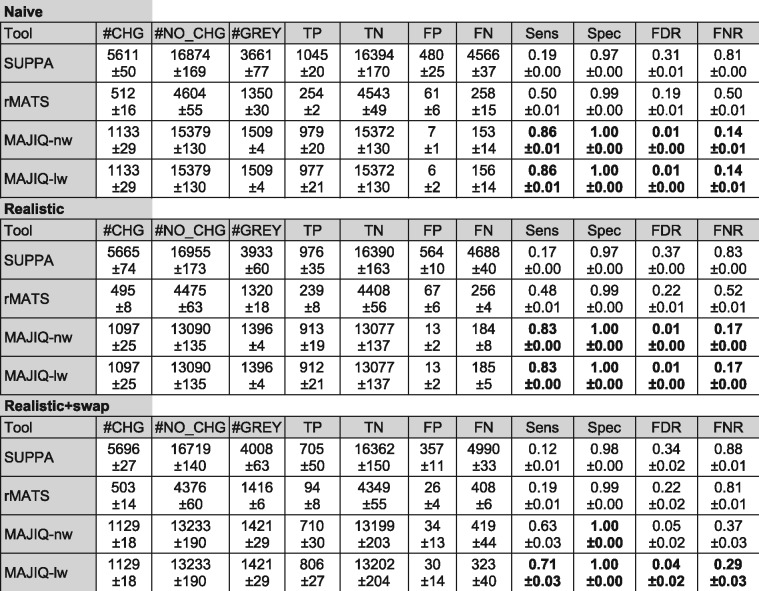
Evaluation using ‘realistic’ synthetic datasets. Each synthetic sample is created to match a real sample in terms of gene expression and a lower bound on transcriptome complexity. Three datasets were created: ‘Naive’ with naive read simulation (uniform coverage, no errors, biases or indels); ‘Realistic’ with more realistic read generation; ‘Realistic + swap’ where one sample in an outlier. All datasets involve three biological replicates per group. Each method was evaluated using its own definition of AS events, which means the number of events is not comparable between methods. CHG are changing events ($|E[\Delta \Psi ]|\ge 20\%$), NO_CHG are non changing events ($|E[\Delta \Psi ]|\le 5\%$), and GREY are events for which $20\%>|E[\Delta \Psi ]|>5\%$ and on which the algorithm is not evaluated. DEXSeq is not included here as it is not able to return dPSI values

Next, we turned to evaluating the algorithms’ performance on real data with and without a sample swap. In all cases, we used three cerebellum versus three liver for the validation Set 2. Set 1 included either 3 cerebellum compared with three liver samples (control, no swap) or two cerebellum and one muscle compared with three livers (swap case). We chose to evaluate these tissues specifically because of the large number of reproducibly changing LSVs between them (Vaquero-Garcia et al., 2016), though similar results were observed for other tissues as well as for a different dataset from (Keane et al., 2011) (see Supplementary Figures). To produce the reproducibility curves discussed below, we used the following procedure. For MAJIQ, N_A was defined as the set of events for which $P(|\Delta \Psi |\ge 0.2)>0.95$ and events were ranked by $|E[\Delta \Psi ]|$, as in (Vaquero-Garcia et al., 2016). rMATS was run with an equivalent threshold of 0.2 and for rMATS, SUPPA, and DEXSeq events were ranked by their respective p-values, with the significance threshold for all three methods set to the recommended P-value ≤ 0.05. We also tried ranking the events by $|E[\Delta \Psi ]|$ (rMATS, SUPPA) and $\hspace{0.17em}{\text{log}}_2\text{fold}\hspace{0.17em}\text{change}$ (DEXSeq), and plotting the RR graph without thresholding at P-value ≤ 0.05, which gave similar results (see Supplementary Figures). Finally, since DEXSeq is not geared for intron retention (IR) we excluded those (see Supplementary Figures including IR).

Figure 5a and matching Supplementary Figures summarize the RR results for the control (no swap) and outlier (swap) cases. As noted in Section 2.3, one immediate observation is the huge difference in the number of events reported as significantly changing (N_A), a consequence of the vastly different statistical criteria and event definition used by the various algorithms. Specifically, MAJIQ, which captures de-novo junctions and may combine multiple classical AS events into a single complex LSV, detects 22 766 events and 15 336 non overlapping ones while rMATS reports 18 732 events and SUPPA, which was run with RefSeq according to authors’ recommendation, only detects 7770 events. rMATS and MAJIQ report roughly 9% of the events as differentially spliced compared with 27% by SUPPA. DEXSeq which measures expression of exonic segments, naturally reports many more units detected (75 871) and finds about 40% of those to be differentially included (see Supplementary Fig. S2e for details).

Open in a separate window

Fig. 5.

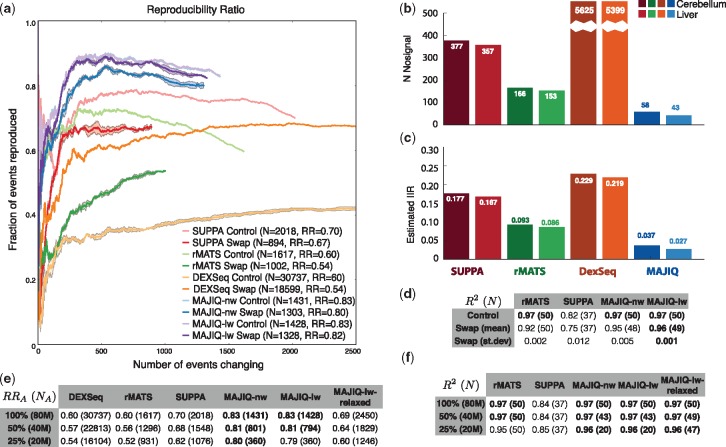
Evaluation using real data. (a)RR plots for detection of DS events between cerebellum and liver, with (Swap, dark line) or without (Control, faded line) a mislabeled muscle. The end of the line marks the point in the graph matching the number of events reported as significantly changing (RR(N_A), see main text). Because DEXSeq report more than 3000 significantly changing exonic segments, we present its extended RR curve in Supplementary Figures. (b) Number of events reported by each methods as significantly changing between two groups of biological replicates from the same condition (light color—liver, dark color—cerebellum). See Supplementary Material for equivalent plots when comparing groups of technical replicates. (c) The IIR, representing the ratio between the number of DS events reported when comparing biological or technical replicates (N_PFP) and the number of events reported when comparing similarly sized groups but from different conditions (N_A, see Section 2.3 for details). See Supplementary Figures for equivalent plots when N_PFP is derived using technical replicates. (d) The same control and swap experimental setup as in (a) with accuracy assessed using 50 RT-PCR experiments from (Vaquero-Garcia et al., 2016). Values represent fraction of variations explained (R²) and the number of events detected in parentheses. DEXSeq is not included here since it does not output $\Psi$ values. Scatterplots are presented in Supplementary Figures. Mean and SD derived by swapping out each of the cerebellum samples. (e, f) Repeating (a) and (d) but with subsets of the FASTQ files to test the effect of read coverage

As shown in Figure 5a, the RR(n) was typically noisy for low n, which is to be expected, but varied greatly between algorithms and between runs with or without an outlier. MAJIQ consistently exhibited higher reproducibility compared with other algorithms regardless of n, with MAJIQ-lw and MAJIQ-nw practically tied in the control case with no outlier ($\text{RR}(N_{\mathrm{A}})=83\%$, overlapping light purple and light blue curves). However, when an outlier was introduced the reproducibility of the previous MAJIQ-nw dropped to 80% (dark blue) while MAJIQ-lw identified more differential LSVs (1410 versus 1426) with higher reproducibility (82%, dark purple). Importantly, the number of reported events did not change much for MAJIQ-lw when the outlier was introduced, dropping by only 7% (1428 versus 1328), while maintaining similar reproducibility. In comparison, other algorithms were much more affected by the introduction of the outlier. Their number of events N_A drop between 40% (rMATS, DEXSeq) to 56% (SUPPA) while reproducibility dropped between 3% (SUPPA) to 6% (rMATS, DEXSeq) at RR(N_A). However, the RR(N_A) numbers by themselves do not capture the entire picture. DEXSeq maintained a RR of around 70% for the control case with n < 2000 compared with its RR(N_A) of only 60%, and all three algorithms suffered a drop of ~15–30% in reproducibility due to the outlier for the most high ranking events.

Next, we assessed the number of events reported by each method as DS between groups of biological or technical replicates from the same two conditions (liver, cerebellum) used in Figure 5a. Figure 5b and c show the resulting putative false positives (N_PFP) and IIR (IIR = $N_{\text{PFP}}/N_{\mathrm{A}}$) for each algorithm for biological replicates. See Supplementary Figures for a similar plot using technical replicates which results in lower IIR, as expected. Overall, MAJIQ maintained significantly lower N_PFP and IIR with DEXSeq exhibiting a particularly high IIR of over 20%.

Using 50 DS events quantified by Vaquero-Garcia et al. (2016) for the same two tissues from Zhang et al. (2014), we quantified the correlation between RNASeq based $E[\Delta \Psi ]$ and the RT-PCR quantifications, with and without an outlier sample. Figure 5b summarizes the accuracy of the various algorithms measured as the fraction of variations explained (R²). We found MAJIQ-lw, MAJIQ-nw, and rMATS gave similar R² values in the control case, with MAJIQ-lw performing the best in the outlier (swap) case. The lower number of events detected by SUPPA may be due to its usage of Refseq only transcripts as recommended by its authors, but may also reflect selection bias as (Vaquero-Garcia et al., 2016) originally selected events detectable by both rMATS and MAJIQ in order to compare these methods. DEXSeq was not included in this analysis since it is not able to produce PSI or dPSI estimates.

Finally, we tested the effect of read coverage levels on the various algorithms. In general, all methods take into account the number of reads that hit an AS event when assessing its statistical significance. Consequently, we do not expect to see a dramatic effect on the reproducibility of events deemed significantly changing (RR) but rather a significant reduction in the number of events detected as differentially spliced (N_A). Unlike other methods, MAJIQ relies solely on junction-spanning reads and is therefore likely to suffer more in detection power if its default parameters are not adjusted accordingly. We therefore tested two different MAJIQ execution configurations. The first is MAJIQ’s default settings, which are particularly conservative. These settings were designed for high reproducibility assuming multiple replicates with an average coverage of ~60 M and read length of 100 bases as in (Zhang et al., 2014). The second configuration, denoted ‘relaxed’, drops the quantifiable filter restrictions to allow the detection of junctions in a single experiment with as few as two reads mapping to two or more unique positions across the junction. We note that the other algorithms we analyzed do not have such coverage specific user adjustable parameters as these do no rely solely on junction spanning reads and as we show are less sensitive to changes in coverage.

By randomly sub-sampling the FASTQ files from (Zhang et al., 2014), read coverage was varied from the original average of 80 million reads (denoted 100%) through 40 million (50%) to 20 million (25%). The RR and detection power of each method evaluated is reported in Figure 5e, and correlations with RT-PCR quantifications in Figure 5f. In general, all methods lose power to detect differentially spliced events as coverage drops. As expected, MAJIQ run with default parameters is the most sensitive to sparse coverage, with detected events dropping up to 75%. When run with the relaxed parameters, MAJIQ-lw loses 50%, while rMATS, SUPPA, and DEXSeq lose 37, 32 and 48% respectively. However, MAJIQ’s conservative settings pay off in consistent high reproducibility of 79–83% compared with 61–70% for MAJIQ-lw with relaxed settings, and generally lower values for other algorithms. Similarly, when evaluating IIR we found MAJIQ-lw relaxed settings slightly increased the IIR by about 4% while detecting many more events overall (see Supplementary Figure). When evaluating the effect of sparse read coverage using the 50 RT-PCR experiments (Fig. 5f), we find a similar picture. It is worth noting that these 50 events were designed by (Vaquero-Garcia et al., 2016) to cover the wide range of read coverage levels across splicing events. Here, SUPPA and rMATS maintain the same number of detected events for all coverage levels and similar R² values. For MAJIQ, the default and the relaxed settings maintain high R² values which compare favorably to the other methods, but the default settings loses 62% of the events (19 versus 50).

4 Discussion

In this article, we developed a new model to automatically detect and downweight outliers in RNA-Seq datasets with replicates for DS analysis. The problem of detecting outliers in batches of biological replicates has not received much attention in the literature. As a result, researchers may include outliers that might affect their results, or discard samples before publication based on some heuristic such as PCA (Conesa et al., 2016). Using such a heuristic to discard samples may also reflect unconscious bias or cause good samples to be lost. Instead, we proposed a model for what constitutes an outlier sample in splicing analysis. This model is supported by our software, MAJIQ, so users can evaluate possible outliers regardless of which pipeline they use.

In addition, we developed an outlier weighing scheme and incorporated it into MAJIQ’s model either at the global, per-sample, level (MAJIQ-gw) or locally at the LSV level (MAJIQ-lw). Using both synthetic data perturbation and real data, we demonstrated that both MAJIQ-gw and MAJIQ-lw can maintain high levels of reproducibility when confronted with outliers. Furthermore, even when a sample is an outlier, using the local weight model (MAJIQ-lw) can help gain detection power by retaining LSVs which are ‘well-behaved’. In addition to sensitivity to outliers, we showed that low read coverage can also affect MAJIQ’s detection power as it relies on junction spanning reads. However, by adjusting MAJIQ’s default parameters, the new MAJIQ-lw was able to maintain high detection power with a moderate price in terms of reproducibility and correlation to RT-PCR, comparing favorably to other algorithms. Given that there is a natural trade-off between detection power and reproducibility, we recommend users decide between default and relaxed parameters based on their needs and dataset specifics.

Another contribution of this work is in developing a framework to tackle the challenge of evaluating DS algorithms based on both real and synthetic data. This work is definitely not the first to tackle this challenge, but most previous work focused on synthetic data using simplifying assumptions about binary AS events or transcript expression levels (Drewe et al., 2013; Entizne et al., 2017; Shen et al., 2014). Instead, we utilize biological replicates and create technical replicates by dividing the original FASTQ files. Using replicates we assess algorithms by using RR plots for DS events between different conditions, and by computing the IIR. The latter allows us to assess putative false positives with respect to DS between conditions and was in good qualitative agreement with FDR values we obtained from the synthetic dataset. We also use an extensive set of RT-PCR experiments from Vaquero-Garcia et al. (2016) to compute R² correlation to the algorithms’ $E[\Psi ]$ estimations from the matching RNASeq data. RT-PCR experiments are the gold standard in the RNA field and are indispensable for validation. In comparison, qPCR used in some other works (Drewe et al., 2013) can help validate significant splicing variations but is generally not considered suitable for quantitative assessment of splicing changes. RT-PCR can serve to measure PSI values as done here, but it must be executed and quantified carefully for this. For example, experiments need to be executed in triplicates with careful reading of the gel bands. Also, PCR primers need to be carefully mapped to each method’s quantified event for valid comparisons, and past studies have mostly focused on classical AS events types rather than the more complex ones (Vaquero-Garcia et al., 2016). In practice, much of the RT-PCR data available in publications have been produced only for validating significant splicing changes and as such may not be suitable for quantitative assessment of DS algorithms. Given these limitations we do not recommend automatic pulling of all available RT-PCR quantification across publications for assessing DS algorithms. Nonetheless, developing good quality sets of RT-PCR validations are important for DS algorithm assessment and we hope the work presented here will help achieve this goal.

Although the new version of MAJIQ compared favorably to other algorithms in the experiments surveyed here, users should keep in mind that different datasets may suffer from other types of noise or biases than those tested here. It is therefore advisable for potential users to always test DS algorithms using the evaluation criteria introduced here, including reproducibility plots, same condition group comparisons, and RT-PCR. To aid such evaluations, we made all the scripts used for this work available at majiq.biociphers.org. Similarly, we also made all datasets, including the synthetic data, available for developers to test against.

Another important point to consider is that the methods tested here differ greatly in the set of features they offer. MAJIQ is the only one that offers the ability to detect complex splicing variations involving more than two alternative junctions, coupled with interactive visualization and genome browser connectivity. It is also capable of supplementing a given transcriptome annotation with reliable de novo junctions detected in the RNA-Seq data, making it less dependent on the exact annotation. Although useful for even normal tissues (Vaquero-Garcia et al., 2016), this feature is particularly relevant for disease studies, cases where uncharacteristic splicing is expected, and for species with poorly annotated transcriptomes. Although some software offers detection of de novo junctions between known splice sites, MAJIQ is able to detect completely novel exons and junctions.

Notably, MAJIQ’s detection of novel exons and junctions comes with a price of algorithmic complexity. MAJIQ first runs a builder which constructs de novo splice graphs per gene, then quantifies the detected LSVs in a second step. Importantly, the builder can be executed once and then used in multiple comparisons. This construction complicates comparison of time and memory to the other algorithms, making it highly context specific. For example, the analysis presented here involved 15 RNA-Seq samples, divided to groups three samples each, and a total of five pairwise comparisons. For this, MAJIQ used ~200 M of memory per node, making it suitable for running on anything from a laptop to an HPC. Running MAJIQ with 16 processes on a 32 Intel Xeon 2.4 GHz cores machine with 64GB of memory took about 3 h for the builder and another 40 m for the pairwise comparisons (each of which can be run in parallel). SUPPA and rMATS-turbo are significantly faster, taking a total of ~35 m (SUPPA) and 1 h (rMATS-turbo) with a similar amount of memory consumption. As for DEXSeq, we found it to be significantly slower and memory heavy, taking up to 1 GB of memory and over 6 h to finish. In addition, the fact DEXSeq does not report PSI or dPSI makes it less suitable for quantitative splicing focused research.

We note the algorithms surveyed here are by no means a complete list of DS methods and other algorithms may offer specific desirable features. For example, VAST-TOOLS (Irimia et al., 2014) offers sensitive detection of micro-exons, and DiffSplice (Hu et al., 2013) offers detection of AS modules in each gene’s splice graph.

There are several important directions in which this work can be extended. First, MAJIQ can be further improved both in terms of memory consumption and running time. More importantly, all the algorithms compared here were designed for datasets with small sets of biological replicates. Although we saw that outlier detection can work even for non biological replicates (see analysis of ρ_t using GTEx samples in Supplementary Figures) we note that large heterogeneous datasets, such as those created in cancer studies or GTEx (GTEx Consortium, 2013), are likely to benefit from different statistical models. Finally, MAJIQ’s improved quantifications can be used to subsequently derive new models for splicing codes and splicing predictions given genetic variations (Barash et al., 2010, 2013; Xiong et al., 2015). Such improvements form a promising path for future algorithm development.

Supplementary Material

Acknowledgements

References