Abstract
Free full text

Guidance on Uncertainty Analysis in Scientific Assessments
Abstract
Uncertainty analysis is the process of identifying limitations in scientific knowledge and evaluating their implications for scientific conclusions. It is therefore relevant in all EFSA's scientific assessments and also necessary, to ensure that the assessment conclusions provide reliable information for decision‐making. The form and extent of uncertainty analysis, and how the conclusions should be reported, vary widely depending on the nature and context of each assessment and the degree of uncertainty that is present. This document provides concise guidance on how to identify which options for uncertainty analysis are appropriate in each assessment, and how to apply them. It is accompanied by a separate, supporting opinion that explains the key concepts and principles behind this Guidance, and describes the methods in more detail.
Short abstract
This publication is linked to the following EFSA Journal article: http://onlinelibrary.wiley.com/doi/10.2903/j.efsa.2018.5122/full
1. Introduction and scope
1.1. Background and Terms of Reference
The European Food Safety Authority requested the Scientific Committee to develop guidance on how to characterise, document and explain uncertainties in risk assessment, applicable to all relevant working areas of EFSA. For full background and Terms of Reference see the accompanying Scientific Opinion (EFSA, 2017).
1.2. Scope, objectives and degree of obligation
This document comprises the Guidance required by the Terms of Reference. More detail on principles and methods used in the Guidance is provided in an accompanying Scientific Opinion (SO) (EFSA Scientific Committee, 2018), together with justification for the approaches taken. These two documents should be used as EFSA's primary guidance on addressing uncertainty. EFSA's earlier guidance on uncertainty in exposure assessment (EFSA, 2007a) continues to be relevant but, where there are differences (e.g. regarding characterisation of overall uncertainty, for the assessment as a whole), the present Guidance and the accompanying Scientific Opinion (EFSA Scientific Committee et al., 2018) take priority. Some case studies were developed during a trial period (EFSA, 2017), and more will become available as the Guidance is implemented. Communicating uncertainty is discussed in Section 16 of the accompanying Scientific Opinion [https://doi.org/10.2903/j.efsa.2018.5122] and guidance on this will be provided in another companion document (EFSA, 2018 in prep.).
In this document, uncertainty is used as a general term referring to all types of limitations in available knowledge that affect the range and probability of possible answers to an assessment question (EFSA Scientific Committee, 2018). The Scientific Committee is of the view that all EFSA scientific assessments must include consideration of uncertainties. Therefore, the application of this Guidance is unconditional for EFSA. Assessments must say what sources of uncertainty have been identified and characterise their overall impact on the assessment conclusion. This must be reported clearly and unambiguously, in a form compatible with the requirements of decision‐makers and any legislation applicable to the assessment in hand [https://doi.org/10.2903/j.efsa.2018.5122].
The Guidance contains a wide range of options to make it applicable to all relevant working areas of EFSA, and adaptable to differing constraints on time and resources. Users are free to select any options that suit the needs of their assessment, provided they satisfy the unconditional requirements stated above. Similarly, EFSA's Panels and Units are encouraged to identify the options relevant to their work and incorporate them into their own guidance documents or procedures.
1.3. How to use this document
This document is intentionally concise. Links to more detailed information in the accompanying Scientific Opinion (EFSA Scientific Committee, 2018) are provided in the format [https://doi.org/10.2903/j.efsa.2018.5122], where n.n is a section number. Terms that are defined in the Glossary of this Guidance are shown in italics where they first appear in the text.
Section 2 of this Guidance distinguishes four main types of assessment, for which different uncertainty analysis approaches are appropriate. Note that where the term ‘assessment’ is used in this document, this refers to scientific assessment as a whole, while ‘analysis’ refers to uncertainty analysis in particular.
It is recommended that users start by consulting Section 2 to identify which type of assessment they are doing, then proceed to the section specific to that type (Sections 3, 4, 5 or 6). Those sections contain flow charts summarising key methods and choices relevant for each type of assessment. Each flow chart is accompanied by numbered notes which provide practical guidance. Some of the footnotes refer to later sections (Sections 7–17) for more detailed guidance, especially on topics that apply to multiple flow charts.
In some of the sections without flow charts, the text is presented as numbered points, for ease of reference by assessors when discussing how to apply this Guidance. In sections where this seems unnecessary, the paragraphs are not numbered.
This Guidance aims to provide sufficient information to carry out the simpler options within each type of assessment, and refers the reader to relevant sections in the Scientific Opinion (EFSA Scientific Committee, 2018) for other options. This Guidance also identifies situations where specialist expertise may be required. Section 13 of the accompanying Scientific Opinion (EFSA Scientific Committee, 2018) contains an overview of all the methods reviewed by the Scientific Committee, indicating what elements of uncertainty analysis they can contribute to and assessing their relative strengths and weaknesses; detailed information and examples for each method are provided in the Annexes of the Opinion.
1.4. Roles
Uncertainty analysis is an integral part of scientific assessment. In this Guidance, those producing a scientific assessment are referred to as ‘assessors’ and those who will use the finished assessment are referred to as ‘decision‐makers’ (the latter includes but is not limited to risk managers). Assessors are responsible for analysis of uncertainty; decision‐makers are responsible for resolving the impact of uncertainty on decision‐making [https://doi.org/10.2903/j.efsa.2018.5122]. Most EFSA assessments are prepared by Working Groups for review and adoption by Panels, and the same is expected for uncertainty analysis. Good engagement between assessors and decision‐makers, and between Working Group and Panel, are essential to ensure that the assessment and uncertainty analyses are fit for purpose.
1.5. Main elements of uncertainty analysis
Uncertainty analysis is the process of identifying and characterising uncertainty about questions of interest and/or quantities of interest in a scientific assessment. A question or quantity of interest may be the subject of the assessment as a whole, i.e. that which is required by the Terms of Reference for the assessment, or it may be the subject of a subsidiary part of the assessment which contributes to addressing the Terms of Reference (e.g. exposure and hazard assessment are subsidiary parts of risk assessment). Questions of interest may be binary (e.g. yes/no questions) or have more than two possible answers, while quantities of interest may be variable or non‐variable [https://doi.org/10.2903/j.efsa.2018.5122].
The main elements of an uncertainty analysis are summarised in Box 1. Most of the elements are always required; others (as identified in the list) depend on the needs of the assessment. Furthermore, the approach to each element varies, and sometimes the order in which they are conducted, depending on the nature or type of each assessment. Therefore, this guidance starts by identifying the main types of assessment, and then uses a series of flow charts to describe the sequence of elements that is recommended for each type.
1.6. Levels of refinement in uncertainty analysis
Most of the elements of uncertainty analysis listed in Box 1 can be conducted at different levels of refinement and effort, analogous to the ‘tiered approaches’ used in some areas of risk assessment. Major choices include whether to assess all uncertainties collectively or divide the uncertainty analysis into parts; whether to quantify uncertainties fully using probabilities and distributions, or partially using probability bounds; and whether to combine uncertainties by expert judgement or calculation. The flow charts in later sections guide assessors through these and other choices, helping them choose the approaches that are best suited to each assessment.
The uncertainty of an assessment is driven primarily by the quantity and quality of available evidence (including data and expert judgement) and how it is used in the assessment. Less refined options for uncertainty analysis are quicker, less complex, and characterise uncertainty more approximately. This may be sufficient for decision‐making in many cases.
More refined options characterise uncertainty more transparently and rigorously, and may result in more precise characterisation of overall uncertainty, although this will always be subject to any limitations in the underlying evidence and assessment methods. However, more refined options are more complex and require more time and specialist expertise. In complex assessments, an iterative approach may be efficient, starting with simpler options and then using the results to target more refined options on the most important uncertainties, whereas in other assessments there may be less scope for iteration. The sequence of flow charts in Sections 3 and 4 is designed to help with these choices.
1.7. Expertise required
It is recommended that at least one expert in each Panel and Working Group should have received training in the use of this Guidance, and that all assessors should have basic training in probability judgements.
Some of the approaches described in later sections require specialist expertise in statistics or expert knowledge elicitation. This may be provided by including relevant experts in the Working Group, or as internal support from EFSA.
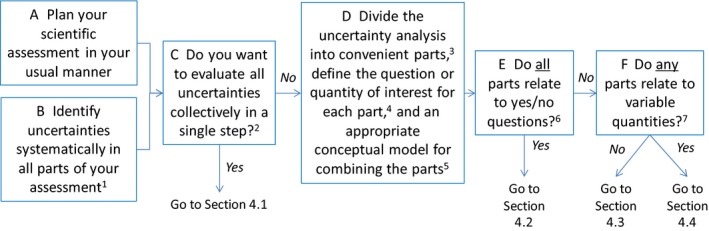
2. Types of scientific assessment
- 1
The recommended approach to uncertainty analysis depends on the nature of the scientific assessment in hand [https://doi.org/10.2903/j.efsa.2018.5122]. Identify which of the following types your assessment most corresponds to and then proceed to the corresponding section for guidance specific to that type.
Standardised assessments. A standardised assessment follows a pre‐established standardised procedure that covers every step of the assessment. Standardised procedures are often used in scientific assessments for regulated products, e.g. for premarket authorisation. They are accepted by assessors and decision‐makers as providing an appropriate basis for decision‐making, and are often set out in guidance documents or legislation. They generally require data from studies conducted according to specified guidelines and specify how those data will be used in the assessment. They may include criteria for evaluating data, and elements for use in the assessment such as assessment factors, default values, conservative assumptions, standard databases and defined calculations. Proceed to Section 3.
Case‐specific assessments. These are needed wherever there is no pre‐established standardised procedure, and the assessors have to develop an assessment plan that is specific to the case in hand. Standardised elements (e.g. default values) may be used for some parts of the assessment, but other parts require case‐specific approaches. Proceed to Section 4.
Development or revision of guidance documents, especially (but not only) those that describe existing standardised procedures or establish new ones. Proceed to Section 6.
Urgent assessments. Assessments that, for any reason, must be completed within an unusually short period of time or with unusually limited resources, and therefore require streamlined approaches to both assessment and uncertainty analysis. Proceed to Section 5.
- 2
In some areas of EFSA's work, the result of a standardised assessment may indicate the need for a ‘refined’ or ‘higher tier’ assessment in which one or more standardised elements are replaced by case‐specific approaches. In principle, the assessment becomes case‐specific at this point, although it may be possible to treat it as a standardised assessment with some non‐standard uncertainties (see Section 3).
- 3
Assessors often distinguish between quantitative and qualitative assessment s. This sometimes refers to the form in which the conclusion of the assessment is expressed: either as an estimate of a quantity of interest (quantitative), or as a verbal response to a question of interest (qualitative). In other cases, an assessment may be described as qualitative because the methods used to reach the conclusion do not involve calculations; e.g. when the conclusions are based on a combination of literature review and narrative reasoning. In all cases, however, the conclusion of a scientific assessment must be expressed in a well‐defined manner, in order to be a proper scientific statement and useful to decision‐makers [https://doi.org/10.2903/j.efsa.2018.5122]. Any well‐defined qualitative conclusion can be considered as an answer to a yes/no question; this is important for uncertainty analysis, because uncertainty about a yes/no question can be expressed quantitatively, using probability [https://doi.org/10.2903/j.efsa.2018.5122]. In general, therefore, the fact that an assessment uses qualitative methods or a conclusion is expressed in qualitative terms does not imply that the uncertainty analysis must be qualitative: on the contrary, it is recommended that assessors should always try to express uncertainty quantitatively, using probability [https://doi.org/10.2903/j.efsa.2018.5122 and https://doi.org/10.2903/j.efsa.2018.5122]. However, qualitative methods of expressing uncertainty also have important uses in uncertainty analysis (see Section 11).
3. Uncertainty analysis for standardised assessments
When performing uncertainty analysis for a standardised assessment it is important to distinguish standard and non‐standard uncertainties (see Section 7.1 for explanation and examples of these). The first step is to identify whether any non‐standard uncertainties are present. If not, no further action is required other than reporting that this is the case (Section 3.1). When non‐standard uncertainties are present, an evaluation of their impact on the result of the standard procedure may be sufficient for decision‐making, as described in Sections 3.2–3.4, depending on how much scope was left for non‐standard uncertainties when calibrating the standardised procedure (if this has been done) [https://doi.org/10.2903/j.efsa.2018.5122]. In other cases, where the non‐standard uncertainties are substantial, the standardised procedure may no longer be applicable and the assessors will need to carry out a case‐specific assessment and uncertainty analysis, as described in Section 4.
Assessors should start with Section 3.1 and follow the instructions that are relevant for the assessment in hand. Refer to the accompanying Scientific Opinion when needed for more information on specific methods (overview tables in https://doi.org/10.2903/j.efsa.2018.5122, summaries in https://doi.org/10.2903/j.efsa.2018.5122 and details in the Annexes of the Scientific Opinion).
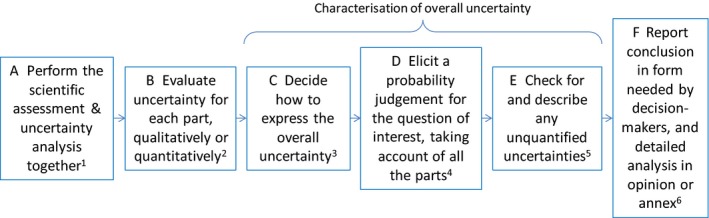
3.1. Checking for non‐standard uncertainties (Figure 1)
3.2. Assessing non‐standard uncertainties collectively
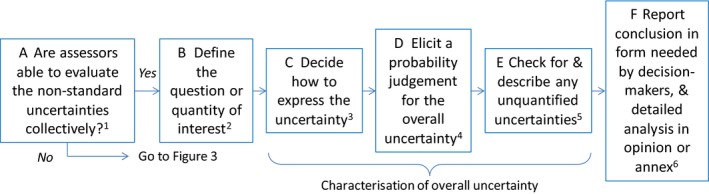
This is the simplest option for assessing non‐standard uncertainties, when assessors are able to evaluate them collectively (Figure 2).
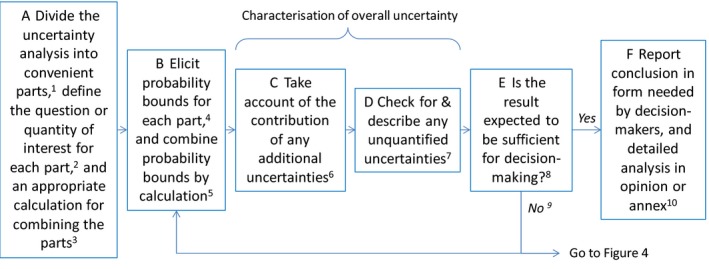
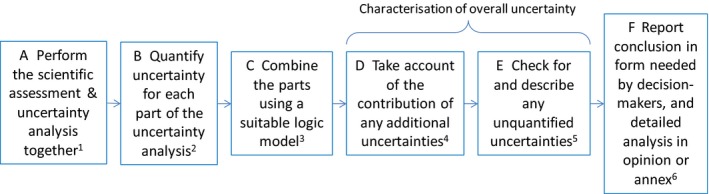
3.3. Assessing non‐standard uncertainties for separate parts of the uncertainty analysis using probability bounds (Figure 3)
4. Uncertainty analysis for case‐specific assessments
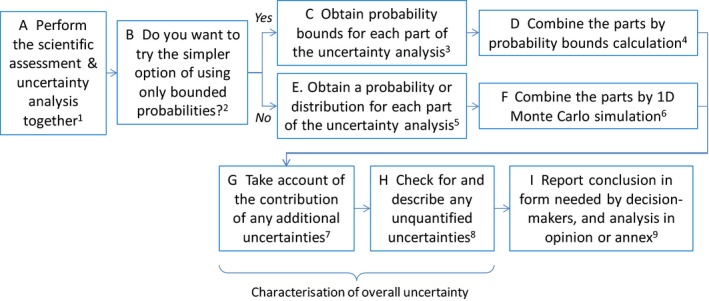
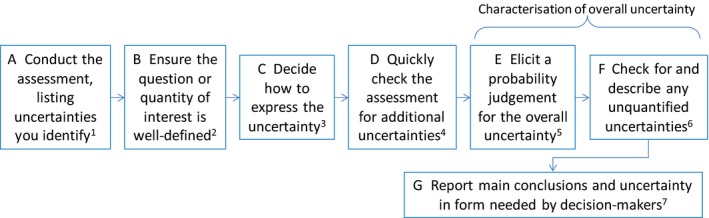
Assessors should start with Figure 5 and follow the instructions that are relevant for the assessment in hand. Refer to the accompanying Scientific Opinion when needed for more information on specific methods (overview tables in https://doi.org/10.2903/j.efsa.2018.5122, summaries in https://doi.org/10.2903/j.efsa.2018.5122 and details in the Annexes of the Scientific Opinion).
Deciding how to handle uncertainty in a case‐specific assessment. Numbered superscripts refer to text notes following the figure. Letters (A, B, C, etc.) are to facilitate reference to specific steps in the figure
The first decision to be taken in Figure 5, after planning the assessment and identifying relevant uncertainties, is whether to divide the uncertainty analysis into parts (see Section 9). When this is done, the subsequent steps depend on the questions or quantities of interest for the assessment and its parts. The figure first separates assessments where no parts have quantities of interest (only questions), then distinguishes those that have only non‐variable quantities of interest from those that include one or more variable quantities of interest. Note that an assessment with some quantities of interest may include some questions of interest, and an assessment with some variable quantities may include both non‐variable quantities and categorical questions. For example, a chemical risk assessment typically includes hazard identification (yes/no question for each type of effect), some quantities that are treated as non‐variable (e.g. the factor for extrapolating from animals to humans), and some quantities that are variable (e.g. exposure): following Figure 5 this would lead to Section 4.4. If an assessment does not fit any of the options identified in the Figure 5, seek specialist advice (Section 1.7) as it may require special treatment (e.g. for questions of interest which have more than two categories). The different types of questions and quantities of interest are discussed in more detail in [https://doi.org/10.2903/j.efsa.2018.5122].
4.1. Assessing uncertainties collectively in a case‐specific assessment
This is the simplest option for assessing uncertainty in case‐specific assessments (Figure 6).
4.2. Evaluating uncertainties separately for parts of the uncertainty analysis that all address yes/no questions
The approach to uncertainty analysis for this type of assessment depends on whether assessors are able to, and wish to, express their uncertainty for all parts using probability and combine them with a probability calculation. Doing so requires that all parts of the uncertainty analysis, and the assessment as a whole, address yes/no questions, and that the reasoning for the assessment is expressed as a formal logic model, of the type described in Section 13. A logic model expresses the reasoning by which the different parts of the assessment are combined using logical operators such as ‘AND’, ‘OR’ and ‘NOT’, e.g. if a AND b then c. Then, if the uncertainty of the answer to the question of interest for each step is expressed using probability, those probabilities can be combined by calculation to derive a probability for the conclusion, which is more reliable than combining them by expert judgement. If the assessors decide to follow this approach, they should proceed to Section 4.2.2.
Alternatively, assessors may prefer to evaluate the uncertainties of the different parts separately (either qualitatively or quantitatively) and combine them by expert judgement, rather than a probability calculation. In this case, uncertainty may be evaluated qualitatively in some or all parts of the assessment, but a probability judgement should be made for the question of interest for the assessment as a whole. If the assessors decide to follow this approach, they should proceed to Section 4.2.1.
In some assessments, some parts of the assessment may address questions that have more than two possible answers or categories rather than being yes/no questions [https://doi.org/10.2903/j.efsa.2018.5122]. Such assessments can still be represented as logic models by reformulating the uncertainty analysis as a series of yes/no questions, considering each of the categories in turn (for example, a chemical may cause multiple types of effect, but each effect can be considered as a yes/no question). If the assessors think it better to treat more than two categories simultaneously, then more complex logic models will be required and specialist help may be needed (Section 1.7).
4.2.1. Combining multiple yes/no questions by expert judgement (Figure 7)
4.3. Evaluating uncertainties separately for different parts of an uncertainty analysis involving non‐variable quantities
This section refers to assessments where each quantitative part is a non‐variable quantity taking only a single real value, e.g. the total number of infected animals entering the EU in a given year. Many non‐variable quantities in scientific assessment are parameters that summarise variable quantities. A common example of this is the mean body weight for a specified population at a specified time. If the assessment includes some parts that address yes/no questions, their uncertainty can be quantified and included in calculation, or treated as an additional uncertainty in the characterisation of overall uncertainty (Figure 9).
4.4. Evaluating uncertainties separately for different parts of an assessment involving variable quantities
This section refers to assessments where at least some of the quantitative parts are variable quantities that take multiple values, such the body weights in a population. If some parts are non‐variable quantities, they can be included accordingly. If the assessment includes some parts addressing yes/no questions, their uncertainty can be quantified and included in calculation, or treated as an additional uncertainty in the characterisation of overall uncertainty (Figure 10).
5. Uncertainty analysis for urgent assessments
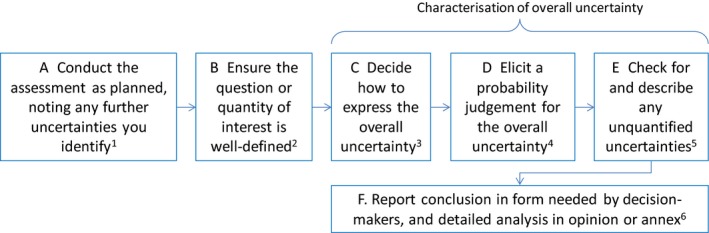
When a scientific assessment is urgent, assessors will need to choose an approach that fits within the available time and any other limitations arising from the urgency of the situation, e.g. limitations in resources and available evidence. Uncertainty analysis must still be included but this flow chart takes the quickest option, evaluating all uncertainties in a single step. This is more approximate than other options but is a reasonable basis for preliminary advice, provided the additional uncertainty implied by the streamlined assessment is reflected in the conclusions (Figure 11).
6. Uncertainty analysis when developing or revising standardised procedures
This section outlines how to conduct an uncertainty analysis when developing or revising a standardised procedure. This will often be necessary when creating or revising guidance documents, as they often contain standardised procedures [https://doi.org/10.2903/j.efsa.2018.5122].
A standardised procedure will, when adopted, be applied repeatedly to a specified class of products or assessment problems. The purpose of uncertainty analysis in this case is to evaluate the probability that the proposed procedure will achieve the management objectives for that procedure to an extent which decision‐makers consider appropriate for that class of products or problems. In other words, it checks whether the procedure is appropriately ‘conservative’, in the sense of providing appropriate cover for the standard uncertainties that normally affect assessments for this class of products or problems. This calibration of the procedure is what justifies its subsequent application to multiple assessments of the specified class without repeating the evaluation of standard uncertainties in every case [https://doi.org/10.2903/j.efsa.2018.5122]. If uncertainty analysis is required for any other purpose during the development of a guidance document, the assessors should treat it as a normal case‐specific assessment (Section 4).
Where an existing procedure is used in more than one area of EFSA's work, e.g. by more than one Panel, its calibration and, if necessary, revision should be undertaken jointly by those involved. Similarly, where a standardised procedure is part of an internationally‐agreed protocol, any changes to it would need to be made in consultation with relevant international partners and the broader scientific community (Figure 12).
7. Identifying uncertainties
7.1. Standard and non‐standard uncertainties
Standard uncertainties are those that are considered (implicitly or explicitly) to be addressed by the provisions of a standardised procedure or standardised assessment element. For example, uncertainties due to within and between species differences in toxicity are often addressed by a default factor of 100 in chemical risk assessment. Similarly, measurement uncertainty in an experimental study is a standard uncertainty if the study followed (without deviations) a study guideline specified in the standard procedure. Standard uncertainties do not need to be reconsidered in each new assessment that follows the standard procedure, because they will have been assessed when the standard procedure was established (see Section 6).
All other uncertainties are non‐standard uncertainties. These include any deviations from a standardised procedure or standardised assessment element that lead to uncertainty regarding the result of the procedure. For example, studies that deviate from the standard guidelines or are poorly reported, cases where there is doubt about the applicability of default values, the use of non‐standard or ‘higher tier’ studies that are not part of the standard procedure, etc. Non‐standard uncertainties are not covered by the allowance for uncertainty that is built into the standard procedure and must therefore be evaluated case‐by‐case, whenever they are present.
Both standard and non‐standard uncertainties may be found in any type of assessment, but the proportions vary. In standardised assessments, there may be few or no non‐standard uncertainties, while in other types of assessment there are generally more.
It is recommended that EFSA's Panels include lists of standard uncertainties within the documentation for standard procedures, as this will help assessors to distinguish standard and non‐standard uncertainties. For the same reason, Panels may find it helpful to develop lists of non‐standard uncertainties which they encounter frequently in their work, or use or adapt existing lists of criteria for evidence appraisal, which serve a similar purpose [see https://doi.org/10.2903/j.efsa.2018.5122].
7.2. Procedure for identifying uncertainties
Every assessment must say what sources of uncertainty have been identified [https://doi.org/10.2903/j.efsa.2018.5122]. For transparency, it is recommended to report them in list or tabular form.
Assessors should systematically examine every part of their assessment for uncertainties, including both the inputs to the assessment (e.g. data, estimates, other evidence) and the methods used in the assessment (e.g. statistical methods, calculations or models, reasoning, expert judgement), to minimise the risk that important uncertainties are overlooked [https://doi.org/10.2903/j.efsa.2018.5122]. In uncertainty analysis for standardised assessments, it is only necessary to identify non‐standard uncertainties (see Section 3.1 and https://doi.org/10.2903/j.efsa.2018.5122).
Uncertainties affecting assessment inputs are identified when appraising the evidence retrieved from literature or from existing databases. Structured approaches to evaluating evidence have been established in many areas of science and are increasingly used in EFSA's work where appropriate [see Table B.45 and Table B.46 in https://doi.org/10.2903/j.efsa.2018.5122]. When these approaches are applicable to the assessment in hand, they should be used. In other assessments, where existing approaches are not applicable, assessors may use the left column of Table 1 as a guide to what types of uncertainty to look for in their assessment inputs. In both cases, assessors should be alert for any additional types of uncertainty beyond those listed in Table 1 or the appraisal approach they are using. For example, external validity is not included in appraisal tools that focus on internal validity only (see https://doi.org/10.2903/j.efsa.2018.5122).
Table 1
Generic list of common types of uncertainty affecting scientific assessments (see https://doi.org/10.2903/j.efsa.2018.5122 for details)
Uncertainties associated with assessment inputs Uncertainties associated with assessment methodology Ambiguity
Accuracy and precision of the measures
Sampling uncertainty
Missing data within studies
Missing studies
Assumptions about inputs
Statistical estimates
Extrapolation uncertainty (i.e. limitations in external validity)
Other uncertainties
Ambiguity
Excluded factors
Distributional assumptions
Use of fixed values
Relationship between parts of the assessment
Evidence for the structure of the assessment
Uncertainties relating to the process for dealing with evidence from the literature
Expert judgement
Calibration or validation with independent data
Dependency between sources of uncertainty
Other uncertainties
Uncertainties affecting the methods used in the assessment are generally not addressed by existing frameworks for evidence appraisal. It is therefore recommended that assessors use the right column of Table 1 (referring to [https://doi.org/10.2903/j.efsa.2018.5122] for details and explanation) as a guide to what types of uncertainty to look for in the methods of their assessment. Again, assessors should be alert for any additional types not listed in Table 1.
Assessors are advised to avoid spending excessive time trying to match uncertainties to the types listed in Table 1 or other frameworks: the purpose of the lists is to facilitate identification of uncertainties, not to classify them.
Assessors should determine which of the uncertainties they identify in an assessment are standard and which are non‐standard (Section 7.1), as this will affect their treatment in subsequent stages of the uncertainty analysis.
8. Prioritising uncertainties
Prioritising sources of uncertainty may be useful at different stages of the assessment and uncertainty analysis. In the early stages, it can be used to select more important uncertainties to be analysed by more refined methods, e.g. to be evaluated individually rather than collectively, to be expressed with probabilities or distributions rather than bounds, to be elicited by more rather than less formal methods, etc. Prioritisation can also be used during the course of an assessment, to identify parts of the assessment where it might be beneficial to search for more data, use more complex models, or invite additional experts. At the end of the assessment, it may be useful to prioritise uncertainties to identify potential areas for further research.
Prioritisation, at any stage of the assessment, should be based on the contribution of individual sources of uncertainty to the uncertainty of the assessment as a whole. This is determined by a combination of the magnitude of each uncertainty and how much it affects the result of the assessment, both of which need to be taken into account [https://doi.org/10.2903/j.efsa.2018.5122].
The relative influence of different uncertainties can be assessed in a simple and approximate way using qualitative methods based on expert judgement. An ordinal scale can be used to express expert judgements of the magnitude and/or direction of impact of each uncertainty on the question or quantity of interest, as in ‘uncertainty tables’ [https://doi.org/10.2903/j.efsa.2018.5122 and https://doi.org/10.2903/j.efsa.2018.5122]. Or separate ordinal scales could be used to express judgements of the magnitude of each uncertainty and its influence, as in the Numeral, Unit, Spread, Assessment and Pedigree (NUSAP) approach [https://doi.org/10.2903/j.efsa.2018.5122].
When the assessment involves a calculation or quantitative model, the contributions of uncertainties about the model inputs can be assessed rigorously by sensitivity analysis. These range from simple ‘what if’ calculations and ‘minimal assessment’ (EFSA, 2014a) to sophisticated sensitivity analyses [see https://doi.org/10.2903/j.efsa.2018.5122] for which specialist help might be required (Section 1.7). The influence of uncertainties relating to choices regarding the structure of the model or assessment may need to be addressed by repeating the assessment with alternative choices. Prioritisation at the early stages of an assessment must necessarily be done by expert judgement or by sensitivity analysis using a preliminary model, as the assessment model is still under development.
9. Dividing the assessment into parts
- 1
Often an assessment will comprise a number of main parts (e.g. exposure and hazard in a chemical risk assessment) and smaller, subsidiary parts (e.g. individual parameters, studies, or lines of evidence within the exposure or hazard assessment).
- 2
The uncertainty analysis may also be divided into parts. Assessors should choose at what level to conduct it:
Evaluate all uncertainties collectively, for the assessment as a whole.
Divide the uncertainty analysis into parts, which evaluate uncertainties separately in major parts of the scientific assessment (e.g. exposure and hazard in a risk assessment). Then, combine the parts of the uncertainty analysis and include also any other identified uncertainties that relate to other parts of the scientific assessment as a whole, so as to characterise the overall uncertainty.
Divide the uncertainty analysis into still smaller parts, corresponding to still smaller parts of the scientific assessment (e.g. every input of a calculation or model). Evaluate uncertainty collectively within each of the smaller parts, combine them into the main parts, and combine those to characterise overall uncertainty for the whole assessment.
- 3
If the uncertainty analysis will be divided into parts, assessors will need to combine them to characterise overall uncertainty. Assessors should define in advance how the parts will be combined, as this will increase transparency and rigour. It is recommended to use a conceptual model diagram (see glossary for explanation) to show how the parts will be combined. The parts may be combined by expert judgement (Section 12.6), or by calculation (Sections 13, 14 or 15) if assessors quantify the uncertainty for each part and can specify an appropriate quantitative or logical model to combine them. Calculation is likely to give more reliable results, but should be weighed against the additional work involved.
- 4
Assessors should judge what is best suited to the needs of each assessment. For example, it may be more efficient to evaluate uncertainty for different parts separately if they require different expertise (e.g. toxicity and exposure). Evaluating all uncertainties collectively (first option in point (2) above) is generally quicker and superficially simpler but requires integrating them all subjectively by expert judgement, which may be less reliable than evaluating different parts of the uncertainty analysis separately, if they are then combined by calculation. For this reason, it is recommended to treat separately those parts of the assessment that are affected by larger uncertainties (identified by a simple initial prioritisation, see Section 8).
- 5
When a part of the scientific assessment is treated separately in the uncertainty analysis, it is not necessary to evaluate immediately all of the uncertainties affecting it; some of them can be set to one side and considered later as part of the overall characterisation of uncertainty, if this is more convenient for the assessor. However, it is recommended that only the lesser uncertainties are deferred to the overall characterisation, since it will be more reliable to combine the larger uncertainties by calculation.
- 6
When the scientific assessment includes a quantitative or logical model, assessors may find it convenient to quantify uncertainty separately for every parameter of the model. In such cases, it will still be necessary to identify additional uncertainties that are not quantified within the model, e.g. uncertainties relating to the structure of the model (see Section 7.2) and take them into account in the characterisation of overall uncertainty (Section 16). In other cases, assessors might find it sufficient to analyse all the uncertainties affecting a model collectively (simplest option in point (2) above), or for major parts of the model without separating the individual parameters (intermediate option in point (2)).
10. Ensuring questions and quantities of interest are well‐defined
- 1
In order to evaluate uncertainty, the questions and/or quantities of interest for the assessment must be well‐defined. This applies both to the assessment as a whole and to different parts of the uncertainty analysis, if it is separated into parts. Any ambiguity in the definition of questions or quantities of interest will add extra uncertainty and make the evaluation more difficult. When a question or quantity of interest is not already well‐defined for the purpose of scientific assessment, assessors should define it well for the purpose of uncertainty analysis.
- 2
A quantity or question of interest is well‐defined if, at least in principle, it could be determined in such a way that assessors would be sure to agree on the answer. A practical way to achieve this is by specifying an experiment, study or procedure that could be undertaken, at least in principle, and which would determine the true answer for the question or quantity with certainty [see https://doi.org/10.2903/j.efsa.2018.5122 for more discussion]. For example:
a well‐defined measure for a quantity of interest, and the time, population or location, and conditions (e.g. status quo or with specified management actions) for which the measure will be considered;
for a question of interest, the presence or absence of one or more clearly‐defined states, conditions, mechanisms, etc., of interest for the assessment, and the time, population or location, and conditions (e.g. status quo or with specified management actions) for which this will be considered;
the result of a clearly‐defined scientific study, procedure or calculation, which is established (e.g. in legislation or guidance) as being relevant for the assessment.
- 3
When drafting the definition of each question or quantity of interest, check each word in turn. Identify words that are ambiguous (e.g. high), or imply a risk management judgement (e.g. negligible, safe). Replace or define them with words that are, as far as possible, unambiguous and free of risk management connotations or, where appropriate, with numbers.
- 4
Sometimes the Terms of Reference for an assessment are very open, e.g. requesting a review of the literature on an area of science. In such cases, assessors should seek to ensure the conclusions they produce either refer to well‐defined quantities, or contain well‐defined statements that can be considered as answers to well‐defined questions, in one of the three forms listed above (point 2, options a–c). This is necessary both for transparency and so that assessors can evaluate and express the uncertainty associated with their conclusions.
11. Qualitative expression of uncertainty
- 1
Qualitative expressions of uncertainty use words or ordinal categories, without quantifying either the range of possible answers or values for the question or quantity of interest, or their probabilities.
- 2
Qualitative expressions are inevitably ambiguous unless accompanied by a quantitative definition. It is therefore recommended to use quantitative expressions when characterising overall uncertainty [https://doi.org/10.2903/j.efsa.2018.5122 and https://doi.org/10.2903/j.efsa.2018.5122]. Nevertheless, qualitative expression is useful in uncertainty analysis, and recommended for use in the following situations:
As a simple approach for prioritising uncertainties (Section 8).
At intermediate steps in uncertainty analysis, to describe individual sources of uncertainty as an aid to quantifying their combined impact by probability judgement (Section 12.6). This may be useful either for individual parts of an assessment (Section 9), or as a preliminary step when characterising the overall uncertainty of the conclusion (Section 16.1).
When quantifying uncertainty by expert judgement, and when communicating the results of that, it may in some cases be helpful to use an approximate probability scale with accompanying qualitative descriptors (Section 12.3).
At the end of uncertainty analysis, for describing uncertainties that the assessors are unable to include in their quantitative evaluation: see Section 16.2 for further guidance on this.
When reporting the assessment, for expressing the assessment conclusion in qualitative terms when this is required by decision‐makers or legislation [https://doi.org/10.2903/j.efsa.2018.5122].
- 3
For the situations identified in 2b above, it is recommended to describe the individual sources of uncertainty with one or more ordinal scales. This will aid consistency and transparency, and help assessors make a balanced overall evaluation of multiple uncertainties when forming a probability judgement about their combined impact. One or more scales may be used (e.g. in weight of evidence, one option could be to define scales for relevance, reliability and consistency, EFSA Scientific Committee, 2017), and they should be defined as part of planning the assessment (EFSA, 2015). Evaluations using the scales could be done more or less formally, using a range of options similar to those for expert elicitation of probability judgements, depending on what is proportionate to the needs of the assessment (see Section 12.6).
- 4
It is recommended that qualitative expressions obtained as in point 3 above are used to inform a quantitative probability judgement of their combined impact on the assessment. They should not be combined by any form of calculation, matrix or fixed rule, unless there is an explicit, reasoned basis for the specific form of calculation, matrix or rule that is chosen [see https://doi.org/10.2903/j.efsa.2018.5122].
12. Quantifying uncertainty using probability
The Scientific Committee recommends that assessors express in quantitative terms the combined impact of as many as possible of the identified uncertainties [https://doi.org/10.2903/j.efsa.2018.5122]. This Guidance uses probability for this purpose [https://doi.org/10.2903/j.efsa.2018.5122]. Probabilities can be specified fully (Section 12.1) or partially (Sections 12.2, 12.3), and obtained from data (Section 12.5) or expert judgement (Section 12.6), as appropriate for the assessment in hand. When data are available, they should be used, and via a statistical analysis if possible. However, there is always some expert judgement involved, even if it is only to choose a statistical model. Uncertainty of variable quantities and dependencies can also be addressed (Sections 12.4, 12.7). The combined impact of two or more sources of uncertainty may be quantified either by direct expert judgement (Section 12.6) or by calculation after quantifying each individual source of uncertainty (Sections 13, 14, 15).
12.1. Probability and probability distributions
Probability is a continuous scale ranging from 0 to 1. It can also be expressed as a percentage, ranging from 0% to 100%, and the latter is used in this Guidance.
For a yes/no question (including whether a non‐variable quantity of interest exceeds a specified value), 0% probability means that the answer is certainly no, 100% probability means it is certainly yes, while probabilities between 0% and 100% represent increasing degrees of certainty that it is yes. For example, a probability of 50% means the answer is equally likely to be yes or no, and 75% means it is three times more likely to be yes than no.
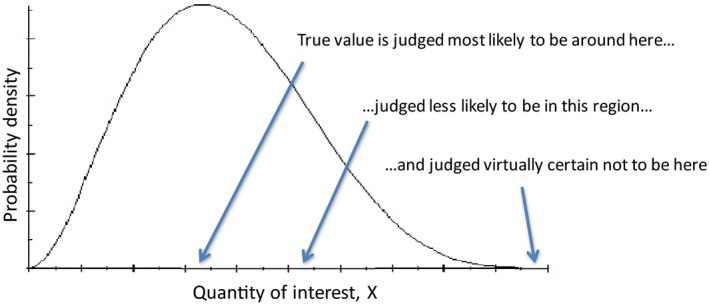
Uncertainty about the value of a non‐variable quantity can be expressed fully by a probability distribution, which shows the relative probability of different values. An example is shown in Figure 13. A probability distribution determines the probability that any specified range of possible values includes the true value of the quantity of interest.
Sometimes a partial expression of uncertainty about the value of a non‐variable quantity is sufficient: the probability that a specified range of possible values includes the true value of the quantity of interest, e.g. the probability that ‘mean exposure exceeds 10 mg/kg bw per day’. Although in the past it has often been implicit that a range contains the true value of a quantity with close to 100% probability, for example when reporting lower and upper bound estimates for exposure, the probability for the range should be specified explicitly.
12.2. Approximate probabilities and probability bounds
When probabilities are obtained by expert judgement rather than from statistical analysis of data, it may be easier to specify a probability approximately by giving a range for the probability. For example, one might specify only that the probability is less than 5%, i.e. between 0% and 5%. The meaning of such a range is that it is judged that the probability would lie in the range if more time was taken to specify the probability precisely.
Combining points 12.1.4 and 12.2.1 yields a probability bound: an approximate probability, specified as a range, that an uncertain non‐variable quantity lies in a specified range of possible values or exceeds a specified value. For example, one might specify that ‘there is less than 10% probability that mean exposure exceeds 10 mg/kg bw per day’. Probability bounds analysis (Section 14.1) can then be used to combine uncertainties expressed in this way.
12.3. Approximate probability scale
When probability judgements are made by semi‐formal expert knowledge elicitation (EKE) procedures or by less formal methods (see Section 12.6), assessors may find it helpful to refer to a standard scale of probability ranges. The approximate probability scale shown in Table 2 is recommended for this purpose in EFSA, and was adapted from a similar scale used by the Intergovernmental Panel on Climate Change [https://doi.org/10.2903/j.efsa.2018.5122].
Table 2
Approximate probability scale recommended for harmonised use in EFSA. See text above for guidance
Probability term Subjective probability range Additional options Almost certain 99–100% More likely than not: > 50% Unable to give any probability: range is 0–100%
Report as ‘inconclusive’, ‘cannot conclude’, or ‘unknown’
Extremely likely 95–99% Very likely 90–95% Likely 66–90% About as likely as not 33–66% Unlikely 10–33% Very unlikely 5–10% Extremely unlikely 1–5% Almost impossible 0–1% When using Table 2, assessors should consider which of the tabulated ranges expresses their judgement of the probability that is required. This could be either the probability of an answer to the question of interest, or the probability that the quantity of interest lies in a specified range. It is emphasised that Table 2 is intended for quantifying uncertainty and not variability. For example, it may be used to express the probability that a specified percentile of exposure exceeds a specified value, but not the proportion of the population who do so. Similarly, it should not be used to express the incidence (risk) of an effect in a population but, if incidence was assessed, Table 2 could be used to express the probability that incidence exceeds a specified level. It can also be used to express the probability that an uncertain qualitative conclusion is true.
Assessors are not restricted to the tabulated ranges: they may use a different range than those listed, if it would better describe their judgement, or give a precise probability if they can.
If assessors are unable to select a single range from the second or third columns of Table 2, they can use more than one range to express their judgement. If assessors feel very uncertain, it may be easier to start with the full set of ranges (i.e. a total range of 0–100%) and then omit any ranges they would not regard as credible, given the available evidence. If they are unable to omit any part of the probability scale, this implies they are unable to make any statement about the probability of the answers or values of interest and should report them as inconclusive or unknown (see Section 16.2 for the implications of this).
The verbal probability terms in Table 2 may be used to aid communication. Assessors’ judgements should be based on the probability ranges, not on the verbal terms. To avoid ambiguity, the verbal terms shown in Table 2 should always be accompanied by the quantitative range in brackets, e.g. ‘Likely (66–90% probability)’, and should not be used for other ranges.
12.4. Quantifying uncertainty for a variable quantity
Any variable quantity should have a specified context of interest for an assessment. For example, the context of interest might be a specified population at a specified time. The context defines a distribution of variability: the relative frequency of occurrence of different values for the quantity. For example, the exposure to or intake of a specified substance during a specified period of time will vary from individual to individual and the variability distribution could be summarised using a histogram if the intake of all individuals was known. However, it is nearly always the situation that there are individuals/cases/places for which the value of the quantity is not known, so the variability distribution is not known exactly and is therefore uncertain. Then quantities such as the mean, or percentiles of variability, are non‐variable but uncertain and uncertainty about them can be expressed using probability.
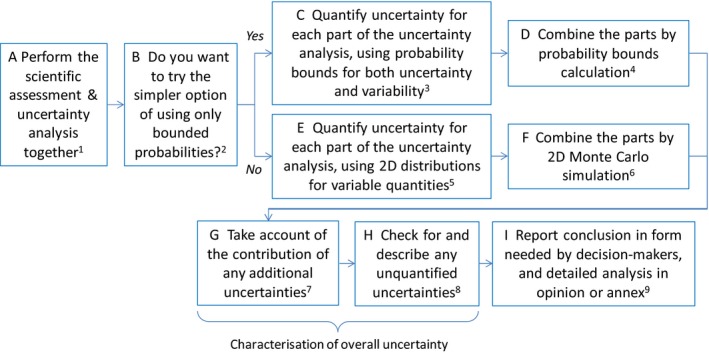
One approach to expressing uncertainty for a variable quantity is to focus on a specified percentile of variability. That percentile is then an uncertain quantity and uncertainty about it can be expressed using a probability distribution or probability bounds (a range with a probability or approximate probability). If there is more than one variable quantity, then it is recommended to begin by using probability bounds, because it may then be possible to use probability bounds analysis to combine the uncertainties (Section 15.1).
If the assessment uses a quantitative model involving more than one variable and probability bounds analysis does not provide sufficient information for decision‐making, it will be necessary to quantify both uncertainty and variability using distributions (see Sections 12.4 and 15.2, https://doi.org/10.2903/j.efsa.2018.5122 and https://doi.org/10.2903/j.efsa.2018.5122). This requires a statistical model for the variability. Parameters in the statistical model are then uncertain quantities and uncertainty about them can be quantified using probability distributions. Statistical expertise is needed (Section 1.7). Section 15.2 provides further detail, including some principles for how to combine uncertainties expressed in this way.
12.5. Obtaining probabilities from data
Where suitable data are available, statistical analysis should be used to derive estimates for the quantity of interest, together with a measure of uncertainty [https://doi.org/10.2903/j.efsa.2018.5122].
Statistical methods for quantifying uncertainty include confidence and prediction intervals, the bootstrap and Bayesian inference [see https://doi.org/10.2903/j.efsa.2018.5122]. Choosing and applying a suitable method may require assistance from a statistician (Section 1.7). Bayesian inference using prior distributions based on expert judgement directly expresses uncertainty about parameters using probabilities which can be combined with other probabilities deriving directly from expert judgement. Traditional non‐Bayesian statistical methods can also be used: confidence and prediction intervals [https://doi.org/10.2903/j.efsa.2018.5122] and output from the bootstrap [https://doi.org/10.2903/j.efsa.2018.5122] can be used as the basis for expert judgements expressed as probabilities. For example, a 95% confidence interval for a parameter might become an expert judgement that there is 95% probability that the true value of the parameter lies in the range given by the confidence interval. https://doi.org/10.2903/j.efsa.2018.5122 discusses when it is reasonable to make such a judgement and when some adjustment of either the interval or its probability might be needed.
Statistical analysis of a data set using a single statistical model quantifies only part of the uncertainty that is present: that part which is reflected in the variability of the data and the sampling scheme which is assumed in the model. Selection of data and statistical model involves additional uncertainty, which must be taken into account. Some of this may be partly addressed within the statistical analysis, e.g. by assessing goodness of fit or using model averaging techniques [https://doi.org/10.2903/j.efsa.2018.5122]. Any uncertainties that are not quantified within the statistical analysis must be taken into account later, by expert judgement, when characterising overall uncertainty (Section 16); this could be facilitated by conducting scenario analysis of alternative statistical models.
12.6. Obtaining probabilities or distributions by expert judgement
All assessments will require expert judgements of probability for at least some uncertainties, except for standard assessments with no non‐standard uncertainties (Section 3.1).
Expert judgement is subject to psychological biases, e.g. over‐confidence (EFSA, 2014a). EFSA's (2014a) guidance describes formal methods of EKE that are designed to counter those biases: these maximise rigour, but require significant time and resource. Semi‐formal EKE [https://doi.org/10.2903/j.efsa.2018.5122] is more streamlined, and probability judgements can also be made by ‘minimal assessment’ (EFSA, 2014a), ‘expert group judgements’ and ‘individual expert judgement’ [https://doi.org/10.2903/j.efsa.2018.5122].
Most methods are described for eliciting distributions, but can be adapted to elicit probabilities or probability bounds, for both yes/no questions and quantities of interest.
Required steps in all methods include ensuring the question or quantity of interest is well‐defined (Section 10), selecting experts with appropriate expertise, deciding how to express the probability judgement (probability, distribution or probability bounds (Sections 12.1 and 12.2), reviewing the available evidence, conducting the elicitation in a manner that mitigates psychological biases, and recording the experts’ rationale for their judgements. All participants should have basic training in making probability judgements (Section 1.7). The methods and results should be documented transparently, including the evidence considered and the experts’ identities, reasoning and judgements, but not who said what.
Formal and semi‐formal EKE should be led by people trained in the elicitation method that is used (Section 1.7). Probability judgements by minimal assessment and expert group judgement can be carried out as part of normal Working Group meetings with little or no specialist support. However, it is recommended that Working Groups seek support (Section 1.7) when first making probability judgements, to help choose methods appropriate for their work.
It is recommended to use less formal methods to prioritise uncertainties (Section 8), and then apply more formal methods to elicit those with most impact on the assessment conclusions. Any limitations in the methods used, e.g. due to time constraints, will make probability judgements more approximate, and should be taken into account when characterising overall uncertainty (Section 16).
All expert judgements, including probability judgements, must be based on evidence and reasoning. Some assessors have concerns about using probability judgements in their assessments, for various reasons. Those concerns are recognised and addressed by this Guidance (see Box 2 and https://doi.org/10.2903/j.efsa.2018.5122).
Most expert judgements will be made either by members of the Working Group conducting the assessment, or by external experts participating in a formal EKE procedure, or a combination of Working Group members and additional experts, depending on what is appropriate in each case. However, for assessments that are to be adopted by a Panel or Scientific Committee, the final assessment is the responsibility and Opinion of the Panel or Committee, who therefore have an important role in peer reviewing and the judgements it includes. It is therefore important to inform and/or consult the Panel or Committee at key steps in the EKE process (EFSA, 2014a). In addition, those conducting an EKE may consider involving Panel or Committee members who have particular expertise in the question at hand.
12.7. Dependencies
Many variable quantities are interdependent, e.g. food intake and body weight.
Sources of uncertainty are dependent when learning more about one would alter the assessors’ uncertainty about the other. For example, getting better data on the toxicity of one chemical may reduce the assessors’ uncertainty about toxicity of a closely related chemical (see [https://doi.org/10.2903/j.efsa.2018.5122]).
Assessors should always consider whether dependencies may be present and, if so, take them into account, because they can have a large impact on the assessment conclusion.
Potential dependencies affecting variability or uncertainty are most easily addressed by probability bounds analysis, because it does not require specification of dependencies (Sections 14.1 and 15.1). However, it accounts for all possible dependencies, so the resulting approximate probability often covers a wide range of probabilities.
Narrower bounds, or precise probabilities or distributions, can be obtained if information on dependencies can be included in the analysis. Calculations with probabilities (Section 13) or distributions (Sections 14.2 15.2) require specification of all potential dependencies. If there is good reason to believe all dependencies are negligible, assuming independence makes calculation much simpler (Section 14.2). When there is reason to believe non‐negligible dependencies may be present, they should be estimated from data or by expert judgement; this will require specialist expertise (Section 1.7).
13. Combining uncertainties for yes/no questions using a logic model
A logic model expresses a yes/no conclusion as a logical deduction from the answers to a series of yes/no questions. When the answers to these questions are uncertain, the conclusion is also uncertain.
The simplest logic models are the ‘and’ and ‘or’ models. In the ‘and’ model, the conclusion is ‘yes’ only if each question has the answer ‘yes’. In the ‘or’ model, the conclusion is ‘yes’ if any of the questions has the answer ‘yes’. More complex models combine ‘and’ and ‘or’ hierarchically to build a tree of reasoning leading to a conclusion, for example taking the output of an ‘or’ submodel for some questions as one input to an ‘and’ model, which might also include other input questions or submodel outputs.
When uncertainty about the answer to each question is expressed using probability, the mathematics of probability can be used to calculate a probability for the conclusion. If precise probabilities are specified for the answers to each question, the result is a precise probability for the conclusion. If an approximate probability is specified for any of the questions, the result is a approximate probability the conclusion. Calculations are fairly straightforward [https://doi.org/10.2903/j.efsa.2018.5122] when uncertainties about answers to questions are independent; otherwise seek specialist advice (Section 1.7).
14. Combining uncertainties by calculation for a quantitative model involving only non‐variable quantities
14.1. Uncertainties expressed using probability bounds
If uncertainty for each input to the model has been quantified using a probability bound (Section 12.2), the method of Probability Bounds Analysis [https://doi.org/10.2903/j.efsa.2018.5122] can be used to deduce a probability bound for the output: an approximate probability that a particular range includes the output value that corresponds to the true values of the inputs.
Two simple versions of the calculation are described in https://doi.org/10.2903/j.efsa.2018.5122. In the first, the output range consists of all possible output values from the model corresponding to input values in the ranges specified for the inputs as part of the probability bounds. The approximate probability for the output range is straightforwardly obtained, using a calculator, from the approximate probabilities for input ranges. The second version applies when the model output is monotonic with respect to each input, i.e. each input either always increases or always decreases the output when the input is increased. The calculation uses approximate probabilities that inputs exceed specified values to compute an approximate probability that the output exceeds the value obtained by using the specified values in the model. If neither simple version is useful, seek specialist advice (Section 1.7). As an example of a simple application, suppose that that the model multiplies an uncertain concentration times an uncertain consumption to obtain an uncertain intake and that the probability that concentration exceeds 10 mg/kg is judged to be less than 10% and that the probability that consumption exceeds 0.2 kg/day is judged to be less than 5%. Then, probability bounds analysis concludes that the probability that intake exceeds 0.2 × 10 = 2 mg/day is less than (10 + 5) = 15%.
The calculation is robust in the sense that it is not affected by possible dependence between uncertainties about inputs. All possible forms of dependence have been taken into account when computing the probability bound for the output.
14.2. Uncertainties expressed using probability distributions
If uncertainty about each input to the model has been expressed using a probability distribution (Section 12.1) and there is no dependence between the uncertainties, the mathematics of probability leads to a probability distribution expressing the combined uncertainty about the output of the model.
The simplest method for computing the probability distribution for the output is one‐dimensional Monte Carlo simulation [https://doi.org/10.2903/j.efsa.2018.5122] which is easily implemented in freely available software or, in some simple cases, in a spreadsheet.
If assessors are not confident about how to express or elicit uncertainty using probability distributions or are not confident about how to carry out one‐dimensional Monte Carlo, seek advice (Section 1.7).
If dependence between uncertainties about inputs (Section 12.7) is considered to be an issue, seek advice (Section 1.7).
15. Combining uncertainties by calculation for a quantitative model involving variable quantities
15.1. Probability bounds analysis for both uncertainty and variability
Probability Bounds Analysis [https://doi.org/10.2903/j.efsa.2018.5122] can be applied to quantitative models which have variable inputs. This is most straightforward when the model output increases when any variable input is increased. For models which are monotonic but with some inputs causing increases and others decreases, the inputs can be redefined so that the model output increases with respect to each input [https://doi.org/10.2903/j.efsa.2018.5122]. It may be possible to apply the method to other models but specialist advice is likely to be needed (Section 1.7).
For each variable input, a percentile of interest should be chosen and a probability bound be provided, expressing uncertainty about the percentile. The result of the calculation is a probability bound for a percentile of the output; the output percentile is determined by doing a probability bounds analysis of the kind described in Section 14.1 but applied to variability rather than uncertainty. For models where output increases with respect to each input, the calculation does not require specialist software or expertise. For details, see https://doi.org/10.2903/j.efsa.2018.5122 which includes a worked example. Otherwise, seek advice (Section 1.7).
The calculation is robust in the sense that it is not affected by possible dependence between the variables and it is also not affected by possible dependence between uncertainties about the chosen percentiles. All possible forms of dependence have been taken into account when computing the probability bound for the output.
15.2. Probability distributions for both variability and uncertainty
As indicated in Section 12.4, a full expression of uncertainty about variability uses probability distributions in two roles: (i) as statistical models of variability; (ii) to express uncertainty about parameters in such models. Using probability to express uncertainty is fundamentally Bayesian and leads naturally to the use of Bayesian inference [https://doi.org/10.2903/j.efsa.2018.5122] and Bayesian graphical models [https://doi.org/10.2903/j.efsa.2018.5122] to provide a full analysis of variability and uncertainty about variability using data and expert judgement.
A full expression of uncertainty about variability is required if the quantitative model has more than one variable input and a probability distribution is needed expressing uncertainty about either: (i) one or more specified percentiles of variability of the model output; or (ii) the proportion of individuals/cases exceeding a specified value of the model output.
In situations where randomly sampled data are available for all variable inputs to a model, the bootstrap [https://doi.org/10.2903/j.efsa.2018.5122] may be used to quantify uncertainty, due to sampling, about variability of model outputs. Alternatively, where uncertainty about all parameters in a statistical model of variability is expressed by expert judgement, possibly informed by data, probability distributions and two‐dimensional Monte Carlo [https://doi.org/10.2903/j.efsa.2018.5122] may be used to compute consequent uncertainty about variability of model output. Where data are available for some inputs and expert judgements for others, Bayesian modelling and inference provide the best solution.
Possible dependence between variables can usually be addressed by an appropriate choice of statistical model for the variability. Dependence between uncertainties relating to parameters in a statistical model may arise simply as a consequence of applying the model to data, in which case Bayesian inference directly quantifies the dependence without need for judgements from experts about dependence. An example of this is the dependency between uncertainty of the mean and variance estimated from a sample of data [https://doi.org/10.2903/j.efsa.2018.5122]. If dependence between uncertainties relating to parameters arises because learning more about one would change the assessors’ judgement of the other, it needs to be addressed by specialist EKE methods (Section 1.7).
Any analysis of the kind described in this section is likely to benefit from specialist statistical expertise, especially in Bayesian modelling and computation (Section 1.7).
16. Characterising overall uncertainty
All assessments must report clearly and unambiguously the impact of uncertainty on the assessment conclusion (Section 1.2). In assessments where the impact of one or more uncertainties cannot be characterised, it must be reported that this is the case and that consequently the assessment conclusion is conditional on assumptions about those uncertainties, which should be specified (see Sections 16.2 and 17).
In standardised assessments where there are no non‐standard uncertainties, these requirements are met simply by reporting that non‐standard uncertainties were checked for and none were found (Section 3.1). For all other assessments, the Scientific Committee recommends that assessors express in quantitative terms the combined impact of as many as possible of the identified uncertainties [https://doi.org/10.2903/j.efsa.2018.5122]. Any uncertainties that the assessors are unable to include in their quantitative evaluation must be described qualitatively [https://doi.org/10.2903/j.efsa.2018.5122, https://doi.org/10.2903/j.efsa.2018.5122 and https://doi.org/10.2903/j.efsa.2018.5122] and presented alongside the quantitative evaluation, so that together they characterise the assessors’ overall uncertainty (note this refers to the overall impact of the identified uncertainties, and does not include ‘unknown unknowns’, See Section 16.2). Three options for this are depicted diagrammatically in Figure 14. In option 1, all identified uncertainties are evaluated collectively in one step: methods for this are, for convenience, described in the earlier sections and flow charts where this approach is used (Figures 2, ,6,6, ,77 and and11).11). In options 2 and 3, uncertainties for some parts of the assessment are quantified and combined separately, and other, additional uncertainties are taken into account when characterising overall uncertainty.
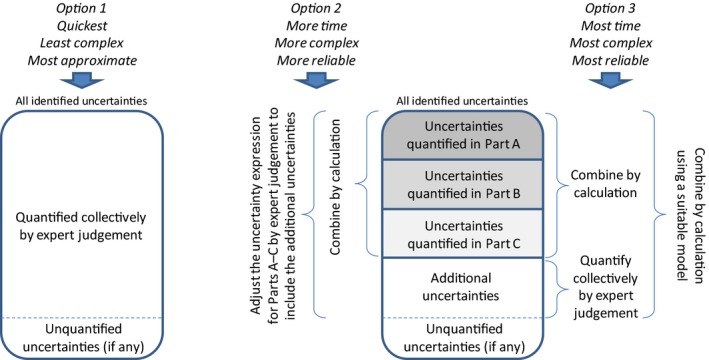
Illustration of options for characterising overall uncertainty. See [https://doi.org/10.2903/j.efsa.2018.5122] for detailed explanation
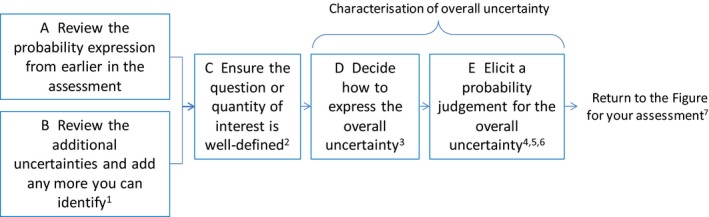
16.1. Taking account of additional uncertainties
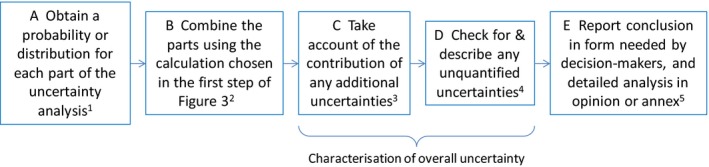
This section describes the approach for taking account of additional uncertainties in assessments where at least some uncertainties have been quantified separately and combined by calculation earlier in the assessment (in Figures 3, ,4,4, ,8,8, ,99 and and10).10). In urgent assessments and assessments using the simpler options for uncertainty analysis, no uncertainties are quantified separately and, for simplicity and speed of use, the approach to overall uncertainty characterisation for those cases (Option 1 in Figure 14) is described in the relevant Sections and Figures earlier in this Guidance (Figures 2, ,6,6, ,77 and and11).11). For all other assessments, where some uncertainties are quantified separately, the earlier Figures will have directed the user to this section, and the user should continue their uncertainty analysis with Figures 15, ,16,16, ,1717 (below).
16.2. Uncertainties that remain unquantified
The Scientific Committee recommends that assessors express in quantitative terms the combined impact of as many as possible of the identified uncertainties, because this avoids the ambiguity of qualitative expression and therefore provides better information for decision‐making [https://doi.org/10.2903/j.efsa.2018.5122]. In theory, probability judgements can be made for any well‐defined question or quantity of interest [https://doi.org/10.2903/j.efsa.2018.5122].
However, it is recognised that in some assessments, there may be some uncertainties that assessors are unable to include in a probability judgement [https://doi.org/10.2903/j.efsa.2018.5122]. In such cases, assessors should produce a probability expression representing the uncertainties that they are able to include, and a qualitative description of the uncertainties that remain unquantified.
If any uncertainties remain unquantified, the quantitative evaluation of uncertainty will be conditional on whatever assumptions have been made about those unquantified uncertainties [https://doi.org/10.2903/j.efsa.2018.5122]. Assessors must choose what assumptions to make: making no explicit assumptions will result in implicit assumptions, often that the unquantified uncertainty has no effect on the question or quantity of interest.
If the assessors are unable to include the unquantified uncertainties in their probability expression, this implies that they can say nothing, even approximately, about how much those unquantified uncertainties might change the assessment conclusion. Therefore, assessors must avoid implying any judgement about this in their qualitative description of the unquantified uncertainties, for example that they are negligible, minor, large, likely, unlikely, etc. If the assessors feel able to use such words this implies that, based on expert judgement, they are in fact able to say something about the impact of those uncertainties. If so, they should return to and revise the probability judgement to include them, at least approximately.
It follows that any uncertainties that remain unquantified, and the assumptions made about them, must be documented explicitly in the assessment and summarised alongside the quantitative expression of uncertainty. This is essential, to provide a proper characterisation of the overall uncertainty. The body of the assessment should include a more detailed description of each unquantified uncertainty, without implying any judgement about their magnitude or likelihood. Assessors should state which parts of the assessment they affect, describe their causes, explain why it was not possible to include them in the quantitative evaluation, state what assumptions have been made about them, and identify any options for reducing them or making them quantifiable [https://doi.org/10.2903/j.efsa.2018.5122].
All scientific assessments, whoever they are done by, are conditional on the expertise of assessors and the scientific knowledge available to them. EFSA addresses this by using appropriate procedures to select experts for participation in assessments, and additional procedures to select experts for participation in expert knowledge elicitation (EFSA, 2014a). In addition, uncertainty analysis represents those uncertainties that the assessors are able to identify and cannot, by definition, include ‘unknown unknowns’. Decision‐makers should be aware that these forms of conditionality are general, applying to all scientific assessment, and it is therefore not necessary to specify them in each assessment report.
17. Addressing uncertainty in conclusions and reporting
For standard assessments where no case‐specific sources of uncertainty have been identified, the EFSA output must at minimum state what standardised procedure was followed and report that non‐standard uncertainties were checked for and none were found (Section 3.1). If the applicability of the standardised procedure to the case in hand is not self‐evident, then an explanation of this should be provided. If non‐standard uncertainties are found, the assessors should report that standard uncertainties in the assessment are accepted to be covered by the standardised procedure and the uncertainty analysis is therefore restricted to non‐standard uncertainties that are particular to this assessment, the analysis of which should then be reported as described below.
In all other assessments, the uncertainty analysis should be reported as described below, although the level of detail may be reduced due to time constraints in urgent assessments.
Uncertainty analysis is part of scientific assessment; so in all cases, it should be reported in a manner consistent with EFSA's general principles regarding transparency (EFSA, 2007b, 2009) and reporting (EFSA, 2014b, 2015). In particular, it is important to list the sources of uncertainty that have been identified and document how they were identified, how each source of uncertainty has been evaluated and how they have been combined, where and how data and expert judgement have been used, what methodological approaches have been used (including models of any type) and the rationale for choosing them, and what the results were. Where the assessment used methods that are already described in other documents, it is sufficient to refer to those.
The location of information on the uncertainty analysis within the assessment report should be chosen to maximise transparency and accessibility for readers. This may be facilitated by including one or more separate sections on uncertainty analysis, which are identifiable in the table of contents.
The Scientific Committee has stated that EFSA's scientific assessments must report clearly and unambiguously what sources of uncertainty have been identified and characterise their overall impact on the assessment conclusion, in a form compatible with the requirements of decision‐makers and any legislation applicable to the assessment in hand [https://doi.org/10.2903/j.efsa.2018.5122].
In some types of assessment, decision‐makers or legislation may stipulate a specified form for reporting assessment conclusions. In some cases, this may comprise qualitative descriptors such as ‘safe’, ‘no concern’, ‘sufficient evidence’, etc. To enable these to be used by assessors without implying risk management judgements requires that assessors and decision‐makers have a shared understanding or definition of the question or quantity of interest and level of certainty associated with each descriptor.
In other cases, decision‐makers or legislation may require that conclusions be stated without qualification by probability expressions. This can be done if assessors and decision‐makers have a shared understanding or definition of the level of probability required for practical certainty about a question of interest, i.e. a level of probability that would be close enough to 100% (answer is certain to be yes) or 0% (certain to be no) for decision‐making purposes. On issues where practical certainty is not achieved, the assessors would report that they cannot conclude, or that the assessment is inconclusive.
In such cases, assessors should also comply with any requirements of decision‐makers or legislation regarding where and how to document the details of the uncertainty analysis that led to the conclusion.
In other cases, where the form for reporting conclusions is not specified by decision‐makers or legislation, the assessment conclusion should include (a) a clear statement of the overall result for those uncertainties that have been quantified and (b) a clear description of unquantified sources of uncertainty, i.e. those that could not be included in the quantitative analysis. The former will generally express the overall quantified uncertainty about the assessment conclusion using probabilities, probability distributions, probability bounds, or ranges from the approximate probability scale (Sections 12.1–12.3). For each unquantified source of uncertainty, the assessors should describe (either in the conclusion or another section, as appropriate) which part(s) of the assessment it arises in, the cause or reason for it, how it affects the assessment (but not how much), why it is difficult to quantify, what assumptions have been made about it in the assessment and what could be done to reduce or better characterise it. Assessors must avoid using any words that imply a judgement about the magnitude or likelihood of the unquantified sources of uncertainty (Section 16.2).
In addition to the detailed reporting of the methods and results of the uncertainty analysis, the assessors should prepare a concise summary of the overall characterisation of uncertainty in format and style suitable for inclusion in the executive summary of the assessment report. This should present, in the simplest terms possible, a quantitative expression of the combined effect on the assessment conclusion of those uncertainties that have been quantified, and a brief description of any unquantified sources of uncertainty.
Assessors must check that there is no incompatibility between the reporting of the uncertainty analysis and the assessment conclusions. In principle, no such incompatibility should occur, because sound scientific conclusions will take account of relevant uncertainties, and therefore should be compatible with an appropriate analysis of those uncertainties. If there appears to be any incompatibility, assessors should review and if necessary revise both the uncertainty analysis and the conclusion to ensure that they are compatible with one another and with what the science will support.
In many assessments, information on the main contributors to the uncertainty of the question or quantity of interest may be useful to decision‐makers, to inform decisions about the need for further work such as data gathering, to support refinement of the assessment. Such information may be generated by methods for prioritising uncertainties (Section 8).
Communicating uncertainty is discussed in [https://doi.org/10.2903/j.efsa.2018.5122] and guidance on communication to different target audiences including decision‐makers is the subject of another companion document (EFSA, 2018, in prep.).
Glossary
- Additional uncertainties
- Term used when some uncertainties have already been quantified, to refer to other uncertainties that have not yet been quantified and need to be taken into account in the characterisation of overall uncertainty
- Ambiguity
- The quality of being open to more than one interpretation. A type or cause of uncertainty that may apply for example to questions for assessment, evidence, models or concepts, and assessment conclusions
- Approximate probability
- A range or bound for a probability
- Approximate probability scale
- A set of approximate probabilities with accompanying verbal probability terms, shown in Section 12.3 of the Guidance and recommended for harmonised use in EFSA scientific assessments
- Assessment factor
- A numerical factor used in quantitative assessment, to represent or allow for extrapolation or uncertainty
- Assessor
- A person conducting a scientific assessment and/or uncertainty analysis
- Calibration
- Used in the Guidance to refer to the process of evaluating whether a standardised procedure is appropriately conservative and, if necessary, adjusting it to achieve this. More specifically, the process of ensuring a standard procedure provides an appropriate probability of achieving a specified management objective to an acceptable extent
- Case‐specific assessment
- Scientific assessments where there is no pre‐established standardised procedure, so the assessors have to develop an assessment plan that is specific to the case in hand. Standardised elements (e.g. default values) may be used for some parts of the assessment, but other parts require case‐specific approaches. Both standardised and case‐specific assessments are used in Applications Management, one of the core processes in EFSA's Process Architecture
- Categorical question
- An assessment question that is expressed as a choice between two or more categories, e.g. yes/no or low/medium/high. Many issues that are expressed as categorical questions refer explicitly or implicitly to quantities (e.g. whether exposure is below a threshold value)
- Characterising uncertainty
- The process of making and expressing an evaluation of uncertainty either for an assessment as a whole or for a specified part of an assessment. Can be performed and expressed either qualitatively or quantitatively
- Collective
- Used in this document to refer to evaluating the combined impact of two or more uncertainties together
- Combine uncertainties
- The process of integrating separate characterisations of two or more uncertainties to produce a characterisation of their combined impact on an assessment or part of an assessment. Can be performed by calculation or expert judgement, and in the latter case either quantitatively or qualitatively
- Conceptual model
- The reasoning developed by assessors in the course of a scientific assessment, which is then implemented as a narrative argument, a logic model, a calculation or a combination of these. Documenting the conceptual model, e.g. as a bullet list, flow chart or graphic, may be helpful to assessors during the assessment and also for readers, if included in the assessment report
- Conditional
- Used in the Guidance to refer to dependence of the quantitative result of an assessment or uncertainty analysis on assumptions made about sources of uncertainty that have not been quantified
- Conservative
- Term used to describe assessments, or parts of assessments (e.g. assumptions, default factors, etc.), that tend to overestimate the severity and/or frequency of an adverse consequence (e.g. overestimate exposure or hazard and consequently risk). Can also be used to refer to underestimation of a beneficial consequence. Conservatism is often introduced intentionally, as a method to allow for uncertainty
- Decision‐maker
- A person with responsibility for making decisions; in the context of this document, a person making decisions informed by EFSA's scientific advice. Includes risk managers but also people making decisions on other issues, e.g. health benefits, efficacy, etc
- Default value or factor
- Pragmatic, fixed or standard value used in the absence of relevant data, implicitly or explicitly regarded as accounting appropriately for the associated uncertainty
- Dependency
- Variable quantities are dependent when they are directly or indirectly related, such that the probability of a given value for one quantity depends on the value(s) of other quantities (e.g. food consumption and body weight). Sources of uncertainty are dependent when learning more about one would alter the assessors’ uncertainty about the other
- Distribution
- A probability distribution is a mathematical function that relates probabilities with specified intervals of a continuous quantity or values of a discrete quantity. Applicable both to random variables and uncertain parameters
- Evidence appraisal
- The process of evaluating the internal validity of evidence and its external validity for the question at hand, in addition to other sources of uncertainties such as imprecision
- Expert group judgement
- The process of eliciting a judgement or judgements from a group of experts without using a formal or semi‐formal elicitation procedure
- Expert judgement
- The judgement of a person with relevant knowledge or skills for making that judgement
- Expert knowledge elicitation (EKE)
- A systematic, documented and reviewable process to retrieve expert judgements from a group of experts, often in the form of a probability distribution
- External validity
- Extent to which the findings of a study can be generalised or extrapolated to the assessment question at hand. It is not an inherent property of the evidence
- Identifying uncertainties
- The process of identifying sources of uncertainty affecting a scientific assessment
- Individual expert judgement
- The process of eliciting a judgement or judgements from a single expert without using a formal or semi‐formal elicitation procedure
- Influence analysis
- The extent to which plausible changes in the overall structure, parameters and assumptions used in an assessment produce a change in the results
- Logic model
- A model expressing a yes/no conclusion as a logical deduction from the answers to two or more yes/no questions
- Management objective
- A well‐defined expression of the outcome required by decision‐makers from a decision, policy or procedure, specifying the question or quantity of interest and the temporal and spatial scale for which it should be assessed. Applied in the Guidance to the calibration of standardised procedures
- Model
- In scientific assessment, usually refers to a mathematical or statistical construct, which is a simplified representation of data or of real world processes, and is used for calculating estimates or predictions. Can also refer to the structure of a reasoned argument or qualitative assessment
- Monte Carlo: one‐dimensional
- A method for making probability calculations by random sampling from one set of distributions, all representing uncertainty about non‐variable quantities or categorical questions
- Monte Carlo: two‐dimensional
- A method for making probability calculations by random sampling from two sets of distributions, one set describing the variability of variable quantities, and the second set representing uncertainty, including uncertainty about the parameters of the distributions describing variability
- Non‐standard uncertainties
- Any deviations from a standardised procedure or standardised assessment element that lead to uncertainty regarding the result of the procedure. For example, studies that deviate from the standard guidelines or are poorly reported, cases where there is doubt about the applicability of default values, or the use of non‐standard or ‘higher tier’ studies that are not part of the standard procedure
- Non‐variable quantity
- A quantity that has a single real or true value
- Ordinal scale
- A scale of measurement comprised of ordered categories, where the magnitude of the difference between categories is not quantified
- Overall uncertainty
- The assessors’ uncertainty about the question or quantity of interest at the time of reporting, taking account of the combined effect of all sources of uncertainty identified by the assessors as being relevant to the assessment
- Parameter
- Parameter is used in this document to refer to quantitative inputs to an assessment or uncertainty analysis, without specifying whether they are variable or not. In most places a non‐variable quantity is implied, consistent with the use of parameter in statistics. However, in some places parameter could refer to a variable quantity, as it is sometimes used in biology (e.g. glucose level is referred to as a blood parameter)
- Parts of the scientific assessment
- Components of a scientific assessment that it is useful to distinguish for the purpose of assessment, e.g. a risk assessment comprises hazard and exposure assessment, and each of these can be subdivided further (e.g. to distinguish individual model parameters, studies, or lines of evidence)
- Parts of the uncertainty analysis
- Parts of an uncertainty analysis that it is useful to distinguish, evaluating uncertainties within each part collectively, and then combining the parts and any additional uncertainties to characterise overall uncertainty. Not necessarily the same as the parts into which the scientific assessment is divided (see text)
- Practical certainty
- A level of probability that would be close enough to 100% (answer is certain to be yes) or 0% (certain to be no) for the purpose of decision‐making. What levels of probability will comprise practical certainty will vary, depending on the context for the decision including the decision options and their respective costs and benefits
- Prioritising uncertainties
- The process of evaluating the relative importance of different sources of uncertainty, to guide decisions on how to treat them in uncertainty analysis or to guide decisions on gathering further data with the aim of reducing uncertainty. Prioritisation is informed by influence or sensitivity analysis
- Probability
- Defined depending on philosophical perspective: (1) the frequency with which sampled values arise within a specified range or for a specified category; (2) quantification of judgement regarding the likelihood of a particular range or category
- Probability bound
- A probability or approximate probability for a specified range of values
- Probability bounds analysis
- A method for combining probability bounds for inputs in order to obtain a probability bound for the output of a deterministic model. It is a special case of the general theory of imprecise probability which provides more ways to obtain partial expressions of uncertainty for the output based on more general partial expressions for inputs
- Probability judgement
- A probability, approximate probability or probability bound obtained by expert judgement
- Protection goal
- A management objective for protection of an entity of interest
- Qualitative assessment
- Sometimes refers to the form in which the conclusion of an assessment is expressed (e.g. a verbal response to a question of interest), or to the methods used to reach the conclusion (not involving calculations), or both
- Qualitative expression of uncertainty
- Expression of uncertainty using words or ordinal scales
- Quantitative expression of uncertainty
- Expression of uncertainty using numeric measures of the range and relative likelihood of alternative answers or values for a question or quantity of interest
- Quantity
- A property or characteristic having a numerical scale
- Quantity of interest
- A quantity that is the subject of a scientific assessment as a whole, or of a part of such an assessment
- Question of interest
- A categorical question that is the subject of a scientific assessment as a whole, or of a part of such an assessment
- Real value
- A synonym for true value (q.v.)
- Resolved
- The actual or hypothetical process of removing an uncertainty by making the measurement or observation needed to obtain the true answer or value for the question or quantity of interest
- Risk management judgement
- The process or result of weighing policy alternatives in consultation with interested parties, considering risk assessment and other legitimate factors, and, if need be, selecting appropriate prevention and control options
- Risk manager
- A type of decision‐maker, responsible for making risk management judgements
- Scientific assessment
- The process of using scientific evidence and reasoning to answer a question or estimate a quantity
- Scope (for non‐standard uncertainties)
- The degree to which a standardised procedure was calibrated to be more conservative than required (e.g. by rounding up an assessment factor), which determines how much opportunity there will be to accommodate the presence of non‐standard uncertainties in individual assessments
- Semi‐formal expert knowledge elicitation
- A structured and documented procedure for eliciting expert judgements that is intermediate between fully formal elicitation and informal expert judgements
- Sensitivity analysis
- A study of how the variation in the outputs of a model can be attributed to, qualitatively or quantitatively, different sources of uncertainty or variability. Implemented by observing how model output changes when model inputs are changed in a structured way
- Standard uncertainties
- Sources of uncertainty that are considered (implicitly or explicitly) to be addressed by the provisions of a standardised procedure or standardised assessment element. For example, uncertainties due to within and between species differences in toxicity are often addressed by a default factor of 100 in chemical risk assessment
- Standardised assessment
- An assessment that follows a standardised procedure (q.v.)
- Standardised procedure
- A procedure that specifies every step of assessment for a specified class or products or problems, and is accepted by assessors and decision‐makers as providing an appropriate basis for decision‐making. Often (but not only) used in scientific assessments for regulated products. Both standardised and case‐specific assessments are used in Applications Management, one of the core processes in EFSA's Process Architecture
- Statistical model
- A probabilistic model of variability, possibly modelling dependence between variables or dependence of one variable on another, for example a family of probability distributions representing alternative possible distributions for a variable or regression or dose‐response models. Usually has parameters which control the detail of distributions or dependence
- True value
- The actual value that would be obtained with perfect measuring instruments and without committing any error of any type, both in collecting the primary data and in carrying out mathematical operations. (OECD Glossary of Statistical Terms, https://stats.oecd.org/glossary/detail.asp?ID=4557)
- Uncertainty
- In this document, uncertainty is used as a general term referring to all types of limitations in available knowledge that affect the range and probability of possible answers to an assessment question. Available knowledge refers here to the knowledge (evidence, data, etc.) available to assessors at the time the assessment is conducted and within the time and resources agreed for the assessment. Sometimes ‘uncertainty’ is used to refer to a source of uncertainty (see separate definition), and sometimes to its impact on the conclusion of an assessment
- Uncertainty analysis
- The process of identifying and characterising uncertainty about questions of interest and/or quantities of interest in a scientific assessment
- Unknown unknowns
- A limitation of knowledge that one is unaware of
- Unquantified uncertainty
- An identified source of uncertainty in a scientific assessment that the assessors are unable to include, or choose not to include, in a quantitative expression of overall uncertainty for that assessment
- Urgent assessment
- A scientific assessment requested to be completed within an unusually short period of time. Part of Urgent Responses Management in EFSA's Process Architecture
- Variability
- Heterogeneity of values over time, space or different members of a population, including stochastic variability and controllable variability. See [https://doi.org/10.2903/j.efsa.2018.5122] for discussion of uncertainty and variability
- Variable quantity
- A quantity that has multiple true values (e.g. body weight measured in different individuals in a population, or in the same individual at different points in time)
- Weight of evidence assessment
- A process in which evidence is integrated to determine the relative support for possible answers to a scientific question
- Well defined
- A question or quantity of interest that has been defined by specifying an experiment, study or procedure that could be undertaken, at least in principle, and would determine the question or quantity with certainty
Notes
Suggested citation: EFSA (European Food Safety Authority) Scientific Committee , Benford D, Halldorsson T, Jeger MJ, Knutsen HK, More S, Naegeli H, Noteborn H, Ockleford C, Ricci A, Rychen G, Schlatter JR, Silano V, Solecki R, Turck D, Younes M, Craig P, Hart A, Von Goetz N, Koutsoumanis K, Mortensen A, Ossendorp B, Martino L, Merten C, Mosbach‐Schulz O and Hardy A, 2018. Guidance on Uncertainty Analysis in Scientific Assessments. EFSA Journal 2018;16(1):5123, 39 pp. 10.2903/j.efsa.2018.5123 [CrossRef]
Requestor: EFSA
Question number: EFSA‐Q‐2013‐00738
Scientific Committee members: Anthony Hardy, Diane Benford, Thorhallur Halldorsson, Michael John Jeger, Helle Katrine Knutsen, Simon More, Hanspeter Naegeli, Hubert Noteborn, Colin Ockleford, Antonia Ricci, Guido Rychen, Josef R Schlatter, Vittorio Silano, Roland Solecki, Dominique Turck and Maged Younes.
Acknowledgements: The Scientific Committee wishes to thank the EFSA staff members Andrea Germini, Nikolaos Georgiadis and Anthony Smith for the support provided to this scientific opinion.
Adopted: 15 November 2017
This publication is linked to the following EFSA Journal article: http://onlinelibrary.wiley.com/doi/10.2903/j.efsa.2018.5122/full
References
- EFSA (European Food Safety Authority), 2007a. Guidance of the Scientific Committee on a request from EFSA related to uncertainties in dietary exposure assessment. EFSA Journal 2006;5(1):438, 54 pp. 10.2903/j.efsa.2007.438 [CrossRef] [Google Scholar]
- EFSA (European Food Safety Authority), 2007b. Transparency in risk assessment carried out by EFSA: guidance document on procedural aspects. EFSA Journal 2006;4(5):353, 16 pp. 10.2903/j.efsa.2006.353 [CrossRef] [Google Scholar]
- EFSA (European Food Safety Authority), 2009. Guidance of the Scientific Committee on Transparency in the Scientific Aspects of Risk Assessments carried out by EFSA. Part 2: general principles. EFSA Journal 2009;7(5):1051, 22 pp. 10.2903/j.efsa.2009.1051 [CrossRef] [Google Scholar]
- EFSA (European Food Safety Authority), 2014a. Guidance on expert knowledge elicitation in food and feed safety risk assessment. EFSA Journal 2014;12(6):3734, 278 pp. 10.2903/j.efsa.2014.3734 [CrossRef] [Google Scholar]
- EFSA (European Food Safety Authority), 2014b. Guidance on statistical reporting. EFSA Journal 2014;12(12):3908, 18 pp. 10.2903/j.efsa.2014.3908 [CrossRef] [Google Scholar]
- EFSA (European Food Safety Authority), 2015. Principles and process for dealing with data and evidence in scientific assessments. Scientific Report. EFSA Journal 2015;13(5):4121, 35 pp. 10.2903/j.efsa.2014.4121 [CrossRef] [Google Scholar]
- EFSA (European Food Safety Authority), 2016. Guidance to develop specific protection goals options for environmental risk assessment at EFSA, in relation to biodiversity and ecosystem services. EFSA Journal 2016;14(6):4499, 50 pp. 10.2903/j.efsa.2014.4499 [CrossRef] [Google Scholar]
- EFSA (European Food Safety Authority), 2017. Event report on the Workshop on the trial of the EFSA guidance document on uncertainty analysis in scientific assessments. EFSA Supporting publication 2017:EN‐1313, 28 pp.
- EFSA (European Food Safety Authority), 2018. in preparation. Guidance on how to communicate on uncertainty of scientific assessments.
- EFSA Scientific Committee , Benford D, Halldorsson T, Jeger MJ, Knutsen HK, More S, Naegeli H, Noteborn H, Ockleford C, Ricci A, Rychen G, Schlatter JR, Silano V, Solecki R, Turck D, Younes M, Craig P, Hart A, Von Goetz N, Koutsoumanis K, Mortensen A, Ossendorp B, Germini A, Martino L, Merten C, Smith A and Hardy A, 2018. Principles and methods behind EFSA's Guidance on Uncertainty Analysis in Scientific Assessment. Scientific Opinion. EFSA Journal 2018;16(1):5122, 282 pp. 10.2903/j.efsa.2018.5122 [CrossRef] [Google Scholar]
- EFSA Scientific Committee , Hardy A, Benford D, Halldorsson T, Jeger MJ, Knutsen HK, More S, Naegeli H, Noteborn H, Ockleford C, Ricci A, Rychen G, Schlatter JR, Silano V, Solecki R, Turck D, Benfenati E, Chaudhry QM, Craig P, Frampton G, Greiner M, Hart A, Hogstrand C, Lambre C, Luttik R, Makowski D, Siani A, Wahlstroem H, Aguilera J, Dorne J‐L, Fernandez Dumont A, Hempen M, Valtue˜na Martınez S, Martino L, Smeraldi C, Terron A, Georgiadis N and Younes M, 2017. Scientific Opinion on the guidance on the use of the weight of evidence approach in scientific assessments. EFSA Journal 2017;15(8):4971, 69 pp. 10.2903/j.efsa.2017.4971 [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
Articles from EFSA Journal are provided here courtesy of Wiley
Full text links
Read article at publisher's site: https://doi.org/10.2903/j.efsa.2018.5123
Read article for free, from open access legal sources, via Unpaywall:
https://efsa.onlinelibrary.wiley.com/doi/pdfdirect/10.2903/j.efsa.2018.5123
HAL Open Archive
https://hal.univ-lille.fr/hal-04388193
Citations & impact
Impact metrics
Article citations
Update of the risk assessment of brominated phenols and their derivatives in food.
EFSA J, 22(10):e9034, 23 Oct 2024
Cited by: 0 articles | PMID: 39444985 | PMCID: PMC11496907
Estimating public health risks of infectious disease events: A Canadian approach to rapid risk assessment.
Can Commun Dis Rep, 50(9):282-293, 05 Sep 2024
Cited by: 0 articles | PMID: 39257839 | PMCID: PMC11383208
Scientific opinion on the tolerable upper intake level for vitamin E.
EFSA J, 22(8):e8953, 02 Aug 2024
Cited by: 1 article | PMID: 39099617 | PMCID: PMC11294871
A developmental neurotoxicity adverse outcome pathway (DNT-AOP) with voltage gate sodium channel (VGSC) inhibition as a molecular initiating event (MiE).
EFSA J, 22(8):e8954, 06 Aug 2024
Cited by: 0 articles | PMID: 39109086 | PMCID: PMC11301258
The use of high expansion foam for stunning and killing pigs and poultry.
EFSA J, 22(7):e8855, 12 Jul 2024
Cited by: 0 articles | PMID: 39005713
Go to all (170) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
The principles and methods behind EFSA's Guidance on Uncertainty Analysis in Scientific Assessment.
EFSA J, 16(1):e05122, 24 Jan 2018
Cited by: 124 articles | PMID: 32625670 | PMCID: PMC7009645
Draft for internal testing Scientific Committee guidance on appraising and integrating evidence from epidemiological studies for use in EFSA's scientific assessments.
EFSA J, 18(8):e06221, 18 Aug 2020
Cited by: 16 articles | PMID: 32831946 | PMCID: PMC7433401
Scientific Committee guidance on appraising and integrating evidence from epidemiological studies for use in EFSA's scientific assessments.
EFSA J, 22(7):e8866, 05 Jul 2024
Cited by: 1 article | PMID: 38974922