Abstract
It is well-known that designing a cluster randomized trial (CRT) requires an advance estimate of the intra-cluster correlation coefficient (ICC). In the case of longitudinal CRTs, where outcomes are assessed repeatedly in each cluster over time, estimates for more complex correlation structures are required. Three common types of correlation structures for longitudinal CRTs are exchangeable, nested/block exchangeable and exponential decay correlations—the latter two allow the strength of the correlation to weaken over time. Determining sample sizes under these latter two structures requires advance specification of the within-period ICC and cluster autocorrelation coefficient as well as the intra-individual autocorrelation coefficient in the case of a cohort design. How to estimate these coefficients is a common challenge for investigators. When appropriate estimates from previously published longitudinal CRTs are not available, one possibility is to re-analyse data from an available trial dataset or to access observational data to estimate these parameters in advance of a trial. In this tutorial, we demonstrate how to estimate correlation parameters under these correlation structures for continuous and binary outcomes. We first introduce the correlation structures and their underlying model assumptions under a mixed-effects regression framework. With practical advice for implementation, we then demonstrate how the correlation parameters can be estimated using examples and we provide programming code in R, SAS, and Stata. An Rshiny app is available that allows investigators to upload an existing dataset and obtain the estimated correlation parameters. We conclude by identifying some gaps in the literature.
Keywords: Sample size, statistical power, clinical trials, cluster autocorrelation coefficient, stepped wedge
Key Messages.
Obtaining an estimate of the intra-cluster correlation coefficient (ICC) to inform sample size calculation for a planned cluster randomized trial (CRT) is one of the most common challenges faced by investigators.
A common strategy is to use a guestimate or a ‘typical value’, but this becomes more challenging in longitudinal CRTs as multiple types of correlation parameters need to be postulated. With the increasing practice of data sharing from trial publications, as well as increasing availability of routinely collected data for outcome assessment, there is an opportunity for researchers to estimate correlation parameters more reliably in advance of a longitudinal CRT.
In this tutorial, we describe three main correlation structures in longitudinal CRTs and demonstrate how to estimate relevant correlation parameters from existing data to inform future trial designs. We provide R, SAS and Stata code that can be used for both repeated cross-sectional and cohort designs. An RShiny app to estimate correlation parameters is available for those without access to statistical software.
Background
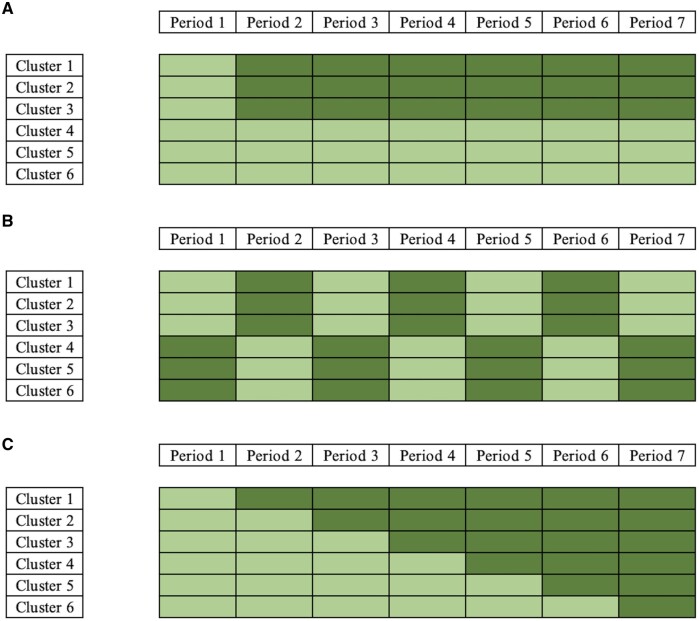
The cluster randomized trial (CRT) is an essential design for evaluating interventions delivered at the group level or when there are scientific or logistical reasons precluding individual randomization.1 Unlike individually randomized trials, CRTs randomize intact groups of participants to either intervention or control conditions. A key characteristic of this design is that the randomization is at the level of the cluster, and individuals within the same cluster are more similar than individuals from different clusters; this should be taken into consideration in the design and analysis.2 The similarity of outcomes within clusters is typically measured by the intra-cluster correlation coefficient (ICC).3 Substantial methodological development for longitudinal CRTs (also referred to as multiple-period CRTs) has taken place in recent years. In a longitudinal design, the outcomes are measured multiple times in each cluster, typically before and after intervention delivery. These outcomes can be measured on different participants over time (i.e. a repeated cross-sectional design) or the same participants (i.e. a cohort design).4 Three major types of longitudinal CRTs are multiple-period before and after parallel-arm (Figure 1a), multiple cross-over5 (Figure 1b) and stepped-wedge cluster randomized trials (SW-CRT) (Figure 1c).6
Figure 1.
Example of different types of longitudinal cluster randomized trials. (a) Multiple-period before and after design. (b) Multiple-period cross-over cluster randomized trial. (c) Stepped-wedge cluster randomized trial. (Light shading: control condition; Dark shading: intervention condition)
Two recent articles have summarized existing sample size calculation methods and statistical models for longitudinal CRTs.7,8 A key feature differentiating existing methods is the type of correlation structure, i.e. how ICCs are assumed to change over time. Available sample size calculators require specification of an assumed correlation structure for the planned design and corresponding estimated correlation parameters. Parameters that must be specified are a within-period ICC, a cluster autocorrelation coefficient (CAC) and, in the case of a cohort design, a within-individual ICC.
A practical challenge for researchers planning a new trial is how to obtain estimates for these coefficients. The choice of correlation structure can affect the sample size requirements and the statistical inferences.8,9 One possibility is to use estimates reported in previously published trials. However, despite the various CONSORT extensions for CRTs recommending that authors report the obtained ICC values for their trials,10,11 adherence to this recommendation has been low.12 Furthermore, even when reported, estimates may not be suitable for longitudinal correlation structures. A database reporting suitable ICC values for a selection of longitudinal CRTs with continuous outcomes has recently become available,13 but the range of outcomes remains limited. With the increasing availability of routinely collected databases that can be used for outcome assessment in a CRT, as well as data availability from published trials, researchers may be able to obtain access to real data for more reliable estimation of ICC values in advance of a new trial. However, researchers may lack knowledge of how to estimate complex correlation parameters from longitudinal clustered data.
In this tutorial, our goal is to provide readers with the tools to estimate correlation parameters required for longitudinal CRTs with continuous and binary outcomes. We first review the main types of mixed-effect statistical models and correlation structures available for longitudinal CRTs and define the required input parameters for sample size calculation under these models. We then describe the required data structure for estimating the relevant correlation values and highlight some practical considerations for implementation. We provide code in R, SAS and Stata to empirically estimate the correlation parameters under repeated cross-sectional and cohort designs and we make available an RShiny app that does not require access to statistical software. We conclude our tutorial by identifying some gaps in the literature.
Available correlation structures for longitudinal CRTs
A common analytical approach for longitudinal CRT is mixed-effects regression with fixed (discrete) effects for periods and treatment.14 In the methodological literature, substantial attention has been paid to the random-effects specification, with three main types of correlation structures defined by what has become known as the Hussey and Hughes (exchangeable) model,15 the Hooper and Girling (nested/block exchangeable) model,16,17 and the Kasza (exponential decay) model.18 A visualization of these three correlation structures is presented in Supplementary File Section 1 (available as Supplementary data at IJE online).
The first statistical model we introduce for longitudinal CRTs was developed by Hussey and Hughes in 2007.15 Assuming a continuous outcome, this model can be expressed as:
| (1) |
where is the outcome of the -th individual from the -th cluster and -th period. The baseline average response (average outcome in the first period under the control condition) is denoted as ; is the random intercept for the cluster, which is assumed to follow the distribution; and is the categorical time effect in the -th period (with for identifiability). The binary treatment indicator is denoted for the -th cluster in the -th period, where 0 is the control and 1 is the intervention condition. is the treatment effect. The error term is denoted by and assumed to be independently and identically distributed as .
This model includes a random intercept for the cluster only, and thus, the ICC is assumed to be constant across different periods (called the exchangeable correlation structure). This may be a rather strong assumption, considering that factors that may influence outcomes can vary over time. Moreover, since the exchangeable model allows the variance of the treatment effect estimate to approach 0 with increasing cluster size,19 use of the exchangeable correlation for designing longitudinal CRTs is not recommended. An improvement is to allow the outcomes of two individuals within the same cluster but in different periods to weaken with increasing time separation; i.e. to allow for a within-period ICC (the correlation between two individuals in the same cluster and the same period) and a different between-period ICC (correlation between two individuals in the same cluster but different periods).
To allow for a different within- and between-period ICC, Hooper et al.16 and Girling and Hemming17 added an additional random cluster-by-period interaction term ( independent to the random intercept for clusters, which is written as:
| (2) |
This model defines a correlation structure referred to as the nested exchangeable correlation.20 The additional random effect allows the cluster means to vary randomly across periods. The within-period and between-period ICCs between any pair of observations in any two periods can be defined as follows:
Within-period ICC (where ):
Between-period ICC:
Note that the between-period ICC is constant in this model regardless of the distance between and . The ratio of the between-period and within-period ICCs is called the CAC. The CAC is typically less than 1; a CAC value of 1 implies the exchangeable correlation.
The Hooper and Girling model was later extended by Kasza et al.,18 where they further allowed the between-period ICC to decay over time. This model can be written as:
| (3) |
where the vector of random cluster-by-period effects in each cluster is assumed to follow the distribution. Kasza et al.18 focused on as an autoregressive (AR(1)) structure where the between-period ICC decays exponentially at the rate of per period. Therefore, this model is referred to as the exponential decay model. For simplicity, the rate of decay per period, r, is called the CAC although it defines a different parameter compared with the Hooper and Girling model.
In the case of binary outcomes, data are often analysed using mixed-effects logistic regression. The mathematical expression of the model under each correlation structure is similar to the above except where the probability of the binary outcome for the -th individual from the -th cluster and -th period and the error term is omitted. The definition of the ICC for binary outcomes, however, is less straightforward. For mixed-effects logistic regression, one simple approach is to work on the latent response scale21 so that the ICC can still be defined as the ratio of the between-cluster variance and the total variance with the residual variance defined as . Under this approach, the within-period ICC and CAC can be defined analogously to the linear mixed model case.
In the case of a cohort design, an additional random effect for the repeated measures on the same individual ) in cluster (denoted as ) may be added to equations (1), (2) and (3) to model a constant correlation in repeated measures on the same individual over time. This random effect is assumed to follow the distribution and defines the within-individual ICC. In this case, the three relevant ICCs can be derived under the nested exchangeable model as:
Within-period ICC (where ):
Between-period ICC:
Within-individual ICC:
In some sample size calculation methods,16,22 an alternative correlation coefficient called the individual autocorrelation coefficient (IAC), defined as , is used to account for the correlation in repeated measures on the same individual in cohort designs.16 The fundamental difference between IAC and within-individual ICC is whether we consider the individual as being sampled from one given cluster or from any cluster. In practice, if using data from a single cluster, IAC may be a more suitable measure, and if using data from several different clusters, then within-individual ICC would be a better measure. In the literature, the cohort design version of a nested exchangeable correlation structure has been referred to as block exchangeable correlation.20
Practical recommendations for estimating correlation parameters from available data
Sample size calculation methods are now available for all three models reviewed in the previous section,8 and have been implemented in major statistical software packages and web-based applications.22–28 The input correlation parameters required under all three models are summarized in Table 1. In most cases, assuming an exchangeable correlation is inappropriate and anti-conservative at the design stage. Therefore, it is preferable to assume an alternative correlation structure and estimate both the within-period ICC and the CAC (in addition to the within-individual ICC or IAC in case of a cohort design). In this section, we provide practical recommendations for estimating values for these correlation parameters in advance of a planned longitudinal CRT. After obtaining estimates, readers can refer to a previously published tutorial for how to use these input parameters to determine the required sample size using any of the available sample size calculators including code and examples.8
Table 1.
Summary of correlation parameters under each correlation structure for repeated cross-sectional and cohort design
| Correlation structure | Correlation parameter | Repeated cross-sectional design | Cohort design |
|---|---|---|---|
| Exchangeable | ICC | ||
| Within-individual ICCa | – | ||
| Nested/block exchangeable | Within-period ICC | ||
| Between-period ICCb | |||
| CACb = | |||
| Within-individual ICCa | – | ||
| Exponential decay | Within-period ICC | ||
| CACb | |||
| Between-period ICCb (Between period and , where ) | |||
| Within-individual ICCa | – | ||
ICC, intra-cluster correlation; CAC, cluster autocorrelation; IAC, individual autocorrelation coefficient.
, variance of the random intercept for clusters.
, variance of the random cluster period effect.
, variance of the random residuals.
, variance of the random intercept for repeated measures on the same individual.
IAC, defined as , may also be used to account for individual repeated measures.
Often only one of CAC and between-period ICC is required for sample size calculation. We present both formulae for completeness. CAC does not indicate the same parameter in each model.
Identification of suitable longitudinal data
To be informative for a planned longitudinal trial, the available data (e.g. from routinely collected databases or previous trial data) should ideally be for the same primary outcome of interest and the same target population, and ideally over multiple intervals corresponding to the period lengths in the planned trial. For example, if an SW-CRT is being planned with step lengths of one month, it would be ideal to have existing data over multiple monthly intervals. It is also recommended that the prior data cover at least the same duration as the planned study. In the case of block/nested exchangeable correlatio, the same duration is required; in the case of exponential decay, a longer duration with more periods may be desirable as it may improve precision of the estimated within-period ICC and CAC per period. Furthermore, the periods in the available dataset should ideally be approximately equally spaced intervals. When the outcomes are measured at unequally spaced intervals or at intervals with lengths that are substantially different from those in the planned study, they may not be suitable for estimating these correlation structures unless the deviation from equal spacing is small.
The minimum required number of clusters to reliably estimate correlation parameters to inform sample size calculation for a longitudinal CRT is unclear. In the case of non-longitudinal CRTs, Eldridge et al.29 addressed the question of the minimum pilot sample size required when using the analysis of variance (ANOVA) estimator for the ICC. They recommended at least 30 clusters to obtain unbiased and accurate ICC estimates for the purpose of sample size calculation. Confidence intervals around estimated ICCs can be useful to assess whether ICCs can be estimated with acceptable precision, but unless the sample size on which the ICC is based is very large, such confidence intervals are likely to be very wide. Thus, Eldridge et al. do not recommend the use of upper confidence limits in the sample size calculation, as this could result in considerably over-powered trials; instead, they recommend using ICC estimates from a range of sources or using information on patterns in ICCs.30–34
To our knowledge, no previous studies have examined the minimum required number of clusters, periods and cluster period sizes to yield reliable sample size estimates for longitudinal CRTs. Li et al.35 examined estimation of correlation parameters for stepped-wedge CRTs with binary outcomes under nested exchangeable and exponential decay structures. In line with the results reported by Eldridge et al.,29 their results suggest that a minimum of 30 clusters may be sufficient to reliably estimate the within-period ICCs but that a larger number of clusters (up to 100 or more) may be needed for the CAC. They proposed the method of matrix-adjusted estimating equations (MAEE) to substantially improve finite-sample inferences for correlation parameters.
Whereas future work is required to make specific recommendations about the minimum requirements for reliable sample size calculations for longitudinal CRTs using mixed-effects regression, we recommend that, when the planned outcome assessments will use routinely collected data, investigators make all efforts to obtain access to historical data for a population of clusters, similar to those being targeted by the trial. Ideally, all available clusters and subjects with eligibility criteria similar to those in the trial (as opposed to only participating clusters) should be used to estimate the correlation parameters. If the available number of clusters is small, a variety of data sources and estimates from published trials, accompanied by a sensitivity analysis across a range of values, is recommended. Estimation of confidence intervals around ICCs is one way to make the uncertainty in its estimation transparent in small samples. For continuous outcomes, a useful resource is the CLustered OUtcome Dataset bank,13 which summarizes empirical ICC and CAC values from a range of longitudinal clustered studies.
Data preparation
Once a suitable dataset has been identified, the data should be structured in ‘long format’, where each row represents one timepoint per individual. In addition to the outcome, the data should at a minimum have indicators for clusters and periods. For data obtained from observational studies, a treatment indicator is not relevant and will not be needed to estimate the correlation parameters; if data are obtained from a previous trial, the treatment indicator is relevant and should be included. For cohort designs, the dataset should also include subject-level indicators. The subject-level identifiers should be recognized as ‘distinct’ among all individuals in the statistical analysis software (e.g. by assigning unique IDs to each individual or by using nested identifiers to differentiate individuals in different clusters). We include templates for minimal datasets required for estimation in the Supplementary File Section 2 (available as Supplementary data at IJE online).
Unlike for cohort designs, subject-level indicators are not strictly necessary for repeated cross-sectional designs with binary outcomes. When privacy concerns exist, and patient-level data are not freely available to investigators planning a new trial, correlation parameters can still be estimated if only summary information is available in the form of numerators (number of patients with the outcome of interest) and denominators (number of eligible patients) in each cluster period. To estimate the correlation parameters in this case, the denominators and numerators must be converted to individual-level binary outcomes first (e.g. an outcome column with 0s and 1s based on denominators and numerators). We provide R and SAS code to achieve this via online code repository [https://rpubs.com/derek6561/estimateicc].
Estimation method for continuous and binary outcomes
The estimation procedure for continuous outcomes is straightforward. Users need to fit a linear mixed-effects model and extract the corresponding variance components to calculate the correlation parameters using formulas provided in Table 1. The procedure for binary outcome is less intuitive. Most existing sample size calculators require the correlation parameters to be specified on the proportions scale. Conventional logistic mixed-effect models return variance components on the logistic scale, which usually yields larger ICC values and should not be used for the purpose of sample size calculation.21,36 Yelland et al.37 discussed several ways to convert ICCs from logistic scale to proportions scale, but these methods are only applicable under exchangeable correlation structures. An alternative approach which has been used in longitudinal CRTs is to fit a linear mixed-effect model (e.g. treating binary outcomes as continuous) to estimate ICCs on the proportions scale.38
Selection of the most appropriate correlation structure
How to select the most appropriate correlation structure for a planned longitudinal CRT is a challenging issue. At the design stage, we may not have adequate information to prespecify the best type of correlation structure (e.g. nested exchangeable versus exponential decay). Information criteria, such as the Akaike information criteria (AIC) and Bayesian information criterion (BIC), for each fitted model can be extracted and may be used as criteria to select the best correlation structures. However, there are limitations to using AIC/BIC for selecting the best models.39 In a simulation study, for continuous outcomes, Rezaei-Darzi et al.40 showed that AIC/BIC only started to become reliable when the number of clusters was larger than 20, the number of periods was larger than six and the cluster period size was larger than 50. When the number of periods is small and the degree of dependence between observations in adjacent periods is large, we generally recommend that the sample size be calculated using the correlation structure providing the most conservative estimate. For example, researchers may conduct a sensitivity analysis to calculate the sample size needed under different structures and use the one returning the largest sample size (usually, either nested/block exchangeable or exponential decay).
Software for estimating the required correlation parameters
Available packages for fitting the three types of correlation structures in R, SAS and Stata are summarized in Table 2. We only provide R and SAS code to fit exponential decay models, as this structure is not available in Stata at the time of submission. For readers without access to R, SAS or Stata, we have built an RShiny app that can estimate correlation parameters under the three correlation structures without the need for any coding [https://douyang.shinyapps.io/estimateICC/]. Users can upload their datasets in comma separated values (CSV) format following the templates we have provided. The RShiny app will calculate the ICC, CAC and within-individual (and IAC) where relevant, and display information criteria automatically. Currently, this app supports both repeated cross-sectional and cohort designs with continuous and binary outcomes. For repeated cross-sectional designs with binary outcomes, users can upload either aggregated or individual-level data.
Table 2.
Procedures to fit linear mixed-effect models for intra-cluster correlation coefficient estimation in each software package
| Software | Procedure | Correlation structures that can be accommodated |
|---|---|---|
| SAS | PROC MIXEDa | Exchangeable |
| Nested/block exchangeable | ||
| Exponential decay | ||
| PROC GLIMMIX | Exchangeable | |
| Nested/block exchangeable | ||
| Exponential decay | ||
| PROC HPMIXEDa | Exchangeable | |
| Nested/block exchangeable | ||
| Exponential decay | ||
| R | lmer in lme4a | Exchangeable |
| Nested/block exchangeable | ||
| lmer in lmerTest | Exchangeable | |
| Nested/block exchangeable | ||
| glmmTMB in glmmTMBa | Exponential decay | |
| lme in nlme | Exchangeable | |
| Nested/block exchangeable | ||
| Stata | mixeda | Exchangeable |
| Nested/block exchangeable | ||
| meglm | Exchangeable | |
| Nested/block exchangeable |
Packages and functions we used in this tutorial.
Computational challenges
When fitting complex mixed-effects models, computational challenges may be expected, especially when the number of clusters is small: models may fail to converge, or negative variance component estimates may be obtained. Unfortunately, there is no simple solution to this problem, but some mitigating strategies for dealing with computational challenges are available.41 In SAS, PROC HPMIXED can be used instead of PROC MIXED to increase the computational speed. In R and Stata, users may try a different optimizer or different estimation methods.
Examples for illustration
In this section, we demonstrate how to estimate the correlation parameters in R, SAS and Stata using data from three real longitudinal CRTs. The code used to do the estimation is available via online code repository [https://rpubs.com/derek6561/estimateicc]. The estimation procedure we used in all three packages is restricted maximum likelihood (REML) estimation. As different software packages use different default algorithms (e.g. in our examples, SAS (PROC MIXED) uses Newton-Raphson, R (lmer) uses NLopt nonlinear optimization and Stata (mixed) uses expectation–maximization optimization) to optimize REML, it is possible that slightly different estimates may be obtained.
Example 1: Repeated cross-sectional design with binary outcome
A repeated cross-sectional SW-CRT was conducted in Guatemala to evaluate the impact of an intervention package (distribution of promotional materials encouraging health centre delivery, education for traditional birth attendants about the importance of health centre delivery, and provider capacity building using simulation training) on maternal and newborn health indicators.42 A total of 33 health centres were grouped by region (six groups in total) and randomized to one of six sequences. For our purposes, we will treat the health centres as independent clusters. There were two baseline periods (five and four months) after which the intervention package was rolled out sequentially, every four months, until all clusters had received four months of intervention exposure. There were four co-primary outcomes measured: number of health centre deliveries, maternal morbidity and perinatal morbidity and mortality. In this example, we will use perinatal morbidity as our outcome. This outcome was measured on different individuals at every period with an average cluster period size of 82.
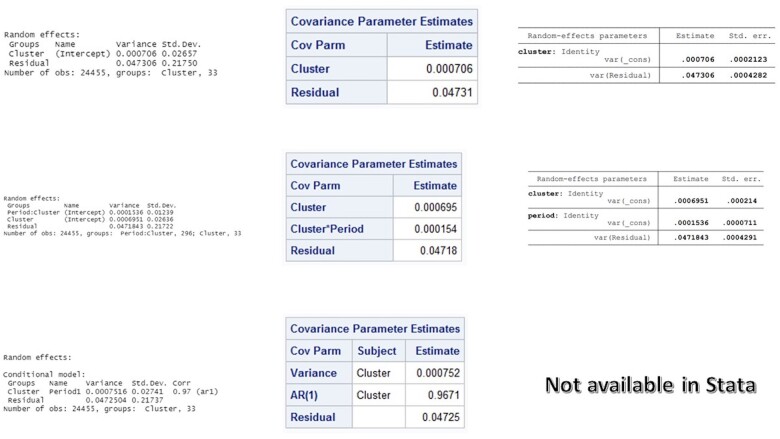
In this trial, the period length was four months. The two baseline periods were not strictly the same but approximately equal. Using data from this trial, we fit the three models described above in R, SAS and Stata. The estimated covariance parameters were extracted from the resulting output and used to estimate the within-period ICC and CAC under the exchangeable, nested exchangeable and exponential decay structures, using the formulae provided in Table 1. The estimated correlation values as well as information criteria obtained from R are displayed in Table 3. To illustrate manual calculations, we present screenshots of the software outputs (Figure 2) and detailed calculations of the within-period ICC and CAC under the nested exchangeable model (Box 1). Similar calculations can be done for exponential decay using the formulae we have provided. In this example, bias-corrected AIC suggested the nested exchangeable model has the best fit, whereas BIC suggested the exchangeable model. Sample size should ideally be calculated under all correlation structures and the most conservative estimate be selected as the final estimate.
Table 3.
Estimated intra-cluster correlation coefficients using R under three different models for the Guatemala, WAVES and OXTEXT-7 trials
| Model | Within-period ICC | Between-period ICC | CAC | Within-individual ICC | AIC a | BIC |
|---|---|---|---|---|---|---|
| Guatemala | ||||||
| Exchangeable | 0.0147 | 0.0147 | 1.0000 | – | –5010.86 | –4943.62 |
| Nested exchangeable | 0.0177 | 0.0145 | 0.8190 | – | –5046.67 | –4941.32 |
| Exponential decay | 0.0157 | – | 0.9671 | – | –5042.02 | –4936.67 |
| WAVES | ||||||
| Exchangeable | 0.0053 | 0.0053 | 1.0000 | 0.8742 | 17 040.74 | 17 085.44 |
| Block exchangeable | 0.0085 | 0.0037 | 0.4302 | 0.8742 | 17 003.37 | 17 054.45 |
| Exponential decay | 0.0099 | – | 0.5733 | 0.8792 | 17 000.91 | 17 052.00 |
| OXTEXT-7 | ||||||
| Exchangeable | 0.0240 | 0.0240 | 1.0000 | 0.3976 | 30 354.49 | 30 482.96 |
| Nested exchangeable | 0.0421 | 0.0229 | 0.5438 | 0.3918 | 30 336.99 | 30 471.88 |
| Exponential decay | 0.0407 | – | 0.8362 | 0.4105 | 30 331.83 | 30 466.71 |
ICC, intra-cluster correlation coefficient; CAC, cluster autocorrelation coefficient; AIC, Akaike information criterion; BIC, Bayesian information criterion.
Bias-corrected version (AICC) was used.
Figure 2.
Screenshots of estimated covariance parameters obtained from R (column 1), SAS (column 2) and Stata (column 3) for a cross-sectional design (Guatemala trial) with continuous outcome using exchangeable model (row 1), nested exchangeable model (row 2), and exponential decay model (row 3)
Box 1.
Example of intra-cluster correlation coefficients calculation using the estimated covariance parameters with a repeated cross-sectional design under nested/block exchangeable model (Guatemala trial)
The intra-cluster correlation coefficients (ICCs) under nested/block exchangeable model can be calculated as:
Within-period ICC:
Between-period ICC:
CAC = 0.819, which is the ratio of between-period and within-period ICC
CAC, cluster autocorrelation coefficient
Example 2: Closed cohort design with continuous outcome
The West Midlands ActiVe lifestyle and healthy Eating in Schoolchildren (WAVES) study43 was a longitudinal parallel-arm CRT conducted in 54 UK primary schools from the West Midlands, to assess the impact of a healthy lifestyle programme on childhood obesity. This 12-month intervention involved healthy eating and physical activity both at school and at home and included 30 min of physical activity every day at school, a 6-week training programme with a football club, information about local family-based physical activities, and workshops on healthy cooking. The continuous outcome, body mass index (BMI), was measured on an average of 27 participants per school (a total of 1467 participants) and was available for approximately 95%, 85%, and 78% of participants at baseline and 15, and 30 months, respectively. Since this is a cohort design, three relevant input parameters are required: within-period ICC, CAC and within-individual ICC. To obtain a complete dataset for demonstration purposes, we used a single imputation generated from the multivariate imputation by chained equations (MICE) algorithm that the cluster indicators as clustering variable, treatment indicator and all available covariates.44
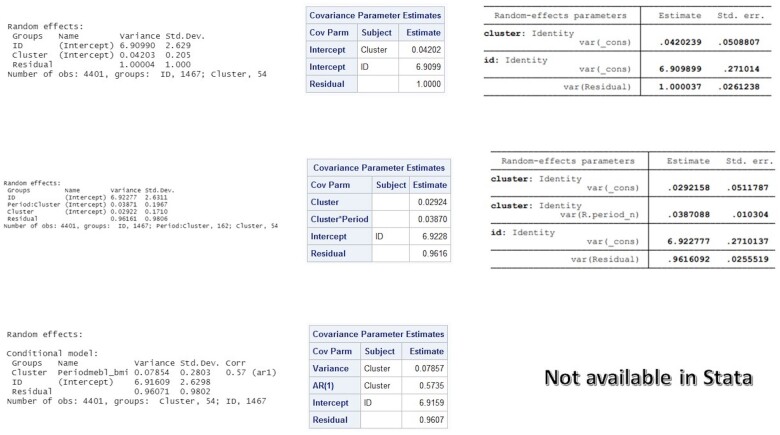
The estimated covariance parameters (Figure 3) were plugged into the corresponding equations for cohort designs (Table 1) to obtain the required correlation values (see Box 2 for calculations). Estimated ICC values and information criteria from the three correlation structures are displayed in Table 3. According to the information criteria, the exponential decay model returned the smallest bias-corrected AIC and BIC.
Figure 3.
Screenshots of estimated covariance parameters obtained from R (column 1), SAS (column 2) and Stata (column 3) for a cohort design (WAVES trial) with continuous outcome using exchangeable model (row 1), exchangeable model (row 2) and exponential decay model (row 3)
Box 2.
Example of intra-cluster correlation coefficients calculation using the estimated covariance parameters with a cohort design under nested/block exchangeable model (WAVES trial)
The intra-cluster correlation coefficients (ICCs) under nested/block exchangeable model can be calculated as:
Within-period ICC:
Between-period ICC:
CAC = 0.430, which is the ratio of between-period and within-period ICC
(This CAC is slightly different from the one in Table 3 due to rounding in ICCs)
Within-individual ICC:
CAC, cluster autocorrelation coefficient
Example 3: Open cohort design with continuous outcome
OXTEXT-745,46 is a SW-CRT conducted in the UK, to assess whether community mental health teams who were offered the ‘Feeling Well with True Colours’ (an intervention originally used for individuals with bipolar disorder) produced better health outcomes for participants in their care. Eleven community mental health teams in the Oxford Health NHS Foundation Trust were randomized to receive the intervention sequentially over 16 months. The primary outcome was the Health of the Nation Outcome Scales (HoNOS) total score (a continuous outcome). The trial used an open cohort design in which participants can enter the study at any time point and can potentially contribute multiple measurements to the trial. The average number of measurements per cluster period was 26. Approximately 50% of the participants contributed more than one measurement and 12% contributed three or more measurements; the average number of measurements per participant over the 16 months of the study was two.
Using data freely available for this trial,45 we fit the three models described above in R, SAS, and Stata. For open cohort designs, three relevant input parameters are required: within-period ICC, CAC and within-individual ICC.47 The estimated covariance parameters were extracted from the resulting output and used to estimate these correlation parameters under the exchangeable, nested exchangeable and exponential decay structures, using the formulae provided in Table 1. The estimated correlation values as well as information criteria obtained from R are displayed in Table 3. According to the information criteria, the exponential decay model returned the smallest bias-corrected AIC48 and BIC. However, given that the sample size in this dataset was relatively small, AIC and BIC may not be reliable, and it may be advisable to calculate the sample size under both nested exchangeable and exponential decay and select the most conservative estimate. Furthermore, since the number of clusters used to estimate the correlation parameters is relatively small, a sensitivity analysis across a range of values should be conducted.
We note that this trial was treated as a repeated cross-sectional design in the CLustered OUtcome Dataset bank.13 The implications for the variance components may be minimal when only a small fraction of participants have repeated measures. Supplementary File Section 3 (available as Supplementary data at IJE online) presents the estimated correlation values when treating all observations as independent.
Discussion
In this tutorial, we considered three main correlation structures for longitudinal CRTs and provided practical recommendations and tools to allow investigators to obtain relevant estimates for a planned longitudinal CRT. Previously published trials may not have reported appropriate correlations, but data collected from such trials may be available under a data sharing agreement allowing estimates to be calculated. Furthermore, when the planned trial will use routinely collected databases for outcome assessment, investigators could potentially access these data (at individual level or in aggregate) to inform the design of their trial. We present three examples in this tutorial to demonstrate how available data can be used to estimate correlation parameters for future designs with continuous or binary outcomes, and with repeated cross-sectional or cohort designs.
For cohort designs, we considered models assuming a constant correlation in repeated measures on the same individual over time, although more complex correlation structures are available. In a proportional decay model for example, both the between-period ICC and the individual-level correlation are allowed to decay exponentially at the same or different rates.20 Unfortunately, software packages that can fit proportional decay models are limited. Furthermore, the models considered in this tutorial assumed measurements are taken in discrete intervals of time; in reality, observations may be taken on a continuous basis.49 Continuous time decay structures for trials with continuous recruitment are available,49 but need further development. In practice, due to privacy issues, granular data allowing users to estimate such continuous time decay structures based on actual times of recruitment may not be available. Approximations may be obtained using a discrete time decay model by assuming participants arrive in equally spaced time intervals as described in Grantham et al.49
In this manuscript, we did not consider covariates when estimating the ICCs. Currently available sample size formulae for longitudinal CRTs are based on models without baseline covariates; see, for example, the review of Li et al.7 In a real application, covariates may be available at the design stage. If the planned analysis includes adjustment for covariates, an adjusted ICC may be a more accurate input design parameter for sample size calculation, but if covariate information is not available at the design stage, using unadjusted ICC estimates may be appropriate and will typically yield a more conservative sample size estimate. When the planned analyses include accounting for treatment effect heterogeneity, multiple ICCs for example, the ICC for the outcome adjusting for covariates and the ICC for the covariates may be needed.50,51 Readers may still be able to apply the methods described here to estimate each ICC and use available sample size formulae for powering the study to detect treatment effect heterogeneity.50,52
In this tutorial, we focused on the situation where a suitable historical dataset has been identified. In the absence of suitable empirical data, researchers may need to use ‘rules of thumb’. For example, a within-period ICC of 0.05 and CAC of 0.8 may be reasonable values for continuous outcomes, although previous studies have suggested that higher values for process measures may be reasonable.30 Several studies have examined patterns in databases of ICC values.13,30–33 For binary outcomes, Campbell et al.30 discussed the relationship between the ICC and prevalence, which can be helpful in choosing an appropriate ICC. Regardless of the choice of ICCs, a sensitivity analysis is strongly recommended to obtain a range of sample sizes under alternative assumptions about the ICC parameters.
There are several gaps in the literature requiring further research. First, estimating correlation parameters for longitudinal trials with binary outcomes is challenging and an under-explored area. Although obtaining estimates on the logistic scale may be straightforward, most sample size calculators based on a mixed-effects model for longitudinal CRTs require estimates on the proportions scale.8 Therefore, a practical strategy is to fit linear mixed-effect models to the data and treat the binary outcome as continuous; this way, one may be able to plug the resulting ICC estimates into the sample size formulae developed for continuous outcome for an approximate calculation (when the effect size of interest is the risk difference). Second, there is no consensus on how to choose the best correlation structure for longitudinal CRTs. In practice, researchers may calculate the sample sizes under both exponential decay and block/nested exchangeable models and choose the structure yielding the most conservative estimate. Third, we have focused on the mixed-effects model framework, which is most commonly used in practice and more accessible in existing software.7,53,54 An alternative approach is generalized estimating equations (GEE).55,56 The GEE approach can be more attractive for binary or count outcomes because the ICCs can be directly parameterized on the natural scale of the outcomes, even when a non-identity link function is used for the outcome model (that is, when the effect size of interest is a relative risk or odds ratio).20,57,58 However, related software for implementing GEE models with longitudinal correlation structures is still being developed, and the associated computational challenges with large cluster sizes have only recently been addressed for cross-sectional designs.35 Fourth, as discussed earlier, future work is required to determine guidelines for minimum required numbers of clusters and cluster period sizes to yield reliable estimates for ICC parameters in longitudinal CRT designs. Additionally, methods for obtaining confidence intervals around estimated within-period ICCs and CACs under nested/block exchangeable and exponential decay correlation structures, under a mixed-effects model framework, require further investigation. Finally, attrition may be present in a cohort design and may be informative, i.e. the missing value in a particular period may depend on the intervention and the outcome in a previous period, as well as other unmeasured factors. Even under non-informative missingness, failure to account for the complex nature of the correlations in the imputation model may lead to incorrect estimation of the correlation parameters based on imputation-completed data. Further work is required to develop appropriate imputation methods for longitudinal CRTs.
Ethics approval
Not applicable.
Supplementary Material
Acknowledgements
We thank Prof. Richard Hooper, Queen Mary University of London, for helpful discussion about the difference between within-individual, intra-cluster correlation and individual autocorrelation. We thank the authors of the WAVES study and the Guatemala trial for providing us with trial data.
Contributor Information
Yongdong Ouyang, Clinical Epidemiology Program, Ottawa Hospital Research Institute, Ottawa, ON, Canada; School of Epidemiology and Public Health, University of Ottawa, Ottawa, ON, Canada.
Karla Hemming, Institute of Applied Health Research, The University of Birmingham, Birmingham, UK.
Fan Li, Department of Biostatistics, Yale School of Public Health, New Haven, CT, USA; Center for Methods in Implementation and Prevention Science, Yale School of Public Health, New Haven, CT, USA.
Monica Taljaard, Clinical Epidemiology Program, Ottawa Hospital Research Institute, Ottawa, ON, Canada; School of Epidemiology and Public Health, University of Ottawa, Ottawa, ON, Canada.
Data availability
There are no new data associated with this article. Some code for data manipulation and model fitting can be found at [https://rpubs.com/derek6561/estimateicc]. A RShiny app used to estimate ICC is available at [https://douyang.shinyapps.io/estimateICC].
Supplementary data
Supplementary data are available at IJE online.
Author contributions
Y.O. led the writing of the manuscript and developed the idea with M.T. M.T. conceived the ideas and co-led the writing. K.H. and F.L. participated in the development of the idea and the method. All authors contributed to writing, drafting and editing the manuscript.
Funding
M.T. and F.L. are supported by the National Institute of Aging (NIA) of the National Institutes of Health (NIH) under Award Number U54AG063546, which funds NIA Imbedded Pragmatic Alzheimer's Disease and AD-Related Dementias Clinical Trials Collaboratory (NIA IMPACT Collaboratory). Y.O. is funded by the Health System Impact Fellowship, which is supported by the Canadian Institutes of Health Research (CIHR). F.L. is supported through a Patient-Centered Outcomes Research Institute® (PCORI® Award ME-2020C3-21072). The statements presented in this article are solely the responsibility of the authors and do not necessarily represent the views of NIH, nor PCORI®, its Board of Governors or Methodology Committee. K.H. is funded by an NIHR Senior Research Fellowship SRF-2017–10-002.
Conflict of interest
None declared.
References
- 1. Donner A. Design and Analysis of Cluster Randomization Trials in Health Research. London: Arnold, 2000. [Google Scholar]
- 2. Kahan BC, Morris TP.. Assessing potential sources of clustering in individually randomised trials. BMC Med Res Methodol 2013;13:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Donner A, Koval JJ.. Design considerations in the estimation of intraclass correlation. Ann Hum Genet 1982;46:271–77. [DOI] [PubMed] [Google Scholar]
- 4. Copas AJ, Lewis JJ, Thompson JA, Davey C, Baio G, Hargreaves JR.. Designing a stepped wedge trial: three main designs, carry-over effects and randomisation approaches. Trials 2015;16:352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Hemming K, Taljaard M, Weijer C, Forbes AB.. Use of multiple period, cluster randomised, crossover trial designs for comparative effectiveness research. BMJ 2020;371:m3800. [DOI] [PubMed] [Google Scholar]
- 6. Hemming K, Lilford R, Girling AJ.. Stepped-wedge cluster randomised controlled trials: a generic framework including parallel and multiple-level designs. Stat Med 2015;34:181–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Li F, Hughes JP, Hemming K, Taljaard M, Melnick ER, Heagerty PJ.. Mixed-effects models for the design and analysis of stepped wedge cluster randomized trials: an overview. Stat Methods Med Res 2021;30:612–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Ouyang Y, Li F, Preisser JS, Taljaard M.. Sample size calculators for planning stepped-wedge cluster randomized trials: a review and comparison. Int J Epidemiol 2022;51:2000–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Ouyang Y, Kulkarni MA, Protopopoff N. et al. Accounting for complex intracluster correlations in longitudinal cluster randomized trials: a case study in malaria vector control. BMC Med Res Methodol 2023;23:64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Campbell MK, Piaggio G, Elbourne DR, Altman DG; CONSORT Group. Consort 2010 statement: extension to cluster randomised trials. BMJ 2012;345:e5661. [DOI] [PubMed] [Google Scholar]
- 11. Hemming K, Taljaard M, Grimshaw J.. Introducing the new CONSORT extension for stepped-wedge cluster randomised trials. Trials 2019;20:68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Ivers NM, Taljaard M, Dixon S. et al. Impact of CONSORT extension for cluster randomised trials on quality of reporting and study methodology: review of random sample of 300 trials, 2000-8. BMJ 2011;343:d5886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Korevaar E, Kasza J, Taljaard M. et al. Intra-cluster correlations from the CLustered OUtcome Dataset bank to inform the design of longitudinal cluster trials. Clin Trials 2021;18:529–40. [DOI] [PubMed] [Google Scholar]
- 14. McCulloch CE, Searle SR, Neuhaus JM.. Generalized, Linear, and Mixed Models. 2nd edn. Hoboken, NJ: John Wiley & Sons; 2008. [Google Scholar]
- 15. Hussey MA, Hughes JP.. Design and analysis of stepped wedge cluster randomized trials. Contemp Clin Trials 2007;28:182–91. [DOI] [PubMed] [Google Scholar]
- 16. Hooper R, Teerenstra S, Hoop ED, Eldridge S.. Sample size calculation for stepped wedge and other longitudinal cluster randomised trials. Stat Med 2016;35:4718–28. [DOI] [PubMed] [Google Scholar]
- 17. Girling AJ, Hemming K.. Statistical efficiency and optimal design for stepped cluster studies under linear mixed effects models. Stat Med 2016;35:2149–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Kasza J, Hemming K, Hooper R, Matthews J, Forbes AB.. Impact of non-uniform correlation structure on sample size and power in multiple-period cluster randomised trials. Stat Methods Med Res 2019;28:703–16. [DOI] [PubMed] [Google Scholar]
- 19. Taljaard M, Teerenstra S, Ivers NM, Fergusson DA.. Substantial risks associated with few clusters in cluster randomized and stepped wedge designs. Clin Trials 2016;13:459–63. [DOI] [PubMed] [Google Scholar]
- 20. Li F. Design and analysis considerations for cohort stepped wedge cluster randomized trials with a decay correlation structure. Stat Med 2020;39:438–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Eldridge SM, Ukoumunne OC, Carlin JB.. The intra-cluster correlation coefficient in cluster randomized trials: a review of definitions. Int Stat Rev Rev Int Stat 2009;77:378–94. I [Google Scholar]
- 22. Hemming K, Kasza J, Hooper R, Forbes A, Taljaard M.. A tutorial on sample size calculation for multiple-period cluster randomized parallel, cross-over and stepped-wedge trials using the Shiny CRT Calculator. Int J Epidemiol 2020;49:979–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Chen J, Zhou X, Li F, Spiegelman D.. swdpwr: a SAS macro and an R package for power calculations in stepped wedge cluster randomized trials. Comput Methods Programs Biomed 2022;213:106522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Ouyang Y, Xu L, Karim ME, Gustafson P, Wong H.. CRTpowerdist: An R package to calculate attained power and construct the power distribution for cross-sectional stepped-wedge and parallel cluster randomized trials. Comput Methods Programs Biomed 2021;208:106255. [DOI] [PubMed] [Google Scholar]
- 25. Baio G, Copas A, Ambler G, Hargreaves J, Beard E, Omar RZ.. Sample size calculation for a stepped wedge trial. Trials 2015;16:354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Hemming K, Girling A.. A menu-driven facility for power and detectable-difference calculations in stepped-wedge cluster-randomized trials. Stata J Promot Commun Stat Stata 2014;14:363–80. [Google Scholar]
- 27. Zhang Y, Preisser JS, Turner EL, Rathouz PJ, Toles M, Li F.. A general method for calculating power for GEE analysis of complete and incomplete stepped wedge cluster randomized trials. Stat Methods Med Res 2023;32:71–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Voldal EC, Hakhu NR, Xia F, Heagerty PJ, Hughes JP.. swCRTdesign: an RPackage for stepped wedge trial design and analysis. Comput Methods Programs Biomed 2020;196:105514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Eldridge SM, Costelloe CE, Kahan BC, Lancaster GA, Kerry SM.. How big should the pilot study for my cluster randomised trial be? Stat Methods Med Res 2016;25:1039–56. [DOI] [PubMed] [Google Scholar]
- 30. Campbell MK, Fayers PM, Grimshaw JM.. Determinants of the intracluster correlation coefficient in cluster randomized trials: the case of implementation research. Clin Trials 2005;2:99–107. [DOI] [PubMed] [Google Scholar]
- 31. Adams G, Gulliford MC, Ukoumunne OC, Eldridge S, Chinn S, Campbell MJ.. Patterns of intra-cluster correlation from primary care research to inform study design and analysis. J Clin Epidemiol 2004;57:785–94. [DOI] [PubMed] [Google Scholar]
- 32. Gulliford MC, Adams G, Ukoumunne OC, Latinovic R, Chinn S, Campbell MJ.. Intraclass correlation coefficient and outcome prevalence are associated in clustered binary data. J Clin Epidemiol 2005;58:246–51. [DOI] [PubMed] [Google Scholar]
- 33. Taljaard M, Donner A, Villar J. et al. ; World Health Organization 2005 Global Survey on Maternal and Perinatal Health Research Group. Intracluster correlation coefficients from the 2005 WHO Global Survey on Maternal and Perinatal Health: implications for implementation research. Paediatr Perinat Epidemiol 2008;22:117–25. [DOI] [PubMed] [Google Scholar]
- 34. Pagel C, Prost A, Lewycka S. et al. Intracluster correlation coefficients and coefficients of variation for perinatal outcomes from five cluster-randomised controlled trials in low and middle-income countries: results and methodological implications. Trials 2011;12:151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Li F, Yu H, Rathouz PJ, Turner EL, Preisser JS.. Marginal modeling of cluster-period means and intraclass correlations in stepped wedge designs with binary outcomes. Biostatistics 2021;23:772–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Wu S, Crespi CM, Wong WK.. Comparison of methods for estimating the intraclass correlation coefficient for binary responses in cancer prevention cluster randomized trials. Contemp Clin Trials 2012;33:869–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Yelland LN, Salter AB, Ryan P, Laurence CO.. Adjusted intraclass correlation coefficients for binary data: methods and estimates from a cluster-randomized trial in primary care. Clin Trials 2011;8:48–58. [DOI] [PubMed] [Google Scholar]
- 38. Martin J, Girling A, Nirantharakumar K, Ryan R, Marshall T, Hemming K.. Intra-cluster and inter-period correlation coefficients for cross-sectional cluster randomised controlled trials for type-2 diabetes in UK primary care. Trials 2016;17:402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Murray DM, Hannan PJ, Wolfinger RD, Baker WL, Dwyer JH.. Analysis of data from group-randomized trials with repeat observations on the same groups. Stat Med 1998;17:1581–600. [DOI] [PubMed] [Google Scholar]
- 40. Rezaei-Darzi E, Kasza J, Forbes A, Bowden R.. Use of information criteria for selecting a correlation structure for longitudinal cluster randomised trials. Clin Trials 2022;19:316–25. [DOI] [PubMed] [Google Scholar]
- 41. Kiernan K, Tao J, Gibbs P.. Tips and Strategies for Mixed Modeling with SAS/STAT® Procedures. 2012. http://support.sas.com/resources/papers/proceedings12/332-2012.pdf (14 June 2022, date last accessed).
- 42. Kestler E, Ambrosio G, Hemming K. et al. An integrated approach to improve maternal and perinatal outcomes in rural Guatemala: a stepped-wedge cluster randomized trial. Int J Gynaecol Obstet 2020;151:109–16. [DOI] [PubMed] [Google Scholar]
- 43. Adab P, Pallan MJ, Lancashire ER. et al. Effectiveness of a childhood obesity prevention programme delivered through schools, targeting 6 and 7 year olds: cluster randomised controlled trial (WAVES study). BMJ 2018;360:k211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Buuren S V, Groothuis-Oudshoorn K.. mice: Multivariate imputation by chained equations in R. J Stat Softw 2011;45:1–67. [Google Scholar]
- 45. Nickless A, Voysey M, Geddes J, Yu L-M, Fanshawe TR.. Mixed effects approach to the analysis of the stepped wedge cluster randomised trial—Investigating the confounding effect of time through simulation. PLoS One 2018;13:e0208876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Bilderbeck A, Price J, Hinds C. et al. OXTEXT: The Development and Evaluation of a Remote Monitoring and Management Service for People with Bipolar Disorder and Other Psychiatric Disorders. NIHR Report for Programme Grants for Applied Research Programme (Reference Number RP-PG-0108–10087). 2015. https://www.journalslibrary.nihr.ac.uk/programmes/pgfar/RP-PG-0108-10087/#/ (7 November 2022, date last accessed)
- 47. Kasza J, Hooper R, Copas A, Forbes AB.. Sample size and power calculations for open cohort longitudinal cluster randomized trials. Stat Med 2020;39:1871–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Hurvich CM, Tsai C-L.. Regression and time series model selection in small samples. Biometrika 1989;76:297–307. [Google Scholar]
- 49. Grantham KL, Kasza J, Heritier S, Hemming K, Forbes AB.. Accounting for a decaying correlation structure in cluster randomized trials with continuous recruitment. Stat Med 2019;38:1918–34. [DOI] [PubMed] [Google Scholar]
- 50. Yang S, Li F, Starks MA, Hernandez AF, Mentz RJ, Choudhury KR.. Sample size requirements for detecting treatment effect heterogeneity in cluster randomized trials. Stat Med 2020;39:4218–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Li F, Chen X, Tian Z, Esserman D, Heagerty PJ, Wang R.. Designing three-level cluster randomized trials to assess treatment effect heterogeneity. Biostatistics 2022;kxac026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Tong G, Esserman D, Li F.. Accounting for unequal cluster sizes in designing cluster randomized trials to detect treatment effect heterogeneity. Stat Med 2022;41:1376–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Barker D, McElduff P, D'Este C, Campbell MJ.. Stepped wedge cluster randomised trials: a review of the statistical methodology used and available. BMC Med Res Methodol 2016;16:69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Li F, Wang R.. Stepped wedge cluster randomized trials: a methodological overview. World Neurosurg 2022;161:323–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Preisser JS, Young ML, Zaccaro DJ, Wolfson M.. An integrated population-averaged approach to the design, analysis and sample size determination of cluster-unit trials. Stat Med 2003;22:1235–54. [DOI] [PubMed] [Google Scholar]
- 56. Preisser JS, Lu B, Qaqish BF.. Finite sample adjustments in estimating equations and covariance estimators for intracluster correlations. Stat Med 2008;27:5764–85. [DOI] [PubMed] [Google Scholar]
- 57. Li F, Turner EL, Preisser JS.. Sample size determination for GEE analyses of stepped wedge cluster randomized trials. Biometrics 2018;74:1450–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Tian Z, Preisser JS, Esserman D, Turner EL, Rathouz PJ, Li F.. Impact of unequal cluster sizes for GEE analyses of stepped wedge cluster randomized trials with binary outcomes. Biom J Biom Z 2022;64:419–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
There are no new data associated with this article. Some code for data manipulation and model fitting can be found at [https://rpubs.com/derek6561/estimateicc]. A RShiny app used to estimate ICC is available at [https://douyang.shinyapps.io/estimateICC].