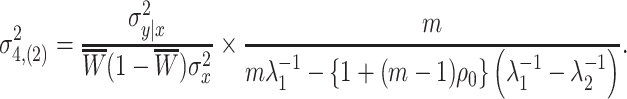SUMMARY
Cluster randomized trials often exhibit a three-level structure with participants nested in subclusters such as health care providers, and subclusters nested in clusters such as clinics. While the average treatment effect has been the primary focus in planning three-level randomized trials, interest is growing in understanding whether the treatment effect varies among prespecified patient subpopulations, such as those defined by demographics or baseline clinical characteristics. In this article, we derive novel analytical design formulas based on the asymptotic covariance matrix for powering confirmatory analyses of treatment effect heterogeneity in three-level trials, that are broadly applicable to the evaluation of cluster-level, subcluster-level, and participant-level effect modifiers and to designs where randomization can be carried out at any level. We characterize a nested exchangeable correlation structure for both the effect modifier and the outcome conditional on the effect modifier, and generate new insights from a study design perspective for conducting analyses of treatment effect heterogeneity based on a linear mixed analysis of covariance model. A simulation study is conducted to validate our new methods and two real-world trial examples are used for illustrations.
Keywords: Design effect, Effect modification, Heterogeneous treatment effect, Intraclass correlation coefficient, Nested exchangeable correlation structure, Power calculation
1. Introduction
Pragmatic cluster randomized trials (CRTs) are increasingly popular for comparative effectiveness research within health care delivery systems based on real-world interventions and broadly representative patient populations. While the average treatment effect (ATE) has typically been the primary focus in planning pragmatic trials, interest is growing in understanding whether the treatment effect varies among prespecified patient subpopulations, such as those defined by demographics or baseline clinical characteristics. By design, the flexible inclusion of a range of clusters and patients to mimic real-world practice in pragmatic trials naturally induces more heterogeneity, an aspect that should be reflected at the design stage and which invites the study of the associated factors that may lead to variation in treatment effects.
While data-driven exploratory heterogeneity of treatment effect (HTE) analysis can be ad hoc and used to generate hypotheses for future studies, confirmatory HTE analysis is often hypothesis driven, and carried out based on prespecified effect modifiers identified from either prior data or subject-matter knowledge (Wang and Ware, 2013). A recent systematic review reported that 16 out of 64 health-related CRTs published between 2010 and 2016 examined HTE among prespecified demographic patient subgroups but also noted a lack of methods for designing CRTs to enable the assessment of confirmatory HTE (Starks and others, 2019). To this end, Yang and others (2020) proposed an analytical power calculation procedure for HTE analysis in CRTs with two-level data where patients are nested in clusters. Although planning CRTs for assessing the ATE only requires accounting for the outcome intraclass correlation coefficient (ICC), planning CRTs for assessing the HTE additionally requires accounting for the covariate-ICC (or equivalently, ICC of the effect modifier). The covariate-ICC captures the fraction of between-cluster covariate variation relative to the total of between- and within-cluster covariate variation and plays an important role in sample size determination for HTE analysis.
Although these two distinct types of ICCs were identified as essential ingredients for estimating the power of the HTE test in two-level CRTs, analytical design formulas are currently unavailable for pragmatic trials exhibiting a three-level structure. As a first example, the Health and Literacy Intervention (HALI) trial in Kenya is a three-level CRT studying a literacy intervention to improve early literacy outcomes (Jukes and others, 2017). In the HALI trial, continuous literacy outcomes are collected for children (participants), who are nested within schools (subclusters), which are further nested in Teacher Advisory Center (TAC) tutor zone (cluster); randomization is carried out at the TAC tutor zone level. Beyond studying the ATE on the literacy outcomes, one may be interested in detecting effect modification by different levels of the baseline literacy measurements to see whether the intervention is more effective in improving spelling or reading test scores among those with lower baseline scores. Power analysis for such an interaction test requires accounting for the covariate-ICCs and outcome-ICCs within each school and across different schools. In a second example, the Strategies to Reduce Injuries and Develop Confidence in Elders (STRIDE) trial (Gill and others, 2021) aims to study the effect of a multifactorial fall prevention intervention program and recruited patients (participants) nested within clinics (subclusters), which were nested in health care systems (clusters); the randomization was at the clinic level and therefore the study can be considered as a subcluster randomized trial. The study included prespecified HTE analysis with patient-level effect modifiers such as age and gender, among others. Suppose the interest lies in detecting potential intervention effect modification by gender on the continuous outcome, concern score for falling, the power analysis for such an interaction test also required accounting for the covariate-ICCs and outcome-ICCs within each clinic and between different clinics. In both examples, as we discuss in Section 2.1, a direct application of the design formula developed in two-level CRTs can result in either conservative or anticonservative sample size estimates; therefore, the three-level hierarchical structure clearly requires new methods that enable a precise understanding of how both participant- and subcluster-level characteristics moderate the impact of new care innovations. Addressing this gap in three-level designs is further complicated by the fact that not only can the randomization be carried out at either the subcluster or cluster level but also the effect modifier can be measured at each level. To date, existing methods for power analysis in three-level trials were mainly developed for studying the ATE, with a closed-form design effect jointly determined by the between-subcluster outcome-ICC and the within-subcluster outcome-ICC (Heo and Leon, 2008; Teerenstra and others, 2010). Dong and others (2018) have developed sample size formulas for HTE analysis with a univariate effect modifier under cluster-level randomization. However, the essential role of covariate-ICCs was neglected in their design formulas, which lead to under-powered trials as we demonstrate in Section 3. Beyond Dong and others (2018), computationally efficient and yet accurate power analysis procedures are lacking to ensure sufficient power for HTE analyses in three-level trials.
In this article, we contribute novel design formulas to address multilevel effect modification in trials with a three-level structure, without restrictions on the level of randomization or the level at which the effect modifier is measured. We characterize a nested exchangeable correlation structure for both the effect modifier and the outcome conditional on the effect modifier and derive new sample size expressions for HTE analysis based on the asymptotic covariance matrix corresponding to a linear mixed analysis of covariance (LM-ANCOVA) model. With a small set of design assumptions, our closed-form expressions can adequately capture key aspects of the data generating processes that contribute to the variance of the interaction effect parameters are a good approximation to the true Monte Carlo variance for the sample size of interest (as we demonstrate in Section 3) and therefore obviate the need for exhaustive power calculations by simulations. Based on either a univariate effect modifier or multivariate effect modifiers, we prove in Section 2 that both the between-subcluster and within-subcluster covariate-ICCs are key elements in the asymptotic variance expression of the HTE estimator. Beyond power analysis for the HTE, in Section 2.3, we point out that the LM-ANCOVA framework can be used for more efficient analyses of the ATE, thus allowing the use of familiar sample size equations for testing the ATE. We report a simulation study to validate our new methods in Section 3 and provide two concrete examples in Section 4. Section 5 concludes.
2. Power analyses for confirmatory HTE analysis in three-level trials
We consider a parallel-arm design with a three-level data structure, including the common scenario where participants (level 1) are nested in subclusters (level 2), which are nested in clusters (level 3). Let 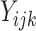 be the outcome from participant
be the outcome from participant  (
( ) from subcluster
) from subcluster 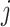 (
(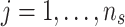 ) in cluster
) in cluster 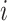 (
(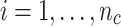 ). For design purposes, we assume each cluster includes an equal number of subclusters (
). For design purposes, we assume each cluster includes an equal number of subclusters (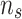 ), and each subcluster includes an equal number of participants (
), and each subcluster includes an equal number of participants ( ). We denote
). We denote 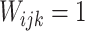 if participant
if participant 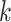 in subcluster
in subcluster 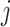 of cluster
of cluster  receives treatment and
receives treatment and 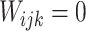 if the participant receives usual care. While randomization is more frequently carried out at the cluster or subcluster level in three-level designs, our framework also allows participant-level randomization as we elaborate on below.
if the participant receives usual care. While randomization is more frequently carried out at the cluster or subcluster level in three-level designs, our framework also allows participant-level randomization as we elaborate on below.
For prespecified HTE analysis with a set of 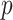 effect modifiers,
effect modifiers, 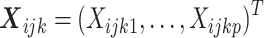 , we consider the following LM-ANCOVA model to formulate the HTE test:
, we consider the following LM-ANCOVA model to formulate the HTE test:
 |
(2.1) |
where 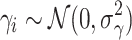 is the random intercept at the cluster level,
is the random intercept at the cluster level, 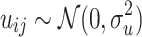 is the random intercept at the subcluster level, and
is the random intercept at the subcluster level, and 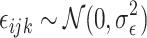 is the participant-level random error. We adopt the conventional assumption in CRTs that the random effects are mutually independent and assume the absence of additional random variations. In model (2.1),
is the participant-level random error. We adopt the conventional assumption in CRTs that the random effects are mutually independent and assume the absence of additional random variations. In model (2.1), 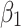 is the intercept parameter,
is the intercept parameter, 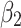 is the main effect of the treatment,
is the main effect of the treatment, 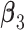 and
and 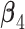 are the main covariate effects and the treatment-by-covariate interactions. The null hypothesis of no systematic HTE across subpopulations defined by
are the main covariate effects and the treatment-by-covariate interactions. The null hypothesis of no systematic HTE across subpopulations defined by 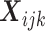 can be formulated as
can be formulated as 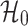 :
: 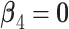 . Putting
. Putting  in the context of a single binary effect modifier where
in the context of a single binary effect modifier where 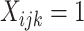 for female and
for female and 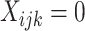 for nonfemale,
for nonfemale, 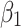 represents the mean outcome among the nonfemale subgroup without receiving treatment,
represents the mean outcome among the nonfemale subgroup without receiving treatment, 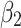 represents the treatment effect for the nonfemale subgroup,
represents the treatment effect for the nonfemale subgroup, 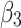 represents the mean outcome difference between the gender subgroups, and the scalar parameter
represents the mean outcome difference between the gender subgroups, and the scalar parameter  encodes the difference in treatment effect between the gender subgroups, and a two-sided HTE test can proceed with the Wald statistic based on a standard normal sampling distribution. Of note, when
encodes the difference in treatment effect between the gender subgroups, and a two-sided HTE test can proceed with the Wald statistic based on a standard normal sampling distribution. Of note, when 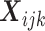 is mean centered, the interpretations of
is mean centered, the interpretations of 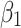 and
and 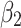 will change (we discuss the interpretation of
will change (we discuss the interpretation of 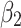 after mean-centering covariates in Section 2.3), but the interpretations of
after mean-centering covariates in Section 2.3), but the interpretations of 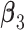 and
and 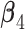 remain unchanged, and therefore mean-centering covariates does not affect the HTE test for
remain unchanged, and therefore mean-centering covariates does not affect the HTE test for 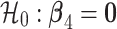 .
.
We assume the allocation ratio to the treatment and control groups is 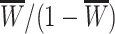 , with
, with  . We consider three design configurations: (i) CRT with randomization at the cluster level such that
. We consider three design configurations: (i) CRT with randomization at the cluster level such that 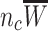 clusters are randomized to treatment and
clusters are randomized to treatment and 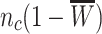 clusters are randomized to usual care; (ii) CRT with randomization at the subcluster level such that within each cluster,
clusters are randomized to usual care; (ii) CRT with randomization at the subcluster level such that within each cluster, 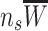 subclusters are randomized to treatment and
subclusters are randomized to treatment and 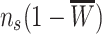 subclusters are randomized to usual care; (iii) individually randomized trial (IRT) with a hierarchical structure such that within each subcluster,
subclusters are randomized to usual care; (iii) individually randomized trial (IRT) with a hierarchical structure such that within each subcluster, 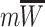 participants are randomized to treatment and
participants are randomized to treatment and 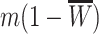 participants are randomized to usual care. In configurations (i) and (ii), we can further write the treatment indicator
participants are randomized to usual care. In configurations (i) and (ii), we can further write the treatment indicator  ,
,  and
and 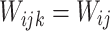 ,
, 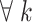 , respectively, but we maintain
, respectively, but we maintain 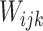 throughout for a more unified presentation. To facilitate the characterization of the covariance parameters, we reparameterize model (2.1) by centering the treatment indicator and obtain
throughout for a more unified presentation. To facilitate the characterization of the covariance parameters, we reparameterize model (2.1) by centering the treatment indicator and obtain
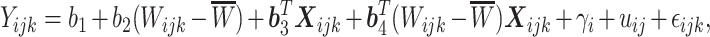 |
(2.2) |
where 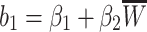 ,
, 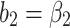 ,
, 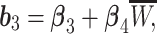 and
and 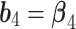 . Let
. Let 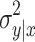 denote the total variance of the outcome conditional on
denote the total variance of the outcome conditional on 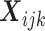 . Under model (2.2),
. Under model (2.2),  . The strength of dependency between two outcomes conditional on covariates can be characterized by two distinct outcome-ICCs. The within-subcluster outcome-ICC describes the strength of dependency between two outcomes within the same subcluster, or
. The strength of dependency between two outcomes conditional on covariates can be characterized by two distinct outcome-ICCs. The within-subcluster outcome-ICC describes the strength of dependency between two outcomes within the same subcluster, or 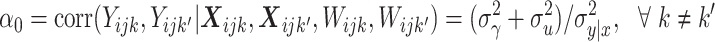 . The between-subcluster outcome-ICC describes the degree of dependency between two outcomes from two different subclusters but within the same cluster, or
. The between-subcluster outcome-ICC describes the degree of dependency between two outcomes from two different subclusters but within the same cluster, or 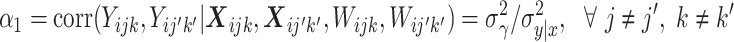 . If we write
. If we write 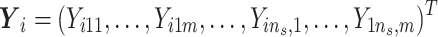 , then the implied correlation structure for
, then the implied correlation structure for  is nested exchangeable (Teerenstra and others, 2010) with the matrix expression given by
is nested exchangeable (Teerenstra and others, 2010) with the matrix expression given by
 |
(2.3) |
where “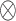 ” refers to the Kronecker operator,
” refers to the Kronecker operator, 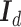 and
and 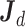 are a
are a 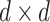 identity matrix and
identity matrix and 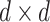 matrix of ones, respectively. Define the collection of design points
matrix of ones, respectively. Define the collection of design points 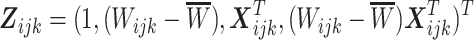 , and
, and 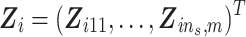 as the design matrix for cluster
as the design matrix for cluster 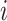 . Given values of the variance components, the best linear unbiased estimator of
. Given values of the variance components, the best linear unbiased estimator of 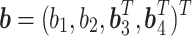 is the generalized least squares (GLS) estimator, given by
is the generalized least squares (GLS) estimator, given by 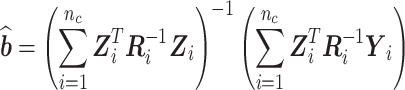 . Furthermore,
. Furthermore,  converges in distribution to a multivariate normal random variate with mean zero and covariance matrix
converges in distribution to a multivariate normal random variate with mean zero and covariance matrix 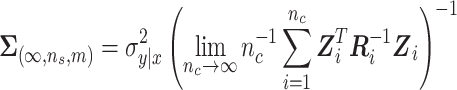 . Then, the asymptotic variance of
. Then, the asymptotic variance of 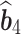 (based on
(based on 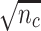 -regime) is the lower-right element of the square matrix
-regime) is the lower-right element of the square matrix 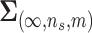 . Design calculations for sample size and power then boil down to explicitly characterizing the key elements of
. Design calculations for sample size and power then boil down to explicitly characterizing the key elements of 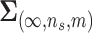 , which we operationalize below.
, which we operationalize below.
2.1. Univariate effect modifier
We first provide the analytical variance expressions when the treatment effect heterogeneity concerns a univariate effect modifier ( ). For testing
). For testing 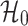 :
: 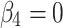 with a two-sided Wald test with type I error rate
with a two-sided Wald test with type I error rate 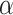 and target power
and target power  , the required number of clusters, number of subclusters per cluster, and subcluster size, (or the total sample size), should satisfy
, the required number of clusters, number of subclusters per cluster, and subcluster size, (or the total sample size), should satisfy 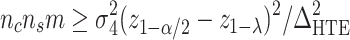 , where
, where 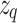 is the
is the 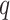 th quantile of the standard normal distribution,
th quantile of the standard normal distribution, 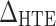 is the interaction effect size and
is the interaction effect size and 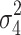 refers to the lower-right element of
refers to the lower-right element of 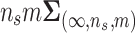 , or
, or 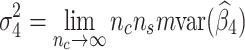 . Notice that
. Notice that 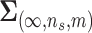 is a function of
is a function of 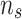 ,
, 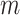 and decreases to zero as
and decreases to zero as 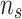 or
or 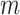 increases. Therefore, we intentionally define
increases. Therefore, we intentionally define 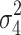 by multiplying
by multiplying 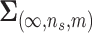 with
with 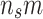 to facilitate efficiency comparison when randomization is conducted at different levels. This way, the limit of
to facilitate efficiency comparison when randomization is conducted at different levels. This way, the limit of 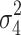 will remain as a constant instead of zero if we also let
will remain as a constant instead of zero if we also let 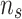 or
or 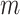 increase. To proceed, we write
increase. To proceed, we write 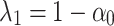 ,
, 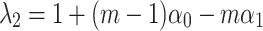 and
and 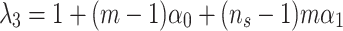 as three distinct eigenvalues of the nested exchangeable correlation structure (2.3) (Li and others, 2018), based on which an explicit inverse is given by
as three distinct eigenvalues of the nested exchangeable correlation structure (2.3) (Li and others, 2018), based on which an explicit inverse is given by  ; this analytical inverse plays a critical role in simplifying
; this analytical inverse plays a critical role in simplifying  . For testing the HTE, we further assume a nested exchangeable correlation structure for the univariate effect modifier such that the marginal correlation matrix for
. For testing the HTE, we further assume a nested exchangeable correlation structure for the univariate effect modifier such that the marginal correlation matrix for 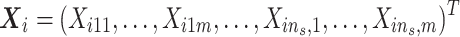 is
is
 |
(2.4) |
where 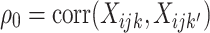 ,
, 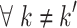 , defines the within-subcluster covariate-ICC and
, defines the within-subcluster covariate-ICC and 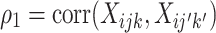 ,
, 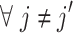 (without restrictions on
(without restrictions on 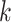 ,
, 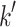 ), defines the between-subcluster covariate-ICC. Figure 1 provides a graphical representation of the data structure in a three-level trial. Defining
), defines the between-subcluster covariate-ICC. Figure 1 provides a graphical representation of the data structure in a three-level trial. Defining 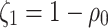 ,
, 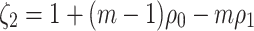 and
and 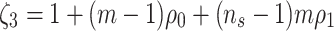 as three distinct eigenvalues of the nested exchangeable correlation structure (2.4), we first establish the following result.
as three distinct eigenvalues of the nested exchangeable correlation structure (2.4), we first establish the following result.
Fig. 1.
A graphical representation of the data structure in a cluster with two subclusters in a three-level trial. Each oval represents a participant (level 1) nested in a subcluster (level 2) nested in the cluster (level 3). The effect modifier  and outcome
and outcome  are measured for each participant with their respective covariate-IC7Cs and outcome-ICCs depicted. A thicker arrow indicates a stronger correlation between variables.
are measured for each participant with their respective covariate-IC7Cs and outcome-ICCs depicted. A thicker arrow indicates a stronger correlation between variables.
Theorem 2.1
Defining
as the marginal variance of the univariate effect modifier, the limit variance
can be expressed as a function of the eigenvalues of the outcome-ICC and covariate-ICC matrices, and is dependent on the level of randomization. (i) When randomization is carried out at the cluster level, we have
(ii) When randomization is carried out at the subcluster level, we have
(iii) When randomization is carried out at the participant level, we have
. (iv) The variances are linearly ordered such that
, with equality obtained in the absence of residual clustering (e.g.,
or
).
The proof of Theorem 2.1 can be found in Appendix A of the Supplementary material available at Biostatistics online. Depending on the level of randomization, Theorem 2.1 provides a cascade of variance expressions to facilitate analytical power calculations. First, in the absence of any residual clustering in a three-level design such that 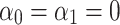 , we can write
, we can write 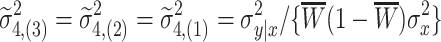 , which is essentially the limit variance of an interaction effect estimator in a simple ANCOVA model without clustering (Shieh, 2009). Therefore, we immediately notice that all three variances share the same form of the variance without clustering,
, which is essentially the limit variance of an interaction effect estimator in a simple ANCOVA model without clustering (Shieh, 2009). Therefore, we immediately notice that all three variances share the same form of the variance without clustering, 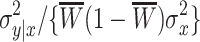 , multiplied by a design effect expression characterizing the nontrivial residual clustering, which we denote by
, multiplied by a design effect expression characterizing the nontrivial residual clustering, which we denote by 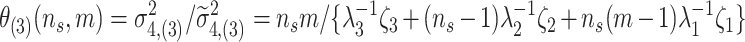 ,
, 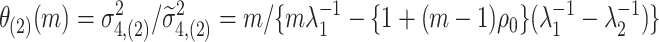 ,
,  , when the randomization unit is the cluster, subcluster, and participant, respectively. When the randomization is at the cluster level, Cunningham and Johnson (2016) showed that the design effect for testing the ATE in a three-level trial is unbounded when the subcluster size
, when the randomization unit is the cluster, subcluster, and participant, respectively. When the randomization is at the cluster level, Cunningham and Johnson (2016) showed that the design effect for testing the ATE in a three-level trial is unbounded when the subcluster size  increases indefinitely. In sharp contrast, with a participant-level effect modifier, the design effect under a three-level CRT is bounded above even if the subcluster size goes to infinity, as
increases indefinitely. In sharp contrast, with a participant-level effect modifier, the design effect under a three-level CRT is bounded above even if the subcluster size goes to infinity, as  . Intuitively, the HTE parameter
. Intuitively, the HTE parameter  corresponds to a participant-level interaction covariate that varies within each subcluster whereas the ATE corresponds to a cluster-level treatment variable that only varies between clusters; this subtle difference underlies the difference in the two design effects. Interestingly, when
corresponds to a participant-level interaction covariate that varies within each subcluster whereas the ATE corresponds to a cluster-level treatment variable that only varies between clusters; this subtle difference underlies the difference in the two design effects. Interestingly, when  , then
, then  and there can even be variance deflation in testing HTE under a three-level CRT relative to an individually randomized trials without clustering. For the subcluster randomized trial,
and there can even be variance deflation in testing HTE under a three-level CRT relative to an individually randomized trials without clustering. For the subcluster randomized trial,  , and the design effect is similarly bounded in the limit. The design effect
, and the design effect is similarly bounded in the limit. The design effect 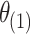 , however, does not depend on
, however, does not depend on 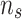 or
or  and shares the same form with the one derived in Cunningham and Johnson (2016) for testing the ATE in a three-level IRT.
and shares the same form with the one derived in Cunningham and Johnson (2016) for testing the ATE in a three-level IRT.
In addition, Theorem 2.1 demonstrates that randomization at a lower level leads to potential efficiency gain for estimating the interaction parameter 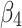 . This ordering result parallels that developed for testing the ATE in three-level designs (Cunningham and Johnson, 2016) and is intuitive because randomization at a lower level allows the within-cluster or within-subcluster comparisons to inform the estimation of the associated parameter. All three variances are increasing functions of the conditional outcome variance
. This ordering result parallels that developed for testing the ATE in three-level designs (Cunningham and Johnson, 2016) and is intuitive because randomization at a lower level allows the within-cluster or within-subcluster comparisons to inform the estimation of the associated parameter. All three variances are increasing functions of the conditional outcome variance 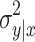 and decreasing functions of the marginal covariate variance
and decreasing functions of the marginal covariate variance 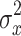 , matching the intuition that explained variation due to the effect modifier can lead to a HTE estimate with higher precision. Similar to the analysis of the ATE in IRTs or CRTs, a balanced design with equal randomization,
, matching the intuition that explained variation due to the effect modifier can lead to a HTE estimate with higher precision. Similar to the analysis of the ATE in IRTs or CRTs, a balanced design with equal randomization, 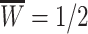 , leads to the largest power for testing
, leads to the largest power for testing 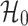 under a fixed sample size. Interestingly, the covariate-ICCs enter the variance for estimating
under a fixed sample size. Interestingly, the covariate-ICCs enter the variance for estimating 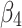 in an orderly fashion, that is,
in an orderly fashion, that is, 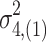 is independent of
is independent of 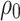 and
and 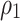 , and
, and  depends on
depends on 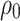 but is free of
but is free of 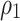 , whereas
, whereas 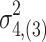 depends on both
depends on both 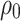 and
and 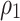 . This observation suggests that the variance of
. This observation suggests that the variance of  only depends on the covariate-ICCs defined within each randomization unit but not between randomization units.
only depends on the covariate-ICCs defined within each randomization unit but not between randomization units.
Theorem 2.1 helps demystify the relationships between the key ICC parameters and design efficiency for estimating the HTE. When randomization is carried out at the cluster level, larger values of covariate-ICCs, 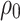 ,
, 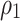 , are always associated with a larger
, are always associated with a larger 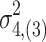 (smaller power). This is expected because larger covariate-ICCs imply less per-participant information for estimating
(smaller power). This is expected because larger covariate-ICCs imply less per-participant information for estimating 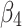 and therefore reduce statistical efficiency. The relationship between
and therefore reduce statistical efficiency. The relationship between 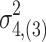 and outcome-ICCs,
and outcome-ICCs, 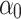 ,
, 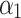 , can be nonmonotone and is graphically explored in Figure S1 of the Supplementary material available at Biostatistics online, where
, can be nonmonotone and is graphically explored in Figure S1 of the Supplementary material available at Biostatistics online, where 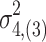 exhibits a parabolic relationship with
exhibits a parabolic relationship with 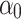 and
and 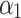 . This implies that a direct application of the existing design formula in Yang and others (2020) by equating
. This implies that a direct application of the existing design formula in Yang and others (2020) by equating 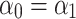 and
and 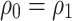 can lead to either conservative or anticonservative predictions for
can lead to either conservative or anticonservative predictions for  and inaccurate sample size results in general. When randomization is carried out at the subcluster level, larger values of between-subcluster outcome-ICC,
and inaccurate sample size results in general. When randomization is carried out at the subcluster level, larger values of between-subcluster outcome-ICC, 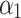 , is always associated with a smaller
, is always associated with a smaller 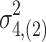 (larger power), whereas a larger value of covariate-ICC,
(larger power), whereas a larger value of covariate-ICC, 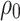 , is always associated with a larger
, is always associated with a larger 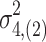 (smaller power). However,
(smaller power). However, 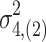 can be nonmonotone in the within-subcluster outcome-ICC,
can be nonmonotone in the within-subcluster outcome-ICC, 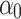 (see Figure S2 of the Supplementary material available at Biostatistics online for a graphical exploration). Finally, when randomization is carried out at the participant level, a larger value of within-subcluster outcome-ICC,
(see Figure S2 of the Supplementary material available at Biostatistics online for a graphical exploration). Finally, when randomization is carried out at the participant level, a larger value of within-subcluster outcome-ICC, 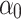 , is always associated with a smaller
, is always associated with a smaller 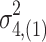 (larger power), whereas
(larger power), whereas 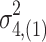 is independent of other ICC parameters. Table 1 provides a concise summary of these relationships and we further expand on these remarks in Appendix B of the Supplementary material available at Biostatistics online.
is independent of other ICC parameters. Table 1 provides a concise summary of these relationships and we further expand on these remarks in Appendix B of the Supplementary material available at Biostatistics online.
Table 1.
Definition of ICC parameters, and a concise summary of the relationships between ICC parameters and the variance of the interaction effect parameter with a univariate participant-level effect modifier ( ), under different levels of randomization
), under different levels of randomization
| Level of randomization | ||||
|---|---|---|---|---|
| ICC | Interpretation | Cluster | Subcluster | Participant |
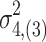
|
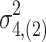
|
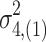
|
||
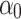
|
The intraclass correlation parameter between outcomes from two participants within the same subcluster |
|
|
|
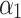
|
The intraclass correlation parameter between outcomes from two participants in two different subclusters |
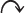
|

|
Indep |
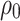
|
The intraclass correlation parameter between covariates from two participants within the same subcluster |
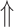
|
|
Indep |
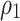
|
The intraclass correlation parameter between covariates from two participants in two different subclusters |

|
Indep | Indep |
“Indep” indicates that the variance is independent of and thus does not change with the specific ICC parameter; “ ” indicates a monotonically increasing relationship; “
” indicates a monotonically increasing relationship; “ ” indicates a monotonically decreasing relationship; and “
” indicates a monotonically decreasing relationship; and “ ” indicates a nonmonotone and likely quadratic relationship.
” indicates a nonmonotone and likely quadratic relationship.
Based on Theorem 2.1, further simplifications of the variance expressions are possible when the effect modifier is measured at the subcluster or cluster level. When the effect modifier is measured at the subcluster level (i.e., 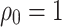 ) we obtain
) we obtain
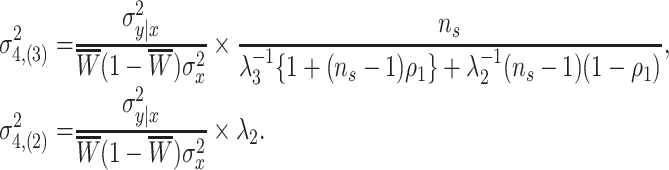 |
(2.5) |
When the effect modifier is measured at the cluster level (i.e., 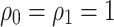 ),
),  reduces to
reduces to 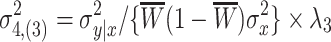 , but
, but 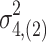 remains identical to (2.5). In both cases,
remains identical to (2.5). In both cases,  is unaffected and remains the same as in Theorem 2.1.
is unaffected and remains the same as in Theorem 2.1.
2.2. Generalization to accommodate multivariate effect modifiers
Although a common practice for confirmatory tests of HTE is to consider a univariate effect modifier, the above analytical sample size procedure can be generalized to jointly test the interaction effects with multivariate effect modifiers. In this case, we write 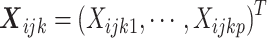 as the set of
as the set of 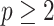 baseline covariates and
baseline covariates and 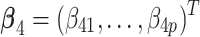 . We are interested in testing the global null hypothesis
. We are interested in testing the global null hypothesis 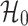 :
: 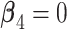 based on a Wald test. From the LM-ANCOVA model (2.2), the scaled GLS estimator
based on a Wald test. From the LM-ANCOVA model (2.2), the scaled GLS estimator  is asymptotically normal with mean zero and variance equal to the lower-right
is asymptotically normal with mean zero and variance equal to the lower-right 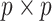 block of
block of 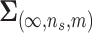 , which is denoted by
, which is denoted by 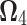 . This motivates a quadratic Wald test statistic
. This motivates a quadratic Wald test statistic 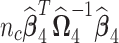 , which converges to a Chi-squared distribution
, which converges to a Chi-squared distribution 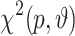 with
with 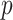 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter 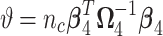 , where
, where 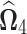 is the estimated covariance matrix of
is the estimated covariance matrix of  . For fixed effect size vector
. For fixed effect size vector 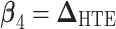 , the corresponding power equation of this Wald test is approximated by
, the corresponding power equation of this Wald test is approximated by
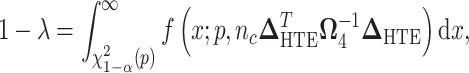 |
(2.6) |
where 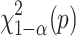 is the
is the 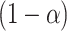 quantile of the central Chi-squared distribution with
quantile of the central Chi-squared distribution with 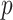 degrees of freedom and
degrees of freedom and 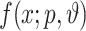 is the probability density function of the
is the probability density function of the  distribution. Fixing any two of
distribution. Fixing any two of 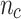 ,
, 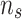 , or
, or 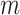 , solving (2.6) for the other argument (for example, using the
, solving (2.6) for the other argument (for example, using the 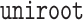 function in
function in 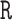 and rounding to the next integer above) readily gives the required sample size to achieve a desired level of power; therefore, sample size determination for HTE analysis with multivariate effect modifiers boils down to the characterization of
and rounding to the next integer above) readily gives the required sample size to achieve a desired level of power; therefore, sample size determination for HTE analysis with multivariate effect modifiers boils down to the characterization of  in explicit forms.
in explicit forms.
In Appendix C of the Supplementary material available at Biostatistics online, assuming a nested block exchangeable correlation structure for the multivariate effect modifiers, we prove a general version of Theorem 2.1. The general results establish the analytical forms of three covariance matrices of the 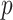 -vector of HTE estimators,
-vector of HTE estimators, 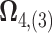 ,
, 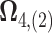 , and
, and 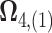 , when randomization is carried out at the cluster level, subcluster level, and participant level, respectively. Furthermore, these covariance matrices have Löwner ordering such that
, when randomization is carried out at the cluster level, subcluster level, and participant level, respectively. Furthermore, these covariance matrices have Löwner ordering such that 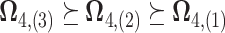 , with equality obtained in the absence of residual clustering (e.g.,
, with equality obtained in the absence of residual clustering (e.g., 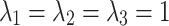 or
or 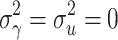 ). Finally, with a univariate effect modifier measured at the participant level, the LM-ANCOVA model (2.1) can also be used to detect contextual effect modification by decomposing the covariate effect into a cluster-level, subcluster-level, and participant-level components to address different effects for the aggregated and lower-level variations (Raudenbush, 1997). Correspondingly,
). Finally, with a univariate effect modifier measured at the participant level, the LM-ANCOVA model (2.1) can also be used to detect contextual effect modification by decomposing the covariate effect into a cluster-level, subcluster-level, and participant-level components to address different effects for the aggregated and lower-level variations (Raudenbush, 1997). Correspondingly, 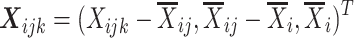 becomes the transformed vector of effect modifiers, and the more general Theorem derived in Appendix C of the Supplementary material available at Biostatistics online can be applied for analytical power analysis with contextual effect modification. We derive those explicit expressions in Appendix D of the Supplementary material available at Biostatistics online as an application of this more general result.
becomes the transformed vector of effect modifiers, and the more general Theorem derived in Appendix C of the Supplementary material available at Biostatistics online can be applied for analytical power analysis with contextual effect modification. We derive those explicit expressions in Appendix D of the Supplementary material available at Biostatistics online as an application of this more general result.
2.3. Connections to sample size requirements for studying the ATE
Even though the primary motivation for model (2.1) is to study HTE with prespecified effect modifiers, the LM-ANCOVA model also implies a covariate-adjusted estimator for the ATE. This is because the conditional ATE given by LM-ANCOVA is 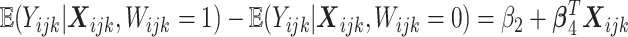 , and therefore the marginal ATE parameter can be given by integrating over the distribution of effect modifiers,
, and therefore the marginal ATE parameter can be given by integrating over the distribution of effect modifiers, 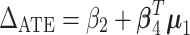 . Often times, a practical strategy is to globally mean center the collection of effect modifiers such that the sample mean is zero. Without loss of generality, we assume
. Often times, a practical strategy is to globally mean center the collection of effect modifiers such that the sample mean is zero. Without loss of generality, we assume 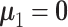 and therefore
and therefore 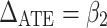 can be interpreted as the covariate-adjusted ATE estimator. Such an observation is akin to the ANCOVA analysis of IRTs, for which model (2.1) is a direct generalization with multiple random effects. Different from prior work on ANCOVA analysis of IRTs without residual clustering (Yang and Tsiatis, 2001), we assume model (2.1) is correctly specified such that an explicit model-based variance expression of the ATE estimator can be used as a basis for study planning. Specifically, we denote the asymptotic variance expression of
can be interpreted as the covariate-adjusted ATE estimator. Such an observation is akin to the ANCOVA analysis of IRTs, for which model (2.1) is a direct generalization with multiple random effects. Different from prior work on ANCOVA analysis of IRTs without residual clustering (Yang and Tsiatis, 2001), we assume model (2.1) is correctly specified such that an explicit model-based variance expression of the ATE estimator can be used as a basis for study planning. Specifically, we denote the asymptotic variance expression of 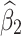 as
as 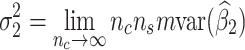 , based on which the generic sample size requirement in a three-level design is
, based on which the generic sample size requirement in a three-level design is 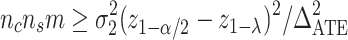 . Based on model (2.1), we provide a final result to facilitate power and sample size determination for testing the ATE in three-level designs (proof in Appendix E of the Supplementary material available at Biostatistics online).
. Based on model (2.1), we provide a final result to facilitate power and sample size determination for testing the ATE in three-level designs (proof in Appendix E of the Supplementary material available at Biostatistics online).
Theorem 2.2
The limit variance expression of the covariate-adjusted ATE estimator depends on the unit of randomization and is at most a function of the outcome-ICCs. (a) When the randomization is carried out at the cluster level, we have
. (b) When randomization is carried out at the subcluster level, we have
. (c) When randomization is carried out at the participant level, we have
. (d) The variances are linearly ordered such that
, and equality is obtained when
(
) and
(
.
Theorem 2.2 implies that the design effect in a three-level design for estimating the ATE, as compared to an unclustered randomized design, is one eigenvalue of the outcome-ICC matrix 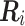 , matching those derived by Cunningham and Johnson (2016) under three-level designs with one subtle difference. In Cunningham and Johnson (2016), the design effects were all derived assuming a linear mixed model without any effect modifiers and therefore the outcome variance and the outcome-ICCs in each eigenvalue are marginal with respect to effect modifiers. In contrast, the design effect expressions implied by Theorem 2.2 are parameterized by outcome variance and outcome-ICCs conditional on effect modifiers. As we demonstrate in Section 3, adjusting for effect modifiers can partially explain the residual variation of the outcomes at any level, and therefore may reduce either the outcome variance or the amount of residual correlation. In such a case, the conditional outcome-ICCs and conditional outcome variance are frequently no larger than their marginal counterparts, and therefore the ATE estimators based on LM-ANCOVA are likely to be more efficient than those under the unadjusted linear mixed model. This improvement in efficiency can directly translate into sample size savings. Finally, if the marginal variance of a univariate effect modifier is a unity such that
, matching those derived by Cunningham and Johnson (2016) under three-level designs with one subtle difference. In Cunningham and Johnson (2016), the design effects were all derived assuming a linear mixed model without any effect modifiers and therefore the outcome variance and the outcome-ICCs in each eigenvalue are marginal with respect to effect modifiers. In contrast, the design effect expressions implied by Theorem 2.2 are parameterized by outcome variance and outcome-ICCs conditional on effect modifiers. As we demonstrate in Section 3, adjusting for effect modifiers can partially explain the residual variation of the outcomes at any level, and therefore may reduce either the outcome variance or the amount of residual correlation. In such a case, the conditional outcome-ICCs and conditional outcome variance are frequently no larger than their marginal counterparts, and therefore the ATE estimators based on LM-ANCOVA are likely to be more efficient than those under the unadjusted linear mixed model. This improvement in efficiency can directly translate into sample size savings. Finally, if the marginal variance of a univariate effect modifier is a unity such that 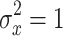 , regardless of the level of randomization, the large-sample variance expression for the covariate-adjusted ATE estimator is identical to the large-sample variance expression for the HTE estimator, when the effect modifier is measured at or above the unit of randomization. Namely,
, regardless of the level of randomization, the large-sample variance expression for the covariate-adjusted ATE estimator is identical to the large-sample variance expression for the HTE estimator, when the effect modifier is measured at or above the unit of randomization. Namely, 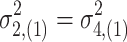 regardless of the measurement level of the effect modifier;
regardless of the measurement level of the effect modifier;  when the effect modifier is measured at the subcluster or cluster level; and
when the effect modifier is measured at the subcluster or cluster level; and  when the effect modifier is measured at the cluster level.
when the effect modifier is measured at the cluster level.
3. Numerical studies
We carry out simulations to assess the finite-sample performance of the proposed sample size procedures for planning three-level trials. Our objectives are (i) assessing the accuracy of the proposed methods for powering three-level trials to detect HTE as well as the ATE and (ii) demonstrating, from a cost-effectiveness perspective, whether the sample size estimates based on Theorem 2.2 can be smaller than those estimated by the approach given in Cunningham and Johnson (2016), for the same level of power. Whenever applicable, we also compare our sample size results with those obtained from Dong and others (2018). To focus on the main idea, throughout we assume a univariate continuous effect modifier measured at the participant level. We consider designs with randomization at each of the three levels, leading to CRTs, subcluster randomized trials, and IRTs with a hierarchical structure. We assume equal randomization with 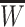 =1/2, and a balanced design with equal numbers of subclusters
=1/2, and a balanced design with equal numbers of subclusters  in each cluster and equal subcluster sizes
in each cluster and equal subcluster sizes 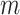 .
.
For the first objective, we fix 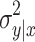 and
and 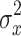 at
at  , nominal type I error
, nominal type I error 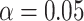 and the desired power level
and the desired power level 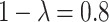 ; the remaining parameters are varied. Under each design, we consider two levels of subcluster sizes
; the remaining parameters are varied. Under each design, we consider two levels of subcluster sizes 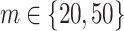 and two values for the number of subclusters per cluster
and two values for the number of subclusters per cluster 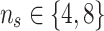 . Since typically
. Since typically 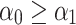 and
and 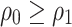 , we chose
, we chose 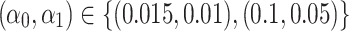 to represent small and moderate conditional outcome-ICC, and
to represent small and moderate conditional outcome-ICC, and 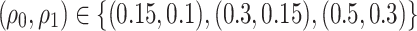 to represent small, moderate, and large covariate-ICCs, based on ranges commonly reported in the CRT literature (Murray and Blitstein, 2003). To ensure that the predicted number of clusters is practical and mostly below
to represent small, moderate, and large covariate-ICCs, based on ranges commonly reported in the CRT literature (Murray and Blitstein, 2003). To ensure that the predicted number of clusters is practical and mostly below 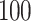 , we set
, we set 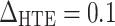 for all randomization scenarios,
for all randomization scenarios, 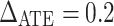 for the CRTs, and
for the CRTs, and 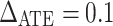 for the subcluster randomized trial or IRT. For each parameter combination, we estimate the number of clusters
for the subcluster randomized trial or IRT. For each parameter combination, we estimate the number of clusters 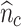 that ensures at least
that ensures at least 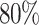 power and round to the nearest even integer above to ensure an exactly equal randomization. We then use the predicted cluster number
power and round to the nearest even integer above to ensure an exactly equal randomization. We then use the predicted cluster number  to simulate correlated outcome data based on the LM-ANCOVA model and compute the empirical power of the Wald test for HTE or the ATE. When the randomization is carried out at the cluster level, we quantify the proportion of explained variation due to the effect modifier (details in Appendix F of the Supplementary material available at Biostatistics online) and use the method of Dong and others (2018) to obtain the required number of cluster
to simulate correlated outcome data based on the LM-ANCOVA model and compute the empirical power of the Wald test for HTE or the ATE. When the randomization is carried out at the cluster level, we quantify the proportion of explained variation due to the effect modifier (details in Appendix F of the Supplementary material available at Biostatistics online) and use the method of Dong and others (2018) to obtain the required number of cluster 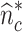 to ensure at least 80
to ensure at least 80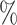 power, as a comparator to our new method.
power, as a comparator to our new method.
We generate the individual-level outcomes using the LM-ANCOVA model (2.1) by fixing 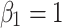 and
and 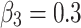 . For the HTE tests under each randomized design, we fix
. For the HTE tests under each randomized design, we fix 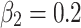 , and
, and  . For studying the empirical power of the Wald test for the covariate-adjusted ATE, we fix
. For studying the empirical power of the Wald test for the covariate-adjusted ATE, we fix  such that
such that 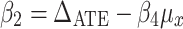 . We generate the correlated effect modifiers based on the linear mixed model,
. We generate the correlated effect modifiers based on the linear mixed model, 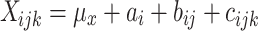 , where the global mean
, where the global mean 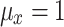 ,
, 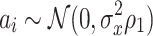 ,
, 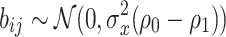 , and
, and 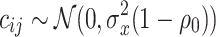 . The cluster-specific random intercept in LM-ANCOVA
. The cluster-specific random intercept in LM-ANCOVA 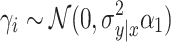 , the subcluster-level random effect
, the subcluster-level random effect 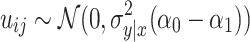 , and the random error
, and the random error  . For each parameter configuration, we generate
. For each parameter configuration, we generate 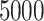 hypothetical trials to evaluate the empirical type I error under the null and empirical power under the alternative. For each hypothetical trial, we fit the LM-ANCOVA model using restricted maximum likelihood estimation and carry out the corresponding Wald test for inference. To evaluate the covariate-adjusted Wald test for the ATE, we first globally mean-center the effect modifier before fitting the LM-ANCOVA. Finally, while the sample size estimation for HTE test and ATE test under a three-level design can generally be based on the standard normal distribution, we consider the
hypothetical trials to evaluate the empirical type I error under the null and empirical power under the alternative. For each hypothetical trial, we fit the LM-ANCOVA model using restricted maximum likelihood estimation and carry out the corresponding Wald test for inference. To evaluate the covariate-adjusted Wald test for the ATE, we first globally mean-center the effect modifier before fitting the LM-ANCOVA. Finally, while the sample size estimation for HTE test and ATE test under a three-level design can generally be based on the standard normal distribution, we consider the 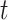 -distribution with the between-within degrees of freedom (
-distribution with the between-within degrees of freedom (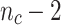 ) only when studying the ATE under a CRT (standard normal distribution will still be used for testing the ATE in both subcluster randomized trials and IRTs). This choice represents an effective small-sample degrees of freedom correction specifically for CRTs with a limited number of clusters (and will have negligible difference from the standard normal when
) only when studying the ATE under a CRT (standard normal distribution will still be used for testing the ATE in both subcluster randomized trials and IRTs). This choice represents an effective small-sample degrees of freedom correction specifically for CRTs with a limited number of clusters (and will have negligible difference from the standard normal when 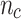 is sufficiently large, also see Chapter 2.4.2 in Pinheiro and Bates (2006)) and has been previously shown to maintain valid type I error rate (Li and others, 2016) in small CRTs for testing the ATE and therefore is adopted to more objectively assess the agreement between empirical and predicted power under that specific scenario. For this scenario, we also confirm in Table S1 of the Supplementary material available at Biostatistics online that the predicted variance of the ATE estimator based on Theorem 2.2 is close to the Monte Carlo variance.
is sufficiently large, also see Chapter 2.4.2 in Pinheiro and Bates (2006)) and has been previously shown to maintain valid type I error rate (Li and others, 2016) in small CRTs for testing the ATE and therefore is adopted to more objectively assess the agreement between empirical and predicted power under that specific scenario. For this scenario, we also confirm in Table S1 of the Supplementary material available at Biostatistics online that the predicted variance of the ATE estimator based on Theorem 2.2 is close to the Monte Carlo variance.
For the second objective, given each effect size  , we still generate the correlated outcome data using the LM-ANCOVA model as the above, but assume that the primary analysis of the ATE is based on a linear mixed model without the effect modifier. Correspondingly, we compute the required sample size using the formulas in the absence of any covariates. To operationalize those formulas, we obtain the total outcome variance marginalizing over the covariate distribution,
, we still generate the correlated outcome data using the LM-ANCOVA model as the above, but assume that the primary analysis of the ATE is based on a linear mixed model without the effect modifier. Correspondingly, we compute the required sample size using the formulas in the absence of any covariates. To operationalize those formulas, we obtain the total outcome variance marginalizing over the covariate distribution, 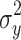 . Furthermore, the unconditional outcome-ICCs can be approximated by
. Furthermore, the unconditional outcome-ICCs can be approximated by  and
and 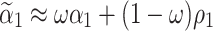 , where the explicit form of
, where the explicit form of 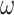 is derived in Appendix F of the Supplementary material available at Biostatistics online. The required sample size for the unadjusted mixed model analysis is then estimated from the Theorem 2.2 but by replacing
is derived in Appendix F of the Supplementary material available at Biostatistics online. The required sample size for the unadjusted mixed model analysis is then estimated from the Theorem 2.2 but by replacing 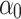 ,
, 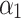 with
with 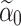 ,
,  , and
, and 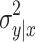 with
with 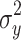 , namely, using the formulas in Cunningham and Johnson (2016). We compared the results with those estimated based on Theorem 2.2 to investigate saving in sample size due to adjustment for the univariate effect modifier. Finally, we also obtain the empirical type I error rate and empirical power by fitting the linear mixed model omitting
, namely, using the formulas in Cunningham and Johnson (2016). We compared the results with those estimated based on Theorem 2.2 to investigate saving in sample size due to adjustment for the univariate effect modifier. Finally, we also obtain the empirical type I error rate and empirical power by fitting the linear mixed model omitting 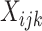 to verify the accuracy of the sample size procedure without the effect modifier.
to verify the accuracy of the sample size procedure without the effect modifier.
3.1. Results
Table 2 provides a summary of the estimated number of clusters using the proposed formula in Theorem 2.1, the empirical size, empirical power as well as predicted power by formula of the Wald test for HTE when 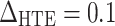 , and when the randomization is carried out at the cluster level (differences from 80
, and when the randomization is carried out at the cluster level (differences from 80 power are due to rounding). The Wald test maintains the nominal type I error rate, which ensures the validity of the subsequent comparisons between the empirical and predicted power. Across all scenarios, the predicted power is in good agreement with the empirical power, even when there are as few as
power are due to rounding). The Wald test maintains the nominal type I error rate, which ensures the validity of the subsequent comparisons between the empirical and predicted power. Across all scenarios, the predicted power is in good agreement with the empirical power, even when there are as few as 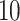 clusters. In Table 2, we also observe that the method of Dong and others (2018) often leads to much smaller sample size estimates (
clusters. In Table 2, we also observe that the method of Dong and others (2018) often leads to much smaller sample size estimates (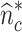 ) than the proposed method and therefore their method is consistently anticonservative. In Appendix F of the Supplementary material available at Biostatistics online, we have re-expressed their design formula using our notation and found that it does not depend on any covariate-ICC parameters. It is apparent from Table 2 that ignoring the covariate-ICC at each level during study planning can result in under-powered CRTs, especially in the presence of nontrivial covariate-ICCs.
) than the proposed method and therefore their method is consistently anticonservative. In Appendix F of the Supplementary material available at Biostatistics online, we have re-expressed their design formula using our notation and found that it does not depend on any covariate-ICC parameters. It is apparent from Table 2 that ignoring the covariate-ICC at each level during study planning can result in under-powered CRTs, especially in the presence of nontrivial covariate-ICCs.
Table 2.
Estimated required number of clusters 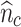 for the HTE test based on the proposed formula, empirical type I error (Emp. size), empirical power (Emp. power), as well as predicted power (Pred. power) for the HTE, test when randomization is at the cluster level. For studying power, the HTE effect size is fixed at
for the HTE test based on the proposed formula, empirical type I error (Emp. size), empirical power (Emp. power), as well as predicted power (Pred. power) for the HTE, test when randomization is at the cluster level. For studying power, the HTE effect size is fixed at 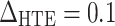 . In the last two columns, we estimate the required sample size
. In the last two columns, we estimate the required sample size 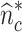 using the method of Dong and others (2018) and obtain the actual predicted power (Actual power) using our formula based on the estimated sample size
using the method of Dong and others (2018) and obtain the actual predicted power (Actual power) using our formula based on the estimated sample size 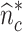 to assess the degree to which the three-level CRT may be under-powered
to assess the degree to which the three-level CRT may be under-powered
| Design parameters | Performance characteristics | Comparator | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
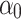
|
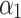
|

|

|

|
Emp. size | Emp. power | Pred. power |
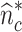
|
Actual power |
| 20 | 4 | 0.015 | 0.010 | 0.150 | 0.100 | 42 | 0.051 | 0.812 | 0.806 | 40 | 0.787 |
| 20 | 4 | 0.015 | 0.010 | 0.300 | 0.150 | 44 | 0.054 | 0.806 | 0.807 | 40 | 0.768 |
| 20 | 4 | 0.015 | 0.010 | 0.500 | 0.300 | 48 | 0.052 | 0.801 | 0.804 | 40 | 0.730 |
| 20 | 4 | 0.100 | 0.050 | 0.150 | 0.100 | 42 | 0.051 | 0.813 | 0.808 | 36 | 0.746 |
| 20 | 4 | 0.100 | 0.050 | 0.300 | 0.150 | 48 | 0.050 | 0.805 | 0.813 | 36 | 0.694 |
| 20 | 4 | 0.100 | 0.050 | 0.500 | 0.300 | 58 | 0.053 | 0.798 | 0.800 | 36 | 0.598 |
| 20 | 8 | 0.015 | 0.010 | 0.150 | 0.100 | 22 | 0.048 | 0.811 | 0.819 | 20 | 0.781 |
| 20 | 8 | 0.015 | 0.010 | 0.300 | 0.150 | 24 | 0.054 | 0.837 | 0.832 | 20 | 0.760 |
| 20 | 8 | 0.015 | 0.010 | 0.500 | 0.300 | 26 | 0.055 | 0.816 | 0.816 | 20 | 0.708 |
| 20 | 8 | 0.100 | 0.050 | 0.150 | 0.100 | 22 | 0.045 | 0.817 | 0.825 | 18 | 0.744 |
| 20 | 8 | 0.100 | 0.050 | 0.300 | 0.150 | 24 | 0.048 | 0.813 | 0.811 | 18 | 0.692 |
| 20 | 8 | 0.100 | 0.050 | 0.500 | 0.300 | 30 | 0.046 | 0.796 | 0.806 | 18 | 0.590 |
| 50 | 4 | 0.015 | 0.010 | 0.150 | 0.100 | 18 | 0.054 | 0.818 | 0.822 | 16 | 0.775 |
| 50 | 4 | 0.015 | 0.010 | 0.300 | 0.150 | 20 | 0.055 | 0.829 | 0.833 | 16 | 0.744 |
| 50 | 4 | 0.015 | 0.010 | 0.500 | 0.300 | 22 | 0.055 | 0.811 | 0.811 | 16 | 0.678 |
| 50 | 4 | 0.100 | 0.050 | 0.150 | 0.100 | 18 | 0.052 | 0.828 | 0.832 | 16 | 0.787 |
| 50 | 4 | 0.100 | 0.050 | 0.300 | 0.150 | 20 | 0.054 | 0.812 | 0.813 | 16 | 0.722 |
| 50 | 4 | 0.100 | 0.050 | 0.500 | 0.300 | 26 | 0.056 | 0.816 | 0.808 | 16 | 0.603 |
| 50 | 8 | 0.015 | 0.010 | 0.150 | 0.100 | 10 | 0.053 | 0.857 | 0.856 | 8 | 0.772 |
| 50 | 8 | 0.015 | 0.010 | 0.300 | 0.150 | 10 | 0.052 | 0.827 | 0.828 | 8 | 0.739 |
| 50 | 8 | 0.015 | 0.010 | 0.500 | 0.300 | 12 | 0.058 | 0.825 | 0.830 | 8 | 0.663 |
| 50 | 8 | 0.100 | 0.050 | 0.150 | 0.100 | 10 | 0.052 | 0.874 | 0.868 | 8 | 0.786 |
| 50 | 8 | 0.100 | 0.050 | 0.300 | 0.150 | 10 | 0.053 | 0.818 | 0.813 | 8 | 0.722 |
| 50 | 8 | 0.100 | 0.050 | 0.500 | 0.300 | 14 | 0.054 | 0.831 | 0.834 | 8 | 0.600 |
Under cluster randomization, Table 3 provides a summary of the estimated number of clusters using the proposed formula in Theorem 2.2, the empirical size, empirical power as well predicted power by formula of the Wald test for the covariate-adjusted ATE when 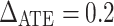 . The Wald test still maintains valid type I error rate, with empirical power close to analytical prediction by our formula. This suggests that our variance expressions are accurate for study design purposes. Interestingly, even though the ATE size is twice the HTE effect size, the required sample size to achieve 80
. The Wald test still maintains valid type I error rate, with empirical power close to analytical prediction by our formula. This suggests that our variance expressions are accurate for study design purposes. Interestingly, even though the ATE size is twice the HTE effect size, the required sample size to achieve 80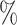 power is not always larger for the HTE test compared to the ATE and can depend on the remaining design parameters. Finally, we demonstrate that ignoring the univariate effect modifier in the study design stage can lead to larger than necessary sample size estimates under a wide range of design configurations (Table S2 of the Supplementary material available at Biostatistics online). In fact, for the same ATE size, we find that the required sample size based on the Cunningham and Johnson (2016) formula may even be
power is not always larger for the HTE test compared to the ATE and can depend on the remaining design parameters. Finally, we demonstrate that ignoring the univariate effect modifier in the study design stage can lead to larger than necessary sample size estimates under a wide range of design configurations (Table S2 of the Supplementary material available at Biostatistics online). In fact, for the same ATE size, we find that the required sample size based on the Cunningham and Johnson (2016) formula may even be 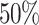 larger than that based on Theorem 2.2, as a result of explained variation. For example, as seen in Table S2 of the Supplementary material available at Biostatistics online, the adjusted outcome-ICCs
larger than that based on Theorem 2.2, as a result of explained variation. For example, as seen in Table S2 of the Supplementary material available at Biostatistics online, the adjusted outcome-ICCs  and
and 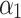 can be substantially smaller than their marginal counterparts,
can be substantially smaller than their marginal counterparts, 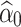 ,
,  , especially when the covariate-ICCs are farther away from zero.
, especially when the covariate-ICCs are farther away from zero.
Table 3.
Estimated required number of clusters 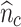 for the covariate-adjusted ATE test based on the proposed formula, empirical type I error (Emp. size), empirical power (Emp. power), as well as predicted power (Pred. power) for the covariate-adjusted ATE test when randomization is at the cluster level. For studying power, the ATE size is fixed at
for the covariate-adjusted ATE test based on the proposed formula, empirical type I error (Emp. size), empirical power (Emp. power), as well as predicted power (Pred. power) for the covariate-adjusted ATE test when randomization is at the cluster level. For studying power, the ATE size is fixed at 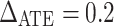
| Design parameters | Performance characteristics | ||||||||
|---|---|---|---|---|---|---|---|---|---|
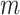
|
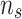
|
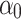
|
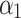
|
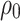
|
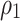
|
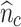
|
Emp. size | Emp. power | Pred. power |
| 20 | 4 | 0.015 | 0.010 | 0.150 | 0.100 | 22 | 0.051 | 0.824 | 0.828 |
| 20 | 4 | 0.015 | 0.010 | 0.300 | 0.150 | 22 | 0.052 | 0.821 | 0.828 |
| 20 | 4 | 0.015 | 0.010 | 0.500 | 0.300 | 22 | 0.054 | 0.821 | 0.828 |
| 20 | 4 | 0.100 | 0.050 | 0.150 | 0.100 | 60 | 0.052 | 0.798 | 0.801 |
| 20 | 4 | 0.100 | 0.050 | 0.300 | 0.150 | 60 | 0.053 | 0.797 | 0.801 |
| 20 | 4 | 0.100 | 0.050 | 0.500 | 0.300 | 60 | 0.053 | 0.796 | 0.801 |
| 20 | 8 | 0.015 | 0.010 | 0.150 | 0.100 | 16 | 0.048 | 0.820 | 0.819 |
| 20 | 8 | 0.015 | 0.010 | 0.300 | 0.150 | 16 | 0.048 | 0.818 | 0.819 |
| 20 | 8 | 0.015 | 0.010 | 0.500 | 0.300 | 16 | 0.051 | 0.814 | 0.819 |
| 20 | 8 | 0.100 | 0.050 | 0.150 | 0.100 | 52 | 0.048 | 0.815 | 0.811 |
| 20 | 8 | 0.100 | 0.050 | 0.300 | 0.150 | 52 | 0.048 | 0.815 | 0.811 |
| 20 | 8 | 0.100 | 0.050 | 0.500 | 0.300 | 52 | 0.049 | 0.813 | 0.811 |
| 50 | 4 | 0.015 | 0.010 | 0.150 | 0.100 | 16 | 0.051 | 0.839 | 0.832 |
| 50 | 4 | 0.015 | 0.010 | 0.300 | 0.150 | 16 | 0.053 | 0.840 | 0.832 |
| 50 | 4 | 0.015 | 0.010 | 0.500 | 0.300 | 16 | 0.055 | 0.837 | 0.832 |
| 50 | 4 | 0.100 | 0.050 | 0.150 | 0.100 | 56 | 0.050 | 0.812 | 0.810 |
| 50 | 4 | 0.100 | 0.050 | 0.300 | 0.150 | 56 | 0.050 | 0.814 | 0.810 |
| 50 | 4 | 0.100 | 0.050 | 0.500 | 0.300 | 56 | 0.050 | 0.813 | 0.810 |
| 50 | 8 | 0.015 | 0.010 | 0.150 | 0.100 | 14 | 0.054 | 0.851 | 0.851 |
| 50 | 8 | 0.015 | 0.010 | 0.300 | 0.150 | 14 | 0.056 | 0.850 | 0.851 |
| 50 | 8 | 0.015 | 0.010 | 0.500 | 0.300 | 14 | 0.059 | 0.842 | 0.851 |
| 50 | 8 | 0.100 | 0.050 | 0.150 | 0.100 | 48 | 0.051 | 0.805 | 0.801 |
| 50 | 8 | 0.100 | 0.050 | 0.300 | 0.150 | 48 | 0.052 | 0.802 | 0.801 |
| 50 | 8 | 0.100 | 0.050 | 0.500 | 0.300 | 48 | 0.054 | 0.802 | 0.801 |
Simulation results for when the randomization is carried at the subcluster level and at the participant level are presented in Tables S3–S8 of the Supplementary material available at Biostatistics online. The patterns are qualitatively similar to the results in Tables 2 and 3 as well as Table S2 of the Supplementary material available at Biostatistics online and confirm that our analytical power procedure can accurately track the empirical power for the Wald test for HTE and ATE. In addition, these results confirm the ordering properties of the variances under different randomized designs, with the cluster-level randomization requiring the largest sample size and the participant-level randomization requiring the smallest sample size, for studying both HTE and the ATE. Finally, we observe that, for studying the ATE, the sample size saving by adjusting for the participant-level effect modifier is often the largest under a CRT and the smallest under an IRT with a hierarchical structure.
4. Two real CRT examples
We illustrate the proposed methods using two real trial examples, with a primary focus on the detection of confirmatory HTE. In both examples, we consider two-sided tests with a nominal 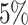 type I error and
type I error and 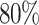 power.
power.
Example 4.1
(The HALI trial). The HALI trial compared the effect of a literacy intervention with usual instruction in terms of students’ literacy outcomes measured by performance on spelling and reading tests (Jukes and others, 2017). The study exhibits a three-level structure since the children participants are nested in schools (subclusters) which are further nested in TAC tutor zones (clusters); and the randomization of literacy intervention is carried out at the TAC level with
. There are approximately
children in each school, and on average
schools per TAC tutor zone. We focus on the
-month spelling score as a continuous outcome and the baseline spelling score as a continuous potential effect modifier. Based on the estimates in Jukes and others (2017), we assume the conditional within-subcluster and between-subcluster outcome-ICCs as
and
. We further assume the within-subcluster and between-subcluster covariate-ICCs
and
. Using Theorem 2.1(a), the required number of TAC tutor zones to detect HTE by the baseline spelling score for a standardized effect size,
(interpreted as the impact due to one standard deviation unit change in baseline spelling score on standard deviation unit change in the 9-month spelling score) is
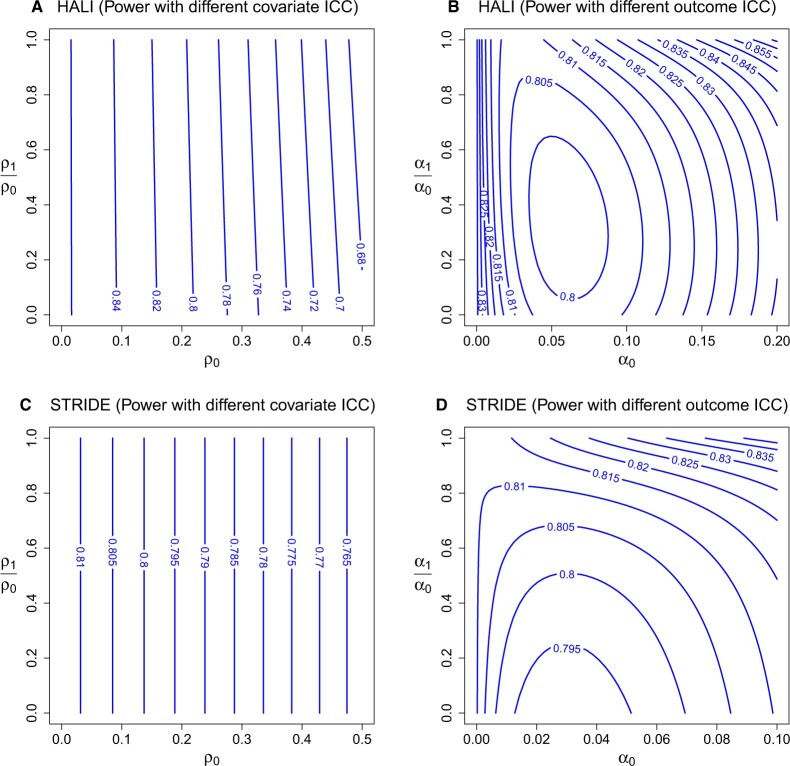
. To explore the sensitivity of power to varying covariate- and outcome-ICC values, we estimate the power of the HTE test by varying
,
with fixed outcome-ICC values, and by varying
,
with fixed covariate-ICCs. The power contours in Figures 2(a) and (b) indicate that the test power is sensitive to the magnitude of within-cluster covariate-ICC, but relatively insensitive to the magnitude of between-cluster covariate-ICC. While larger values of the within-cluster covariate-ICC can reduce the power of the HTE test to below
, variations of the outcome-ICCs within the range we considered maintain the power of the HTE test above
.
Fig. 2.
Estimated power contours for studying the heterogeneous treatment effect in the HALI and STRIDE trials as a function of the covariate and outcome-ICCs. (a) and (b) are based on the participant-level continuous effect modifier, baseline spelling score, in the HALI CRT (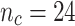 ,
, 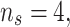 and
and 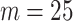 ), while (c) and (d) are based on the participant-level binary effect modifier, SRH, in the STRIDE subcluster randomized trial (
), while (c) and (d) are based on the participant-level binary effect modifier, SRH, in the STRIDE subcluster randomized trial (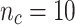 ,
,  and
and 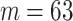 ).
).
Example 4.2
(The STRIDE Trial). The STRIDE trial was a subcluster randomized trial comparing the effectiveness of a multifactorial fall prevention intervention program versus enhanced usual care on patient’s health outcomes (Gill and others, 2021). The study randomized primary care clinics to intervention conditions with allocation probability
and measured outcomes at the participant level; the clinics were nested within health centers, thus exhibiting a three-level structure. Each health center included about
clinics, and the average clinic size was
. In this illustrative example, we considered the concern score for falling as a continuous outcome and self-rated health (SRH; measures whether one has good/excellent SRH) as a binary effect modifier measured at the participant level (Gill and others, 2021). We assumed the conditional within-subcluster and between-subcluster outcome-ICCs as
and
, and further assumed the within-subcluster covariate-ICC
. Using Theorem 2.1(b),
health centers would be required to detect HTE moderated with the SRH for a standardized effect size
(interpreted as the impact due to change in SRH on the standard deviation unit change in the concern score). To additionally explore the sensitivity of power to varying covariate- and outcome-ICC values, we present the power contours in Figures 2(c) and (d) as in Example 4.1. In particular, Figure 2(c) confirms that larger values of
can decrease the power of the HTE test, but varying
has no effect on the test power in a subcluster randomized trial. Varying values of the outcome-ICCs generally do not result in an under-powered HTE test, except when
and
(a scenario with a moderate within-cluster outcome-ICC but a small between-subcluster outcome-ICC), in which case the power appears just below
. Overall, these two examples illustrate how our design expressions can be effectively operationalized in practical design situations and emphasize the critical role of the within-subcluster covariate-ICC in determining the power of the HTE test.
5. Concluding remarks
While prespecified HTE analysis has been a recognized goal in randomized trials, guidance to date on planning pragmatic trials involving clusters with HTE analysis is scarce. Through analytical derivations, we contribute a cascade of new variance expressions to allow for rigorous and yet computationally efficient design of pragmatic CRTs to power confirmatory HTE analysis with effect modifiers measured at each level, addressing a critical methodological gap in designing definitive pragmatic CRTs. Compared to the design of IRTs with HTE analysis (Brookes and others, 2004), the design of CRTs with HTE analysis requires more complex considerations due to the multilevel data structure and additional design parameters, especially the ICCs of the outcome as well as the effect modifier. While recent advancements in computational tools have made the use of a simulation-based power calculation an attractive alternative to analytical power predictions in clustered designs, such an approach is typically time-consuming and can quickly become impractical due to the need to search across multidimensional parameter spaces and repeatedly fitting multilevel models. Our proposed design formulas not only reduce the associated computational issues, but, more importantly, identify key aspects of the data generating processes that contribute to the study power. For example, the power of the HTE test is only affected by the HTE effect size but not the ATE size. Furthermore, the power of the HTE test only depends on the covariate-ICCs defined within each randomization unit but not between randomization units. Regardless of the level of randomization, the variance of the interaction effect estimator from the LM-ANCOVA model is proportional to the ratio of the conditional outcome variance and the variance of the effect modifier. In the context of a binary effect modifier, for example, the variance of the effect modifier is a function of the mean, and it follows that the variance of the interaction effect estimator reaches its minimum when the prevalence of the effect modifier is 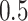 (holding all other factors constant). These insights greatly simplify power analysis by obviating the need to exhaust ancillary design parameters as would otherwise be required in a simulation-based power calculation procedure, and can possibly provide a basis for deriving optimal designs for testing effect modification.
(holding all other factors constant). These insights greatly simplify power analysis by obviating the need to exhaust ancillary design parameters as would otherwise be required in a simulation-based power calculation procedure, and can possibly provide a basis for deriving optimal designs for testing effect modification.
There are additional aspects that we do not address in this article but remain important topics for future research. First, we have assumed equal cluster sizes to arrive at the main results. In a two-level CRT, Tong and others (2021) recently developed a correction factor for the variance formula of the HTE estimator under variable cluster sizes and found that the impact of cluster size variation is minimal with an participant-level effect modifier but can be more substantial with a cluster-level effect modifier. We anticipate these findings can be generalizable to three-level designs, although a careful derivation is needed to obtain the explicit correction factors when only the number of participants varies across subclusters, or only the number of subclusters varies across clusters, or both. Second, our design expressions developed under the LM-ANCOVA model are at best an approximation for three-level designs with a binary outcome. Analytical design formulas for powering the HTE test with a binary outcome that explicitly acknowledge the binomial variance structure warrant additional research. Finally, it would be worthwhile to generalize our results to further accommodate random covariate effects as an additional source of random variation. In general, the asymptotic variance expression tends to be analytically less tractable under random coefficients models and therefore requires a separate development.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Contributor Information
Fan Li, Department of Biostatistics, Yale University School of Public Health, New Haven, CT 06510, USA.
Xinyuan Chen, Department of Mathematics and Statistics, Mississippi State University, MS 39762, USA.
Zizhong Tian, Division of Biostatistics and Bioinformatics, Department of Public Health Sciences, Pennsylvania State University, Hershey, PA 17033, USA.
Denise Esserman, Department of Biostatistics, Yale University School of Public Health, New Haven, CT 06510, USA.
Patrick J Heagerty, Department of Biostatistics, University of Washington, Seattle, WA 98195, USA.
Rui Wang, Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA 02115, USA and Department of Population Medicine, Harvard Pilgrim Health Care Institute and Harvard Medical School, Boston, MA 02215, USA.
Software
R code for implementing the proposed methods, simulations, and data examples are available at https://github.com/BillyTian/code_3levelHTE.
Supplementary material
Supplementary material is available at http://biostatistics.oxfordjournals.org.
Funding
Research in this article was supported by a Patient-Centered Outcomes Research Institute Award (PCORI
(PCORI Award ME-2020C3-21072). This work was also partially supported by the Yale Clinical and Translational Science Award (UL1TR001863). The statements presented in this article are solely the responsibility of the authors and do not necessarily represent the views of PCORI
Award ME-2020C3-21072). This work was also partially supported by the Yale Clinical and Translational Science Award (UL1TR001863). The statements presented in this article are solely the responsibility of the authors and do not necessarily represent the views of PCORI or its Board of Governors or Methodology Committee.
or its Board of Governors or Methodology Committee.
References
- Brookes, S. T., Whitely, E., Egger, M., Smith, G. D., Mulheran, P. A., and Peters, T. J. (2004). Subgroup analyses in randomized trials: risks of subgroup-specific analyses: power and sample size for the interaction test. Journal of Clinical Epidemiology 57, 229–236. [DOI] [PubMed] [Google Scholar]
- Cunningham, T. and Johnson, R. (2016). Design effects for sample size computation in three-level designs. Statistical Methods in Medical Research 25, 505–519. [DOI] [PubMed] [Google Scholar]
- Dong, N., Kelcey, B. and Spybrook, J. (2018). Power analyses for moderator effects in three-level cluster randomized trials. The Journal of Experimental Education 86, 489–514. [Google Scholar]
- Gill, T.M., Bhasin, S., Reuben, D.B., Latham, N.K., Araujo, K., Ganz, D.A., Boult, C., Wu, A.W., Magaziner, J., Alexander, N. and Wallace, R.B. (2021). Effect of a multifactorial fall injury prevention intervention on patient well-being: the stride study. Journal of the American Geriatrics Society 69, 173–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heo, M. and Leon, A. (2008). Statistical power and sample size requirements for three level hierarchical cluster randomized trials. Biometrics 64, 1256–1262. [DOI] [PubMed] [Google Scholar]
- Jukes, M.C., Turner, E.L., Dubeck, M.M., Halliday, K.E., Inyega, H.N., Wolf, S., Zuilkowski, S.S. and Brooker, S.J. (2017). Improving literacy instruction in Kenya through teacher professional development and text messages support: A cluster randomized trial. Journal of Research on Educational Effectiveness 10, 449–481. [Google Scholar]
- Li, F., Lokhnygina, Y., Murray, D.M., Heagerty, P.J. and DeLong, E.R. (2016). An evaluation of constrained randomization for the design and analysis of group-randomized trials. Statistics in Medicine 35, 1565–1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li, F., Turner, E. and Preisser, J. (2018). Sample size determination for gee analyses of stepped wedge cluster randomized trials. Biometrics 74, 1450–1458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, D. and Blitstein, J. (2003). Methods to reduce the impact of intraclass correlation in group-randomized trials. Evaluation Review 27, 79–103. [DOI] [PubMed] [Google Scholar]
- Pinheiro, J. and Bates, D. (2006). Mixed-Effects Models in S and S-PLUS. New York: Springer Science & Business Media. [Google Scholar]
- Raudenbush, S. (1997). Statistical analysis and optimal design for cluster randomized trials. Psychological Methods 2, 173. [DOI] [PubMed] [Google Scholar]
- Shieh, G. (2009). Detecting interaction effects in moderated multiple regression with continuous variables power and sample size considerations. Organizational Research Methods 12, 510–528. [Google Scholar]
- Starks, M.A., Sanders, G.D., Coeytaux, R.R., Riley, I.L., Jackson, L.R., Brooks, A.M., Thomas, K.L., Choudhury, K.R., Califf, R.M. and Hernandez, A.F. (2019). Assessing heterogeneity of treatment effect analyses in health-related cluster randomized trials: a systematic review. PLoS One 14, e0219894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teerenstra, S., Lu, B., Preisser, J.S., Van Achterberg, T. and Borm, G.F. (2010). Sample size considerations for GEE analyses of three-level cluster randomized trials. Biometrics 66, 1230–1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong, G., Esserman, D. and Li, F. (2021). Accounting for unequal cluster sizes in designing cluster randomized trials to detect treatment effect heterogeneity. Statistics in Medicine, 41, 1376–1396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, R. and Ware, J. (2013). Detecting moderator effects using subgroup analyses. Prevention Science 14, 111–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, L. and Tsiatis, A. (2001). Efficiency study of estimators for a treatment effect in a pretest–posttest trial. The American Statistician 55, 314–321. [Google Scholar]
- Yang, S., Li, F., Starks, M.A., Hernandez, A.F., Mentz, R.J. and Choudhury, K.R. (2020). Sample size requirements for detecting treatment effect heterogeneity in cluster randomized trials. Statistics in Medicine 39, 4218–4237. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.