Short abstract
Algorithms that take advantage of repeated measurements yield more accurate and more stable clusters.
Abstract
Clustering is a common methodology for the analysis of array data, and many research laboratories are generating array data with repeated measurements. We evaluated several clustering algorithms that incorporate repeated measurements, and show that algorithms that take advantage of repeated measurements yield more accurate and more stable clusters. In particular, we show that the infinite mixture model-based approach with a built-in error model produces superior results.
Background
The two most frequently performed analyses on gene-expression data are the inference of differentially expressed genes and clustering. Clustering is a useful exploratory technique for gene-expression data as it groups similar objects together and allows the biologist to identify potentially meaningful relationships between the objects (either genes or experiments or both). For example, in the work of Eisen et al. [1] and Hughes et al. [2], cluster analysis was used to identify genes that show similar expression patterns over a wide range of experimental conditions in yeast. Such genes are typically involved in related functions and are frequently co-regulated (as demonstrated by other evidence such as shared promoter sequences and experimental verification). Hence, in these examples, the function(s) of gene(s) could be inferred through 'guilt by association' or appearance in the same cluster(s).
Another common use of cluster analysis is to group samples by relatedness in expression patterns. In this case, the expression pattern is effectively a complex phenotype and cluster analysis is used to identify samples with similar and different phenotypes. Often, there is the additional goal of identifying a small subset of genes that are most diagnostic of sample differences. For example, in the work of Golub et al. [3] and van't Veer et al. [4], cluster analysis was used to identify subsets of genes that show different expression patterns between different types of cancers.
There are numerous algorithms and associated programs to perform cluster analysis (for example, hierarchical methods [5], self-organizing maps [6], k-means [7] and model-based approaches [8-10]) and many of these techniques have been applied to expression data (for example [1,11-14]). Whereas one might anticipate that some algorithms are inherently better for cluster analysis of 'typical' gene-expression data, nearly every software vendor is compelled to provide access to most published methods. Hence, the biologist wishing to perform cluster analysis is faced with a dizzying array of algorithmic choices and little basis on which to make a choice. In addition, in nearly all published cases, cluster analysis is performed on gene-expression data for which no estimates of error are available - for example, the expression data do not contain repeated measurements for a given data point. Such algorithms do not take full advantage of repeated data when it is available. In this paper we address two questions. First, how well do different clustering algorithms perform on both real and synthetic gene expression data? And second, can we improve cluster quality by using algorithms that take advantage of information from repeated measurements?
Introduction to cluster analysis
A dataset containing objects to be clustered is usually represented in one of two formats: the data matrix and the similarity (or distance) matrix. In a data matrix, rows usually represent objects to be clustered (typically genes), and columns usually represent features or attributes of the objects (typically experiments). An entry in the data matrix usually represents the expression level or expression ratio of a gene under a given experiment. The similarity (or distance) matrix contains the pairwise similarities (or dissimilarities) between each pair of objects (genes or experiments).
There are many similarity measures that can be used to compute the similarity or dissimilarity between a pair of objects, among which the two most popular ones for gene expression data are correlation coefficient and Euclidean distance. Correlation is a similarity measure, that is, a high correlation coefficient implies high similarity, and it captures the directions of change of two expression profiles. Euclidean distance is a dissimilarity measure, that is, a high distance implies low similarity, and it measures both the magnitudes and directions of change between two expression profiles.
Most clustering algorithms take the similarity matrix as input and create as output an organization of the objects grouped by similarity to each other. The most common algorithms are hierarchical in nature. Hierarchical algorithms define a dendrogram (tree) relating similar objects in the same subtrees. In agglomerative hierarchical algorithms (such as average linkage and complete linkage), each object is initially assigned to its own subtree (cluster). In each step, similar subtrees (clusters) are merged to form the dendrogram. Cluster similarity can be computed from the similarity matrix or the data matrix (see Sherlock [15] or Sharan et al. [16] for reviews of popular clustering algorithms for gene-expression data).
Once a clustering algorithm has grouped similar objects (genes and samples) together, the biologist is then faced with the task of interpreting these groupings (or clusters). For example, if a gene of unknown function is clustered together with many genes of similar, known function, one might hypothesize that the unknown gene also has a related function. Or, if biological sample 'A' is grouped with other samples that have similar states or diagnoses, one might infer the state or diagnosis of sample 'A'. However, before one does subsequent laboratory work to confirm a hypothesis or, more important, makes a diagnosis based on the results of cluster analysis, a few questions need to be asked. The first is how reproducible are the clustering results with respect to re-measurement of the data. Then, what is the likelihood that the grouping of the unknown sample or gene of interest with other known samples or genes is false (due to noise in the data, inherent limitations of the data or limitations in the algorithm)? And finally, is there a better algorithm that will reduce errors in clustering results?
Related work
Kerr and Churchill [17] applied an analysis of variance model and bootstrapping to array data to assess stability of clusters (for example, 'if one re-measured the data and did the same analysis again, would the same genes/samples group together?'). In their approach, the original data was re-sampled using variability estimates and cluster analysis was performed using the re-sampled data. This post-hoc analysis uses variability estimates to provide a good indication of cluster stability. However, this method does not improve the overall clustering results, it only provides an indication of the reproducibility of the clusters with a given dataset and algorithm.
Hughes et al. [2] analyzed their yeast datasets using the commercial software package Resolver (Rosetta Inpharmatics, Kirkland, WA). Resolver was developed with a built-in error model that is derived from repeated data obtained on the array platform of interest. Resolver uses this error model and available repeated data to estimate the error in expression ratios for each gene sampled. In addition, as described below and in [2], Resolver's clustering algorithms use the error estimates to weigh the similarity measures. This results in lower weights for data points with lower confidence in the cluster analysis. The net result of this treatment (as we show below) is an improvement in both cluster accuracy and cluster stability.
Medvedovic et al. [18] have taken a different approach by adopting the Bayesian infinite mixture model (IMM) to incorporate repeated measurements in cluster analysis. They postulated a probability model for gene-expression data that incorporates repeated data, and estimated the posterior pairwise probabilities of coexpression with a Gibbs sampler. They showed that the estimated posterior pairwise distance allowed for easy identification of unrelated objects. These posterior pairwise distances can be clustered using average linkage or complete linkage hierarchical algorithms.
Our contributions
We have implemented several approaches to take advantage of repeated measurements in cluster analysis and performed an empirical study evaluating clustering results using both real and synthetic gene-expression datasets. We tested several different clustering algorithms and similarity measure combinations on the same datasets and evaluated the quality of each approach using the same criteria. We also assessed four different approaches to clustering repeated array data: clustering the averaged expression levels over the repeated measurements; using variability estimates in similarity measures (assigning low weights to noisy data points); clustering the repeated measurements as individual data points and assigning them to the same subtrees in agglomerative hierarchical algorithms; and an IMM-based approach with built-in error models for repeated data. We use two assessment criteria to evaluate clustering results: cluster accuracy (comparing clustering results to known external knowledge of the data); and cluster stability (the consistency of objects clustered together on synthetic remeasured data). In addition, we extended the IMM-based approach and the variability-weighted approach. We also created synthetic array datasets with error distributions taken from real data. These synthetic data in which the clusters are known are crucial for the development and testing of novel clustering algorithms.
Over a variety of clustering algorithms, we showed that array data with repeated measurements yield more accurate and more stable clusters. When repeated measurements are available, both the variability-weighted similarity approach and the IMM-based approach improve cluster accuracy and cluster stability to a greater extent than the simple approach of averaging over the repeated measurements. The model-based approaches (hierarchical model-based algorithm [8] and the IMM approach [18]) consistently produce more accurate and more stable clusters.
Results
Overview of our empirical study
In our empirical study, we compare the quality of clustering results from a variety of algorithms on array data with repeated measurements. We use two methods to assess cluster quality: cluster accuracy and cluster stability. External validation compares clustering results to known independent external knowledge of which objects (genes, experiments or both) should cluster together [19]. A clustering result that agrees with the external knowledge is assumed to be accurate. However, for most biological data, there is little or no a priori knowledge of this type. We also evaluate the stability of clusters with respect to synthetic remeasured array data. That is, if one remeasures the array data, how often are objects clustered together in the original data assigned to the same clusters in the remeasured data?
In this section, we discuss the clustering algorithms implemented, approaches to clustering repeated measurements, and the real and synthetic datasets used in our empirical study. We will also discuss assessment of cluster quality in greater detail. Finally, we present and discuss results of our study.
Test algorithms and similarity measures
We studied the performance of a wide variety of clustering algorithms, including several agglomerative hierarchical algorithms (average linkage, centroid linkage, complete linkage and single linkage), a divisive hierarchical algorithm called DIANA [20], k-means [7], a graph-theoretic algorithm called CAST [21], a finite Gaussian mixture model-based hierarchical clustering algorithm from MCLUST [8], and an IMM-based approach [18]. Agglomerative hierarchical clustering algorithms successively merge similar objects (or subtrees) to form a dendrogram. To evaluate cluster quality, we obtain clusters from the dendrogram by stopping the merging process when the desired number of clusters (subtrees) is produced. The objects in these subtrees form the resulting clusters. Except for the two model-based approaches, all other clustering algorithms require a pairwise similarity measure. We used both correlation and Euclidean distance in our empirical study.
How to cluster array data with repeated measurements
Average over repeated measurements
The simplest approach is to compute the average expression levels over all repeated measurements for each gene and each experiment, and store these average expression levels in the raw data matrix. The pairwise similarities (correlation or distance) can be computed using these average expression values. This is the approach taken in the vast majority of published reports for which repeated measurements are available.
Variability-weighted similarity measures
The averaging approach does not take into account the variability in repeated measurements. Hughes et al. [2] proposed an error-weighted clustering approach that uses error estimates to weigh expression values in pairwise similarities such that expression values with high error estimates are down-weighted. These error-weighted pairwise similarities are then used as inputs to clustering algorithms. Hughes et al. [2] developed an error model that assigns relatively high error estimates to genes that show greater variation in their repeated expression levels than other genes at similar abundance in their control experiments. In our empirical study, we use variability estimates instead of error estimates in the weighted similarity measures. Intuitively, gene expression levels that show larger variations over the repeated measurements should be assigned lower confidence (weights). We use either the standard deviation (SD) or coefficient of variation (CV) as variability estimates. Let us illustrate this approach with an example: suppose our goal is to compute the variability-weighted correlation of two genes G1 and G2. For each experiment, we compute the SD or CV over the repeated measurements for these two genes. Experiments with relatively high variability estimates (SD or CV) are down-weighted in the variability-weighted correlation of G1 and G2 (see Materials and methods for mathematical definitions of these weighted similarities).
Hierarchical clustering of repeated measurements
An alternative idea is to cluster the repeated measurements as individual objects in hierarchical clustering algorithms. The idea is to initialize the agglomerative algorithm by assigning repeated measurements of each object to the same subtrees in the dendrogram. In each successive step, two subtrees containing repeated measurements are merged. This approach of forcing repeated measurements into the same subtrees is abbreviated as FITSS (forcing into the same subtrees). In addition to heuristically based hierarchical algorithms (such as average linkage, complete linkage, centroid linkage and single linkage), we also investigate the performance of clustering repeated data with MCLUST-HC, which is a model-based hierarchical clustering algorithm from MCLUST [8].
IMM-based approach
Medvedovic et al. [18] postulated a probability model (an infinite Gaussian mixture model) for gene-expression data which incorporates repeated data. Each cluster is assumed to follow a multivariate normal distribution, and the measured repeated expression levels follow another multivariate normal distribution. They used a Gibbs sampler to estimate the posterior pairwise probabilities of coexpression. These posterior pairwise probabilities are treated as pairwise similarities, which are used as inputs to clustering algorithms such as average linkage or complete linkage hierarchical algorithms. They showed that these posterior pairwise probabilities led to easy identification of unrelated objects, and hence are superior to other pairwise similarity measures such as Euclidean distance.
The model published in Medvedovic et al. [18] assumes that the variance between repeated measurements of the same genes is homogeneous across all experiments. We call this model the spherical model. We extended the IMM approach to include an elliptical model, in which repeated measurements may have different variance across the experiments. In other words, genes may have different noise levels in the spherical model, while both genes and experiments may have different noise levels in the elliptical model.
Table 1 summarizes the clustering algorithms and similarity measures implemented in our empirical study, and the corresponding methods to cluster repeated data.
Table 1.
Summary of various clustering approaches used in our empirical study
| Clustering algorithms | Similarity measures | Approach to repeated data |
| Hierarchical agglomerative (average linkage, centroid linkage, complete linkage, single linkage) | Correlation/distance | Average over repeated measurements variability-weighted similarity. Force into the same subtree (FITSS)* |
| k-means | Correlation/distance | Average over repeated measurements variability-weighted similarity |
| CAST | Correlation/distance | Average over repeated measurements variability-weighted similarity |
| DIANA (hierarchical divisive) | Correlation/distance | Average over repeated measurements variability-weighted similarity |
| MCLUST-HC† | None | Average over repeated measurements. Force into the same subtree (FITSS)* |
| IMM | None | Built-in error models (spherical, elliptical) |
*FITSS refers to clustering the repeated measurements as individual objects and force the repeated measurements into the same subtrees. †MCLUST-HC denotes a model-based hierarchical clustering algorithm as implemented in the hcVVV function in the 2002 version of MCLUST.
Datasets
Assessment of cluster accuracy requires datasets for which there is independent knowledge of which objects should cluster together. For most biological data, there is little or no a priori knowledge of this type. In addition, to develop and test clustering algorithms that incorporate repeated measurements, we require datasets for which repeated measurements or error estimates are available. Unfortunately, very few publicly available datasets meet both criteria. Repeated microarray measurements are, unfortunately, still rare in published data. In addition, one rarely has a priori knowledge of which objects should cluster together. This is especially the case when we are grouping in the gene dimension. To overcome these limitations, we used both real and synthetic datasets in our empirical study. Some of these data will be described in the following sections (and see Materials and methods for details).
Completely synthetic data
Because independent external knowledge is often unavailable on real data, we created synthetic data that have error distributions derived from real array data. We use a two-step process to generate synthetic data. In the first step, data are generated according to artificial patterns such that the true class of each object is known. We created six equal-sized classes, of which four are sine waves shifted in phase relative to each other (a periodic pattern) and the remaining two classes are represented by linear functions (non-periodic). In the second step, error is added to the synthetic patterns using an experimentally derived error distribution. The error for each data point is randomly sampled (with replacement) from the distribution of standard deviations of log ratios over the repeated measurements on the yeast galactose data (described below). The error-added data are generated from a random normal distribution with mean equal to the value of the synthetic pattern (from the first step), and SD equal to the sampled error. The signal-to-noise of the synthetic data is adjusted by linearly scaling the error before adding it to the pattern. We generate multiple synthetic datasets with 400 data points, 20 attributes, 1, 4 or 20 repeated measurements and 2 different levels of signal-to-noise (low and high noise levels). In our synthetic data, all genes in each class have identical patterns (before error is added). The cluster structure of real data will, in general, be less distinguishable than that of these synthetic data. Hence, it is of interest to study the performance of various clustering approaches as a function of noise level in the synthetic data. Figure 1a,1b shows the expression profiles of the classes in typical datasets with four repeated measurements at low and high noise levels respectively.
Figure 1.
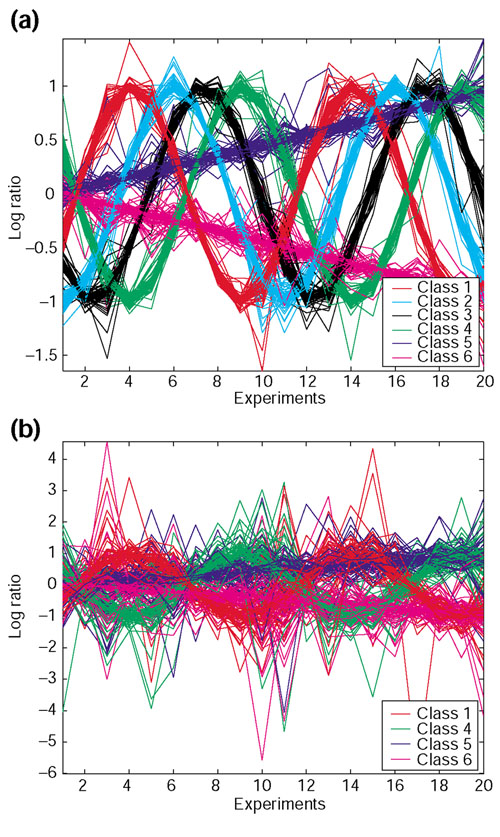
Expression profiles of the classes in typical completely synthetic datasets with four repeated measurements. (a) Low noise level; (b) high noise level. For each class, the log ratios are plotted against the experiment numbers, and each class is shown in a different color. There are four sine (periodic) classes with different phase shifts and two linear (non-periodic) classes. Only four (out of six) classes are shown in (b) for clarity.
Real data: yeast galactose data
In the yeast galactose data of Ideker et al. [22], four replicate hybridizations were performed for each cDNA array experiment. We used a subset of 205 genes that are reproducibly measured, whose expression patterns reflect four functional categories in the Gene Ontology (GO) listings [23] and that we expect to cluster together. On this data, our goal is to cluster the genes, and the four functional categories are used as our external knowledge. That is, we evaluate algorithm performance by how closely the clusters reproduce these four functional categories.
Synthetic remeasured data
To generate synthetic remeasured array data to evaluate cluster stability, we need an error model that describes repeated measurements. Ideker et al. [24] proposed an error model for repeated cDNA array data in which the measured fluorescent intensity levels in each of the two channels are related to their true intensities by additive, multiplicative and random error parameters. The multiplicative error parameters represent errors that are proportional to the true intensity, while the additive error parameters represent errors that are constant with respect to the true intensity. The measured intensity levels in the two channels are correlated such that genes at higher intensities have higher correlation. Ideker et al. [24] estimated these parameters (additive, multiplicative and correlation parameters) from repeated cDNA array data using maximum likelihood, and showed that this model gives reasonable estimates of the true expression intensities with four repeated measurements. We used this error model to estimate the true intensity for each gene, and the correlation, additive and multiplicative error parameters on the yeast galactose data. We generate synthetic remeasured data by generating the random error components in the model from the specified random distributions.
Assessment of cluster quality
Cluster accuracy
To assess algorithm performance, we need a statistic that indicates the agreement between the external knowledge and the clustering result. A clustering result can be considered as a partition of objects into groups. In all subsequent discussion, the term 'class' is used to refer to the external knowledge, while the term 'cluster' refers to the partitions created by the algorithm. Assuming known categories (classes) of objects are available, we can compare clustering results by assessing the agreement of the clusters with the classes. Unfortunately, the results of a given cluster analysis may merge partitions that the external knowledge indicates should be separate or may create additional partitions that should not exist. Hence, comparison of clusters with classes is not as simple as counting which objects are placed in the 'correct' partitions. In fact, with some datasets and algorithms, there is no obvious relationship between the classes and the clusters.
The adjusted Rand index [25] is a statistic designed to assess the degree of agreement between two partitions. On the basis of an extensive empirical study, Milligan and Cooper [26] recommended the adjusted Rand index as the measure of agreement even when comparing partitions with different numbers of clusters. The Rand index [27] is defined as the fraction of agreement, that is, the number of pairs of objects that are either in the same groups in both partitions or in different groups in both partitions, divided by the total number of pairs of objects. The Rand index lies between 0 and 1. When the two partitions agree perfectly, the Rand index is 1. The adjusted Rand index [25] adjusts the score so that its expected value in the case of random partitions is 0. A high adjusted Rand index indicates a high level of agreement between the classes and clusters.
Cluster stability
A few recent papers suggested that the quality of clusters could be evaluated via cluster stability, that is, how consistently objects are clustered together with respect to synthetic remeasured data. The synthetic remeasured data is created by randomly perturbing the original data using error parameters derived from repeated measurements. For example, Kerr and Churchill [17] and Li and Wong [28] generated randomly perturbed data from cDNA and oligonucleotide arrays respectively to identify objects that are consistently clustered.
In our empirical study, we assess the level of agreement of clusters from the original data with clusters from the synthetic remeasured data by computing the average adjusted Rand index over all the synthetic datasets. We also compute the average adjusted Rand index between all pairs of clustering results from the randomly remeasured data. A high average adjusted Rand index implies that the clusters are stable with respect to data perturbations and remeasurements. The external knowledge is not used in computing cluster stability.
Completely synthetic data at low noise level
Table 2a,2b shows selected results on cluster accuracy and cluster stability on the completely synthetic datasets with four simulated repeated measurements. Table 2a,2b show results from average linkage, complete linkage and centroid linkage hierarchical algorithms, k-means, MCLUST-HC (a hierarchical model-based clustering algorithm from MCLUST) and IMM. Both single linkage and DIANA produce very low-quality and unstable clusters and their adjusted Rand indices are not shown. For each clustering approach, we produced six clusters (which is the number of classes). The results from CAST are not shown because the input parameter cannot be tuned to produce exactly six clusters in many cases. The FITSS column refers to the method of forcing repeated measurements into the same subtrees. Because k-means is not hierarchical, its results are not available (NA) under the FITSS column. Both centroid linkage hierarchical algorithm and k-means algorithm require the raw data matrix as input, so we cannot apply these two algorithms to cluster the posterior pairwise probabilities from the IMM approach.
Table 2.
Cluster accuracy and stability on the completely synthetic data with four repeated measurements at low noise level
| (a) Cluster accuracy* | ||||||
| Algorithm | Similarity measure/model | Average | SD-weighted | CV-weighted | FITSS | IMM |
| Average linkage | Elliptical | NA | NA | NA | NA | 0.957 (0.089) |
| Complete linkage | Elliptical | NA | NA | NA | NA | 0.957 (0.090) |
| MCLUST-HC | NA | 0.930 (0.100) | NA | NA | 0.902 (0.123) | NA |
| Average linkage | Distance | 0.877 (0.191) | 0.927 (0.100) | 0.876 (0.192) | 0.804 (0.155) | NA |
| Centroid linkage | Distance | 0.840 (0.178) | 0.927 (0.100) | 0.927 (0.100) | 0.840 (0.178) | NA |
| k-means | Distance | 0.877 (0.191) | 0.927 (0.100) | 0.876 (0.192) | NA | NA |
| Average linkage | Spherical | NA | NA | NA | NA | 0.926 (0.102) |
| Complete linkage | Distance | 0.925 (0.102) | 0.876 (0.192) | 0.925 (0.103) | 0.840 (0.179) | NA |
| Complete linkage | Spherical | NA | NA | NA | NA | 0.897 (0.088) |
| Centroid linkage | Correlation | 0.765 (0.115) | 0.575 (0.179) | 0.527 (0.141) | 0.765 (0.115) | NA |
| Average linkage | Correlation | 0.764 (0.114) | 0.576 (0.201) | 0.597 (0.210) | 0.718 (0.222) | NA |
| k-means | Correlation | 0.764 (0.114) | 0.707 (0.140) | 0.652 (0.116) | NA | NA |
| Complete linkage | Correlation | 0.755 (0.116) | 0.584 (0.189) | 0.599 (0.194) | 0.609 (0.201) | NA |
| (b) Cluster stability † | ||||||
| Algorithm | Similarity measure/model | Average | SD-weighted | CV-weighted | FITSS | IMM |
| Average linkage | Distance | 0.970 (0.055) | 0.998 (0.003) | 0.998 (0.002) | 0.979 (0.018) | NA |
| Centroid linkage | Distance | 0.984 (0.025) | 0.998 (0.002) | 0.986 (0.027) | 0.984 (0.025) | NA |
| k-means | Distance | 0.954 (0.062) | 0.998 (0.003) | 0.967 (0.070) | NA | NA |
| Average linkage | Correlation | 0.958 (0.054) | 0.832 (0.095) | 0.854 (0.060) | 0.984 (0.025) | NA |
| Complete linkage | Distance | 0.968 (0.041) | 0.923 (0.131) | 0.981 (0.037) | 0.918 (0.055) | NA |
| Average linkage | Elliptical | NA | NA | NA | NA | 0.961 (0.081) |
| Complete linkage | Elliptical | NA | NA | NA | NA | 0.960 (0.083) |
| Centroid linkage | Correlation | 0.959 (0.054) | 0.861 (0.119) | 0.866 (0.026) | 0.959 (0.054) | NA |
| k-means | Correlation | 0.958 (0.054) | 0.693 (0.144) | 0.634 (0.098) | NA | NA |
| Complete linkage | Correlation | 0.947 (0.067) | 0.580 (0.140) | 0.671 (0.100) | 0.915 (0.049) | NA |
| MCLUST-HC | NA | 0.935 (0.089) | NA | NA | 0.916 (0.066) | NA |
| Average linkage | Spherical | NA | NA | NA | NA | 0.852 (0.089) |
| Complete linkage | Spherical | NA | NA | NA | NA | 0.779 (0.091) |
*Each entry shows the average adjusted Rand index of the corresponding clustering approach with the six classes. We ran our experiments on five randomly generated synthetic datasets, and show the average results with the SD of the adjusted Rand index in brackets. A high average adjusted Rand index represents close agreement with the classes on average. †Each entry shows the average adjusted Rand index of the original clustering result with clusters from remeasured data. The SD of the average adjusted Rand indices over five sets of randomly generated synthetic remeasured data is shown in brackets. A high average adjusted Rand index means that clusters from remeasured data are in close agreement with clusters from the original data. The external knowledge is not used in evaluating cluster stability. For both parts of the table, the maximum average adjusted Rand index of each row is shown in bold. The algorithms (rows) are sorted in descending order of the maximum average adjusted Rand index in each row.
In terms of cluster accuracy, the elliptical model of IMM produced the highest level of agreement (adjusted Rand index = 0.957) with the six classes, and the hierarchical model-based clustering algorithm (MCLUST-HC) also produced clusters with high agreement (adjusted Rand index = 0.930) with the six classes. Within the same clustering algorithm, different similarity measures and different methods to deal with repeated measurements yield different cluster accuracy. For example, average linkage hierarchical algorithm produced more accurate clusters with Euclidean distance (variability-weighted or average over-repeated measurements) than correlation. The variability-weighted similarity approach produced more accurate clusters using SDs as the variability estimates than using the CVs. It is also interesting to note that SD-weighted correlation produced relatively low-quality clusters, whereas SD-weighted distance produced relatively accurate clusters. The FITSS approach of forcing repeated measurements into the same subtrees in hierarchical clustering algorithms does not yield high cluster accuracy.
In terms of cluster stability, most clustering approaches yield stable clusters (with average adjusted Rand indices above 0.900) except the spherical model of the IMM approach. This is because the spherical model assumes homogeneous variability for each gene across the experiments (which is not true on this synthetic data).
Completely synthetic data at high noise level
Tables 3a,3b show the results on cluster accuracy and cluster stability on the completely synthetic data with four repeated measurements at high noise level. Even at a higher noise level, the elliptical model of IMM produced much more accurate clusters (average adjusted Rand index = 0.911 and 0.910 using average linkage or complete linkage) than all other approaches (SD-weighted distance and k-means produced an average adjusted Rand index of 0.801). In general, the relative rankings of various clustering approaches at high noise level are similar to those at low noise level, except that the model-based hierarchical approach (MCLUST-HC) produced less accurate clusters than the SD-weighted distance approach using the heuristically based algorithms.
Table 3.
Cluster accuracy and stability on the completely synthetic data with four repeated measurements at high noise level
| (a) Cluster accuracy* | ||||||
| Algorithm | Similarity measure/model | Average | SD-weighted | CV-weighted | FITSS | IMM |
| Average linkage | Elliptical | NA | NA | NA | NA | 0.911 (0.122) |
| Complete linkage | Elliptical | NA | NA | NA | NA | 0.910 (0.123) |
| k-means | Distance | 0.326 (0.136) | 0.801 (0.037) | 0.666 (0.098) | NA | NA |
| Complete linkage | Distance | 0.498 (0.113) | 0.798 (0.144) | 0.660 (0.098) | 0.014 (0.030) | NA |
| Centroid linkage | Distance | 0.000 (0.000) | 0.762 (0.113) | 0.315 (0.156) | 0.000 (0.000) | NA |
| Average linkage | Distance | 0.000 (0.000) | 0.713 (0.217) | 0.256 (0.071) | 0.000 (0.000) | NA |
| MCLUST-HC | NA | 0.608 (0.173) | NA | NA | 0.480 (0.052) | NA |
| Average linkage | Spherical | NA | NA | NA | NA | 0.589 (0.212) |
| Complete linkage | Spherical | NA | NA | NA | NA | 0.559 (0.358) |
| k-means | Correlation | 0.556 (0.121) | 0.499 (0.130) | 0.394 (0.194) | NA | NA |
| Average linkage | Correlation | 0.389 (0.151) | 0.519 (0.159) | 0.378 (0.081) | 0.291 (0.130) | NA |
| Complete linkage | Correlation | 0.450 (0.122) | 0.518 (0.159) | 0.484 (0.156) | 0.341 (0.112) | NA |
| Centroid linkage | Correlation | 0.358 (0.097) | 0.261 (0.101) | 0.215 (0.096) | 0.358 (0.097) | NA |
| (b) Cluster stability | ||||||
| Algorithm | Similarity measure/model | Average | SD-weighted | CV-weighted | FITSS | IMM |
| Average linkage | Elliptical | NA | NA | NA | NA | 0.948 (0.099) |
| Average linkage | Distance | 0.208 (0.075) | 0.932 (0.049) | 0.812 (0.138) | 0.381 (0.103) | NA |
| Centroid linkage | Distance | 0.211 (0.087) | 0.920 (0.097) | 0.779 (0.169) | 0.211 (0.087) | NA |
| Complete linkage | Elliptical | NA | NA | NA | NA | 0.912 (0.113) |
| k-means | Distance | 0.508 (0.153) | 0.882 (0.165) | 0.686 (0.147) | NA | NA |
| Average linkage Correlation | Correlation | 0.721 (0.060) | 0.782 (0.083) | 0.692 (0.103) | 0.855 (0.015) | NA |
| Complete linkage | Distance | 0.429 (0.105) | 0.803 (0.159) | 0.582 (0.083) | 0.126 (0.025) | NA |
| Centroid linkage | Correlation | 0.731 (0.130) | 0.497 (0.109) | 0.430 (0.099) | 0.731 (0.130) | NA |
| k-means | Correlation | 0.719 (0.070) | 0.515 (0.046) | 0.382 (0.132) | NA | NA |
| Average linkage | Spherical | NA | NA | NA | NA | 0.674 (0.094) |
| MCLUST-HC | NA | 0.584 (0.093) | NA | NA | 0.527 (0.026) | NA |
| Complete linkage | Correlation | 0.580 (0.044) | 0.497 (0.094) | 0.493 (0.057) | 0.353 (0.046) | NA |
| Complete linkage | Spherical | NA | NA | NA | NA | 0.472 (0.288) |
*Each entry shows the average adjusted Rand index of the corresponding clustering approach with the six classes. We ran our experiments on five randomly generated synthetic datasets, and show the average results with the standard deviation of the adjusted Rand index in brackets. A high average adjusted Rand index represents close agreement with the classes on average. †Each entry shows the average adjusted Rand index of the original clustering result with clusters from remeasured data. The standard deviation of the average adjusted Rand indices over five sets of randomly generated synthetic remeasured data is shown in brackets. A high average adjusted Rand index means that clusters from remeasured data are in close agreement with clusters from the original data. The external knowledge is not used in evaluating cluster stability. In both parts of the table, the maximum average adjusted Rand index of each row is shown in bold. The algorithms (rows) are sorted in descending order of the maximum average adjusted Rand index in each row.
At high noise level, the approach of averaging over the repeated measurements produced relatively low-quality clusters, especially when Euclidean distance is used (for example, both average linkage and centroid linkage produced an average adjusted Rand index of 0). In addition, the quality of clusters produced using Euclidean distance deteriorates more rapidly than correlation at high noise level. The SD-weighted distance approach produced substantial improvement in cluster quality over the approach of averaging over repeated measurements using the same algorithms at high noise level.
In terms of cluster stability (see Table 3b), the following three approaches yield average adjusted Rand index above 0.900: the elliptical model of the IMM approach; the SD-weighted distance using average linkage and centroid linkage. It is interesting that the spherical model of the IMM approach produces unstable clusters at both high and low noise levels.
Yeast galactose data
Table 4a,4b show selected results on cluster accuracy and cluster stability on real yeast galactose data. The true mean column in Table 4a refers to clustering the true mean data (estimated with the error model suggested by Ideker et al. [24]) instead of clustering the repeated measurements. For each clustering approach, we produced four clusters (which is the number of functional categories). The highest level of cluster accuracy (adjusted Rand index = 0.968 in Table 4a) was obtained with several algorithms: centroid linkage hierarchical algorithm with Euclidean distance and averaging over the repeated measurements; hierarchical model-based algorithm (MCLUST-HC); complete linkage hierarchical algorithm with SD-weighted distance; and IMM with complete linkage. Clustering with repeated measurements produced more accurate clusters than clustering with the estimated true mean data in most cases.
Table 4.
Cluster accuracy and stability on yeast galactose data
| (a) Cluster accuracy* | |||||||
| Algorithm | Similarity measure/model | Average | SD-weighted | CV-weighted | FITSS | True mean | IMM |
| Centroid linkage | Distance | 0.968 | 0.849 | 0.802 | 0.968 | 0.159 | NA |
| MCLUST-HC | NA | 0.968 | NA | NA | 0.968 | 0.806 | NA |
| Complete linkage | Distance | 0.957 | 0.968 | 0.957 | 0.643 | 0.695 | NA |
| Complete linkage | Spherical | NA | NA | NA | NA | NA | 0.968 |
| Complete linkage | Elliptical | NA | NA | NA | NA | NA | 0.968 |
| Centroid linkage | Correlation | 0.942 | 0.807 | 0.753 | 0.942 | 0.942 | NA |
| k-means | Correlation | 0.871 | 0.640 | 0.827 | NA | 0.897 | NA |
| Average linkage | Spherical | NA | NA | NA | NA | NA | 0.897 |
| Average linkage | Elliptical | NA | NA | NA | NA | NA | 0.897 |
| Average linkage | Distance | 0.858 | 0.858 | 0.847 | 0.869 | 0.159 | NA |
| Average linkage | Correlation | 0.866 | 0.817 | 0.841 | 0.865 | 0.857 | NA |
| k-means | Distance | 0.857 | 0.857 | 0.767 | NA | 0.159 | NA |
| Complete linkage | Correlation | 0.677 | 0.724 | 0.730 | 0.503 | 0.744 | NA |
| (b) Cluster stability † | |||||||
| Algorithm | Similarity measure/model | Average | SD-weighted | CV-weighted | FITSS | IMM | |
| Complete linkage | Elliptical | NA | NA | NA | NA | 0.998 | |
| Complete linkage | Spherical | NA | NA | NA | NA | 0.991 | |
| Average linkage | Distance | 0.820 | 0.985 | 0.914 | 0.650 | NA | |
| MCLUST-HC | NA | 0.963 | NA | NA | 0.916 | NA | |
| Complete linkage | Distance | 0.927 | 0.937 | 0.830 | 0.441 | NA | |
| Centroid linkage | Distance | 0.893 | 0.924 | 0.841 | 0.893 | NA | |
| Average linkage | Spherical | NA | NA | NA | NA | 0.923 | |
| k-means | Distance | 0.905 | 0.867 | 0.798 | NA | NA | |
| Average linkage | Elliptical | NA | NA | NA | NA | 0.895 | |
| Centroid linkage | Correlation | 0.889 | 0.758 | 0.644 | 0.889 | NA | |
| Average linkage | Correlation | 0.842 | 0.842 | 0.855 | 0.828 | NA | |
| k-means | Correlation | 0.799 | 0.709 | 0.781 | NA | NA | |
| Complete linkage | Correlation | 0.655 | 0.700 | 0.666 | 0.577 | NA | |
*Each entry shows the adjusted Rand index of the corresponding clustering approach with the four functional categories. A high adjusted Rand index represents close agreement with the external knowledge. †Each entry shows the average adjusted Rand index of the original clustering result with clusters from ten synthetic re-measured datasets. A high average adjusted Rand index means that clusters from synthetic remeasured data are in close agreement with clusters from the original dataset. For both parts of the table, the maximum adjusted Rand index of each row is shown in bold. The algorithms (rows) are sorted in descending order of the maximum average adjusted Rand index in each row. The external knowledge is not used in evaluating cluster stability.
Table 4b shows that different clustering approaches lead to different cluster stability with respect to remeasured data. Similar to the results from the completely synthetic data, Euclidean distance tends to produce more stable clusters than correlation (both variability-weighted and average over repeated measurements). Clustering results using FITSS were less stable than the variability-weighted approach and the averaging over repeated measurements approach.
SD produced more accurate and more stable clusters than CV in the variability-weighted similarity approach, especially when Euclidean distance is used. In addition, the model-based approaches (MCLUST-HC and IMM) produced relatively accurate and stable clusters on this data.
Effect of different numbers of repeated measurements
To study the effect of different numbers of repeated measurements on the performance of various clustering approaches, we generated completely synthetic data with different numbers of simulated repeated measurements for each data point. Specifically, we generated 1, 4, or 20 repeated measurements at both the low and high noise levels. The quality of clustering results on datasets with higher numbers of repeated measurements is usually higher (Table 5). For example, using the same algorithms and same similarity measures cluster accuracy is considerably improved with synthetic datasets of four repeated measurements relative to datasets with no repeated measurement. With 20 repeated measurements, Euclidean distance is less sensitive to noise, and the SD-weighted distance approach produces comparable cluster accuracy to IMM. This is probably because the variability estimates computed over 20 repeated measurements are much more robust than those with four repeated measurements. Nevertheless, the elliptical model of IMM consistently produced the most accurate clusters over different numbers of simulated repeated measurements and different noise levels.
Table 5.
Cluster accuracy on the completely synthetic datasets with different numbers of repeated measurements
| Number of repeated measurements | Noise | Similarity measure/mode | Average | SD-weighted | IMM |
| 1 | Low | Correlation | 0.680 | NA | NA |
| 1 | Low | Distance | 0.789 | NA | NA |
| 1 | Low | Spherical | NA | NA | 0.804 |
| 1 | Low | Elliptical | NA | NA | 0.804 |
| 1 | High | Correlation | 0.259 | NA | NA |
| 1 | High | Distance | 0.000 | NA | NA |
| 1 | High | Spherical | NA | NA | 0.395 |
| 1 | High | Elliptical | NA | NA | 0.395 |
| 4 | Low | Correlation | 0.764 | 0.576 | NA |
| 4 | Low | Distance | 0.877 | 0.927 | NA |
| 4 | Low | Spherical | NA | NA | 0.926 |
| 4 | Low | Elliptical | NA | NA | 0.957 |
| 4 | High | Correlation | 0.389 | 0.519 | NA |
| 4 | High | Distance | 0.000 | 0.713 | NA |
| 4 | High | Spherical | NA | NA | 0.589 |
| 4 | High | Elliptical | NA | NA | 0.911 |
| 20 | Low | Correlation | 0.854 | 0.701 | NA |
| 20 | Low | Distance | 0.891 | 0.964 | NA |
| 20 | Low | Spherical | NA | NA | 0.962 |
| 20 | Low | Elliptical | NA | NA | 0.957 |
| 20 | High | Correlation | 0.602 | 0.651 | NA |
| 20 | High | Distance | 0.590 | 0.819 | NA |
| 20 | High | Spherical | NA | NA | 0.688 |
| 20 | High | Elliptical | NA | NA | 0.953 |
Cluster accuracy on the completely synthetic data with different numbers of repeated measurements and different noise levels using average linkage hierarchical clustering algorithm. For each number of repeated measurements and noise level, the highest average adjusted Rand index is shown in bold. As we generated five random synthetic datasets, the results shown are averaged over five synthetic datasets.
Discussion
We showed that different approaches to clustering array data produce clusters of varying accuracy and stability. We also showed that the incorporation of error estimates estimated from repeated measurements improves cluster quality. We also show that the elliptical model of IMM consistently produced more accurate clustering results than other approaches using both real and synthetic datasets, especially at high noise levels. The variability-weighted approach tends to produce more accurate and more stable clusters when used with Euclidean distance than the simple approach of averaging over the repeated measurements. In addition, the SD-weighted distance usually produces more accurate and more stable clusters than the CV-weighted distance. In general, the results are consistent across both real and synthetic datasets.
Limitations
In all the above results, we produced clustering results in which the number of clusters was set equal to the number of classes. In agglomerative hierarchical clustering algorithms (for example, average linkage), we successively merged clusters until the desired number of clusters, K, is reached, and considered the K subtrees as our K clusters, whereas in other algorithms the number of clusters was provided as input. A concern is that using a fixed number of clusters will force different classes into the same cluster owing to one or more outliers occupying a cluster. In such cases, the adjusted Rand index might improve with a larger number of clusters.
However, we chose to use a fixed number of clusters for several reasons. First, with the exception of the model-based algorithms, all other clustering algorithms (directly or indirectly) require the number of clusters as input. Even with the model-based algorithms, the number of clusters can only be estimated. In MCLUST-HC, the number of clusters can be estimated using a statistical score (see [29]). In the IMM approach, the number of clusters can be estimated from the posterior distribution of clustering results (see [18]). Second, it is very difficult, if not impossible, to compare cluster quality over a range of different clustering algorithms when the number of clusters is not fixed. Finally, increasing the number of clusters does not always yield better clusters or higher Rand indices (data not shown).
There are also some limitations with the external criteria for the real datasets used in our empirical study. With the yeast galactose data, we used a subset of 205 genes, which contains many genes previously shown to be strongly co-regulated and which reflect four functional categories in the GO listings [23]. This subset of genes may be biased in the sense that they are not chosen entirely independently of their expression patterns. In addition, there may be good biological reasons why some genes in the chosen set of 205 should not cluster into groups segregated by the GO classifications.
Distributions of variability-weighted similarity measures
The essence of the variability-weighted similarity approach is that the pairwise similarities take into account the variability in repeated measurements. In an attempt to understand the effect of variability between repeated measurements on these similarity measures, we computed the correlation coefficients between all pairs of genes in the yeast galactose data and plotted the distribution of the fraction of gene pairs against correlation coefficient by averaging over repeated measurements and against SD-weighted correlation in Figure 2. The distribution of CV-weighted correlation is similar to that of SD-weighted.
Figure 2.
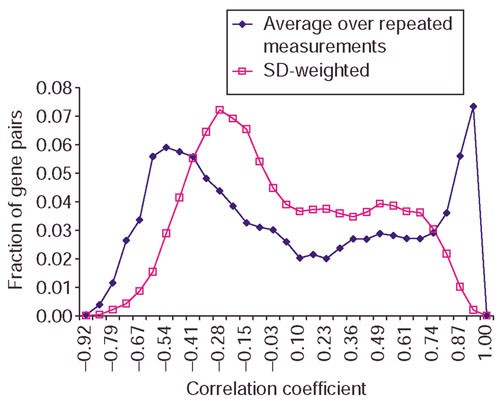
Distribution of the fraction of gene pairs against correlation coefficient. Correlation coefficients are computed from averaging over repeated measurements and using SD over repeated measurements as weights on the yeast galactose data. There are more gene pairs with correlation coefficients around 0 and fewer gene pairs with correlation coefficients near 1 when SD-weighted correlation is used.
Figure 2 shows that when SD is used in variability-weighted correlation, there are more gene pairs with correlation coefficients around 0 and fewer gene pairs with correlation coefficients near 1. Figure 3 shows the distribution of Euclidean distance by averaging over the repeated measurements and the SD-weighted distance on the same data. There are more gene pairs with distance close to zero when variability estimates are used to weigh distance. This shows that weighing similarity measures with variability estimates produces more conservative estimates of pairwise similarities.
Figure 3.
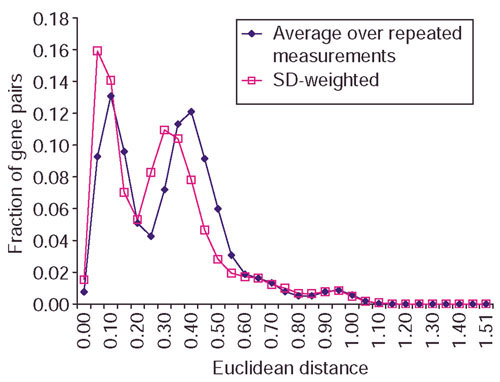
Distribution of the fraction of gene pairs against Euclidean distance. Euclidean distances are computed from averaging over repeated measurements and using SD over repeated measurements as weights on the yeast galactose data. There are more gene pairs with Euclidean distances near 0 when SD-weighted distance is used.
Moreover, we showed that on average, variability-weighted similarity measures (both correlation and distance) computed from repeated measurements produced pairwise similarities closer to the true similarity than similarity measures computed from data with no repeated measurement. In our simulation experiment, we computed the true pairwise correlation and distance between all pairs of genes on the estimated true mean yeast galactose data (using the error model in Ideker et al. [24]). We also computed the variability-weighted correlation and distance between all pairs of genes on the synthetic remeasured data generated from the same error parameters and mean intensities as the yeast galactose data. In addition, we computed correlation and distance using only one of the repeated measurements in the remeasured data. Then, we compared the average deviation of the variability-weighted similarity measures from the truth, and the average deviation of the similarity measures on the data with no repeated measurements to the truth (see Materials and methods for detailed results).
Modified variability-weighted approach
One of the drawbacks of the current definitions of the variability-weighted similarity approach is that only noisy experiments are down-weighted, whereas noisy genes are not. Suppose we have a dataset in which some genes are noisier than others, but the noise levels across the experiments stay relatively constant. In this scenario, the variability-weighted approach would not improve cluster quality. Genes expressed at low levels are frequently expressed at low levels across all experiments and usually have higher variability (see Figure 4). Hence, unless we filter out low-intensity genes, the weighting methods developed by Hughes et al. ([2] and see Materials and methods) will not down-weight these genes. We attempted to correct for this effect by removing the normalizing factor in the definition of variability-weighted distance (see Materials and methods for mathematical definitions). This improved the clustering accuracy when Euclidean distance was used. However, we did not see improvement using this method with correlation as the similarity measure.
Figure 4.
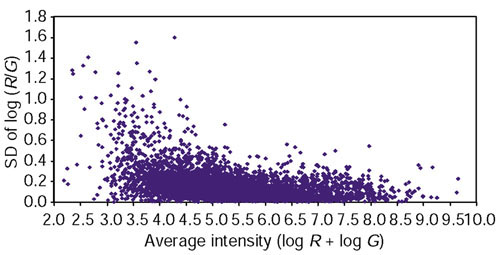
Distribution of error plotted against intensity. The SDs over the log ratios from repeated measurements are plotted against the average intensities over repeated measurements in a typical experiment on the yeast galactose data.
Conclusions
Our work shows that clustering array data with repeated measurements can significantly improve cluster quality, especially when the appropriate clustering approach is applied. Different clustering algorithms and different methods to take advantage of repeated measurements (not surprisingly) yield different clusters with different quality. In practice, many clustering algorithms are frequently run on the same dataset and the results most consistent with previous beliefs are published. A better approach would be to use a clustering algorithm shown to be the most accurate and stable when applied to data with similar signal-to-noise and other characteristics as the data of interest. In this work, we analyzed both real and completely synthetic data with many algorithms to assess cluster accuracy and stability. In general, the model-based clustering approaches produce higher-quality clusters, especially the elliptical model of the IMM. In particular, the higher the noise level, the greater the performance difference between the IMM approach and other methods.
For the heuristically based approaches, average linkage hierarchical clustering algorithm combined with SD-weighted Euclidean distance also produces relatively stable and accurate clusters. On the completely synthetic data, we showed that the infinite mixture approach works amazingly well with only four repeated measurements, even at high noise levels. The variability-weighted approach works almost as well as the IMM with 20 repeated measurements. From our results on the synthetic data, we showed that there is significant improvement in cluster accuracy from one to four repeated measurements using IMM at both low and high noise levels (Table 5). However, there is no substantial improvement in cluster accuracy from 4 to 20 repeated measurements with the IMM approach (Table 5).
There are many possible directions of future work, both methodological and experimental. Because the elliptical model of IMM produces very high-quality clusters, it would be interesting to develop a similar error model in the finite model-based framework on MCLUST and to compare the performance of the finite versus infinite mixture approaches. Another practical methodological development would be to incorporate the estimation of missing data values into the model-based approaches. It would also be interesting to develop other variability-weighted similarity measures that would down-weight both noisy genes and noisy experiments.
In terms of future experimental work, we would like to evaluate the performance of various clustering algorithms on array data with repeated measurements on more real datasets. One of the difficulties we encountered is that there are very few public datasets that have both repeated measurements and external criteria available. We would greatly appreciate it if readers would provide us with access to such datasets as they become available.
Materials and methods
Datasets
Yeast galactose data
Ideker et al. [22] studied galactose utilization in yeast using cDNA arrays by deleting nine genes on the galactose utilization pathway in the presence or absence of galactose and raffinose. There are a total of 20 experiments (nine single-gene deletions and one wild-type experiment with galactose and raffinose, nine deletions and one wild-type without galactose and raffinose). Four replicate hybridizations were performed for each experiment. We used a subset of 205 genes from this data, whose expression patterns reflect four functional categories in the GO [23].
Synthetic remeasured cDNA data
Let xijr and yijr be the fluorescent intensities of the two channels (fluorescent dyes) for gene i, experiment j and repeated measurement r, where i = 1, ..., G, j = 1, .., E, r = 1, .., R. For the yeast galactose data, G is approximately 6,000, E is 20 and R is 4. Ideker et al. [24] proposed an error model for replicated cDNA array data in which the observed fluorescent intensity levels are related to their true expression levels by the following model:
![]()
where (μxij, μyij) are the true mean intensity levels for gene i under experiment j in the two channels. The multiplicative error parameters in the two channels (εxijr, εyijr) are assumed to follow the bivariate normal distribution with mean 0, SDs σεxj, σεyj and correlation ρεj. Similarly, the additive error parameters (δxijr, δyijr) are assumed to follow the bivariate normal distribution with mean 0, SDs σδxj, σδyj and correlation ρδj. The gene-independent parameters (σεxj, σεyj, ρεj, σδxj, σδyj, ρδj) and the gene-dependent parameters (μxij, μyij), where i = 1, ..., G and j = 1, ..., E, are estimated by maximum likelihood [24].
Using this error model, we estimate the true expression intensities for each gene and the gene-independent parameters for each of the 20 experiments in the yeast galactose data. From the gene independent parameters (σεxj, σεyj, ρεj, σδxj, σδyj, ρδj), we generate random (εxijr, εyijr) and (δxijr, δyijr) from the bivariate normal distributions. Hence, we can generate random remeasured data (and log ratios) using the estimated true mean intensities (μxij, μyij).
Completely synthetic data
The completely synthetic datasets consist of 400 data points (genes), 20 attributes (experiments) and 6 classes. Let φ(i,j) be the artificial pattern of gene i and experiment j before error is added, and suppose gene i belongs to class k. Four of the six classes follow the periodic sine function (φ(i,j) = sin (2πj/10 - ωk)), and the remaining two classes follow the non-periodic linear function (φ(i,j) = j/20 or φ(i,j) = -j/20), where i = 1, 2, 3, ..., 400, j = 1, 2, 3, ..., 20, k = 1, 2, 3, 4 and ωk is a random phase shift between 0 and 2π. Let X(i,j,r) be the error-added value for gene i, experiment j and repeated measurement r. Let the randomly sampled error be σij for gene i and experiment j, and X(i,j,r) is generated from a random normal distribution with mean equal to φ(i,j), and SD equal to σij.
We define the signal-to-noise ratio of a synthetic dataset to be the ratio of the range of signals (in our case, 1-(-1) = 2) to the average sampled error. For the completely synthetic data shown in Figure 1a,1b the signal-to-noise ratios are 14.3 and 2.5 respectively.
Missing data
The yeast galactose dataset [22] contains approximately 8% of missing data values. There are many possible sources of missing data values, for example, low signal-to-noise ratios, dust or scratches on slides. As the current versions of MCLUST [30] and the IMM implementation [18] do not handle missing data values, we impute the missing data values. We experimented with two imputation methods, namely model-based multiple imputation [31] as implemented in Splus, and weighted k-nearest neighbors (KNNimpute) [32]. We found that data after KNNimpute produce higher-quality clusters than data after model-based multiple imputation. Therefore, we applied KNNimpute to the yeast galactose data before applying the model-based approaches.
Notations and similarity measures
Suppose there are G genes, E experiments, and R repeated measurements. Denote the measured expression level from repeated measurement r of gene g under experiment e as Xger, where g = 1, ..., G, e = 1, ..., E and r = 1, ..., R. Let D be the raw data matrix such that D(g,e) represents the average expression level over R repeated measurements for gene g under experiment e, that is,
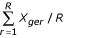 ,
,
where g = 1, ..., G, e = 1, ..., E. The correlation coefficient between a pair of genes i and j (i,j = 1, .., G) is defined as
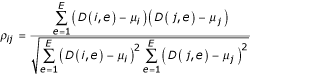
where
![]()
is the average expression level of gene i over all E experiments. The Euclidean distance between a pair of genes i and j (i,j = 1, .., G) is defined as
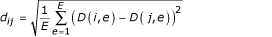 .
.
Similarly, we can define correlation and Euclidean distance between a pair of experiments by swapping the positions of the gene and experiment indices.
Variability-weighted similarity measures
Hughes et al. [2] defined error-weighted similarity measures that weight expression values with error estimates such that expression values with relatively high errors are down-weighted. Let σge be the error estimate of the expression level of gene g under experiment e, where g = 1, ..., G and e = 1, ..., E. The error-weighted correlation between a pair of genes i and j is defined as
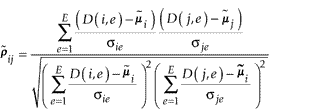
where
![]()
is the weighted average expression level of gene i. Similarly, the error-weighted Euclidean distance [2] is defined as
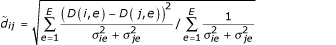 .
.
In our empirical study, variability estimates are used instead of error estimates. In particular, we use either the SD or CV over the R repeated measurements as σge. These variability-weighted similarity measures serve as inputs to many clustering algorithms.
Modified variability-weighted distance
The above definitions of variability-weighted correlation and distance down-weight noisy experiments in computing the pairwise similarity, but would not work in the case of noisy genes. Consider two pairs of genes, (X, Y) and (W, Z), such that D(X,e) = D(W,e) and D(Y,e) = D(Z,e) and σXe = σYe <<σWe = σZe for all experiments e. In other words, the expression patterns of gene X and gene W are identical, so are the patterns of gene Y and gene Z. The levels of noise (or variability) are constant across all the experiments for each pair of genes, but genes (W,Z) are much more noisy than genes (X,Y). Using the above definitions of variability-weighted similarity, 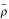 XY =
XY = 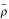 WZ and
WZ and  XY =
XY =  WZ. Intuitively, one would expect the pairwise similarity between genes (W,Z) to be lower than that of genes (X,Y) because genes (W,Z) are more noisy. We experimented with a modified definition of variability-weighted distance by removing the scaling factor in the denominator:
WZ. Intuitively, one would expect the pairwise similarity between genes (W,Z) to be lower than that of genes (X,Y) because genes (W,Z) are more noisy. We experimented with a modified definition of variability-weighted distance by removing the scaling factor in the denominator:
![]()
This modified definition tends to give slightly better clusters (see Additional data files and [33]).
Clustering algorithms
Agglomerative hierarchical algorithms
In agglomerative hierarchical clustering algorithms [5], each object is initially assigned to its own cluster (subtree), and the number of initial clusters is equal to the number of objects. Similar clusters (subtrees) are successively merged to form a dendrogram. In each merging step, the number of clusters (subtrees) is reduced by one. This merging process is repeated until the desired number of clusters, K, is produced. The objects in these K subtrees form the resulting K clusters, and the hierarchical structures of the subtrees are ignored.
Different definitions of cluster similarity yield different clustering algorithms. In a single linkage hierarchical algorithm, the cluster similarity of two clusters is the maximum similarity between a pair of genes, one from each of the two clusters. In a complete linkage hierarchical algorithm, the cluster similarity is defined as the minimum similarity between a pair of genes, one from each of the two clusters. In an average linkage hierarchical algorithm, the cluster similarity of two clusters is the average pairwise similarity between genes in the two clusters. In a centroid linkage hierarchical algorithm, clusters (subtrees) are represented by the mean vectors of the clusters, and cluster similarity is defined as the similarity between the mean vectors.
k-means
K-means [7] is a classic iterative clustering algorithm, in which the number of clusters is an input to the algorithm. Clusters are represented by centroids, which are cluster centers. The goal of k-means is to minimize the sum of distances from each object to its corresponding centroid. In each iteration, each gene is assigned to its closest centroid. After the gene reassignment, new centroids are computed. The steps of assigning genes to centroids and computing new centroids are repeated until no genes are moved between clusters. In our implementation, we use the clusters from average linkage hierarchical algorithm to compute initial centroids to start k-means.
MCLUST
The finite Gaussian mixture model-based approach assumes that each cluster follows the multivariate normal distribution with model parameters that specify the location and shape of each cluster. MCLUST [8] implements the expectation-maximization (EM) algorithm for clustering via finite Gaussian mixture models, as well as model-based hierarchical clustering algorithms, with optional cross-cluster constraints. MCLUST also includes a clustering function (hcVVV) that uses model-based hierarchical clustering to initialize the EM algorithm. Because the current version of MCLUST does not have any mechanism to incorporate repeated measurements, but does allow initializations at nontrivial partitions, we initialize the hierarchical model-based algorithm with subtrees containing repeated measurements. We use the most general model (unconstrained) for hierarchical clustering, which allows each cluster to have different volume, orientation and shape. This approach is abbreviated as MCLUST-HC.
IMM
The IMM approach uses a Gibbs sampler to estimate the posterior pairwise probabilities. The Gibbs sampler requires two sets of parameters for input: initialization parameters (random seed and the initial number of mixture components) and convergence parameters (initial annealing coefficient, the rate of 'cooling' and the 'burn-in' period). A posterior distribution with multiple peaks could result in Gibbs samplers' inability to escape from a suboptimal peak. The role of the annealing coefficient [34] is to flatten the posterior distribution of clustering results and thus alleviate the difficulty in transitioning between high-probability regions that are separated by regions of low probability, which is a common problem of Gibbs samplers in general [35]. Burn-in corresponds to the number of initial iterations that the Gibbs sampler takes to converge to the posterior distribution, and the burn-in iterations are not used in calculating posterior pairwise probabilities. We tuned the convergence parameters by running independent samplers with different initialization parameters, and chose the set of convergence parameters that yielded the highest correlation between pairwise probabilities over different runs and over different random perturbations of the data. Using this simple principle, we identified a single combination of the annealing parameters that resulted in excellent convergence in all datasets we analyzed, including some not reported in this paper. This combination consisted of the initial annealing coefficient of 0.01, rate of cooling of 0.999 and the burn-in of 10,000 iterations. For investigators analyzing their own data, we suggest that they run at least five independent Gibbs samplers with this combination of parameters from five different initial numbers of clusters and establish that all five converge to the same posterior distribution. This can be done by calculating correlation between posterior pairwise probabilities from different runs. Alternatively, the adjusted Rand index can be used for comparing clustering results generated by different runs of the Gibbs sampler. If the correlations or adjusted Rand indices suggest that all five samplers did not converge to the same solution, investigators should try increasing the annealing coefficient (to say 0.9995) and the burn-in number of iterations (to say 20,000), and repeat the process. The Readme.txt file that accompanies the IMM software describes these parameters in detail.
CAST
The cluster affinity search technique (CAST) [21] is an iterative algorithm, in which objects are added to or removed from the current cluster until there are no more similar objects to be added and no more dissimilar objects to be removed. At this point, the current cluster is assumed to be done. A new cluster is started and the iterative process of adding and removing objects is repeated until all objects are assigned to clusters. The inputs to the algorithm include the pairwise similarities and a parameter that indirectly controls the number of clusters.
DIANA
DIANA [20] is a hierarchical divisive clustering algorithm, in which we start with all objects in one cluster. In each step, clusters are successively split to form two clusters until the desired number of clusters is reached. The cluster with maximum diameter (maximum pairwise dissimilarity) is split in each step. Let us call this the current cluster. The most dissimilar element in the current cluster is identified to start a new cluster. An object in the current cluster is moved to the new cluster if the average similarity with the new cluster is higher than that with the current cluster.
Completely synthetic data with different numbers of repeated measurements
Table 5 shows some selected results produced using average linkage hierarchical algorithm on the completely synthetic data over varying numbers of repeated measurements and different noise levels. In general, increasing the number of repeated measurements increases cluster accuracy (average adjusted Rand index with respect to the six classes). The elliptical model of IMM produced superior quality of clusters, especially at high noise levels.
Simulation experiment: variability-weighted similarity
We computed the true pairwise correlation and Euclidean distance between all pairs of genes on the estimated true mean yeast galactose data. Denote the correlation between estimated true means for gene i and gene j as 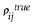 . We generated synthetic re-measured datasets using the same error parameters and true mean intensities of the yeast galactose data. Let the variability-weighted correlation for gene i and gene j be
. We generated synthetic re-measured datasets using the same error parameters and true mean intensities of the yeast galactose data. Let the variability-weighted correlation for gene i and gene j be 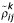 , and the correlation computed using only one of the repeated measurements, r (no repeated data) be
, and the correlation computed using only one of the repeated measurements, r (no repeated data) be 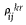 , where k is one of the randomly generated synthetic remeasured data.
, where k is one of the randomly generated synthetic remeasured data.
The column |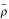 - ρtrue| in Table 6 shows the average of
- ρtrue| in Table 6 shows the average of 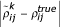 over all pairs of genes i, j, and all randomly remeasured datasets k, while the column |ρr - ρtrue| shows the average of
over all pairs of genes i, j, and all randomly remeasured datasets k, while the column |ρr - ρtrue| shows the average of 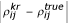 over all pairs of genes i, j, all randomly remeasured datasets k, and all repeated measurements r. The corresponding results using distance are also shown in Table 6, which shows that on average the variability-weighted similarities are closer to the 'truth' than similarities computed from data with no repeated measurement.
over all pairs of genes i, j, all randomly remeasured datasets k, and all repeated measurements r. The corresponding results using distance are also shown in Table 6, which shows that on average the variability-weighted similarities are closer to the 'truth' than similarities computed from data with no repeated measurement.
Table 6.
Simulation results
| Number of remeasured datasets | Number of repeated measurements | Correlation | |
Correlation |ρr - ρtrue| | Distance | |
Distance |dr - dtrue| |
| 100 | 4 | 0.01383 | 0.01454 | 0.00379 | 0.00476 |
| 100 | 10 | 0.01044 | 0.01440 | 0.00364 | 0.00472 |
| 10 | 20 | 0.05298 | 0.08162 | 0.02029 | 0.02653 |
| 10 | 100 | 0.04591 | 0.08147 | 0.01997 | 0.02660 |
The average deviation of the variability-weighted similarity from the true similarity (|![]() - ρtrue| and |
- ρtrue| and |![]() - dtrue|), and the average deviation of the true similarity from the similarity measures computed with no repeated measurements (|ρr - ρtrue| and |dr - dtrue|).
- dtrue|), and the average deviation of the true similarity from the similarity measures computed with no repeated measurements (|ρr - ρtrue| and |dr - dtrue|).
Additional data files
Datasets (both real and synthetic) and the software (executables and documentation) used in this work are available as additional files and from our website [33]. They comprise additional results (Additional data file 1), documentation (Additional data file 2), bytecode files for hierarchical agglomerative algorithms (Additional data file 3), bytecode files for k-means (Additional data file 4), bytecode files for hierarchical agglomerative algorithms using FITSS (Additional data file 5), subset of 205 genes from yeast data (Additional data files 6, 7, 8), and the completely synthetic datasets (Additional data files 9, 10, 11, 12, 13, 14). Our website [33] also has external links to publicly available software, yeast galactose data and lung cancer data.
Supplementary Material
Additional results
Documentation
Bytecode files for hierarchical agglomerative algorithms
Bytecode files for k-means
Bytecode files for hierarchical agglomerative algorithms using FITSS
A subset of 205 genes from yeast data
A subset of 205 genes from yeast data
A subset of 205 genes from yeast data
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset
Acknowledgments
Acknowledgements
We thank Vesteinn Thorsson for providing us with the yeast galactose data, and Chris Fraley and Adrian Raftery for their valuable comments. We also acknowledge the following publicly available software packages: MCLUST [30], Vera and SAM [24], KNNimpute [32], dCHIP [36] and the BioConductor project. R.E.B. and K.Y.Y. are supported by NIH-NIDDK grant 5U24DK058813-02. M.M. is supported by NIEHS grants 2P30 ES06096-11 and ES04908-12.
Contributor Information
Ka Yee Yeung, Email: [email protected].
Roger E Bumgarner, Email: [email protected].
References
- Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci USA. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes TR, Marton MJ, Jones AR, Roberts CJ, Stoughton R, Armour CD, Bennett HA, Coffey E, Dai H, He YD, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- van't Veer LJ, Dai H, van de Vijver MJ, He YD, Hart AA, Mao M, Peterse HL, van der Kooy K, Marton MJ, Witteveen AT, et al. Gene expression profiling predicts clinical outcome of breast cancer. Nature. 2002;415:530–536. doi: 10.1038/415530a. [DOI] [PubMed] [Google Scholar]
- Hartigan JA. Clustering Algorithms. New York: John Wiley and Sons; 1975. [Google Scholar]
- Kohonen T. Self-organizing Maps. Berlin/Heidelberg: Springer-Verlag; 1997. [Google Scholar]
- MacQueen J. Some methods for classification and analysis of multivariate observations. In: University of California Press, editor. In Proc 5th Berkeley Symp Math Stat Probability. Cam LML, Neyman J; 1965. pp. 281–297. [Google Scholar]
- Fraley C, Raftery AE. Model-based clustering, discriminant analysis, and density estimation. J Am Stat Assoc. 2002;97:611–631. [Google Scholar]
- McLachlan GJ, Basford KE. Mixture Models: Inference and Applications to Clustering. New York: Marcel Dekker; 1988. [Google Scholar]
- McLachlan GJ, Peel D. Finite Mixture Models. New York: Wiley; 2000. [Google Scholar]
- Tamayo P, Slonim D, Mesirov J, Zhu Q, Kitareewan S, Dmitrovsky E, Lander ES, Golub TR. Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. Proc Natl Acad Sci USA. 1999;96:2907–2912. doi: 10.1073/pnas.96.6.2907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavazoie S, Huges JD, Campbell MJ, Cho RJ, Church GM. Systematic determination of genetic network architecture. Nat Genet. 1999;22:281–285. doi: 10.1038/10343. [DOI] [PubMed] [Google Scholar]
- McLachlan GJ, Bean RW, Peel D. A mixture model-based approach to the clustering of microarray expression data. Bioinformatics. 2002;18:413–422. doi: 10.1093/bioinformatics/18.3.413. [DOI] [PubMed] [Google Scholar]
- Yeung KY, Fraley C, Murua A, Raftery AE, Ruzzo WL. Model-based clustering and data transformations for gene expression data. Bioinformatics. 2001;17:977–987. doi: 10.1093/bioinformatics/17.10.977. [DOI] [PubMed] [Google Scholar]
- Sherlock G. Analysis of large-scale gene expression data. Curr Opin Immunol. 2000;12:201–205. doi: 10.1016/s0952-7915(99)00074-6. [DOI] [PubMed] [Google Scholar]
- Sharan R, Elkon R, Shamir R. In Ernst Schering Workshop on Bioinformatics and Genome Analysis. Berlin: Springer-Verlag; 2002. Cluster analysis and its applications to gene expression data. pp. 83–108. [DOI] [PubMed] [Google Scholar]
- Kerr MK, Churchill GA. Bootstrapping cluster analysis: assessing the reliability of conclusions from microarray experiments. Proc Natl Acad Sci USA. 2001;98:8961–8965. doi: 10.1073/pnas.161273698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medvedovic M, Sivaganesan S. Bayesian infinite mixture model based clustering of gene expression profiles. Bioinformatics. 2002;18:1194–1206. doi: 10.1093/bioinformatics/18.9.1194. [DOI] [PubMed] [Google Scholar]
- Jain AK, Dubes RC. Algorithms for Clustering Data Englewood Cliffs. NJ: Prentice Hall; 1988. [Google Scholar]
- Kaufman L, Rousseeuw PJ. Finding Groups in Data: An Introduction to Cluster Analysis. New York: John Wiley and Sons; 1990. [Google Scholar]
- Ben-Dor A, Shamir R, Yakhini Z. Clustering gene expression patterns. J Comput Biol. 1999;6:281–297. doi: 10.1089/106652799318274. [DOI] [PubMed] [Google Scholar]
- Ideker T, Thorsson V, Ranish JA, Christmas R, Buhler J, Eng JK, Bumgarner RE, Goodlett DR, Aebersold R, Hood L. Integrated genomic and proteomic analyses of a systemically perturbed metabolic network. Science. 2001;292:929–934. doi: 10.1126/science.292.5518.929. [DOI] [PubMed] [Google Scholar]
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, et al. Gene Ontology: tool for the unification of biology. Nat Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ideker T, Thorsson V, Siegel AF, Hood L. Testing for differentially-expressed genes by maximum-likelihood analysis of microarray data. J Comput Biol. 2000;7:805–817. doi: 10.1089/10665270050514945. [DOI] [PubMed] [Google Scholar]
- Hubert L, Arabie P. Comparing partitions. J Classification. 1985;2:193–218. [Google Scholar]
- Milligan GW, Cooper MC. A study of the comparability of external criteria for hierarchical cluster analysis. Multivar Behav Res. 1986;21:441–458. doi: 10.1207/s15327906mbr2104_5. [DOI] [PubMed] [Google Scholar]
- Rand WM. Objective criteria for the evaluation of clustering methods. J Am Stat Assoc. 1971;66:846–850. [Google Scholar]
- Li C, Wong WH. Model-based analysis of oligonucleotide arrays: model validation, design issues and standard error application. Genome Biol. 2001;2:research0032.1–0032.11. doi: 10.1186/gb-2001-2-8-research0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banfield JD, Raftery AE. Model-based Gaussian and non-Gaussian clustering. Biometrics. 1993;49:803–821. [Google Scholar]
- Fraley C, Raftery AE. MCLUST: software for model-based clustering, discriminant analysis, and density estimation. Technical Report No 415 Seattle, WA: Department of Statistics, University of Washington. 2002. ftp://ftp.u.washington.edu/public/mclust/tr415.pdf
- Schafer JL. Analysis of Incomplete Multivariate Data. London: Chapman and Hall; 1997. [Google Scholar]
- Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Botstein D, Altman RB. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17:520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- University of Washington (Microbiology): public microarray data download site http://www.expression.washington.edu/public
- Medvedovic M, Succop P, Shukla R, Dixon K. Clustering mutational spectra via classification likelihood and Markov chain Monte Carlo algorithm. J Agric, Biol Environ Stat. 2001;6:19–37. [Google Scholar]
- Jennison C. Discussion on the meeting on the Gibbs sampler and other Markov chain Monte Carlo methods. J R Stat Soc Ser B (Methodological) 1993;55:54–56. [Google Scholar]
- Li C, Wong WH. Model-based analysis of oligonucleotide arrays: expression index computation and outlier detection. Proc Natl Acad Sci USA. 2001;98:31–36. doi: 10.1073/pnas.011404098. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional results
Documentation
Bytecode files for hierarchical agglomerative algorithms
Bytecode files for k-means
Bytecode files for hierarchical agglomerative algorithms using FITSS
A subset of 205 genes from yeast data
A subset of 205 genes from yeast data
A subset of 205 genes from yeast data
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset
A completely synthetic dataset


