Optimal design for informative protocols in xenograft tumor growth inhibition experiments in mice

Giulia Lestini; France Mentré; Paolo Magni

doi:10.1208/s12248-016-9924-z

. Author manuscript; available in PMC: 2018 Mar 1.

Published in final edited form as: AAPS J. 2016 Jun 15;18(5):1233–1243. doi: 10.1208/s12248-016-9924-z

Optimal design for informative protocols in xenograft tumor growth inhibition experiments in mice

Giulia Lestini ^1,^2,^*, France Mentré ¹, Paolo Magni ²

PMCID: PMC5660732 PMID: 27306546

Abstract

Tumor growth inhibition (TGI) models are increasingly used during preclinical drug development in oncology for the in vivo evaluation of antitumor effect. Tumor sizes are measured in xenografted mice, often only during and shortly after treatment, thus preventing correct identification of some TGI model parameters. Our aims were i) to evaluate the importance of including measurements during tumor regrowth; ii) to investigate the proportions of mice included in each arm. For these purposes, optimal design theory based on the Fisher information matrix implemented in PFIM4.0 was applied. Published xenograft experiments, involving different drugs, schedules and cell lines, were used to help optimize experimental settings and parameters using the Simeoni TGI model. For each experiment, a two-arm design, i.e. control vs treatment, was optimized with or without the constraint of not sampling during tumor regrowth, i.e. “short” and “long” studies, respectively. In long studies, measurements could be taken up to 6 grams of tumor weight, whereas in short studies the experiment was stopped three days after the end of treatment. Predicted relative standard errors were smaller in long studies than in corresponding short studies. Some optimal measurement times were located in the regrowth phase, highlighting the importance of continuing the experiment after the end of treatment. In the four-arm designs, the results showed that the proportions of control and treated mice can differ. To conclude, making measurements during tumor regrowth should become a general rule for informative preclinical studies in oncology, especially when a delayed drug effect is suspected.

Introduction

The in vivo evaluation of antitumor effect is an important step of preclinical drug development in oncology. Experimental models in rodents have been developed in recent decades to assess the antitumor effect of a new compound (1). Among in vivo preclinical studies, the most popular is the xenograft model (2), that is the human tumor transplanted into animals. Most recent xenograft experiments have been performed on athymic nude mice (3), which are mice with reduced capacity to reject foreign cells. The common practice is either to implant tumor fragments subcutaneously or to inject tumor cells into the flank of athymic mice (4). When the tumor has reached the desired volume, mice are randomized into control and treatment arms receiving either a vehicle (control arm) or the compound to be tested at different dose levels or with different drug administration schedules (treatment arms). Tumor sizes are measured at repeated time points during the study and specific metrics are then calculated to assess tumor activity in the different arms (5). The main purpose of those studies is to quantify the inhibition of tumor growth provided by the treatment, which depends on dose, time and dosing regimen (4,6). For this reason, mathematical models able to dissect system-related from drug-related parameters have been proposed to describe and predict the antitumor effect of a new compound. We chose to use the Simeoni tumor growth inhibition(TGI) model (7,8)for in vivo evaluation of antitumor effect in xenografted mice. The Simeoni TGI model is a pharmacokinetic-pharmacodynamic (PKPD) model in which the dose of an anticancer compound is linked, through concentration, to the inhibition of tumor growth. By searching for papers that cite the model and looking at author affiliations, we observed that the model is widely used in both industry and academia. It has been used for analysis of hundreds of single-agent experiments in preclinical studies in industry(4,9)and was recently used to evaluate interaction effects when drugs are administered in combination (9). Xenograft data may be analyzed by various methods. One method is the “naïve pooled data” (NPD) approach (10) in which the model can be fitted using standard nonlinear regression. In this approach parameter estimation is straightforward but does not model all sources of variability, so no information about the differences between subjects is considered. Nonlinear mixed effects models (NLMEMs) (11–13) are a popular alternative approach. This method is more complex than NPD, but has been increasingly used in the biomedical field as it keeps all the data of all subjects.

Before performing the experiment, it is important to define an appropriate design, which implies there has to be a good balance between the number of subjects, the number of samples per subject and the timing of sampling, and the doses, in line with the experimental conditions. As reported in (4), until now preclinical studies have been rarely designed using optimal design strategies. When planning a study it is crucial to choose a good design as it can play an important part in parameter estimation (14), and poor design can lead to inconclusive studies. As recommended in (4), designing experiments with optimal design strategies would lead to more informative studies and ensure more precise parameter estimates for the selected model.

There are two main approaches to design evaluation. The first, by trial simulation, involves parameter estimation using numerous simulated datasets and thus is a time-consuming method (15). The second approach, which avoids simulation, relies on the Cramer-Rao inequality, which states that the inverse of the Fisher information matrix (FIM) is the lower bound of the variance-covariance matrix of any unbiased parameter estimate. Several criteria based on FIM have been proposed. One is the D-optimality criterion, which consists in maximizing the determinant of FIM, considering all model parameters. In NLMEMs there is no closed form of the likelihood and thus of FIM, therefore an approximation method must be used. Mentré et al. (16) first introduced the first-order (FO) linearization method and further approximations have been developed since. FIM is implemented in several optimal design software programs for NLMEMs(17,18). These are: PFIM (19,20), PopED(21), PopDes(22) and POPT (23). These tools allow for design evaluation/optimization by computing FIM and the D-optimality criterion (24), and it was shown in (17) that they all provided the same answer when using the same FO approximation of FIM.

The aim of this study was thus to apply optimal design strategies to the xenograft experiments analyzed with the Simeoni TGI model, to derive some general rules that could be used as guidelines for future preclinical studies in this field, and to assess the impact of suboptimal design. More specifically, in vivo tumor size measurements in xenograft experiments are often taken only during and shortly after treatment(25,26), possibly preventing correct identification of some parameters of TGI models(27). The first objective of this study was to assess quantitatively in two-arm experiments, i.e. one control and one treatment arm, the difference in terms of precision of parameter estimation of taking samples only during and shortly after the treatment administration, or also later, during the tumor regrowth phase, by using standard nonlinear regression or an NLMEM. The main idea behind this thought is that the time efficacy index (TEI), which is a secondary parameter of the Simeoni TGI model that is linked to the drug potency parameter, is estimated better when considering regrowth (8). Although many institutions have already had the common intuition that sampling during tumor regrowth would allow for more informative studies, to our knowledge this was never proven before.

The second objective of this work was to investigate the influence of including arms with different doses or different drug administration schedules in the trials, as well as the number of treated and control mice to be used in the experiments, when using NLMEMs.

Materials and Methods

Experimental Settings

Several xenograft experiments were selected from the literature (7,28) involving various drugs with various modes of action, different drug administration schedules and cell lines. The compounds tested in the experiments considered were paclitaxel and 5-fluorouracil (5-FU), which are available on the market, and two drugs (Drug A and Drug B) synthesized by Pharmacia (7). The A2780 human ovarian carcinoma and HCT116 colon carcinoma cell lines were used. Tumor fragments were subcutaneously implanted into the left flank of athymic nude mice and, one week after tumor inoculation, mice bearing a palpable tumor were randomized into control and treatment arms. Tumor dimensions were measured using calipers and the tumor masses w were calculated at each time t with the following formula reported in (7):

w = \frac{l \cdot z}{2} ρ

(1)

where l is the length of the tumor measured in mm and z is the tumor squared width expressed inmm². It was assumed that the density ρ was equal to 1 mg/mm³ for tumor tissue such that the tumor weight w is expressed in mg.

A schematic description of selected experiments is reported in Table I. Experimental settings for experiments 1, 2, 9 and 10 were taken from (28), whereas the information for the other experiments was found in (7).

Table I.

Experimental and optimal designs settings, and results for “long” (first row) and “short” (second row) studies in the two-arm experiments, i.e. control and treatment arm, selected from reference (7) and (28)

Experimental settings											Optimal design settings and results
Exp	Drug	Daily Dose (mg/kg)	Treatment		Dosing frequency	TGI Parameters^a			Ref	n	Sampling window treatment/control arms (days)	Optimal designs in treatment arm (days)	Optimal design in control arm (days)
			Starting day	Last day		Fixed effects (λ₀,λ₁,w₀, k₁,k₂)	Variance of random effects ( $ω_{λ_{0}}^{2}, ω_{λ_{1}}^{2}, ω_{k_{1}}^{2}, ω_{k_{2}}^{2}$ )	St. deviation of residual error (σ_inter, σ_slope)^b
			1	paclitaxel		30	8	16						every 4 days	0.238, 0.14, 0.049, 0.117, 6.3910⁻⁴	0.138,0.063	(28)	1	8–68/8–48 8–19/8–19	8, 28, 63, 68 8, 12, 18, 19	8, 12, 44, 48 8, 11, 18, 19
2	drug B	120	9	12	bid	0.269, 0.397, 0.022, 0.631, 2.7210⁻⁴		0.118,0.07	(28)	1	9–33/9–27 8–15/8–15	9, 15, 23, 33 8, 13, 14, 15	9, 15, 25, 27 8, 9, 14, 15
3	paclitaxel	30	13	21	every 4 days	0.311, 0.656, 0.033, 0.968, 6.2910⁻⁴		0,0.063	(7)	1	9–31/9–19 9–24/9–19	9, 15, 23, 27 9, 16, 22, 24	9, 13, 18, 19 9, 13, 18, 19
4	paclitaxel	30	8	16	every 4 days	0.273,0.814, 0.055, 0.968, 6.2910⁻⁴		0.138,0.063	(7)	1	8–30/8–18 8–19/8–18	14, 18, 26, 30 8, 11, 12, 19	8, 9, 15, 18 8, 9, 15, 18
5	5-FU	50	8	29	every 4 weeks	0.215,0.412, 0.065, 0.056, 20.2110⁻⁴		0.138,0.063	(7)	1	8–47/8–24 8–32/8–24	8, 23, 41, 47 8, 24, 28, 32	8, 12, 22, 24 8, 12, 22, 24
6	drug A	15	9	19	qd	0.349,0.363,0.010, 0.405, 3.4510⁻⁴		0.118,0.07	(7)	1	9–37/9–26 9–22/9–22	9, 21, 35, 37 9, 10, 19, 22	9, 13, 25, 26 9, 13, 21, 22
7	drug B	30	13	17	bid	0.309, 0.796, 0.034, 0.517, 2.8910⁻⁴		0,0.07	(7)	1	9–23/9–18 9–20/9–18	9, 15, 19, 23 9, 15, 19, 20	9, 14, 17, 18 9, 14, 17, 18
8	drug B	83	9	15	7-day infusion	0.369, 0.511, 0.016, 0.615, 2.9310⁻⁴		0,0.063	(7)	1	8–32/8–20 8–18/8–18	8, 18, 22, 24 8, 16, 17, 18	8, 12, 18, 20 8, 12, 17, 18
9	paclitaxel	30	8	16	every 4 days	0.238, 0.14, 0.049, 0.117, 6.3910⁻⁴	0.002, 0.177, 0.053, 1.580	0.138,0.063	(28)	4	8–68/8–48 8–19/8–19	27, 44, 48, 68 11, 12, 18, 19	8, 11, 12, 49 11, 12, 18, 19
10	drug B	120	9	12	bid	0.269, 0.397, 0.022, 0.631, 2.7210⁻⁴	0.014,0.017,2.080,0.360	0.118,0.07	(28)	7	9–33/9–27 8–15/8–15	10, 16, 22, 33 11, 13, 14, 15	10, 16, 26, 27 11, 13, 14, 15

Open in a new tab

For experiments 1–8 an individual approach was used therefore n=1 mouse was included in each arm. For the population experiments 9 and 10, n=4 and n=7 mice were included in each arm, respectively. The route was i.v. bolus for all experiments except for experiment 8, which was i.v. infusion. Inter individual variability on parameter w₀ was set to 0.

TGI parameters units are as following: λ₀(day⁻¹), λ₁(g · day⁻¹), w₀(g), k₁(day⁻¹), k₂(ng⁻¹ · ml · day⁻¹)

Parameter values for σ_inter and σ_slope were only available for the experiments in reference (28), therefore they were arbitrarily defined for the experiments from (7)

Tumor Growth Inhibition Model

The Simeoni TGI model is built based on the assumption that tumor growth follows an exponential curve in the early phases followed by linear growth (5,7). The unperturbed growth model for untreated mice is expressed with the following differential equation (7):

\frac{d w (t)}{d t} = \frac{λ_{0} \cdot w (t)}{{[1 + {(\frac{λ_{1}}{λ_{0}} \cdot w (t))}^{ψ}]}^{\frac{1}{ψ}}} w (0) = w_{0}

(2)

where w₀ is the tumor weight at inoculation time, and λ₀ and λ₁ are parameters describing the rate of exponential and linear growth, respectively. The parameter ψ is set to 20 ensuring a sharp system transfer from first-order growth (exponential) to zero-order growth (linear) (7). With this model, if the tumor weight w(t) is small the denominator of equation 2 can be approximated to 1 and then the tumor growth is given by λ₀ · w(t); whereas when w(t) is large, 1 can be neglected in the denominator and the tumor growth is approximated by λ₁. The system-related parameters of the unperturbed model are therefore: λ₀, λ₁ and w₀.

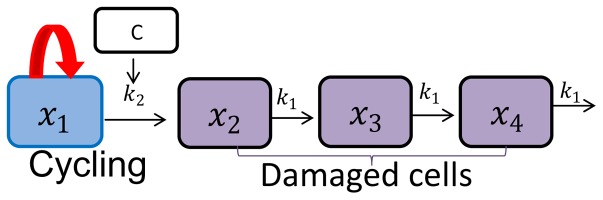
In the treatment arms the action of the antitumor compound prevents the proliferation of a proportion of tumor cells, which go through a three-stage chain at a constant rate of damage k₁, with different levels of impairment, and then, eventually, die. The antitumor potency is characterized by the constant parameter k₂, which is proportional to c(t) · x₁(t), where c(t) is the drug concentration, which can be predicted with a PK model, and x_i(t) are the proliferating cells in w(t). A schematic representation of the perturbed growth model is reported in Figure 1.

Fig. 1 — Schematic representation of Simeoni TGI model. The first box represents the proliferating cells for which the tumor growth is characterized by an exponential growth followed by a linear growth. k₂ is the parameter related to drug potency, C is the plasma concentration of the anticancer agent and k₁ is the parameter related to the rate of death of the tumor cells.

The perturbed growth model for treated mice is described with the following system of differential equations(7):

\frac{d x_{1} (t)}{d t} = \frac{λ_{0} \cdot x_{1} (t)}{{[1 + {(\frac{λ_{1}}{λ_{0}} \cdot w (t))}^{ψ}]}^{\frac{1}{ψ}}} - k_{2} \cdot c (t) \cdot x_{1} (t) \frac{d x_{2} (t)}{d t} = k_{2} \cdot c (t) \cdot x_{1} (t) - k_{1} x_{2} (t) \frac{d x_{3} (t)}{d t} = k_{1} [x_{2} (t) - x_{3} (t)] \frac{d x_{4} (t)}{d t} = k_{1} [x_{3} (t) - x_{4} (t)] w (t) = x_{1} (t) + x_{2} (t) + x_{3} (t) + x_{4} (t) c (t) = 0 for 0 < t \leq t_{0}

(3)

where t₀ represents the time of beginning of treatment. Before the start of treatment, the concentration c(t)is equal to 0 and the model follows an unperturbed growth, with w(t) = x₁(t). After time t₀, the model follows a perturbed growth and w(t) = x₁(t) + x₂(t) + x₃(t) + x₄(t).

The parameters of the perturbed growth model therefore are: λ₀, λ₁, w₀, and k₁, k₂, which are the system-related and drug-related parameters, respectively.

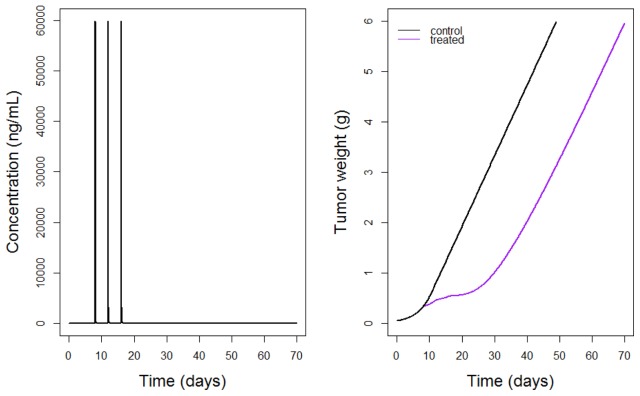
For each proposed experiment a PK model was used in order to predict the c(t) needed for the treatment arm in the TGI model. The PK model and its parameter values were taken from the literature (7,28). For experiments 1 to 7 of Table I a two-compartment model with intravenous (i.v.) bolus was used, whereas in experiment 8 a two-compartment model with continuous i.v. infusion was used. Figure 2 shows the simulated PK model and TGI model for experiments 1 and 9 of Table I.

Fig. 2 — Simulated PK (left) and PD (right) for experiments 1 and 9 of Table I. The PK is a two compartment model i.v. bolus with multiple doses administration (of 30 mg/kg given every 4 days for 3 times). The PD is the TGI model for a two-arm experiment with control arm (black curve) and treatment arm (purple curve).

Statistical Model

In standard nonlinear regression, the vector y_i of observations y_i₁, …, y_{in_i} measured from the subject i at times ξ_i = (t_i₁, … t_{in_i}) is defined with y_i = f(θ_i, ξ_i) + ε_i where f is the nonlinear structural model describing the tumor growth over time and ξ_i is the elementary design composed of n_i sampling times. θ_i is the vector of p individual parameters and ε_i is the vector of residual error following a normal distribution ε_i ~ N(0, Σ(θ, ξ_i)) with Σ(θ, ξ_i) = diag(σ_inter + σ_slope × f(θ_i, ξ_i))². σ_inter is the parameter for the additive error and σ_slope for proportional error. The individual parameters vector is γ′ = (θ_i, σ_inter, σ_slope).

In NLMEMs all samples of all individuals are analyzed simultaneously. The individual parameters θ_i for the i^th subject is modeled as θ_i = μe^η_i with a fixed effect μ, which represents the median values of the parameter in the population, and a random effect η_i ~ N(0, Ω), where $Ω = diag (ω_{1}^{2}, \dots, ω_{p}^{2})$ accounts for the between-subject variability. The population parameter vector is $Φ^{'} = (μ_{1}, \dots, μ_{p}, ω_{1}^{2}, \dots ω_{p}^{2}, σ_{inter}, σ_{slope})$ .

All parameter values used in this article are given in Table I and were estimated from real experiments in (7) for experiments 3 to 8, and in (28) for experiments 1,2,9 and 10. Moreover, experiments 1 and 2 have the same mean parameter values as experiments 9 and 10, respectively, and experiments A and B in Table II have same TGI model parameters as those of experiments 9 and 10 in Table I.

Table II.

Experimental and optimal designs settings and results in four-arm design experiments from reference (28)

Experimental settings							Optimal design settings and results

Exp	Drug	Daily Dose (mg/kg)	Treatment		Dosing frequency (Route: i.v. bolus)	Allowed sampling window (days)	Optimal design (Scenario 1)			Optimal design (Scenario 2)

			Starting day	Last day			Optimized times (days)	n (optimized)	D-optimal criterion	Optimized times (days)	n (fixed)	D-optimal criterion
A	paclitaxel	0				8–48	11, 26, 29, 41, 47, 68	6	2100	8, 11, 14, 17, 47, 49	4	1924
		20	8	16	every 4 days	8–68		0		8, 11, 14, 32, 56, 68	4
		30	8	16	every 4 days	8–68		0		8, 11, 23, 44, 47, 68	4
		40	8	16	every 4 days	8–68	8, 11, 14, 17, 47, 49	10		11, 23, 26, 29, 41, 68	4

B	drug B	0				9–27	9, 11, 17, 23, 25, 27	10	4708	9, 10, 11, 16, 26, 27	7	4643
		60	9	12	bid	9–33	9, 11, 15, 23, 31, 33	9		10, 11, 16, 22, 32, 33	7
		60	9	9	tid	9–29		0		9, 12, 14, 20, 28, 29	7
		60	9	19	qd	9–35	9, 11, 13, 21, 27, 35	9		11, 14, 22, 27, 34, 35	7

Open in a new tab

TGI parameters for experiment A and B are those of experiment 9 and 10 of Table I, respectively.

Optimal design strategy

Criterion and optimization

For optimal design we used the D-optimal criterion, which corresponds to the maximization of the determinant of the individual or population FIM, corresponding to the minimization of the confidence region associated with the individual or population parameter estimates. The reported optimality criterion is the determinant to the power 1/p, where p is the total number of estimated parameters in the model. A search for optimal measurement times was performed using the Fedorov-Wynn algorithm implemented in the R function PFIM, in the PFIM 4.0 program (19,29), in which both individual and population FIMs can be computed.

Together with the optimal design, PFIM returns the predicted relative standard error (pRSE) in % for each model parameter, and pRSE is defined as:

pRSE (p) = \frac{S E (\hat{φ})}{φ} \times 100

(4)

where SE (φ̂) is the expected standard error of parameter φ.

Two-arm designs

All experiments described in Table I were used for the first objective of the present study, that is to assess quantitatively the difference in precision of parameter estimates in two-arm experiments, when taking 4 measurement samples only during and shortly after the treatment period, compared with taking measurements also later, in the tumor regrowth phase. In experiments 1 to 8 only one mouse per arm was included in order to perform individual design optimization. This can be viewed as an NPD approach where mean data are fitted, hence assuming that they come from a single mouse. In experiments 9 and 10, 4 and 7 mice were assigned to each arm, respectively, such that population design optimization could be computed.

For each experiment two scenarios were thus considered. a “short study”, in which it was possible to measure only until three days after the end of the treatment period in order to mimic the frequently adopted setting of those preclinical studies, and a “long study”, in which measurements could be taken also later, after the end of the treatment period, during the tumor regrowth phase, but for ethical reasons only up to a tumor weight of 6 grams. Note that 6 grams is an overestimated threshold adopted to emphasize the impact on precision of parameter estimates in short versus long studies. See the discussion for more details. The two scenarios therefore only differ in the chosen range of allowed sampling times, in the optimal design settings. The parameters were used to simulate the tumor weight with and without treatment for each experiment, to define the time when a tumor weight of 6 grams was reached. Allowed sampling time ranges for the two scenarios are reported in Table I under the “Sampling window” column for both treatment and control arms, first line for the short study and second line for the long study. Note that in the long study treatment arms should have larger allowed sampling time windows compared with those for the corresponding control arms, as treated mice reached a tumor weight of 6 grams later, because of the treatment effect.

The allowed sampling times were chosen based on the time ranges defined for each experiment. In short studies, a dense grid for each day in the range was set as the allowed sampling times, except for experiment 5 in which the allowed times were allocated every other day. In long studies the allowed sampling times were allocated every other day, if the last time in the range was before day 38, every three/four days if the last time in the range was before day 50 and every four or five days for the long studies of experiments 1 and 9, in which the last allowed time was day 68.

Optimization of sampling times from the allowed sampling window was performed simultaneously in control and treatment arms for each selected experiment and for short and long studies. In the individual design optimization, for experiments 1 to 8, the model was implemented as a two responses model, each response corresponding to one arm. For experiments 9 and 10 and population design optimization, as the Fedorov-Wynn algorithm would also optimize the proportion of subjects per arm, two steps were used to get the optimal times with a fixed number of mice per arm. The model was implemented as a single response model with a two-arm design. As currently in PFIM, the same allowed sampling window should be set for the two arms—the treatment arm window was chosen, as it includes all the possible times for both arms. Optimal design was performed and the optimal times obtained were stored. For the control arm, optimal times exceeding the allowed range were replaced by the last possible times. We then performed two-arm design evaluation of all possible combinations of 4 times among the optimal times found in the previous step for a fixed number of mice in each arm. The two-arm design with the combination that led to the highest criterion was defined as the optimal design. pRSE (%) were used to compare long and short studies in all the experiments, knowing that the lower pRSE (%) would guarantee the more precise parameter estimates for the study considered.

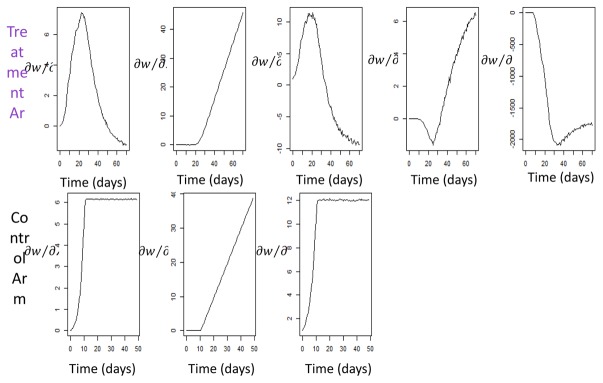
Graphs of sensitivity functions, i.e. partial derivatives of the Simeoni TGI model prediction with respect to each parameter, were used to visualize the impact of each model parameter through time. Sensitivity functions with respect to each parameter provide knowledge on the design values (e.g. tumor weight measurement time) leading to the greatest information, i.e. the times for which the square of the sensitivity function is maximal. Figure 3 displays the graph of sensitivity functions for experiments 1 and 9. The PFIM input and output files for experiment 1 are reported in the supplementary material.

Fig. 3 — Graphs of sensitivity functions of tumor weight (w) versus time for TGI parameters in treatment arm and control arm obtained for experiments 1 and 9 of Table I.

Four-arm designs

The second objective of this study was to apply optimal design in the context of four-arm designs, i.e. one control and three treatment arms, with i) different doses per arm or ii) different drug administration schedules per arm. The experiments used for this purpose were experiments A and B reported in Table II, which were analyzed by an NLMEM. Experiment A had three different doses of 20, 30 and 40 mg/kg in each treatment arm, respectively, whereas experiment B had three different drug administration schedules: i.v. bolus bid, i.e. twice a day, in treatment arm 1, i.v. bolus tid, i.e. three times a day, in treatment arm 2 and i.v. bolus qd, i.e. once daily, in treatment arm 3. The allowed sampling time ranges for treatment and control arms were defined as before, using the criterion of stopping the study when the tumor weight reached 6 grams.

In a first scenario, 6 sampling times from the allowed sampling times were optimized with the Fedorov-Wynn algorithm. The initial design for experiment A consisted of 4 mice per arm at 6 times; 8, 17, 20, 26, 29, 35 days, arbitrarily chosen. The same was true for experiment B, where the initial design consisted of 7 mice per arm at the 6 times: 11, 13, 15, 17, 19, 21 days. Using the Fedorov-Wynn algorithm in PFIM for optimization could lead to some arms being dropped from the experiment. The model was implemented as a one-response model and in a first scenario the four-arm design was optimized using the same approach that was applied to optimize the two-arm design for experiments 9 and 10 of Table I, with the exception that the arms and number of mice per arm were those found to be optimal with the Fedorov-Wynn algorithm instead of being fixed.

As it might be useful to keep all the arms, in a second scenario a different approach was used. First, 3 two-arm designs were optimized (control and treatment arms 1, 2 or 3) with 4 mice and 7 mice in each arm of experiments A and B, respectively. Optimal design of the 3 two-arm designs was obtained using the same approach as that used for experiments 9 and 10 of Table I. The four-arm design with the previously obtained optimal times for each arm could then be evaluated, keeping fixed the number of mice per arm.

Results

Two-arm designs

Optimal sampling times obtained simultaneously in control and treatment arms of all the selected experiments in short and long studies are reported in Table I. In long studies, some optimal times were located in the regrowth phase of treatment arms, highlighting the importance of continuing the experiment after the end of the treatment. These results were obtained for all two-arm experiments, i.e. one treatment and one control arm, either when only one subject was assigned per arm, as for experiments 1 to 8, or when more mice were included in each arm, as for experiments 9 and 10, using a population approach.

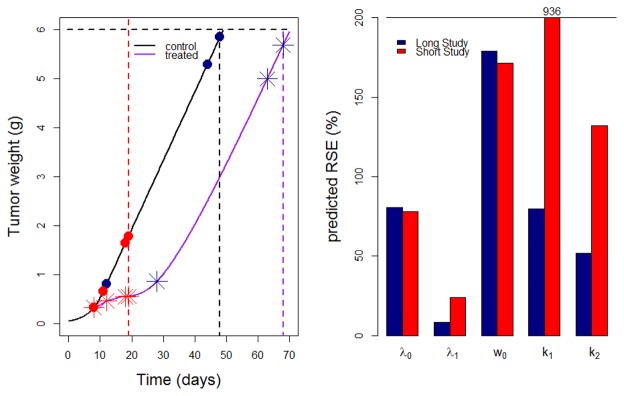
Graphs showing results for experiment 1 are reported in Figure 4. In the graph on the left it is noticeable that two out of four optimal sampling times obtained in the long study lie on the last times of the curve. In the graph on the right it is evident that pRSE (%) of the Simeoni TGI model parameters obtained in long studies (blue bars) were better than those obtained in the short study (red bars) of the corresponding experiment. Sensitivity graphs related to experiments 1 and 9 (Figure 3) provide a visual check of the impact of model parameters through time for those experiments. When focusing on the fixed effects of the drug-related parameters k₁ and k₂, it is noticeable that they start to be informative, i.e. the curve stops being constant at 0, when the treatment is given (day 8), and they both reach an optimum after the end of treatment, at around day 25 and day 35, respectively. Similar reasoning regarding sensitivity graphs was possible for the other experiments, but it was chosen not to report all the graphs in the article.

Fig. 4 — Optimal times (left) in the long study (dark blue symbols) and short study (red symbols) and predicted RSE (%) in TGI model parameters (right) for experiment 1 of Table I. In the left panel red dashed lines define the end of the short study; dashed black and purple lines define the end of the long study for control and treatment arm, respectively.

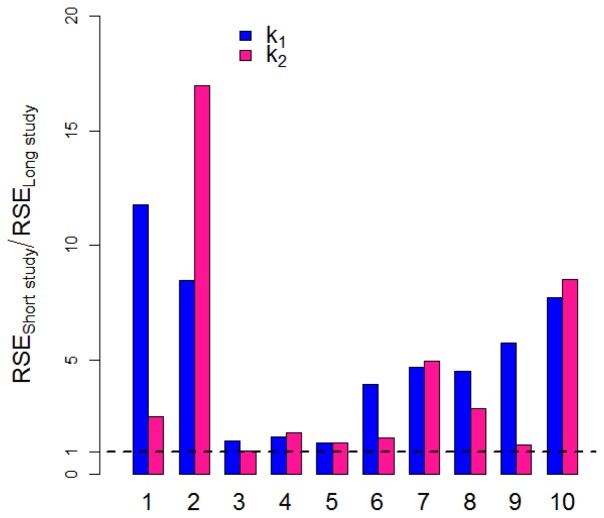
Ratios of pRSE (%) from short to long studies (Figure 5) were calculated for all experiments reported in Table I for the treatment-related parameters k₁ and k₂. The ratio was greater than 1 in all experiments, proving that pRSE (%) in long studies were better than the corresponding pRSE (%) in short studies.

Fig. 5 — Ratio of predicted RSE (%) of short study to long study in two-arm designs for drug related parameters k₁ (blue bars) and k₂ (pink bars) for the experiments listed in Table I.

Four-arm designs

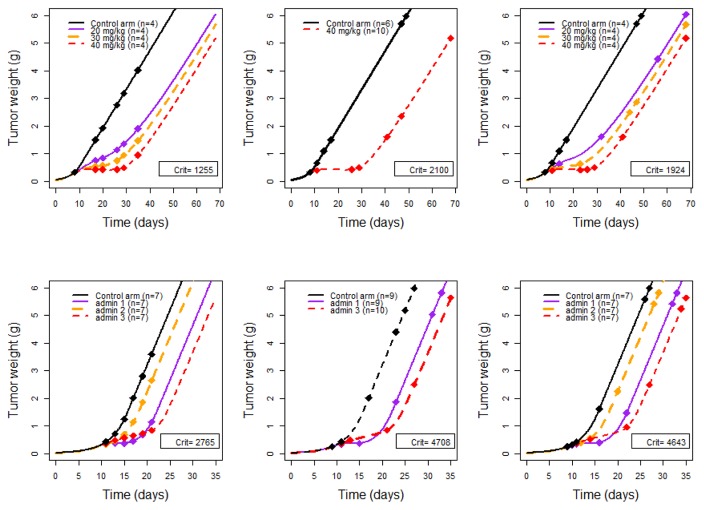
For experiment A in Table II, not surprisingly it was found that the highest dose (40 mg/kg) gave the greatest information, indeed although the initial design had four arms with 4 mice per arm, the design obtained after the optimization of FIM was a two-arm design with 6 control mice, 37.5% of the total number, and 10 treated mice, 62.5% of the total number, at the highest dose (40 mg/kg). The criterion obtained for the optimal design was 2100, which is much higher than the criterion obtained for the initial design of 1255, i.e. an increase of efficiency of 1.67. The criterion obtained for the four-arm design with 4 mice per arm was 1924, i.e. a small loss of efficiency of 0.92 from the optimal design, but a gain of efficiency of 1.53 from the initial design. An evaluation of the first optimal two-arm design was performed including 8 mice in each arm to investigate the loss of having 50% of control and treated mice instead of 37.5% and 62.5%, respectively. The criterion found was 2049, i.e. a small loss of efficiency of 0.98. Graphs showing the initial design, the two-arm design and the four-arm design are in Figure 6, top panel.

Fig. 6 — From left to right, initial design, optimal design for first scenario and optimal design for second scenario (i.e. with fixed proportions of mice per arm) for Exp A (top panel) and Exp B (bottom panel). D-optimal criteria (“Crit”) obtained for each design are specified inside each corresponding graph.

For experiment B the criterion obtained with the initial design was 2765 and the optimal design obtained was a three-arm design, thus only one arm was “excluded” from the optimal design. treatment arm 2 with tid treatment. The proportions of treated and control mice were approximately the same as for the first example: 64% treated, of which 9 mice in both treatment arms 1 and 3, and 36% controls, which is 10 mice. The criterion obtained was 4708, i.e. an increase of efficiency of 1.70. The criterion obtained for the four-arm design with 7 mice per arm was 4643, i.e. a small loss of efficiency of 0.99 from the optimal design, but a gain of efficiency of 1.68 from the initial design. Graphs showing the initial design, the three-arm design and the four-arm design are in Figure 6, bottom panel.

Discussion

Optimal design strategies have rarely been applied to experiments concerning the in vivo evaluation of antitumor effect in xenografted mice (4), and none of them, to our knowledge, have approached the question using optimal design theory. Some work on design of xenograft experiments has been published(30), but the focus was on comparing treatment and control groups, disregarding the correct estimation of drug-related parameters. The use of optimal design will ensure more informative studies and provide measurement times that guarantee the smallest pRSE for the model parameters. In the present work, optimal design was performed for the Simeoni TGI model, for different sets of experiments, in order to answer some important questions arising from these studies.

Optimal design strategies applied in two-arm design experiments, i.e. control vs treatment, showed that studies curtailed three days after the end of treatment administration led to much higher pRSE of the drug-related parameters k₁ and k₂, compared with those obtained in longer studies, where for ethical reasons tumor growth measurements could only be taken until tumor weight reached 6 grams. This result proved that short studies would likely prevent correct identification of parameters k₁ and k₂, whereas long studies should ensure more precise estimates of Simeoni TGI model parameters, leading to a more informative study. This can be considered as a proof-of-concept study, where the hypothesis has been stated in the past by many laboratories and in(27), but has never been proved before, to our knowledge. Graphs of sensitivity functions through time (Figure 3) showed the time points in which Simeoni TGI model parameters were more informative in each experiment, underlying the fact that parameters k₁ and k₂ increase their impact starting from the treatment period, and continuing also afterwards, during the regrowth phase. These results were observed in all the experiments of Table I, where either individual or population approaches were used. Moreover, those experiments were performed for different cell lines, drugs and drug administration schedules. Furthermore, the optimal sampling times reported in Table I were located in the last part of the regrowth phase at least two out of four times, which partially supports the initial intuition that sampling during the tumor regrowth phase would ensure more informative studies.

In some laboratories experiments stop when the tumor reaches 2 grams (5), disregarding the fact that the regrowth rate may be well visible and then model parameters could be well estimated. Furthermore, other researchers stop analyzing when the tumor weight in the control group reaches the maximum allowed by the Institutional Animal Care and Use Committee (IACUC) (31), which corresponds to 4 grams. This may be an issue for the estimation of drug-related parameters, in cases where the tumor in treatment group has not started regrowing by the time the control group has reached a tumor weight of 4 grams. Note that 6 grams is an overestimated threshold adopted to emphasize the impact on precision of parameter estimates in short versus long studies. However, results are substantially confirmed also choosing lower limits. It should also be considered that longer studies may cost more than short studies. A cost-efficacy analysis could be performed in order to define a good balance between information acquisition and cost, as envisaged in our study.

The conclusion drawn from the results discussed in this first part is that making measurements during tumor regrowth should become a general rule for informative preclinical studies in oncology, independently of adopting standard nonlinear regression or an NLMEM approach.

Using a population approach, we further investigated the application of optimal design strategies to four-arm designs in two experiments with several mice included in each arm, considering for the three treatment arms either three different doses or three different drug administration schedules and the same dose. The former optimal design experiment led to the expected conclusion that the treatment arm with the highest dose would provide the greatest information, and the other treatment arms were excluded from the optimal design. We may suspect that in cases where the relationship between drug concentration and cell killing effect is not linear, intermediate doses might be selected by the optimal design, but these analyses were not performed in this work. In preclinical trials intermediate doses are often studied to answer other experimental questions, e.g. toxicology studies. We therefore evaluated an optimal four-arm design including also intermediate doses and using same number of mice in each arm. We found that keeping the intermediate doses did not lead to a large loss of information, compared with the optimal two-arm design obtained with the highest doses. For the latter experiment with different dosing regimens, the same optimal design strategy was employed. In the optimal design one treatment arm with a “poor” drug administration schedule was excluded, but in the optimal four-arm design evaluation with same number of mice per arm it was again found that this experiment did not greatly reduce the information yielded by the study. For both experiments the proportions of mice were approximately 63% treated mice (divided in the treatment arms) and 37% control mice. As computation of FIM is independent of the number of subjects, these proportions should remain the same when performing the same experiment with a different number of mice in the initial design.

In this work, the design variable to be optimized was the sampling time, but dose and dosing regimen could also be considered as design variables. It would be interesting for future studies to investigate the impact of dosing for longer compared with shorter times.

In optimizing design, it is necessary to define the model and parameter values for the model at the beginning of the analysis. In practice, the values for the parameters can be taken from previous experiments. The estimation of parameters from well-planned experiments based on these D-optimal designs provides better estimates than the initial ones and optimal design can be generated with this new set of parameters for subsequent studies. For laboratories in which xenograft experiments are routinely performed, optimal design could be applied in a sequential manner, to fine-tune the experimental design. A limitation of this work is that the model parameters were assumed to be true and error-free. Indeed, the D-optimality used here does not handle uncertainty in parameters. To introduce uncertainty in the parameters, several robust design criteria (32–34) have been developed in recent years, based on the assumption of assigning prior distributions for the parameters, rather than constraining them to a fixed value. An alternative to robust design methods could be to apply two-stage adaptive design (35), e.g. starting the experiment with a small number of mice in the first cohort, and then performing a second part of the experiment with a better design. Moreover, considering the model as true could also be a limitation. The concept of robustness could be extended across models, leading to model averaging criteria (36), which could be considered for application in future studies.

We would like to stress the fact that in the present work the performance of the optimal designs in long and short studies was compared based on the predicted precision of the model parameters. Complementary to this analysis, Monte Carlo simulations could be performed to obtain the empirical precision and biases of the parameter estimates, considering that parameter estimation would be computed for a certain number of simulated datasets, for which responses are simulated at the optimal times found in the optimal design analysis. The Monte Carlo approach could thus be considered for use in future studies.

An additional limitation of this work is that the number of sampling times to be optimized was kept low, i.e. either 4 or 6 times for each experiment described in Table I and Table II, respectively. But it may be important for researchers to take more measurements in long studies, to keep track of tumor size more frequently. In practice, measurements are taken at a higher frequency, also considering the fact that caliper readings are relatively inexpensive.

Another limitation of our work relates to software limitations. It would be interesting to introduce more flexibility into the design optimization settings by requiring optimal time ranges instead of optimal fixed times.

Conclusion

To conclude, this work was a first attempt to provide some general guidelines for preclinical xenograft experiments and proved that optimal design can help us perform more informative preclinical tumor growth inhibition studies, by measuring tumor growth for longer after the end of treatment, thus ensuring more precise model parameter estimation and hence better translation into clinical studies.

Acknowledgments

The research leading to these results has received support from the Innovative Medicines Initiative Joint Undertaking under grant agreement n° 115156, resources of which are composed of financial contributions from the European Union’s Seventh Framework Programme (FP7/2007-2013) and EFPIA companies’ in kind contribution. The DDMoRe project is also financially supported by contributions from Academic and SME partners. This work does not necessarily represent the view of all DDMoRe partners.

References

1.Bernard A, Kimko H, Mital D, Poggesi I. Mathematical modeling of tumor growth and tumor growth inhibition in oncology drug development. Expert Opin Drug Metab Toxicol. 2012 Sep;8(9):1057–69. doi: 10.1517/17425255.2012.693480. [DOI] [PubMed] [Google Scholar]
2.Kelland LR. Of mice and men: values and liabilities of the athymic nude mouse model in anticancer drug development. Eur J Cancer Oxf Engl 1990. 2004 Apr;40(6):827–36. doi: 10.1016/j.ejca.2003.11.028. [DOI] [PubMed] [Google Scholar]
3.Mattern J, Bak M, Hahn EW, Volm M. Human tumor xenografts as model for drug testing. Cancer Metastasis Rev. 1988 Nov;7(3):263–84. doi: 10.1007/BF00047755. [DOI] [PubMed] [Google Scholar]
4.Simeoni M, De Nicolao G, Magni P, Rocchetti M, Poggesi I. Modeling of human tumor xenografts and dose rationale in oncology. Drug Discov Today Technol. 2013 Sep;10(3):e365–72. doi: 10.1016/j.ddtec.2012.07.004. [DOI] [PubMed] [Google Scholar]
5.Bissery MC, Vrignaud P, Lavelle F, Chabot GG. Experimental antitumor activity and pharmacokinetics of the camptothecin analog irinotecan (CPT-11) in mice. Anticancer Drugs. 1996 Jun;7(4):437–60. doi: 10.1097/00001813-199606000-00010. [DOI] [PubMed] [Google Scholar]
6.Rocchetti M, Poggesi I, Germani M, Fiorentini F, Pellizzoni C, Zugnoni P, et al. A pharmacokinetic-pharmacodynamic model for predicting tumour growth inhibition in mice: a useful tool in oncology drug development. Basic Clin Pharmacol Toxicol. 2005 Mar;96(3):265–8. doi: 10.1111/j.1742-7843.2005.pto960325.x. [DOI] [PubMed] [Google Scholar]
7.Simeoni M, Magni P, Cammia C, De Nicolao G, Croci V, Pesenti E, et al. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004 Feb 1;64(3):1094–101. doi: 10.1158/0008-5472.can-03-2524. [DOI] [PubMed] [Google Scholar]
8.Magni P, Simeoni M, Poggesi I, Rocchetti M, De Nicolao G. A mathematical model to study the effects of drugs administration on tumor growth dynamics. Math Biosci. 2006 Apr;200(2):127–51. doi: 10.1016/j.mbs.2005.12.028. [DOI] [PubMed] [Google Scholar]
9.Terranova N, Germani M, Del Bene F, Magni P. A predictive pharmacokinetic pharmacodynamic model of tumor growth kinetics in xenograft mice after administration of anticancer agents given in combination. Cancer Chemother Pharmacol. 2013 Aug;72(2):471–82. doi: 10.1007/s00280-013-2208-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Magni P, Bertoldo A, Vicini P. 7 - Population Modelling. In: Cobelli EC, editor. Modelling Methodology for Physiology and Medicine (Second Edition) [Internet] Oxford: Elsevier; 2014. pp. 131–58. [cited 2015 Nov 17] Available from: http://www.sciencedirect.com/science/article/pii/B9780124115576000070. [Google Scholar]
11.Lavielle M. Mixed Effects Models for the Population Approach: Models, Tasks, Methods and Tools. Chapman and Hall/CRC; 2014. p. 383. [Google Scholar]
12.Lalonde RL, Kowalski KG, Hutmacher MM, Ewy W, Nichols DJ, Milligan PA, et al. Model-based drug development. Clin Pharmacol Ther. 2007 Jul;82(1):21–32. doi: 10.1038/sj.clpt.6100235. [DOI] [PubMed] [Google Scholar]
13.Smith BP, Vincent J. Biostatistics and Pharmacometrics: Quantitative Sciences to Propel Drug Development Forward. Clin Pharmacol Ther. 2010 Aug 1;88(2):141–4. doi: 10.1038/clpt.2010.136. [DOI] [PubMed] [Google Scholar]
14.al-Banna MK, Kelman AW, Whiting B. Experimental design and efficient parameter estimation in population pharmacokinetics. J Pharmacokinet Biopharm. 1990 Aug;18(4):347–60. doi: 10.1007/BF01062273. [DOI] [PubMed] [Google Scholar]
15.Holford N, Ma SC, Ploeger BA. Clinical trial simulation: a review. Clin Pharmacol Ther. 2010 Aug;88(2):166–82. doi: 10.1038/clpt.2010.114. [DOI] [PubMed] [Google Scholar]
16.Mentré F, Mallet A, Baccar D. Optimal design in random-effects regression models. Biometrika. 1997 Jun 1;84(2):429–42. [Google Scholar]
17.Nyberg J, Bazzoli C, Ogungbenro K, Aliev A, Leonov S, Duffull S, et al. Methods and software tools for design evaluation in population pharmacokinetics pharmacodynamics studies. Br J Clin Pharmacol. 2015;79(1):6–17. doi: 10.1111/bcp.12352. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Mentré F, Chenel M, Comets E, Grevel J, Hooker A, Karlsson M, et al. Current Use and Developments Needed for Optimal Design in Pharmacometrics: A Study Performed Among DDMoRe’s European Federation of Pharmaceutical Industries and Associations Members. CPT Pharmacomet Syst Pharmacol. 2013 Jun;2(6):e46. doi: 10.1038/psp.2013.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Mentré F, Thu Thuy N, Lestini G, Dumont C PFIM group. PFIM 4.0: new features for optimal design in nonlinear mixed effects models using R. PAGE 2014 Abstr 3032 [Internet] Available from: [ http://www.page-meeting.org/default.asp?abstract=3032]
20.Bazzoli C, Retout S, Mentré F. Design evaluation and optimisation in multiple response nonlinear mixed effect models: PFIM 3.0. Comput Methods Programs Biomed. 2010 Apr;98(1):55–65. doi: 10.1016/j.cmpb.2009.09.012. [DOI] [PubMed] [Google Scholar]
21.Nyberg J, Ueckert S, Strömberg EA, Hennig S, Karlsson MO, Hooker AC. PopED: an extended, parallelized, nonlinear mixed effects models optimal design tool. Comput Methods Programs Biomed. 2012 Nov;108(2):789–805. doi: 10.1016/j.cmpb.2012.05.005. [DOI] [PubMed] [Google Scholar]
22.Gueorguieva I, Ogungbenro K, Graham G, Glatt S, Aarons L. A program for individual and population optimal design for univariate and multivariate response pharmacokinetic pharmacodynamic models. Comput Methods Programs Biomed. 2007 Apr;86(1):51–61. doi: 10.1016/j.cmpb.2007.01.004. [DOI] [PubMed] [Google Scholar]
23.http://www.winpopt.com/.
24.Atkinson A, Donev A, Tobias R. Optimum Experimental Designs, with SAS. 2007. (Oxford Statistical Science Series) [Google Scholar]
25.Nagy Z, Baghy K, Hunyadi-Gulyas E, Micsik T, Nyir G, Racz G, et al. Evaluation of 9-cis retinoic acid and mitotane as antitumoral agents in an adrenocortical xenograft model. Am J Cancer Res. 2015 Nov 15;5(12):3645–58. [PMC free article] [PubMed] [Google Scholar]
26.Chang L, Gong F, Cai H, Li Z, Cui Y. Combined RNAi targeting human Stat3 and ADAM9 as gene therapy for non-small cell lung cancer. Oncol Lett. 2016 Feb;11(2):1242–50. doi: 10.3892/ol.2015.4018. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
27.Rocchetti M, Germani M, Del Bene F, Poggesi I, Magni P, Pesenti E, et al. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth after administration of an anti-angiogenic agent, bevacizumab, as single-agent and combination therapy in tumor xenografts. Cancer Chemother Pharmacol. 2013 May;71(5):1147–57. doi: 10.1007/s00280-013-2107-z. [DOI] [PubMed] [Google Scholar]
28.Simeoni M, Poggesi I, Germani M, De Nicolao G, Rocchetti M. Population modeling of tumor growth inhibition in vivo: application to anticancer drug development. PAGE 2004 Abstr 503 [Internet] Available from: [ www.page-meeting.org/?abstract=503]
29.PFIM [Internet] [cited 2014 Mar 10]. Available from: http://www.pfim.biostat.fr/
30.Hather G, Liu R, Bandi S, Mettetal J, Manfredi M, Shyu W-C, et al. Growth Rate Analysis and Efficient Experimental Design for Tumor Xenograft Studies. Cancer Inform. 2014 Dec 9;13(Suppl 4):65–72. doi: 10.4137/CIN.S13974. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Tumor Policy for Mice and Rats » Research Committees » Boston University *Internet+ *cited 2016 Apr 4]. Available from: http://www.bu.edu/orccommittees/iacuc/policies-and-guidelines/tumor-policy-for-mice-and-rats/
32.Dodds MG, Hooker AC, Vicini P. Robust population pharmacokinetic experiment design. J Pharmacokinet Pharmacodyn. 2005 Feb;32(1):33–64. doi: 10.1007/s10928-005-2102-z. [DOI] [PubMed] [Google Scholar]
33.Tod M, Rocchisani JM. Comparison of ED, EID, and API criteria for the robust optimization of sampling times in pharmacokinetics. J Pharmacokinet Biopharm. 1997 Aug;25(4):515–37. doi: 10.1023/a:1025701327672. [DOI] [PubMed] [Google Scholar]
34.Vajjah P, Duffull SB. A generalisation of T-optimality for discriminating between competing models with an application to pharmacokinetic studies. Pharm Stat. 2012 Dec;11(6):503–10. doi: 10.1002/pst.1542. [DOI] [PubMed] [Google Scholar]
35.Lestini G, Dumont C, Mentré F. Influence of the Size of Cohorts in Adaptive Design for Nonlinear Mixed Effects Models: An Evaluation by Simulation for a Pharmacokinetic and Pharmacodynamic Model for a Biomarker in Oncology. Pharm Res. 2015 Oct;32(10):3159–69. doi: 10.1007/s11095-015-1693-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Hoeting J, Madigan D, Raftery A, Volinsky C. Bayesian model averaging: a tutorial. Stat Sci. 1999 Nov 1;14(4):382–417. [Google Scholar]

[R1] 1.Bernard A, Kimko H, Mital D, Poggesi I. Mathematical modeling of tumor growth and tumor growth inhibition in oncology drug development. Expert Opin Drug Metab Toxicol. 2012 Sep;8(9):1057–69. doi: 10.1517/17425255.2012.693480. [DOI] [PubMed] [Google Scholar]

[R2] 2.Kelland LR. Of mice and men: values and liabilities of the athymic nude mouse model in anticancer drug development. Eur J Cancer Oxf Engl 1990. 2004 Apr;40(6):827–36. doi: 10.1016/j.ejca.2003.11.028. [DOI] [PubMed] [Google Scholar]

[R3] 3.Mattern J, Bak M, Hahn EW, Volm M. Human tumor xenografts as model for drug testing. Cancer Metastasis Rev. 1988 Nov;7(3):263–84. doi: 10.1007/BF00047755. [DOI] [PubMed] [Google Scholar]

[R4] 4.Simeoni M, De Nicolao G, Magni P, Rocchetti M, Poggesi I. Modeling of human tumor xenografts and dose rationale in oncology. Drug Discov Today Technol. 2013 Sep;10(3):e365–72. doi: 10.1016/j.ddtec.2012.07.004. [DOI] [PubMed] [Google Scholar]

[R5] 5.Bissery MC, Vrignaud P, Lavelle F, Chabot GG. Experimental antitumor activity and pharmacokinetics of the camptothecin analog irinotecan (CPT-11) in mice. Anticancer Drugs. 1996 Jun;7(4):437–60. doi: 10.1097/00001813-199606000-00010. [DOI] [PubMed] [Google Scholar]

[R6] 6.Rocchetti M, Poggesi I, Germani M, Fiorentini F, Pellizzoni C, Zugnoni P, et al. A pharmacokinetic-pharmacodynamic model for predicting tumour growth inhibition in mice: a useful tool in oncology drug development. Basic Clin Pharmacol Toxicol. 2005 Mar;96(3):265–8. doi: 10.1111/j.1742-7843.2005.pto960325.x. [DOI] [PubMed] [Google Scholar]

[R7] 7.Simeoni M, Magni P, Cammia C, De Nicolao G, Croci V, Pesenti E, et al. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004 Feb 1;64(3):1094–101. doi: 10.1158/0008-5472.can-03-2524. [DOI] [PubMed] [Google Scholar]

[R8] 8.Magni P, Simeoni M, Poggesi I, Rocchetti M, De Nicolao G. A mathematical model to study the effects of drugs administration on tumor growth dynamics. Math Biosci. 2006 Apr;200(2):127–51. doi: 10.1016/j.mbs.2005.12.028. [DOI] [PubMed] [Google Scholar]

[R9] 9.Terranova N, Germani M, Del Bene F, Magni P. A predictive pharmacokinetic pharmacodynamic model of tumor growth kinetics in xenograft mice after administration of anticancer agents given in combination. Cancer Chemother Pharmacol. 2013 Aug;72(2):471–82. doi: 10.1007/s00280-013-2208-8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Magni P, Bertoldo A, Vicini P. 7 - Population Modelling. In: Cobelli EC, editor. Modelling Methodology for Physiology and Medicine (Second Edition) [Internet] Oxford: Elsevier; 2014. pp. 131–58. [cited 2015 Nov 17] Available from: http://www.sciencedirect.com/science/article/pii/B9780124115576000070. [Google Scholar]

[R11] 11.Lavielle M. Mixed Effects Models for the Population Approach: Models, Tasks, Methods and Tools. Chapman and Hall/CRC; 2014. p. 383. [Google Scholar]

[R12] 12.Lalonde RL, Kowalski KG, Hutmacher MM, Ewy W, Nichols DJ, Milligan PA, et al. Model-based drug development. Clin Pharmacol Ther. 2007 Jul;82(1):21–32. doi: 10.1038/sj.clpt.6100235. [DOI] [PubMed] [Google Scholar]

[R13] 13.Smith BP, Vincent J. Biostatistics and Pharmacometrics: Quantitative Sciences to Propel Drug Development Forward. Clin Pharmacol Ther. 2010 Aug 1;88(2):141–4. doi: 10.1038/clpt.2010.136. [DOI] [PubMed] [Google Scholar]

[R14] 14.al-Banna MK, Kelman AW, Whiting B. Experimental design and efficient parameter estimation in population pharmacokinetics. J Pharmacokinet Biopharm. 1990 Aug;18(4):347–60. doi: 10.1007/BF01062273. [DOI] [PubMed] [Google Scholar]

[R15] 15.Holford N, Ma SC, Ploeger BA. Clinical trial simulation: a review. Clin Pharmacol Ther. 2010 Aug;88(2):166–82. doi: 10.1038/clpt.2010.114. [DOI] [PubMed] [Google Scholar]

[R16] 16.Mentré F, Mallet A, Baccar D. Optimal design in random-effects regression models. Biometrika. 1997 Jun 1;84(2):429–42. [Google Scholar]

[R17] 17.Nyberg J, Bazzoli C, Ogungbenro K, Aliev A, Leonov S, Duffull S, et al. Methods and software tools for design evaluation in population pharmacokinetics pharmacodynamics studies. Br J Clin Pharmacol. 2015;79(1):6–17. doi: 10.1111/bcp.12352. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] 18.Mentré F, Chenel M, Comets E, Grevel J, Hooker A, Karlsson M, et al. Current Use and Developments Needed for Optimal Design in Pharmacometrics: A Study Performed Among DDMoRe’s European Federation of Pharmaceutical Industries and Associations Members. CPT Pharmacomet Syst Pharmacol. 2013 Jun;2(6):e46. doi: 10.1038/psp.2013.19. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] 19.Mentré F, Thu Thuy N, Lestini G, Dumont C PFIM group. PFIM 4.0: new features for optimal design in nonlinear mixed effects models using R. PAGE 2014 Abstr 3032 [Internet] Available from: [ http://www.page-meeting.org/default.asp?abstract=3032]

[R20] 20.Bazzoli C, Retout S, Mentré F. Design evaluation and optimisation in multiple response nonlinear mixed effect models: PFIM 3.0. Comput Methods Programs Biomed. 2010 Apr;98(1):55–65. doi: 10.1016/j.cmpb.2009.09.012. [DOI] [PubMed] [Google Scholar]

[R21] 21.Nyberg J, Ueckert S, Strömberg EA, Hennig S, Karlsson MO, Hooker AC. PopED: an extended, parallelized, nonlinear mixed effects models optimal design tool. Comput Methods Programs Biomed. 2012 Nov;108(2):789–805. doi: 10.1016/j.cmpb.2012.05.005. [DOI] [PubMed] [Google Scholar]

[R22] 22.Gueorguieva I, Ogungbenro K, Graham G, Glatt S, Aarons L. A program for individual and population optimal design for univariate and multivariate response pharmacokinetic pharmacodynamic models. Comput Methods Programs Biomed. 2007 Apr;86(1):51–61. doi: 10.1016/j.cmpb.2007.01.004. [DOI] [PubMed] [Google Scholar]

[R23] 23.http://www.winpopt.com/.

[R24] 24.Atkinson A, Donev A, Tobias R. Optimum Experimental Designs, with SAS. 2007. (Oxford Statistical Science Series) [Google Scholar]

[R25] 25.Nagy Z, Baghy K, Hunyadi-Gulyas E, Micsik T, Nyir G, Racz G, et al. Evaluation of 9-cis retinoic acid and mitotane as antitumoral agents in an adrenocortical xenograft model. Am J Cancer Res. 2015 Nov 15;5(12):3645–58. [PMC free article] [PubMed] [Google Scholar]

[R26] 26.Chang L, Gong F, Cai H, Li Z, Cui Y. Combined RNAi targeting human Stat3 and ADAM9 as gene therapy for non-small cell lung cancer. Oncol Lett. 2016 Feb;11(2):1242–50. doi: 10.3892/ol.2015.4018. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]

[R27] 27.Rocchetti M, Germani M, Del Bene F, Poggesi I, Magni P, Pesenti E, et al. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth after administration of an anti-angiogenic agent, bevacizumab, as single-agent and combination therapy in tumor xenografts. Cancer Chemother Pharmacol. 2013 May;71(5):1147–57. doi: 10.1007/s00280-013-2107-z. [DOI] [PubMed] [Google Scholar]

[R28] 28.Simeoni M, Poggesi I, Germani M, De Nicolao G, Rocchetti M. Population modeling of tumor growth inhibition in vivo: application to anticancer drug development. PAGE 2004 Abstr 503 [Internet] Available from: [ www.page-meeting.org/?abstract=503]

[R29] 29.PFIM [Internet] [cited 2014 Mar 10]. Available from: http://www.pfim.biostat.fr/

[R30] 30.Hather G, Liu R, Bandi S, Mettetal J, Manfredi M, Shyu W-C, et al. Growth Rate Analysis and Efficient Experimental Design for Tumor Xenograft Studies. Cancer Inform. 2014 Dec 9;13(Suppl 4):65–72. doi: 10.4137/CIN.S13974. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] 31.Tumor Policy for Mice and Rats » Research Committees » Boston University *Internet+ *cited 2016 Apr 4]. Available from: http://www.bu.edu/orccommittees/iacuc/policies-and-guidelines/tumor-policy-for-mice-and-rats/

[R32] 32.Dodds MG, Hooker AC, Vicini P. Robust population pharmacokinetic experiment design. J Pharmacokinet Pharmacodyn. 2005 Feb;32(1):33–64. doi: 10.1007/s10928-005-2102-z. [DOI] [PubMed] [Google Scholar]

[R33] 33.Tod M, Rocchisani JM. Comparison of ED, EID, and API criteria for the robust optimization of sampling times in pharmacokinetics. J Pharmacokinet Biopharm. 1997 Aug;25(4):515–37. doi: 10.1023/a:1025701327672. [DOI] [PubMed] [Google Scholar]

[R34] 34.Vajjah P, Duffull SB. A generalisation of T-optimality for discriminating between competing models with an application to pharmacokinetic studies. Pharm Stat. 2012 Dec;11(6):503–10. doi: 10.1002/pst.1542. [DOI] [PubMed] [Google Scholar]

[R35] 35.Lestini G, Dumont C, Mentré F. Influence of the Size of Cohorts in Adaptive Design for Nonlinear Mixed Effects Models: An Evaluation by Simulation for a Pharmacokinetic and Pharmacodynamic Model for a Biomarker in Oncology. Pharm Res. 2015 Oct;32(10):3159–69. doi: 10.1007/s11095-015-1693-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.Hoeting J, Madigan D, Raftery A, Volinsky C. Bayesian model averaging: a tutorial. Stat Sci. 1999 Nov 1;14(4):382–417. [Google Scholar]

PERMALINK

Optimal design for informative protocols in xenograft tumor growth inhibition experiments in mice

Giulia Lestini

France Mentré

Paolo Magni

Abstract

Introduction