Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 Mar 5.
Published in final edited form as: J Comput Chem. 2019 Nov 13;41(6):528–537. doi: 10.1002/jcc.26098

A minimal membrane metal transport system: Dynamics and energetics of mer proteins

Hyea Hwang *,†, Anthony Hazel ‡, Peng Lian †,§, Jeremy C Smith †,, James C Gumbart ‡,∥, Jerry M Parks †,**
PMCID: PMC7263448  NIHMSID: NIHMS1593338  PMID: 31721253

Abstract

The mer operon in bacteria encodes a set of proteins and enzymes that impart resistance to environmental mercury toxicity by importing Hg2+ and reducing it to volatile Hg(0). Because the reduction occurs in the cytoplasm, mercuric ions must first be transported across the cytoplasmic membrane by one of a few known transporters. MerF is the smallest of these, containing only two transmembrane helices and two pairs of vicinal cysteines that coordinate mercuric ions. In this work, we use molecular dynamics simulations to characterize the dynamics of MerF in its apo and Hg2+-bound states. We find that the apo state positions one of the cysteine pairs closer to the periplasmic side of the membrane, while in the bound state the same pair approaches the cytoplasmic side. This finding is consistent with the functional requirement of accepting Hg2+ from the periplasmic space, sequestering it on acceptance, and transferring it to the cytoplasm. Conformational changes in the TM helices facilitate the functional interaction of the two cysteine pairs. Free-energy calculations provide a barrier of 16kcal/mol for the association of the periplasmic Hg2+-bound protein MerP with MerF and 7kcal/mol for the subsequent association of MerF’s two cysteine pairs. Despite the significant conformational changes required to move the binding site across the membrane, coarse-grained simulations of multiple copies of MerF support the expectation that it functions as a monomer. Our results demonstrate how conformational changes and binding thermodynamics could lead to such a small membrane protein acting as an ion transporter.

Keywords: MerF, mercury transport, membrane transporter, free-energy calculations, molecular dynamics

Graphical Abstract

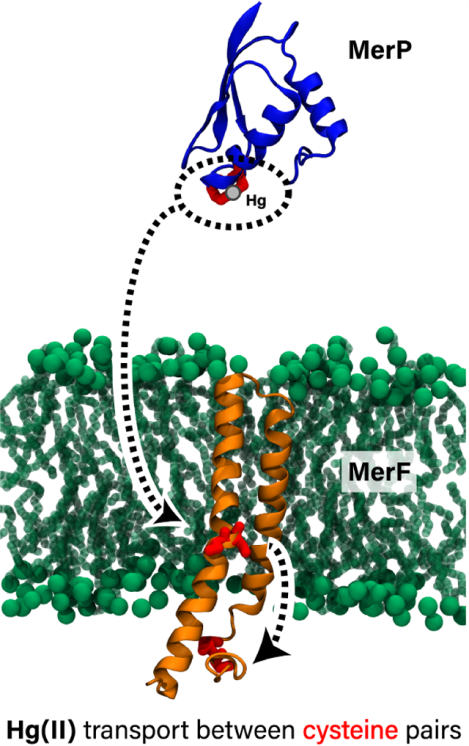
graphic file with name nihms-1593338-f0001.jpg

Mercury-resistant bacteria import Hg2+ ions across the cytoplasmic membrane by means of the two-transmembrane-helix transport protein MerF. The authors have characterized the dynamics and energetics of MerF using molecular dynamics simulations and free-energy calculations. They find that the conformation of MerF is adaptable, shifting to receive the ion from the periplasm and deliver it to the cytoplasm. The results reveal how such a small protein can transport mercury across the membrane.

INTRODUCTION

Mercury (Hg) is a non-essential element that is toxic to living organisms. In its oxidized Hg2+ and methylated [CH3Hg]+ forms, it binds strongly to the sulfhydryl groups of Cys residues in proteins, leading to deleterious effects on various cellular functions. Consequently, many Gram-positive and Gram-negative bacteria possess the Hg resistance (mer) operon, a suite of genes that confer these organisms with the ability to survive in environments with high concentrations of Hg.1

The mer operon encodes at a minimum a mercuric reductase, MerA, which catalyzes the reduction of Hg2+ to Hg(0), and a regulator, MerR, which initiates transcription in the presence of sufficiently high intracellular concentrations of Hg2+. However, genes encoding additional proteins and enzymes involved in Hg resistance are often present. In so-called “broad spectrum” Hg-resistant bacteria, the organomercurial lyase, MerB, catalyzes the cleavage of the Hg–C bond in methylmercury to produce Hg2+ and CH4. A periplasmic metallochaperone and several α-helical membrane-bound proteins facilitate the transfer of Hg into the cytoplasm, where demethylation of methylmercury and reduction of Hg2+ to Hg(0) occur.2

The metallochaperone MerP scavenges Hg2+ in the periplasm and transfers it to transmembrane transporters such as MerF, which then transport Hg2+ across the membrane into the cytoplasm for reduction by MerA.3 MerP consists of a heavy metal-associated (HMA) domain that is present in many heavy metal transport and detoxification proteins and includes two conserved cysteines in a CXXC configuration that bind Hg2+ with high affinity.

The transmembrane transporters MerC, MerT4 and MerF contain four, three, and two α-helices, respectively. The smallest of the mer transport proteins, MerF (Pfam PF11431) has a molecular mass of only 8.7 kDa and consists solely of a simple helix-loop-helix domain with two pairs of cysteine residues. Evidence for MerF’s ability to transport Hg2+ comes from genetically manipulated Escherichia coli in which mercury volatization increased significantly under the expression of individual Mer proteins, including MerF, as well as combinations of them.5,6 However, more direct in vitro assays have yet to demonstrate that MerF alone is capable of transport. If confirmed, it would make MerF the smallest Hg2+ transmembrane transporter in the mer operon and also one of the smallest known transporters.5

To date, all available structures of MerF (Pfam00403) have been determined by NMR spectroscopy in solution3 or in the solid state7–10 (Table 1). In early studies, truncated variants of the integral membrane core were used,3,7,8 but more recent structures include the full-length 81-residue protein from Morganella morganii.9,10 Similarly, the majority of published structures of MerP (Pfam00403) were determined by solution NMR11–13. However, one structure of the oxidized (i.e., disulfide) form of full-length MerP from Cupriavidus metallireducens CH34 was determined at 2.0 Å resolution using X-ray diffraction.14

Table 1:

Experimentally determined structures of MerF and MerP.

PDB entry Author, Year Technique Sequence length Notes
MerF
1WAZ Howell, 2005 Solution NMR 46
2H3O De Angelis, 2006 Solid-state NMR 61
2LJ2 Das, 2012 Solid-state NMR 60
2M67 Lu, 2013 Solid-state NMR 81
2MOZ Tian, 2014 Solid-state NMR 81
MerP
1AFI Steele, 1997 Solution NMR 72 Reduced form
1AFJ Steele, 1997 Solution NMR 72 Hg2+-bound
2HQI Qian, 1998 Solution NMR 72
1DVW Veglia, 2000 Solution NMR 18 Hg2+-bound
1OSD Serre, 2004 X-ray diffraction 87 Oxidized (disulfide)
Open in a new tab

Mer proteins and enzymes exploit the high affinity of Hg for S by using pairs of cysteine residues to orchestrate the acquisition, controlled transport, and transformation of toxic Hg species to less toxic elemental Hg(0). The mechanism of intramolecular transfer of Hg2+ from a pair of surface-exposed cysteines at the C-terminus of MerA to a pair of active-site cysteines was investigated with quantum mechanical/molecular mechanical (QM/MM) calculations.15 It was found that Hg2+ is always coordinated by at least two cysteine thiolates. During handoff from one pair of cysteines to another, a trigonal Hg(Cys)3 intermediate is formed. This step is assisted by acid/base chemistry performed by nearby residues to deprotonate the cysteine thiols prior to Hg binding and protonate thiolates upon its departure. The biological advantage of this tightly controlled handling of intracellular Hg2+ is that it is not released until it has been reduced to Hg(0).16

Previous studies have demonstrated chemical aspects of Hg binding and transfer in Mer enzymes, but the free energy landscapes associated with the conformational changes that occur prior to intra- and inter-molecular transfer of Hg2+ among Mer transport proteins remain largely unexplored. Here, to characterize its conformational landscape we perform all-atom and coarse-grained molecular dynamics (MD) simulations of MerF as well as free-energy calculations of MerF and MerF with MerP. We find that the positioning of a key binding site on MerF depends on whether or not Hg2+ is bound. We also quantify the free energy required to bring this binding site to either side of the membrane to interact with MerP (periplasmic surface) or the other MerF binding site (cytoplasmic surface), finding that, although large, the energy required is not insurmountable.

METHODS

Force field parameterization of Cys-Hg2+-Cys

The Lennard-Jones parameters for Hg(II) were taken from Fuchs et al.17, as used previously18. We optimized force field parameters for Hg(SCH2CH3)2 using the Force Field Toolkit (ffTK)19, which is implemented in VMD.20

Because Hg exhibits strong relativistic effects, during the parameterization procedure we used the Stuttgart-Dresden (SDD) scalar relativistic effective core potential (ECP) and corresponding basis set to describe Hg. As is customary for MM force field parameterization, we used the 6–31G(d) basis set for all other atoms. In addition, we used hybrid density functional theory instead of wavefunction theory. Thus, the geometry of Hg(SCH2CH3)2 was optimized with Gaussian 1621 at the B3LYP/SDD/6–31G(d) level of theory, where SDD refers to the Stuttgart-Dresden scalar relativistic ECP and basis set.22 Vibrational frequencies and water interaction energies (Fig. S1 and Table S1) were calculated at the same level of theory. To optimize the MM partial charges, we fitted the MM water interaction energies to the corresponding quantum chemical values. Only the charges of Hg, SG, and CB were optimized, as shown in Fig. 1.

Figure 1:

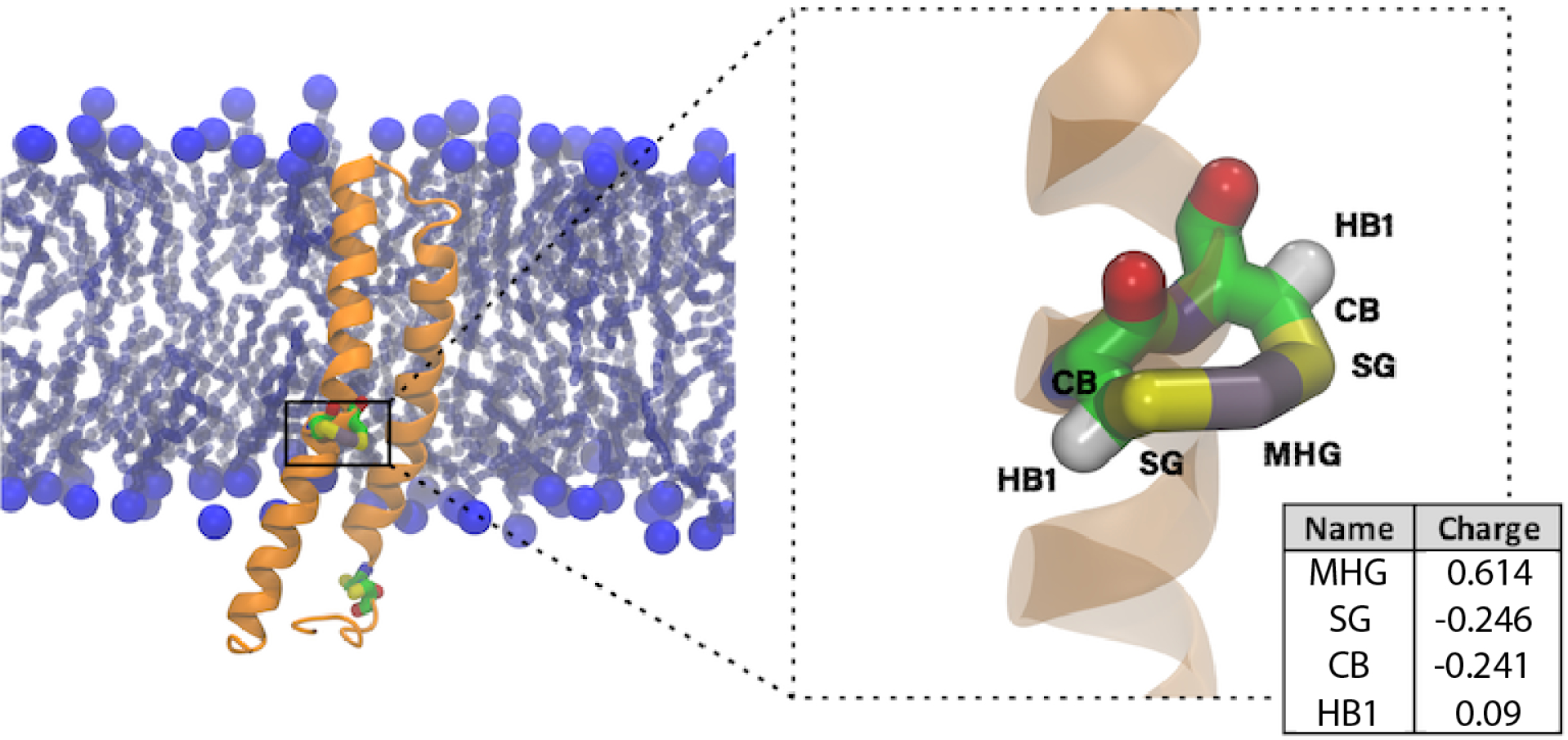
Figure 1:

Open in a new tab

MerF (orange) in the DMPC lipid bilayer with Hg2+ binding sites (Cys21/Cys22 and Cys71/Cys72) highlighted in a licorice representation. The upper leaflet faces the periplasm and the lower leaflet faces the cytoplasm. Phosphorus atoms are shown as large blue spheres and lipid tails are shown in light blue licorice representation. The partial charges for each atom in -C-S-Hg-S-C- (Cys21-Hg2+-Cys22) are shown in the table on the bottom right.

We also assessed the accuracy of the SDD ECP for Hg by comparing it to a more accurate all-electron relativistic approximation. Specifically, we used the zeroth-order regular approximation23 (ZORA) to optimize the geometry of Hg(SCH2CH3)2 and calculate water interaction energies for this complex. We again used the B3LYP24–26 density functional approximation and performed all ZORA calculations with Orca version 3.0.3.27 ZORA requires the use of specialized basis sets, so we compared the SDD/6–31G(d) geometry to that obtained with ZORA/Def2-TZVPP, in which the segmented all-electron relativistically contracted (SARC-ZORA) basis set28 was used for Hg and the Def2-TZVPP basis set was used for all other elements. The optimized geometries are nearly identical (0.034 Å RMSD), with the main difference arising from slightly longer Hg-S bonds with SDD (2.38 Å) than with ZORA (2.35 Å). Thus, the geometry of the complex computed with the SDD ECP is accurate.

The 6–31G(d) basis set is incompatible with ZORA, so to compare water interaction energies computed with an ECP and with ZORA we performed SDD/Def2-TZVPP and ZORA/Def2-TZVPP calculations. The water interaction energies computed with the SDD ECP are very similar to the corresponding all-atom ZORA calculations (Tables S2 and S3), with a mean signed error (MSE) of only −0.06 kcal/mol, showing that the SDD ECP performs accurately. We also compared the original SDD/6–31G(d) water interaction energies (Table S1) with the ZORA/Def2-TZVPP values (Table S3). In this case, the use of the 6–31G(d) basis set results in a substantial overstabilization of the interaction energies (MSE = −1.68 kcal/mol). Although it is tempting to use the higher level of theory for the parameterization, doing so would be inconsistent with the standard CHARMM approach and would result in imbalanced intermolecular interactions. Thus, we opted to use the B3LYP/SDD/6–31G* calculations as the basis for our MM force field parameterization. The force-field topology and parameters are provided in the Supporting Information.

System construction

All-atom systems.

We used the solution NMR structure10 of MerF (PDB:2MOZ) with the mutated residues (Ser21, Ser22, Ser71 and Ser72) replaced with Cys. We first constructed two systems, one with and one without Hg2+ at the Cys21/Cys22 binding site, in a 1,2-dimyristoyl-sn-glycero-3-phosphorylcholine (DMPC) membrane, which was used for reconstitution of the protein in experiments3,7–10. To investigate the effect of lipid composition on the dynamic properties of the protein, we additionally built two more systems for each with a “Top6” membrane, which contains the top six lipids found in the Escherichia coli inner membrane29,30. Lastly, we modeled MerFt (PDB:2H3O), a truncated 60-residue construct spanning the integral membrane helix-loop-helix region of MerF, embedded in a DMPC membrane.

The periplasmic Hg2+-binding protein MerP (PDB:1AFJ)11 was placed in a water box and equilibrated for 50ns before placing it above the MerF-embedded membrane in the periplasm. All systems were solvated with water, and ions were added to neutralize the system at a concentration of 150 mM NaCl. The final system sizes ranged from 36,000 to 125,000 atoms.

Coarse-grained systems.

In coarse-grained (CG) simulations, small groups of atoms are treated as single particles, allowing for much longer simulation time scales than with an all-atom representation. Here, the Martini force field31 was used. We constructed three models with different concentrations of MerF. The CG15, CG25, and CG35 systems contained 15, 25, and 35 MerF monomers, respectively. The initial area of the membrane was 30 nm × 30 nm for all the systems, requiring 2,517 (CG15), 2,401 (CG25), and 2,314 (CG35) lipids. An approximately 3:1 ratio of POPE:POPG lipids was used, which is a simple mimic of a bacterial cytoplasmic membrane30. The system was solvated with ~20Å of water on both sides of the membrane (36–37,000 water beads), and 581 (CG15), 521 (CG25), or 461 (CG35) Na+ ions were added to neutralize the systems. The final size of each system was between 72,000 and 73,000 beads.

MD simulation

All-atom.

The energy of each system was minimized for 1000 steps, after which the solvent was equilibrated while the peptide backbone was restrained for an additional 2 ns. MD simulations were carried out with NAMD32. The CHARMM36m force field33,34 and TIP3P water model35 were used to describe the protein and solvent/ions, respectively. The temperature was maintained at 300 K using Langevin dynamics and the pressure was kept at 1 atm using the Langevin piston method36. A 2-fs time step was used. The short-range non-bonded interactions and the bonded terms were evaluated every time step, and non-bonded terms and long-range electrostatic interactions were updated every 2 fs and 4 fs, respectively. Long-range electrostatic interactions were calculated using the particle-mesh Ewald (PME) method37. Lennard-Jones interactions were cut off at 12Å, and a force-based switching function was used beginning at 10Å. System setup and analysis were performed using VMD20, and all analysis was done on the last 400ns of the 500-ns production runs.

Coarse-grained.

CG simulations were carried out with NAMD32 with notable differences from the all-atom simulations. A time step of 30fs was used. Short-range non-bonded interactions were cut off at 12Å with a Martini-specific switching function beginning at 9Å applied. No long-range interactions were included (i.e., no PME). The temperature and pressure were controlled using the same approaches as for the all-atom simulations.

Free-energy calculations

MerF-MerF.

To quantify the conformational change required to bring Hg2+-bound Cys21/Cys22 near Cys71/Cys72 in MerF, we used a system containing MerF in the Top6 membrane. Hg2+ was coordinated by Cys21 and Cys22, which are located inside the membrane. A steered MD simulation in which Hg2+ was pulled toward the sulfur atom of Cys72 at 1Å/ns was used to generate the initial windows for a subsequent replica-exchange umbrella sampling (REUS) simulation38–40. In the REUS simulation, a set of 25 windows covering the distance range of 3Å to 24Å was used. Window spacing and force constants were chosen to produce a typical exchange rate between neighboring windows of 0.2–0.4 (minimum of 0.12 and maximum of 0.51). After sorting the resulting trajectories, the potential of mean force (PMF) was determined using the weighted histogram analysis method (WHAM)41. Convergence was achieved after 16ns/window (400ns in total), judged by the root-mean-square difference in the PMFs of 0.34kcal/mol between the PMF after 12ns/window and that after 16ns/window. The PMF with its standard deviation is plotted in Fig. S2.

MerP-MerF.

For quantifying the association of MerP’s Hg2+-bound Cys14/Cys17 and Cys21/Cys22 of MerF, we used a system containing MerF in the Top6 membrane and MerP placed above the membrane, with Hg2+ coordinated by Cys14 and Cys17 of MerP. A steered MD simulation in which Hg2+ was pulled toward the sulfur of MerF residue Cys21 at 1Å/ns was used to generate windows spaced every 3–10Å along the separation pathway. These windows, located at separations of 3, 6, 9, 12, 15, 20, 25, 30, 40, 50, and 60Å, were then equilibrated for 80ns (separations less than 25Å) or ~20ns (separations greater than 20Å). The equilibrated windows were then used to seed a subsequent replica-exchange umbrella sampling (REUS) simulation38–40. In this simulation, 66 windows were evenly spaced from a distance of 3Å to 68Å, with force constants chosen from a range of 2.0–3.5kcal/mol·Å2. Each window was simulated for 8ns for total simulation time of 528ns. Because the barrier to approach was high (~20kcal/mol), a second REUS simulation was initiated using the same initial configurations but a different set of force constants. After 9ns/window (594ns in total), the free energy of the MerP-MerF associated state was much lower at 7.5kcal/mol. PMFs from these 1D attempts are provided in Fig. S3.

The 1D REUS simulations showed a significant separation of the two MerF transmembrane helices as the Hg–Cys21 distance approached 0. Initiation of this separation varied between REUS runs and was not consistent across the individual windows. To track it, we calculated the angle between the center of mass of the backbone atoms of (i) residues 25 to 40, (ii) residues 41 to 45, and (iii) residues 46 to 66 (illustrated in Fig. 3 below). Using the final coordinates from each window of the second 1D REUS simulation, we then ran ~25ns of metadynamics along this MerF angle, where a Gaussian hill of height 0.1kcal/mol and width 1° was added to the potential energy function every 1000 time steps. Each metadynamics system was also restrained along the Hg–Cys21 distance coordinate using the same harmonic restraint from the 1D REUS simulations. We then chose starting coordinates from these metadynamics simulations on a 1Å × 5° grid, which resulted in a total of 1481 windows. We ran 15ns/window of 2D REUS simulations, for a total simulation time of 22.2μs, with harmonic force constants of 2kcal/mol·Å2 and 0.1kcal/mol·deg2. for the distance and angle coordinates, respectively. The average exchange rate between neighboring windows was 0.19 (minimum of 0.04 and maximum 0.44), with >99% falling between 0.1–0.4 and >40% between 0.2–0.4. The first 5ns of each window was discarded before calculating a 2D PMF using a modified version of the WHAM code from Alan Grossfield41 that uses the method of direct inversion in the iterative subspace (DIIS)42. Convergence was monitored by examining 1D PMFs along the Hg–Cys21 distance calculated by integrating out the MerF angle coordinate from the 2D PMFs using 1ns/window blocks of the REUS simulations (Fig. S4). The RMS distance was 0.15kcal/mol between the 1D PMFs calculated using 5 to 13ns/window and that calculated using 5 to 15ns/window, and 0.34kcal/mol for the corresponding 2D PMFs.

Figure 3:

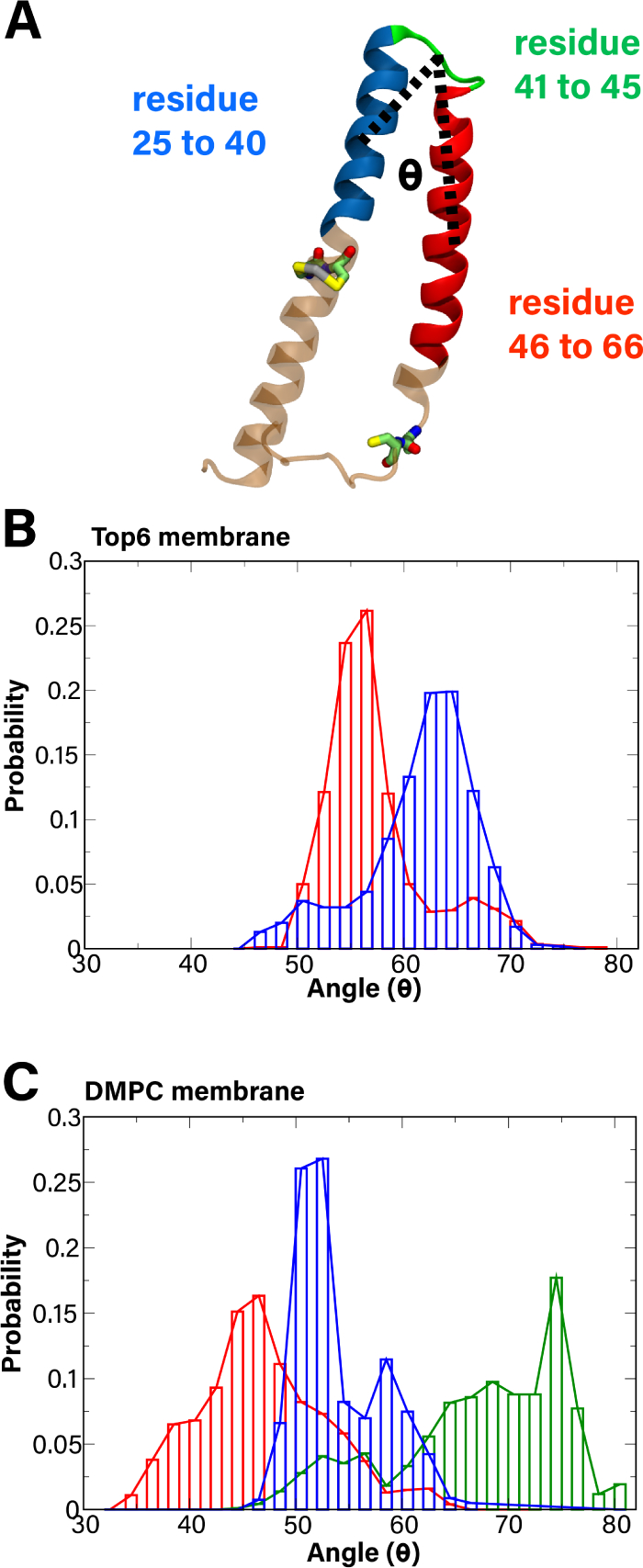
Figure 3:

Open in a new tab

MerF inter-helical angle. (A) A representation of the calculated angle (black dotted line) between the center of mass of the backbone atoms of residues 25 to 40 (blue), residues 41 to 45 (green), and residues 46 to 66 (red). (B,C) Histograms of measured angle of MerF’s TM helices are shown for the Top6 membrane system (B) and DMPC membrane (C). The apo and Hg(II)-bound state of Cys21/Cys22 are shown in blue and red, respectively. The result of truncated MerF (MerFt) with no Hg bound is shown in green in C. These histograms are averages from the last 400 ns of two separate runs of 500 ns for each system.

RESULTS

We performed all-atom MD simulations to obtain insight into the structural properties of two states of full-length MerF (with and without Hg2+ bound) as well as a truncated MerF (MerFt). The energetics of Hg-mediated association between MerF’s two cysteine pairs as well as between MerF and MerP were also studied using replica-exchange umbrella sampling (REUS) to calculate potentials of mean force (PMFs). Finally, we used a coarse-graining method to create and simulate systems with multiple copies of MerF.

All-atom simulations

Because it is presumably necessary for the first MerF binding site (Cys21/Cys22) to be near the periplasmic membrane surface to receive Hg2+, we investigated how this site is positioned with and without Hg2+ bound. We monitored the distance along the membrane normal between the head groups of the outer leaflet and the binding site, and created a histogram combining the results of two runs (0.8μs in total for each system). For both the Top6 and DMPC membranes, the binding site of the apo state of MerF stays closer to the periplasmic membrane surface compared to MerF with Hg2+ bound (Fig. 2). On average, the distances between the periplasmic membrane surface (upper leaflet in Fig. 1) of the Top6 membrane and the first binding site are 26.8 Å and 30.6 Å for the apo and bound states, respectively. While these distances do not demonstrate exposure to the periplasmic membrane surface, they indicate that when there is no Hg2+ bound to Cys21/Cys22 in MerF, it moves closer to this surface, whereas coordination of Hg2+ results in it moving farther from the surface. For the DMPC membrane, the distances are 29.5 Å and 32.6 Å for the apo and bound states, respectively; both values are larger than those of Top6 membrane (Fig. 2). The truncated MerF (MerFt) has a wider distance distribution than the other systems (Fig. 2B, green), which indicates that its Cys21/22 binding site can fluctuate more. This finding was expected because MerFt lacks the charged residues at its N- and C-termini, so the core TM domain and its binding site can move closer to or farther from the periplasmic surface of the membrane without needing to accommodate charged residues at the cytoplasmic membrane interface.

Figure 2:

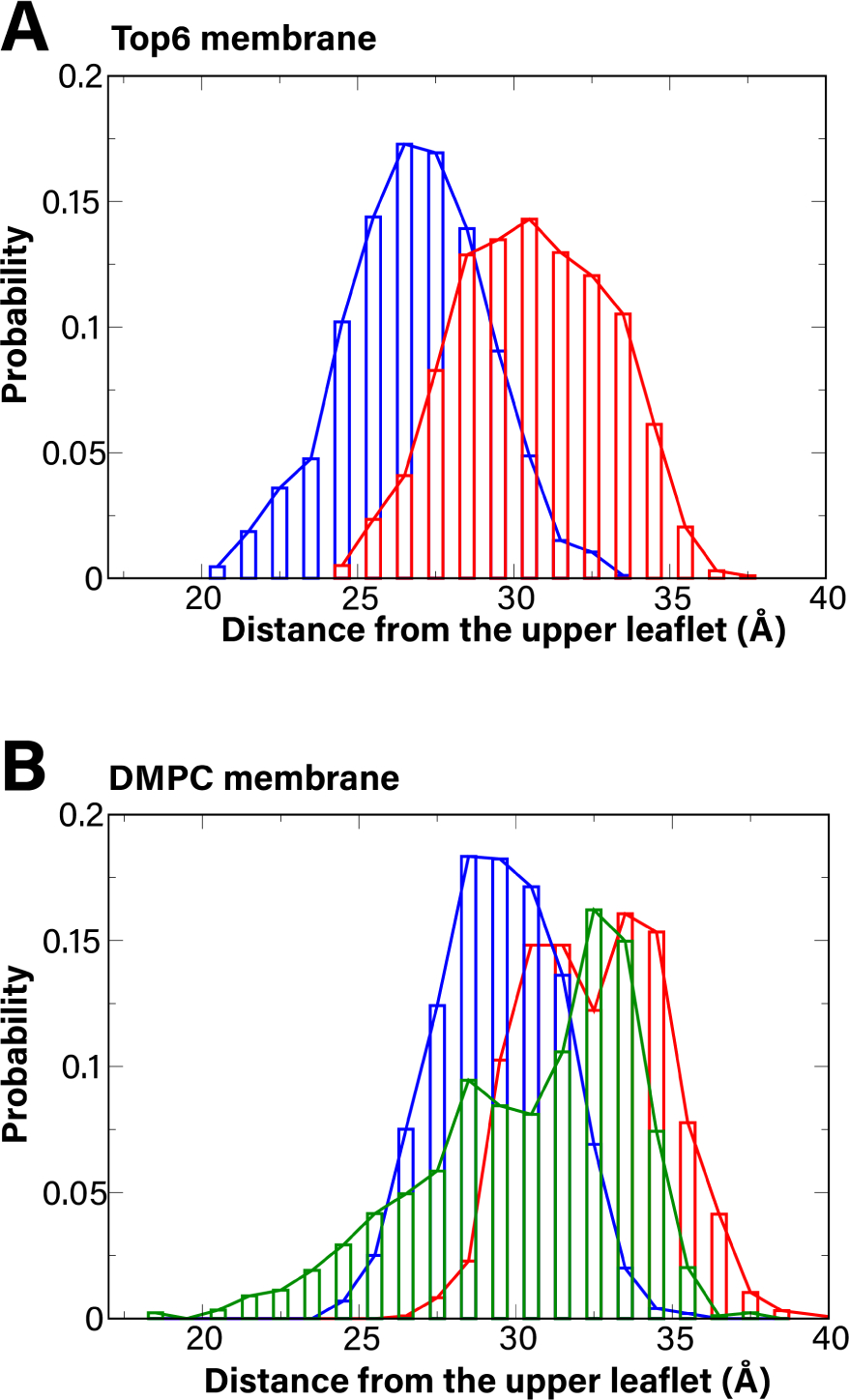
Figure 2:

Open in a new tab

Histograms of measured distance between the upper leaflet of the membrane and the first Hg2+ binding site (Cys21/Cys22) for the Top6 membrane system (A) and DMPC membrane system (B). The apo and Hg-bound state of Cys21/Cys22 are shown in blue and red respectively. The result of truncated MerF (MerFt) with no Hg2+ bound is in green in B. These histograms are averages from the last 400 ns of two separate runs of 500 ns for each system.

We also calculated the angle between the two TM helices in MerF for all the systems (defined in Methods), as we observed in our free-energy calculations (described below) that a change in this angle is necessary to bring the Cys21/Cys22 binding site to the periplasmic surface. The histograms plotted in Fig. 3 combine the results of two runs (0.8 μs for each system) for all systems. Hg2+-bound MerF has a smaller angle on average between its two TM helices (56.3 ± 4.9° and 45.8 ± 7.7° for the Top6 and DMPC membranes, respectively) than that of apo MerF (60.6 ± 5.2° and 53.0 ± 3.9° for the Top6 and DMPC membranes, respectively). Just as for the distance distributions, MerFt has the widest range of measured angles, with the highest average value of 65.5 ± 9.5° and a maximum interhelical angle of 80.1°.

The distance between the periplasmic membrane surface and the first binding site (Cys21/Cys22), as well as the angle between its two helices suggest how MerF’s conformation could influence its function. In the apo state, Cys21/Cys22 presumably need to be close to the periplasmic membrane surface to acquire Hg2+ from MerP. In this case, the distance to the membrane surface would be small (Fig. 2) and the angle between the two helices would be large (Fig. 3). Subsequently, when Hg2+ is bound to MerF, the first binding site (Cys21/Cys22) moves away from the periplasmic membrane surface (i.e., larger distance) and the two TM helices would likely be closer together (i.e., smaller interhelical angle). These conformational changes bring the first and second binding site (Cys71/Cys72) closer to each other, which is necessary for the transfer of Hg2+ between these two cysteine pairs. However, we note that the measured distance between Cys pairs when Hg2+ is bound to Cys21/Cys22 is still too large for transfer.

Energetics of conformational change in MerF

The directionality of Hg2+ movement across the membrane will be dictated by the difference in concentrations on each side. In vivo, uptake occurs because the cytoplasmic reduction of Hg2+ to Hg(0) results in an inward electrochemical gradient of Hg2+. Here we assume that MerA will acquire Hg2+ from MerF and reduce it to Hg(0), ensuring continued uptake from the periplasm to the cytoplasm. For MerF to transport Hg2+ requires direct handoff of the ion from one vicinal cysteine pair to the other. In the NMR structure (PDB 2M67), these pairs of residues are ~15Å apart, which is too long to support a direct transfer of the ion in that conformation. Therefore, to assess the likelihood of such a transfer, we calculated a potential of mean force (PMF) as a function of the distance between one pair (Cys21/Cys22) coordinating an Hg2+ ion and the other pair without an ion bound (Cys71/Cys72).

In the NMR structures, the two pairs of cysteines, which were mutated to serine, are around 10–12 Å apart (PDB 2MOZ) and 18–23 Å apart (PDB 2M67). The latter distance corresponds to the minimum in the PMF (Fig. 4A). Bringing the two cysteine pairs closer to one another initially only requires movement of the free pair, which is on the unstructured C-terminus in the cytoplasm (Fig. 4D), and results in practically no change in the PMF. To get closer, the first TM helix begins to bend (Fig. 4C,D), aided by a nearly universally conserved proline at residue 25, which is present in 96.5% of over 3,500 MerF sequences (see Fig. S5 for a sample of sequences). Although the proline leaves 1–2 polar groups along the backbone unable to form hydrogen bonds, in nearly half of the analyzed REUS trajectories, a water molecule is present in its vicinity inside the membrane, less than 10 Å from the surface.

Figure 4:

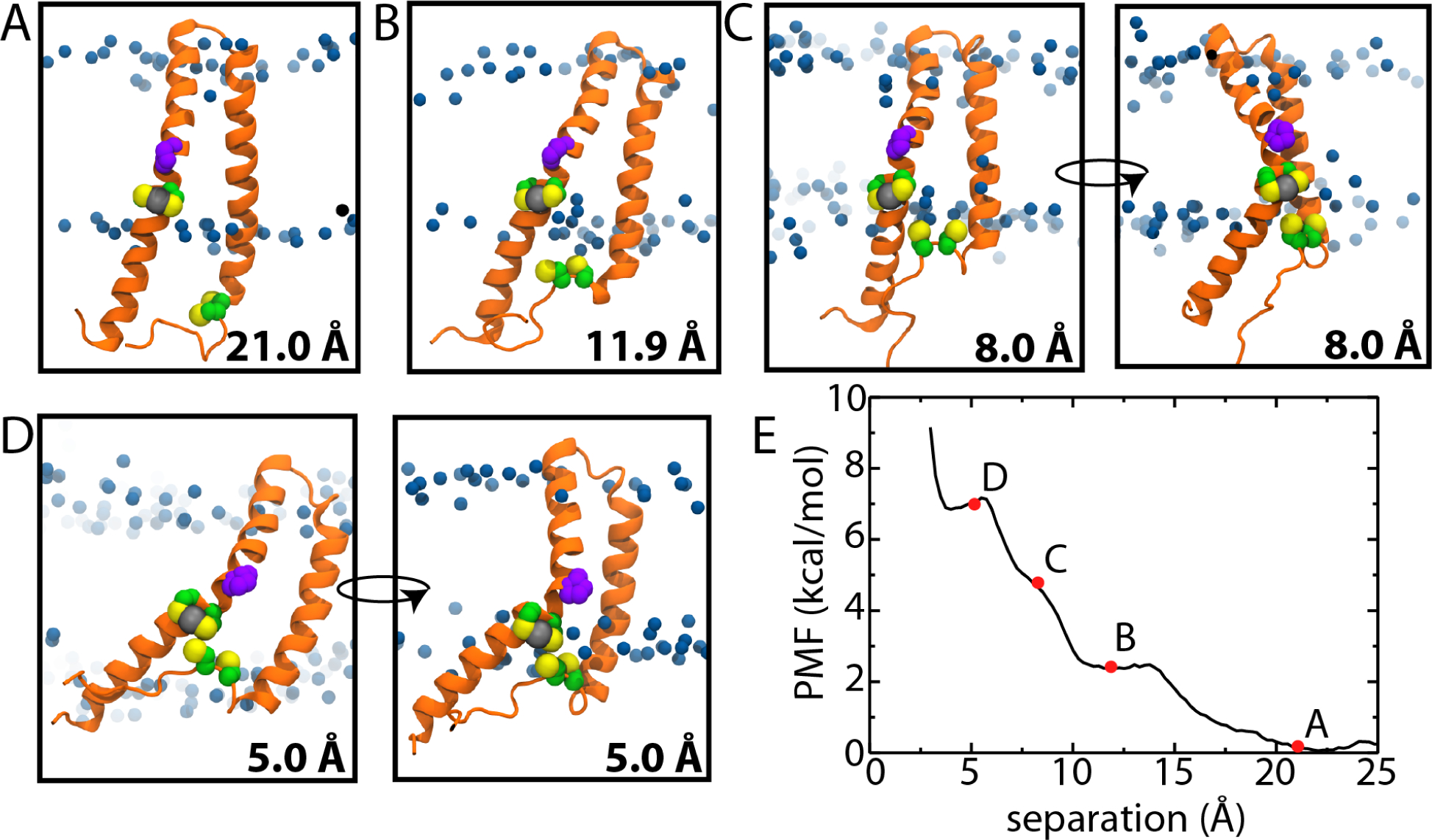
Figure 4:

Open in a new tab

Conformational changes associated with handoff of Hg2+ in MerF. (A-D) Snapshots from the REUS simulations at the specified distances. MerF is shown in orange, with the four cysteines shown as green and yellow spheres and Pro25 in purple. Hg is shown as a grey sphere coordinated by Cys21/Cys22 while Cys71/Cys72 approach from outside the membrane. The blue spheres are the C2 carbons of the lipid tails, indicating the extent of the hydrophobic region. In C and D, two views are shown with one rotated by ~90° with respect to the other. (E) PMF versus distance between the two pairs of cysteines. Snapshots in A-D are taken from the points labeled. Cys71/Cys72 were modeled as neutral thiols in the simulations. See Fig. S2 for the standard deviation of the PMF.

Although bringing the pairs of cysteines together requires MerF to change its conformation in the membrane, the associated free energy change is relatively modest. At 10-Å separation, the rise in the PMF is only 3.0 ± 1.4 kcal/mol (Fig. 4E). At shorter separations, the bend in the first TM helix becomes more pronounced and the PMF rises to 5.0 ± 1.4 kcal/mol at 8 Å. At this point, reducing the separation farther distorts the membrane as well, as the second pair of free cysteines on the unstructured C-terminus moves toward the membrane center (Fig. 4D). However, at no point does this pair enter the hydrophobic region of the membrane. Despite modest distortion of both the protein and the membrane, the energetic cost to bring the cysteine pairs within 5 Å of each other is only 7.1 ± 1.7 kcal/mol. This activation energy is sufficiently small to allow for relatively rapid association of the cysteine pairs and transfer of Hg2+.

We also simulated the post-transfer state, with Hg2+ bound to Cys71/Cys72 instead, for 100ns. The separation between the cysteine pairs increased quickly to ~15Å within 20ns and remained between 10 and 15Å for the rest of the simulation (Fig. S6). Cys71/Cys72 with the bound Hg2+ remained on the membrane surface. The reverse process, in which Cys71/Cys72 transfers Hg2+ to Cys21/Cys22, is not thermodynamically forbidden; however, it is presumably prevented by subsequent transfer to the mercuric reductase (MerA) in the cytoplasm43.

Energetics of MerP and MerF association

Before MerF can transport Hg2+ across the cytoplasmic membrane, it must first receive it from the periplasm. The most obvious candidate is MerP, the periplasmic Hg2+ binding protein. While an early attempt to detect an interaction between MerF and MerP was unsuccessful5, a later study demonstrated a roughly two-fold increase in uptake by MerF and MerP compared to MerF alone6. Given that both of MerF’s pairs of cysteines are positioned near the cytoplasmic membrane surface (one inside the membrane and one outside), how MerP could deliver Hg2+ to MerF is unclear. To determine a possible pathway, we calculated a two-dimensional PMF as a function of the MerP-MerF distance and the angle between MerF’s two TM helices. The second reaction coordinate (MerF angle) was found to aid sampling of MerF’s conformational flexibility (see Methods). To avoid including the kinked region in MerF’s first TM helix, we defined it as beginning at Pro25 (see Methods).

In all states sampled, MerP interacted with the membrane. In equilibrium simulations, even when MerP was initially placed away from the membrane, it quickly adsorbed to it. This adsorption is due to 5–10 hydrogen bonds that form primarily between basic residues and lipid head groups, especially the negatively charged lipids. For example, Lys22 forms a hydrogen bond with the membrane in 66% of sampled states; other residues forming a hydrogen bond roughly half the time include Lys23, Lys27, Lys33, Glu39, and Arg41. In particular, all six of these residues formed hydrogen bonds with lipids when Hg-bound MerP approached MerF’s cysteines.

Initially, approach of the Hg-bound MerP requires very little change in energy (up to ~30 Å separation) as MerP surveys the membrane surface (Fig. 5A–C). In this low-energy region of the PMF (0–5 kcal/mol), the angle of MerF’s helices consistently fluctuates around 60° (Fig. 5F), which is in line with the typical value for apo MerF (60.6 ± 5.2°; Fig. 3B). However, because MerF’s Cys21/Cys22 are typically 20–30 Å from the periplasmic membrane surface, further reduction in separation between them and MerP requires a conformational change in MerF (Fig. 5D). The angle between its helices begins increasing in order to bring Cys21/Cys22 closer to the membrane surface, rising to ~95° at the point of closest approach (Fig. 5E). This increase is necessitated by a number of charged residues at the cytoplasmic ends of MerF (Lys2, Asp3, Lys5, Arg9 along with Arg64, Lys65, Arg66, Asp69) and one at the hinge (Asp44) that prevent either terminus from being pulled into the membrane during MerP-MerF association.

Figure 5:

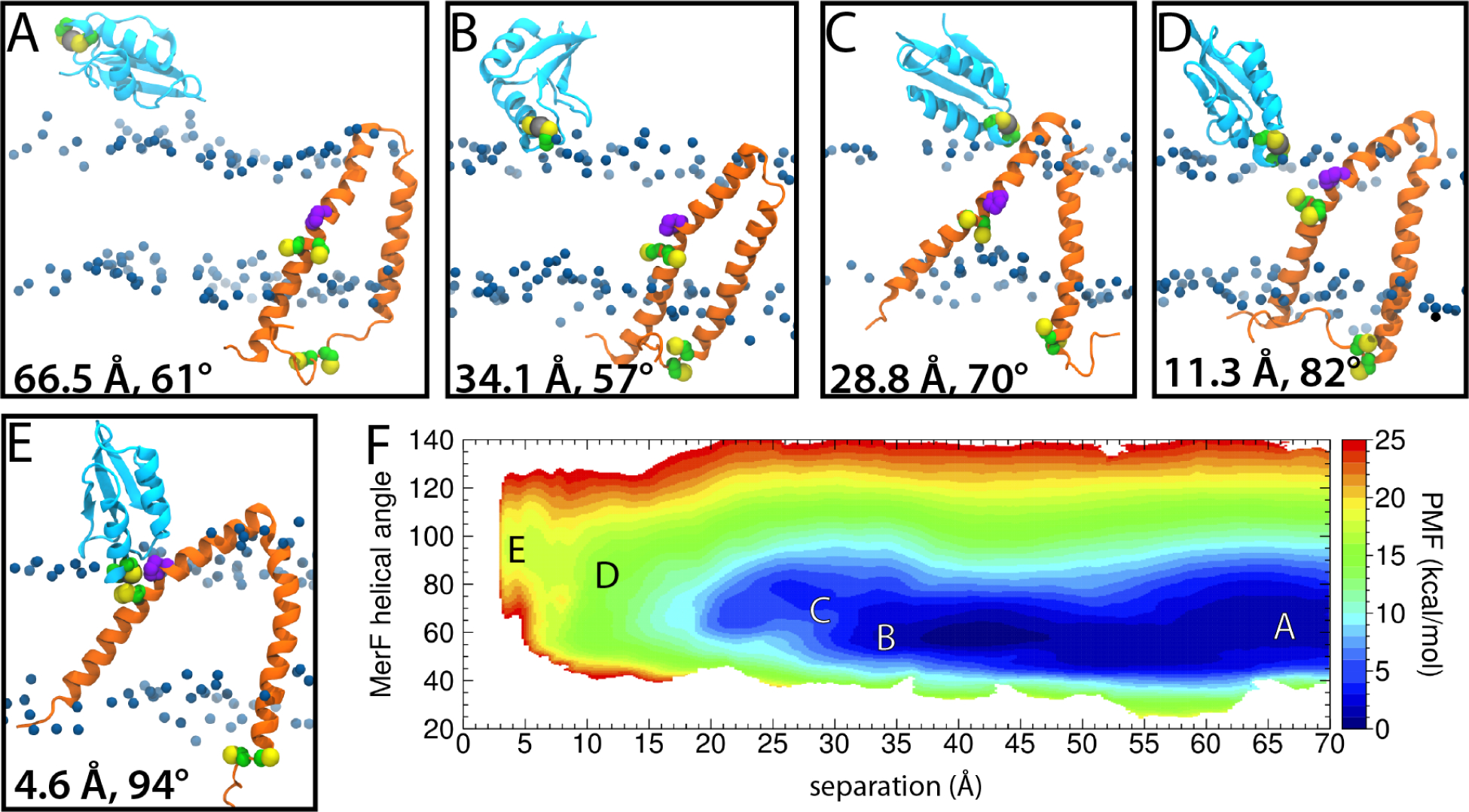
Figure 5:

Open in a new tab

Association of Hg2+-bound MerP and MerF. (A-E) Snapshots from 2D REUS simulations at the specified distances and angles. MerF is shown in orange and MerP in cyan. All cysteines are shown as green and yellow spheres and Pro25 of MerF is in purple. The ion is shown as a grey sphere coordinated by Cys14/Cys17 of MerP. The blue spheres are the C2 carbons of the lipid tails, indicating the extent of the hydrophobic region. (F) PMF as a function of the distance between Hg2+ and Cys21 of MerF and the angle of MerF’s TM helices. Snapshots in A-E are taken from the points labeled.

We also integrated the 2D PMF along the angle coordinate to produce a 1D PMF as a function of separation (Fig. S4). While the energetic cost of bringing MerP’s Cys14/Cys17 and MerF’s Cys21/Cys22 together is apparently high (16.2 ± 0.8kcal/mol relative to the fully separated state), we observed a number of favorable interactions, including the aforementioned hydrogen bonds between MerP and the lipid head groups. To assess the stability of this state, we took a frame from the REMD calculation in which the Hg2+ bound to MerP is 3.5Å from MerF’s Cys21 and ran it without any external forces applied for 2μs. We found that the distance was maintained around 5–7Å for 800ns, increasing to 11Å for another 700ns. Only after 1.5μs did MerP begin to move away from the membrane interior (Fig. S7). The apparent stability of the bound state suggests that it is either metastable or that the PMF is not truly converged due to slowly evolving degrees of freedom, e.g., membrane reorganization44,45.

Coarse-grained simulations of multiple copies of MerF

Although it is assumed that MerF functions as a monomer5, the large free energy required to bring its vicinal cysteine pair into contact with MerP leaves uncertain the mechanism of transfer of Hg2+ from the periplasm. Inspired by the existence of other Mer proteins with more than two helices5, we considered the possibility that MerF could form dimers or even higher-order oligomers. To explore this possibility, we constructed three coarse-grained (CG) systems with different concentrations of MerF denoted CG15 (15 MerF monomers), CG25 (25 MerF), and CG35 (35 MerF) in a ~30nm × 30nm 3:1 POPE:POPG membrane. Coarsegraining is used to access simulation scales, both in size and time, that cannot be reached with an all-atom representation. Each system was run for 3μs. The proteins were initially placed at random positions and orientations by rotating each about its z axis (i.e., normal to the membrane, Fig. 6).

Figure 6:

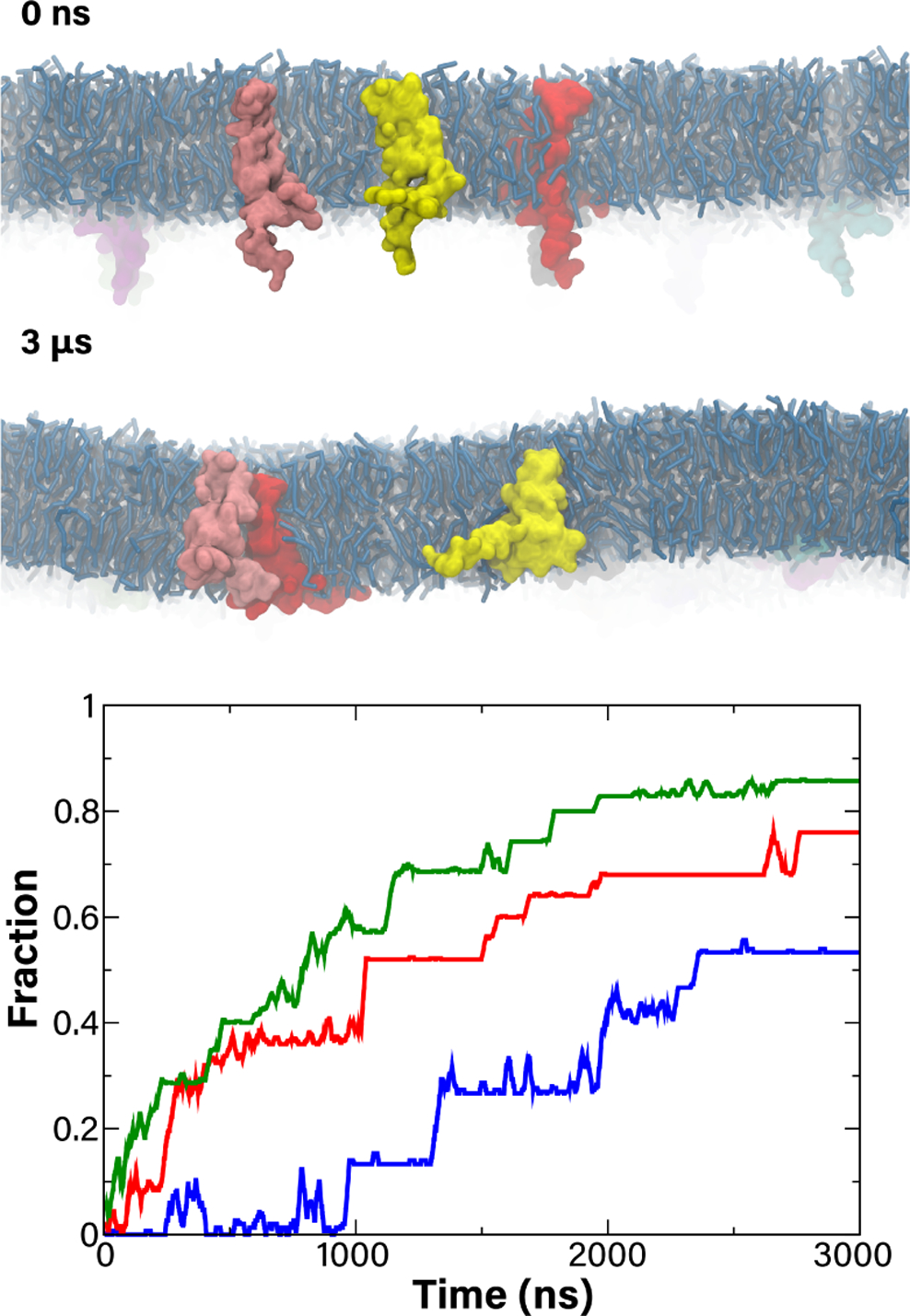
Figure 6:

Open in a new tab

(top) Side view of initial (0 ns) and final (3 μ) structures of the CG15 system. Lipids are in pale blue licorice and MerF monomers are in various colors. (bottom) The fraction of formed dimers over time for all three systems; CG15 in blue, CG25 in red, and CG35 in green.

While the simulations started with all monomers essentially dispersed, clusters began forming within the first 100ns for the denser CG25 and CG35 systems and within the first 1μs for the CG15 system. The fraction of MerF copies in a cluster of any size is plotted in Fig. 6 (bottom). This fraction goes up for all systems, apparently stabilizing within 2μs for CG25 and CG35 at 0.76 and 0.86, respectively, and 2.5μs for CG15 at 0.53. For comparison, we also generated 3,000 random distributions for each system (akin to a previous study on lipid mixing46), finding much lower degrees of clustering at 0.14±0.12 (CG15), 0.26±0.12 (CG25), and 0.37±0.10 (CG35). However, excessive aggregation has been recently noted for Martini coarse-grained models47, indicating that the irreversible formation of clusters we observed is likely anomalous. Even with a high degree of clustering, the MerF monomers were often in unproductive orientations and would be unable to share a Hg2+ ion. Over the last 1μs of the CG15 and CG25 simulations, we found on average fewer than 2% of MerF copies had a Cys21/Cys22 pair within 8Å of Cys71/Cys72 from a neighboring MerF; even for the dense CG35 simulation, this number rose only to 10%. Thus, we conclude that even if multiple MerF copies were to associate in vivo, such an association is unlikely to enhance Hg2+ transport.

DISCUSSION

Mercuric ion reduction is a key process in bacterial mercury resistance. As the reductase is located in the cytoplasm, the ion must first be transported across the cytoplasmic membrane, made possible by a number of transporters. The smallest of these is MerF, a two TM-helix protein that is nonetheless believed to move Hg2+ across the membrane, apparently without the input of external energy.5,6 Here, we have examined the dynamics and energetics of MerF, with and without Hg2+ bound, in different membrane environments to resolve the mechanism of transport.

In both a Top6 membrane, representative of the E. coli inner membrane, and a DMPC membrane, often used in experiments3,7–10, the Cys21/Cys22 pair in MerF embedded in the membrane migrated closer to the periplasmic membrane surface when Hg2+ was bound than when it was not (Fig. 2). This finding suggests a model of MerF function in which Cys21/Cys22 can approach the periplasm to receive Hg2+ from MerP near the surface. This approach would be made possible by an increase in the inter-helical angle, which is larger for apo MerF than for Hg2+-bound MerF (Fig. 3). However, our free-energy calculations for MerP-MerF association found an energetic penalty of 16 kcal/mol for Cys21/Cys22 in MerF to reach MerP near the periplasmic membrane surface, which is too large to support Hg2+ transfer. Other factors, however, may reduce this penalty, such as the presence of other proteins in the vicinity, which may induce or at least enhance the formation of membrane defects. In addition, we have not accounted for the energetic cost of chemical steps including changes in metal coordination and any associated protonation/deprotonation events that occur during inter- or intramolecular Hg2+ transfer.

While our choice of collective variables, namely distances and an inter-helical angle, for the free-energy calculations are intuitive, they are not necessarily the ideal descriptor(s) of the reaction path48. Other possibilities considered include, e.g., a “tilt” of MerF into the membrane plane, which may expose MerF’s Cys21/22 to the periplasm. The true reaction coordinate, which typically is a concerted motion of the protein(s), likely involves all of these simpler descriptors49,50. Thus, our choice of variables to bias may limit the physical relevance of the obtained free energies. Finally, it remains possible that, due to our choice of variables, we did not adequately sample very slowly evolving degrees of freedom, e.g., membrane reorganization44,45.

When Hg2+ is bound to Cys21/Cys22, the pair of cysteines is closer to the cytoplasmic side of the membrane (Fig. 2) and, correspondingly, closer to Cys71/Cys72 near the Cterminus, although contact was never observed in equilibrium simulations. Based on this observation, we hypothesized that, upon receiving Hg2+ from MerP, MerF’s Cys21/Cys22 pair transfers it to Cys71/Cys72. The conformational free energy required to bring the Cys pairs within 5Å of each other and effect this handoff is relatively small at ~7kcal/mol. After receiving the Hg2+ ion, Cys71/Cys72 presumably transfers it to MerA in the cytoplasm.

MerF sequences display significant sequence conservation (Fig. S5). The two cysteine pairs are nearly universally conserved, owing to their presumed function in transporting Hg2+. Other important residues include two prolines, Pro25 near the first cysteine pair (Cys21/Cys22) and Pro49 near the periplasmic hinge between the two TM helices. These prolines disrupt secondary structure at these points, a key feature that supports movement of Cys21/Cys22 in the membrane. Pro4, which is present near the N-terminus in the cytoplasm, is highly conserved as well. A number of charged residues are conserved as well, including an absolutely conserved negative charge (Asp or Glu) at the periplasmic hinge, and a predominance of positively charged residues at the cytoplasmic termini of MerF. These residues likely anchor MerF on both sides of the membrane during its significant conformational changes during function. In addition, they establish the proper topology of MerF during synthesis and insertion by the Sec translocon via the “positive inside rule”51,52. A highly conserved Asp is also present just upstream of the Cys71/Cys72 pair. For transfer of Hg2+ to occur between Cys21/Cys22 and Cys71/Cys72, either Cys71 or Cys72 would need to be deprotonated to enable nucleophilic attack on Hg. Presumably, a residue near Cys71/Cys72 would deprotonate one or both cysteines and then subsequently protonate the thiolate leaving groups of the other Cys pair, analogous to the mechanism of intramolecular Hg2+ transfer proposed for MerA15. An obvious candidate for this role is Asp69.

In total, our results indicate how MerF could function as a metal ion transporter despite having only two TM helices. Targeted mutations, e.g., to the conserved prolines, as well as the introduction of disulfide cross links that hold the two helices together could be used to test the role of MerF dynamics suggested here. Further work, both computational and experimental, could also focus on whether this flexibility is found in other Mer transporters, such as MerC and MerT, neither of which is structurally resolved yet. Clearly, much can be learned about protein-membrane interactions, dynamics, and transport from this deceptively simple system.

Supplementary Material

SI

ACKNOWLEDGMENTS

This work was supported by the U.S. Department of Energy (DOE) Office of Science, Biological and Environmental Research, Subsurface Biogeochemical Research (SBR) Program through the Mercury Science Focus Area Program (SFA) at Oak Ridge National Laboratory (ORNL), which is managed by UT-Battelle LLC for the U.S. DOE under Contract No. DE-AC05-00OR22725. H.H. was supported by a U.S. Department of Energy Office of Science Graduate Student Research (SCGSR) fellowship. The SCGSR program is administered by the Oak Ridge Institute for Science and Education for the DOE under contract number DE-SC0014664. J.C.G. acknowledges support from National Institutes of Health Grant R01-GM123169. Computational resources were provided through the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by NSF Grant OCI-1053575.

Footnotes

Additional Supporting Information may be found in the online version of this article.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SI
NIHMS1593338-supplement-SI.pdf (1.4MB, pdf)

RESOURCES