Abstract
We examine the effects of applied electric fields on neuronal synchronization. Two-compartment model neurons were synaptically coupled and embedded within a resistive array, thus allowing the neurons to interact both chemically and electrically. In addition, an external electric field was imposed on the array. The effects of this field were found to be nontrivial, giving rise to domains of synchrony and asynchrony as a function of the heterogeneity among the neurons. A simple phase oscillator reduction was successful in qualitatively reproducing these domains. The findings form several readily testable experimental predictions, and the model can be extended to a larger scale in which the effects of electric fields on seizure activity may be simulated.
Keywords: synchrony, electric fields, phase response, seizure, control
1. Introduction
There has recently been a growing interest in states of sustained activity within neuronal networks, and it has been suggested that such states may form the dynamical underpinnings of working memory (Wang, 2001), orientation tuning (Hansel and Sompolinsky, 1996), maintenance of head direction (Sharp et al., 2001), and perhaps other neuronal phenomena such as ocular saccade control (Aksay et al., 2001). States of sustained activity have also been implicated in pathological phenomena. Epileptic seizures, for example, are pathological dynamics whose hallmark is an abnormally prolonged and computationally dysfunctional state with sustained activation of groups of neurons. Although it has long been believed that seizures are highly synchronous events (Penfield and Jasper, 1954; Kandel et al., 1991), recent work calls this into question (Netoff and Schiff, 2002). Interestingly, recent theoretical treatments of models exhibiting sustained working memory activity have also suggested that such activity might be supported by collectively asynchronous states (Gutkin et al., 2001).
The ability to interact with and modify such collective neuronal dynamical states would be of great interest. Steady DC electrical fields applied to brain tissue have been shown to transiently suppress seizure activity (Gluckman et al., 1996). More recently, fields adjusted with a simple adaptive feedback algorithm have been employed to achieve more sustained seizure suppression (Gluckman et al., 2001). It remains unclear, however, how such mechanisms achieve this effect.
There is at present no adequate theoretical or numerical framework available to study how macroscopic electric fields modulate complex neuronal dynamics. It is not even clear what sort of state modulation—increasing or decreasing synchrony, for example—is required to achieve seizure suppression. Such a framework would find application not only in the design of seizure suppression technology, but also in the design of neural prosthetics where neuronal interactions need to be carefully manipulated.
As a first step towards achieving this goal, we have designed a simple model system to study how electric fields affect synchronization in model neurons. We use a quasi-one-dimensional array of neurons to emphasize the spatial structure of neurons in the direction parallel to the surface of the brain. An important feature of our model is a resistive network, which represents the conductive brain tissue in which the neurons are embedded (Traub, 1985). An applied electric potential perpendicular to this array simulates electrodes placed on the brain for the application of electric fields and for the measurement of extracellular local differential voltages.
The paper is organized as follows. In Section 2, we describe the computational neuronal model used in our simulation and we give some mathematical background for our subsequent phase analysis. In Section 3, we present our results, as well as an analysis of our observed synchrony transition using a reduced phase model. In Section 4, we summarize our results and propose some neurophysiologically relevant predictions that might be testable in future experiments. A detailed and complete description of our numerical model and the parameters we used can be found in the Appendices.
A report of related preliminary results has appeared previously (Park, 2003).
2. Methods
2.1. Two-Compartment Neurons Embedded in a Resistive Array
We based our numerical experiments on a computational model that we have explicitly designed to include electric field interactions (Gluckman, 1998). The presence of an electric field induces spatial polarization in neurons (Chan and Nicholson, 1986; Chan et al., 1988; Tranchina and Nicholson, 1986), and therefore, the minimal individual neuronal unit must have at least two spatially separated compartments. We therefore chose the two-compartment Pinsky-Rinzel (PR) model neuron, which consists of a dendrite and a soma compartment separated by a finite conductance gc (Pinsky and Rinzel, 1994). A schematic representation of the PR model neuron is shown in Fig. 1(a). The dendritic compartment contains a passive leakage current, a capacitive current, and three voltage-dependent ionic currents. The soma compartment contains only two voltage-dependent ionic currents, as well as passive leakage and capacitive currents. Steady currents can also be injected independently into each compartment.
Figure 1.
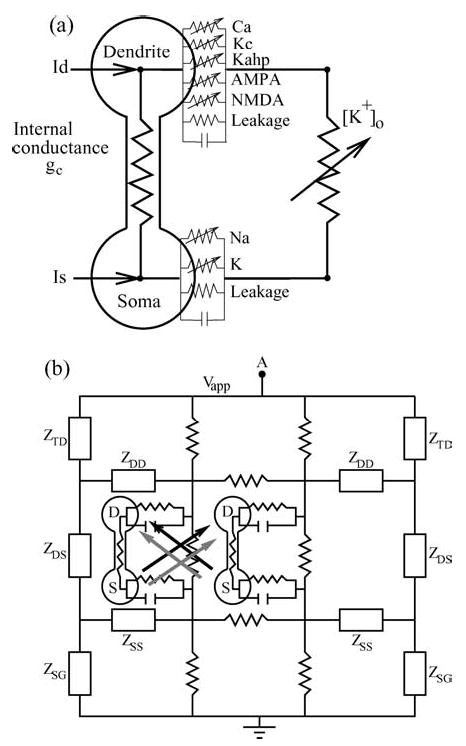
(a) Currents and conductances for a single PR neuron. (b) Synaptically-coupled neurons embedded within a resistive array modeling the extracellular medium. Black and gray arrows indicate excitatory synaptic coupling through the NMDA and AMPA channels respectively. Z indicates the equivalent terminal resistors corresponding to a resistive array of infinite extent. (TD, DS, SG, SS, DD stands for Top-Dendrite, Dendrite-Soma, Soma-Ground, Soma-Soma, and Dendrite-Dendrite, respectively.)
For the present work, two such neurons are embedded in parallel within an array of resistors which models the extracellular medium; see Fig. 1(b). The terminal resistors on both ends of the array are chosen to match the impedance characteristics of an array of infinite extent. An externally applied electric field is modeled by imposing a potential difference Vapp between point ‘A’ and ground. The existence of this resistive array also allows the neurons to communicate ephaptically. Finally, the neurons are synaptically coupled to each other via both NMDA and AMPA channels. Complete details regarding the resistive array, various currents, rate functions, and other model parameters are presented in the Appendices.
The focus of our investigation is to study the synchronization properties of a heterogeneous network of neurons under the influence of an applied electric field. To accomplish this goal, we modulate the applied potential difference Vapp and we adjust the degree of heterogeneity within the network by varying the internal conductance gc between the neurons’ somatic and dendritic compartments. The entire system of differential equations was integrated using a 4th order Runge-Kutta algorithm with a fixed integration time step.
2.2. The Measurement of Phase from Spike Times and the Synchrony Measure
Throughout this study, we specifically define neuronal synchrony in terms of the phase locking between the neurons’ spiking activity. In general, uncoupled heterogeneous neurons will spike at different rates. When these neurons are coupled together, one would expect these different spiking frequencies to “pull” toward a common mean frequency if the heterogeneity is not too large (Winfree, 1980; Kuramoto, 1984). The spike timings of the coupled neurons are expected to “phase-lock” to each other with a possible non-zero phase lag Ψ0. With still stronger coupling, the (non-identical) neurons might also spike at nearly the same time, i.e., Ψ0 → 0, in addition to spiking at the same rate. In this study, we consider two heterogeneous neurons to be synchronized if they simply phase lock to each other. We do not impose the stronger condition of exact synchrony with zero phase lag. The goal of this study is to examine the relationship between the phase-locked state, the applied electric field, and the degree of heterogeneity among the neurons.
Our procedure for assigning a phase to a given neuron’s activity is as follows. A voltage threshold for the somatic voltage Vs is chosen, and the spike times tn , where n = 1, 2, 3. . . , are defined as the times when Vs crosses this threshold.1 Then, the phase corresponding to the activity of neuron i at an arbitrary time t between its nth and (n + 1)th spike (tn(i) ≤ t < tn+1(i)) is defined as . Thus, the phase increases linearly by 2π between successive spikes (see Fig. 2(a) and (b)).
Figure 2.
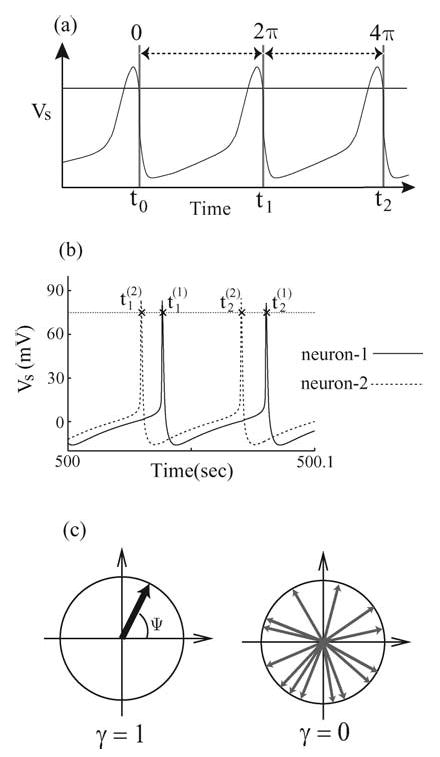
(a) Determination of the phase of a neuron’s spike by a threshold. The threshold is indicated by the horizontal solid line, and Vs is the somatic transmembrane voltage. (b) Typical tracings of the somatic transmembrane voltages from two coupled neurons within the network. Here, tn(m) indicates the spike times associated with the mth neuron’s nth threshold crossing. (c) Schematic illustration of the distribution of the relative phase ψ(t) as phasors on a unit circle. The left diagram depicts a state of perfect synchrony in which all relative phases are clustered together. The synchrony index γ attains its maximal value of one in this case. The right diagram illustrates an incoherent state in which the relative phases are randomly distributed over the unit circle and the phase synchrony index γ is close to zero.
A general n:m phase-locked state can be defined by the condition |nφ2 − mφ1 − Ψ0| < ɛ, where n and m are integers (n, m = 1, 2, 3 . . .), φ1 and φ2 are the phases of the two neurons, Ψ0 is a constant phase lag between 0 and 2π , and ɛ is a small constant (Rosenblum et al., 1996; Pikovsky et al., 2000).2 For the parameter range that we examined, the 1:1 phase-locked state was observed predominately, i.e., |φ2(t) − φ1(t) − Ψ0| < ɛ. In our analysis, we introduce the relative phase Ψ(t) = φ2(t ) − φ1(t) between the two neurons. From the definition of phase given above, Ψ(t) is simply the instantaneous phase of neuron-2, φ2(t ), when neuron-1 completes its k-th cycle at time t = tk(1):
In terms of this relative phase, the degree of phase-locking can be quantified by the synchronization indexn γ (Kuramoto, 1984; Pikovsky et al., 2001), defined as
where 〈〉 is an average over the number of spiking events (N ), which we set to 10000 in most of our simulations. If one assigns a two-dimensional unit vector (a phasor) to each relative phase measurement of Ψ, then γ gives the magnitude of the vector sum of all the phasors (see Fig. 2(c)). One can imagine that in the incoherent case, all measurements of Ψ(tk(1)) and the corresponding phasors will be uniformly distributed on a unit circle and γ should approach zero for large N. On the other hand, if the neurons are phase-locked, the distribution of the relative phase Ψ(tk(1)) will cluster around the locked value, Ψ0, and γ should approach its maximal value of one (see Fig. 2(c)).
3. Results
3.1. Natural Frequency Mismatch
In this section, we present results on the synchronization characteristics of our coupled neurons as the strength of the externally applied electric field and the heterogeneity parameter Δgc are varied. Figure 3 illustrates the variation of the synchrony index γ as the applied electric field is modulated in the case of two nearly identical neurons (solid squares) and two very different neurons (open circles). For inhibitory (negative) electric fields, the neurons tend to phase-lock with each other, and there is a range of moderate inhibitory field where the spiking ceases (see gap in the figure). Larger negative fields can depolarize the dendrites and paradoxically “excite” the neurons back into phase-locked spiking behavior.3 Qualitatively, this response to negative inhibitory fields is consistent across different levels of parameter mismatch.
Figure 3.
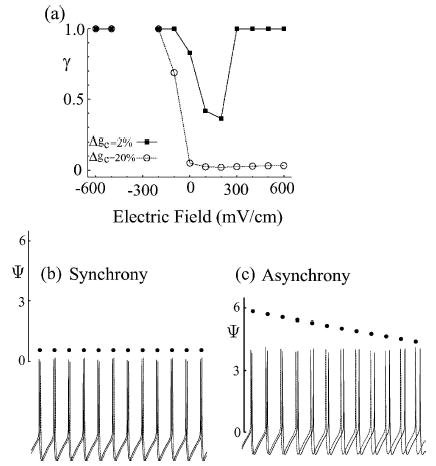
(a) Plots of the synchrony index γ as a function of the applied electric field for the cases of low (Δgc = 2%) and high (Δgc = 20%) levels of neuronal disparity. (b) and (c) Sample tracings of the relative phases ψ(t) and the somatic transmembrane voltages in the synchronous state (Δgc = 2%) and the asynchronous state (Δgc = 20%) as shown in (a). The electric field strength is fixed at 600 mV/cm in this example.
However, with excitatory (positive) electric fields, we observed a more complex network synchrony response as a function of the applied electric field and of heterogeneity. Neurons with a small parameter mismatch first desynchronize at moderate excitatory fields, and then resynchronize at larger excitatory fields.4 Neurons with a large parameter mismatch become desynchronized as the strength of excitation becomes stronger, and remains so. This result is consistent with the report of Golomb and Hansel (2000), who found that in sufficiently heterogeneous ensembles, increasing coupling tends to desynchronize the network. We show in Figs. 3(b) and (c) tracings of the somatic voltage from the two neurons at large excitatory fields (E = 600 mV/cm) in the synchronous and the asynchronous cases just described. In the synchronous case (Fig. 3(b)), the spiking from the two neurons phase-lock, and this behavior is reflected in the constant relative-phase (solid dots) plotted in the graph. In Fig. 3(c), we illustrate the asynchronous case in which the relative phase between the two neurons monotonically drifts in time.
A more complete illustration of our network’s synchronous behavior is presented in Fig. 4(a). In this figure, we show the γ index as a function of both the applied electric field strength and the parameter mismatch Δgc. We discuss several prominent features. An extensive asynchronous region is present for large excitatory fields and large neuronal disparity, in agreement with Golomb and Hansel (2000). Moderate inhibitory fields tend to induce phase locking even when neuronal disparity is large. Larger inhibitory fields suppress collective network activity. This is consistent with in vitro seizure suppression experiments (Gluckman et al., 1996, 2001). Lastly, the reemergence of phase-locked spiking activity under the largest negative fields is also seen. Among these general characteristics, the most interesting feature of this phase diagram is the boundary between the phase-locked and asynchronous (phase-drifting) states under an applied excitatory field. For small neuronal disparity there is a regime (see the wedged region indicated in Fig. 4) where moderately strong excitatory fields desynchronize the network, but an even stronger field leads to resynchronization. The threshold for this transition at small neuronal disparities is seen in Fig. 4(a) to increase with increasing Δgc.
Figure 4.
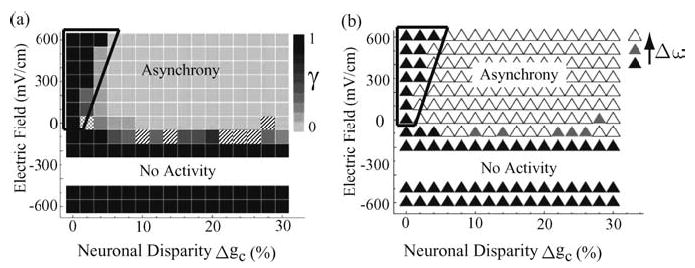
(a) Plot of the synchrony index γ as a function of the applied electric field E and the neuronal disparity Δgc. Higher-order synchrony states (n:m, n, m > 1) are indicated by hatched boxes. 1:2 synchrony states were observed at E = −100 mV/cm, Δgc = 10%, 14%, and Δgc = 22–26%; a 3:4 synchrony state was observed at E = 0, Δgc = 28%. The meshed box (at, E = 0, Δ gc = 2%) marks an intermittent non-locked state where phase drifting alternates with a relatively prolonged fluctuating but bounded phase locked transient state; for a finite measurement time, the value of the synchrony index γ was spuriously elevated from zero. (b) A plot of the natural frequency mismatch Δω as a function of the applied electric field E and the neuronal disparity Δ gc. Black triangles indicate cases where Δω < Δω*; open triangles indicate cases where Δω > Δω*; and gray triangles denote cases where Δω ~ Δω*. One should note the noticeable correspondence between the synchrony (asynchrony) regions in (a) and the regions in (b) with Δω < Δω*(Δ ω > Δω*). The observed critical threshold Δω* correctly predicts the wedged region where, for fixed Δgc, the coupled network desynchronizes and re-synchronizes as the strength of the applied electric field is increased from zero.
We now argue that the transition to synchrony in the network including the wedged region can be explained using a simple phase oscillator model (Winfree, 1980; Cohen et al., 1982; Kuramoto, 1984; Ermentrout and Kopell, 1984). Specifically, the boundary between the synchronous and the asynchronous states is highly correlated with the degree of natural frequency mismatch among the individual units within the network. To illustrate this connection, we plotted the degree of natural frequency mismatch Δω between the neurons in isolation as a function of the applied electric field and neuronal disparity in Fig. 4(b). For each neuron in isolation, its intrinsic natural frequencyω is measured with the same parameters as in the coupled network and subjected to the same applied electric field. The natural frequency mismatch Δ ω is then simply the difference in theω values between the neurons. By comparing Figs. 4(a) and (b), one can see that there exists a critical value of natural frequency mismatch Δω* such that for Δω > Δω*, the network is in the asynchronous state, and for Δω < Δω*, the neurons phase lock to each other. The critical value Δω* was empirically determined in our numerical experiment to be approximately 0.63 rad/s. It is remarkable that this simple criterion reproduces the observed synchrony transition boundary so well. In particular, it correctly predicts that for small neuronal disparity (Δgc < 6%), increasing the (excitatory) electric field first desynchronizes and then resynchronizes the network (see the wedged region in Fig. 4(b)). To clarify this point, Fig. 5 (lower panel) shows the decrease in Δω as a function of the increasing (excitatory) electric field strength at Δgc = 4%. One can understand this result by noting that each individual neuron’s spiking rate is a monotonically increasing concave-down function with respect to the applied electric field (see Fig. 5—top panel). This behavior is biologically reasonable since the spiking rate of a neuron will ultimately be limited. Thus, as the spiking rate increases with increasing excitatory fields, the corresponding incremental change between two different neurons is smaller. In the small disparity regime, an initial frequency mismatch might be larger than Δω* at low excitatory fields (so that the network is asynchronous when coupled), but it might become small enough with increasing excitatory fields such that the difference between the spiking rates of the two neurons decreases below the critical level Δω*. Thus, at sufficiently high excitatory field, phase locking is observed.
Figure 5.
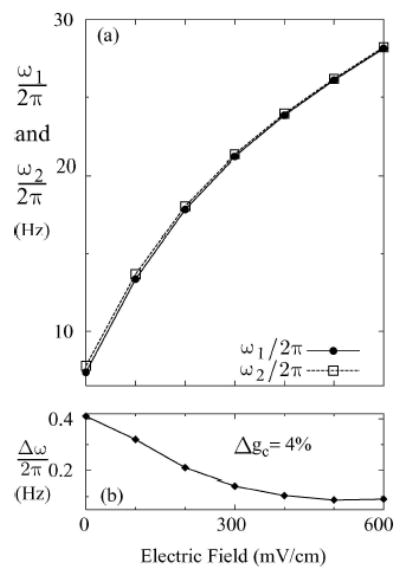
(a) A plot showing the dependence of the mean natural frequencies (ω1 and ω2) of two heterogeneous neurons (Δgc = 4%) on the applied electric field. (b) The difference between the natural frequencies (Δω= ω2 − ω1) as a function of the applied electric field.
In our discussion so far, we have focused on the simplest 1:1 phase locked state. Within the parameter range of our study, we have observed a few cases where the two neurons are synchronized at higher-order n : m phase locked states (cross-hatched squares in Fig. 4(a)). If Ω1 and Ω2 are the observed frequencies of the coupled neurons, the n : m phase locked state is characterized by the condition: nΩ2 − mΩ1 = 0 (Pikovsky et al., 2001). These higher order locked states are expected to occur when the natural frequencies of the two neurons in isolation are roughly in the same rational ratios, i.e.,ω1/ω2 ≈ n/m (Ermentrout, 1981; Pikovsky et al., 2001). Figure 6 gives some examples of the values of Δgc (10%, 14%, and 24%) at E = −100 (mV/cm) where the natural frequencies of the neurons give the approximate rational ratios 3/4, 2/3 and 1/2. To demonstrate these n:m phase locked states, we plotted ΔΩ = nΩ2 − mΩ1 as a function of Δgc for four different combinations of n and m (see Fig. 7). Since Δgc is functionally related to Δω and is a direct measure of the difference between the individual uncoupled neurons, Δgc serves as the detuning parameter for this analysis. The n:m phase locked state in these detuning curves are indicated as plateau regions with Δ Ω = 0. As one can see from Fig. 7, the plateau regions correspond to ranges in Δgc where ω1/ω2 ≈ 1(0% ≤ Δgc ≤ 4%), 1/2 (22% ≤ Δgc ≤ 26%), 2/3(13% ≤ Δgc ≤ 14.2%), and 3/4 (9.9% ≤ Δgc ≤ 10.3%).5
Figure 6.
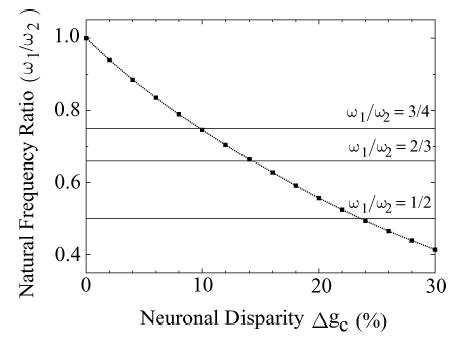
The ratio of the natural frequencies (ω1/ω2) of two uncoupled neurons under the influence of an applied electric field (E = −100 mV/cm) is plotted as a function of the neuronal disparity Δgc(%). The intersections between this curve and the horizontal lines indicate where the natural frequency ratios attain the rational values 1/2, 2/3, and 3/4. These crossing points occur near Δgc = 24% (1/2), Δgc = 14% (2/3), and Δgc = 10% (3/4).
Figure 7.
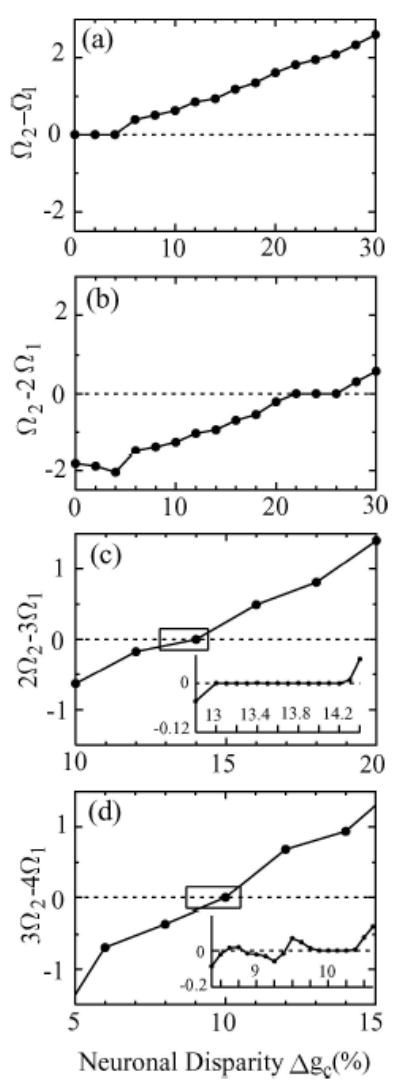
Plots of frequency differences Ω2 − Ω1 of mutually coupled neurons as a function of the neuronal disparity Δgc(%) for the case E = −100 mV/cm. The plateaus indicate the n:m phase-locked states with (a) Ω1 : Ω2 = 1:1, (b) 1:2, (c) 2:3, and (d) 3:4. The locations of these plateaus correspond to similar ranges in Δgc in Fig. 6 where the natural frequency mismatches are in the same n/m ratios.
3.2. Phase Response
In our network, the dynamics of the individual units are determined by the Pinsky-Rinzel equations, which include many state variables. Nevertheless, the resulting dynamics in our chosen parameter range are predominately periodic spikes. This periodic behavior can typically be reduced to a simple phase equation under a suitable parameterization and the assumption of weak coupling. Various authors (Rand and Holmes, 1980; Cohen et al., 1982; Kuramoto, 1984; Ermentrout and Kopell, 1984) have given detailed descriptions for similar phase reductions in different biological systems. For the following discussion, we assume that the reduced phase equation for the ith uncoupled neuron can be written as
where φi is the phase of the ith neuron, and ωi (E, gc(i)) is the natural frequency of the ith neuron in isolation (i.e., without any synaptic or electrical couplings between neurons). Note that ωi depends explicitly on the externally applied electric field E and the internal conductance gc.
With two or more neurons mutually coupled together as in our network, we follow Refs. (Kuramoto, 1984; Cohen et al., 1982; Ermentrout and Kopell, 1984) and further assume that the input from the presynaptic neuron is not so strong that it significantly alters the form of the spike. From our numerical simulations, this is a valid assumption for almost the entire range of parameters examined. Under this assumption, the network of coupled phase oscillators can be written as
where the sum is over all neurons (j) which are connected to the ith neuron. In general, we expect the coupling function fi (E, φj − φi) to depend on the applied electric field E and the relative phase of the neurons. In the case of only two mutually coupled neurons, we can explicitly write down the following reduced dynamical equations:
| (1) |
where Ψ = φ2 − φ1 is the relative phase between neuron-1 and neuron-2.
To understand the dynamics of phase locking within this network, one can consider the temporal evolution of the relative phase Ψ by subtracting the previous two equations,
| (2) |
where Δω ≡ ω2 − ω1 is the mismatch in the natural frequencies of the two individual neurons in isolation and Δf ≡ f1 − f2, the phase sensitivity function, is simply the difference between the coupling functions. For identical neurons with symmetric coupling, f1(ψ) = f2(− ψ) = f (ψ) and Δf (ψ) will simply be twice the odd part of f (ψ), i.e., 2 fodd(ψ) = f (ψ) −f (−ψ). For non-identical neurons, Δf (ψ) will typically contain both even and odd parts. For a pair of neurons to phase lock to each other, the necessary condition is , i.e., the relative phase Ψ is constant. For a particular choice of the parameters E and Δgc, the natural frequency mismatch of the neurons, Δω, is constant and Δf is a function of the phase difference Ψ only. Requiring the right hand side of Eq. (2) to be zero, the condition for phase-locking becomes
| (3) |
where Ψ* is the locked phase lag between the two neurons. A schematic illustration of this phase-locked criterion is given in Fig. 8. The dashed line is the constant value of Δω and the solid line is the function Δ f (Ψ). The crossing points (indicated by the three small circles) are the possible phase-locked equilibrium states predicted by this reduced phase model for a particular choice of applied electric field E and Δgc. The stability of these phase-locked states is given by the sign of the local slope of Δf (Ψ) at these locations. For example, Ψ*b is a stable equilibrium with . One can understand the stability argument by noticing that for Ψ slightly less than ψ*b, Δf (ψ) < Δω so that . Then, in time, Ψ will increase toward Ψ*b from the left. Similarly, for Ψ slightly larger than Ψ*b, Δf (Ψ) > Δω and so that Ψ will decrease toward Ψ*b from the right. By a similar argument, one can see that the remaining two phase-locked states at ψ*a and ψ*c are unstable equilibria. In summary, if one can obtain the phase sensitivity function Δf (Ψ) and the natural frequency mismatch Δω for the ensemble at a given choice of E and Δgc, one can then use the reduced phase model to predict the stable phase lags Ψ*b for the two locked neurons from a graph similar to Fig. 8.
Figure 8.
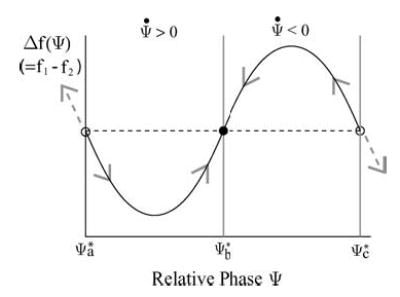
A schematic diagram of the phase sensitive function Δ f as a function of the relative phase Ψ between the two neurons. The phase-locked states correspond to the locations where Δf (solid line) is equal to the natural frequency mismatch Δω (dashed straight line). The stability of these equilibrium states depends on the local slope of Δf . In particular, the stable phase-locked state at Ψ*b (filled circle) has a positive local slope for Δf , and the unstable phase-locked states at Ψ*a or Ψ*c (open circles) have negative local slopes for Δf.
To get a conceptual picture of the synchrony transition for a pair of heterogeneous neurons, we discuss a canonical example for illustrative purposes. Consider the simple example in which f and Δf are given by Figs. 9(a) and (b). The coupling function f is basically given by its canonical form of (a0 + a1 cos(ψ) + b1 sin(ψ)) (Ermentrout, 1996) and Δf is simply the anti-symmetric part of f. Furthermore, since the elicitation of spikes in one neuron from another neuron cannot be instantaneous, this coupling function f will typically be phase shifted by a small amount δ. One should in general expect this phase shift to be influenced by the synaptic time constants of the NMDA or the AMPA channels, the time constant in the kinetics of the membrane, and the conduction velocity between neurons (not modeled here).
Figure 9.
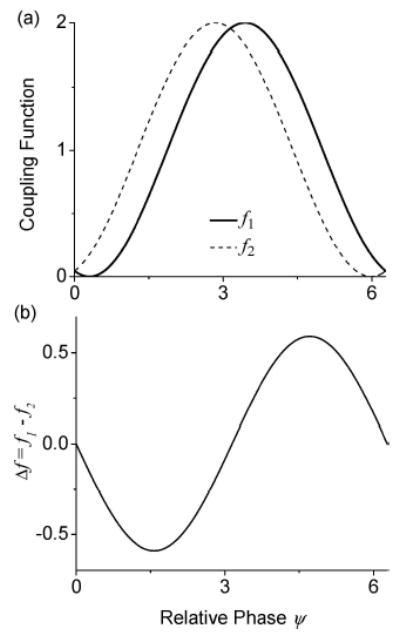
(a) An illustration of the coupling functions: f1 = 1 + cos(Ψ−π−δ) (solid line) and f2 = f1(2π − Ψ) = 1+cos(Ψ−π+δ) (dashed line). Here, the cosine curve has been phase shifted by π so that the strongest phase response from a neuron occurs near Ψ = π and the parameter related to synaptic delay, δ, was chosen to be 0.3. Compared with the canonical form f(ψ) = a0 + a1 cos(ψ) + b1 sin(ψ), we have a0 = 1, a1 = cos(π− δ), and b1 = sin(π − δ) for f1 and a0 = 1, a1 = cos(π + δ), and b1 = sin(π + δ) for f2. (b) A plot of the phase sensitivity function, Δ f = f1 − f2.
To analyze the phase-locked states of this idealized model, we need to compare Δf (Ψ) with Δω. For identical neurons, the natural frequency mismatch Δω is zero. Then according to Eq. (3), there will be two phase-locked equilibria at Ψ* = 0(2π ) and π (Fig. 9(b)). Of these two phase-locked states, only the solution at Ψ* = π has a positive slope. Thus, Ψ* = π (the anti-locked state) is the only stable equilibrium. For non-identical neurons, Δω will be non-zero and its value will depend on the parameter mismatch Δgc between the two neurons and the applied electric field E. Depending on the sign of Δω, the relative phase Ψ* of the stable phase-locked state will either decrease (Δω < 0) or increase (Δω > 0) away from the anti-locked phase. There are two special relative phase values ΨLc and ΨRc corresponding to the left (negative) and the right (positive) peaks of the Δf (Ψ) function. These are, respectively, the smallest and the largest locked relative phases possible for the system. The critical values for this coupling threshold are achieved when Δω = Δf (ΨLc) or Δf (ΨRc). These two values also define the range of allowed frequency mismatch (Δf (ΨLc) ≤ Δω ≤ Δf (ΨRc)) where phase-locking between the two neurons is possible. For Δω outside this range, a non-locked phase drifting state between the two neurons is expected. One should note that, for non-identical neurons, an exact phase-locked state with Ψ = 0 is not expected to be stable in this simplified model. Biologically, this is a reasonable conclusion since synaptic coupling cannot be instantaneous, and no two neurons are exactly identical.
The key advantage of this phase model description is that it predicts the synchronization characteristics of the coupled network from the knowledge of the individual neurons, namely: their natural frequencies and coupling functions. We now apply this formalism to our model system. For a given level of applied electric field E and internal conductance gc, the natural frequency ω(E, gc) for a particular neuron can be determined simply by taking the inverse of the average of the spiking rate.6 The coupling functions f1,2(E , φj − φi) in the reduced phase model can be rigorously calculated using the averaging technique described in Refs. (Ermentrout and Kopell, 1984; Hansel et al., 1995; Ermentrout, 1996). In brief, suppose a pair of neurons is described by the following dynamical equations:
where X is a multi-dimensional vector describing the state of the neuron, F1 and F2 prescribe the intrinsic dynamics of the neurons in isolation, and G1 and G2 are the coupling functions between the two neurons. It can be shown that when the long-term dynamics of the individual neurons are stable limit cycles and the coupling strength ɛ is small, then the above nonlinear equations can be reduced to a pair of phase equations as in Eq. (1). The coupling functions f1,2 in the phase equations can then be expressed as a time-averaged quantity involving the original coupling functions G1,2 as follows:
| (4) |
where X0(t ) is the period-P limit cycle of neuron j in isolation and X*(t), called the adjoint solution, is determined by the linearized dynamical equation
where [DX F]T is the transpose of the Jacobian matrix of F(X) with respect to the state variable X. X*(t) is then further normalized according to the condition X*(t) · X′0 (t) = 1, where the prime denotes the rate of change of the vector field along the periodic orbit X0(t). This procedure is elegantly implemented in the publicly available software package XPPAUT (Ermentrout, 2002).
Alternatively, one can measure the coupling function f (E, φj − φi) of one neuron with respect to another by a sampling method. One can employ a pair of unidirectionally coupled subsystems. For two mutually coupled neurons, we decompose the system as shown in Fig. 10. In Fig. 10(a), neuron-1 receives synaptic input from neuron-2 only and one measures the rate of change of neuron-1’s phase, concurrently with φ1 and φ2. Then, the quantity gives an estimate of f1(E, φ2 − φ1) for a particular phase difference Ψ = φ2 − φ1. In some cases, the two neurons phase lock with each other under uni-directional coupling. In this latter situation, one can still sample f1(E, φ2 − φ1) by periodically perturbing the pair of neurons by a sufficiently large applied electric field or by injecting current, and measuring during the system’s transient back toward the phase-locked state.
Figure 10.
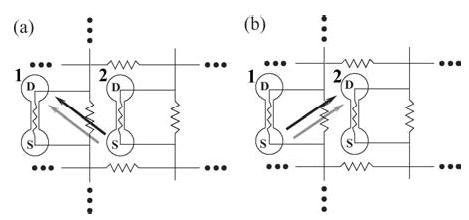
Two uni-directionally coupled PR neurons. (a) The case when neuron-2 drives neuron-1 and (b) the case when neuron-1 drives neuron-2. NMDA and AMPA excitatory synapses are denoted by black and gray arrows, respectively.
Figure 11 is an example of the coupling function calculated using Eq. (4) for a PR neuron embedded within a resistive network with an excitatory applied electric field. The inset is a close approximation to this function using the sampling method described above. Both of these methods agree qualitatively with the canonical functional form of the coupling function, and the δ phase shift due to synaptic delay can be clearly seen in the graph.
Figure 11.
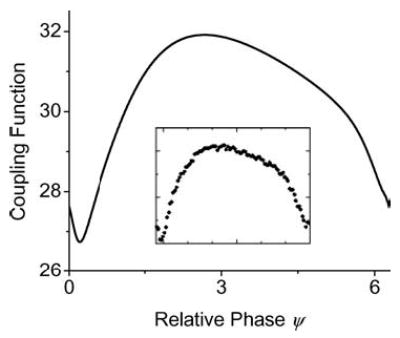
A sample coupling function f (Ψ) obtained for a PR neuron embedded within a resistive array with an applied electric field (E = 600 mV/cm). All parameters for the PR neuron are as quoted in Table 2 (Appendix) and gc = 2.1 mS/cm2. The solid curve was calculated using XPPAUT and the data points in the inset were calculated using the alternative sampling method described in the text.
Since the neurons are coupled both synaptically and electrically through the resistive network, one can in principle tease out their separate contributions to f (ψ). This can easily be done by utilizing Eq. (4) and taking the time average of, respectively, the synaptic current Isyn and/or the effective current term gc VDSout resulting from the electric polarization between the two chambers (see Appendixes A and B for details on these two terms). In Fig. 12, we have plotted the coupling function for a neuron with the same parameters as in Fig. 11 but with no externally applied electric field. In this case, we have chosen no applied electric field because we simply want to examine the phase response of a neuron purely due to the firing of its neighbor within the resistive array. Figures 12(a) and (b) are, respectively, the graphs for the coupling function f (ψ) with and without Isyn. Since the neuron remains embedded within the resistive array, the firing of the neighboring neuron can still have a modulating effect on its firing time even when Isyn = 0. However, as one can see from this graph, the contribution to the coupling function from the ephaptic coupling (Fig. 12(b)) is substantially smaller than the contribution from the synaptic channels (Fig. 12(a)). Nonetheless, since it is the difference between the coupling functions Δf (E, Ψ) that is important in determining the phase-locked criterion, this small contribution plays a significant role in determining the synchronization properties of the neurons. Furthermore, it is important to note that in contrast to the larger but positive-definite contribution from the excitatory synapes, the ephaptic contribution can be both positive and negative. Thus, the ephaptic connection has the potential to both advance and retard the phase of the next spike of the postsynaptic neuron.
Figure 12.

The coupling function f (ψ) obtained for a PR neuron embedded within a resistive array without an applied electric field (E = 0 mV/cm): (a) with both synaptic and ephaptic coupling, (Isyn ≠ 0), (b) with ephaptic coupling only (Isyn = 0). All other parameters for the PR neuron are as quoted in Table 2 (appendix) and gc = 2.1 mS/cm2.
To illustrate the utility of the reduced phase model in analyzing the synchronization among our PR neurons, we consider three examples respectively in the locked in-phase state, the phase drifting state, and the locked anti-phase state.
Our example for the in-phase locked state is from two non-identical phase-locked neurons. The parameters were E = 600 mV/cm, gc(1) = 2.1 mS/cm2, and gc(2) = 2.058 mS/cm2. From the direct simulation of this system, the ensemble has a single locked state with a phase-lag between the two neurons near Ψ = 5.7 rad (see Fig. 13(c)). The coupling functions f1, 2 for both neurons were calculated using XPPAUT and the results are graphed in Fig. 13(a). The phase sensitivity curve Δf for these two coupled neuron is shown in Fig. 13(b). Note that it crosses the natural frequency mismatch Δω = 0.5 rad/sec line near its right positive peak. The stable equilibrium state predicted from this crossing point roughly agrees with the phase locked value of Ψ = 5.7 rad observed in the full model (Fig. 13(c)). As we have discussed previously, as Δω increases, the stable equilibrium moves toward the in-phase regime near Ψ = 0 (or 2π ). Due to the intrinsic synaptic delays, the locked phase between the two neurons cannot be exactly at Ψ = 0 (or 2π). This slight phase lag in the in-phase locked neurons is exactly what we have observed in our simulation.
Figure 13.
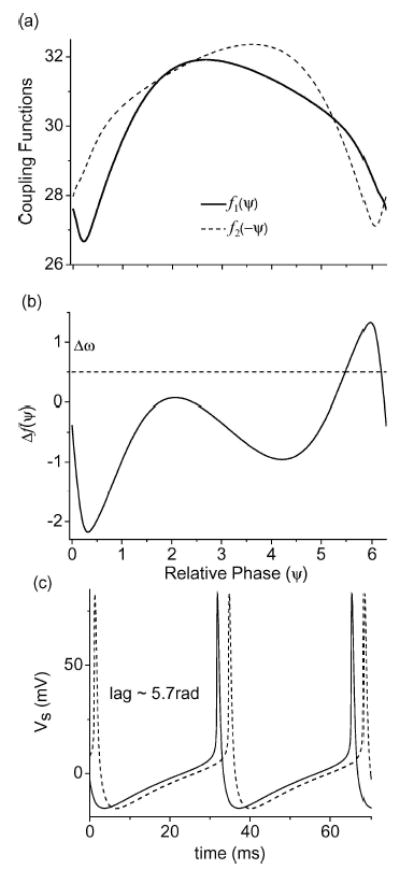
An example of the in-phase synchrony state (E = 600 mV/cm and Δgc = 2%). (a) The numerically obtained coupling functions f1 and f2 using the averaging method implemented in XPPAUT. The vertical scale for f1 and f2 is in units of rad/sec. (b) The phase sensitivity function Δf obtained by subtracting the two coupling functions. Δω = 0.5 rad/sec is also plotted in (b) as a horizontal dotted line. The in-phase locked state is located where Δf and Δω intersect. The stable in-phase locked state is predicted to have a phase lag near Ψ = 2π. (c) Voltage traces of Vs for the two neurons in the full simulation showing the phase lag near Ψ = 2π.
The next example is for the case when the two neurons do not phase lock to each other. The parameters were chosen in the asynchronous region with E = 200 mV/cm, gc(1) = 2.1 mS/cm2, and gc(2) = 1.68 mS/cm2. In this case, the phases of the two coupled PR neurons drift with respect to each other, as can be seen in Fig. 14(b). Again, using XPPAUT, we have calculated the coupling functions for these two neurons in the reduced phase model and the phase sensitivity graph Δf is plotted in Fig. 14(a). As one can see from this graph, Δω does not intersect Δf at all, and the two neurons are not expected to phase lock. This is what is observed in the actual numerical experiment.
Figure 14.
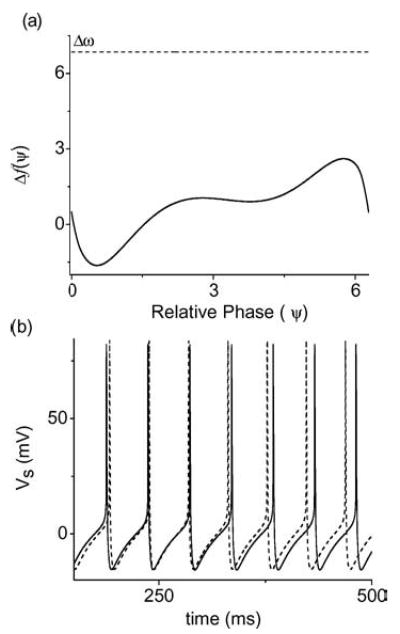
An example of the phase-drifting state (E = 200 mV/cm and Δgc = 20%). (a) The phase sensitivity function Δf =f1 − f2 obtained using XPPAUT. The dotted line is the natural frequency mismatch Δω = 6.53 rad/s for the two non-identical neurons. In this example, Δf does not intersect Δω and the reduced phase model predicts no phase-locked state. (b) Voltage traces of Vs for the two neurons in the full simulation showing the predicted phase-drifting dynamics.
The last example is for the anti-phase locked state. As we have seen in our simplified phase model (Fig. 8) previously, identical neurons (Δgc = 0%) with excitatory coupling typically phase lock in the anti-phase state (Hansel, 1995). For E = 200 mV/cm and gc(1,2) = 2.1 mS/cm2, Δω is zero and Δf is given in Fig. 15(a). As expected, this curve crosses Δω = 0 near Ψ = π. However, upon magnification, one can see that Δf actually has three zeros in this region with the left and right zeros being stable and the middle one at ψ = π being unstable. Therefore, the reduced phase model predicts that there should be two distinct locking regions near the anti-locked state. We ran many trials (2000) of our numerical experiment using the full model of the coupled PR neurons and formed a histogram of the observed locked relative phases (see Fig. 15(c)). From this histogram, we found two main clusters on either sides of Ψ = π which indicate a multi-stable phase-locked state in this anti-phase regime. The two peaks of the histogram align closely with the two predicted locked phases. However, if one examines the histogram closely, one notices that there is a spread to the two histogram peaks. This indicates additional structure in the anti-synchronous regime for the two-coupled PR neurons. We speculate that the ephaptic coupling through the intercellular medium may play a subtle role in modulating the synchronization between these two neurons within this multi-stable region.
Figure 15.
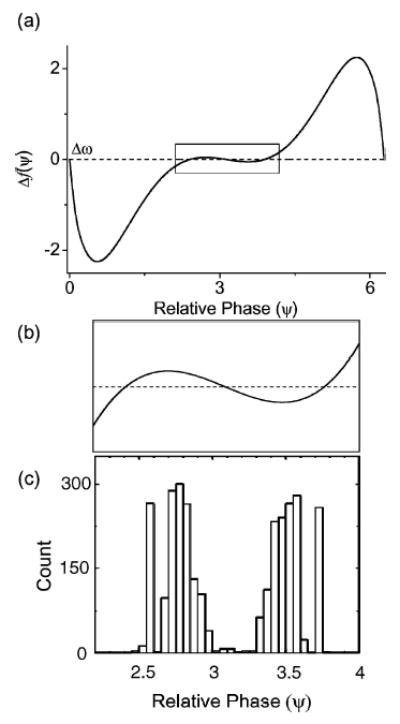
An example of the anti-phase locked state (E = 200 mV/cm and Δgc = 0%) with identical neurons. (a) The phase sensitivity function Δf = f1 − f2 obtained using XPPAUT. For identical neurons, Δω = 0 rad/s and the equilibrium states should be located where Δf = 0. (b) The boxed region in (a) is magnified near the anti-phase locked state at Ψ = π. The magnification reveals that there are three equilibrium states in this region with one unstable equilibrium at the exact anti-phase locked state and two stable equilibria on either side. (g) A histogram (with 2000 trials) of the measured relative phases of two mutually coupled PR neurons in this anti-phase locked state. One can identify two main clusters in this histogram corresponding roughly to the two predicted stable equilibrium states within this anti-phase locked regime.
4. Conclusions
We have shown that excitatory electric fields can have synchronizing and desynchronizing effects depending upon the heterogeneity of the neurons and the strength of the applied electric field. For weak excitatory fields, a careful modulation of the field amplitude might be able to push a network across a synchronization boundary established by the natural frequency mismatch of the neurons. Such a prediction is quite testable in laboratory experiments.
Inhibitory applied fields were noted to suppress neuronal activity at modest field strength, but surprisingly to increase activity and to synchronize neurons at larger field strengths. In recent simulations, we have demonstrated that this effect is due to dendritic activation, and a reversal of intraneuronal current flow during initial field application from dendrite-to-soma to soma-to-dendrite (Munyan et al., unpublished observations). Again, such a prediction is readily testable in future experiments.
We further employed a phase oscillator formalism to attempt to simplify the neuronal interactions using phase sensitivity curves for each individual neuron. Such an analysis is instructive in that it readily permits dissection of the synaptic and ephaptic coupling effects on phase, and permits predictions regarding the conditions required for synchronization. Although ephaptic effects are generally small, there are clear regimes of phase where ephaptic coupling plays an important role (Traub, 1985). Since recent experimental work (Francis et al., 2003) has demonstrated the exquisite sensitivity of neurons to weak electric fields, such ephaptic coupling may have a more important role in neuronal network synchronization than is generally appreciated. Furthermore, our entire approach, which focuses on polarization effects, is one that is operative in the weak electric field regime. Stronger applied fields and their associated currents can induce depolarization block, a regime where field orientation is no longer relevant (Bikson et al., 2001).
Larger scale simulations will be required in order to begin to replicate biological effects more accurately. Although we study dimensionally similar (quasi-1D) topologies in brain slice experiments, a more accurate representation of the connectivity of excitatory and inhibitory neurons is required before a complete model of seizure suppression can be constructed. Since the computational complexity of such networks increases rapidly with size, the prospect of generating qualitative predictions about synchronization or desynchronization from a reduced phase model approach is highly attractive.
Acknowledgments
We are grateful to R. Traub for helpful discussions. This work was supported by NIH grants K02MH01493 (SJS), K25MH01963 (EB), and R01MH50006 (SJS, PS, BJG).
Appendix A: The Neuron Model
The PR neuron (Pinsky and Rinzel, 1994) is a lumped two-chamber model with transmembrane potentials for the somatic and the dendritic chambers governed by the following equations (also see Fig. 1(a)),
| (A1.1) |
| (A1.2) |
The various ionic, synaptic, and leakage currents are defined as:
Id and Is are the injected currents into the soma and the dendrite and IDS in ≡ gc(Vdin − Vsin) is the current that flows between the two chambers of the neuron. Here, gc is the internal conductance between the soma and the dendrite, and (Vdin − Vsin) is the intracellular voltage difference between the two chambers. The heterogeneity between the neurons within our network is adjusted through this internal conductance parameter gc Specifically, gc(1) = 2.1 (mS/cm2), and where Δgc = 0 – 30%.
The geometric factors p and (1 − p) characterize the proportion of area occupied by the soma and the dendrite, respectively, so that all currents listed above except IDSin, Id, and Is are in units of μA/cm2. In the original PR neuron, Isyn is also defined as the total current into the dendrite compartment as are the other injected currents Id and Is. Thus, the synaptic term in the original PR neuron reads Isyn/(1 − p). In our model, we explicitly assume Isyn to be the synaptic current per unit membrane area of the dendrite so that the synaptic current term appears as above without the1/(1 − p) factor.
In addition to the current balance equations for the transmembrane potentials, the kinetics of the gating variables for the different ionic channels is governed by the following equations:
where
with y = h, n, s, c, and q.
The specific choices for the different α and β function listed above are provided in Table 1. The dynamics of the intracellular Ca2+ concentration is given by
Table 1.
Rate functions.
| Gating variable | Forward rate function (ms−1) | Backward rate function (ms−1) |
|---|---|---|
| Na+ channel (INa) activation; m | ||
| Na+ channel (INa) inactivation; h | ||
| K+ channel (IKDR) activation; n | βn = 0.25 · exp(0.5 − 0.025 · Vs) | |
| Ca2+ channel (ICa) activation; s | ||
| Ca2+ activated K +(IKC) activation; c | ||
| βc = 0 Vd > 50.0 | ||
| K+AHP channel (IKAHP) activation; q | αq = min(0.00002 · Ca, 0.01) | βq = 0.001 |
and χ(Ca) = min(Ca/250, 1). Lastly, the weighting functions for the two synaptic conductances (NMDA and AMPA) are governed by the following differential equations:
In these equations, the sum is over all pre-synaptic neurons and H(x) refers to the Heaviside step function, i.e., H(x) = 1 if x ≥ 0 and H(x) = 0 if x < 0. All other parameters for the PR neuron used in our model are summarized in Table 2.
Table 2.
Parameters.
| Parameters | Values (Unit) |
|---|---|
| p: soma area/total membrane area | 0.5 (unitless) |
| Area: total membrane area | 6 × 10−6 (cm2)a (soma radius of 5 μm) |
| gc: coupling conductance between two compartments | 1.5–2.1 (mS/cm2) |
| cm: membrane capacitance | 3.0 (μF/cm2) |
| Reversal potentials | |
| (w.r.t. reference potential-60 mV) | (mV) |
| VNa | 120 |
| VCa | 140 |
| VK | −38.56 ([K+]o = 3.5 (mM)) |
| VL | 0 |
| Vsyn | 60 |
| Channel conductances | (mS/cm2) |
| gL | 0.1 |
| GNa | 30 |
| gKDR | 15 |
| gCa | 10 |
| gKAHP | 0.8 |
| gKC | 15 |
| gNMDA | 0.03 |
| gAMPA | 0.0045 |
| Injected currents | (μA/cm2) |
| Is | 0 |
| Id | 0.7 |
From personal communications with G. Ascoli.
Appendix B. Resistive Array
To model the electric field interaction among neurons within the extracellular medium, we embedded two (or more) PR neurons within a resistive array as shown in Fig. A1. Although we have only shown a pair of PR neurons in this graph, a natural extension to a larger number of neurons in a quasi-one-dimensional array can easily be done by repeating the single neuron unit horizontally along the chain (Munyan et al., unpublished data). In the following three subsections, we describe in detail the modifications needed to implement this electric field interaction for two PR neurons embedded within the array.
Figure A1.
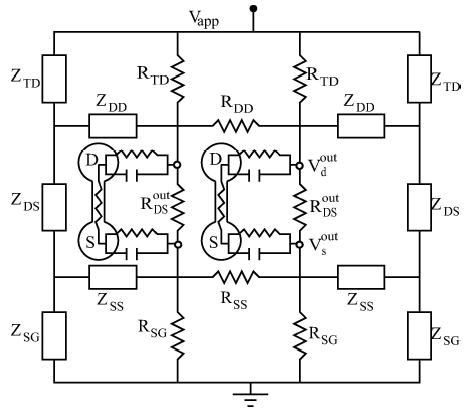
Detailed structure of the resistive array with terminal resistors and embedded PR neurons. All resistance values are listed in Table 3.
B.1. Ephaptic Coupling Through the Resistive Array
Figure A1 is a circuit diagram for the resistive array with two embedded PR neurons. In this figure, the bulk resistors are labeled by ‘R’ and the equivalent terminators are labeled as ‘Z’. (Please see the next subsection for a discussion of how these terminal resistances were chosen to model an infinite resistive array.) An externally applied electric field is modeled by the potential difference Vapp imposed between the top and bottom plates of the array. The neural activities of the two neurons couple into the array as currents passing into the four connection points indicated in the figure (see the small open circles in Fig. A1). Consider the top-left connection point in Fig. A1, where all the currents of Eq. (A1) (including the capacitive current) pass from the dendrite chamber into the array. By applying Kirchhoff’s rules at all junctions and closed loops within the resistive array at a particular instant of time, one can write down a linear matrix equation relating the resistor values within the array and the inputs to the array. In particular, these inputs are Vapp and the currents from the neurons. The solution of this linear matrix equation gives the instantaneous current/voltage values along all branches of the array. We are particularly interested in the voltage difference VDSout = Vd out − Vsout between the extracellular nodes where the dendrite and soma are connected to the resistive array. This voltage difference induces a polarization between the two chambers of the neurons. In particular, note that the current IDSin which flows through the neuron’s internal conductance connecting the two chambers is modulated by VDSout. Without the resistive array, we have IDSin ≡ gc(Vdin − Vsin) = gc(Vd − Vs ) as in the original Pinsky-Rinzel model. For a neuron embedded within the resistive array, we have
| (A2) |
since the extracelluar nodes outside the two chambers are no longer at the same potential and VDSout is non-zero (Note that, by definition, we have Vd,s = Vd,sin − Vd,sout). Algorithmically, we solve a linear matrix equation at each time step to calculate VDSout in terms of the instantaneous activity of both neurons, i.e., VDSout is a linear function of VD and VS from both neurons. Then, by Eq. (A2), VDSout affects the transmembrane potentials VD and VS in the next time step through the Pinsky-Rinzel equations Eq. (A1).
B.2. Equivalent Resistances for an Extended Infinite Array
The resistive lattice which models the extracellular medium is set up effectively as an array of infinite extent by the use of equivalent terminal resistors. To obtain these equivalent terminators, one can consider the two circuits given in Fig. A2. As in our previous disscusion, the bulk resistors are labeled by ‘R’ and the equivalent terminators on the right side of the array are labeled ‘Z’. (Although our discussion is for the terminators on the right side the array, the left equivalent terminators can be obtained through a similar argument.) If the terminal resistances are chosen correctly, then for given voltage inputs (V1 and V2), the currents (i1 and i2) flowing through the top circuit (Fig. A2 (a)) should be equal to the currents ( j1 and j2) flowing through the bottom circuit (Fig. A2 (b)).
Figure A2.
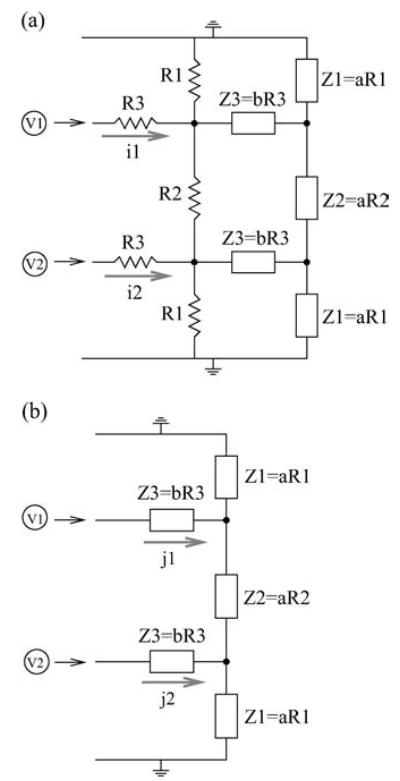
Two circuit diagrams for obtaining terminal resistances equivalent to an array of infinite extent. The voltage sources are indicated as V1 and V2, and the top and bottom plates are grounded. (a) The network contains both the bulk resistors indicated as R, and the terminators indicated as Z. For the relation between resistors and terminators, see Table 3. In the table, R1, R2, and R3 are associated with RT D (or RSG ), RDSout , and RD D (or RSS) respectively. (b) This set-up contains the terminal resistances, and they are chosen to be proportional to the bulk resistances: Z1 = aR1, Z2 = aR2, and Z3 = bR3, where ‘a’ and ‘b’ are the coefficients of proportionality.
For this particular arrangement of resistors, a simple way to solve for these equivalent terminators is to assume that the bulk resistors and the terminal resistors are proportional to each other as shown in Fig. A2 with two free parameters a and b. Then, by imposing the condition that i1 = j1 and i2 = j2 as mentioned above, one can solve for the required proportionality a and b. In our numerical simulation, a = 0.0756826 and b = 2.38394 were used. Other resistance values employed in our resistive network array are given in Table 3.
Table 3.
Resistance values.
| Resistance between | Ratios of resistances | Equivalent resistances |
|---|---|---|
| Dendrite and Soma | RTDout = 0.1RDSin | ZDS = a RDSout |
| Top plate and Dendrite | RTD = 12RDSout | ZTD = a RTD |
| Dendrite and Dendrite | RDD = 0.1RDSout | ZDD = bRDD |
| Soma and Soma | RSS = 0.1RDSout | ZSS = b RSS |
| Soma and Ground | RSG = 12RDSout | ZSG = a RSG |
Note: All resistance values are expressed in ratios to the nominal resistance value .
B.3. Relation between Extracellular Postassium Concentration ([K+]o) and the Resistive Network
In designing this resistive network, the relation between the extracelluar potassium concentration [K+]o and the resistivity in the extracellular medium has also been taken into account. Choices in [K+]o can be adjusted through the resistances chosen in our resistive network. Physiologically, increasing [K+]o increases cell swelling, which in turn decreases the extracellular volume space as well as the cross-sectional area of the extracellular medium. Since the cross-sectional area of the extracellular medium and its resistance are reciprocally related, the extracellular resistance value RDSout should increase with elevated levels of extracellular [K+]o. One can model this dependence by the following linear relation,
where RDSin is the intracellular resistance and is inversely proportional to gc. Thus, as [K+]o is increased from 3.5 (mM) to 8.5 (mM), the ratio r(= RDSout / RDSin) increases from 0.1 to 0.15. With a given fixed value of RDSin, this implies an increase in the extracellular resistance value RDSout from ~8(MΩ) to ~12(MΩ), an increase of approximately 33%. This variation in extracellular resistance is consistent with experimental measurements of extracellular volume in terms of [K+]o in hippocampal pyramidal CA1 and CA3 neurons (McBain et al., 1990).
Footnotes
Action Editor: G. Bard Ermentrout
The downward crossing of the threshold is chosen here since the rate of change of the membrane voltage for these neurons is greater in the downward direction. Therefore, the timing of the spike can be more accurately measured.
This condition, which allows the relative phase to fluctuate around ψ0, can be used to describe phase locking in both regular and chaotic oscillations. In the latter case, this phenomenon is usually called ‘phase synchronization’ (Rosenblum et al., 1996).
A similar phenomena is observed in a larger network of PR neurons (Munyan et al., unpublished data).
Hansel (1995) showed that two neurons with excitatory coupling cannot synchronize (phase-locked with ψ0 = 0). Our observation of synchronization with an excitatory field does not contradict with this result since we do not restrict our synchrony criterion to have ψ0 = 0.
It is observed that the value for the critical natural frequency mismatch Δω* in the simpler 1:1 phase-locked states does not apply universally to the Δω = nω2 −mω1 observed in the n:m phase-locked states.
Due to the nonlinearity of PR neurons, the spiking events are mostly periodic but in reality there are small fluctuations about this mean rate. Nonetheless, we have found that these small fluctuations do not significantly alter the predicted locked behavior.
References
- Aksay E, Gamkrelidze G, Seung HS, Baker R, Tank DW. In vivo intracellular recording and perturbation of persistent activity in a neural integrator. Nature Neuroscience. 2001;4:184–193. doi: 10.1038/84023. [DOI] [PubMed] [Google Scholar]
- Bikson M, Lian J, Hahn PJ, Stacey WC, Sciortino C, Durand DM. Suppression of epileptiform activity by high frequency sinusoidal fields in rat hippocampal slices. Journal of Physiology. 2001;531:181–191. doi: 10.1111/j.1469-7793.2001.0181j.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan CY, Houndsgaard J, Nicholson C. Effects of electric fields on transmembrane potential and excitability of turtle cerebellar Purkinje cells in vitro. Journal of Physiology (London) 1988;402:751–771. doi: 10.1113/jphysiol.1988.sp017232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan CY, Nicholson C. Modulation by applied electric fields of Purkinje and stellate cell activity in the isolated turtle cerebellum. Journal of Physiology (London) 1986;371:89–114. doi: 10.1113/jphysiol.1986.sp015963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen AH, Holmes PJ, Rand RH. The nature of the coupling between segmental oscillators of the lamprey spinal generator for locomotion: A mathematical model. Journal of Mathematical Biology. 1982;13:345–369. doi: 10.1007/BF00276069. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB. n:m Phase-locking of weakly coupled oscillators. Journal of Mathematical Biology. 1981;12:327–342. [Google Scholar]
- Ermentrout GB, Kopell N. Frequency plateaus in a chain of weakly coupled oscillators, I. SIAM Journal of Mathematical Analysis. 1984;15:215–237. [Google Scholar]
- Ermentrout GB. Type I membranes, phase resetting curves, and synchrony. Neural Computation. 1996;8:979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Kleinfeld D. Traveling electrical waves in cortex: insights from phase dynamics and speculation on a computational role. Neuron. 2001;29(1):33–44. doi: 10.1016/s0896-6273(01)00178-7. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB (2002) Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students, in Software, Environments, and Tools, SIAM, Philadelphia. (Free software downloading available at http://www.math.pitt.edu/~bard/xpp/xpp.html)
- Francis JT, Gluckman BJ, Schiff SJ. Sensitivity of Neurons to Weak Electric Fields. Journal of Neuroscience. 2003;23:7255–7261. doi: 10.1523/JNEUROSCI.23-19-07255.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gluckman BJ, Neel EJ, Netoff TI, Ditto WL, Spano ML, Schiff SJ. Electric field suppression of epileptiform activity in hippocampal slices. Journal of Neurophysiology. 1996;76:4202–4205. doi: 10.1152/jn.1996.76.6.4202. [DOI] [PubMed] [Google Scholar]
- Gluckman BJ, Nguyen H, Weinstein SL, Schiff SJ. Adaptive electric field suppression of epileptic seizures. Journal of Neuroscience. 2001;21:590–600. doi: 10.1523/JNEUROSCI.21-02-00590.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gluckman BJ, So P, Netoff TI, Spano ML, Schiff SJ. Stochastic resonance in mammalian neuronal networks. Chaos. 1998;8:588–598. doi: 10.1063/1.166340. [DOI] [PubMed] [Google Scholar]
- Golomb D, Hansel D. The number of synaptic inputs and the synchrony of large, sparse neuronal networks. Neural Computation. 2000;12:1095–1139. doi: 10.1162/089976600300015529. [DOI] [PubMed] [Google Scholar]
- Gutkin BS, Lang CR, Colby CL, Chow CC, Ermentrout GB. Turning on and off with excitation: The role of spike-timing asynchrony and synchrony in sustained neural activity. Journal of Computational Neuroscience. 2001;11:121–134. doi: 10.1023/a:1012837415096. [DOI] [PubMed] [Google Scholar]
- Hansel D, Mato G, Meunier C. Synchrony in excitatory neural networks. Neural Computation. 1995;7:307–337. doi: 10.1162/neco.1995.7.2.307. [DOI] [PubMed] [Google Scholar]
- Hansel D, Sompolinsky H. Chaos and synchrony in a model of a hypercolumn in visual cortex. Journal Computational Neuroscience. 1996;3:7–34. doi: 10.1007/BF00158335. [DOI] [PubMed] [Google Scholar]
- Kandel ER, Schwartz JH, Jessell TM (1991) Principles of Neural Science, 3rd ed. Appleton & Lange, Norwalk CT.
- Kuramoto Y (1984) Chemical Oscillations, Waves, and Turbulence. Springer, Berlin.
- McBain CJ, Traynelis SF, Dingledine R. Regional variation of extracellular space in the hippocampus. Science. 1990;249:674–677. doi: 10.1126/science.2382142. [DOI] [PubMed] [Google Scholar]
- Munyan B, So P, Barreto E, Schiff SJ (2003), unpublished.
- Netoff TI, Schiff SJ. Decreased neuronal synchronization during experimental seizures. Journal of Neuroscience. 2002;22:7297–7307. doi: 10.1523/JNEUROSCI.22-16-07297.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park EH, So P, Barreto E, Schiff SJ. Electric field modulation of synchronization in neuronal networks. Neurocomputing. 2003;52–54:169–175. [Google Scholar]
- Penfield W, Jasper H (1954) Epilepsy and the functional anatomy of the human brain. Little, Brown and Co., Boston MA, p. 896.
- Pikovsky AS, Rosenblum MG, Kurths J. Phase synchronization in regular and chaotic systems. International Journal of Bifurcation and Chaos. 2000;10:2291–2306. [Google Scholar]
- Pikovsky AS, Rosenblum MG, Kurths J (2001) Synchronization a Universal Concept in Nonlinear Sciences. Cambridge University Press, Cambridge UK.
- Pinsky PF, Rinzel J (1994) Intrinsic and network rhythmogenesis in a reduced Traub model for CA3 neurons. Journal of Computational Neuroscience 1: 39–60. The erratum for this paper, published in volume 2, on page 275 (1995). [DOI] [PubMed]
- Rand RH, Holmes PJ. Bifurcation of periodic motions in two weakly coupled van der Pol oscillators. International Journal of Nonlinear Mechanics. 1980;15:387–399. [Google Scholar]
- Rosenblum MG, Pikovsky AS, Kurths J. Phase synchronization of chaotic oscillators. Physical Review Letters. 1996;76:1804–1807. doi: 10.1103/PhysRevLett.76.1804. [DOI] [PubMed] [Google Scholar]
- Sharp PE, Blair HT, Cho J. The anatomical and computational basis of the rat head-direction cell signal. Trends Neuroscience. 2001;24:289–94. doi: 10.1016/s0166-2236(00)01797-5. [DOI] [PubMed] [Google Scholar]
- Stein PSG (1976) Mechanisms of interlimb phase control. In: R Herman, S Grillner, P Stein, D Stuart, eds. Neural Control of Locomotion. Plenum Press, New York, NY, pp. 465–487.
- Tranchina D, Nicholson C. A model for the polarization of neurons by extrinsically applied electric fields. Biophysical Journal. 1986;50:1139–1159. doi: 10.1016/S0006-3495(86)83558-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Traub RD, Dudek FE, Taylor CP, Knowles WD. Simulation of hippocampal afterdischarges synchronized by electrical interactions. Neuroscience. 1985a;14:1033–1038. doi: 10.1016/0306-4522(85)90274-x. [DOI] [PubMed] [Google Scholar]
- Wang X-J. Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. 2001;24:455–63. doi: 10.1016/s0166-2236(00)01868-3. [DOI] [PubMed] [Google Scholar]
- Winfree AT (1980) The geometry of biological time. Springer, New York, NY.


