Abstract
In recent times, COVID-19 pandemic has posed certain challenges to transportation companies due to the restrictions imposed by different countries during the lockdown. These restrictions cause delay and/ or reduction in the number of trips of vehicles, especially, to the regions with higher restrictions. In a pandemic scenario, regions are categorized into different groups based on the levels of restrictions imposed on the movement of vehicles based on the number of active cases (i.e., number of people infected by COVID-19), number of deaths, population, number of COVID-19 hospitals, etc. The aim of this study is to formulate and solve a fixed-charge transportation problem (FCTP) during this pandemic scenario and to obtain transportation scheme with minimum transportation cost in minimum number of trips of vehicles moving between regions with higher levels of restrictions. For this, a penalty is imposed in the objective function based on the category of the region(s) where the origin and destination are situated. However, reduction in the number of trips of vehicles may increase the transportation cost to unrealistic bounds and so, to keep the transportation cost within limits, a constraint is imposed on the proposed model. To solve the problem, the Genetic Algorithm (GA) has been modified accordingly. For this purpose, we have designed a new crossover operator and a new mutation operator to handle multiple trips and capacity constraints of vehicles. For numerical illustration, in this study, we have solved five example problems considering three levels of restrictions, for which the datasets are generated artificially. To show the effectiveness of the constraint imposed for reducing the transportation cost, the same example problems are then solved without the constraint and the results are analyzed. A comparison of results with existing algorithms proves that our algorithm is effective. Finally, some future research directions are discussed.
Keywords: Transportation Problem, COVID-19 Pandemic scenario, Fixed-charge, Multiple vehicles, Genetic algorithm
Graphical abstract
1. Introduction
Transportation problem is an important problem in operations research, since it is directly linked with the economy of a country and inflation. It is one of the most studied problem due to its applications in wide field of topics, which includes transportation network, supply chain and logistics, manufacturing industries, location routing, etc. The first model of transportation network was developed by Hitchcock [1] in 1941, which is known as the classical transportation problem (CTP). Since CTP belongs to the class of linear programming problem, it is solvable in polynomial time. Many researchers developed exact and approximate algorithms to solve such kind of problems. Some of the earliest works on transportation and its associated problems are reported in [2], [3], [4], [5]. To make the transportation problem (TP) more realistic, Hirsch and Dantzig [6] incorporated fixed cost into the transportation problem (TP), and named the resulting problem as the fixed-charge transportation problem (FCTP). A FCTP considers the involvement of two types of costs, variable cost and fixed cost. The variable cost depends on the quantity of an item to be transported, whereas the fixed cost is incurred for a route being used and is independent of the quantity of item. Some examples of fixed cost may include toll tax on highways, docking charge at ports, warehouse setup cost, etc. Later, Balinski [7] formulated the FCTP mathematically. The inclusion of fixed cost result in discontinuities in the objective function and consequently, makes the problem complex. Moreover, the FCTP is NP-hard [8], [9] and cannot be solved by the traditional algorithms used to solve TPs. The FCTP is thus a classic example of a combinatorial optimization problem. In the last decade or so, researchers mainly focused on approximate methods (heuristics and metaheuristics) to solve the FCTP and its variants due to less computational time over the existing exact methods. Gen et al. [10] adopted the spanning tree representation into the Genetic Algorithm, which they named spanning tree-based Genetic Algorithm (st-GA), to solve the FCTP. Then, the algorithm is extended for the bicriteria FCTP. The result shows better performance of the st-GA than the matrix-based GA with respect to computational time. Hajiaghaei-Keshteli [8] used the Prüfer number representation with certain modifications to design a GA based on spanning tree that overcome the limitations of some earlier works [10], [11]. The major advantage of this method is that, it guarantees the generation of feasible chromosomes only unlike the aforementioned works. Molla-Alizadeh-Zavardehi [12] modeled a cost minimizing capacitated fixed-charge transportation problem for a two-stage supply chain network, in which some locations are to be selected as distribution centers to transport different quantities of an item to customers. Then, they used two algorithms, namely, Genetic Algorithm (GA) and Artificial Immune Algorithm (AIA) to solve the NP-hard problem. A comparison of the results obtained show better performance of AIA over GA in terms of both, the solution quality and the robustness, especially for large size problems. Xie and Jia [13] formulated a FCTP with the variable cost in the quadratic form (nonlinear FCTP, in short NFCTP). Due to non-linearity, NFCTP is more difficult to solve than the FCTP. To better absorb the non-linear structure of NFCTP, a hybrid genetic algorithm named NFCTP-HGA is developed that uses minimum cost flow algorithm as decoder. Numerical experiments proved better performance of the algorithm with respect to computational time, memory usage, efficiency and robustness. Lofti & Tavakkoli-Moghaddam [14] adapted the GA with a priority based encoding, which is a modified version of the priority based encoding proposed by Gen et al. [15] to adapt with the FCTP structure. Balaji et al. [16] formulated a truck load constraints (FCT-TLC) problem, a special case of the FCTP, in which it is assumed that the quantity of items to be transported from an origin exceed the capacity of the vehicle, and consequently, may require more than one trip to transport the whole quantity. The FCT-TLC is then solved using two algorithms, namely, Genetic Algorithm (GA) and Simulated Annealing (SA). Computational results performed on twenty test examples shows that SA produces the same or better quality solutions than GA.
Some researchers also considered two or more of cost, transport time, profit, etc. as objectives that are conflicting in nature and posed the FCTP as multi-objective optimization problem. Biswas et al. [17] formulated a solid multi-objective FCTP with non-linear cost function. The uncertainties in some parameters are also considered in the form of interval numbers, and an equivalent formulation of the problem is presented in interval environment. Then, suitable genetic operators are developed, and incorporated into the non-dominated sorting genetic algorithm-II (NSGA-II) [18] to solve the problem in crisp environment. The FCTP with interval objectives is solved using an extended NSGA-II to cope with interval objectives. Numerical experiments are performed and the results are compared with another metaheuristic SPEA2 (Strength Pareto Evolutionary Algorithm 2), implementing the same genetic operators. Roy et al. [19] modeled a multi-objective FCTP considering the parameters of objective functions to be random rough variables and the parameters corresponding to demand and supply to be rough variables. The problem is first converted into a deterministic form using an expected value operator, and is then solved using three different procedures, namely, the fuzzy programming, global criterion and -constrained method. The result shows the better performance of -constrained method over other methods. Midya and Roy [20] considered a multi-objective FCTP (named as MOFCTP), in which all the parameters are taken to be imprecise and measured using rough intervals. The MOFCTP is converted into deterministic form using rough programming and is then solved using two methods, namely, fuzzy programming method and linear weighted sum method. A comparison of results show better performance of the linear weighted sum method. Ghosh et al. [21] formulated a multi-objective solid FCTP (named as MOFCSTP) considering all the parameters and variables as triangular intuitionistic fuzzy numbers (TIFNs) having membership and non-membership function. The modeled MOFCSTP is first reduced to an interval-valued intuitionistic fuzzy transportation problem (IVIFTP) using -cut, and then into an equivalent crisp problem using an accuracy function. Then, the crisp problem is solved using the methods fuzzy programming (FP), intuitionistic fuzzy programming (IFP) and goal programming (GP). The results show that IFP performs best among the applied methods. Biswas and Pal [22] formulated a multi-objective solid FCTP, considering fixed capacities of modes of transport that are different for each mode. New genetic operators (crossover and mutation) are designed to deal with the capacity constraint. The problem is then solved using a modified NSGA-II, obtained by incorporating the genetic operators. Some numerical examples are solved using the modified NSGA-II and the results are compared with two other metaheuristics on the basis of various performance metrics, which indicates towards the overall supremacy of the modified NSGA-II.
In recent years, researchers solved different variants of FCTP considering multiple items [23], [24], [25], multiple vehicles/conveyances [17], [26], [27], [28] and capacity constraints of conveyances (modes of transport) [12], [22]. Some researchers also considered the uncertainties of different parameters and measured the uncertainties using interval [17], [29], fuzzy [23], [30], [31], rough [19] and fuzzy-rough [31].
Recently, due to the COVID-19 pandemic, interests are growing among researchers to adapt different network models such as manufacturing industry, supply chain, transportation and logistics for the changed scenario. Amankwah-Amoah [32] presented a conceptual framework of business firm’s responses due to restrictions imposed in business activities in the ongoing COVID-19 pandemic. Then, considering the global airline industry as case study, different strategic responses such as changes in in-flight service, flight cancellations, pursue emergency aids and financial supports are analyzed, which provide few outlines for the service providers for recovery. Mogaji [33] studied the impact of COVID-19 over a long period on transportation in Lagos State of Nigeria, where the restrictions are difficult to maintain considering practical scenarios. Then, some feasible strategies are outlined based on ‘avoid-shift-improve’ for the policymakers, both in private and public sectors. The time lag between recognizing a problem and the time of activation of a policy on a system is studied by Bian et al. [34]. A detection process is developed computing the change point using likelihood ratio, regression value and a Bayesian change point detection method. Then, as a case study, two cities of U. S. are investigated which reveal that the nationwide declaration of emergency has no impact on policy lag, while the two policies ‘stay-at-home’ and ‘reopening’ has certain lead effect. In addition to these, some works on supply chains and logistics in COVID-19 pandemic includes that given in [35], [36], [37], [38], [39], [40], [41], [42], [43], respectively.
1.1. Motivation
From the literature survey, it is evident that most countries imposed restrictions which greatly affect the transportation system of items (both essential and non-essential). Thus, the existing models of transportation problem (TP) are based on the assumption that there is no such restrictions in the movement of vehicles and suitable for normal scenario only. Moreover, in most of the works on TP (in particular fixed-charge transportation problem (FCTP)), it is considered that a vehicle can avail at most one trip to a destination. However, in real-world scenario, the amount of an item available at an origin may exceed the total capacity of all the vehicles, and hence, one or more vehicles may need more than one trip to satisfy the demand at a destination. In the existing works, none of the researchers has considered that the number of trips of a vehicle to a destination can be more than one, except Balaji et al. [16]. However, the number of trips of a vehicle to a destination can be more than one, and must be considered into the formulation, since for a FCTP, the number of trips contribute to the fixed cost, total time and total profit (in case of shipping of perishable items).
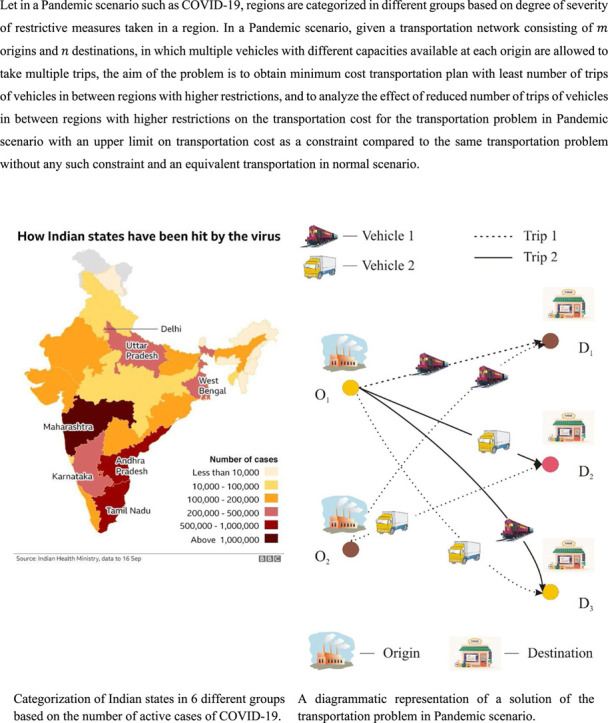
In pandemic scenario, regions are categorized in different groups depending upon the level of restriction in a region persistent over a certain period of time. The level of restriction in a region is dependent on various factors such as number of active cases (i.e., number of people infected), number of deaths, population density, number of COVID-19 hospitals and number of migrant workers returned or might return to a region. Thus, in pandemic scenario, for origins and destinations that are situated in regions with higher restrictions, the number of trips of vehicles need to be reduced in such a way that, a balance between the supply and demand of item(s) is maintained. However, reducing the number of trips of vehicles may increase the transportation cost to an unrealistic bound. Thus, a transportation company needs to find a proper balance between the transportation cost and the reduction in number of trips of vehicles considering the levels of restriction imposed in different regions. Hence, planning of transportation scheme in a pandemic scenario is a challenging task for transportation companies, and consideration of a new type of transportation plan becomes necessary. However, there is no such work available in the literature, which motivated us to formulate a transportation model for pandemic scenario and to solve it. This model is also applicable in emergency scenarios such as major earthquakes, floods and other natural calamities in which only a limited number of trips of some particular types of vehicles can be availed.
1.2. Our proposed contribution
In this paper, we first formulate a fixed cost transportation model for a homogeneous item in COVID-19 pandemic scenario, in which regions are categorized in groups depending upon the level of restrictions on the mobility of freight vehicles. It is also considered that more than one type of vehicles are available at each origin, and each vehicle may take more than one trip to the same or different destinations, where the capacity of each vehicle is not the same. For an origin and a destination, the variable cost of a unit item and the fixed-charge varies for each vehicle, which also varies for different pairs of an origin and a destination. The aim of the problem is to obtain a minimum cost transportation plan with minimum number of trips of vehicles moving from origins to destinations that are situated in regions with higher levels of restrictions. For this, the problem is posed as a single-objective optimization problem (SOOP), in which minimization of transportation cost is considered as the objective function. Moreover, to minimize the number of trips of vehicles from origins to destinations situated in regions with higher levels of restrictions, a penalty is imposed in the objective function for each trip of a vehicle that depends upon the level of restrictions of the two regions. To keep the transportation cost within realistic bound, a constraint is imposed with an upper bound on transportation cost. Then, the problem is solved using a Genetic Algorithm (GA) based approach, in which newly designed genetic operators (crossover and mutation) are incorporated to handle multiple trips and capacity constraints of vehicles. Some numerical examples of the proposed model are generated artificially, in which three levels of restrictions are considered for the regions associated with the origins and destinations. To prove that the imposed constraint plays a crucial role, the same examples are solved without considering the constraint. Thereafter, the same examples are solved in normal scenario, i.e., ignoring any categorization of regions and the results are analyzed. The performance of our algorithm is also compared with three existing works, considering a particular instance of our proposed FCTP model. Finally, some future research directions are discussed.
The organization of the rest of the paper is as follows. In Section 2, the notations and abbreviations are presented. The mathematical model of the FCTP in pandemic scenario is given in Section 3. The solution methodology is discussed in Section 4. Section 5 contains the experimental results with discussion. Finally, in Section 6, conclusions are drawn with the lines of further research directions are discussed.
2. Notations
The notations used to formulate and to solve the problem are the following.
| : | Size of initial population | |
| : | Maximum number of iterations (Termination criterion) | |
| : | Crossover probability | |
| : | Mutation probability | |
| : | Set of origins | |
| : | Set of destinations | |
| : | Set of vehicles available at each origin | |
| : | Quantity of the item available at origin | |
| : | Demand of the item at destination () | |
| : | Capacity of vehicle () | |
| : | Variable transportation cost per unit of item from an origin to a destination by a vehicle | |
| : | Fixed-charge incurred for transportation of a positive quantity of the item from an origin to a destination using a vehicle | |
| : | Decision variable denoting unknown quantity of the item to be transported from origin to a destination in trip of a vehicle | |
| : | Total transportation cost in transportation of units of the item from an origin to a destination in trip of a vehicle | |
| : | Number of trips taken by the vehicle from origin corresponding to the chromosome/solution | |
| : | A Boolean variable, which takes the value 1, if a positive quantity of the item is transported in trip of the vehicle from origin to destination , otherwise it takes the value 0. | |
| : | Upper limit on transportation cost | |
List of abbreviations:
| Abbreviation | Explanation |
|---|---|
| TP | Transportation problem |
| CTP | Classical transportation problem |
| FCTP | Fixed-charge transportation problem |
| SOOP | Single objective optimization problem |
| MOOP | Multi-objective optimization problem |
| GA | Genetic algorithm |
| NSGA-II | Non-dominated sorting genetic algorithm-II |
| LSR | Level of Severity of Restriction |
| NP-hard | Non-deterministic polynomial-time hard |
| SPEA2 | Strength Pareto Evolutionary Algorithm 2 |
3. Mathematical formulation of a FCTP in pandemic scenario
In this section, we present the mathematical formulations of a FCTP in pandemic scenario. In this model, we consider the FCTP to be balanced, since, to solve an unbalanced FCTP, it is first converted into a balanced one. In case of a balanced FCTP, the sum of availabilities of the item at all the origins is equal to the sum of demands of the item at all the destinations, i.e., .
3.1. Fixed-charge transportation problem in pandemic scenario
Consider a transportation network consisting of origins, say, and destinations, say, . Let in COVID-19 pandemic, the regions associated with the origins and destinations be divided in categories, say, , arranged in increasing order of levels of restrictions. Let there be types of vehicles available at each origin, where each vehicle may take one or more trips to same or different destinations and the capacity of each vehicle being different. The unit variable cost of the item and the fixed cost corresponding to the vehicle to transport from origin to destination vary for different pairs of origins and destinations. Let for a trip of a vehicle from an origin to a destination situated in regions and , respectively, let be the penalty to be imposed on the objective function. The penalty depends only on the level of restrictions in the two regions and , i.e., the penalty is large if the level of restrictions is high and vice-versa. A higher value of penalty will restrict the vehicles to take less number of trips between an origin and a destination.
| (1) |
subject to
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Here, represents the total transportation cost (the sum of the total variable cost and the total fixed-charge) associated with the transportation of units of the item from origin to destination in trip of the vehicle , and is given by for the linear form of FCTP, and for the quadratic form of FCTP (non-linear). From here on, we shall call the quadratic form of FCTP as the non-linear FCTP.
The objective function (1) represents the minimization of the total transportation cost (i.e., the sum of total variable cost and total fixed-charge) associated with the transportation of different units of the item from all the origins to all the destinations using one or more trips of the vehicles. Eqs. (2), (3) represent, respectively the supply and demand constraints of the item at the origins and destinations. Eq. (4) represents the capacity constraint of the vehicles, Eq. (5) shows that the FCTP is balanced, whereas, the non-negativity restrictions of the decision variables are given in (6).
A special case:
If in the proposed model of FCTP, we consider the restrictions of each region to be in zero level (i.e., the LSR value of each region is considered as zero), then the problem gets reduced to a FCTP in normal scenario given as follows.
| (7) |
subject to the same constraints and non-negativity restrictions considered in the FCTP without any upper limit on transportation cost. In this case, the penalty for each pair of origin and destination becomes zero.
4. Solution methodology
In this paper, we solve the proposed model of FCTP in pandemic scenario presented in (7) using a GA based approach with suitable modifications. For this, a new crossover and a new mutation operator are designed and incorporated into the algorithm. In the following subsections, we discuss some components of GA such as generation of a chromosome, crossover and mutation, in details.
4.1. Generation of chromosome
Many researchers have used different encoding procedures to represent individual chromosomes, such as matrix representation [17], [28], [44], spanning tree [9], [10], [11], [13] and priority-based encoding [14] to solve FCTP and its variants. Among these, the encoding procedures, namely, spanning tree and priority-based encoding are suitable for FCTPs, in which only one type of vehicle with no capacity constraint are available for each pair of an origin and a destination, and a vehicle can ship items to a destination in one trip at most. Thus, it is very difficult to incorporate these encoding procedures into our proposed FCTP. Moreover, these representations need encoding and decoding procedure to understand the transportation scheme corresponding to a solution. So, we use the matrix representation to represent an individual chromosome. As the decision variable has four indices, a four-dimensional matrix is used to represent a chromosome. The process of generation of a chromosome is given in Algorithm 1.
To constitute an initial population of size , Algorithm 1 is repeatedly used. We now illustrate the process of generation of a chromosome for the proposed model of FCTP with two origins, three destinations and two vehicles using Algorithm 1.
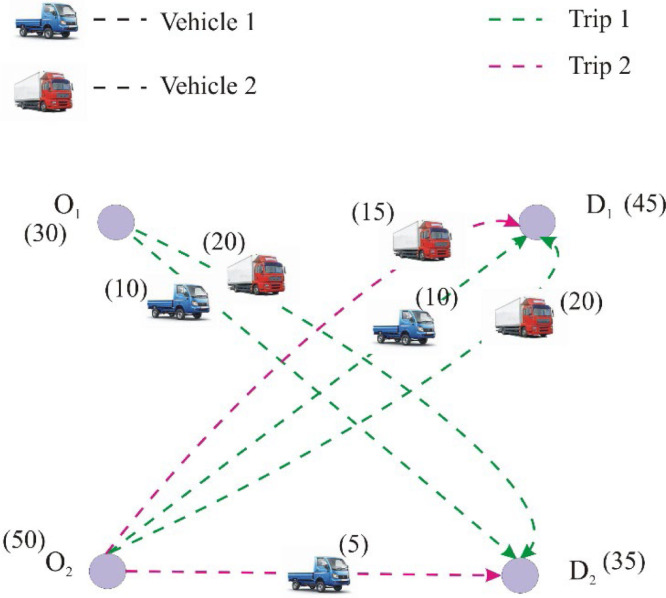
Example 1
Let us consider a transportation network consisting of two origins , two destinations and , be two vehicles capable of carrying 10 and 20 units of the item, respectively, are available at each origin. Let the availability of the item at the origins be 30, 50 units and the demand for the items at the destinations be and 45, 35 units, respectively.
The process of generation of a chromosome for Example 1 is described below.
Iteration 1: Initially, Set , , , . Then . Also, set ; ; and (Step 1). Let the origin , the destination and the vehicle be selected (Step 2). Since , the value of is changed to 1 (Step 3). Now, and the updated values are and (Step 4). Since the value of , we go to Step 2.
Iteration 2: Let the origin , the destination and the vehicle be selected (Step 2). Since , the value of is changed to 1 (Step 3). Now, and the updated values are and (Step 4). Since becomes 0, the value of is changed to 1 and the updated values are . Since the value of , we go to Step 2.
Iteration 3: Let the origin , the destination and the vehicle be selected (Step 2). Since , the value of is changed to 1 (Step 3). Now, and the updated values are and (Step 4). Since the value of , we again go to Step 2.
Iteration 4: Let the origin , the destination and the vehicle be selected (Step 2). Now, . Thus, and the updated values become and (Step 4). Since becomes 0, the value of is changed to 1 and the updated values are . Since the value of , we go to Step 2.
Iteration 5: Let the origin , the destination and the vehicle be selected (Step 2). Since , the value of is changed to 1 (Step 3). Now, and the updated values become , and (Step 4). Since the value of , we go to Step 2.
Iteration 6: Let the origin , the destination and the vehicle be selected (Step 2). Now, . Thus, and the updated values are and (Step 4). Since the value of , the process of generation of chromosome is completed.
The generated chromosome is given in Table 1 and the transportation scheme is represented diagrammatically in Fig. 1.
Table 1.
A chromosome generated for Example 1 using Algorithm 1.
| Origin |
|
|
||||||
|---|---|---|---|---|---|---|---|---|
| Destination |
|
|
|
|||||
| – | – | – | – | 10 | – | 20 | 30 | |
| 10 | – | 20 | 15 | 5 | – | – | 50 | |
| 45 | 35 | |||||||
Fig. 1.
Transportation scheme corresponding to the chromosome given in Table 1.
After the initial population is constituted, the fitness value of each chromosome is evaluated. In this paper, the binary tournament selection is used.
4.2. Crossover
In this paper, we develop a new crossover for the proposed model of FCTP. In this crossover, two child chromosome are obtained from two parent chromosomes, the selection of parent chromosomes being random from the mating pool. The process of generation of a child chromosome say, from two parent chromosomes and using the proposed crossover is provided in Algorithm 2.
After both the child chromosomes are obtained, the best two chromosomes among the parent and child chromosomes are selected to constitute the population of next generation.
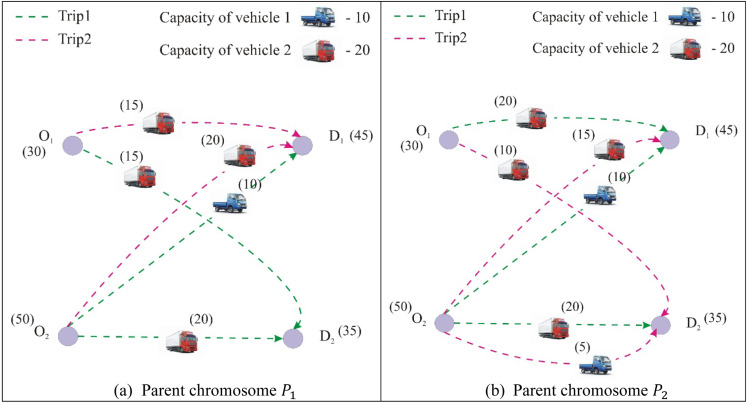
Let us now illustrate the procedure of the proposed crossover two particular chromosomes and of the transportation network considered in Example 1. The chromosomes and are given in Table 2, the transportation network for which are represented diagrammatically in Fig. 2. Here, we illustrate the process of generation of a child chromosome only, the process of generation of the other child being similar.
Table 2.
Matrix representation of the parent chromosomes and .
|
|
|
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Origin |
|
|
|
|
||||||||||||
| Destination |
|
|
|
|
|
|
|
|
||||||||
| – | – | – | 15 | – | – | 15 | – | – | – | 20 | – | – | – | – | 10 | |
| 10 | – | – | 20 | – | – | 20 | – | 10 | – | – | 15 | – | 5 | 20 | – | |
Fig. 2.
Diagrammatic representation of parent chromosomes and chosen for performing crossover.
Generation of a child chromosome from the parent chromosomes and :
At first, assign , , , , , and (Step 1). We have, and (Step 2). Assign (Step 3).
Let us choose . Thus, and . Also select (Step 4). Since , we change the value of to 1 (Step 5). Then and , i.e., an amount of 20 units of the items is transported from the origin to the destination in first trip of vehicle originating from . Then , , , , , and (Step 6). Since , we go to Step 4.
Since , we can choose . Let us choose . Thus, and . Also select (Step 4). Since , we change the value of to 1 (Step 5). Then and , i.e., an amount of 20 units of the items is transported from the origin O2 to the destination in first trip of vehicle originating from . Then , , , , , and (Step 6). Since , we go to Step 4.
Since , we can choose . Let us choose . Thus, and . Also select (Step 4). Since , we change the value of to 1 (Step 5). Then and , i.e., an amount of 10 units of the items is transported from the origin to the destination in first trip of vehicle originating from . Then , , , , , and (Step 6). Since becomes 0, and (Step 7). Again, , we go to Step 4.
Since , , and , we can choose . Let us choose . Thus, and . Also select (Step 4). Since , we change the value of to 1 (Step 5).
Then and , i.e., an amount of 5 units of the item is transported from the origin O2 to the destination in first trip of vehicle originating from . Then, , , , , , and (Step 6). Since becomes 0, , , and (Step 7). Again, since , we go to Step 4.
Since , , and , the only value that can be chosen is . Thus, and . Also, select (Step 4). We have . Thus, and , i.e., an amount of 10 units of the items is transported from the origin O2 to the destination in second trip of vehicle originating from . Then , , , , , and (Step 6). Since , we go to Step 4.
Since , , and , the only value that can be chosen is . Thus, and . Let us choose (Step 4). We have . Thus, and , i.e., an amount of 15 units of the items is transported from the origin O2 to the destination in the second trip of vehicle originating from . Then , , , , , and (Step 6). Since , the generation of the child chromosome is completed.
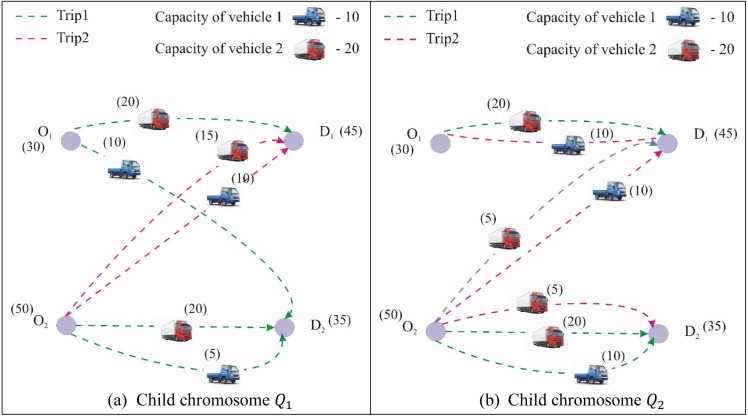
The child chromosomes and obtained from the parent chromosomes and are given in Table 3. The diagrammatic representation of and are given in Fig. 3.
Table 3.
Matrix representation of the children and .
|
|
|
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Origin |
|
|
|
|
|||||||||||||
| Destination |
|
|
|
|
|
|
|
|
|||||||||
| – | – | 20 | – | 10 | – | – | – | – | 10 | 20 | – | – | – | – | – | – | |
| – | 10 | – | 15 | 5 | – | 20 | – | – | 10 | – | – | 5 | 10 | – | 20 | 5 | |
Fig. 3.
Child chromosomes and obtained by applying the proposed crossover.
4.3. Mutation
In this paper, a new mutation suitable for the proposed problem is developed. The process of the proposed mutation operation is described in Algorithm 3.
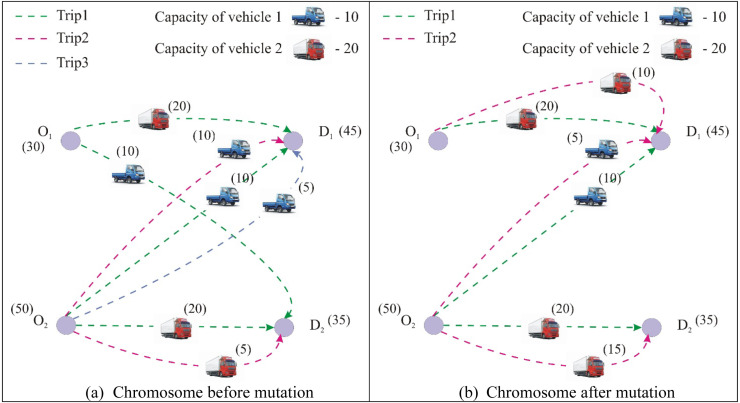
Let us illustrate the process of the proposed mutation for a particular chromosome , as given in Table 4, for which the transportation scheme is represented diagrammatically in Fig. 4(a). Let the chromosome to be obtained after the mutation be .
Table 4.
Matrix representation of the chromosomes before and after mutation.
| Chromosome before mutation |
Chromosome after mutation |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Origin |
|
|
|
|
||||||||||
| Destination |
|
|
|
|
|
|||||||||
| – | – | 20 | 10 | – | – | – | 20 | 10 | ||||||
| 10 | 5 | – | – | – | 20 | 15 | 10 | 10 | 5 | 20 | 5 | |||
Fig. 4.
Chromosomes before and after mutation.
Assign and (Step 1). Let us select and , . We get (Step 2). Again, let us select and , and (Step 3-5). Then and the updated values are obtained as , . Also, since and , the value of is decreased by 1 i.e., (Step 6). Next, we have and select the vehicle say, (Step 7). Since , the value of is increased by 1 i.e., (Step 8). Then and (Step 9). Since , we go to Step 11 ( Step 10 ).
We have and select the vehicle say, (Step 11). Now, and we obtain and hence , . Also, since , the value of is increased by 1 i.e., (Step 13). Since , we again go to Step 11 and select a vehicle say, . Now, and we obtain and hence , (Step 13). Since , the process is completed and is given in Table 4. A diagrammatic representation of the chromosome after mutation is given in Fig. 4(b).
5. Experimental results
For experimental purpose, we consider five numerical examples of the proposed model of FCTP of different size, which are then solved using the algorithm. In this section, we first discuss the dataset generation and the parameter settings used. Then, the numerical examples are solved using the algorithm and the results are analyzed. Finally, the performance comparison with existing methods are presented. The configuration of the system in which the program is executed: Intel® x-64 based processor CPU N3700 @ 1.60 GHz with 4.0 GB RAM.
5.1. Dataset
The proposed model is different from the existing models of FCTP, and so, we generate new datasets according to our model. For experimental purpose, we consider five numerical examples of the same size given in Lofti & Tavakkoli-Moghaddam [14] (i.e., and 20 × 30). Thus, for these numerical examples, we take the availability and demands for the item as given in Lofti & Tavakkoli-Moghaddam [14]. We consider two vehicles, say, and with capacities 10 and 20 units, respectively, corresponding to each numerical example. The variable and fixed costs corresponding to the vehicles and for the numerical example with 20 origins and 30 destinations are generated randomly within the ranges and , and are presented in Appendix. The variable and fixed cost matrices for a numerical example of smaller size, say, (where ) is taken as the sub-matrix of order , starting from the north-west corner of the corresponding matrix of size 20 × 30. For each numerical example, we categorize the regions in three groups, in which the level of restrictions are ‘high’, ‘medium’ and ‘low’, and are marked in ‘Red’, ‘Orange’ and ‘Green’, respectively. The list of origins and destinations belonging to each group are presented in Table 5.
Table 5.
Categorization of origins and destinations for the numerical examples.
| # Example | Category of origins | Category of destinations |
|---|---|---|
| 1 | Green: 1; Orange: 2, 4; Red: 3 | Green: 3, 5; Orange: 1,2; Red: 4 |
| 2 | Green: 1, 5; Orange: 2, 4; Red: 3 | Green: 3, 5, 10; Orange: 1, 2, 8, 9;Red: 4, 6, 7 |
| 3 | Green: 1, 5, 9; Orange: 2, 4, 7, 8; Red: 3, 6, 10 | Green: 3, 5, 10; Orange: 1,2, 8, 9;Red: 4, 6, 7 |
| 4 | Green: 1, 5, 9; Orange: 2, 4, 7, 8; Red: 3, 6, 10 | Green: 3, 5, 10, 14, 17; Orange: 1, 2, 8, 9, 12, 15, 16,19; Red: 4, 6, 7, 11, 13, 18, 20 |
| 5 | Green: 1, 5, 9, 14, 17; Orange: 2, 4, 7, 8, 12, 15, 16, 19; Red: 3, 6, 10, 11, 13, 18, 20 | Green: 3, 5, 10, 14, 17, 23, 28; Orange: 1,2, 8, 9, 12, 15, 16,19, 21, 22, 26, 29, 30; Red: 4, 6, 7, 11, 13, 18, 20, 24, 25, 27. |
5.2. Parameter settings
To obtain the best possible solution using the algorithm, the control parameters of the algorithm such as and are set to values that produce promising results in preliminary testing. The parameter values of used to solve the numerical examples of different size are shown in Table 6. The values of the parameters and are taken as 0.8 and 0.15 for each numerical example.
Table 6.
Parameters used to solve the numerical examples.
| Cost function | Classical |
Linear fixed- charge |
Non-linear fixed- charge |
|||
|---|---|---|---|---|---|---|
| # Numerical example | ||||||
| 1 | 100 | 100 | 100 | 100 | 100 | 150 |
| 2 | 100 | 100 | 100 | 100 | 150 | 200 |
| 3 | 100 | 150 | 150 | 200 | 200 | 250 |
| 4 | 200 | 200 | 200 | 250 | 200 | 300 |
| 5 | 300 | 400 | 300 | 400 | 300 | 400 |
5.3. Results and discussion
In this section, we describe the method for computation of penalty for the proposed FCTP, which depends upon the level of restriction of the regions in which the origins and the destinations are located. The purpose of imposing penalty in the objective function is to lower the number of trips of vehicles if the level of restriction in the regions are ‘high’. For this purpose, we associated a numerical value corresponding to each category of regions, and term as Level of Severity of Restriction (LSR) value. The process of computation of penalty is given as follows.
In a pandemic scenario, if the regions be categorized in different groups, say, , then the region is assigned a LSR value that lies between 1 and in the relative ranking of the regions when arranged in increasing order of level of restrictions. The LSR value of a region is assigned zero, when no restrictions are imposed in a region. For a trip of any vehicle from an origin to a destination located in regions and respectively, the penalty is denoted by , and computed as , where is a large positive number and are the LSR values of the regions and respectively. For solving the numerical examples, we have chosen the value of as 100.0.
Explanation:
The reason of including the terms and in the penalty function is to consider higher penalty when either of the situation occurs, (i) at least one of the regions in which an origin or a destination situated takes large LSR value, i.e., the restriction is high (ii) the difference in LSR values of the two regions associated with a tour of any vehicle is large, i.e., the level of restriction in one of the two regions is low, whereas, the level restriction in the other region is high.
Let us illustrate the process of computation of penalty for a particular example. For this, let us consider the transportation network given in Example 1 (Ref. Section 4.1.). Let us consider that the regions be categorized in three groups, and are marked in ‘Red’, ‘Orange’ and ‘Green’. Then, the penalty for a single trip of a vehicle for different possible combinations of LSR values corresponding to an origin and a destination is given in Table 7.
Table 7.
Computation of penalty in a trip for all possible categories of regions.
| Category of region in which origin is situated | LSR value of origin | Category of region in which destination is situated | LSR value of destination | Penalty value |
|---|---|---|---|---|
| Green | 0 | Green | 0 | 0 |
| Green | 0 | Orange | 1 | |
| Green | 0 | Red | 2 | |
| Orange | 1 | Green | 0 | |
| Orange | 1 | Orange | 1 | |
| Orange | 1 | Red | 2 | |
| Red | 2 | Green | 0 | |
| Red | 2 | Orange | 1 | |
| Red | 2 | Red | 2 |
In this section, we discuss the results obtained for the five numerical examples solved for each of the problems, namely, the proposed FCTP (given in (7)), the corresponding problem without any constraint on transportation cost and the problem in normal scenario (given in (8)). Each of the problems are solved taking three different forms of the cost function, viz., the linear fixed-charge form, quadratic fixed-charge form (non-linear) and the reduced classical form (a special case of the fixed charge forms in which the fixed costs are taken to be zero). Consequently, a total of 15 instances are solved for each problem, and a total of 45 instances are solved in this paper. The best found objective function value, penalty value and the total number of trips for each example corresponding to the linear and quadratic form of cost function are presented in Table 8 and Table 9, respectively. The corresponding results for the reduced CTP are presented in Table 10. Due to the randomness nature of GA, 20 independent runs are taken for each instance of a numerical example.
Table 8.
Information summary of results for the numerical examples of the proposed FCTP with the linear fixed-charge form of cost function.
| Scenario | Normal |
Pandemic |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Without consideration of upper limiton transportation cost as constraint |
Without consideration of upper limit ontransportation cost as constraint |
With consideration of upper limit ontransportation cost as constraint |
||||||||||||
| # Numerical example (Size) | Best found objective function value (A) | Penalty (B) | Total no. of trips (B) | Best found objective function value | Penalty | % Increase in objective function value with respect to (A) | Total no. of trips | % Decrease in penalty with respect to (B) | Upper limit on total transportation cost | Best found objective function value | Penalty | % Increase in objective function value with respect to (A) | Total no. of trips | % Decrease in penalty with respect to (B) |
| 1 (4 × 5) | 1619 | 16 | 12 | 1779 | 11 | 9.88 | 10 | 31.25 | 1750 | 1711 | 14 | 5.68 | 11 | 12.5 |
| 2 (5 × 10) | 2324 | 24 | 15 | 3041 | 18 | 30.85 | 17 | 25.0 | 2600 | 2591 | 24 | 11.49 | 17 | 0.0 |
| 3 (10 × 10) | 2713 | 27 | 20 | 3504 | 20 | 29.16 | 18 | 25.93 | 2850 | 2815 | 25 | 3.76 | 19 | 7.41 |
| 4 (10 × 20) | 4248 | 48 | 29 | 5539 | 33 | 30.39 | 30 | 31.25 | 5000 | 4980 | 39 | 17.23 | 28 | 18.75 |
| 5 (20 × 30) | 7069 | 70 | 47 | 9341 | 62 | 32.14 | 51 | 11.43 | 8500 | 8403 | 64 | 18.87 | 50 | 8.57 |
Table 9.
Information summary of results for the numerical examples of the proposed FCTP with the quadratic fixed-charge form of cost function.
| Scenario | Normal |
Pandemic |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Without consideration of upper limiton transportation cost as constraint |
Without consideration of upper limit on transportation cost as constraint |
With consideration of upper limit on transportation cost as constraint |
||||||||||||
| # Numerical example (Size) | Best found objective function value (A) | Penalty (B) | Total no. of trips (C) | Best found objective function value | Penalty | % Increase in objective function value with respect to (A) | Total no. of trips | % Decrease in penalty with respect to (B) | Upper limit on total transportation cost | Best found objective function value | Penalty | % Increase in objective function value with respect to (A) | Total no. of trips | % Decrease in penalty with respect to (B) |
| 1 (4 × 5) | 8489 | 30 | 23 | 16060 | 11 | 89.19 | 11 | 63.33 | 10000 | 9765 | 17 | 15.03 | 14 | 43.33 |
| 2 (5 × 10) | 11996 | 54 | 38 | 22082 | 18 | 84.08 | 18 | 66.67 | 15500 | 14835 | 27 | 23.67 | 22 | 50.0 |
| 3 (10 × 10) | 11765 | 56 | 36 | 25250 | 19 | 112.41 | 20 | 66.07 | 16000 | 15996 | 26 | 35.96 | 21 | 53.57 |
| 4 (10 × 20) | 20376 | 103 | 67 | 45522 | 32 | 123.41 | 30 | 68.93 | 35000 | 34649 | 40 | 70.05 | 36 | 61.16 |
| 5 (20 × 30) | 31050 | 156 | 106 | 66304 | 62 | 113.54 | 51 | 60.26 | 42000 | 41814 | 86 | 34.67 | 66 | 44.87 |
Table 10.
Information summary of results for the numerical examples of the reduced CTP.
| Scenario | Normal |
Pandemic |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Without consideration of upper limiton transportation cost as constraint |
Without consideration of upper limit on transportation cost as constraint |
With consideration of upper limit on transportation cost as constraint |
||||||||||||
| #Numerical example (Size) | Best found objective function value (A) | Penalty (B) | Total no. of trips (C) | Best found objective function value | Penalty | % Increase in objective function value with respect to (A) | Total no. of trips | % Decrease in penalty with respect to (B) | Upper limit for total transportation cost | Best found objective function value | Penalty | % Increase in objective function value with respect to (A) | Total no. of trips | % Decrease in penalty with respect to (B) |
| 1 (4 × 5) | 665 | 21 | 15 | 923 | 11 | 38.80 | 10 | 47.62 | 800 | 778 | 12 | 16.99 | 10 | 33.33 |
| 2 (5 × 10) | 1000 | 31 | 21 | 1341 | 18 | 34.1 | 17 | 41.94 | 1250 | 1214 | 19 | 21.4 | 16 | 23.81 |
| 3 (10 × 10) | 962 | 41 | 26 | 1818 | 19 | 88.98 | 19 | 53.66 | 1250 | 1248 | 23 | 29.73 | 18 | 30.77 |
| 4 (10 × 20) | 1779 | 58 | 37 | 2815 | 33 | 58.23 | 31 | 43.10 | 2300 | 2296 | 38 | 29.06 | 33 | 10.81 |
| 5 (20 × 30) | 2775 | 108 | 70 | 4481 | 64 | 61.48 | 54 | 40.74 | 3550 | 3536 | 69 | 27.42 | 49 | 30.0 |
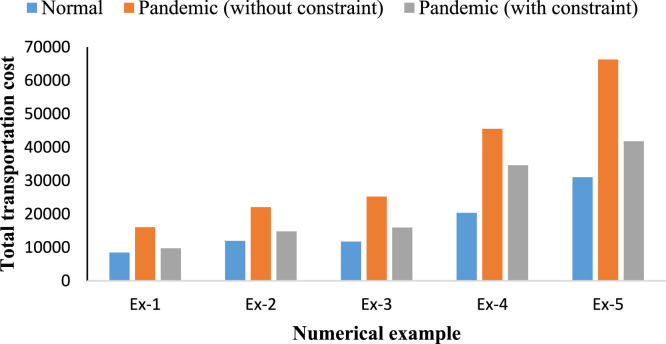
The result shows that the transportation cost for each numerical example of the problem in pandemic scenario without the constraint is more in comparison to normal scenario, and for certain examples, the difference in transportation cost is significantly high. However, the set upper limit on transportation cost is effective in reducing the transportation cost. The percentage increase in transportation cost for the two problems (with and without constraint) in pandemic scenario with respect to the problem in normal scenario are computed for each form of the cost function and given in Table 8, Table 9, Table 10.
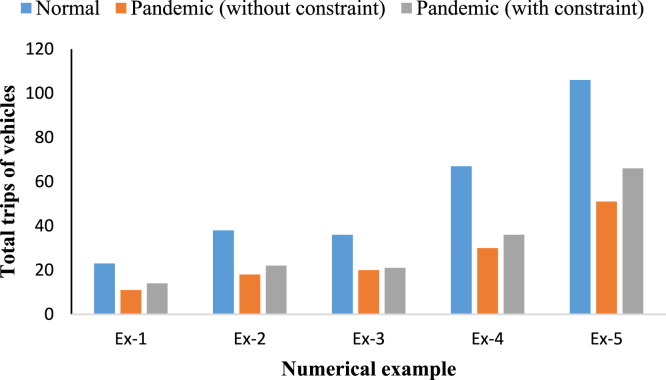
Since the penalty value is a measure of the number of trips between regions with different levels of restrictions (i.e., LSR values), we have computed the expected penalty for each example of the problem in normal scenario given in Eq. (8) considering the same categorization of regions, and presented in respective tables. The result shows that the penalty value is less for the FCTP with constraint as compared to normal scenario, and thus, the trips are restricted to less number between regions with higher restrictions for the proposed FCTP with constraint. The penalty value further decreases for the FCTP without the constraint, and hence, the number of trips between regions with higher restrictions is further less. This is due to either of the two reasons (i) availability of alternate origin–destination pairs with less restrictions, or (ii) availability of alternate origin–destination pairs with lesser difference in LSR values. For each numerical example, the total transportation cost corresponding to the three problems is presented in Fig. 5, whereas, the total number of trips corresponding to the problems is presented in Fig. 6, considering the quadratic fixed-charge form of cost function. The average computational time (in CPU seconds) for each instance of the numerical examples are given in Table 11.
Fig. 5.
Variation of total transportation cost corresponding the three problems for each numerical example.
Fig. 6.
Variation of total number of trips corresponding the three problems for each numerical example.
Table 11.
Average computational time (in CPU seconds).
| Scenario | Normal |
Pandemic |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Cost function # Numerical example () |
Classical | Linear fixed-charge | Non-linear fixed-charge | Classical | Linear fixed-charge | Non-linear fixed-charge | Classical | Linear fixed-charge | Non-linear fixed-charge |
| 1 | 0.74 | 0.78 | 1.11 | 0.76 | 0.77 | 1.08 | 0.77 | 0.89 | 1.05 |
| 2 | 4.47 | 1.49 | 4.77 | 4.37 | 1.62 | 4.38 | 4.41 | 1.59 | 4.70 |
| 3 | 13.63 | 4.26 | 14.17 | 13.34 | 4.17 | 13.63 | 13.54 | 4.10 | 13.78 |
| 4 | 32.96 | 22.26 | 34.92 | 33.19 | 22.12 | 33.53 | 32.86 | 21.99 | 33.71 |
| 5 | 144.72 | 193.43 | 286.67 | 142.59 | 192.24 | 260.19 | 143.70 | 193.17 | 267.18 |
5.4. Performance comparison
To compare the results obtained using our algorithm with existing works, we consider the problem in normal scenario, and only type of vehicle is available at each origin. Moreover, it is also considered that a vehicle can take one trip at most to a destination. In this paper, we compare the results obtained using our algorithm with the works of Jo et al. [11], Xie and Jia [13] and Lofti & Tavakkoli-Moghaddam [14]. We also compare the computational time, wherever possible.
For each numerical example of the above mentioned works, we consider the cost function to be linear and non-linear (quadratic). A comparison of results for the numerical examples given in Jo et al. [11] and Xie and Jia [13] with priority-based genetic algorithm (pb-GA), spanning-tree genetic algorithm (st-GA) and LINGO software are presented in Table 12 and Table 13, respectively. A comparison of the best, average and worst objective function value(s) corresponding to the best solution among our algorithm, pb-GA and st-GA for the numerical examples given in Lofti & Tavakkoli-Moghaddam [14] are presented in Table 14, Table 15. Due to randomness nature of Genetic Algorithms, our algorithm is run 10 times for each numerical example. The average computational time (ACT) (in CPU seconds) for the numerical examples of Lofti & Tavakkoli-Moghaddam [14] using our algorithm are also presented in Table 14, Table 15. The priority-based encoding of the solutions obtained for the numerical examples in [14] using our algorithm are presented in Table 16. In each of the Table 12, Table 13, Table 14, Table 15, the best among the compared approaches are shown in bold. Moreover, since the dataset (variable and fixed cost) for the numerical examples solved in the work by Balaji et al. [16] are not given, we could not compare the performance of our algorithm with theirs.
Table 12.
Comparison of results for the numerical examples from Jo et al. [11].
Table 13.
Comparison of results for the numerical examples from Xie et al. [13].
| Algorithm(s) | Linear FCTP |
Non-linear FCTP |
||
|---|---|---|---|---|
| Size of problem |
||||
| 8 × 16 | 20 × 20 | 8 × 16 | 20 × 20 | |
| st-GA | – | – | 805941 | 3878824 |
| Pb-GA | – | – | – | – |
| LINGO | 54,570 | – | – | – |
| Our proposed algorithm | 43,395 | 1,66,366 | 712542 | 3767542 |
Table 14.
Comparison of results for the numerical examples from Lofti & Tavakkoli-Moghaddam [14] of linear FCTP.
| # Problem | Size of problem | Parameters used |
St-GA |
Pb-GA |
Our proposed algorithm |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| popsize | maxgen | Best | Average | Worst | ACT (in seconds) | Best | Average | Worst | ACT (in seconds) | Best | Average | Worst | ACT (in seconds) | ||
| 1 | 4 × 5 | 10 | 500 | 9291 | 9364 | 9486 | 4.875 | 9291 | 9295 | 9304 | 3.25 | 9168 | 9253.0 | 9338 | 4.65 |
| 2 | 5 × 10 | 20 | 500 | 12899 | 13481 | 13996 | 11.54 | 12718 | 12734 | 12818 | 5.81 | 12718 | 12840.4 | 13009 | 5.96 |
| 3 | 10 × 10 | 30 | 500 | 14844 | 15621 | 16222 | 62.63 | 13987 | 14074 | 14113 | 23.62 | 13934 | 14072.6 | 14192 | 26.74 |
| 4 | 10 × 20 | 30 | 700 | 26036 | 27260 | 28309 | 180.8 | 22095 | 22284 | 22656 | 62.79 | 22095 | 22428.2 | 23200 | 68.84 |
| 5 | 20 × 30 | 30 | 700 | 44453 | 45473 | 45988 | 472.7 | 32526 | 33796 | 34843 | 136.2 | 32526 | 33796 | 34843 | 157.6 |
| 6 | 30 × 50 | 50 | 1000 | 76738 | 77777 | 78706 | 2893.1 | 55143 | 55912 | 56731 | 721.5 | 55143 | 56433.6 | 61506 | 853.5 |
Table 15.
Comparison of results for the numerical examples from Lofti & Tavakkoli-Moghaddam [14] of non-linear FCTP (quadratic cost function).
| # Problem | Size of problem | Parameters used |
St-GA |
Pb-GA |
Our proposed algorithm |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Popsize | Maxgen | Best | Average | Worst | ACT (in seconds) | Best | Average | Worst | ACT (in seconds) | Best | Average | Worst | ACT (in seconds) | ||
| 1 | 4 × 5 | 20 | 500 | 77,798 | 78,270 | 78,479 | 9.938 | 78,458 | 78,458 | 78,458 | 6.314 | 48490 | 50089.6 | 51386 | 6.314 |
| 2 | 5 × 10 | 30 | 500 | 67,854 | 72,659 | 77,016 | 37.199 | 63,571 | 65,596 | 66,067 | 17.998 | 51839 | 52304.8 | 52973 | 17.998 |
| 3 | 10 × 10 | 30 | 500 | 63,469 | 68,345 | 71,537 | 62.755 | 55,075 | 55,342 | 55,846 | 25.149 | 48105 | 48655.4 | 49114 | 25.149 |
| 4 | 10 × 20 | 30 | 500 | 128,655 | 134,559 | 140,397 | 133.96 | 96,161 | 97,673 | 100,081 | 46.0 | 80884 | 82677.6 | 84119 | 46.0 |
| 5 | 20 × 30 | 50 | 1000 | 189,109 | 198,289 | 208,863 | 1176.1 | 126,462 | 128,056 | 129,879 | 325.36 | 113108 | 114450.4 | 115966 | 325.36 |
| 6 | 30 × 50 | 50 | 1000 | 397,082 | 406,872 | 414,957 | 2870.4 | 226,679 | 229,265 | 233,888 | 723.15 | 195264 | 200334.8 | 204067 | 723.15 |
Table 16.
Priority-based representation of best solutions obtained using our proposed algorithm.
| Problem | Solution |
|---|---|
| 1La | 8-9-2-6-3-4-5-7-1 |
| 1Lb | 5-8-9-7-2-1-4-6-3 |
| 2La | 11-13-7-2-9-15-5-4-14-12-6-1-10-3-8 |
| 2Lb | 8-12-11-4-2-13-15-6-14-9-7-10-1-3-5 |
| 3La | 18-3-19-2-7-12-20-9-15-5-8-16-10-14-6-1-13-4-11-17 |
| 3Lb | 7-17-3-12-2-20-14-10-9-13-16-11-4-19-18-6-15-5-1-8 |
| 4La | 24-2-25-14-7-27-5-13-26-23-12-29-28-19-16-21-15-8-11-30-18-22-3-4-6-1-10-17-20-9 |
| 4Lb | 30-10-17-7-2-23-27-6-16-11-8-14-24-13-22-5-18-26-25-29-12-21-1-3-19-9-20-28-15-4 |
| 5La | 6-45-32-21-44-50-46-27-38-22-13-8-12-29-2-34-43-17-40-48-42-10-25-41-49-36-20-16-4-28-18-35-3-11-19-9-26-47-33-39-7-24-1-30-14-15-31-23-5-37 |
| 5Lb | 24-46-22-5-45-38-3-37-34-30-2-35-40-20-36-15-44-43-7-49-42-32-18-41-50-26-10-11-28-13-1-23-12-33-6-31-39-48-14-25-29-27-47-9-4-16-21-8-19-17 |
| 6La | 5-34-42-2-52-80-27-24-23-74-69-59-16-40-61-44-30-9-77-78-72-10-55-7-79-57-51-21-67-75-15-62-48-76-45-19-68-41-54-66-18-32-63-58-29-53-56-71-12-36-39-50-3-6-64-1-37-47-43-14-33-49-22-38-35-26-20-4-28-60-46-70-11-31-73-25-17-8-65-13 |
| 6Lb | 32-28-38-8-70-80-74-78-2-23-63-69-64-77-59-11-16-62-46-79-67-57-9-65-75-19-52-30-58-71-66-53-56-73-44-3-6-72-14-61-51-26-49-36-68-35-48-39-42-21-50-31-24-76-40-12-34-43-5-33-15-4-22-54-7-10-55-1-27-20-45-25-47-29-13-37-41-17-60-18 |
Linear FCTP.
Non-linear FCTP.
Table 12 reveals that our proposed algorithm is able to attain the best solution available in the literature corresponding to the linear and non-linear (quadratic) cost function for the numerical examples of size 4 × 5 and 5 × 10 (Jo et al. [11]). The same set of solutions are also obtained using the LINGO software. It is also seen, for the numerical example of size 4 × 5 with non-linear (quadratic) cost function, the worst solution is obtained using the pb-GA. Moreover, for each numerical example corresponding to the linear and non-linear (quadratic) cost function, the worst solution is obtained using the spanning-tree genetic algorithm (st-GA), except for the numerical example of size 4 × 5 with non-linear (quadratic) cost function.
From Table 13, it is observed that our proposed algorithm produces the best solutions corresponding to linear and non-linear (quadratic) form of the cost function for each numerical example. The LINGO software is able to solve the numerical example of size 8 × 16 with linear cost function only. The solutions obtained using st-GA for the numerical examples of size 8 × 16 and 20 × 20 with non-linear cost function are the worst among all the compared algorithms. Since the running time and performance statistics such as, average and worst objective function values for the works of Jo et al. [11] and Xie and Jia [13] are not reported, we only compare the best solutions.
From Table 14, it is observed that for the same parameter settings, our algorithm is able to attain the existing best solutions for the numerical examples of size 520 and 20 × 30 with linear cost function. For the other numerical examples of size 410 and 30 × 50 with linear cost function, our algorithm produces better solutions. However, our algorithm produces better solutions than the best known solutions for each numerical example with non-linear (quadratic) cost function, and are reported in Table 15. For each numerical example corresponding to linear and non-linear cost function, the average of the objective function values in 10 consecutive runs obtained using our proposed algorithm are better than the st-GA. When compared with pb-GA, the average objective function value is better for some numerical examples only corresponding to linear cost. However, better average objective function value is obtained for each numerical example corresponding to the non-linear cost. The worst among the solutions in 10 consecutive runs are obtained for each numerical example, which shows that for the linear cost, the worst objective function value obtained using our algorithm is less only for the numerical example of size 20 × 30. But, for the non-linear cost function, the worst objective function value obtained using our algorithm is least for each numerical example. From Table 14, Table 15, it is seen that though the average computational time (ACT in seconds) for our algorithm is marginally higher than pb-GA, it is much less than st-GA.
6. Conclusion
In the recent COVID-19 pandemic, most countries categorized regions in different groups and imposed restrictions of different levels in the movement of vehicles (which includes freight vehicles). The level of restriction in a region is based upon many factors that includes number of active cases, population density, number of migrant workers, etc. Consequently, in this scenario, transportation of items is a challenging task for the transportation companies. In this paper, we presented a model of FCTP for a homogeneous item suitable for pandemic scenario, in which multiple vehicles are available at each origin, each with different capacity, and each vehicle is allowed to take multiple trips to one or more destinations. The aim of this problem is to obtain minimum cost transportation plan from a set of origins to a set of destinations situated in regions with different levels of restrictions, so that the number of trips of vehicles moving between regions with higher levels of restrictions (i.e., higher LSR values) is less. For this, a penalty is imposed in the objective function for each such trip. Since the reduction in trips may increase the transportation cost to unrealistic bounds, a constraint is imposed considering an upper limit on transportation cost. The problem is then solved using a genetic algorithm based approach. For this, a new crossover and a new mutation are developed to deal with multiple trips of vehicles moving to one or more destinations. The datasets for five numerical examples are generated artificially, in which the regions are categorized in three different groups. The regions are marked in Red, Orange and Green in the decreasing order of level of restriction. For each numerical example, the cost function is taken to be in three different forms, namely, linear fixed-charge, non-linear fixed-charge and classical. To prove the effectiveness of the imposed constraint, each numerical example is solved without considering the constraint. The results show that the constraint is effective in reducing the transportation cost. Thereafter, the numerical examples are solved considering the problem in normal scenario, and a comparison of results with the earlier two problems is made in terms of transportation cost and number of trips between regions with higher level of restrictions. The results show that the transportation cost is least for the transportation problem in normal scenario, whereas, the total number of trips of all the vehicles moving between regions with level of restriction high is least for the transportation problem in pandemic scenario without any constraint on transportation cost.
Scope of future work
In future, one may be consider one or more of the following natural extensions of the problem solved in this paper.
-
(i)
Formulating a transportation problem for multiple items in pandemic scenario, in which items are categorized in different groups based on priority (For example, medicinal items may be given the top priority, the items related to grocery may be given the next priority and the items related to electronics and cosmetics may be given the last priority), and items need to be delivered at destinations maintaining the order of priority.
-
(ii)
Setting a restriction on the amount of an item a consumer can order from an origin (producer).
-
(iii)
Setting a restriction on the maximum number of origins (producer) from which a consumer may order.
-
(iv)
Consideration of transshipment problems (such as [45], [46], [47] etc.) through the origin and consumer nodes.
Apart from these, one may develop some other heuristics (such as Particle Swarm Optimization [48], Ant Colony Optimization [49], Whale Optimization [50] or some other heuristic/metaheuristic algorithm) and compare the result with that obtained in this paper. While comparing the results with other heuristics, the same crossover and mutation proposed may be used or some other genetic operators may be newly developed.
CRediT authorship contribution statement
Amiya Biswas: Conceptualization, Methodology, Resources, Writing – original draft. Sankar Kumar Roy: Writing – review & editing, Formal analysis, Supervision. Sankar Prasad Mondal: Methodology, Review & validation.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors would like to thank the anonymous referees for their valuable comments which are helpful to greatly improve the quality of the paper.
Appendix.
Table A.1.
Variable cost matrices (for unit quantity) corresponding to the TP with origins, destinations and 2 vehicles at each origin.
| Vehicle 1 | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 7 | 5 | 7 | 12 | 11 | 6 | 9 | 6 | 6 | 6 | 4 | 6 | 6 | 7 | 12 | 12 | 9 | 11 | 11 | 5 | 11 | 12 | 9 | 6 | 4 | 10 | 7 | 8 | 12 |
| 5 | 10 | 6 | 5 | 11 | 5 | 10 | 11 | 8 | 11 | 5 | 9 | 11 | 7 | 11 | 12 | 4 | 10 | 7 | 12 | 8 | 8 | 8 | 5 | 12 | 8 | 4 | 9 | 9 | 8 |
| 8 | 9 | 5 | 8 | 10 | 10 | 7 | 7 | 9 | 10 | 5 | 10 | 6 | 10 | 11 | 11 | 8 | 9 | 8 | 11 | 6 | 10 | 4 | 10 | 12 | 12 | 12 | 12 | 8 | 9 |
| 5 | 10 | 5 | 5 | 12 | 11 | 11 | 7 | 12 | 7 | 4 | 12 | 11 | 4 | 7 | 7 | 11 | 9 | 4 | 4 | 5 | 6 | 10 | 4 | 11 | 7 | 10 | 10 | 4 | 6 |
| 6 | 6 | 10 | 7 | 7 | 10 | 12 | 12 | 11 | 10 | 7 | 11 | 7 | 12 | 9 | 10 | 7 | 7 | 7 | 7 | 7 | 6 | 7 | 11 | 6 | 5 | 6 | 4 | 12 | 6 |
| 4 | 5 | 6 | 10 | 7 | 7 | 5 | 4 | 7 | 12 | 10 | 8 | 8 | 4 | 5 | 4 | 9 | 8 | 5 | 10 | 9 | 6 | 12 | 4 | 5 | 6 | 5 | 5 | 4 | 4 |
| 5 | 4 | 4 | 6 | 8 | 7 | 9 | 10 | 5 | 10 | 7 | 12 | 5 | 12 | 10 | 7 | 10 | 6 | 9 | 12 | 12 | 6 | 5 | 10 | 4 | 4 | 12 | 5 | 12 | 12 |
| 4 | 5 | 10 | 11 | 7 | 5 | 12 | 12 | 9 | 4 | 10 | 4 | 12 | 9 | 10 | 8 | 10 | 5 | 10 | 7 | 4 | 8 | 7 | 4 | 5 | 7 | 11 | 11 | 6 | 11 |
| 8 | 6 | 12 | 5 | 11 | 4 | 4 | 10 | 10 | 10 | 11 | 5 | 8 | 8 | 11 | 12 | 12 | 6 | 4 | 8 | 7 | 12 | 12 | 10 | 10 | 11 | 11 | 8 | 7 | 5 |
| 4 | 9 | 5 | 10 | 8 | 4 | 10 | 8 | 10 | 8 | 12 | 6 | 9 | 5 | 11 | 5 | 4 | 10 | 8 | 12 | 5 | 11 | 11 | 11 | 7 | 8 | 7 | 5 | 10 | 10 |
| 4 | 11 | 6 | 4 | 8 | 10 | 4 | 4 | 4 | 8 | 8 | 12 | 11 | 4 | 12 | 7 | 4 | 10 | 4 | 8 | 9 | 4 | 4 | 5 | 9 | 7 | 7 | 4 | 7 | 5 |
| 8 | 5 | 10 | 9 | 5 | 12 | 4 | 12 | 12 | 4 | 6 | 5 | 11 | 4 | 6 | 10 | 5 | 4 | 7 | 12 | 6 | 11 | 12 | 6 | 12 | 7 | 8 | 7 | 5 | 9 |
| 6 | 7 | 10 | 12 | 12 | 12 | 11 | 4 | 9 | 9 | 11 | 11 | 10 | 9 | 9 | 10 | 4 | 10 | 10 | 8 | 10 | 12 | 6 | 7 | 4 | 5 | 8 | 6 | 6 | 9 |
| 11 | 8 | 4 | 8 | 7 | 10 | 5 | 4 | 8 | 11 | 7 | 7 | 9 | 4 | 10 | 4 | 9 | 11 | 10 | 4 | 4 | 7 | 11 | 6 | 9 | 11 | 5 | 4 | 4 | 6 |
| 8 | 9 | 10 | 8 | 11 | 12 | 12 | 11 | 10 | 8 | 9 | 4 | 11 | 12 | 11 | 6 | 10 | 7 | 4 | 8 | 6 | 4 | 9 | 4 | 4 | 5 | 11 | 4 | 4 | 9 |
| 6 | 8 | 12 | 12 | 10 | 10 | 9 | 9 | 8 | 6 | 11 | 11 | 4 | 7 | 9 | 12 | 10 | 6 | 4 | 10 | 8 | 6 | 11 | 5 | 4 | 9 | 4 | 9 | 9 | 4 |
| 5 | 11 | 6 | 11 | 9 | 12 | 9 | 12 | 7 | 11 | 6 | 5 | 8 | 6 | 9 | 4 | 12 | 6 | 4 | 11 | 12 | 9 | 11 | 8 | 8 | 12 | 5 | 8 | 8 | 8 |
| 7 | 8 | 5 | 9 | 6 | 10 | 7 | 9 | 7 | 10 | 6 | 9 | 11 | 10 | 10 | 7 | 8 | 7 | 9 | 6 | 5 | 7 | 9 | 4 | 9 | 4 | 10 | 10 | 7 | 5 |
| 4 | 8 | 7 | 5 | 4 | 8 | 9 | 5 | 11 | 12 | 11 | 4 | 9 | 8 | 8 | 4 | 9 | 10 | 7 | 4 | 4 | 9 | 7 | 9 | 7 | 12 | 8 | 4 | 8 | 11 |
| 12 | 8 | 6 | 7 | 7 | 4 | 9 | 12 | 6 | 7 | 11 | 11 | 8 | 5 | 4 | 12 | 5 | 10 | 8 | 9 | 10 | 8 | 12 | 11 | 11 | 6 | 8 | 6 | 4 | 12 |
| Vehicle 2 | |||||||||||||||||||||||||||||
| 4 | 12 | 5 | 4 | 4 | 8 | 5 | 9 | 5 | 5 | 4 | 4 | 10 | 6 | 5 | 11 | 12 | 5 | 6 | 7 | 8 | 12 | 11 | 5 | 8 | 8 | 5 | 12 | 10 | 5 |
| 12 | 9 | 11 | 11 | 7 | 12 | 5 | 6 | 6 | 6 | 5 | 4 | 6 | 12 | 6 | 6 | 8 | 6 | 5 | 8 | 7 | 9 | 5 | 4 | 8 | 9 | 8 | 9 | 8 | 12 |
| 10 | 5 | 8 | 8 | 4 | 10 | 5 | 5 | 12 | 6 | 5 | 5 | 6 | 6 | 11 | 9 | 8 | 4 | 9 | 7 | 8 | 12 | 10 | 9 | 12 | 5 | 5 | 5 | 10 | 7 |
| 5 | 5 | 9 | 7 | 7 | 7 | 4 | 9 | 8 | 4 | 9 | 7 | 12 | 11 | 9 | 10 | 5 | 4 | 8 | 8 | 5 | 12 | 6 | 11 | 6 | 5 | 12 | 5 | 5 | 7 |
| 8 | 6 | 8 | 11 | 9 | 12 | 5 | 10 | 6 | 7 | 8 | 11 | 11 | 7 | 9 | 7 | 11 | 9 | 6 | 6 | 4 | 7 | 12 | 6 | 6 | 12 | 6 | 12 | 4 | 7 |
| 7 | 8 | 7 | 11 | 7 | 12 | 10 | 6 | 7 | 10 | 10 | 11 | 8 | 8 | 12 | 5 | 11 | 8 | 8 | 11 | 8 | 6 | 6 | 5 | 9 | 6 | 4 | 9 | 12 | 4 |
| 10 | 4 | 7 | 4 | 10 | 8 | 10 | 5 | 10 | 5 | 12 | 7 | 10 | 7 | 9 | 8 | 6 | 6 | 12 | 10 | 4 | 6 | 4 | 4 | 7 | 7 | 4 | 8 | 10 | 4 |
| 8 | 7 | 4 | 9 | 5 | 8 | 4 | 11 | 10 | 11 | 10 | 9 | 12 | 8 | 12 | 9 | 10 | 6 | 11 | 7 | 10 | 9 | 9 | 10 | 10 | 4 | 11 | 8 | 6 | 8 |
| 8 | 8 | 9 | 7 | 5 | 10 | 11 | 5 | 9 | 8 | 10 | 4 | 11 | 8 | 8 | 11 | 4 | 12 | 11 | 9 | 7 | 8 | 5 | 12 | 6 | 9 | 10 | 11 | 5 | 12 |
| 7 | 7 | 6 | 12 | 8 | 7 | 8 | 5 | 6 | 11 | 7 | 11 | 11 | 6 | 6 | 5 | 4 | 6 | 4 | 11 | 9 | 7 | 6 | 8 | 5 | 6 | 12 | 9 | 12 | 4 |
| 7 | 6 | 5 | 9 | 12 | 8 | 10 | 7 | 9 | 12 | 5 | 12 | 10 | 11 | 5 | 12 | 12 | 12 | 12 | 10 | 8 | 6 | 12 | 9 | 11 | 4 | 9 | 10 | 9 | 8 |
| 8 | 10 | 10 | 7 | 6 | 8 | 11 | 12 | 9 | 7 | 10 | 9 | 5 | 7 | 7 | 4 | 5 | 4 | 4 | 4 | 10 | 6 | 5 | 9 | 11 | 12 | 7 | 8 | 7 | 4 |
| 12 | 9 | 8 | 8 | 12 | 11 | 12 | 9 | 8 | 6 | 10 | 5 | 11 | 11 | 9 | 5 | 12 | 8 | 5 | 10 | 6 | 10 | 12 | 7 | 6 | 11 | 6 | 10 | 4 | 7 |
| 8 | 12 | 10 | 12 | 5 | 8 | 8 | 4 | 4 | 4 | 5 | 10 | 5 | 12 | 9 | 8 | 5 | 6 | 12 | 4 | 12 | 6 | 10 | 9 | 9 | 11 | 7 | 10 | 6 | 7 |
| 11 | 8 | 5 | 9 | 5 | 6 | 4 | 10 | 5 | 11 | 8 | 6 | 8 | 9 | 5 | 11 | 12 | 4 | 11 | 9 | 12 | 8 | 11 | 7 | 5 | 6 | 5 | 6 | 10 | 5 |
| 10 | 8 | 9 | 9 | 11 | 11 | 11 | 9 | 8 | 10 | 7 | 10 | 12 | 12 | 6 | 12 | 8 | 12 | 10 | 7 | 9 | 9 | 11 | 5 | 4 | 10 | 7 | 12 | 4 | 11 |
| 12 | 8 | 7 | 8 | 4 | 12 | 4 | 9 | 9 | 6 | 7 | 12 | 12 | 4 | 9 | 6 | 10 | 5 | 12 | 8 | 6 | 8 | 11 | 11 | 8 | 11 | 9 | 11 | 9 | 9 |
| 10 | 8 | 4 | 11 | 10 | 11 | 10 | 11 | 7 | 4 | 4 | 8 | 4 | 4 | 7 | 9 | 4 | 4 | 8 | 12 | 6 | 8 | 6 | 5 | 7 | 10 | 10 | 10 | 6 | 4 |
| 6 | 10 | 6 | 4 | 6 | 4 | 11 | 4 | 11 | 5 | 11 | 9 | 8 | 11 | 9 | 11 | 6 | 7 | 9 | 8 | 7 | 10 | 4 | 7 | 11 | 5 | 11 | 6 | 11 | 4 |
| 7 | 4 | 11 | 9 | 4 | 4 | 7 | 9 | 11 | 5 | 8 | 8 | 9 | 12 | 6 | 5 | 8 | 6 | 7 | 12 | 11 | 8 | 9 | 9 | 11 | 5 | 10 | 9 | 5 | 8 |
Table A.2.
Fixed-charge matrices corresponding to the TP with origins, destinations and 2 vehicles at each origin.
| Vehicle 1 | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 85 | 115 | 90 | 55 | 105 | 105 | 120 | 100 | 120 | 115 | 125 | 95 | 100 | 80 | 55 | 80 | 125 | 65 | 55 | 110 | 60 | 70 | 70 | 115 | 85 | 65 | 90 | 85 | 50 | 60 |
| 60 | 80 | 110 | 95 | 120 | 90 | 110 | 55 | 110 | 70 | 85 | 95 | 50 | 75 | 100 | 55 | 50 | 120 | 60 | 95 | 100 | 55 | 50 | 90 | 110 | 50 | 60 | 70 | 80 | 70 |
| 120 | 125 | 125 | 100 | 60 | 50 | 80 | 70 | 55 | 65 | 100 | 55 | 105 | 60 | 110 | 65 | 110 | 100 | 115 | 105 | 105 | 105 | 100 | 80 | 125 | 90 | 110 | 80 | 125 | 90 |
| 55 | 85 | 100 | 95 | 95 | 75 | 125 | 65 | 120 | 70 | 50 | 80 | 70 | 70 | 85 | 120 | 85 | 60 | 80 | 85 | 125 | 55 | 90 | 75 | 100 | 70 | 70 | 95 | 95 | 110 |
| 95 | 75 | 55 | 125 | 65 | 80 | 120 | 115 | 100 | 50 | 100 | 50 | 55 | 95 | 80 | 85 | 50 | 125 | 50 | 95 | 65 | 65 | 75 | 105 | 55 | 75 | 125 | 90 | 125 | 85 |
| 95 | 80 | 80 | 100 | 60 | 105 | 55 | 95 | 110 | 75 | 110 | 80 | 115 | 100 | 60 | 60 | 125 | 60 | 110 | 110 | 120 | 80 | 85 | 75 | 55 | 50 | 50 | 85 | 80 | 90 |
| 60 | 65 | 60 | 75 | 60 | 55 | 105 | 55 | 70 | 60 | 110 | 55 | 100 | 105 | 90 | 105 | 125 | 100 | 60 | 55 | 55 | 90 | 85 | 100 | 125 | 125 | 55 | 95 | 85 | 115 |
| 75 | 95 | 65 | 75 | 55 | 110 | 85 | 110 | 110 | 90 | 85 | 85 | 85 | 65 | 50 | 105 | 70 | 95 | 75 | 110 | 50 | 80 | 115 | 70 | 115 | 70 | 65 | 95 | 90 | 75 |
| 90 | 125 | 50 | 75 | 60 | 100 | 105 | 100 | 75 | 55 | 100 | 65 | 50 | 80 | 85 | 65 | 100 | 110 | 85 | 50 | 60 | 115 | 100 | 65 | 70 | 50 | 105 | 100 | 55 | 70 |
| 115 | 80 | 95 | 50 | 70 | 90 | 105 | 60 | 105 | 85 | 105 | 115 | 100 | 120 | 95 | 60 | 110 | 100 | 110 | 70 | 115 | 95 | 60 | 120 | 65 | 110 | 100 | 55 | 65 | 55 |
| 65 | 55 | 115 | 75 | 80 | 100 | 80 | 110 | 55 | 95 | 125 | 120 | 120 | 125 | 110 | 110 | 60 | 120 | 85 | 95 | 115 | 65 | 85 | 115 | 95 | 90 | 105 | 125 | 70 | 105 |
| 125 | 65 | 60 | 50 | 70 | 80 | 100 | 60 | 85 | 90 | 75 | 75 | 95 | 90 | 65 | 55 | 90 | 55 | 65 | 60 | 95 | 85 | 60 | 85 | 105 | 95 | 55 | 125 | 65 | 95 |
| 90 | 70 | 100 | 100 | 80 | 70 | 85 | 65 | 75 | 70 | 95 | 120 | 100 | 60 | 60 | 55 | 65 | 100 | 100 | 100 | 50 | 125 | 90 | 65 | 105 | 115 | 65 | 115 | 85 | 105 |
| 100 | 60 | 50 | 100 | 55 | 100 | 65 | 105 | 115 | 90 | 65 | 105 | 50 | 65 | 70 | 55 | 105 | 110 | 55 | 85 | 105 | 70 | 100 | 85 | 105 | 120 | 80 | 50 | 125 | 120 |
| 65 | 60 | 70 | 85 | 70 | 80 | 125 | 105 | 90 | 50 | 55 | 125 | 85 | 120 | 70 | 80 | 115 | 60 | 80 | 80 | 85 | 90 | 90 | 115 | 70 | 70 | 100 | 115 | 60 | 75 |
| 85 | 110 | 70 | 75 | 90 | 85 | 95 | 60 | 60 | 55 | 115 | 110 | 95 | 90 | 65 | 60 | 90 | 115 | 125 | 105 | 115 | 70 | 50 | 75 | 70 | 105 | 100 | 95 | 125 | 120 |
| 110 | 100 | 125 | 75 | 90 | 65 | 125 | 105 | 110 | 70 | 85 | 65 | 80 | 75 | 100 | 85 | 60 | 120 | 80 | 125 | 50 | 80 | 95 | 120 | 50 | 85 | 65 | 95 | 70 | 110 |
| 120 | 95 | 60 | 55 | 95 | 105 | 50 | 80 | 50 | 115 | 95 | 90 | 125 | 60 | 115 | 60 | 65 | 105 | 55 | 50 | 100 | 55 | 105 | 60 | 125 | 110 | 75 | 65 | 85 | 70 |
| 70 | 120 | 60 | 125 | 80 | 115 | 90 | 115 | 85 | 115 | 120 | 105 | 55 | 70 | 65 | 105 | 65 | 125 | 70 | 90 | 105 | 105 | 75 | 75 | 85 | 125 | 110 | 90 | 80 | 60 |
| 80 | 125 | 90 | 125 | 100 | 85 | 115 | 90 | 90 | 105 | 55 | 60 | 60 | 95 | 90 | 55 | 95 | 95 | 110 | 115 | 110 | 125 | 75 | 105 | 70 | 105 | 120 | 50 | 90 | 90 |
| Vehicle 2 | |||||||||||||||||||||||||||||
| 94 | 121 | 99 | 61 | 112 | 112 | 128 | 109 | 126 | 125 | 134 | 100 | 107 | 85 | 63 | 85 | 133 | 71 | 63 | 115 | 69 | 80 | 79 | 120 | 94 | 72 | 100 | 95 | 58 | 67 |
| 67 | 88 | 117 | 101 | 130 | 97 | 119 | 62 | 119 | 76 | 95 | 101 | 57 | 83 | 107 | 61 | 59 | 125 | 65 | 102 | 106 | 64 | 58 | 98 | 119 | 55 | 65 | 78 | 89 | 80 |
| 127 | 130 | 132 | 108 | 70 | 59 | 87 | 79 | 63 | 73 | 109 | 63 | 110 | 69 | 120 | 70 | 118 | 105 | 122 | 115 | 115 | 111 | 105 | 87 | 135 | 97 | 117 | 90 | 134 | 98 |
| 64 | 93 | 106 | 102 | 101 | 84 | 131 | 73 | 130 | 77 | 56 | 88 | 77 | 80 | 93 | 126 | 92 | 69 | 88 | 94 | 135 | 63 | 97 | 81 | 109 | 78 | 75 | 102 | 100 | 115 |
| 105 | 82 | 60 | 133 | 74 | 85 | 127 | 120 | 106 | 58 | 108 | 57 | 64 | 103 | 90 | 91 | 55 | 132 | 60 | 102 | 70 | 75 | 81 | 113 | 62 | 85 | 135 | 95 | 131 | 92 |
| 102 | 85 | 86 | 109 | 66 | 114 | 61 | 103 | 119 | 83 | 120 | 89 | 121 | 108 | 67 | 69 | 135 | 66 | 115 | 115 | 129 | 89 | 95 | 85 | 60 | 57 | 56 | 95 | 89 | 96 |
| 65 | 75 | 68 | 83 | 69 | 62 | 114 | 63 | 76 | 68 | 116 | 64 | 106 | 114 | 99 | 110 | 133 | 106 | 66 | 61 | 63 | 98 | 91 | 106 | 133 | 132 | 61 | 103 | 90 | 121 |
| 83 | 100 | 70 | 83 | 61 | 120 | 94 | 117 | 120 | 99 | 91 | 95 | 92 | 72 | 57 | 115 | 80 | 101 | 83 | 117 | 60 | 90 | 120 | 79 | 123 | 75 | 74 | 103 | 99 | 80 |
| 95 | 131 | 58 | 85 | 70 | 107 | 111 | 108 | 82 | 63 | 105 | 70 | 60 | 87 | 92 | 75 | 105 | 116 | 91 | 56 | 65 | 120 | 107 | 71 | 75 | 56 | 110 | 108 | 64 | 80 |
| 121 | 85 | 101 | 58 | 75 | 99 | 112 | 65 | 111 | 90 | 114 | 121 | 107 | 125 | 102 | 67 | 118 | 108 | 116 | 78 | 124 | 103 | 65 | 130 | 73 | 118 | 105 | 63 | 71 | 64 |
| 72 | 65 | 120 | 85 | 89 | 108 | 85 | 116 | 62 | 105 | 133 | 129 | 130 | 131 | 118 | 117 | 66 | 127 | 91 | 100 | 120 | 75 | 90 | 124 | 100 | 100 | 115 | 134 | 78 | 111 |
| 130 | 74 | 67 | 59 | 79 | 89 | 105 | 68 | 92 | 96 | 82 | 81 | 100 | 96 | 70 | 62 | 96 | 63 | 74 | 67 | 104 | 90 | 67 | 93 | 111 | 103 | 62 | 132 | 72 | 102 |
| 95 | 80 | 107 | 106 | 85 | 80 | 90 | 70 | 85 | 78 | 103 | 127 | 107 | 68 | 67 | 63 | 75 | 108 | 107 | 109 | 59 | 134 | 96 | 75 | 115 | 124 | 74 | 123 | 91 | 111 |
| 107 | 65 | 55 | 106 | 64 | 106 | 70 | 111 | 123 | 98 | 73 | 110 | 59 | 71 | 80 | 61 | 115 | 116 | 61 | 94 | 115 | 80 | 109 | 95 | 114 | 126 | 87 | 56 | 130 | 129 |
| 71 | 70 | 80 | 91 | 75 | 88 | 134 | 112 | 96 | 60 | 60 | 133 | 93 | 130 | 76 | 85 | 121 | 65 | 86 | 87 | 95 | 97 | 99 | 121 | 77 | 80 | 109 | 123 | 67 | 82 |
| 94 | 118 | 79 | 84 | 98 | 93 | 102 | 67 | 68 | 62 | 122 | 115 | 101 | 99 | 73 | 68 | 100 | 120 | 130 | 110 | 121 | 76 | 56 | 82 | 78 | 114 | 108 | 105 | 135 | 125 |
| 115 | 105 | 135 | 85 | 100 | 74 | 131 | 112 | 120 | 76 | 95 | 73 | 90 | 81 | 109 | 90 | 65 | 127 | 88 | 131 | 58 | 86 | 102 | 129 | 59 | 92 | 70 | 105 | 75 | 120 |
| 127 | 101 | 70 | 64 | 101 | 113 | 59 | 87 | 58 | 125 | 104 | 99 | 133 | 65 | 123 | 65 | 71 | 110 | 63 | 58 | 107 | 60 | 110 | 67 | 135 | 118 | 81 | 73 | 94 | 75 |
| 78 | 126 | 65 | 131 | 87 | 124 | 95 | 123 | 93 | 121 | 130 | 111 | 62 | 76 | 74 | 113 | 74 | 134 | 77 | 99 | 113 | 110 | 80 | 81 | 95 | 134 | 120 | 96 | 87 | 66 |
| 85 | 130 | 97 | 131 | 108 | 94 | 120 | 98 | 99 | 112 | 65 | 65 | 68 | 100 | 97 | 63 | 101 | 101 | 119 | 124 | 115 | 130 | 84 | 111 | 79 | 114 | 130 | 56 | 98 | 99 |
References
- 1.Hitchcock F.L. The distribution of a product from several resources to numerous localities. J. Math. Phys. 1941;20:224–230. [Google Scholar]
- 2.Arsham H., Kahn A.B. A simplex-type algorithm for general transportation problems: An alternating to stepping-stone. J. Oper. Res. Soc. 1989;40:581–590. [Google Scholar]
- 3.Bhatia H.L., Swarup K., Puri M.C. Time-cost trade-off in a transportation problem. Opsearch. 1976;13:129–142. [Google Scholar]
- 4.Charnes A., Cooper W.W. The stepping stone method of explaining linear programming calculations in transportation problems. Manage. Sci. 1954;1:49–69. [Google Scholar]
- 5.Wagner H.M. On a class of capacitated transportation problems. Manage. Sci. 1959;5(3):304–318. [Google Scholar]
- 6.Hirsch W.M., Dantzig G.B. Rand Corporation Memorandum Number 1383, Santa Monica, California. 1954. Notes on linear programming, Part XIX: The fixed charge problem. [Google Scholar]
- 7.Balinski M.L. Fixed-cost transportation problems. Nav. Res. Logist. Q. 1961;8(1):41–54. [Google Scholar]
- 8.Hajiaghaei-Keshteli M., Molla-Alizadeh-Zavardehi S., Tavakkoli-Moghaddam R. Addressing a nonlinear fixed-charge transportation problem using a spanning tree-based genetic algorithm. Comput. Ind. Eng. 2010;59(2):259–271. [Google Scholar]
- 9.El-Sherbiny M.M., Alhamali R.M. A hybrid particle swarm algorithm with artificial immune learning for solving the fixed charge transportation problem. Comput. Ind. Eng. 2013;64(2):610–620. [Google Scholar]
- 10.Gen M., Li Y., IDA K. Spanning tree-based genetic algorithm for bicriteria fixed charge transportation problem. J. Jpn. Soci. Fuzzy Theory Syst. 2000;12(2):295–303. [Google Scholar]
- 11.Jo J., Li Y., Gen M. Nonlinear fixed charge transportation problem byspanning tree-based genetic algorithm. Comput. Ind. Eng. 2007;53:290–298. [Google Scholar]
- 12.Molla-Alizadeh-Zavardehi S., Hajiaghaei-Keshteli M., Tavakkoli-Moghaddam R. Solving a capacitated fixed-charge transportation problem by artificial immune and genetic algorithms with a Prüfer number representation. Expert Syst. Appl. 2011;38(8):10462–10474. [Google Scholar]
- 13.Xie F., Jia R. Nonlinear fixed charge transportation problem by minimum cost flow- based genetic algorithm. Comput. Ind. Eng. 2012;63:763–778. [Google Scholar]
- 14.Lofti M.M., Tavakkoli-Moghaddam R. A genetic algorithm using priority-based encoding with new operators for fixed charge transportation problems. Appl. Soft Comput. 2013;13(5):2711–2726. [Google Scholar]
- 15.Gen M., Altiparmak F., Lin L. A genetic algorithm for two-stage transportation problem using priority-based encoding. OR Spectrum. 2006;28(3):337–354. [Google Scholar]
- 16.Balaji A.N., Nilakantan J.Mukund., Nielsen I., Jawahar N., Ponnambalam S.G. Solving fixed charge transportation problem with truck load constraint using metaheuristics. Ann. Oper. Res. 2019;273(1):207–236. [Google Scholar]
- 17.Biswas A., Shaikh A.A., Niaki S.T.A. Multi-objective non-linear fixed charge transportation problem with multiple modes of transportation in crisp and interval environments. Appl. Soft Comput. 2019;80:628–649. [Google Scholar]
- 18.Deb K., Pratap A., Agarwal S., Meyarivan T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002;6(2):182–197. [Google Scholar]
- 19.Roy S.K., Midya S., Yu V.F. Multi-objective fixed-charge transportation problem with random rough variables. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2018;26(06):971–996. [Google Scholar]
- 20.Midya S., Roy S.K. Multi-objective fixed-charge transportation problem using rough programming. Int. J. Oper. Res. 2020;37(3):377–395. [Google Scholar]
- 21.Ghosh S., Roy S.K., Ebrahimnejad A., Verdegay J.L. Multi-objective fully intuitionistic fuzzy fixed-charge solid transportation problem. Complex Intell. Syst. 2021;7(2):1009–1023. [Google Scholar]
- 22.Biswas A., Pal T. A comparison between metaheuristics for solving a capacitated fixed charge transportation problem with multiple objectives. Expert Syst. Appl. 2021;170 [Google Scholar]
- 23.Giri P.K., Maiti M.K., Maiti M. Fully fuzzy fixed charge multi-item solid transportation problem. Appl. Soft Comput. 2015;27:77–91. [Google Scholar]
- 24.Roy S.K., Midya S., Weber G.W. Multi-objective multi-item fixed-charge solid transportation problem under twofold uncertainty. Neural Comput. Appl. 2019;31(12):8593–8613. [Google Scholar]
- 25.Majumder S., Kundu P., Kar S., Pal T. Uncertain multi-objective multi-item fixed charge solid transportation problem with budget constraint. Soft Comput. 2019;23(10):3279–3301. [Google Scholar]
- 26.Yang L., Liu L. Fuzzy fixed charge solid transportation problem and algorithm. Appl. Soft Comput. 2007;7:879–889. [Google Scholar]
- 27.Zhang B., Peng J., Li S., Chen L. Fixed charge solid transportation problem in uncertain environment and its algorithm. Comput. Ind. Eng. 2016;102:186–197. [Google Scholar]
- 28.Molla-Alizadeh-Zavardehi S., Nezhad S.S., Tavakkoli-Moghaddam R., Yazdani M. Solving a fuzzy fixed charge solid transportation problem by metaheuristics. Math. Comput. Modelling. 2013;57(5–6):1543–1558. [Google Scholar]
- 29.Safi M.R., Razmjoo A. Solving fixed charge transportation problem with interval parameters. Appl. Math. Model. 2013;37(18–19):8341–8347. [Google Scholar]
- 30.Kundu P., Kar S., Maiti M. A fixed charge transportation problem with type-2 fuzzy variables. Inform. Sci. 2014;255:170–186. [Google Scholar]
- 31.Ghosh S., Roy S.K. Fuzzy-rough multi-objective product blending fixed-charge transportation problem with truck load constraints through transfer station. RAIRO: Recherche OpErationnellé. 2021;55(2923) [Google Scholar]
- 32.Amankwah-Amoah J. Note: mayday, mayday, mayday! responding to environmental shocks: insights on global airlines’responses to COVID-19. Transp. Res. E Logist. Transp. Rev. 2020 doi: 10.1016/j.tre.2020.102098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mogaji E. Impact of COVID-19 on transportation in Lagos, Nigeria. Transp. Res. Interdiscip. Perspect. 2020;6 doi: 10.1016/j.trip.2020.100154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bian Z., Zuo F., Gao J., Chen Y., Venkata S.S.C.P., Bernardes S.D., et al. Time lag effects of COVID-19 policies on transportation systems: A comparative study of New York City and Seattle. Transp. Res. A Policy Prac. 2021;145:269–283. doi: 10.1016/j.tra.2021.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Govindan K., Mina H., Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: A case study of coronavirus disease 2019 (COVID-19) Transp. Res. E Logist. Transp. Rev. 2020;138 doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. E Logist. Transp. Rev. 2020;136 doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Gupta R., Rathore B., Biswas B. Impact of COVID-19 on supply chains: lessons learned and future research directions. Int. J. Qual. Reliab. Manag. 2021 [Google Scholar]
- 38.Butt A.S. Supply chains and COVID-19: impacts, countermeasures and post-COVID-19 era. Int. J. Logist. Manage. 2021 [Google Scholar]
- 39.Butt A.S. Mitigating the effects of COVID-19: an exploratory case study of the countermeasures taken by the manufacturing industry. J. Bus. Ind. Mark. 2021 [Google Scholar]
- 40.Reza M.N.H., Jayashree S., Malarvizhi C.A.N., Rauf M.A., Jayaraman K., Shareef S.H. The implications of industry 4.0 on supply chains amid the COVID-19 pandemic: a systematic review. F1000Research. 2021;10(1008):1008. doi: 10.12688/f1000research.73138.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shi X., Liu W., Zhang J. Present and future trends of supply chain management in the presence of COVID-19: a structured literature review. Int. J. Logist. Res. Appl. 2021:1–30. [Google Scholar]
- 42.Choi T.M. Innovative bring-service-near-your-home operations under corona-virus (COVID-19/SARS-CoV-2) outbreak: Can logistics become the messiah? Transp. Res. E Logist. Transp. Rev. 2020;140 doi: 10.1016/j.tre.2020.101961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hirata E., Matsuda T. Uncovering the impact of COVID-19 on shipping and logistics. Marit. Bus. Rev. 2021 [Google Scholar]
- 44.Mollanoori H., Tavakkoli-Moghaddam R., Triki C., Hajiaghaei-Keshteli M., Sabouhi F. Extending the solid step fixed-charge transportation problem to consider two-stage networks and multi-item shipments. Comput. Ind. Eng. 2019;137 [Google Scholar]
- 45.Herer Y.T., Tzur M., Yücesan E. The multilocation transshipment problem. IIE Trans. 2006;38(3):185–200. [Google Scholar]
- 46.Hoppe B., Tardos É. The quickest transshipment problem. Math. Oper. Res. 2000;25(1):36–62. [Google Scholar]
- 47.Özdemir D., Yücesan E., Herer Y.T. Multi-location transshipment problem with capacitated transportation. European J. Oper. Res. 2006;175(1):602–621. [Google Scholar]
- 48.Kennedy J., Eberhart R. Proceedings of ICNN’95-International Conference on Neural Networks, Vol. vol. 4. IEEE; 1995. Particle swarm optimization; pp. 1942–1948. [Google Scholar]
- 49.Dorigo M., Birattari M., Stutzle T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006;1(4):28–39. [Google Scholar]
- 50.Mirjalili S., Lewis A. The whale optimization algorithm. Adv. Eng. Softw. 2016;95:51–67. [Google Scholar]