Abstract
In biomedical research, the replicability of findings across studies is highly desired. In this study, we focus on cancer omics data, for which the examination of replicability has been mostly focused on important omics variables identified in different studies. In published literature, although there have been extensive attention and ad hoc discussions, there is insufficient quantitative research looking into replicability measures and their properties. The goal of this study is to fill this important knowledge gap. In particular, we consider three sensible replicability measures, for which we examine distributional properties and develop a way of making inference. Applying them to three The Cancer Genome Atlas (TCGA) datasets reveals in general low replicability and significant across-data variations. To further comprehend such findings, we resort to simulation, which confirms the validity of the findings with the TCGA data and further informs the dependence of replicability on signal level (or equivalently sample size). Overall, this study can advance our understanding of replicability for cancer omics and other studies that have identification as a key goal.
Keywords: replicability measure, quantitative properties, cancer omics data analysis
Background
In biomedical research, it is desirable to have robust findings. In this aspect, there are two closely related but distinct concepts: reproducibility and replicability. Reproducibility is defined as ‘obtaining consistent results using the same data and codes as the original study’ [1]. It involves following consistent principles and sufficiently publishing programs and information on data analysis procedures. There has been a myriad of studies on reproducibility [2, 3]. Reproducibility itself is not enough to ensure the high-quality of research findings. In this article, we focus on replicability, which is defined as ‘obtaining consistent results across studies aimed at answering the same scientific question using new data or other new computational methods’ [1]. It is noted that reproducibility and replicability are closely related. For example, generating the same findings from the same data using the same methods is essential for achieving replicability across studies.
Although replicability is desirable in all subfields of biomedicine [4], it may have different focuses in different subfields. For example, clinical trial studies may demand not only consistent qualitative results (for example, whether the treatment effects are significant or not) but also compatible quantitative results (for example, the estimated hazard ratios are ‘close enough’). In this article, we focus on cancer omics data analysis, which may be mostly at an earlier exploratory stage. As in most cases, there is still a lack of consensus on which omics variables (for example, Single Nucleotide Polymorphisms, gene expressions) are important for cancer outcomes/phenotypes, most of the existing cancer omics research still focuses on identification and strives to achieve consistent identification results across studies. Our literature review suggests that some cancer omics publications, in particular the recent ones, have touched on replicability [5–9]. For example, some have discussed which findings have also been made in all existing publications (i.e. full replicability), have been made in some but not other publications (i.e. partial replicability), or are completely new (i.e. a lack of replicability).
Many factors can potentially affect replicability [10, 11]. For example, higher differences in sample characteristics, differences in analysis methods, smaller sample sizes, lower signal-to-noise ratios and more complex data distributional properties may potentially reduce replicability. This has been discussed in published studies [12–15] and is not the focus of this study.
Although replicability has drawn broad attention (for example, there are more than 60 000 publications in Pubmed that involve ‘cancer replicability’), our own limited literature review suggests that there is still insufficient attention to the measures of replicability. In quite a few studies, a simple count (or percentage) of findings that have also been made in another study (or multiple selected studies) has been used to quantify replicability [16–19]. However, replicability assessment itself is usually not the focus of these studies. Shi et al. [20] considered the index-based and correlation-based measures, however, did not dig deeper into properties of these measures. There has also been some context-specific effort. For example, repfdr [21], SCREEN [22] and MAMBA [23] have been developed to assess replicability for Genome-Wide Association Meta-Analysis.
Motivated by the significance of replicability and insufficient attention to the measures of replicability, this study targets filling an important knowledge gap by examining multiple replicability measures that take different perspectives, studying their distributional properties, and making direct comparisons based on empirical data. It can complement the existing studies that discuss (the lack of) replicability for specific diseases, outcomes and datasets. Quantifying replicability is also essential for many other fields such as engineering, social science, economics and others. The tools developed in this study have the potential of being applied to those fields too. In addition, this study may also serve as the prototype for developing other, more sophisticated replicability measures and studying their properties.
Data preparation
Replicability may be more of an applied (as opposed to theoretical) problem. In some published studies, data are generated from parametric models. Such data may have simpler distributional properties than that generated by real studies. For example, some simulated data have autoregressive or blocked correlation structures, under which many correlations are zero. In contrast, data from real studies often have more complex correlation structures. To this end, our empirical examination is based on The Cancer Genome Atlas (TCGA) data. TCGA is a public cancer data repository. It has published comprehensive omics (and clinical and imaging) data on 33 cancer types and over 11 000 cancer patients. TCGA data have been extensively analyzed for many different purposes. Compared to some other data resources, it may excel with a more carefully designed and clearly described quality control, leading to higher data quality [24]. Some TCGA data-based studies have included discussions related to replicability [7, 25–27].
We choose three common cancers, namely skin cutaneous melanoma (SKCM), lung squamous cell carcinoma (LUSC) and lung adenocarcinoma (LUAD). Here it is noted that our goal is not to draw conclusions for specific cancers, and the choice of cancers may not be critical. For cancer outcome, we consider overall survival, which is of essential importance for these three and many other cancers. For covariates, we consider clinical/demographic variables and gene expressions. In the literature, the analysis of ‘cancer overall survival ~ clinical/demographic variables + omics variables’ has been popular.
To ensure full reproducibility, we provide a detailed description of data collection and processing in the Supplementary Material. All analyzed data are publicly available and directly downloaded from the NCI Genomic Data Commons Data Portal (https://portal.gdc.cancer.gov/). The final sample sizes are 406 (SKCM), 484 (LUSC) and 493 (LUAD). As a representative example, the data processing flowchart for SKCM is presented in Figure 1. The three datasets are briefly summarized in Table 1.
Figure 1.
Flowchart of data processing for SKCM.
Table 1.
Summary of sample characteristics
| SKCM | LUSC | LUAD | |
|---|---|---|---|
| Sample size | 406 | 484 | 493 |
| Clinical outcomes | |||
| Overall survival (days): median (range) | 1029 (0, 10 346) | 653(0, 5287) | 653 (0, 7248) |
| Event | 191 (47.0%) | 206 (42.6%) | 178 (36.1%) |
| Clinical/demographic variablesa | |||
| Age at diagnosis | 59.3 (15.6) | 67.8 (8.4) | 65.8 (9.8) |
| Race (White) | 387 (95.3%) | 338 (69.8%) | 378 (76.7%) |
| Gender (Male) | 252 (62.1%) | 358 (74.0%) | 226 (45.8%) |
| Prior malignancy (Yes) | 19 (4.7%) | 58 (12.0%) | 80 (16.2%) |
| Prior treatment (Yes) | 9 (4.7%) | ||
| AJCC pathologic stage | |||
| I, IA, IB | 76 (18.7%) | 241 (49.8%) | 270 (54.8%) |
| II, IIA, IIB | 139 (34.2%) | 154 (31.8%) | 118 (23.9%) |
| III, IIIA, IIIB, IIIC or IV | 191 (47.0%) | 89 (18.4%) | 105 (21.3%) |
| Radiation therapy (Yes) | 123 (30.3%) | 68 (14.0%) | 104 (21.1%) |
| Pharmaceutical therapy (Yes) | 156 (38.4%) | 135 (27.9%) | 179 (36.3%) |
| Additional exposure variables | |||
| Cigarettes per day | 2.46 (1.88) | 1.58 (1.63) | |
| BMI | |||
| Obese | 65 (16.0) | ||
| Normal and underweight | 152 (37.4) | ||
| Not reported | 189 (46.6) | ||
aContinuous variable: mean (standard deviation), categorical variable: count (percentage).
Identification of important genes
Many methods have been developed to identify important gene expressions (and other omics measurements) associated with cancer overall survival (and other outcomes) [28–30]. Replicability can be directly affected by the choice of analysis methods [10]. To make our analysis more relevant, we adopt the ‘simplest’ and highly popular methods. We note that it is not our intention to draw conclusions on specific analysis methods and that similar replicability analysis can be conducted with other analysis methods.
In general, there are two families of analysis methods: marginal and joint, depending on whether one gene or a large number of genes are analyzed at a time. Marginal analysis proceeds as follows: (1) For a specific gene, assume the Cox model, and fit the model ‘overall survival – clinical/demographic variables, additional exposure variables + gene expression,’ which can be realized using R package survival [31]. Extract the P-value for the gene expression. (2) Repeat step (1) for all gene expressions. (3) With all the P-values, adjust for multiple comparisons. In particular, we consider the Bonferroni approach with a cutoff of 0.1 [32] (main text) and the false discovery rate (FDR) approach with a target FDR of 0.1 [33] (see Supplementary Materials available online). It is also possible to adopt other cutoffs (which is not expected to change the qualitative conclusions) and other less popular multiple adjustments approaches.
For joint analysis, we assume the Cox model and consider the partial likelihood function. For regularized estimation and variable selection, we apply elastic net [34], which is a penalization approach built on the ridge and Lasso penalties and realized using R package glmnet [35]. With this approach, all gene expressions and clinical/demographic and additional exposure variables are analyzed in a single model. The α parameter is set as 0.5, balancing the two penalties. The tuning parameter 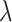 is selected using 3-fold cross validation. In particular, data are randomly split into three subsets with equal sizes. Two subsets are combined, serve as the training data and are analyzed using the elastic net approach under a specific
is selected using 3-fold cross validation. In particular, data are randomly split into three subsets with equal sizes. Two subsets are combined, serve as the training data and are analyzed using the elastic net approach under a specific 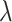 value. With the training set estimate and testing data (the left-out subset), the log partial likelihood is computed. The three subsets are repeatedly left out. From a sequence of
value. With the training set estimate and testing data (the left-out subset), the log partial likelihood is computed. The three subsets are repeatedly left out. From a sequence of 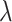 values, the one corresponding to the largest average partial likelihoods is selected as the optimal. Gene expressions with non-zero estimates under the optimal tuning parameter value are identified as important.
values, the one corresponding to the largest average partial likelihoods is selected as the optimal. Gene expressions with non-zero estimates under the optimal tuning parameter value are identified as important.
The analyses described above and many published ones are not robust. In the Supplementary Materials, we also consider a robust estimation, which demonstrates that replicability analysis can also be coupled with robustness if desirable.
Replicability evaluation involves at least two datasets. In our analysis, we create two datasets by equally splitting the original data. This can effectively reduce the lack of replicability caused by differences in cohorts, measurement techniques, data preprocessing, etc. As described below, to avoid an ‘unlucky’ split, we repeat the splitting multiple times.
Replicability measures
We consider three replicability measures, all of which are easy to implement and intuitive and have roots in published literature. In the following description, we consider two studies. When one study is evaluated against multiple studies, one possibility is to consider each pair and then take average. The second possibility is to combine the multiple studies/findings into one and then proceed as follows.
A measure based on gene name matching (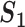 )
)
The simplest measure is to count how many important genes identified in a study are also identified in another study. It is closely related to the index-based measure in Shi et al. [20] and the Jaccard index. Assume that two studies identify  and
and  genes, respectively, with
genes, respectively, with 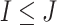 . We create a
. We create a  dimensional matrix
dimensional matrix 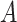 , with the
, with the 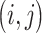 th element
th element 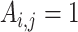 if gene
if gene  of the first study and gene
of the first study and gene 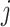 of the second study have the same name. Otherwise,
of the second study have the same name. Otherwise, 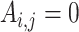 . That is, replicability is concluded only if the gene names match exactly. We define replicability measure:
. That is, replicability is concluded only if the gene names match exactly. We define replicability measure:
 |
where the denominator 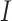 realizes normalization.
realizes normalization. 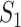 takes the smallest value of 0, when the two lists of genes have no overlap; and it equals 1, if the shorter list is a subset of the longer one. A higher value indicates a higher level of replicability.
takes the smallest value of 0, when the two lists of genes have no overlap; and it equals 1, if the shorter list is a subset of the longer one. A higher value indicates a higher level of replicability.
Denote 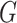 as the number of genes. When we randomly select two sets of genes with sizes
as the number of genes. When we randomly select two sets of genes with sizes 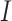 and
and 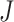 , it is possible that
, it is possible that 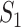 is not zero. That is, we may observe spurious replicability. Define
is not zero. That is, we may observe spurious replicability. Define 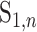 as the resulting value of
as the resulting value of 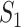 if
if 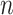 out of
out of  genes are matched. Under the null when two sets of genes are random, we have the expectation of
genes are matched. Under the null when two sets of genes are random, we have the expectation of 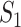 :
:
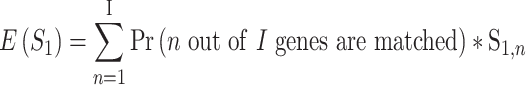 |
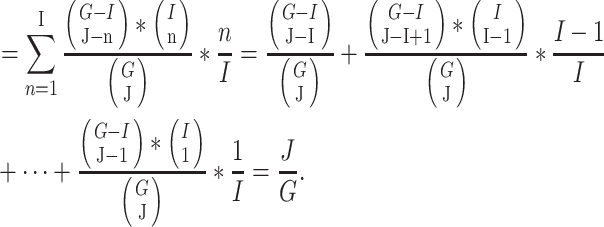 |
Apparently, if an observed 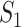 value is close to this expectation, replicability should not be concluded. In practice, an alternative but less accurate way of calculating
value is close to this expectation, replicability should not be concluded. In practice, an alternative but less accurate way of calculating 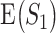 is to randomly select
is to randomly select 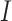 and
and 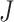 genes and calculate
genes and calculate 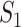 , repeat many times, and then take average.
, repeat many times, and then take average.
A measure based on correlation (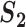 )
)
If two genes with different names have identical expression values, any statistical analysis cannot distinguish them. If they have highly correlated expression values, then statistically speaking, they are highly similar. As such, if each of those two genes is identified in a study, then the two studies should be concluded as having high replicability. This cannot be realized using 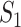 and has motivated the correlation-based measure.
and has motivated the correlation-based measure.
Using notations similar to those in Section “A measure based on gene name matching (S1),” we create a  dimensional matrix
dimensional matrix 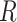 , with the
, with the 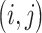 th element equal to
th element equal to 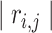 , where
, where 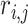 is the correlation coefficient between genes
is the correlation coefficient between genes 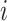 and
and 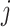 . In our analysis, datasets are combined to calculate correlations. In practice when sharing data are not feasible, correlations can be calculated as the averages from individual datasets. We further define
. In our analysis, datasets are combined to calculate correlations. In practice when sharing data are not feasible, correlations can be calculated as the averages from individual datasets. We further define 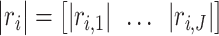 as the
as the 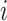 th row and
th row and 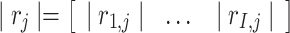 as the
as the 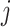 th column in
th column in 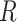 . The second replicability measure is defined as:
. The second replicability measure is defined as:
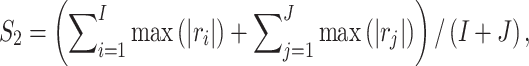 |
which is the average of the maximum absolute correlation coefficients across rows and columns. Different from with 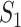 ,
, 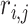 takes a non-integer value and can describe partial replicability.
takes a non-integer value and can describe partial replicability. 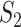 takes value between 0 and 1, with a larger value indicating higher replicability. It shares some similar spirit with the RV coefficient, which has been adopted in multiple studies to assess the degree of overlapping findings. Unlike for
takes value between 0 and 1, with a larger value indicating higher replicability. It shares some similar spirit with the RV coefficient, which has been adopted in multiple studies to assess the degree of overlapping findings. Unlike for 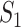 , there is not a simple analytic calculation of its expectation. With practical data, we estimate its expectation by randomly selecting
, there is not a simple analytic calculation of its expectation. With practical data, we estimate its expectation by randomly selecting 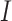 and
and 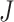 genes, calculate
genes, calculate 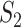 (which is under the null and denoted as
(which is under the null and denoted as 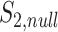 ), repeat
), repeat 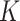 times, and then take average. That is,
times, and then take average. That is, 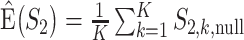 .
.
A measure incorporating pathway information (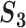 )
)
Measure 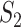 can accommodate genes that have different names but are ‘statistically overlapping.’ Measure
can accommodate genes that have different names but are ‘statistically overlapping.’ Measure 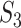 is developed to accommodate genes that are ‘functionally overlapping.’ Some published studies have drawn conclusions based on omics measurements’ functionalities. That is, replicability is indicated if the same biological functionalities/mechanisms are identified in different studies. Here we incorporate pathway information in measuring replicability. Other functional information, for example gene ontology (GO) terms, can be incorporated in the same manner. The calculation includes the following steps:
is developed to accommodate genes that are ‘functionally overlapping.’ Some published studies have drawn conclusions based on omics measurements’ functionalities. That is, replicability is indicated if the same biological functionalities/mechanisms are identified in different studies. Here we incorporate pathway information in measuring replicability. Other functional information, for example gene ontology (GO) terms, can be incorporated in the same manner. The calculation includes the following steps:
1) Extract pathway information, for example, from Kyoto Encyclopedia of Genes and Genomes (KEGG), and identify the pathway(s) each gene belongs to.
2) For the first set of
 identified genes, assume that they belong to
identified genes, assume that they belong to 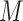 pathways. For
pathways. For 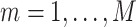 , calculate the weight:
, calculate the weight:
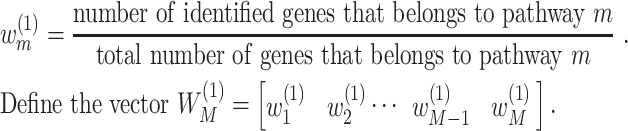 |
For the second set of 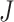 identified genes, conduct a similar calculation. Denote
identified genes, conduct a similar calculation. Denote 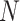 as the number of unique pathways,
as the number of unique pathways, 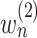 as the weight for pathway
as the weight for pathway 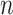 , and
, and 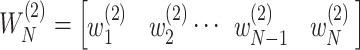 .
.
For 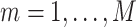 and
and 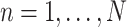 , create an
, create an 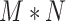 dimensional matrix
dimensional matrix 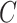 , with the
, with the 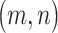 th element
th element 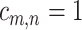 , if pathway
, if pathway 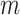 of the first study matches pathway
of the first study matches pathway 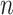 of the second study, and
of the second study, and 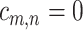 otherwise.
otherwise.
Denote 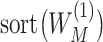 and
and 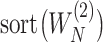 as
as 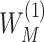 and
and 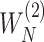 sorted in a descending manner, respectively. Assume that
sorted in a descending manner, respectively. Assume that 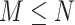 . Further denote
. Further denote 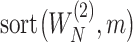 as the sub-vector composed of the first
as the sub-vector composed of the first 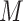 components of
components of 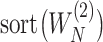 .
.
3) The replicability measure is defined as:
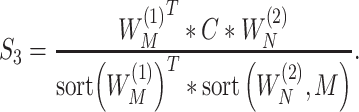 |
This calculation is more complicated but still intuitive. In particular, replicability is defined at the pathway level. That is, we quantify how strongly the two sets of identified pathways overlap. Pathways have different sizes. The weights  ’s have been designed to account for the ‘strength of evidence’: if a larger number of genes from a specific pathway are identified, then the evidence is stronger. The denominator of
’s have been designed to account for the ‘strength of evidence’: if a larger number of genes from a specific pathway are identified, then the evidence is stronger. The denominator of 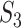 has been designed so that it can be normalized to be within [0,1], with a larger value indicating a higher level of replicability. Calculating the expectation of
has been designed so that it can be normalized to be within [0,1], with a larger value indicating a higher level of replicability. Calculating the expectation of 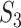 under the null can be realized in the same Monte Carlo way as above. Specifically,
under the null can be realized in the same Monte Carlo way as above. Specifically, 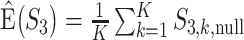 , where
, where 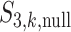 is the value of
is the value of 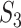 for the sets of randomly selected
for the sets of randomly selected 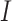 and
and 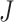 genes in the
genes in the 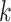 th round of random sampling. Here we note that although pathway (and other functionality) information has been extensively referred to in the discussion of overlapping findings, the existing works are qualitative, and there has been a lack of rigorous measure as the proposed.
th round of random sampling. Here we note that although pathway (and other functionality) information has been extensively referred to in the discussion of overlapping findings, the existing works are qualitative, and there has been a lack of rigorous measure as the proposed.
Remarks: The first measure is based on exact matching. It is easily and clearly defined and can be generalized to many other settings/scientific domains. It also has the strictest definition. With the second measure, the choice of correlation may need to be data dependent. For example, for omics (and other) data with categorical distributions, rank correlation may be more sensible than Pearson’s correlation. It is noted that, in different studies, the same sets of identification may lead to different 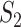 values, as the correlations are calculated based on present data. This is different from
values, as the correlations are calculated based on present data. This is different from 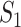 and
and 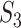 . This measure may be the most sensible if there existing high correlations among variables. With
. This measure may be the most sensible if there existing high correlations among variables. With 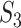 , it is noted that there are different ways of defining functionalities, and different definitions may lead to different replicability values. In addition, our knowledge of functionality is still evolving, and the value of
, it is noted that there are different ways of defining functionalities, and different definitions may lead to different replicability values. In addition, our knowledge of functionality is still evolving, and the value of  may need update along with the identification of new functionality. Moreover, in other scientific domains, the definition of functionality may need to be revised. This measure may be the most sensible when the underlying mechanisms are of interest.
may need update along with the identification of new functionality. Moreover, in other scientific domains, the definition of functionality may need to be revised. This measure may be the most sensible when the underlying mechanisms are of interest.
Application to the TCGA data
For each dataset, we randomly split into two equal-sized subsets. Both marginal and joint analyses are conducted on the two subsets. With 100 random splittings (that correspond to system-generated random seeds, which may lead to some randomness in the results), the numbers of identified genes and pathways are summarized in Table 2. As in the literature, significant differences across cancers and between marginal and joint analysis are observed. Significant variations across splittings are also observed.
Table 2.
Analysis of TCGA data: numbers of identified genes and pathways. Mean (sd) in each cell
| Data | SKCM | LUSC | LUAD | |||
|---|---|---|---|---|---|---|
| Marginal | Joint | Marginal | Joint | Marginal | Joint | |
| Number of genes | 377 (169) | 63 (40) | 24 (24) | 73 (50) | 81 (57) | 71 (43) |
| Number of pathways | 264 (41) | 145 (64) | 74 (52) | 150 (81) | 163 (65) | 158 (71) |
We then conduct the following replicability analysis. (i) For each split and the corresponding two sets of identified genes (under marginal and joint analysis separately), we calculate 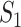 ,
, 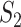 and
and 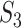 values. With 100 random splittings, we obtain their mean and standard deviation (sd) values. (ii) As described in Section “Replicability measures,” we calculate the replicability measures under the null, where the two sets of findings are simply randomly selected. With multiple values under the null, we construct 95% confidence intervals. This shares some similar spirit with the permutation-based inference. It is noted that, although intuitively sensible, its theoretical validity has not been rigorously established. We consider two types of confidence intervals: two-sided and one-sided. We then calculate the percentages of the replicability measures obtained in (i) that are below, within and above the 95% confidence intervals. On a special note, in some joint analyses, none of the genes are selected and concluded as important, which leads to ‘invalid’ replicability measures. In this case, when calculating summary statistics and visualizing measures, we exclude results from those splittings that lead to empty identification.
values. With 100 random splittings, we obtain their mean and standard deviation (sd) values. (ii) As described in Section “Replicability measures,” we calculate the replicability measures under the null, where the two sets of findings are simply randomly selected. With multiple values under the null, we construct 95% confidence intervals. This shares some similar spirit with the permutation-based inference. It is noted that, although intuitively sensible, its theoretical validity has not been rigorously established. We consider two types of confidence intervals: two-sided and one-sided. We then calculate the percentages of the replicability measures obtained in (i) that are below, within and above the 95% confidence intervals. On a special note, in some joint analyses, none of the genes are selected and concluded as important, which leads to ‘invalid’ replicability measures. In this case, when calculating summary statistics and visualizing measures, we exclude results from those splittings that lead to empty identification.
The results are summarized in Table 3 and Figure 2 (Bonferroni with cutoff 0.1) in the main text as well as Table 2 and Figure 1 (FDR with cutoff 0.1), and Table 4 and Figure 2 (robust estimation) in the Supplementary Materials, which reveal the following. (i) Significant differences across measures are observed. The  values tend to be very low, with the only exception of the marginal analysis of the SKCM data. By accounting for ‘partial replicability’ attributable to statistical correlation and similar functionality, measures
values tend to be very low, with the only exception of the marginal analysis of the SKCM data. By accounting for ‘partial replicability’ attributable to statistical correlation and similar functionality, measures 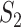 and
and 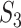 have significantly larger values. The
have significantly larger values. The  and
and  values are different, and there is a lack of obvious pattern, suggesting that both measures can be needed. (ii) Significant differences are observed between marginal and joint analysis, with joint analysis having smaller values. For example, for SKCM and
values are different, and there is a lack of obvious pattern, suggesting that both measures can be needed. (ii) Significant differences are observed between marginal and joint analysis, with joint analysis having smaller values. For example, for SKCM and  , the marginal and joint analysis have replicability measure values 0.75 and 0.38, respectively. As such, in the discussion of replicability, the adopted methods need to be clearly specified and fully accounted for – this has not been given full attention in some published studies. (iii) Significant differences are observed across datasets, even though exactly the same procedures are followed. For example, for marginal analysis and
, the marginal and joint analysis have replicability measure values 0.75 and 0.38, respectively. As such, in the discussion of replicability, the adopted methods need to be clearly specified and fully accounted for – this has not been given full attention in some published studies. (iii) Significant differences are observed across datasets, even though exactly the same procedures are followed. For example, for marginal analysis and 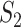 , the three datasets have replicability measure values 0.75 (SKCM), 0.25 (LUSC) and 0.39 (LUAD). This result suggests that the discussion of replicability needs to be domain specific. (iv) Strong replicability is observed for some analysis. For example, for SKCM, marginal analysis and
, the three datasets have replicability measure values 0.75 (SKCM), 0.25 (LUSC) and 0.39 (LUAD). This result suggests that the discussion of replicability needs to be domain specific. (iv) Strong replicability is observed for some analysis. For example, for SKCM, marginal analysis and 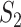 , all of the 100 replicability measure values are above the upper bound of both the two-sided and one-side 95% confidence interval, suggesting significant replicability. However, quite a few irreplicable findings are also observed. For example, for LUSC, joint analysis, and
, all of the 100 replicability measure values are above the upper bound of both the two-sided and one-side 95% confidence interval, suggesting significant replicability. However, quite a few irreplicable findings are also observed. For example, for LUSC, joint analysis, and 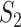 , 97.4% of the replicability measure values are below the lower bound of the two-sided confidence interval, and 100% within the one-sided confidence interval. This result may seem somewhat counterintuitive, in the sense that the findings from the observed data should not be worse than random. A possible reason is that the two datasets that generated by splitting are not fully iid. That is, the lack of inherent replicability may be caused by findings sensitive to data splitting.
, 97.4% of the replicability measure values are below the lower bound of the two-sided confidence interval, and 100% within the one-sided confidence interval. This result may seem somewhat counterintuitive, in the sense that the findings from the observed data should not be worse than random. A possible reason is that the two datasets that generated by splitting are not fully iid. That is, the lack of inherent replicability may be caused by findings sensitive to data splitting.
Table 3.
Analysis of TCGA data: summary of replicability measures
| Measure |
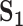 a
a
|

|

|
||
|---|---|---|---|---|---|
| SKCM | Marginal | Observed | 0.49 (0.14) | 0.75 (0.05) | 0.91 (0.09) |
| Under the null: 2.5% Mean 95% 97.5% |
0.05 (0.01) 0.09 (0.02) 0.12 (0.03) 0.13 (0.03) |
0.53 (0.03) 0.55 (0.03) 0.56 (0.03) 0.56 (0.03) |
0.67 (0.06) 0.74 (0.04) 0.8 (0.03) 0.8 (0.03) |
||
| Below 95% Above or at 95% |
1 (1%) 99 (99%) |
0 (0) 100 (100%) |
5 (5%) 95 (95%) |
||
| Below 2.5% 2.5–97.5% Above 97.5% |
0 (0) 4 (4%) 96 (96%) |
0 (0) 0 (0) 100 (100%) |
3 (3%) 4 (4%) 93 (93%) |
||
| Joint | Observed | 0.02 (0.04) | 0.38 (0.04) | 0.37 (0.14) | |
| Under the null: 2.5% Mean 95% 97.5% |
0 (0) 0.02 (0.01) 0.06 (0.03) 0.07 (0.04) |
0.38 (0.07) 0.43 (0.06) 0.47 (0.04) 0.48 (0.04) |
0.17 (0.1) 0.31 (0.09) 0.46 (0.08) 0.5 (0.07) |
||
| Below 95% Above or at 95% |
76 (78.4%) 21 (21.6%) |
96 (99.0%) 1 (1.0%) |
74 (76.3%) 23 (23.7%) |
||
| Below 2.5% 2.5–97.5% Above 97.5% |
0 (0) 93 (95.9%) 4 (4.1%) |
60 (61.9%) 36 (37.1%) 1 (1.0%) |
2 (2.1%) 79 (81.4%) 16 (16.5%) |
||
| LUSC | Marginal | Observed | 0 (0.01) | 0.25 (0.05) | 0.13 (0.1) |
| Under the null: 2.5% Mean 95% 97.5% |
0 (0) 0.01 (0.01) 0.04 (0.06) 0.08 (0.06) |
0.24 (0.05) 0.3 (0.04) 0.36 (0.04) 0.37 (0.04) |
0.03 (0.04) 0.14 (0.05) 0.33 (0.06) 0.39 (0.05) |
||
| Below 95% Above or at 95% |
45 (45%) 55 (55%) |
99 (99%) 1 (1%) |
94 (94%) 6 (6%) |
||
| Below 2.5% 2.5–97.5% Above 97.5% |
0 (0) 99 (99%) 1 (1%) |
44 (44%) 55 (55%) 1 (1%) |
8 (8%) 91 (91%) 1 (1%) |
||
| Joint | Observed | 0.03 (0.03) | 0.31 (0.05) | 0.35 (0.15) | |
| Under the null: 2.5% Mean 95% 97.5% |
0 (0) 0.02 (0.01) 0.05 (0.02) 0.07 (0.06) |
0.37 (0.06) 0.4 (0.05) 0.43 (0.05) 0.44 (0.04) |
0.24 (0.12) 0.37 (0.11) 0.5 (0.09) 0.53 (0.08) |
||
| Below 95% Above or at 95% |
56 (71.8%) 22 (28.2%) |
78 (100%) 0 (0) |
75 (96.2%) 3 (3.8%) |
||
| Below 2.5% 2.5–97.5% Above 97.5% |
0 (0) 75 (96.2%) 3 (3.8%) |
76 (97.4%) 2 (2.6%) 0 (0) |
3 (3.8%) 74 (94.9%) 1 (1.3%) |
||
| LUAD | Marginal | Observed | 0.08 (0.04) | 0.39 (0.04) | 0.32 (0.1) |
| Under the null: 2.5% Mean 95% 97.5% |
0 (0) 0.02 (0.01) 0.06 (0.03) 0.08 (0.04) |
0.36 (0.04) 0.39 (0.03) 0.42 (0.03) 0.43 (0.03) |
0.22 (0.07) 0.36 (0.07) 0.5 (0.06) 0.53 (0.05) |
||
| Below 95% Above or at 95% |
24 (24%) 76 (76%) |
90 (90%) 10 (10%) |
98 (98%) 2 (2%) |
||
| Below 2.5% 2.5–97.5% Above 97.5% |
0 (0) 62 (62%) 38 (38%) |
20 (20%) 75 (75%) 5 (5%) |
20 (20%) 79 (79%) 1 (1%) |
||
| Joint | Observed | 0.05 (0.04) | 0.33 (0.04) | 0.35 (0.14) | |
| Under the null: 2.5% Mean 95% 97.5% |
0 (0) 0.02 (0.01) 0.06 (0.05) 0.08 (0.06) |
0.36 (0.06) 0.39 (0.05) 0.42 (0.05) 0.43 (0.05) |
0.21 (0.11) 0.35 (0.1) 0.49 (0.07) 0.52 (0.07) |
||
| Below 95% Above or at 95% |
45 (47.9%) 49 (52.1%) |
94 (100%) 0 (0) |
89 (94.7%) 5 (5.3%) |
||
| Below 2.5% 2.5–97.5% Above 97.5% |
0 (0) 84 (89.4%) 10 (10.6%) |
78 (83.0%) 16 (17.0%) 0 (0) |
2 (2.1%) 88 (93.6%) 4 (4.3%) |
||
aFor observed and under the null, mean (sd). For 95% CI, count (percentage).
Figure 2.

Analysis of TCGA data: replicability measures. Left/right: marginal/joint analysis. x-axis: value of replicability measure; y-axis: one horizontal line corresponds to one split.
Table 4.
Analysis of simulated data: numbers of identified genes and pathways. Mean (sd)
| Dataa | SKCM_S | LUSC_S | LUAD_S | |||
|---|---|---|---|---|---|---|
| Marginal | Joint | Marginal | Joint | Marginal | Joint | |
| Number of genes | 918 (264) | 70 (35) | 144 (106) | 67 (43) | 670 (239) | 82 (36) |
| Number of pathways | 312 (12) | 162 (54) | 198 (64) | 147 (74) | 301 (18) | 172 (56) |
aThis is the counterpart of Table 2 for the simulated data.
The above observations may be somewhat ‘disappointing.’ With data splitting, the two generated datasets should contain similar information. However, they do not lead to similar findings with high replicability. Potential reasons may include the limited sample sizes, significant differences across samples and high ‘noises,’ all of which may make findings sensitive to data splitting. In addition, the signal levels of genes on survival may be limited, negatively impacting replicability. The observations made here will be further ‘validated’ using simulation in the next section, where we will also look into one of the most impactful contributing factors. In the literature, there are studies that have key properties (for example, overall sample size, number of events, signal levels, etc.) comparable to our analyzed data, and they contain discussions on replicating published findings (or not). The above analysis suggests that such discussions may not be very meaningful in that high replicability may not be expected in the first place. In recent literature, there has been effort in designing alternative analysis methods that may help improve replicability. For example, integrative analysis [36–39] pools multiple datasets/studies to increase sample size and improve the accuracy of identification, which can lead to improved replicability. Bayesian [40] and information-incorporating [41, 42] approaches can directly take published findings into consideration in estimation, making new findings ‘closer’ to published ones and hence improving replicability.
A closer look VIA simulation
A validation of the TCGA data analysis results
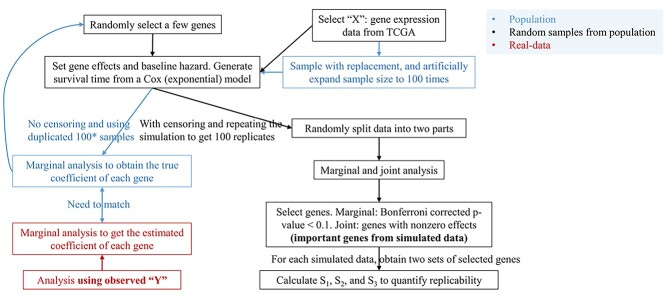
The observations reported in Section “Application to the TCGA data” are based on somewhat limited data. In particular, for a specific cancer, although multiple splittings are conducted, they are based on a single original dataset. It is possible that the outcomes in the original data are extremely ‘lucky’ (or ‘unlucky’) such that the findings may not be sufficiently informative. To further examine this problem, we resort to data-based simulation. The simulation and analysis workflow is presented in Figure 3 and consists of the following steps.
Figure 3.
Workflow of the simulation study conducted in Section ‘A validation of the TCGA data analysis results.’
1) For SKCM, LUSC and LUAD, randomly sample gene expressions with replacement (note that, to retain the correlation structures, all gene expressions of a subject need to be sampled together), and increase the sample size by 100 times.
2) Generate survival times from a Cox model. In particular, the baseline hazard function is set as
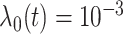 (that is, an exponential model). Randomly select 30 genes and assign them as important (with nonzero coefficients). The non-zero coefficients are also generated randomly. However, they need to be adjusted via trial and error – additional details are provided in Step 3).
(that is, an exponential model). Randomly select 30 genes and assign them as important (with nonzero coefficients). The non-zero coefficients are also generated randomly. However, they need to be adjusted via trial and error – additional details are provided in Step 3).-
3) With the generated data, conduct marginal Cox regression analysis, and obtain the marginal regression coefficients. Note that, with a huge sample size, the estimates should be very close to the (unknown) ‘true values’. Adjust the selected genes and their coefficients in Step 2), such that the ‘distribution’ of the absolute marginal regression coefficients resembles that of the observed data (here the ‘distance’ between the two distributions is defined as the average of the absolute differences between matched pairs). We have the following remarks for this step.
Gene expressions are correlated. As such, the non-zero coefficients specified in Step 2) cannot be taken as the true values of the underlying model – this subtle point has been neglected in some published studies. Instead, the nonzero coefficients for marginal analysis (and joint analysis) need to be calculated. In principle, this can be done analytically. However, this is expected to be highly complex. We resort to a large, simulated dataset to approximate the population.
There are perhaps infinitely many ways for specifying genes and their coefficients so that the marginal absolute regression coefficient distribution matches that of the observed data. In what follows, only results from one set of simulation are presented. However, it is noted that a few other settings have been examined and led to similar observations.
4) Simulate 100 datasets under the same settings (baseline hazard, set of important genes and their coefficients, etc.), where the sample size is equal to that of the original data. Censoring times are further generated from independent Uniform distributions, and the distribution parameters are adjusted so that the observed censoring rates are similar to those of the original data.
5) With the simulated data, analyses similar to those reported in Section “Application to the TCGA data” are conducted. We skip the FDR analysis and robust estimation, making analysis and discussion more concise, and considering that the FDR analysis and joint robust estimation do not seem to change the main observations and that the marginal robust estimation leads to limited discoveries. Taking into consideration the above TCGA data analysis results, we only report the two-sided 95% confidence interval results here to make the presentation more concise.
In this simulation, we attempt to closely mimic the observed data. In particular, the gene expressions contain the same information as the original data. The associations between the gene expressions and survival, as measured by the absolute marginal regression coefficients, also highly resemble. Compared to the data analysis reported in Section “Application to the TCGA data”, the survival outcomes are fully independently simulated, and as such, this analysis may somewhat better mimic replicability analysis with completely independent data.
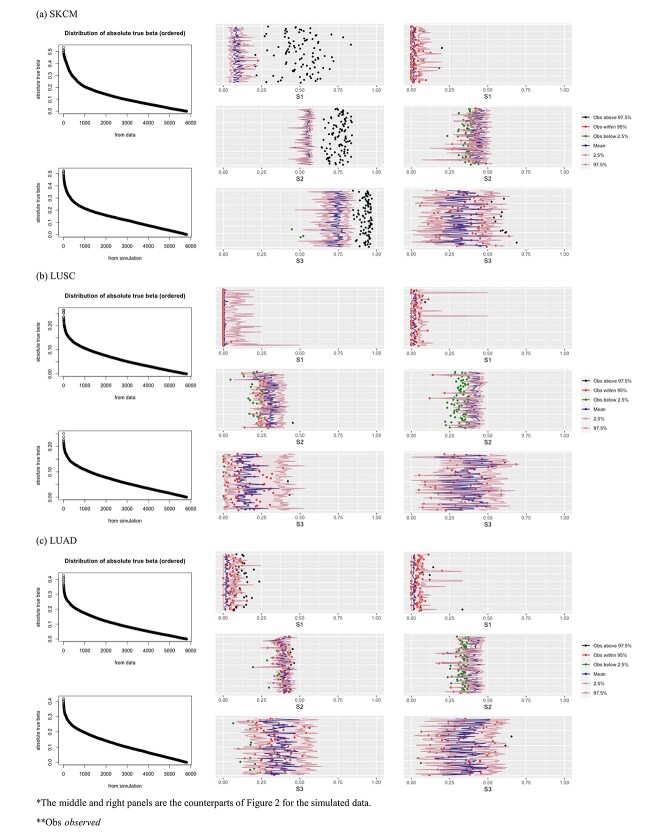
The results are summarized in Tables 4 and 5 as well as Figure 4, which correspond to Tables 2 and 3 and Figure 2 for the real data analysis. To differentiate, for example, LUSC_S indicates the simulated data based on the LUSC data. Overall, this simulation confirms the observations reported in Section “Application to the TCGA data”, with significant differences observed between marginal and joint analysis, between gene- and pathway-based analysis, and across cancer types. Low-to-moderate replicability is observed. The levels of replicability and inference results are compatible to those in Section “Application to the TCGA data”. For example, for SKCM, 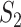 , and marginal analysis, results from both the simulated and observed data indicate high replicability with values 0.82 (all above 97.5%) and 0.75 (all above 97.5%), respectively. With joint analysis, both results fail to suggest replicability with similar values: 0.04 (
, and marginal analysis, results from both the simulated and observed data indicate high replicability with values 0.82 (all above 97.5%) and 0.75 (all above 97.5%), respectively. With joint analysis, both results fail to suggest replicability with similar values: 0.04 (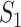 ), 0.40 (
), 0.40 (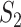 ), 0.35 (
), 0.35 (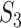 ) for the simulated data, and 0.02 (
) for the simulated data, and 0.02 ( ), 0.38 (
), 0.38 (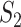 ), 0.37 (
), 0.37 (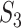 ) for the observed data. In addition, differences across datasets as reported in Section “Application to the TCGA data” are also observed with the simulated datasets. For example, for marginal analysis and
) for the observed data. In addition, differences across datasets as reported in Section “Application to the TCGA data” are also observed with the simulated datasets. For example, for marginal analysis and 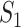 , the three real datasets have mean values 0.49 (SKCM), 0 (LUSC) and 0.08 (LUAD); and the three simulated datasets have mean values 0.65 (SKCM_S), 0.11 (LUSC_S) and 0.46 (LUAD_S). Here it is noted that the quantitative results differ between the observed and simulated data; however, the main patterns (for example, the SKCM data have high replicability, while the LUSC data have low replicability) are the same. The overall higher replicability measure values of the simulated data may be explained by the fact that the simulated data are relatively simpler: for example, the Cox (exponential) model is relatively simpler, and there is no human/measurement error.
, the three real datasets have mean values 0.49 (SKCM), 0 (LUSC) and 0.08 (LUAD); and the three simulated datasets have mean values 0.65 (SKCM_S), 0.11 (LUSC_S) and 0.46 (LUAD_S). Here it is noted that the quantitative results differ between the observed and simulated data; however, the main patterns (for example, the SKCM data have high replicability, while the LUSC data have low replicability) are the same. The overall higher replicability measure values of the simulated data may be explained by the fact that the simulated data are relatively simpler: for example, the Cox (exponential) model is relatively simpler, and there is no human/measurement error.
Table 5.
Analysis of simulated data: summary of replicability measures
| Measureb |
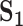 a
a
|
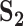
|
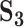
|
||
|---|---|---|---|---|---|
| SKCM_S | Marginal | Observed | 0.65 (0.1) | 0.82 (0.04) | 0.95 (0.04) |
| Under the null:2.5% Mean 97.5% |
0.16 (0.04) 0.19 (0.04) 0.21 (0.04) |
0.62 (0.02) 0.63 (0.02) 0.64 (0.02) |
0.86 (0.03) 0.89 (0.02) 0.92 (0.02) |
||
| 95% CI: below within above |
0 (0) 0 (0) 100 (100%) |
0 (0) 0 (0) 100 (100%) |
2 (2%) 6 (6%) 92 (92%) |
||
| Joint | Observed | 0.04 (0.03) | 0.4 (0.04) | 0.35 (0.1) | |
| Under the null:2.5% Mean 97.5% |
0 (0) 0.02 (0.01) 0.06 (0.03) |
0.41 (0.05) 0.45 (0.04) 0.49 (0.03) |
0.21 (0.08) 0.35 (0.08) 0.52 (0.05) |
||
| 95% CI: below within above |
0 (0) 85 (85.9%) 14 (14.1%) |
64 (64.6%) 31 (31.3%) 4 (4%) |
1 (1%) 97 (98%) 1 (1%) |
||
| LUSC_S | Marginal | Observed | 0.11 (0.08) | 0.45 (0.07) | 0.46 (0.15) |
| Under the null:2.5% Mean 97.5% |
0.01 (0.01) 0.03 (0.02) 0.08 (0.02) |
0.41 (0.04) 0.44 (0.04) 0.46 (0.03) |
0.37 (0.15) 0.49 (0.13) 0.62 (0.09) |
||
| 95% CI: below within above |
0 (0) 44 (44%) 56 (56%) |
22 (22%) 45 (45%) 33 (33%) |
12 (12%) 84 (84%) 4 (4%) |
||
| Joint | Observed | 0.03 (0.03) | 0.32 (0.04) | 0.33 (0.14) | |
| Under the null:2.5% Mean 97.5% |
0 (0) 0.02 (0.01) 0.06 (0.03) |
0.35 (0.06) 0.39 (0.05) 0.43 (0.04) |
0.19 (0.11) 0.33 (0.11) 0.51 (0.07) |
||
| 95% CI: below within above |
0 (0) 87 (93.5%) 6 (6.5%) |
75 (80.6%) 18 (19.4%) 0 (0) |
4 (4.3%) 85 (91.4%) 4 (4.3%) |
||
| LUAD_S | Marginal | Observed | 0.46 (0.1) | 0.71 (0.04) | 0.85 (0.06) |
| Under the null:2.5% Mean 97.5% |
0.11 (0.03) 0.14 (0.03) 0.17 (0.04) |
0.55 (0.02) 0.56 (0.02) 0.58 (0.02) |
0.8 (0.04) 0.85 (0.04) 0.88 (0.03) |
||
| 95% CI: below within above |
0 (0) 0 (0) 100 (100%) |
0 (0) 0 (0) 100 (100%) |
11 (11%) 64 (64%) 25 (25%) |
||
| Joint | Observed | 0.04 (0.03) | 0.38 (0.04) | 0.36 (0.12) | |
| Under the null:2.5% Mean 97.5% |
0 (0) 0.02 (0.01) 0.06 (0.02) |
0.38 (0.05) 0.41 (0.04) 0.45 (0.03) |
0.24 (0.09) 0.38 (0.08) 0.54 (0.06) |
||
| 95% CI: below within above |
0 (0) 82 (82%) 18 (18%) |
66 (66%) 32 (32%) 2 (2%) |
6 (6%) 94 (94%) 0 (0) |
||
aFor observed and under the null, mean (sd). For 95% CI, count (percentage).
bThis is the counterpart of Table 3 for the simulated data.
Figure 4.
Analysis of simulated data: replicability measures. Left: distributions of the absolute values of the marginal regression coefficients (upper: observed; lower: simulated). Middle/right: marginal/joint analysis.
A closer look into effect size
Many factors may affect replicability. Among them, the most important may be effect size and correlation structure. With respect to correlation, loosely speaking, a more complex correlation structure makes it harder to accurately identify important variables. Compared to, for example, means and variances, there has been less research on correlations among omics measurements for cancer. In addition, with a large number of omics measurements, there is not a simple way of quantifying the complexity of correlation.
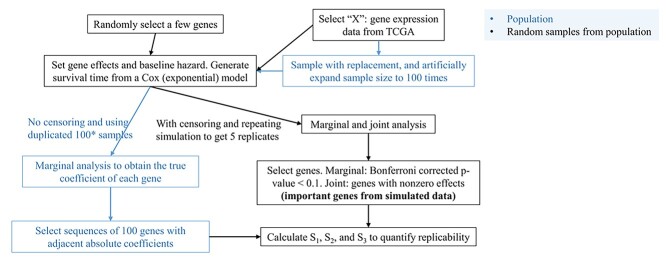
In this subsection, we look into effect size, which has been more extensively examined and can be easier to quantify [43]. It is first noted that, for the Cox and many other models, effect size is proportional to regression coefficient times the square root of sample size. In this subsection, we fix sample size and examine the impact of regression coefficients of gene expressions on replicability. As in the previous subsection, we again resort to data-based simulation. The workflow is presented in Figure 5 and consists of the following steps.
Figure 5.
Workflow of the simulation study conducted in Section ‘A closer look into effect size.’
1) Randomly sample the observed gene expressions with replacement, and increase the sample size by 100 times.
2) Randomly select 15 genes, and set as important. Their nonzero coefficients are set as
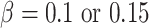 , corresponding to two signal levels. Set the baseline hazard function
, corresponding to two signal levels. Set the baseline hazard function 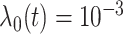 , and generate survival times from a Cox (exponential) model.
, and generate survival times from a Cox (exponential) model.3) With the generated data, conduct marginal Cox regression analysis. With a huge sample size, the estimated coefficients are expected to be very close to the (unknown) ‘true values.’ These estimates are ordered based on their absolute magnitudes.
4) Simulate five additional datasets under the same generating model but with sample size equal to the original data. For these five datasets, generate censoring times from independent Uniform distributions.
5) With the above steps, both ‘population’ and ‘sample’ data are obtained. With the sample data, both the marginal and joint analyses are conducted, and important genes are identified.
6) With the ordered regression coefficients obtained in Step 3), create multiple sets of important genes, with the first set containing genes #1–#100, the second set containing genes #2–#101 and so on. Then, evaluate replicability of the important genes identified from the sample data against the truly important sets.
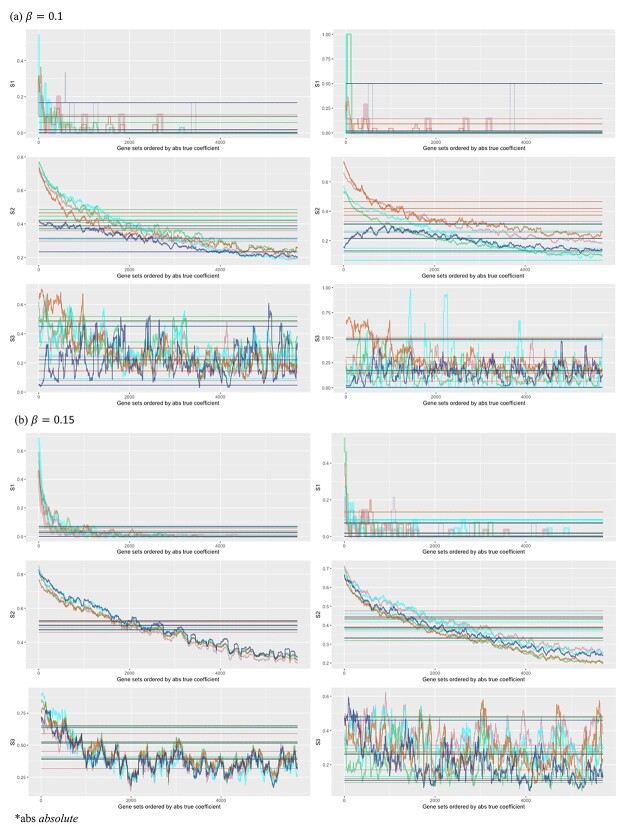
The overall simulation strategy is coherent with above. There are a few points worth noting. Here we assess replicability against the ‘true.’ It is easy to see that if two studies are both replicable with respect to a common reference, then they should have a high replicability value. We use two ways to vary signal levels. First, two different regression coefficient levels are considered in data generation. Second, we look at multiple truly important sets, which contain different signal levels. We use five simulated datasets to reduce the possibility of extreme simulation – more can be considered in the same manner but may negatively affect graphical presentation. The results are summarized in Figure 6. The x-axis contains 5700 values, where each value corresponds to the comparison against a truly important set. For example, x = 1000 corresponds to the set containing genes with absolute true coefficients ranking from 1000 to 1100. The five colors correspond to the five simulated datasets. The ‘fluctuating’ lines represent the observed replicability measures, and the horizontal lines are the 97.5%, mean, and 2.5% of the measures under the null.
Figure 6.
Analysis of simulated data: replicability measures for five simulated datasets. For each signal level, left/right: marginal/joint analysis.
Several observations are made. Significant differences are observed across the three measures and between marginal and joint analysis. Among the three, the second measure has the ‘most monotone’ curves (that is, a more obvious decreasing pattern as gene rankings decrease). As expected, stronger signals (a large value of 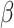 and genes with higher rankings) lead to higher replicability. Comparing against the values under the null can provide some insight into the signal levels needed to generate findings with sensible replicability. Significant variations across the five simulated datasets are observed, which should raise a ‘warning sign’ to practical data analysis – the high or low replicability observed for a specific dataset may be attributed to randomness.
and genes with higher rankings) lead to higher replicability. Comparing against the values under the null can provide some insight into the signal levels needed to generate findings with sensible replicability. Significant variations across the five simulated datasets are observed, which should raise a ‘warning sign’ to practical data analysis – the high or low replicability observed for a specific dataset may be attributed to randomness.
Concluding remarks
The importance of replicability in cancer omics and other studies has been fully recognized. Different from the existing literature, in this article, we have focused on the techniques for quantifying replicability. Through analytic and numeric examinations, we have presented the key properties of three sensible measures. Beyond effect size, replicability may also depend on other factors (for example, correlation), which can be more challenging to examine and are deferred to future research. This study, in particular the numerical analysis based on the TCGA and simulated data, inevitably has limitations. There can be other replicability measures (although they may take more complicated forms and/or be less intuitive), and they can be potentially examined in the same manner. Similar to other data, findings based on the TCGA data may not be fully generalizable. The simulation settings have been somewhat limited. However, TCGA data have been widely analyzed, and our findings have merit of their own. In addition, there has been no indication that TCGA data have unique distributional properties. As such, compatible findings may be expected with other data. The simulated data, although limited, have already revealed important properties.
Key Points
Replicability is of essential importance in cancer omics research. Although there has been extensive attention, quantitative research on replicability remains limited.
There are multiple sensible and broadly applicable replicability measures. Their key properties are examined in this article.
In the analysis of TCGA data, in general, low replicability and significant across-data variations are observed.
Simulations ‘verify’ the data analysis findings and further demonstrate the dependence of replicability on effect size.
Supplementary Material
Acknowledgements
We thank the editor and reviewers for their careful review and insightful comments, which have led to a significant improvement of this article.
Author Biographies
Jiping Wang is a PhD student in the Department of Biostatistics at Yale School of Public Health.
Hongmin Liang is a PhD student in the Department of Statistics at School of Economics, Xiamen University.
Qingzhao Zhang is an associate professor in the Department of Statistics, School of Economics and Wang Yanan Institute for Studies in Economics, Xiamen University.
Shuangge Ma is a professor in the Department of Biostatistics at Yale School of Public Health.
Contributor Information
Jiping Wang, Department of Biostatistics, Yale School of Public Health, New Haven, CT, USA.
Hongmin Liang, Department of Statistics, School of Economics, Xiamen University, Xiamen, Fujian, China.
Qingzhao Zhang, Department of Statistics, School of Economics, Xiamen University, Xiamen, Fujian, China; The Wang Yanan Institute for Studies in Economics, Xiamen University, Xiamen, Fujian, China.
Shuangge Ma, Department of Biostatistics, Yale School of Public Health, New Haven, CT, USA.
Funding
A Yale Cancer Center pilot award and National Institutes of Health CA121974 and CA196530.
Data availability
Data analyzed in this study are publicly available at The Cancer Genome Atlas (TCGA) Data Repository, Harmonized Cancer Datasets Genomic Data Commons Data Portal https://portal.gdc.cancer.gov/.
References
- 1. National Academies of Sciences, Engineering, and Medicine. Reproducibility and replicability in science. Washington, DC: Tha National Academies Press, 2019. [PubMed] [Google Scholar]
- 2. Collaboration OS. Estimating the reproducibility of psychological science. Science 2015;349:aac4716. [DOI] [PubMed] [Google Scholar]
- 3. Goodman SN, Fanelli D, Ioannidis JP. What does research reproducibility mean? Sci Transl Med 2016;8:341ps312-341ps312. [DOI] [PubMed] [Google Scholar]
- 4. Ioannidis JP. Why most published research findings are false. PLoS Med 2005;2:e124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Wirapati P, Sotiriou C, Kunkel S, et al. . Meta-analysis of gene expression profiles in breast cancer: toward a unified understanding of breast cancer subtyping and prognosis signatures. Breast Cancer Res 2008;10:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Verleyen W, Ballouz S, Gillis J. Positive and negative forms of replicability in gene network analysis. Bioinformatics 2016;32:1065–73. [DOI] [PubMed] [Google Scholar]
- 7. Rashid NU, Li Q, Yeh JJ, et al. . Modeling between-study heterogeneity for improved replicability in gene signature selection and clinical prediction. J Am Stat Assoc 2020;115:1125–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Subramanian J, Subramanian J. Gene expression–based prognostic signatures in lung cancer: ready for clinical use? J Natl Cancer Inst 2010;102:464–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Bueno R, Richards WG, Harpole DH, et al. . Multi-institutional prospective validation of prognostic mRNA signatures in early stage squamous lung cancer (alliance). J Thorac Oncol 2020;15:1748–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Waldron L, Haibe-Kains B, Culhane AC, et al. . Comparative meta-analysis of prognostic gene signatures for late-stage ovarian cancer. J Natl Cancer Inst 2014;106:dju04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Ioannidis J, Ntzani EE, Trikalinos TA, et al. . Replication validity of genetic association studies. Nat Genet 2001;29:306–9. [DOI] [PubMed] [Google Scholar]
- 12. Sotiriou C, Piccart MJ. Taking gene-expression profiling to the clinic: when will molecular signatures become relevant to patient care? Nat Rev Cancer 2007;7:545–53. [DOI] [PubMed] [Google Scholar]
- 13. Lusa L, McShane LM, Reid JF, et al. . Challenges in projecting clustering results across gene expression–profiling datasets. J Natl Cancer Inst 2007;99:1715–23. [DOI] [PubMed] [Google Scholar]
- 14. Paquet ER, Hallett MT. Absolute assignment of breast cancer intrinsic molecular subtype. J Natl Cancer Inst 2015;107:dju357. [DOI] [PubMed] [Google Scholar]
- 15. Ein-Dor L, Zuk O, Domany E. Thousands of samples are needed to generate a robust gene list for predicting outcome in cancer. Proc Natl Acad Sci U S A 2006;103:5923–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Shi X, Shen S, Liu J, et al. . Similarity of markers identified from cancer gene expression studies: observations from GEO. Brief Bioinform 2014;15:671–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ma S, Huang J, Moran MS. Identification of genes associated with multiple cancers via integrative analysis. BMC Genomics 2009;10:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Michiels S, Koscielny S, Hill C. Prediction of cancer outcome with microarrays: a multiple random validation strategy. Lancet 2005;365:488–92. [DOI] [PubMed] [Google Scholar]
- 19. Venet D, Dumont JE, Detours V. Most random gene expression signatures are significantly associated with breast cancer outcome. PLoS Comput Biol 2011;7:e1002240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Shi X, Yi H, Ma S. Measures for the degree of overlap of gene signatures and applications to TCGA. Brief Bioinform 2015;16:735–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Heller R, Yaacoby S, Yekutieli D. repfdr: a tool for replicability analysis for genome-wide association studies. Bioinformatics 2014;30:2971–2. [DOI] [PubMed] [Google Scholar]
- 22. Amar D, Shamir R, Yekutieli D. Extracting replicable associations across multiple studies: empirical Bayes algorithms for controlling the false discovery rate. PLoS Comput Biol 2017;13:e1005700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. McGuire D, Jiang Y, Liu M, et al. . Model-based assessment of replicability for genome-wide association meta-analysis. Nat Commun 2021;12:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Tomczak K, Czerwińska P, Wiznerowicz M. The Cancer Genome Atlas (TCGA): an immeasurable source of knowledge. Contemp Oncol (Pozn) 2015;19:A68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Acha-Sagredo A, Uko B, Pantazi P, et al. . Long non-coding RNA dysregulation is a frequent event in non-small cell lung carcinoma pathogenesis. Br J Cancer 2020;122:1050–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Shen A, Fu H, He K, et al. . False discovery rate control in cancer biomarker selection using knockoffs. Cancer 2019;11:744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Nguyen HT, Xue H, Firlej V, et al. . Reference-free transcriptome signatures for prostate cancer prognosis. BMC Cancer 2021;21:1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Witten DM, Tibshirani R. Survival analysis with high-dimensional covariates. Stat Methods Med Res 2010;19:29–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Ma S, Huang J. Penalized feature selection and classification in bioinformatics. Brief Bioinform 2008;9:392–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Knudsen S (ed). Cancer Diagnostics with DNA Microarrays. John Wiley & Sons, 2006. [Google Scholar]
- 31. Therneau TM, Lumley T. Package ‘survival’. R Top Doc 2015;128:33–6. [Google Scholar]
- 32. Bonferroni C. Teoria statistica delle classi e calcolo delle probabilita. Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commericiali di Firenze 1936;8:3–62. [Google Scholar]
- 33. Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc B Methodol 1995;57:289–300. [Google Scholar]
- 34. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Series B Stat Methodology 2005;67:301–20. [Google Scholar]
- 35. Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw 2010;33:1. [PMC free article] [PubMed] [Google Scholar]
- 36. Yengo L, Sidorenko J, Kemper KE, et al. . Meta-analysis of genome-wide association studies for height and body mass index in∼ 700000 individuals of European ancestry. Hum Mol Genet 2018;27:3641–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Xue A, Wu Y, Zhu Z, et al. . Genome-wide association analyses identify 143 risk variants and putative regulatory mechanisms for type 2 diabetes. Nat Commun 2018;9:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Singh A, Shannon CP, Gautier B, et al. . DIABLO: an integrative approach for identifying key molecular drivers from multi-omics assays. Bioinformatics 2019;35:3055–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Gomez-Cabrero D, Abugessaisa I, Maier D, et al. . Data integration in the era of omics: current and future challenges. BMC Syst Biol 2014;8:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Beaumont MA, Rannala B. The Bayesian revolution in genetics. Nat Rev Genet 2004;5:251–61. [DOI] [PubMed] [Google Scholar]
- 41. Stingo FC, Chen YA, Tadesse MG, et al. . Incorporating biological information into linear models: a Bayesian approach to the selection of pathways and genes. Ann Appl Stat 2011;5:1978–2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Spencer AV, Cox A, Lin WY, et al. . Incorporating functional genomic information in genetic association studies using an empirical Bayes approach. Genet Epidemiol 2016;40:176–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Olejnik S, Algina J. Measures of effect size for comparative studies: applications, interpretations, and limitations. Contemp Educ Psychol 2000;25:241–86. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data analyzed in this study are publicly available at The Cancer Genome Atlas (TCGA) Data Repository, Harmonized Cancer Datasets Genomic Data Commons Data Portal https://portal.gdc.cancer.gov/.