Abstract
We present a novel physically-intuitive mathematical formulation to investigate the effects of a fully-constrained generic tendon routing (GTR) on the correlation between tension loss and deformation behavior of a variable-curvature tendon-driven continuum manipulator (TD-CM). The proposed model can account for distributed friction forces/moments along a GTR path that have been typically ignored in the previous approaches (e.g., the well-known frictionless Cosserat rod model). For the first time, the internal distributed forces on a GTR are expressed using three physically-intuitive generic functions. Solely relying on the known actuation input(s), the proposed mathematical formulation can also solve the entangled and unknown correlation between GTR, internal distributed forces, tension loss and deformation behavior of TD-CMs. To evaluate the performance of the proposed approach, we performed various simulation studies using eight different GTR paths. Additionally, we fabricated two different types of TD-CMs with different GTRs to experimentally evaluate the efficacy and performance of the proposed mathematical framework. The results demonstrate the proposed model can successfully and accurately (i.e., about <10% error) capture the trends of substantial tension loss (e.g., about <50%) on fully constrained GTRs, which reveals the importance of considering tension loss in modeling these TD-CMs.
Keywords: Medical Robots and Systems, Tendon-driven Continuum Manipulator (TD-CM), Generic Tendon Routing, Distributed Friction Effects
I. Introduction
TENDON-Driven Continuum Manipulators (TD-CMs) have been the essential component of various recent surgical robotics systems developed for orthopedics (e.g., [1]), single-port (e.g., [2]), and ophthalmological (e.g., [3]) surgical interventions. This is mainly due to their excellent features such as inherent compliance, small form factor, and lightweight that allow for smaller surgical incisions, less trauma, and safe procedures [4]. Generic tendon routing (GTR) can expand TD-CMs’ workspace and allow a single tendon to actuate a one-segment TD-CM to bend in variable curvatures along its body [5]. Such advantages of routed tendons provide for greater accessibility to hard-to-reach sites and can be utilized for a variety of interventions demanding TD-CMs to transverse through complex trajectories to avoid obstacles and sensitive tissues or internal organs.
Although there are benefits in using TD-CMs with GTR in narrow and confined spaces, tendons often cause issues such as tension loss and hysteresis phenomenon during pulling and releasing phases of actuation, which subsequently affect the deformation behavior of TD-CMs [4], [6], [7]. Such highly nonlinear entangled correlation between distributed friction and deformation behavior of TD-CMs makes tension loss modeling very challenging [7], especially when considering a manipulator with GTR. Of note, internal distributed friction forces along the tendon channel can be significantly amplified due to the GTR and subsequently exacerbates the tension loss of TD-CMs [8]. To address these adverse effects influencing the design, fabrication, force and shape sensing, and control of these manipulators, it is essential to develop a comprehensive analytical model that considers the effect of GTR on distributed friction force and subsequently tension loss and deformation behavior of TD-CMs.
As we have reviewed in our previous studies (i.e., [7] and [8]), most of the existing approaches in modeling deformation behavior of TD-CMs–including piecewise constant-curvature (e.g., [9], [10]) and variable-curvature (e.g., [11], [12]) models–completely ignore the internal distributed friction effects on tension loss and deformation behavior of TD-CMs. Although there are studies that consider friction effects while modeling TD-CMs and tendon-sheath systems, most of them rely on either simplifying models and assumptions such as lumped-parameter model [13], predefined/known tendon configuration (e.g., tendon wrap angle [14] and tendon curvature distribution [15]), TD-CM deformation [16], concentrated point friction and normal forces [13], or experimental measurements for identifying system parameters in some specific configurations [17]. To address these limitations, in [7], [8] and [18], we proposed an analytical model that can completely describe the unknown correlation between the internal forces, deformation behaviors, and/or external loads of TD-CMs without requiring such a priori known information. Nevertheless, similar to the most of the proposed friction-less and friction-based models in the literature, these models do not consider the effect of GTR on the tension loss and deformation behavior of TD-CMs.
The advantages of reshaping configurations and expanding the design space of TD-CMs via GTR have been demonstrated and investigated in various studies. For instance, Rucker et al. [5] developed a model of TD-CMs based on Cosserat rod theory with general tendon routing. Starke et al. [19] studied the influence of helical tendon routing on the workspace of TD-CMs and Oliver-Butler et al. [20] investigated the stiffness of TD-CMs with prescribed tendon displacements and parallel/converging tendon routing. Nevertheless, like most of the models developed based on the Cosserat rod theory, the GTR effects on the entangled relationship between the tension loss and deformation behavior of TD-CMs were not considered in these studies. Additionally, the performance of these models have only been evaluated in TD-CMs with partially-constrained tendon paths [21]. As described in [6] and our previous studies [7], [8], [18], tendon tension drop in TD-CMs with fully-constrained tendons is very evident (e.g., > 40%) and cannot be ignored, especially when a tendon is routed in a curved tendon channel. Recently, Chitalia.et al. [22], [23] developed a steerable robot with a partially-constrained tendon routing to expand its workspace. A simple Coulomb friction model and capstan equation [23] were used to model friction effects of tendon. To the best of our knowledge, despite TD-CMs with partially-constrained tendon routings, there is still a lack of comprehensive model that can capture the effect of GTR on tension loss in TD-CMs with fully-constrained curved routed tendons.
To address the aforementioned limitations and as the major independent contributions of this study over our previous works (i.e., [7], [8] and [18]): (1) we introduce a physically-intuitive mathematical formulation that uses three functions to completely capture the effects of fully-constrained GTR on the entangled relationship between tension loss and planar deformation behavior of TD-CMs. The proposed model is based on the Cosserat rod theory (e.g., [5], [24]), which makes it more generic and extendable. It also quantitatively visualizes and provides an intuitive understanding of the GTR effects on tension distribution, and distributed internal forces in TD-CMs; (2) the proposed formulation can account for distributed friction forces/moments along the GTR path that has been typically ignored in the previous modeling in the literature (e.g., [5], [6], [21] ); (3) it can model and solve the entangled and unknown correlation between the GTR, distributed friction forces, distributed normal forces, tension loss along the routed tendon, and planar deformation behavior of TD-CMs solely relying on known actuation input(s); (4) we presents a new algorithm (i.e., Algorithm 1) to provide an approach for capturing the three phases of hysteresis behavior observed in TD-CMs; and (5) we design a novel experimental setup including two molded TD-CMs with different fully-constrained GTR paths. These two manipulators were sensorized with two load cells to measure tendon routing effects on tension loss during both pulling and releasing of routed tendon actuation.
II. MODELING FRAMEWORK
A. Problem Statement
To completely consider the effect of GTR on tension loss and deformation behavior of a generic variable-curvature TD-CM with planar bending shown in Fig. 1, we develop a new modeling framework that has the following new features:
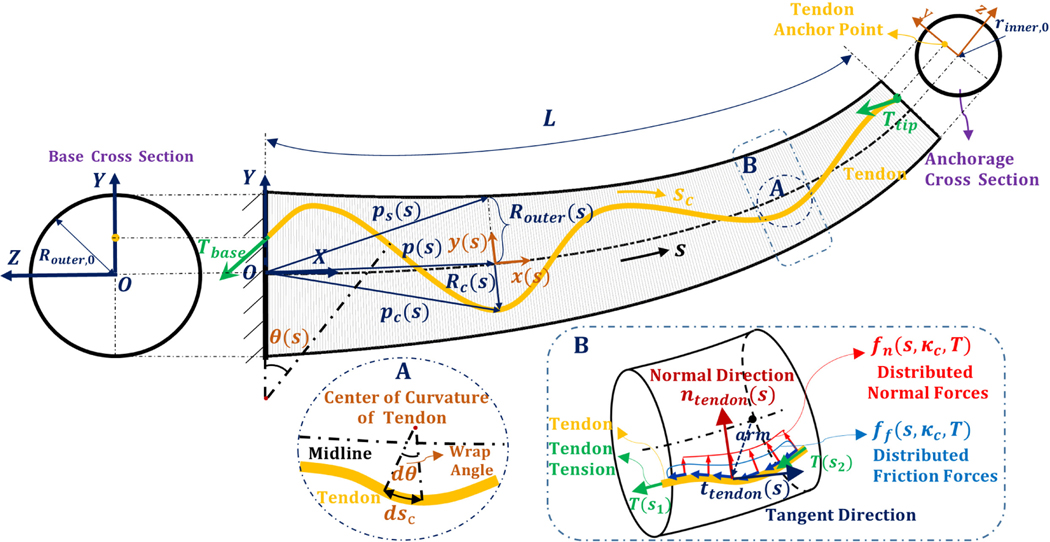
Fig. 1.
Conceptual illustration of a variable-curvature TD-CM with GTR and planar deformation behavior. The zoomed region A shows the tendon wrap angle of a GTR, while the zoomed region B illustrates the internal distributed forces along a GTR. θ(s) denotes the total angle swept by the tendon from the base to a current point s on the tendon
Remark 1: As shown in Fig. 1, for a TD-CM with a GTR, the arc length along a routed tendon sc is not necessarily equal to the midline arc length s (i.e.,). Thus, the developed models in our previous studies (i.e., [7], [8] and [18]) with this assumption are not valid for TD-CMs with a GTR and may cause modeling inaccuracies. Therefore, unlike our previous studies, the proposed modeling framework takes into account this difference and generalizes our previous models in which tendons were limited to a parallel or straight routing. This feature enables expanding the design and work spaces of TD-CMs with GTR by accurately modeling their tension loss and deformation behavior.
Remark 2: The proposed modeling framework is derived based on a new mathematical formulation that uses three physically-intuitive generic functions to describe internal distributed forces on a GTR. It also introduces new concepts of “tension loss factor” and “projection factor” to provide insights of tendon-tension transmission loss in TD-CMs. This framework can be easily incorporated in the Cosserat rod theory (e.g., [5], [24]), which makes it more generic, physically-intuitive, and extendable.
Assumption 1: In this study, we assume a TD-CM with a fully-constrained GTR that causes planar deformation behavior. We also neglect tendons’ elongation and backlash effects.
B. Distributed Forces along a GTR
To develop a more accurate model and consider the difference between tendon arc length sc and TD-CM’s midline arc length s, the kinematics of a GTR is thoroughly derived in this section. As shown in Fig. 1, the position vector of the GTR is first expressed as follows:
| (1) |
where p(s) denotes the position vector of TD-CM’s midline and denotes a vector from origin of the body frame to the corresponding point on the routed tendon. Using this definition, the arc length sc along the routed tendon can be expressed as:
| (2) |
where denotes the two norm throughout this paper. Using (2), we can define the differential as:
| (3) |
where and represent the partial derivative of position in the x and y directions with respect to s, respectively. Of note, denotes the differentiation with respect to s throughout this paper. As shown in the zoomed region B of Fig. 1, to model distributed forces along a GTR, the directions associated with the tendon tension T(s), distributed normal force and distributed friction need to be obtained. Here, and are functions of tendon curvature and tendon tension profile T(s). During actuation, a tendon slides along the curved channel in which tendon tension T(s) and distributed friction are both in the tangent direction while distributed normal force is in the direction of tendon curvature . The tangent direction of the curve can be described using arc length parameterization sc as follows:
| (4) |
By the chain rule and using (2) and (3), we can write: . Hence, (4) can be expressed as [5]:
| (5) |
Also, tendon tension T(s) along the arc length parameter s is a function of tendon wrap angle θ(s) (shown in Fig. 1) [8] and using (5) can be written as:
| (6) |
where denotes the direction vector of tendon tension. Tbase is the input tension at the base of the TD-CM. As for the exponential term, (where [8]) indicates the sliding direction of the curved tendon along the channel, while µ is the frictional coefficient of the sliding motion. Here we use a Coulomb friction model and the tendon loading/motion is quasi-static (e.g., [6], [16], [25]). Also, represents the tendon wrap angle shown in the zoomed region A of Fig. 1. Of note, the tendon curvature κc is non-negative [26].
Remark 3: In (6), the ”tension loss factor” captures the tendon-tension transmission loss phenomenon of TD-CMs with GTR. Of note, in contrast with the well-known frictionless Cosserat-rod models (e.g., [5], [11]), this equation can take into account the effects of distributed friction forces on tension loss and deformation behavior of TD-CMs.
Remark 4: Unlike previous studies (e.g., [15], [17], [16]), in the implementation of (6), there is no need for a priori known information or experimental measurements on tendon’s configuration (e.g., wrap angle or tendon curvature distribution) or TD-CM’s configuration (e.g., robot’s shape). The only known variable in this equation is the input actuating tension Tbase which includes the applied tendon tension history and the other variables are not required to be known a priori.
Using (3), (5), and the Frenet–Serret Formulas [26], the further differentiations of pc(s) can be obtained as follows:
| (7) |
Throughout the paper, denotes the cross product of two vectors. Using (7), parameter in (6) can be expressed as:
| (8) |
The direction of tendon curvature (i.e., ) can also be obtained using (7):
| (9) |
As shown in the zoomed region B of Fig. 1, internal distributed forces are functions of tendon’s curvature, and tension distribution:
| (10) |
| (11) |
Derivation of (10) and (11) can be found in Appendix A. Substituting (5), (6), (8), and (9) into (10) and (11), the distributed normal force can be written as:
| (12) |
The distributed friction force can also be derived as:
| (13) |
In (12), is defined as the “projection factor” that can “project” tendon tension to the distributed normal force. Similarly, in (13), is defined as the “projection factor” that can “project” tendon tension to distributed friction force. Therefore, we can use a general physically-intuitive form to express the internal distributed forces as follow:
| (14) |
where represents or .
Remark 5: Equation (13) gives the analytical form of distributed friction force along a routed tendon of TD-CMs, which either has been ignored or not been investigated by all the previous studies of both frictionless Cosserat-rod models (e.g., [5], [11]) and tendon-sheath systems (e.g., [15], [16]).
Remark 6: Equation (14) generalizes and provides a physically-intuitive understanding of internal distributed forces. When tendon tension is transmitted from the base of TD-CMs to a point on the curved routed tendon, it first experiences an exponential tension loss and then is “projected” to the normal and tangent directions of the tendon curve. The “projection factor” is characterized by the tendon configurations (e.g., tendon position and curvature) and the friction coefficient.
C. Distributed Moment on the TD-CM’s Midline
The distributed moment that a routed tendon applies to the TD-CM’s midline consists of the contributions from the anchor point force (see Fig. 1) and the described internal distributed forces. The anchor point moment is the cross product of the arm vector and the anchor point force vector:
| (15) |
Distributed moment can also be expressed as the integral of the cross product of the arm vector and the distributed forces as follows:
| (16) |
where represents the sum of the internal distributed normal force and the distributed friction force along the GTR. Similar to (16), external distributed moment can be written as:
| (17) |
where denotes the distributed forces along the TD-CM’s body and is the position vector of a point on the TD-CM’s surface (shown in Fig. 1). Now, using the static equilibrium equation, we can relate the GTR effects as well as the internal and external distributed loads to the deformation behavior of TD-CMs [8]:
| (18) |
where E is the Young’s modulus and I(s) is the second moment of area of the TD-CM’s cross sections. is the angular rate of change of the TD-CM’s configuration [8].
To solve such highly nonlinear model expressed in (18) with exponential terms in the integral calculation, we have developed an iterative solution algorithm. This algorithm requires the solution of the friction-less Cosserat-rod model (e.g., [11], [5]) in the first iteration. The obtained solution will then be used as an initial guess for iteratively solving the proposed friction-based model. More details of sovling equation (18) can be found in references [7], [8] and [18].
To capture the tension loss due to the friction and particularly hysteresis behavior of tendon-tension transmission in TD-CMs, we propose a procedure summarized in Algorithm 1. In this algorithm, we particularly need to obtain the direction of motion/friction of tendons to calculate the sign of during the tendons’ actuation phases and identify the three pulling, transition, and releasing phases observed in TD-CMs experiencing tension loss [6], [16]. As shown in lines 1–5 of Algorithm 1, during the pulling phase, we first apply tendon tension Tbase quasi-statically at TD-CM’s base from an initial zero to a maximum tendon tension Tbase max. During this phase, the entire tendon moves towards proximal/base side of the manipulator and tension distribution decreases since the friction force accumulates along the length (i.e., ) [6], [16]. Using the known λ(s) and for each applied Tbase, we can calculate the tension at the TD-CM’s tip Ttip by solving equilibrium equation (18). Obviously, among these calculated Ttip, the maximum output Ttip_max is associated with the maximum applied Tbase.
After the pulling phase, we start releasing the tendon in which the TD-CM first experiences a transition phase [6], [16]. In this phase, part of tendon moves from base toward the distal/tip end of manipulator and more specifically to a “sign transition point of λ(s)” while tension distribution is increased–due to the accumulated friction force in the opposite direction of tendon’s motion. Of note, beyond the “sign transition point of λ(s)”, there is no tendon motion and no change is observed in the tension distribution (i.e., λ(s) is partially −1 and partially +1) [6], [16]. Therefore, the maximum measured output tension at the TD-CM tip (i.e., Ttip_max) stays constant until the input tension at the base is below an unknown certain value that needs to be calculated. To obtain the whole transition phase, we need to find an input tension that can lead to a switch from a transition phase to a releasing phase where the entire tendon moves towards the distal end and tension distribution increases due to the accumulation of friction force along the entire length (i.e., ). Therefore, as summarized in lines 6–15 of Algorithm 1, during releasing tendon, if input tension is greater than , TD-CM will be in the transition phase in which output tension at the tip stays constant; otherwise, TD-CM is in the releasing phase. Using known λ(s) and Tbase, the output Ttip can be calculated by solving (18). Of note, by setting and using the Ttip_max as the input, equation (18) can be solved backward to calculate .
III. Simulation and Experimental Validations
A. Simulations
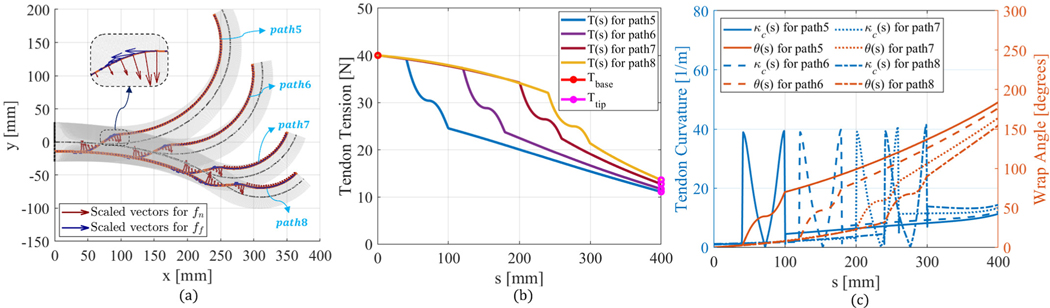
To evaluate the capability of the proposed model, we conducted simulations on a conical-shape TD-CM with 8 different GTR paths (i.e., path 1∼8), shown in Fig. 2 and Fig. 3. The TD-CM geometry is defined using the parameters shown in Fig. 1 i.e.,: L = 400 mm, Router,0 = 30 mm, and router,0 = 15 mm. To investigate the GTR effects on tension loss of TD-CMs, the simulations of the considered eight GTR paths (i.e., path 1∼8) are performed with identical input tensions (i.e., Tbase = 60 N and Tbase = 40 N in Fig. 2 and Fig. 3, respectively). In general, as shown in Fig. 2 and Fig. 3, we have considered two different classes of GTRs. Fig. 2(a) illustrates a single curved tendon passing through a converging sinusoidal wave path (i.e., path 1∼4) from TD-CM base to the tip. Among these GTR paths, path 1∼3 are defined based on equation (19), while path 4 is defined based on equation (20) and the parameters detailed in Table I.
Fig. 2.
Simulation results of the considered four GTR paths (i.e., converging sinusoidal wave path 1~4) with input tension Tbase = 60 N: (a) Comparison and illustration of the deformation behaviors and internal distributed forces (i.e., fn and ff) along the GTR between these four different paths; (b) Comparison of the tendon tension losses along the midline arc length s; and (c) Comparison of the curvatures and wrap angles along the midline arc length s.
Fig. 3.
Simulation results of the considered four GTR paths (i.e., straight-sine-straight path 5~8) with input tension Tbase = 40 N: (a) Comparison and illustration of the deformation behaviors and internal distributed forces (i.e., fn and ff) along the GTR between these four different paths; (b) Comparison of the tendon tension losses along the midline arc length s; and (c) Comparison of the curvatures and wrap angles along the midline arc length s.
TABLE I.
GTR Pathparameters
| Items | Rmax : mm | Rmin : mm | nsine | σ |
|---|---|---|---|---|
| path 1 | 15 | 7.5 | 10 | 0.1 |
| path 2 | 15 | 7.5 | 10 | 0.3 |
| path 3 | 15 | 7.5 | 10 | 0.9 |
| path 4 | 20 | 8 | 5 | / |
| Items | r1 : mm | r2 : mm | w1 : mm | w2 : mm |
|
| ||||
| path 5 | −14 | 14 | 40 | 100 |
| path 6 | −14 | 14 | 120 | 180 |
| path 7 | −14 | 14 | 200 | 260 |
| path 8 | −14 | 14 | 240 | 300 |
| (19) |
| (20) |
Moreover, in Fig. 3(a), a multi-segment GTR path of straight-sine-straight (i.e., path 5∼8) is considered and expressed by (21) and the parameters detailed in Table I.
Algorithm 1:
Solving the proposed model in pulling, transition, and releasing phases

|
| (21) |
Fig. 2(a) and Fig. 3(a) compare the TD-CM deformation behavior as well as the distributed forces (i.e., fn and ff) along the routed tendon between these GTR paths. Fig. 2(b) and Fig. 3(b) illustrate the tendon tension distribution profile along the arc length parameter s. Fig. 2(c) and Fig. 3(c) show the tendon curvature distribution and wrap angle along the arc length parameter s. Of note, to solely investigate the effects of GTR and remove the influence of other factors, the distributed gravitational force is not considered in these simulations. However, in the performed experimental studies, the TD-CMs are under the influence of distributed gravitational loads and this effect has been considered in the modeling procedure.
B. Experiments
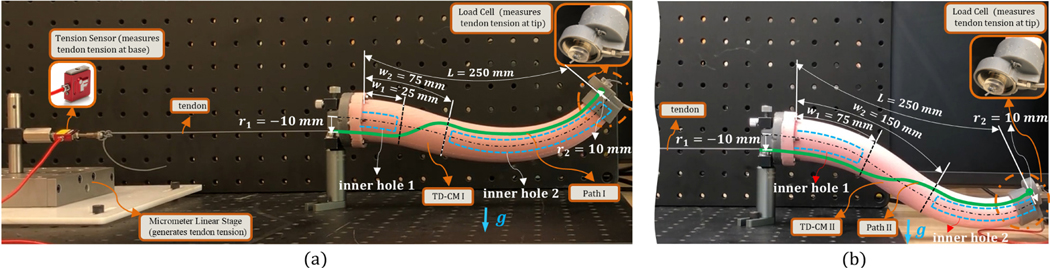
As shown in Fig. 4, to experimentally evaluate the performance of the proposed friction-based model, we molded two TD-CMs (i.e., TD-CM I and TD-CM II) with different GTR paths (i.e., path I and path II, respectively). The dimensions of these robots are identical and defined using the parameters shown in Fig. 1, i.e., L = 250 mm, Router,0 = 20 mm and router,0 = 13 mm. As shown in Fig. 4(a), the diameter of the inner hole 1 of TD-CM I is 14 mm and its depth is 20 mm. The diameter of the inner hole 2 is 14 mm and its depth is 170 mm. The diameter of the inner hole 1 of TD-CM II is 14 mm with 70 mm length and the diameter of the inner hole 2 is 14 mm with 95 mm length (Fig. 4(b)). The GTR path I (shown in Fig. 4(a)) of TD-CM I and path II (shown in Fig. 4(b)) of TD-CM II are both defined based on (21). Details of parameters and experimental setup are shown in Fig. 4. More information about this setup can be found in [8].
Fig. 4.
Experimental setup for (a) TD-CM I with tendon path I and (b) TD-CM II with tendon path II.
During the experimental process, we first pulled the tendon using the linear actuation mechanism to continuously generate input tendon tensions at the TD-CM base (i.e., Tbase = 0 N∼45 N with 5 N increment). In the pulling phase, we simultaneously measured the corresponding tension at the TD-CM tip using the aforementioned load cell. Similarly, we released the tendon and measured the tension at the tip of TD-CM (i.e., releasing/unbending phase) at the end of the bending phase. Of note, we repeated all experiments three times. Fig. 5 shows the tendon-tension transmission loss of the GTR in path I of TD-CM I from experiments, the proposed model, and the friction-less model output results during both bending and unbending phases. Similarly, Fig. 6 compares the tension transmission loss of the GTR in TD-CM II with path 2 from experiments, proposed model prediction, and friction-less model prediction during both bending and unbending phases.
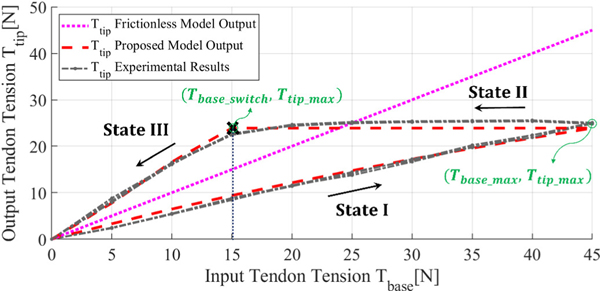
Fig. 5.
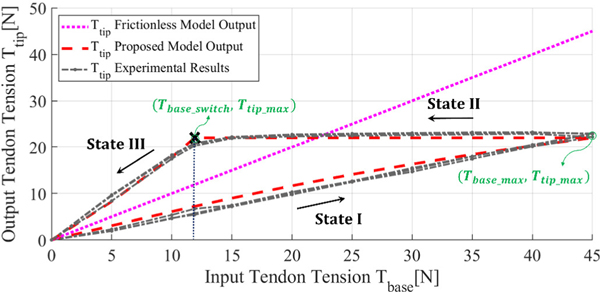
Experimental results for TD-CM I with tendon path I and input tension ranging from Tbase = 0 ∼ 45 N with a 5 N increment. The red dashed line, the magenta dotted line, and the gray dash-dot lines show the tendon tension at the tip of the TD-CM I from the proposed model, friction-less model, and experiments, respectively. States I, II, and III represent the pulling, transition, and releasing phases, respectively. The predicted and measured tensions in three repeated trials have the mean absolute percentage error of 9.98% and the mean absolute error of 0.91 N. Input tension Tbase_switch leads to a switch from a transition phase to a releasing phase.
Fig. 6.
Experimental results for TD-CM II with tendon path II and input tension ranging from Tbase = 0 ∼ 45 N with a 5 N increment. The red dashed line, the magenta dotted line, and the gray dash-dot lines show the tendon tension at the tip of the TD-CM II from the proposed model, friction-less model, and experiments, respectively. States I, II, and III represent pulling, transition, and releasing phases, respectively. The predicted and measured tensions in three repeated trials have the mean absolute percentage error of 7.10% and the mean absolute error of 0.85 N. Input tension Tbase_switch leads to a switch from a transition phase to a releasing phase.
IV. Results and Discussion
As clearly observed in Fig. 2(a) and Fig. 2(b), for an identical input tensions, converging sinusoidal wave GTR paths with different amplitudes create distinct tension losses and deformation behaviors for the TD-CM. For instance, as the amplitude of the sine curve of path 1∼3 increases, the TD-CM’s tension loss significantly increases from 41.5 N to 59.7 N (i.e., from 69.2% to 99.5% loss shown in Fig. 2(b)), which subsequently creates a smaller deformation behavior due to the increase of the distributed friction forces. The distributed friction force in Fig. 2(a) is larger at the crests and troughs in which the amplitude of tendon’s curvature is greater (see Fig. 2(c)). It is worth noting that when the sine-wave GTR path crosses the midline of the TD-CM (shown in the path 4 of Fig. 2(a)) and the number of the sine-wave cycles decreases, the TD-CM bends in a variable-curvature undulating pattern.
In Fig. 3(a), although the sine-wave segment (i.e., the middle segment of the considered multi-segment straight-sine-straight GTR paths) is identical for the performed simulations, the difference in their locations creates a completely distinct deformation behavior for the manipulator. For instance, as the location of the sine wave segment moves from proximal end to the distal end of the TD-CM, the parts near the TD-CM base experience a higher deformation whereas the the parts near the tip bend less. As shown in Fig. 3(b) and Fig. 3(c), similarly, the patterns of tension distribution profile caused by the sine-wave segment also move from the proximal end to the distal end of the TD-CM.
As shown in Fig. 4, path I has a “steeper slope“ than path II because of the shorter distance of the sine wave in path I. Thus, the tendon’s curvature distribution and wrap angle of path I are larger than those of path II, which explain why path I has larger increasing cumulative distributed friction and tension loss. Notably, although identical input tension is applied in the experiments for TD-CM I and TD-CM II, they have distinct deformation behavior due to the difference in their GTR paths and subsequently internal distributed forces between path I and path II. Although we do not directly compare the shape of TD-CM between the experiments and simulation prediction, due to the interconnected/correlated relation between the tension loss and curvature/shape of the TD-CM (check (18)), the experimental results indirectly demonstrate the accuracy of the model in predicting the shape of TD-CM in these experiments. The obtained prediction mean absolute percentage errors (i.e., 9.98% for TD-CM I and 7.10% for TD-CM II) for the total of 120 readings (i.e., repeated pulling and releasing experiments for three times and for both TD-CM I and TD-CM II with different GTRs) clearly support this justification.
Fig. 5 and Fig. 6 demonstrate the calculated three different hysteresis phases–labeled by States I, II, and III denoting the pulling, transition, and releasing phases, respectively [8]–using the proposed Algorithm 1 for both TD-CM I and TD-CM II. As can be seen, the proposed algorithm can successfully capture the mentioned three phases for both TD-CMs. A transition phase is observed between the end of the pulling phase and beginning of the releasing phase, in which the output tension at the TD-CM tip stays constant (i.e., Ttip_max = 22.0 N and Ttip_max = 23.9 N shown in Fig. 5 and Fig. 6, respectively) until the input tension at the base is below a certain value [8]. The input tension Tbase_switch that can lead to a switch (i.e., marked by a black “×”) from transition phase to releasing phase is 11.9 N and 15 N for TD-CM I and TD-CM II, respectively. Of note, such a difference is caused by the considered different GTR paths (i.e., path I and path II). Moreover, the transition phases for the GTR paths are obviously larger than those of straight tendon routing paths experimented in [8], which could be partly due to the longer tendon arc length and larger accumulative distributed friction forces. Of note, the proposed algorithm models hysteresis behavior in sequential orders of pulling, transition and releasing, and in the future, we will extend the work in which these phases are not sequential.
V. Conclusion
In this paper, a comprehensive physically-intuitive mathematical formulation was proposed that can capture the effects of a fully-constrained GTR on tension loss and deformation behavior of TD-CMs with planar bending. We successfully showed that this model can solve the entangled and coupled relation between GTR, distributed friction, and deformation behavior of TD-CMs solely relying on the known input tension. The conducted simulation (i.e., 8 different GTR cases) and experimental studies on two different GTRs and TD-CMs, with 120 readings in total, provided qualitative, quantitative, and intuitive understandings of the GTR effects on tendon-tension transmission loss and deformation behavior of TD-CMs. The proposed model and solution algorithm successfully captured the trends of tension loss and three states of the hysteresis phenomenon on different GTR paths (MAPE error < 10%). The obtained significant tension loss (i.e., about 50% ) in our studies demonstrated that the distributed friction effects cannot be simply ignored in TD-CMs with GTR, especially when the tendon is fully constrained.
Although, in this study, we focused on modeling a TD-CM with planar deformation, in the future, we will extend the current mathematical framework to model TD-CMs with partially- and fully-constrained GTRs with 3D deformation behavior. We will also verify the obtained TD-CM’s bending shape and tension loss with experimental results. Another interesting topic would be incorporating dynamic and presliding friction that are ignored in the current modeling framework.
Supplementary Material
Acknowledgments
This paper was recommended for publication by Editor Jessica Burgner-Kahrs upon evaluation of the Associate Editor and Reviewers’ comments.
This work is supported by the National Institute Of Biomedical Imaging and Bioengineering of the National Institutes of Health under Award Number R21EB030796.
Appendix A
For a small material element dsc along the GTR, the mathematical relationship between the infinitely small change in tendon tension T, friction force , and normal force can be described as: and (see [7] and [18]). Since and (forces per unit sc [5]) and (see (3)), we can obtain:
References
- [1].Alambeigi F, Bakhtiarinejad M, Sefati S, Hegeman R, Iordachita I, Khanuja H, and Armand M, “On the use of a continuum manipulator and a bendable medical screw for minimally invasive interventions in orthopedic surgery,” IEEE Transactions on Medical Robotics and Bionics, vol. 1, no. 1, pp. 14–21, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Choi H, Kwak H-S, Lim Y-A, and Kim H-J, “Surgical robot for single-incision laparoscopic surgery,” IEEE Transactions on Biomedical Engineering, vol. 61, no. 9, pp. 2458–2466, 2014. [DOI] [PubMed] [Google Scholar]
- [3].Gupta A, Singh S, Gonenc B, Kobilarov M, and Iordachita I, “Toward sclera-force-based robotic assistance for safe micromanipulation in vitreoretinal surgery,” in 2017 IEEE SENSORS. IEEE, 2017, pp. 1–3. [DOI] [PMC free article] [PubMed]
- [4].Simaan N, Yasin RM, and Wang L, “Medical technologies and challenges of robot-assisted minimally invasive intervention and diagnostics,” Annual Review of Control, Robotics, and Autonomous Systems, vol. 1, pp. 465–490, 2018. [Google Scholar]
- [5].Rucker DC and Webster III RJ, “Statics and dynamics of continuum robots with general tendon routing and external loading,” IEEE Transactions on Robotics, vol. 27, no. 6, pp. 1033–1044, 2011. [Google Scholar]
- [6].Subramani G. and Zinn MR, “Tackling friction-an analytical modeling approach to understanding friction in single tendon driven continuum manipulators,” in 2015 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2015, pp. 610–617. [Google Scholar]
- [7].Liu Y, Ahn S, Yoo U, Cohen A, and Alambeigi F, “Toward analytical modeling and evaluation of curvature-dependent distributed friction force in tendon-driven continuum manipulators,” in 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 2020, pp. 8823–8828. [Google Scholar]
- [8].Liu Y. and Alambeigi F, “Effect of external and internal loads on tension loss of tendon-driven continuum manipulators,” IEEE Robotics and Automation Letters, vol. 6, no. 2, pp. 1606–1613, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Webster III RJ and Jones BA, “Design and kinematic modeling of constant curvature continuum robots: A review,” The International Journal of Robotics Research, vol. 29, no. 13, pp. 1661–1683, 2010. [Google Scholar]
- [10].Camarillo DB, Milne CF, Carlson CR, Zinn MR, and Salisbury JK, “Mechanics modeling of tendon-driven continuum manipulators,” IEEE transactions on robotics, vol. 24, no. 6, pp. 1262–1273, 2008. [Google Scholar]
- [11].Renda F, Cianchetti M, Giorelli M, Arienti A, and Laschi C, “A 3d steady-state model of a tendon-driven continuum soft manipulator inspired by the octopus arm,” Bioinspiration & biomimetics, vol. 7, no. 2, p. 025006, 2012. [DOI] [PubMed] [Google Scholar]
- [12].Boyer F, Lebastard V, Candelier F, and Renda F, “Dynamics of continuum and soft robots: A strain parameterization based approach,” IEEE Transactions on Robotics, vol. 37, no. 3, pp. 847–863, 2020. [Google Scholar]
- [13].Kato T, Okumura I, Kose H, Takagi K, and Hata N, “Tendon-driven continuum robot for neuroendoscopy: validation of extended kinematic mapping for hysteresis operation,” International journal of computer assisted radiology and surgery, vol. 11, no. 4, pp. 589–602, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Sun Z, Wang Z, and Phee SJ, “Elongation modeling and compensation for the flexible tendon–sheath system,” IEEE/ASME Transactions on Mechatronics, vol. 19, no. 4, pp. 1243–1250, 2013. [Google Scholar]
- [15].Agrawal V, Peine WJ, and Yao B, “Modeling of transmission characteristics across a cable-conduit system,” IEEE Transactions on Robotics, vol. 26, no. 5, pp. 914–924, 2010. [Google Scholar]
- [16].Khoshnam M. and Patel RV, “Robotics-assisted control of steerable ablation catheters based on the analysis of tendon-sheath transmission mechanisms,” IEEE/ASME Transactions on Mechatronics, vol. 22, no. 3, pp. 1473–1484, 2017. [Google Scholar]
- [17].Roy R, Wang L, and Simaan N, “Modeling and estimation of friction, extension, and coupling effects in multisegment continuum robots,” IEEE/ASME Transactions on Mechatronics, vol. 22, no. 2, pp. 909–920, 2016. [Google Scholar]
- [18].Liu Y, Yoo U, Ha S, Atashzar SF, and Alambeigi F, “Influence of antagonistic tensions on distributed friction forces of multisegment tendon-driven continuum manipulators with irregular geometry,” IEEE/ASME Transactions on Mechatronics, 2021. [DOI] [PMC free article] [PubMed]
- [19].Starke J, Amanov E, Chikhaoui MT, and Burgner-Kahrs J, “On the merits of helical tendon routing in continuum robots,” in 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2017, pp. 6470–6476. [Google Scholar]
- [20].Oliver-Butler K, Till J, and Rucker C, “Continuum robot stiffness under external loads and prescribed tendon displacements,” IEEE Transactions on Robotics, vol. 35, no. 2, pp. 403–419, 2019. [Google Scholar]
- [21].Rao P, Peyron Q, Lilge S, and Burgner-Kahrs J, “How to model tendon-driven continuum robots and benchmark modelling performance,” Frontiers in Robotics and AI, vol. 7, p. 223, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Chitalia Y, Jeong S, Deaton N, Chern JJ, and Desai JP, “Design and kinematics analysis of a robotic pediatric neuroendoscope tool body,” IEEE/ASME Transactions on Mechatronics, vol. 25, no. 2, pp. 985–995, 2020. [Google Scholar]
- [23].Chitalia Y, Wang X, and Desai JP, “Design, modeling and control of a 2-dof robotic guidewire,” in 2018 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2018, pp. 32–37. [Google Scholar]
- [24].Antman SS, “Nonlinear problems of elasticity,” Springer, 1995. [Google Scholar]
- [25].Jung Y. and Bae J, “Torque control of a series elastic tendon-sheath actuation mechanism,” IEEE/ASME Transactions on Mechatronics, 2020.
- [26].Mate A, “The frenet-serret formulas,” Brooklyn Collage Of The City University Of New York, izdano, vol. 19, 2017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.