Abstract
Objective:
Fusion of magnetic resonance imaging (MRI) breast images with microwave tomography is accomplished through a soft prior technique, which incorporates spatial information (from MRI), i.e. accurate boundary location of different regions of interest, into the regularization process of the microwave image reconstruction algorithm.
Methods:
Numerical experiments were completed on a set of 3D breast geometries derived from MR breast data with different parenchymal densities, as well as a simulated tumor to evaluate performance over a range of breast shapes, sizes and property distributions.
Results:
When the soft prior regularization technique was applied, both permittivity and conductivity relative root mean square error (RRMSE) values decreased by more than 87% across all breast densities, except in two cases where the error decrease was only 55% and 78%. In addition, the incorporation of structural priors increased contrast between tumor and fibroglandular tissue by 59% in permittivity and 192% in conductivity.
Conclusion:
This study confirmed that the soft prior algorithm is robust in 3D and can function successfully across a range of complex geometries and tissue property distributions.
Significance:
This study demonstrates that our microwave tomography is capable of recovering accurate tissue property distributions when spatial information from MRI is incorporated through soft prior regularization.
Keywords: Breast Cancer, Microwave Tomography, MRI, Multimodality Imaging, Soft Prior Regularization
1. Introduction
Magnetic resonance imaging (MRI) is now commonly used in a wide range of applications including for conventional structural imaging, functional imaging and various types of contrast enhanced imaging [1]–[3]. It is involved in screening of high-risk breast cancer patients [4], in diagnosing tumors from benign conditions in cases of ambiguous findings with x-ray, mammography or ultrasound [5] and in monitoring neoadjuvant chemotherapy [6]. Breast MRI offers high spatial resolution and produces 3D maps of internal structures such as fibroglandular tissue, adipose and chest wall. It also accesses challenging anatomical areas such as the axilla region, which can be problematic for other modalities (e.g., x-ray mammography) [4]. The high sensitivity of breast MRI is achieved via gadolinium contrast injection [7], but its specificity suffers accordingly because gadolinium is a generalized, non-targeted vascular agent [8], [9]. Gadolinium is generally considered to be safe except for patients with compromised kidney function where it can cause complications [10] More recently, instances of gadolinium passing through the blood brain barrier have been observed [11], although the long-term health consequences of the phenomenon are unknown. Despite its high costs and some performance limitations, MR is still considered an important breast imaging resource [12].
Microwave imaging has been shown to be specific to variations in normal tissue and also appears to distinguish cancers from other benign abnormalities. For normal tissue, in vivo data indicate property differences exist between different breast densities [13]–[15]. While much of the property differences can be attributed to variations in bulk water fraction, other factors appear to be involved [16], [17]. In terms of receiver operating characteristic (ROC) analysis for classifying breast abnormalities as benign or malignant, area under the curve was 0.86 for microwave imaging [18] which is comparable to published results for MR [19] provided cancers were greater than 1 cm in size. The microwave conductivity is a particularly useful diagnostic at microwave frequencies, since it has been shown to correlate well with near infrared (NIR) oxygenated hemoglobin values which are known to be good predictors of tumor presence [15]. Some uncertainty exists in terms of breast tissue dielectric properties relative to tumor based on ex vivo measurements [20]–[25]; at least in part because assumptions underpinning use of microwave probe devices may not hold in the breast tissue measurement setting [26], [27].
Efforts to recover the dielectric properties of tissue directly from MRI measurement data at lower frequencies (Larmor–128 MHz for a 3T MRI scanner) have been presented [28], [29]. However, these interesting approaches do not eliminate the need for higher frequency information, especially since tissue dielectric properties exhibit multiple relaxations over a broad frequency range that directly impact their values for any given frequency [30–32].
Thus, microwave imaging is an attractive option for breast imaging because signals are non-ionizing, significant dielectric property contrast for tumor appears to exist, and the technology can be produced at low cost in large quantities [33]. Technical advances have progressed to the point where promising clinical studies have been reported [13], [18], [34]–[36].
Work is currently being performed to combine the high spatial resolution and soft tissue contrast of MRI synergistically with the more specific attributes of microwave imaging [37]. Integration of the two systems is a formidable task because: (1) the metallic microwave antennas distort the MR images, (2) the microwave liquid coupling is difficult to manage and poses space challenges within an MRI scanner bore, and (3) the MR radio frequency (RF) signals interfere with the microwave data acquisition. An early prototype [37] demonstrated that these hardware challenges can be overcome. On the software integration side, we developed a soft prior algorithm as the primary means of combining the multi-modality imaging data available from the two systems [16], [38], [39]. More specifically, the MR data is transformed into a finite element mesh with segmented zones for adipose and fibroglandular tissue [38]. In addition, a penalty term is imposed on the Gauss-Newton iterative image reconstruction scheme that encourages property uniformity within these predefined regions but allows different zones to seek different property values [39]. The net effect is recovery of microwave property images with steep property gradients between zones and relatively homogeneous distributions within zones [39]. The property estimates within each region are more accurate than those obtained without spatial priors in two-and three-dimensional (2D and 3D) numerical simulation and phantom experiments [16], [39].
While 2D microwave image reconstruction with the soft prior approach has been validated in numerical simulation and phantom experiments utilizing conical forms and a range of complex shapes, including data from actual breast and calcaneus bone exams [38], [39], the experience in 3D has been more limited [16]. We recently evaluated the 3D algorithmic analogue in numerical simulations to assess its sensitivity to errors in the location, size and contrast of an object. We also tested the algorithm with a breast phantom where the MRI and microwave data were acquired at different times [16]. However, the algorithm has not previously been evaluated in simulated breast phantoms with patient-derived anatomical shapes and tissue compositions. In this study, we explore the capabilities of the 3D algorithm using MRI-based breast geometries from the University of Wisconsin image repository [40]. The paper presents an overview of the soft prior algorithm and describes how the synthetic microwave data was generated from image data obtained from the Wisconsin repository. Results derived from MR breast data with four different densities and a simulated tumor are considered to assess the accuracy and robustness of the algorithm. Comparisons with non-prior images illustrate quantitative benefits. Discussion of issues that will be confronted when progressing towards actual patient exams is also included.
II. Methods
A. Image Reconstruction
Microwave imaging is based on determining the distribution of constitutive parameters within tissue represented by the complex wave number squared, k2, which can be written as
| (1) |
where r is the 3D position vector within the imaging domain, ω is the angular frequency, j is the imaginary unit, µ0 is the free-space permeability, and ε and σ are the electrical permittivity and conductivity, respectively [41]. Estimation of the dielectric properties embodied in k2 is driven by known microwave excitations and resulting measured data through the finite difference time domain (FDTD) algorithm [42]. Following this step, differences between 3D measured (Em) and computed (Ec(k2)) electric field vectors are minimized through an iterative Levenberg-Marquardt (LM) technique [43] with a variance stabilizing transformation [44]. Tikhonov regularization [45] also occurs to impose additional constraints to stabilize the reconstruction procedure. In our algorithm, the objective function is defined as
| (2) |
where Γm and Γc are the log magnitudes, and ϕm and ϕ c are the associated phases of the measured and computed field vectors, respectively [44], [46], [47], λ is the Tikhonov regularization parameter, L is a positive definite, dimensionless regularization matrix, and is a prior estimate of k2 In our case, the starting dielectric property distributions were uniform and began with the values of the surrounding coupling bath which are known and can be measured independently. The objective function Ω in (2) can be minimized iteratively based on the property update vector, , at iteration as follows:
| (3) |
where J is the Jacobian matrix, which has dimensions 2M × 2N, and consists of derivatives of the log magnitude and phases of the computed field values (M is the number of measurements) with respect to the property values at each node (N is the total number of nodes) in a 3D tetrahedral-element reconstruction mesh. Updates of the property distribution at each iteration are formed according to
| (4) |
When no prior information about the tissue being imaged is available, the L matrix in (3) is an identity matrix, which applies a homogeneously distributed smoothing effect to the dielectric property estimates. We refer to this instance as the “no prior” case. However, when prior information on internal structure is available, for example from MRI, a heterogeneouslydistributed smoothing of the property estimates occurs within subzones of the imaging domain. In this case, known as the “soft prior” approach [16], [38], [39], segmented MR images define a volumetric reconstruction mesh in which areas of interest such as adipose, fibroglandular, and tumor regions are identified. Spatial locations of these property estimates are incorporated into the reconstruction through regularization matrix, L, in (3). Specifically, given two nodes, i and j, in the reconstruction mesh, the corresponding entry in L is 1 if i = j, 0 if i and j are located in different regions, and –(NR)−1 if i and j belong to the same region, R, containing 𝑁R + 1 nodes [38], [39]. The soft prior technique does not force property estimates within identified regions to be constant, but favors uniformity (i.e. penalizes region heterogeneity) within these pre-selected regions. In addition, when two different regions share the same boundary, the smoothing across their common interface is penalized/absent [16]. In our previous and current studies, the choice of λ is derived empirically.
B. Anatomically-Realistic Numerical Phantom Experiments
B.1. Breast Models:
The breast numerical phantom experiments presented in this work are based on anatomically realistic MRI-derived geometries obtained from the University of Wisconsin Cross-Disciplinary Electromagnetics Laboratory (UWCEM) phantom repository [40]. Breast internal features were derived from T1-weighted MRIs of non-patient volunteers with four different radiographic densities, defined by the American College of Radiology [48]: fatty, F (<25% glandular tissue), scattered, S (25–50% glandular), heterogeneously dense, HD (51–75% glandular), and extremely dense, XD (>75% glandular). The original breast models included a ~1.5 mm skin layer. However, since our microwave imaging system operates at relatively low frequencies (~1–2 GHz) and we use a lossy coupling bath in addition to a log-transformed algorithm which emphasizes more centrally located features [44], [49]–[52], the skin layer was not evaluated as a separate region but was incorporated in the surrounding adipose tissue compartment. Based on initial simulations, omitting the skin layer was found to have minimal impact on reconstructed images. Nonetheless, analyzing the effects of including the skin into the model as a distinct region is an important and interesting topic that we plan to explore in detail in future. Moreover, different types of adipose as well as fibroglandular tissues were combined into single adipose and fibroglandular regions for simplicity. Chest wall was removed from the imaging domain to mimic the microwave field-of-view used previously [37].
B.2. Numerical Simulation and Reconstruction Meshes:
The numerical breast models described in the previous section were segmented into regions of interest (adipose and fibroglandular) to create 3D meshes with z = 0 defined to be the center of the mesh in the vertical (coronal) direction. Synthetic data were generated on uniform 3D rectangular FDTD grids ([20.6–21.4] cm × [20.6–21.4] cm × [12.82–18.5] cm with [0.23–0.29] cm spacing), while dielectric property distributions were estimated on various 3D tetrahedral–element meshes. For the 3D numerical microwave data generation, the antenna array transmitted and received the signals at equally spaced (0.5 or 1 cm) vertical positions, at which 16 (transmitters) ×15 (receivers) measurements were collected in each plane. For a more detailed description of our imaging system please refer to [14], [47]. During image reconstruction, only data from receivers in the same plane were used for each transmitter. The 3D no prior images were reconstructed on a uniform mesh representing the reconstruction area defined by the boundary of the simulated breast region consisting of 10,500–12,500 nodes and 56,000–69,000 tetrahedral elements (typically 3–4 mm in element edge length). Soft prior images were reconstructed on more customized meshes (11,000–13,500 nodes and 61,000–75,000 tetrahedral elements), in which higher nodal density was deployed along specific region boundaries (adipose and fibroglandular regions) defined by the MRI segmentation. Fig. 1 shows sample 3D (a) no prior and (b) soft prior reconstruction meshes from a scattered breast with a synthetic tumor approximately 5 mm in radius placed in the fibroglandular zone.
Fig. 1.
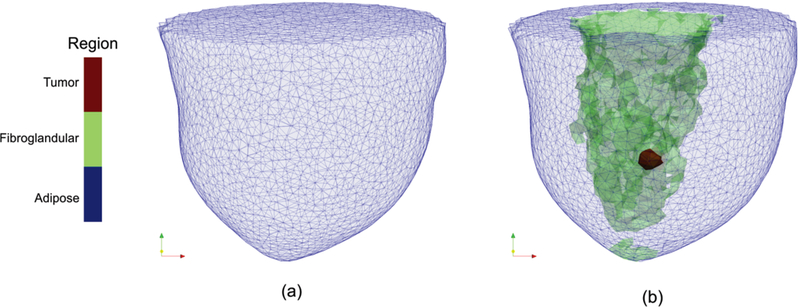
Sample 3D (a) no prior and (b) soft prior reconstruction meshes from a scattered breast with a synthetic tumor approximately 5 mm in radius. The no prior mesh consisted of 12303 nodes and 67019 tetrahedral-elements, whereas the soft prior reconstruction mesh was composed of 12867 nodes and 70789 tetrahedral-elements. Elements associated with the adipose, fibroglandular, and tumor regions in (b) are colored in blue, green, and red, respectively (see color online version).
For comparison purposes, we also used our 2D finite element (FE) algorithm [44] to reconstruct some of the breast images in which case a 2D mesh with 559 uniformly distributed nodes and 1044 triangular-elements was involved.
B.3. Dielectric Properties:
Dielectric property values used in the numerical phantom experiments (at 1300 MHz) are listed in Table I [14]. Background properties represent measured values for mixtures of glycerin:water coupling baths (86:14% for fatty and scattered, and 80:20% for HD and XD cases). In addition, we used εr = 59.3 and σ = 1.54 S/m [24] for a synthetic tumor (Tu) of approximately 5 mm in radius, which was inserted within the fibroglandular region in the scattered breast.
TABLE I.
Dielectric properties of the background medium, adipose, and fibroglandular tissues used in the numerical phantom experiments for different breast densities at 1300 MHz
| Breast Type |
Background Medium |
Adipose (Adp) | Fibroglandular (Fg) |
|||
|---|---|---|---|---|---|---|
| εr |
σ (S/m) |
εr |
σ (S/m) |
εr | σ (S/m) | |
| Fatty | 13.6 | 0.87 | 8.0 | 0.17 | 8.8 | 0.195 |
| Scattered | 13.6 | 0.87 | 9.0 | 0.21 | 14.5 | 0.32 |
| HD | 22.4 | 1.26 | 12.8 | 0.36 | 21.0 | 0.61 |
| XD | 22.4 | 1.26 | 16.5 | 0.60 | 28.0 | 0.89 |
B.4. Added Noise:
In order to account for measurement uncertainty, −100 dBm synthetic noise was introduced into the simulated data, which provides sufficient error margin, since in practice, the noise floor of our system is close to −135 dBm [44]. The noise was defined by KTB where k is Boltzmann’s constant (1.381E −23 J/K), is the temperature in Kelvin, and is the bandwidth [53]. The −100 dBm noise level corresponds to a temperature of 298 K and a sampling time of 41.2 nsec. In this case, the transmitted signal is 1 mW (0 dBm). The synthetic noise was generated with a random number generator having a Gaussian distribution. The amplitude of the distribution was set to reflect the −100 dBm level.
C. Error Analysis, Average Values, and Contrast Enhancements
In order to evaluate the dielectric properties recovered with and without spatial priors quantitatively, the relative root mean square errors (RRMSER) in the region of interest, R, (which could be adipose, Adp, fibroglandular, Fg, or tumor, Tu) were calculated as
| (5) |
where NR is the number of reconstruction nodes in region R, is the reconstructed dielectric property value (either permittivity or conductivity) at node n, and is the true value of the selected dielectric property at that location. Permittivity and conductivity RRMSE associated with all numerical phantom experiments (for various breast densities and inclusion of a small tumor) were calculated and summarized, accordingly.
To quantify how much incorporation of structural priors increased contrast between any two regions R1 and R2 (Adp, Fg, and Tu), the percentage of contrast enhancement was calculated as:
| (6) |
where and are the no prior (NP) and soft prior (SP) contrasts , respectively, of the average reconstructed properties in region with respect to those in region , and were calculated as
| (7) |
Larger represents more contrast enhancement between regions R1 and R2 resulting from the incorporation of prior structural information. can be computed regardless of the average property values. However, in order to compare among different regions consistently, R1 and R2 must be also chosen consistently (i.e. either R1 as the lower and R2 as the higher value property region, or vice versa.)
III. Results
We compared 2D and 3D reconstructed dielectric property profiles using the no prior and soft prior regularization algorithms, and studied how different breast densities affected performance. We also performed a comparison of 3D reconstructed no prior and soft prior images from a scattered breast numerical phantom experiment with a small synthetic tumor.
A. No Prior Spatial Information vs. Soft Prior Regularization
Figure 2 shows (a) 2D, (b) 3D no prior, and (c) 3D soft prior reconstructed permittivity (top row) and conductivity (bottom row) images of the scattered breast numerical phantom experiment with no tumor inclusion. For visualization purposes, 6 horizontal slices (2 cm apart) approximately parallel to the chest wall (coronal slices) through the 3D image volume are presented. The 2D reconstructions also include the matching background medium surrounding the breast. While the fibroglandular region is evident in all cases, the dielectric properties are much closer to their actual values in both permittivity and conductivity images in the soft prior case. Specifically, average property estimates from the adipose and fibroglandular regions were εr Adp = 9.0, σ Adp = 0.21 S/m, and εr Fg = 14.3, σ Fg = 0.33 S/m, respectively. The corresponding actual values were εr Adp = 9.0, σ Adp = 0.21 S/m, and εr Fg = 14.5, σFg = 0.32 S/m, respectively. Moreover, adding internal priors notably reduced the level of property variations in both the adipose and fibroglandular regions in the images. The 3D no prior RRMSE associated with the adipose and fibroglandular regions was 10% and 17% in permittivity, and 23% and 18% in conductivity images, respectively, whereas when soft prior regularization was used, the corresponding RRMSEs were reduced to 0.1% and 1.4% in permittivity, and 2.2% and 3.9% in conductivity.
Fig. 2.
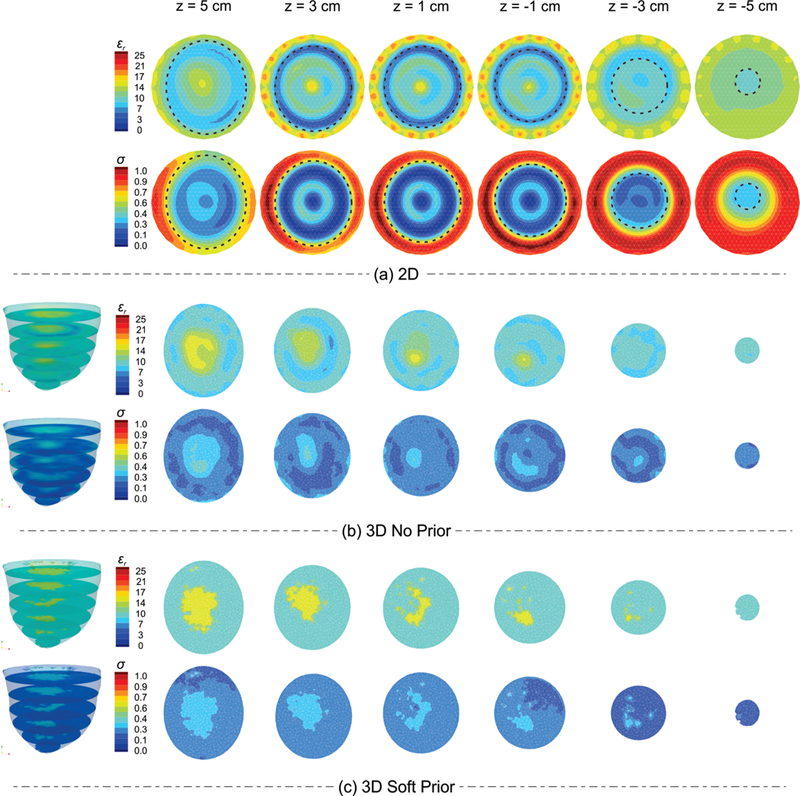
(a) 2D, (b) 3D no prior, and (c) 3D soft prior reconstructed permittivity (top row) and conductivity (bottom row) images of the scattered breast numerical phantom experiment with no tumor inclusion. Dashed-lines on the 2D images correspond to the outline of the breast.
B. Different Breast Densities
The 3D dielectric property maps of the anatomically-realistic numerical phantoms with the 4 radiographic breast densities described in Section II.B.3 were reconstructed using no spatial priors as well as soft priors. Fig. 3 shows representative permittivity (top row) and conductivity (bottom row) images from the three algorithms for two representative planes (z = 3 and z = 0 cm) for (a) fatty, (b) scattered, (c) heterogeneously dense, and (d) extremely dense breasts, respectively. The averaged soft prior recovered properties for each breast density are listed in Table II, whereas the corresponding actual values are listed in Table I. For each 3D case, the corresponding RRMSEs associated with the adipose and fibroglandular regions were calculated, and the results are presented in Fig. 4 and listed in Table III (in APPENDIX). When the soft prior regularization technique was applied, both permittivity and conductivity RRMSE values decreased by more than 87% across all breast densities, except in a few cases–i.e. RRMSE decreased by 55% in the fatty εr Fg and 78% in the scattered σ Fg instances. These results suggest that more overall improvement (across all regions) occurs with soft prior regularization in the higher breast density cases.
Fig. 3.
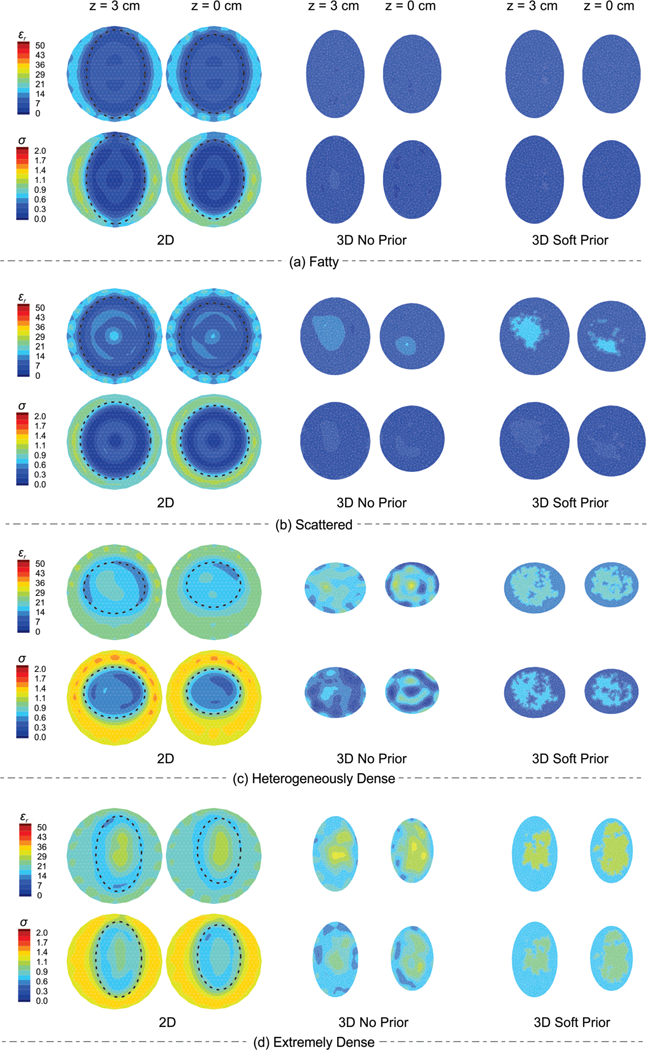
Representative permittivity (top row) and conductivity (bottom row) images from the 2D, 3D no prior, and 3D soft prior reconstructions for two representative planes (z = 3 and z = 0 cm) for (a) fatty, (b) scattered, (c) heterogeneously dense, and (d) extremely dense breasts numerical phantoms, respectively. Dashed-lines on the 2D images correspond to the outline of the breast.
TABLE II.
Averaged soft prior recovered dielectric properties of the adipose and fibroglandular tissues from the numerical phantom experiments with different breast densities.
| Breast Type | Adipose (Adp) | Fibroglandular (Fg) | ||
|---|---|---|---|---|
| εr | σ(S/m) | εr | σ(S/m) | |
| Fatty | 8.03 | 0.1777 | 8.11 | 0.1990 |
| Scattered | 8.99 | 0.214 | 14.30 | 0.332 |
| HD | 13.06 | 0.374 | 20.76 | 0.621 |
| XD | 16.58 | 0.615 | 27.81 | 0.890 |
Fig. 4.
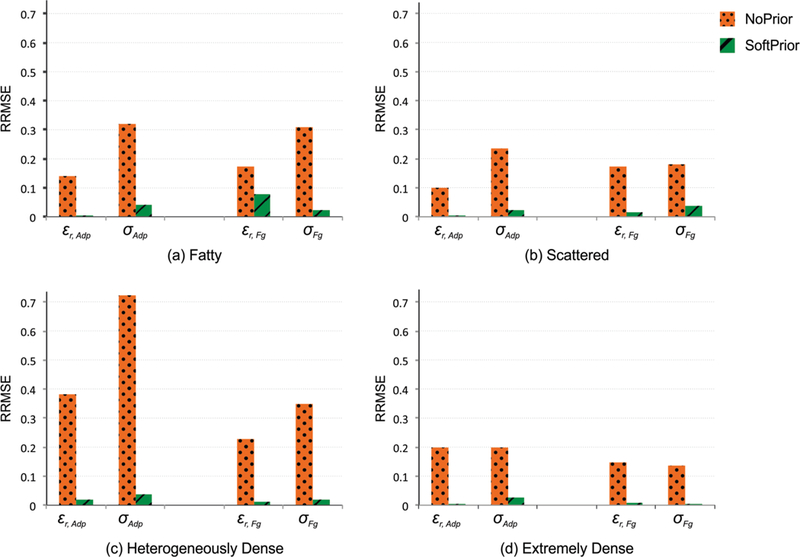
No prior vs. soft prior RRMSE for reconstructed permittivity and conductivity values in adipose (Adp) and fibroglandular (Fg) regions from the (a) fatty, (b) scattered, (c) heterogeneously dense, and (d) extremely dense breast numerical phantoms. For comparison purposes, the RRMSE scales are the same (0–0.8) in all the cases.
C. Tumor Inclusion
Fig. 5 shows 3D reconstructed (a) permittivity and (b) conductivity images from the scattered breast numerical phantom experiment with a synthetic tumor ~5 mm in radius, using soft prior regularization. For visualization purposes, the outline of the reconstructed breast (adipose tissue) is displayed as a point cloud. In addition, horizontal slices for the z = 0 plane, along with iso-surface thresholds of εr = 14 and σ = 0.31 S/m for fibroglandular, and εr = 32 and σ = 1.13 S/m for the tumor were applied to the reconstructed 3D images. Despite the relatively small size of the malignancy, soft prior regularization successfully characterized the inclusion in both permittivity and conductivity images.
Fig. 5.
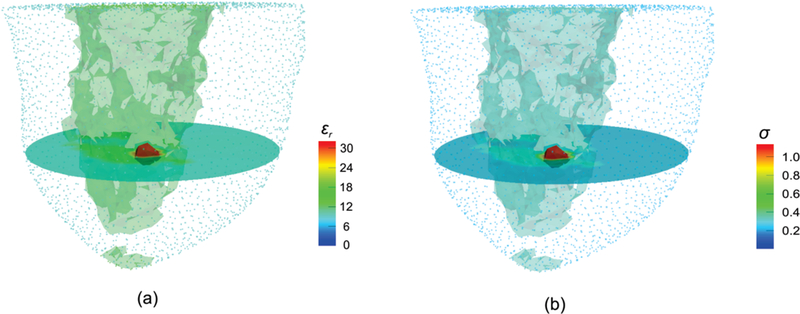
3D reconstructed (a) permittivity and (b) conductivity profiles of the scattered breast numerical phantom experiment with a tumor inclusion of ~5 mm in radius, using the soft prior regularization. Iso-surface thresholds of εr Fg = 14 and σFg = 0.31 S/m (Fg), and εr Tu = 32 and σTu = 1.13 S/m (Tu) were applied to visualize the reconstructed volume of the fibroglandular and target tumor regions, respectively.
To compare the 3D reconstructed dielectric property profiles recovered with and without spatial priors, five horizontal slices (coronal planes) at z = 2, 1, 0, −1, and −2 cm were extracted. Fig. 6 shows the corresponding (a) no prior and (b) soft prior permittivity (top row) and conductivity (bottom row) results. While the tumor is detected in both cases, soft prior images are notably superior not only in terms of tumor size/location, but also its dielectric property values. Since the spherical inclusion was centered at z = 0 with a radius of 5 mm, the tumor should only appear in the horizontal slice at z = 0 cm. In the no prior case, the reconstructed tumor was larger than its actual size; it appeared in 3 slices (z = 1, 0, and −1 cm). In addition, despite the high contrast between tumor and its background fibroglandular tissue, the inclusion only appeared in the reconstructed permittivity images when no spatial priors were used. The permittivity and conductivity RRMSEs associated with the tumor region were 69% and 75%, respectively, for the no prior case, which reduced to 46% and 26% when soft prior regularization was applied. Moreover, the incorporation of structural priors increased contrast between tumor and fibroglandular tissue (CETu/Fg) by 59% in permittivity and 192% in conductivity. A complete list of computed contrast enhancements for different regions of interest is summarized in Table IV in the APPENDIX.
Fig. 6.

Anatomically coronal slices of 3D a) no prior and b) soft prior permittivity (top row) and conductivity (bottom row) images of the scattered breast with a synthetic spherical tumor of 5 mm in radius.
IV. Discussion
Overall, the results suggest a unique opportunity may exist to fuse MRI and microwave tomography for improved specificity when characterizing breast abnormalities. These numerical experiments demonstrate that the dielectric properties of breast tissue constituents can be recovered accurately over a comprehensive range of radiographic densities when spatial priors are encoded into the process. The study also considered the problem of recovering a small tumor embedded in fibroglandular tissue. While this example was promising, the current algorithm was unable to recover the exact tumor properties, although estimates were still well in excess of the surrounding values. We intend to investigate and characterize these limitations and explore ways of further optimizing the algorithm in future studies. Towards this end, numerical experiments conducted over a broader frequency range and possibly incorporating multi-frequency methods are of interest and can be adaptable fully to the soft prior process. In addition, assessments of performance for different sized tumors placed in various locations within the breast demand further study.
Numerical studies have previously shown good agreement between recovered properties and exact values for different tissue types, and for cases with small tumor inclusions [54]–[56] However, in each of these instances, starting values close to the true dielectric properties were provided prior to initiation of the reconstruction process, and in most practical clinical situations, this property information will not be available. Other studies have shown examples of alternative regularization approaches without the need for prior information [57]. While promising, relatively idealized examples have been reported to date, and greater challenges will occur when these techniques are used to recover images from actual measurement data. In the experiments presented here, priors were provided on the spatial distributions of tissue types in the breast but not on their dielectric property values. More specifically, starting dielectric property distributions were uniform and began with the values of the surrounding coupling bath which are known and can be measured prior to each patient exam [17].
The 3D spatial priors can be determined with commercial software using simple thresholding to distinguish tissues within the MR data [58]–[60]. We have previously adapted this approach in a pilot clinical study involving 2D imaging [36]. The incorporation of 3D spatial priors into the reconstruction algorithm does not increase computational time since information is integrated through regularization matrix, L, in (3) which is computed only once. However, preprocessing MRI images in order to segment regions of interest and creating customized soft prior reconstruction meshes does impose additional effort. Acquiring high quality breast MRI in the presence of an array of microwave antennas is also challenging, as is the acquisition of microwave data while operating in an MRI scanner bore.
Confirming the success of a 3D algorithm as operational over a range of breast densities in conjunction with previous efforts to acquire microwave imaging data simultaneously with an MR exam offers a pathway towards clinical implementation and may present an option for breast imaging without contrast injection. Contrast-enhanced MRI with gadolinium is, perhaps, the most sensitive breast imaging exam, but is not very specific. Further, gadolinium is not safe for all patients, especially those with compromised kidney function [10]. New safety concerns have been raised as a result of gadolinium leaking into the brain [58] Here, microwave imaging when combined with MRI may offer an alternative way to achieve specificity without the need for contrast agents, and is a focus of future research.
V. Conclusion
These experiments demonstrate that microwave tomography is capable of recovering accurate tissue property distributions when spatial information from MRI is incorporated through soft prior regularization. Improvement is substantial and minimizes ambiguity at tissue interfaces. This study confirmed that the soft prior algorithm is robust in 3D and can function successfully across a range of complex geometries and tissue property distributions. Gains were realized without the aid of priors on the property values, themselves. A preliminary example involving accurate characterization of the dielectric properties of a small tumor embedded in fibroglandular tissue with a complex, anatomically realistic (patient derived) geometry was successful. While further studies are needed to optimize the detection of tumors, the results presented here, in conjunction with previous advances to deploy our microwave antenna array in an MRI scanner, set the stage for clinical implementation and testing.
Acknowledgments
This work was supported in part by the NIH/NCI Grant # RO1 CA191227-01.
Appendix
TABLE III.
RRMSE values calculated for the reconstructed permittivity and conductivity profiles in adipose (Adp) and fibroglandular (Fg) regions in the fatty, scattered, heterogeneously dense, and extremely dense breast numerical phantom experiments.
| RRMSE | Fatty | Scattered | HD | XD | ||||
|---|---|---|---|---|---|---|---|---|
| No Prior |
Soft Prior |
No Prior |
Soft Prior |
No Prior |
Soft Prior |
No Prior |
Soft Prior |
|
| εr Adp | 0.141 | 0.004 | 0.100 | 0.001 | 0.382 | 0.020 | 0.198 | 0.005 |
| σAdp | 0.319 | 0.042 | 0.236 | 0.021 | 0.723 | 0.037 | 0.197 | 0.025 |
| εr Fg | 0.174 | 0.078 | 0.171 | 0.013 | 0.228 | 0.011 | 0.146 | 0.006 |
| σFg | 0.309 | 0.021 | 0.179 | 0.038 | 0.348 | 0.018 | 0.136 | 0.001 |
TABLE IV.
Percentage of contrast enhancement (% CE) between regions of interest (R1/R2) when structural priors are applied to the scattered breast numerical phantom experiment with a synthetic tumor.
| % CER1/R2 | Scattered with Tumor Inclusion | |
|---|---|---|
| εr | σ | |
| Fg/Adp | 13.7 | 14.0 |
| Tu/Adp | 81.0 | 233.1 |
| Tu/Fg | 59.2 | 192.3 |
Contributor Information
Amir H. Golnabi, Department of Mathematical Sciences and the Center for Quantitative Obesity Research (CQOR), Montclair State University, Montclair, NJ USA (phone: 1-973-655-7226).
Paul M. Meaney, Thayer School of Engineering, Dartmouth College, Hanover, NH USA., Department of Electrical Engineering, Chalmers University of Technology, Gothenburg, Sweden..
Shireen D. Geimer, Thayer School of Engineering, Dartmouth College, Hanover, NH USA.
Keith D. Paulsen, Thayer School of Engineering and Department of Radiology, Geisel School of Medicine, Dartmouth College, Hanover, NH USA., Norris Cotton Cancer Center and Advanced Surgical Center, Dartmouth Hitchcock Medical Center, Lebanon, NH USA..
References
- [1].Symms M, “A review of structural magnetic resonance neuroimaging,” j. Neurol. Neurosurg. Psychiatry, vol. 75, no. 9, pp. 1235–1244, Sep. 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Smith SM et al. , “Advances in functional and structural MR image analysis and implementation as FSL,” NeuroImage, vol. 23, pp. S208–S219, Jan. 2004. [DOI] [PubMed] [Google Scholar]
- [3].Tofts PS et al. , “Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols,” J. Magn. Reson. Imaging JMRI, vol. 10, no. 3, pp. 223–232, Sep. 1999. [DOI] [PubMed] [Google Scholar]
- [4].Rautiainen S et al. , “Preoperative Axillary Staging with 3.0-T Breast MRI: Clinical Value of Diffusion Imaging and Apparent Diffusion Coefficient,” PLOS ONE, vol. 10, no. 3, p. e0122516, Mar. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Peters NHGM, Borel Rinkes IHM, Zuithoff NPA, Mali WPTM, Moons KGM, and Peeters PHM, “Meta-Analysis of MR Imaging in the Diagnosis of Breast Lesions,” Radiology, vol. 246, no. 1, pp. 116–124, Jan. 2008. [DOI] [PubMed] [Google Scholar]
- [6].Sharma U, Danishad KKA, Seenu V, and Jagannathan NR, “Longitudinal study of the assessment by MRI and diffusion-weighted imaging of tumor response in patients with locally advanced breast cancer undergoing neoadjuvant chemotherapy,” NMR Biomed, vol. 22, no. 1, pp. 104–113, Jan. 2009. [DOI] [PubMed] [Google Scholar]
- [7].Dao TH, Rahmouni A, Campana F, Laurent M, Asselain B, and Fourquet A, “Tumor recurrence versus fibrosis in the irradiated breast: differentiation with dynamic gadolinium-enhanced MR imaging.,” Radiology, vol. 187, no. 3, pp. 751–755, Jun. 1993. [DOI] [PubMed] [Google Scholar]
- [8].Orel SG and Schnall MD, “MR imaging of the breast for the detection, diagnosis, and staging of breast cancer,” Radiology, vol. 220, no. 1, pp. 13–30, Jul. 2001. [DOI] [PubMed] [Google Scholar]
- [9].Bartella L, Smith CS, Dershaw DD, and Liberman L, “Imaging breast cancer,” Radiol. Clin. North Am, vol. 45, no. 1, pp. 45–67, Jan. 2007. [DOI] [PubMed] [Google Scholar]
- [10].Perazella MA, “Current Status of Gadolinium Toxicity in Patients with Kidney Disease,” Clin. J. Am. Soc. Nephrol, vol. 4, no. 2, pp. 461–469, Feb. 2009. [DOI] [PubMed] [Google Scholar]
- [11].Gulani V, Calamante F, Shellock FG, Kanal E, and Reeder SB, “Gadolinium deposition in the brain: summary of evidence and recommendations,” Lancet Neurol, vol. 16, no. 7, pp. 564–570, Jul. 2017. [DOI] [PubMed] [Google Scholar]
- [12].Lehman CD and Schnall MD, “Imaging in breast cancer: Magnetic resonance imaging,” Breast Cancer Res, vol. 7, no. 5, Oct. 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Fear EC, Bourqui J, Curtis C, Mew D, Docktor B, and Romano C, “Microwave breast imaging with a monostatic radar-based system: A study of application to patients,” IEEE Trans. Microw. Theory Tech, vol. 61, no. 5, pp. 2119–2128, May 2013. [Google Scholar]
- [14].Meaney PM et al. , “Initial clinical experience with microwave breast imaging in women with normal mammography,” Acad. Radiol, vol. 14, no. 2, pp. 207–218, Feb. 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Poplack SP et al. , “Electromagnetic Breast Imaging: Average Tissue Property Values in Women with Negative Clinical Findings,” Radiology, vol. 231, no. 2, pp. 571–580, May 2004. [DOI] [PubMed] [Google Scholar]
- [16].Golnabi AH, Meaney PM, and Paulsen KD, “3D microwave tomography of the breast using prior anatomical information: 3D microwave tomography using prior anatomical information,” Med. Phys, vol. 43, no. 4, pp. 1933–1944, Mar. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Meaney PM, Geimer SD, and Paulsen KD, “Two-step inversion with a logarithmic transformation for microwave breast imaging,” Med. Phys, vol. 44, no. 8, pp. 4239–4251, Aug. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Poplack SP et al. , “Electromagnetic Breast Imaging: Results of a Pilot Study in Women with Abnormal Mammograms,” Radiology, vol. 243, no. 2, pp. 350–359, May 2007. [DOI] [PubMed] [Google Scholar]
- [19].Bluemke DA et al. , “Magnetic resonance imaging of the breast prior to biopsy,” JAMA, vol. 292, no. 22, pp. 2735–2742, Dec. 2004. [DOI] [PubMed] [Google Scholar]
- [20].Chaudhary SS, Mishra RK, Swarup A, and Thomas JM, “Dielectric properties of normal & malignant human breast tissues at radiowave & microwave frequencies,” Indian J. Biochem. Biophys, vol. 21, no. 1, pp. 76–79, Feb. 1984. [PubMed] [Google Scholar]
- [21].Surowiec AJ, Stuchly SS, Barr JB, and Swarup A, “Dielectric properties of breast carcinoma and the surrounding tissues,” IEEE Trans. Biomed. Eng, vol. 35, no. 4, pp. 257–263, Apr. 1988. [DOI] [PubMed] [Google Scholar]
- [22].Joines WT, Zhang Y, Li C, and Jirtle RL, “The measured electrical properties of normal and malignant human tissues from 50 to 900 MHz,” Med. Phys, vol. 21, no. 4, pp. 547–550, Apr. 1994. [DOI] [PubMed] [Google Scholar]
- [23].Lazebnik M et al. , “A large-scale study of the ultrawideband microwave dielectric properties of normal, benign and malignant breast tissues obtained from cancer surgeries,” Phys. Med. Biol, vol. 52, no. 20, pp. 6093–6115, Oct. 2007. [DOI] [PubMed] [Google Scholar]
- [24].Sugitani T et al. , “Complex permittivities of breast tumor tissues obtained from cancer surgeries,” Appl. Phys. Lett, vol. 104, no. 25, p. 253702, Jun. 2014. [Google Scholar]
- [25].Martellosio A et al. , “Dielectric Properties Characterization From 0.5 to 50 GHz of Breast Cancer Tissues,” IEEE Trans. Microw. Theory Tech, vol. 65, no. 3, pp. 998–1011, Mar. 2017. [Google Scholar]
- [26].Meaney PM, Gregory AP, Epstein NR, and Paulsen KD, “Microwave open-ended coaxial dielectric probe: interpretation of the sensing volume re-visited,” BMC Med. Phys, vol. 14, no. 1, pp. 1–11, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Salahuddin S, Porter E, Meaney PM, and O’Halloran M, “Effect of logarithmic and linear frequency scales on parametric modelling of tissue dielectric data,” Biomed. Phys. Eng. Express, vol. 3, no. 1, p. 015020, Feb. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Balidemaj E et al. , “CSI-EPT: A Contrast Source Inversion Approach for Improved MRI-Based Electric Properties Tomography,” IEEE Trans. Med. Imaging, vol. 34, no. 9, pp. 1788–1796, Sep. 2015. [DOI] [PubMed] [Google Scholar]
- [29].Leijsen RL, Brink WM, van den Berg CAT, Webb AG, and Remis RF, “3-D Contrast Source Inversion-Electrical Properties Tomography,” IEEE Trans. Med. Imaging, vol. 37, no. 9, pp. 2080–2089, Sep. 2018. [DOI] [PubMed] [Google Scholar]
- [30].Gabriel C, Gabriel S, and Corthout E, “The dielectric properties of biological tissues: I. Literature survey,” Phys. Med. Biol, vol. 41, no. 11, pp. 2231–2249, Nov. 1996. [DOI] [PubMed] [Google Scholar]
- [31].Gabriel S, Lau RW, and Gabriel C, “The dielectric properties of biological tissues: II. Measurements in the frequency range 10 Hz to 20 GHz,” Phys. Med. Biol, vol. 41, no. 11, pp. 2251–2269, Nov. 1996. [DOI] [PubMed] [Google Scholar]
- [32].Gabriel S, Lau RW, and Gabriel C, “The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues,” Phys. Med. Biol, vol. 41, no. 11, pp. 2271–2293, Nov. 1996. [DOI] [PubMed] [Google Scholar]
- [33].Fear EC, Meaney PM, and Stuchly MA, “Microwaves for breast cancer detection?,” IEEE Potentials, vol. 22, no. 1, pp. 12–18, Feb. 2003. [Google Scholar]
- [34].Porter E, Coates M, and Popovic M, “An Early Clinical Study of Time-Domain Microwave Radar for Breast Health Monitoring,” IEEE Trans. Biomed. Eng, vol. 63, no. 3, pp. 530–539, Mar. 2016. [DOI] [PubMed] [Google Scholar]
- [35].Preece AW, Craddock I, Shere M, Jones L, and Winton HL, “MARIA M4: clinical evaluation of a prototype ultrawideband radar scanner for breast cancer detection,” J. Med. Imaging, vol. 3, no. 3, p. 033502, Jul. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Meaney PM et al. , “Microwave imaging for neoadjuvant chemotherapy monitoring: initial clinical experience,” Breast Cancer Res, vol. 15, no. 2, pp. 1–16, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Meaney PM et al. , “Integration of microwave tomography with magnetic resonance for improved breast imaging,” Med. Phys, vol. 40, no. 10, p. 103101, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Golnabi AH, Meaney PM, Geimer SD, and Paulsen KD, “Comparison of no-prior and soft-prior regularization in biomedical microwave imaging,” J. Med. Phys, vol. 36, no. 3, pp. 159–170, Jul. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Golnabi AH, Meaney PM, and Paulsen KD, “Tomographic microwave imaging with incorporated prior spatial information,” IEEE Trans. Microw. Theory Tech, vol. 61, no. 5, pp. 2129–2136, May 2013. [Google Scholar]
- [40].Burfeindt MJ et al. , “MRI-Derived 3-D-Printed Breast Phantom for Microwave Breast Imaging Validation,” IEEE Antennas Wirel. Propag. Lett, vol. 11, pp. 1610–1613, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Solymar L, Walsh D, and Syms RRA, Electrical properties of materials, Ninth edition. Oxford: Oxford University Press, 2014. [Google Scholar]
- [42].Taflove A and Hagness SC, Computational electrodynamics: the finite-difference time-domain method, 3rd ed. Boston: Artech House, 2005. [Google Scholar]
- [43].Marquardt DW, “An Algorithm for Least-Squares Estimation of Nonlinear Parameters,” J. Soc. Ind. Appl. Math, vol. 11, no. 2, pp. 431–441, Jun. 1963. [Google Scholar]
- [44].Meaney PM, Fang Q, Rubaek T, Demidenko E, and Paulsen KD, “Log transformation benefits parameter estimation in microwave tomographic imaging,” Med. Phys, vol. 34, no. 6, pp. 2014–2023, Jun. 2007. [DOI] [PubMed] [Google Scholar]
- [45].Tikhonov AN and Arsenin VI, Solutions of ill-posed problems Washington : New York: Winston; distributed solely by Halsted Press, 1977. [Google Scholar]
- [46].Kelley CT, Iterative methods for linear and nonlinear equations Philadelphia: Society for Industrial and Applied Mathematics, 1995. [Google Scholar]
- [47].Meaney PM, Paulsen KD, Pogue BW, and Miga MI, “Microwave image reconstruction utilizing log-magnitude and unwrapped phase to improve high-contrast object recovery,” IEEE Trans. Med. Imaging, vol. 20, no. 2, pp. 104–116, Feb. 2001. [DOI] [PubMed] [Google Scholar]
- [48].“Breast Imaging Reporting and Data System (BI-RADS®),” American College of Radiology, 2003.
- [49].Grzegorczyk TM, Meaney PM, Jeon SI, Geimer SD, and Paulsen KD, “Importance of phase unwrapping for the reconstruction of microwave tomographic images,” Biomed. Opt. Express, vol. 2, no. 2, 315–330, Jan. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Meaney PM, Shubitidze F, Fanning MW, Kmiec M, Epstein NR, and Paulsen KD, “Surface wave multipath signals in near-field microwave imaging,” Int. J. Biomed. Imaging, vol. 2012, p. 697253, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Meaney PM, Fanning MW, Geimer SD, and Paulsen KD, “Mutual coupling in a tomographic imaging system,” in 2009 3rd European Conference on Antennas and Propagation, Berlin, DE, 2009, 2948–2949. [Google Scholar]
- [52].Fang Q, Meaney PM, and Paulsen KD, “Singular value analysis of the Jacobian matrix in microwave image reconstruction,” IEEE Trans. Antennas Propag, vol. 54, no. 8, pp. 2371–2380, Aug. 2006. [Google Scholar]
- [53].Skolnik MI, Introduction to radar systems, Third edition. Boston, Mass. Burr Ridge, IL Dubuque, IA: McGraw Hill, 2001. [Google Scholar]
- [54].Shea JD, Kosmas P, Hagness SC, and Van Veen BD, “Three-dimensional microwave imaging of realistic numerical breast phantoms via a multiple-frequency inverse scattering technique: Microwave imaging of realistic numerical breast phantoms,” Med. Phys, vol. 37, no. 8, pp. 4210–4226, Jul. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Miao Z and Kosmas P, “Multiple-Frequency DBIM-TwIST Algorithm for Microwave Breast Imaging,” IEEE Trans. Antennas Propag, vol. 65, no. 5, pp. 2507–2516, May 2017. [Google Scholar]
- [56].Catapano I et al. , “On quantitative microwave tomography of female breast,” Prog. Electromagn. Res, vol. 97, pp. 75–93, 2009. [Google Scholar]
- [57].Bai F, Franchois A, and Pizurica A, “3D Microwave Tomography with Huber Regularization Applied to Realistic Numerical Breast Phantoms,” Prog. Electromagn. Res, vol. 155, pp. 75–91, 2016. [Google Scholar]
- [58].Rueden CT et al. , “ImageJ2: ImageJ for the next generation of scientific image data,” BMC Bioinformatics, vol. 18, no. 1, Dec. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].CIBC, Seg3D: Volumetric Image Segmentation and Visualization. NIH Center for Integrative Biomedical Computing at the University of Utah Scientific Computing and Imaging (SCI) Institute, 2016.
- [60].Heiberg E, Sjögren J, Ugander M, Carlsson M, Engblom H, and Arheden H, “Design and validation of Segment-freely available software for cardiovascular image analysis,” BMC Med. Imaging, vol. 10, no. 1, Dec. 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]


