Graph convolutional network and self-attentive for sequential recommendation

Collaborative filtering

Collaborative filtering (CF) is a popular approach in recommendation systems that involves learning latent features, or embeddings, to represent users and items. The prediction is then performed based on these embedding vectors. Matrix factorization is one of the early CF models, where users’ interaction history is not explicitly considered, and only the user ID is projected to the embedding. However, subsequent research has shown that incorporating user interaction history can improve the quality of embeddings and prediction performance.

An example of this is the utilization of user interaction history in predicting numerical ratings, as demonstrated by SVD++ (Koren, 2008). Additionally, Neural Attentive Item Similarity (NAIS) assigns varying degrees of importance to items present in the interaction history, leading to more accurate item ranking predictions (He et al., 2018). The key to these enhancements lies in leveraging the subgraph structure of a user’s interaction history, particularly considering their one-hop neighbors, which effectively enhances the process of embedding learning.

To further leverage the subgraph structure, Wang et al. (2019) propose NGCF, a state-of-the-art CF model inspired by graph convolution network (GCN) (Wu et al., 2019). NGCF adopts the propagation rule of GCN, which involves feature transformation, neighborhood aggregation, and nonlinear activation, to refine embeddings. While NGCF has shown promising results, it inherits many operations from GCN without justifying their relevance to the CF task. This design choice introduces unnecessary complexity, particularly when applied to user-item interaction graphs, where each node has only a one-hot ID without rich attribute information. LightGCN (He et al., 2020) introduces a novel approach that propagates user and item embeddings linearly onto the user-item interaction graph, leveraging the weighted summation of embeddings learned across all layers as the ultimate embedding. This method exhibits significant performance improvements over NGCF, as evidenced by our experimental results.

Sequential recommendation

Sequential recommendation has garnered significant research attention in recent years, aiming to accurately capture users’ dynamic interests by modeling their past behavior sequences. Early approaches in this field focused on utilizing Markov chains to model item-to-item transaction patterns. For instance, FPMC combined Markov chains with matrix factorization techniques to integrate sequential patterns and users’ general interests (Rendle, Freudenthaler & Schmidt-Thieme, 2010).

In light of the rise of deep learning, a multitude of deep sequential recommendation models have emerged, harnessing neural networks to capture both long-term and short-term preferences from behavioral sequences. Recurrent neural networks (RNNs) gained prominence due to their ability to encode sequential dependencies. For example, GRU4Rec employed gated recurrent units (GRUs) to model user interests (Hidasi et al., 2015). Another avenue of research delved into the use of convolutional neural networks (CNNs) for sequential recommendation (Yan et al., 2019).

The success of attention mechanisms in natural language processing tasks has motivated its adoption in sequential recommendation. Attention-based models have shown promise in capturing complex dependencies in behavior sequences. SASRec introduced the use of unidirectional attention mechanisms to assign adaptive weights to interacted items (Kang & McAuley, 2018). BERT4Rec improved upon this approach by employing bidirectional attention mechanisms with a Cloze task (Sun et al., 2019). LSAN proposed a light-weight approach with a temporal context-aware embedding and a twin-attention network (Li et al., 2021). ASReP addressed data sparsity by leveraging a attention mechanism on revised user behavior sequences (Liu et al., 2021b). DuoRec (Qiu et al., 2022) introduces innovative techniques to improve semantic preservation and address the representation degeneration problem in recommendation systems.

Contrastive learning for recommendation

Contrastive learning (CL) has garnered significant attention in various research domains such as computer vision, natural language processing, and recommender systems. In the context of recommender systems, the focus of contrastive learning lies in optimizing mutual information between positively transformed data samples while simultaneously enhancing the discriminability of negative samples. Traditional recommender systems often rely on large amounts of labeled user behavioral data, which are often difficult to obtain and may result in subpar recommendations for new users and rare items. In contrast, contrastive learning, with its label-free self-supervised learning approach, exhibits remarkable advantages in recommender systems.

Early works in contrastive learning for recommendation focused on utilizing deep neural networks (DNNs) to enhance collaborative filtering-based recommendation leveraging item attributes (Yao et al., 2020). These models utilized a two-tower architecture to compare positive and negative samples and learn effective item representations. Another line of research employed contrastive learning within graph neural networks (GCNs) to improve collaborative filtering methods using only item IDs as features (Wu et al., 2020).

In the domain of sequential recommendation, contrastive self-supervised learning (SSL) has been utilized to capture associations among items, subsequences, and characteristics found in user behavior sequences (Zhou et al., 2020). These models adopt an end-to-end training approach, incorporating contrastive SSL throughout the entire training phase. Nonetheless, this unified training methodology facilitates information sharing between the SSL and next-item prediction tasks, eliminating the need for separate fine-tuning and pre-training stages, potentially constraining overall performance enhancement. To overcome this limitation, recent studies have proposed multi-task training frameworks incorporating a contrastive objective to improve user representations (Xie et al., 2020; Liu et al., 2021a). Furthermore, a novel approach named ICLRec, presented by Chen et al. (2022), introduces clustering techniques to extract users’ intent distributions from their behavior sequences. By leveraging clustering, ICLRec identifies distinct patterns of user intent embedded within the data.

Problem settings

Let V and U represent the sets of items and users, respectively. We denote a user $u\in U$ interaction sequence as $S_u=\{v_1,v_2,....,v_T\}$, where T is the total number of items in the sequence, and the items are ordered chronologically. Each item $v_i\in S_u$ is associated with an order index $i=1,2,...,T$, indicating its position in the sequence. Our objective is to create a prioritized list of the top K items that user $u$ is highly likely to visit in the subsequent time step T + 1.

Embedding layer

We expound on the representation of a user, denoted as $u$, and an item, denoted as $i$, through their respective embedding vectors, $e_u\in {\mathbb{R}}^d$ (for user $u$) and $e_i\in {\mathbb{R}}^d$ (for item $i$), where $d$ signifies the embedding dimension. The described process can be the creation of a parameter matrix, which operates akin to an embedding look-up table:

$$E_u=[e_{u_1},e_{u_2},...,e_{u_t}]$$

$$E_i=[e_{i_1},e_{i_2},...,e_{i_m}]$$where $t$ represents the total number of users, while $m$ corresponds to the total number of items. For the input sequence $S_u=\{v_1,v_2,...,v_n\}$, data augmentation techniques such as masking, cropping, noising, and reordering are applied to obtain two augmented sequence ${S_u}^{\mathrm{\prime }}=\{{v_1}^{\mathrm{\prime }},{v_2}^{\mathrm{\prime }},...,{v_n}^{\mathrm{\prime }}\}$ and ${S_u}^{\mathrm{\prime }\mathrm{\prime }}=\{{v_1}^{\mathrm{\prime }\mathrm{\prime }},{v_2}^{\mathrm{\prime }\mathrm{\prime }},...,{v_n}^{\mathrm{\prime }\mathrm{\prime }}\}$. Then, based on the $E_i$ table, we can acquire their embedding $E_{S_u}=\{e_{v_1},e_{v_2},...,e_{v_n}\}\in {\mathbb{R}}^{n\times d}$, $E_{{S_u}^{\mathrm{\prime }}}=\{e_{{v_1}^{\mathrm{\prime }}},e_{{v_2}^{\mathrm{\prime }}},...,e_{{v_n}^{\mathrm{\prime }}}\}\in {\mathbb{R}}^{n\times d}$ and $E_{{S_u}^{\mathrm{\prime }\mathrm{\prime }}}=\{e_{{v_1}^{\mathrm{\prime }\mathrm{\prime }}},e_{{v_2}^{\mathrm{\prime }\mathrm{\prime }}},...,e_{{v_n}^{\mathrm{\prime }\mathrm{\prime }}}\}\in {\mathbb{R}}^{n\times d}$.

Interaction graph convolution layer

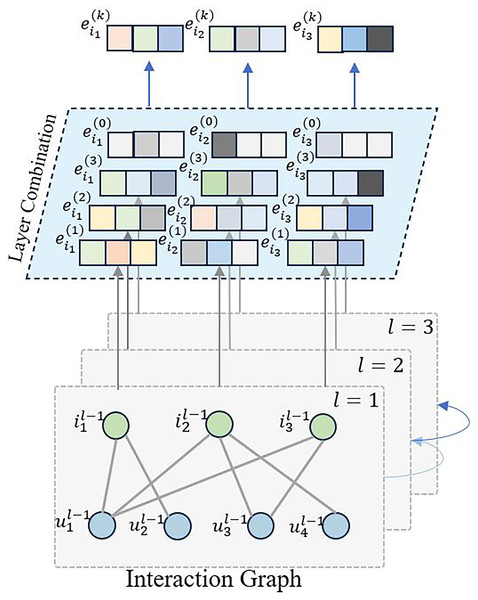
LightGCN (He et al., 2020) incorporates graph convolution neural networks into collaborative filtering, taking into account the latent relationships between users and items, as well as between items themselves. However, during prediction, it does not consider the temporal order of item sequences. Therefore, in this work, we leverage graph convolution neural networks to extract latent embedding information, with a focus on capturing the sequential characteristics of items, as illustrated in Fig. 1.

Based on the training data, we construct the user-item interaction matrix $\mathbf{R}\in {\mathbb{R}}^{t\times m}$ and the item-user interaction matrix ${\mathbf{R}}^T\in {\mathbb{R}}^{m\times t}$. With these matrices in place, we define the graph convolution network as follows:

$${\mathbf{e}}_u^{(k+1)}=\sum _{i\in {\mathcal{N}}_u}\frac{1}{\sqrt{|N_u|}\sqrt{|N_i|}}{\mathbf{e}}_i^{(k)}$$

$${\mathbf{e}}_i^{(k+1)}=\sum _{u\in {\mathcal{N}}_i}\frac{1}{\sqrt{|{\mathcal{N}}_i|}\sqrt{|{\mathcal{N}}_u|}}{\mathbf{e}}_u^{(k)}$$where ${\mathbf{e}}_i^{(k+1)}$ represents the updated representation of node $i$ in the $k+1$st iteration. The sum is taken over all the neighboring nodes $u$ of node $i$ denoted by ${\mathcal{N}}_i$. The term $\frac{1}{\sqrt{|{\mathcal{N}}_i|}\sqrt{|{\mathcal{N}}_u|}}$ is a normalization factor that accounts for the degree of nodes $i$ and $u$, and ${\mathbf{e}}_u^{(k)}$ is the representation of node $u$ in the $k$-th iteration. When $k=0$, we initialize $e_i^{(0)}=e_i\in E_i$ and $e_u^{(0)}=e_u\in E_u$. This update rule is used in graph convolution networks to aggregate neighboring node features and update the representation of each node in the graph.

As items undergo multiple graph convolutions, and the sequence model focuses solely on item sequences for recommendations, we extract only the item embedding representations for the subsequent layers. We aggregate the outputs of various convolution layers to obtain the graph embedding representation for item $i$.

$e_i^{(k)}=\frac{1}{K}{\displaystyle \sum _{k=0}^K{e}_i^{(k)}}$where K represents the number of graph convolution layers utilized in the model.

Self-attention layer

To represent the temporal order within a sequence, we employ positional embedding. Assuming the positional embedding is represented as $P\in {ℝ}^{n\times d}$, we add it to the embedding of the behavioral sequence:

$$\widehat{{\mathbf{E}}_{\mathbf{p}}}=\left[\begin{array}{c}{\mathbf{e}}_{v_1}^{(k)}+{\mathbf{P}}_1\\ {\mathbf{e}}_{v_2}^{(k)}+{\mathbf{P}}_2\\ \cdots \\ {\mathbf{e}}_{v_n}^{(k)}+{\mathbf{P}}_n\end{array}\right]{\widehat{{\mathbf{E}}_{\mathbf{p}}}}^{\mathrm{\prime }}=\left[\begin{array}{c}{\mathbf{e}}_{v_1\mathrm{\prime }}^{(k)}+{\mathbf{P}}_1\\ {\mathbf{e}}_{v_2\mathrm{\prime }}^{(k)}+{\mathbf{P}}_2\\ \cdots \\ {\mathbf{e}}_{v_n\mathrm{\prime }}^{(k)}+{\mathbf{P}}_n\end{array}\right]{\widehat{{\mathbf{E}}_{\mathbf{p}}}}^{\mathrm{\prime }\mathrm{\prime }}=\left[\begin{array}{c}{\mathbf{e}}_{{v_1}^{\mathrm{\prime }\mathrm{\prime }}}^{(k)}+{\mathbf{P}}_1\\ {\mathbf{e}}_{{v_2}^{\mathrm{\prime }\mathrm{\prime }}}^{(k)}+{\mathbf{P}}_2\\ \cdots \\ {\mathbf{e}}_{{v_n}^{\mathrm{\prime }\mathrm{\prime }}}^{(k)}+{\mathbf{P}}_n\end{array}\right]$$we incorporate self-attention mechanism and feed-forward network layers:

$${\mathbf{E}}_{\mathbf{A}}=\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\widehat{{\mathbf{E}}_{\mathbf{p}}}{\mathbf{W}}^Q,\widehat{{\mathbf{E}}_{\mathbf{p}}}{\mathbf{W}}^K,\widehat{{\mathbf{E}}_{\mathbf{p}}}{\mathbf{W}}^V)$$

$$\mathbf{F}=\mathrm{R}\mathrm{e}\mathrm{L}\mathrm{U}({\mathbf{E}}_{\mathbf{A}}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)}){\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}$$where the matrices $W^Q,W^K,W^V\in {\mathbb{R}}^d\times d$ and the matrices $Q,K,V\in {\mathbb{R}}^{n\times d}$. ${\mathbf{W}}^{(1)}$ and ${\mathbf{W}}^{(2)}\in {\mathbb{R}}^{d\times d}$ serve as parameter matrices, while ${\mathbf{b}}^{(1)}$ and ${\mathbf{b}}^{(2)}\in {\mathbb{R}}^d$ represent bias vectors. The attention mechanism is expressed as follows:

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathbf{Q},\mathbf{K},\mathbf{V})=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x} (\frac{\mathbf{Q}{\mathbf{K}}^{\mathbf{T}}}{\sqrt{d}})\mathbf{V}$$

Similarly, from ${\widehat{{\mathbf{E}}_{\mathbf{p}}}}^{\mathrm{\prime }}$ and ${\widehat{{\mathbf{E}}_{\mathbf{p}}}}^{\mathrm{\prime }\mathrm{\prime }}$, we can obtain ${\mathbf{F}}^{\mathrm{\prime }}$ and ${\mathbf{F}}^{\mathrm{\prime }\mathrm{\prime }}$.

Recommendation learning

For the output sequence $\mathbf{F}=\{f_1,f_2,...,f_n\}$ of the feed-forward network (FFN), we can compute the binary cross-entropy loss at each step of the recommendation model:

$${\mathcal{L}}_{\mathrm{R}\mathrm{e}\mathrm{c}}=-\sum _{t\in [1,2,\dots ,n-1]}\log (\sigma (f_t\cdot e_{v_{t+1}}))-\log (\sigma (f_n\cdot e_{v_{\hat{y}}}))-\sum _{t\in [1,2,\dots ,n]}\sum _{j\notin {\mathcal{S}}^u}\log (1-\sigma (f_t\cdot e_{v_j}))$$where $f_i$ represents the output of the $i$-th FFN of the model. $\hat{y}$ represents the index of the target item at position n+1 in the sequence within $E_i$. $\sigma$ denotes the sigmoid function. $e_{v_{\hat{y}}}$ signifies the embedding representation of the training label.

Instance-wise contrastive learning

For a training batch $\mathbf{B}=\{{\mathbf{F}}_1,{\mathbf{F}}_2,...,{\mathbf{F}}_b,{{\mathbf{F}}_1}^{\mathrm{\prime }},{{\mathbf{F}}_2}^{\mathrm{\prime }},\dots {{\mathbf{F}}_b}^{\mathrm{\prime }},{{\mathbf{F}}_1}^{\mathrm{\prime }\mathrm{\prime }},{{\mathbf{F}}_2}^{\mathrm{\prime }\mathrm{\prime }},\dots ,{{\mathbf{F}}_b}^{\mathrm{\prime }\mathrm{\prime }}\}$, where $b$ is the number of original sequences, and $3\cdot b$ is the total number of sequences in one batch, comprising the original sequences and their two augmented sequences, we aim to maximize the similarity between ${\mathbf{F}}_i$ and its corresponding augmented sequences ${{\mathbf{F}}_i}^{\mathrm{\prime }}$ and ${{\mathbf{F}}_i}^{\mathrm{\prime }\mathrm{\prime }}$, as well as the similarity between the two augmented sequences themselves. Additionally, we seek to minimize the similarity between ${\mathbf{F}}_i$, ${{\mathbf{F}}_i}^{\mathrm{\prime }}$, ${{\mathbf{F}}_i}^{\mathrm{\prime }\mathrm{\prime }}$, and the other sequences in the batch, thereby achieving contrastive learning. Hence, we can compute the InfoNCE loss for the batch $\mathbf{B}$:

$$L_{\text{CL}}(F_i,F_i^{\prime })=\raisebox{1ex}{$-\text{log}{e}^{(\text{sim}(F_i,F_i^{\prime }))/\tau }$}\!\left/ \!\raisebox{-1ex}{${\displaystyle {\sum }_{j=1,j\ne i}^b\left[e^{\text{sim}(F_i,F_j)/\tau }+e^{\text{sim}(F_i,F_j^{\prime })/\tau }+e^{(\text{sim}(F_i,F_j^{\prime \prime }))/\tau }\right]}$}\right.$$

$${\mathcal{L}}_{\mathrm{I}\mathrm{C}\mathrm{L}}=\sum _{i=1}^b[{\mathcal{L}}_{\mathrm{C}\mathrm{L}}({\mathbf{F}}_i,{\mathbf{F}}_i^{\mathrm{\prime }})+{\mathcal{L}}_{\mathrm{C}\mathrm{L}}({\mathrm{F}}_i^{\mathrm{\prime }},{\mathbf{F}}_i^{\mathrm{\prime }\mathrm{\prime }})+{\mathcal{L}}_{\mathrm{C}\mathrm{L}}({\mathbf{F}}_i^{\mathrm{\prime }\mathrm{\prime }},{\mathbf{F}}_i)]$$where $\mathrm{s}\mathrm{i}\mathrm{m}(\cdot )$ represents the tensor similarity function, which is used to calculate the similarity between tensors.

Prototype contrastive learning

Prototype contrastive learning aims to learn feature representations by comparing the similarity between samples and prototypes. This process makes the feature representations of similar samples closer while pushing those of dissimilar samples further apart, resulting in the formation of distinct clusters. Typically, this learning is conducted after multiple rounds of training, specifically when the instance contrastive learning loss approaches relative stability. We interpret the embedding encoding of a user’s entire sequence as the representation of their long-term interest. Generally, users with similar behavioral sequences exhibit close long-term interest embeddings. Hence, adopting prototype contrastive learning can bring the embedding encodings of similar behavioral sequences closer, placing them within the same category. This approach is advantageous for recommendation systems as it facilitates recommending similar items to users with shared interests.

We apply k-means clustering M times to the embedding representations of all user sequences in the data. For each iteration m $(1\le m\le M)$, we randomly select several points as the initial cluster centroids, denoted as $C=\{c_1^m,c_2^m,...,c_{|C|}^m\}$. After several iterations of clustering in the $m$-th run, we fix the cluster centroids. Subsequently, we define the function:

$$g({\overline{f}}_i)=\arg \underset{j}{min}d({\overline{f}}_i,c_j^m)$$where $d({\overline{f}}_i,c_j^m)=\sqrt{{\sum }_{k=1}^d{({\overline{f}}_{i,k}-c_{j,k}^m)}^2}$, ${\overline{f}}_i=\frac{1}{|{\mathbf{F}}_i|}{\sum }_{f_i\in {\mathbf{F}}_i}{f}_i$, and the function $g(\cdot )$ assists in identifying the nearest cluster centroid $c_j$ for each averaged embedding ${\overline{f}}_i$ calculated as the mean of all embeddings $f_i$ within the set ${\mathbf{F}}_i$. We leverage pre-iterated cluster centers for contrastive learning and compute the loss function as follows:

$${\mathcal{L}}_{\mathrm{P}\mathrm{C}\mathrm{L}}^m({\overline{f}}_i,c_{g_{({\overline{f}}_i)}}^m)=-\log \frac{e^{({\overline{f}}_i\cdot c_{g_{({\overline{f}}_i)}}^m)}}{{\sum }_{j=0,j\ne g_{({\overline{f}}_i)}}^{|C|}{e}^{({\overline{f}}_i\cdot c_j^m)}}.$$

$${\mathcal{L}}_{\mathrm{P}\mathrm{C}\mathrm{L}}({\overline{f}}_i)=\frac{1}{M}\sum _{m=0}^M{\mathcal{L}}_{\mathrm{P}\mathrm{C}\mathrm{L}}^m({\overline{f}}_i,c_{g_{({\overline{f}}_i)}}^m)$$

Multi-task learning

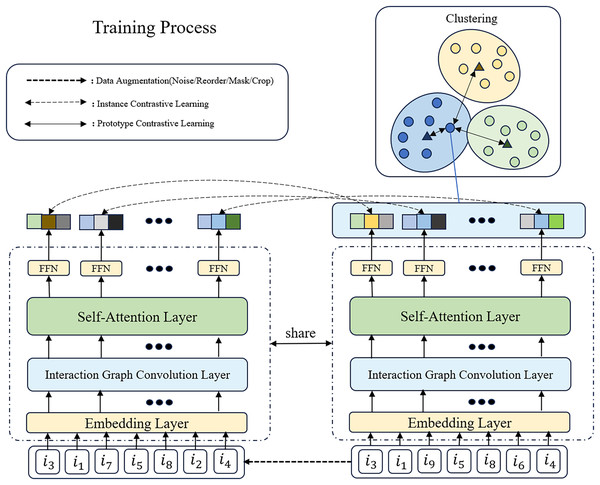
To enhance model performance, data efficiency, and generalization capability, and to address challenges such as data scarcity and overfitting, we adopt a multitask learning approach, as shown in Fig. 2, to integrate recommendation, instance contrastive learning, and prototype contrastive learning tasks. Specifically, we jointly optimize the loss functions of these tasks:

$$\mathcal{L}={\mathcal{L}}_{\mathrm{R}\mathrm{e}\mathrm{c}}+\lambda \cdot {\mathcal{L}}_{\mathrm{I}\mathrm{C}\mathrm{L}}+\beta \cdot {\mathcal{L}}_{\mathrm{P}\mathrm{C}\mathrm{L}}$$where $\lambda$ and $\beta$ are adjustable parameters used to balance the importance of the losses.

Experimental setting

Overall performance

Through the analysis of Table 2, we can observe the results obtained by various methods on different datasets. we observe that incorporating sequential patterns in user behavior sequences enhances the performance of sequential models like SASRec and Caser, surpassing the non-sequential approach BPR-MF. This highlights the significance of mining sequential patterns, with GRU4Rec also exhibiting improved results over BPR-MF in the deep learning era. Furthermore, Caser, leveraging a convolutional module to stack sequential tokens as a matrix, performs on par with GRU4Rec. Moreover, SASRec stands out as the pioneer in utilizing uni-directional attention for sequence encoding, demonstrating its superiority over previous deep learning-based models by significantly improving performance. With the rise of contrastive learning techniques in recommendation systems, BERT4Rec, S3-Rec, and CL4SRec have all leveraged contrastive learning to enhance model performance, surpassing pure sequential recommendation models. However, the two-stage training strategy employed in S3-Rec obstructs information sharing between tasks, resulting in suboptimal outcomes. On the contrary, CL4SRec consistently outperforms other baselines, showcasing the efficacy of contrastive self-supervised learning in enriching sequence representations at an individual user level. The additional objective employed by CL4SRec, entailing two distinct views of the same sequence, significantly contributes to its superior performance. Subsequently, the emergence of ICLRec method combines the advantages of previous approaches and introduces user intent extraction techniques, which also rely on contrastive learning methods, resulting in significant improvements. Finally, our proposed GSASRec model achieves even greater improvements compared to ICLRec. In contrast, we enhance the model’s representational capacity by leveraging graph convolutional techniques on the user-item interaction graph. Moreover, we perform multiple prototype clustering to mitigate noise interference and introduce a data augmentation method for instance-based contrastive learning.

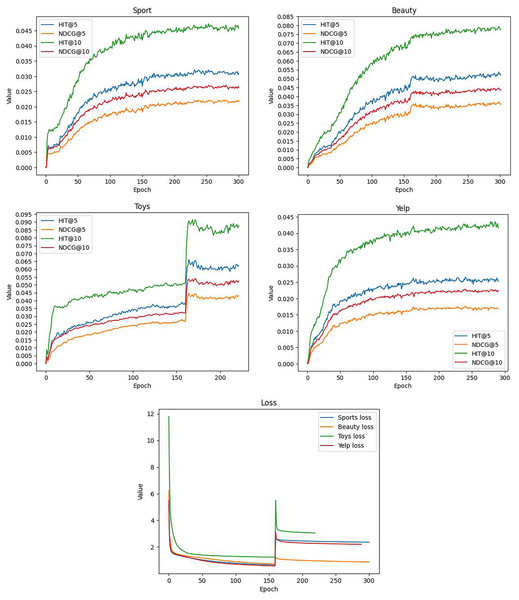
Figure 3 presents the model’s performance at each epoch. It is important to highlight that we introduced the prototype contrastive learning loss at epoch 160, as depicted in Fig. 3E. This led to a noticeable increase in the computed loss values, resulting in distinctive fluctuations and an overall upward trend in the curves, particularly evident in the Toys (Fig. 3C) and Beauty (Fig. 3B) datasets.

Ablation study

Impact of parameters $\lambda$ and $\beta$

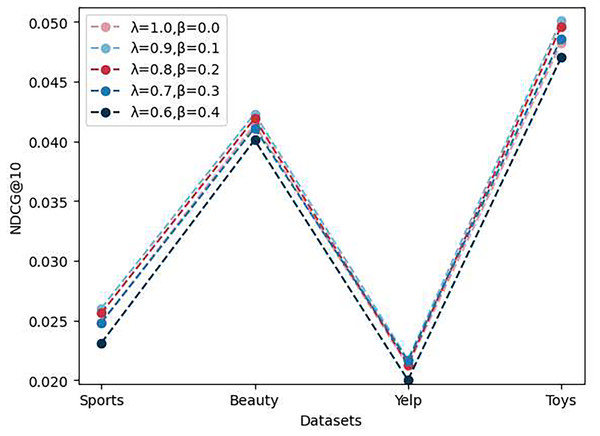
As shown in Fig. 4, to evaluate the impact of loss function weights on the model’s performance, we conducted experiments with multiple sets of $\lambda$ and $\beta$ values and assessed the model’s NDCG@10 performance on four different datasets. The results indicate that the model performs best when $\lambda$ is set to 0.9 and $\beta$ to 0.1. However, when $\beta$ is set to 0 or greater than 0.1, the model’s performance deteriorates. We attribute this to the introduction of the prototype contrast loss, which results in the prototype contrast loss value becoming much larger than the instance contrast loss value after a certain number of epochs. Consequently, the model overly emphasizes the prototype contrast task and does not continue to optimize the sequence recommendation task and the instance contrast task. Therefore, it is necessary to reasonably reduce the weight of the prototype contrast task.

Impact of model components on recommendation performance

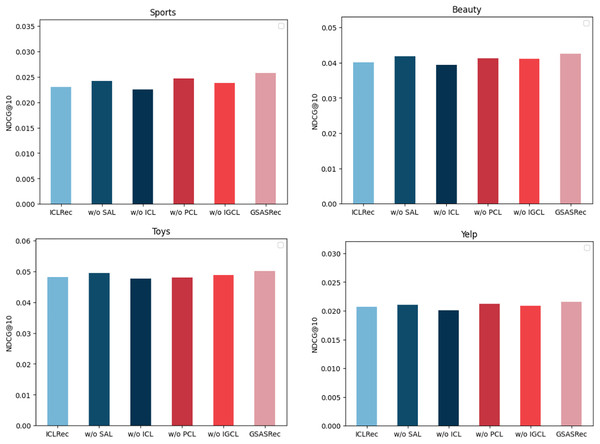
To validate the effectiveness of various model architectures and methods thoroughly, we conducted comprehensive ablation experiments on four diverse datasets, leveraging the widely accepted NDCG@10 metric for evaluation. The conducted ablation experiments involved systematically removing specific functionalities from our proposed model, GSASRec, in order to gauge their individual contributions to the overall performance.

In Fig. 5, we present the insightful results obtained from these ablation experiments. Each abbreviation in the figure represents a specific functionality removed from the GSASRec model. ‘w/o’ stands for ‘without,’ indicating the absence of the corresponding functionality. Specifically, ‘ICL’ represents Instance-wise contrastive learning, ‘PCL’ refers to prototype contrastive learning, ‘IGCL’ signifies the interaction graph convolution layer and ‘SAL’ denotes the self-attention layer, when the self-attention layer is removed, we employ the embeddings of individual items obtained from the graph convolution layer (GCL) as the objects for contrastive learning. Additionally, we employed ‘ICLRec’ as the baseline model, representing the best-performing model from the instance-wise contrastive learning methods. The outcomes of the ablation experiments are highly informative. It is evident that instance-wise contrastive learning has a substantial and positive impact on the model’s overall performance, indicating its crucial role in enhancing recommendation accuracy. Following closely is the self-attention layer, which also demonstrates its significance in contributing to improved recommendation results. Moreover, the results highlight the importance of prototype contrastive learning, particularly for the Toys dataset, where it exhibits a noteworthy influence on enhancing recommendation performance. This observation emphasizes the versatility of our proposed model across different datasets and the potential of prototype contrastive learning in addressing specific domain challenges. Furthermore, the interaction graph convolution layer stands out as a significant component in our model, consistently leading to substantial performance improvements across all the evaluated datasets. This finding underlines the efficacy of incorporating graph-based interactions to capture complex relationships between users and items, reinforcing the importance of leveraging graph-based learning methods in recommendation systems.

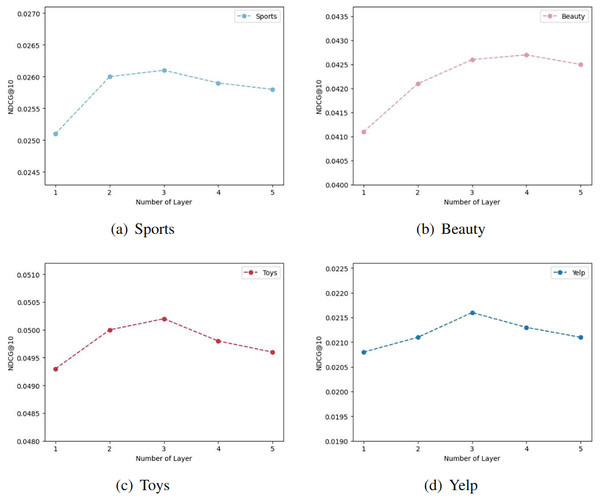
Impact of layer combination

In our model, we aggregate the outputs of k convolutional layers to obtain the embedding representation. The choice of different k values significantly influences the effectiveness of the model’s embedding representation. Figure 6 illustrates the effects of varying convolutional layer depths on four distinct datasets. The term ‘Number of Layer’ corresponds to the upper limit of k values in the model. The curve trends in the figure are generally consistent, with the model’s performance peaking at the third layer in most cases. However, for the Beauty dataset (Fig. 6B), the performance of the four-layer graph convolutional network slightly outperforms that of the third layer. Consequently, we can infer that the suboptimal performance for k values below three may stem from the model’s inability to fully capture the complex relationships and features present in the graph data. Shallow graph convolutional networks might be limited in their ability to propagate information among local neighbor nodes, making it difficult to capture global structures and longer-range dependencies. As the number of convolutional layers increases, the model progressively expands its receptive field, utilizing more extensive graph structure information for feature propagation and learning. Nevertheless, excessively deep networks may encounter issues of vanishing or exploding gradients, leading to a plateau in model performance beyond 3 or 4 layers.