Abstract

Methods

Unfolded Ensembles. The protein sequence-culling server pisces (41) is used to select x-ray structures of the 2,020 chains of >20 residues with a maximum R factor of 0.3 and a resolution of better than 2 Å. A coil library is constructed from these proteins by retaining only internal residues within stretches of four or more residues that lie outside of helices, sheets, and turns (25). End effects are reduced by removing residues adjacent to structured regions. Unfolded conformations are built by initially assigning each residue to one of five Ramachandran basins (α_R, β, PPII, α_L, and γ; see Fig. 6, which is published as supporting information on the PNAS web site) based on their frequencies in the coil library.

A residue's basin frequencies depend on the identity and conformation of the neighboring residues. However, the size of the coil library is insufficient to consider the simultaneous influence of both of the neighbors' sequence and conformation. Hence, we adopt a strategy based on pairs (dimers) of residues. The monomer basin frequencies, P(a_i, b_i), are converted into energy units by

[1]

where a_i is the identity of the ith amino acid that resides in the b_i Ramachandran basin. Similarly, the joint probability, called the dimer library, of finding two consecutive residues a_i and a_i+1 in basins b_i and b_i+1 gives

[2]

Combining Eqs. 1 and 2 enables expressing the NN correlation energy term δU(a_i, b_i, a_i+1, b_i+1) in terms of probabilities derived from the coil library

[3]

The local interactions that dominate the structure of the polypeptide chain can now be modeled by an energy function that includes first neighbor effects. An individual residue contributes U(a_i, b_i), and an additional term δU(a_i, b_i, a_i+1, b_i+1) from each of the neighbors combines to give the total statistical potential for a polypeptide with N residues

[4]

An equilibrium ensemble of peptide chains is generated from Monte Carlo simulations with this energy function. The elementary transitions consist of choosing a Ramachandran basin for randomly determined residues and then accepting or rejecting the transition according to the standard Monte Carlo criteria. Once the basins are assigned, the specific ,ψ backbone angles within the basin are selected from occurrences in the coil library for each residue type, independent of NN effects.

To remove steric overlap, the ,ψ angles are nudged within the basin of each amino acid by minimizing a simple excluded volume energy function for intrabasin relaxation with two terms. The first term is a hard sphere energy contribution for the main-chain heavy atoms (N, C^α, C, and O) and the C^β, side-chain β-carbons. This hard sphere interaction is the same as that used in the program scwrl3 (42). The second term accounts for steric interactions between main-chain atoms and the remaining side chains and involves a soft-sphere interaction that depends on the side groups through two parameters, the location of the center of mass of the side group with respect to the main-chain atoms and a “virtual” soft-sphere radius that encompasses 90% of the total volume explored by the side-chain atoms when all allowed rotameric states are sampled. We also generate an ensemble by switching off the interaction term associated with the side-chain atoms.

The long-range energy function is minimized by using a simulated annealing algorithm. The elementary transition is a change in ,ψ angles within the already assigned basin. These angles are chosen from the coil library described earlier, taking into account both the chemical and conformational identity of the given residue. Finally, side chains and hydrogen atoms are added to the chain backbone by using scwrl (42) and reduce (43), respectively.

RDC. The RDC between the amide nitrogen and proton is given by

[5]

where P₂(x) = (3x² – 1)/2. D_max contains details of the bond lengths and the magnitudes of the magnetic moments. The orientation dependence emerges through θ, the angle between the NH bond vector and the magnetic field. The proportionality factor D_max is constant for the NH bonds considered here, so we focus attention on the average of P₂.

Results and Discussion

We generate ensembles of unfolded structures for which the Ramachandran basin frequencies for each amino acid are assigned according to its identity, followed by the specification of the explicit ψ, angles obtained from the PDB. The basin assignment either uses or neglects information on the chemical and conformational identity of neighboring residues. A comparison of these ensembles for several protein sequences with experimental data provides insight both into the ability of these ensembles to recapitulate the experimental results as well as the importance of NN effects.

Radius of Gyration. Polypeptide dimensions often follow a simple scaling law for a long polymer with N monomers, R_g = aN^b, where the prefactor a depends on local structure, and the exponent b depends on solvent quality. The exponent b is ≈1/3 for collapsed polymers (poor solvent conditions), ≈0.6 in good solvent conditions, and ≈1/2 in ideal θ solvents. More recent and reliable experimental values are a = 2.04 ± 0.17Å and b = 0.59 ± 0.01, obtained by using small-angle scattering for a set of 28 unfolded proteins (8). Because our model incorporates excluded volume constraints, accurate estimates are expected for the exponent b, but the prefactor a is more sensitive to the details of local structure.

Unfolded ensembles of 10 proteins are generated separately with and without inclusion of NN effects (Fig. 1). Generally, the R_g values from our models are ≈10% larger than the experimental values. When NN interactions are neglected, we obtain a = 2.7 ± 0.4 Å and b = 0.57 ± 0.03 (data not shown). The agreement with experiment improves slightly when NN interactions are included (a = 1.9 ± 0.3 Å and b = 0.64 ± 0.03). When side-chain interactions are ignored in the simulated annealing step, more compact conformations are found, with a = 2.35 ± 0.3 Å and b = 0.58 ± 0.02. The exponent b is nearly the same in all of the cases, as anticipated for any self-avoiding random-walk model at large enough length scales.

Open in a separate window

Fig. 1.

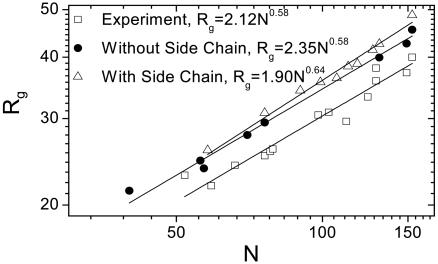
Global conformation. The radius of gyration (R_g) vs. the number of residues (N) for 10 proteins is computed for an unfolded ensemble generated with and without NN effects. The data in both cases are fit to R_g = aN^b. Values are shown for the following: Ub (76 aa, PDB ID code 1UBQ, 16,000 structures), apoMb (153 aa, PDB ID code 1BVC, 5,000 structures), eglin C (70aa, PDB ID code 1CSE, 5,000 structures), and the staphylococcal nuclease (Snase, PDB ID code 1SNQ, 5,000 structures) fragment Δ131Δ, composed of residues 10–140, Calcyclin (Rabbit, Ca²⁺, PDB ID code 1a03, chain A, 90 aa, 1,000 structures), Ig light and heavy chains (PDB ID code 43c9, chains C and B, 113 and 118 aa, 1,000 structures of each), ileal lipid-binding protein (PDB ID code 1eio, chain A, 127, 1,000 structures), bovine pancreatic trypsin inhibitor (PDB ID code 1BPI, 58 aa, 1,000 structures), and B*5301(PDB ID code 1a1o, chain B, 99 aa, 1,000 structures). Dividing the ensembles in half yields essentially identical results.

Comparison with Experimental RDC Patterns. Considered individually, random walks are anisotropic even though the ensemble average is isotropic (44). The principal axes for each unfolded conformation are determined by diagonalizing the moment of inertia tensor. For simplicity, the degree of alignment of all molecules is assumed to be the same, although it may in reality be higher for configurations with higher aspect ratios (ARs). This hypothesis is tested below by calculating RDCs with all of the conformations weighted by varying powers of their ARs, ARⁿ. The major axis is aligned parallel or perpendicular to the direction of stretched or compressed gel channels, respectively. The orientation of the NH bond vector is evaluated relative to the magnetic field.

In practice, evaluating the RDCs for any residue involves two averages. The first average is over all orientations of the molecular axis with respect to the magnetic field for each conformation, whereas the second average is over the ensemble of different chain conformations. The first average yields the value of P₂ for a perfectly aligned chain, multiplied by a factor Δ that describes the average degree of departure from perfect alignment of the principal axis with respect to the magnetic field for each individual chain conformation. Because Δ depends on the nature of the aligning medium, which is poorly understood, we assume Δ to be a constant overall scale factor that is chosen empirically in comparisons between calculated and experimental RDCs. For the proteins investigated, we obtain 100 ≤ D_maxΔ ≤ 800, and Δ increases with protein length, suggesting a common alignment mechanism.

We provide a detailed analysis for apomyoglobin (apoMb), ubiquitin (Ub), the Snase fragment Δ131Δ, and eglin C, whose RDCs have been measured in weakly aligning media under chemically denaturing conditions (1, 10, 29). Although computations have been performed for magnetic fields parallel and perpendicular to the principal molecular axis, the results for Ub and eglin C are only presented for perpendicular alignment, whereas apoMb and Δ131Δ are described by using parallel alignment, corresponding to the experimental conditions of stretched or compressed gels, respectively. Geometrically, upon averaging over all possible molecular rotations about the major axis, the RDCs for a parallel molecular alignment are –1/2 times those for a perpendicular alignment, as observed in apoMb (29).

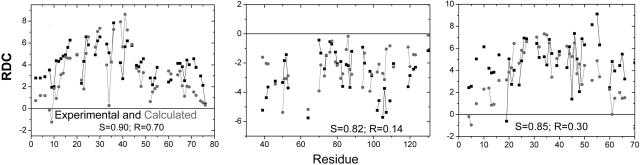
The computed RDCs for the amide NH vectors of the four proteins are almost always of a single sign (Figs. ​(Figs.22 and ​and3).3). Particularly for apoMb and Ub, the computed variation agrees with the irregular pattern observed experimentally. In contrast, the D_NH values for an idealized, uniform random-flight polypeptide are similar for all residues, except for a decreased correlation with the molecular axis for residues closer to the ends (33), which produces a V-shaped curve (Fig. 2C). The calculated and measured RDC patterns of real proteins, however, deviate considerably from this smooth, idealized curve, exhibiting significant residue-to-residue variation. This variation indicates the existence of local structural correlations in unfolded proteins that an idealized random-flight polypeptide fails to capture.

Open in a separate window

Fig. 2.

Local conformation. (A) Calculated (gray) and experimental (black) RDCs for apoMb in 10% acrylamide (29). The calculated RDCs are obtained by averaging 5,000 structures generated by using a PDB-based statistical potential derived from the coil library and excluded volume constraints. RDCs are calculated without (Left) and with (Right) NN effects on backbone conformations. RDCs are presented for all of the residues except prolines and those for which there are no NH resonances. Scale factor is defined as D_maxΔ. S is defined as dot product of the two RDC patterns (Eq. 6). (B) RDCs for an idealized random ensemble generated without NN effects for ALA₅₀ polypeptide [with equal probabilities (1/3) for the three major basins].

Open in a separate window

Fig. 3.

Comparison of calculated (gray) and experimental (black) RDCs for ensembles with NN correlations for chemically denatured Ub (Left), eglin C (12% acrylamide; Right) (10), and Δ131Δ (12% acrylamide; Center) (1).

The ensemble generated by using our coil library captures the local interactions remarkably well as it successfully mimics the relative residue-to-residue variation for apoMb and Ub and, to a lesser extent, elgin C and Δ131Δ (Figs. ​(Figs.22 and ​and3;3; the scatter plot of calculated and observed RDC values is provided in Fig. 7A, which is published as supporting information on the PNAS web site). In addition to providing the Pearson coefficient for the scatter plots, we provide a measure that reflects correlations in the alignment of neighboring residues with respect to the global alignment. This measure is the dot product of the calculated and observed RDC patterns

[6]

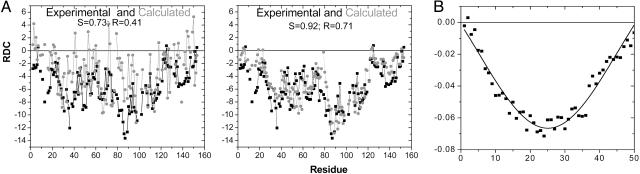
where i is the residue index. A quantitative estimate of the correlations between the calculated and experimental data are obtained by comparing S values with the mean and standard deviation (SD) for a randomized distribution obtained by independently shuffling the order for both the observed and calculated RDCs. The observed S values for apoMb, Ub, elgin, and Δ131Δ are 8, 5, 2, and 1.5 SDs above the mean of their respective random distributions. It is unclear why apoMb exhibits the best agreement, although differences in the acrylamide percentage are known to alter RDC patterns (28), suggesting that the experimental conditions of apoMb best match our model.

The agreement between the calculated and observed RDC pattern gets poorer when NN effects are neglected for apoMb (R = 0.71 → 0.41, S = 0.92 → 0.73; Figs. ​Figs.22 and 7B) and the other proteins (data not shown). This result stresses the importance of correlations in the unfolded state associated with the chemical and conformational identities of neighboring residues.

The preference for extended conformations and the global alignment along the long axis of the chain results in nearly all of the RDCs having the same sign (Figs. ​(Figs.22 and ​and3).3). The sign depends only on whether the gel is compressed or stretched. Backbone NH vectors of residues in the β and PPII conformations are oriented nearly perpendicular to the long axis, whereas those in the α conformation are oriented nearly parallel. The magnitude of the RDC is proportional to P₂(cosθ), which reflects the orientation of the bond vector relative to the applied magnetic field, assumed for now to be parallel to the long molecular axis. In such geometries, the extended and α conformations have P₂(cosθ) ~ –1/2 and 1, respectively. Accordingly, the average value of the angular term can be roughly approximated by using their relative probabilities, P₂(cosθ) ~ –1/2(P_β + P_PPII) + (P_α). Because the frequencies of the two extended conformations generally exceed those for helical conformers by >2:1 for nearly all residues in our coil library (P_β:P_PPII:P_α = 33:36:27), RDCs are mostly negative in this geometry. Conversely, in compressed gels where the alignment is perpendicular to the principal axis, nearly all RDCs are positive, as observed and computed.

Different Libraries. To test the robustness of our model, we compute the RDCs for apoMb by using four additional libraries with very different conformational frequencies. Agreement with experiment worsens when the ensemble is based on entire PDB library, which is dominated by α conformers (Fig. 4A; P_β:P_PPII:P_α = 27:18:53). Even the signs of the computed RDCs no longer agree because of the dominance of α conformers. We also computed the RDCs from a library of all residues outside helices (Fig. 4B; P_β:P_PPII:P_α= 43:27:26). Although the relative frequencies of β and PPII conformers have nearly inverted, their sum is similar to that in our coil library. As a result, the correlation between computed and measured RDCs is similar to the original correlation. The correlation degrades slightly if turns are also included (Fig. 4C; P_β:P_PPII:P_α= 23:33:37) because of higher α frequencies. The agreement improves for the fourth library that comprises residues outside helices, sheets, and turns but includes the biased terminal residues of the remaining fragments (Fig. 4D; P_β:P_PPII:P_α = 32:42:22). Overall, the best correlation is obtained with our original coil library, but reasonable good agreement also emerges for the other libraries in which the fraction of extended conformers is similar.

Open in a separate window

Fig. 4.

Alternative libraries for generating unfolded ensembles. Calculated (gray) and experimental (black) RDCs for apoMb. The calculated RDCs are obtained by averaging 5,000 structures generated by using four different PDB-based statistical potentials that incorporate NN effects and excluded volume constraints. The 3D plot in each image is the probability distribution in the Ramachandran plane for each of the libraries. The axes pointing to left and right are ψ and angles, respectively.

The NMR experiments are conducted with proteins residing in a concentrated denaturant solution, which stabilizes nonnative conformations. Our coil library is culled from high-resolution crystal structures and refers to irregular conformations in a “protein-like environment.” In the coil library, extended PPII and β backbone conformations dominate over the bent α conformers, in accord with experimental results for peptides where substantial amounts of PPII are observed (24, 45–47). The preference for extended over α conformations might even be enhanced under denaturing conditions where the protein is in good solvent conditions because of the increased backbone exposure of β and PPII conformers (18).

The unfolded ensemble produced with the coil library lacks hydrogen-bonded structures. There are very few stretches of four or more α conformers, which could constitute authentic helical structures. This situation is well-matched to experiment; little residual structure likely exists in the chemically denatured states (18) of the four proteins. Under acidic denaturing conditions, however, some helical structure is present in apoMb (29) and acylcoenzyme A binding protein (ACBP) (11). The change from extended to helical geometry equates to an ≈90° rotation in the average N–H direction relative to the long axis, as a result of which the observed RDCs change, sometimes even switching sign. Therefore, our coil library best represents the denatured state of a protein in high denaturant concentrations where the protein is devoid of significant residual hydrogen-bonded structure.

Stretched Conformations Dominate the RDC Signal. We investigate whether a correlation exists between the magnitude of the RDCs and the AR of the individual members in the ensemble of unfolded state proteins. High ARs are expected for individual chains in any random-walk model even though the ensemble average is spherical (33, 44). The AR is defined as , where I_x, I_y, and I_z are the moments of inertia for the given conformation in ascending order.

For Ub's unfolded ensemble, we partitioned the AR distribution into three nearly equal fractions, AR ≤ 2, 2 < AR < 2.5, and AR ≥ 2.5 (Fig. 5). As the AR increases, the RDCs increase in magnitude, although the residue-to-residue pattern remains largely unchanged. The most extended third contributes ≈60% of the ensemble's average signal. These most stretched members of the ensemble have the largest β and PPII percentages.

Open in a separate window

Fig. 5.

AR and RDCs. Shown are AR distribution for the 16,000 chains comprising the unfolding ensemble of Ub. The ensemble is partitioned into three nearly equal fractions, AR ≤ 2, 2 < AR < 2.5 and AR ≥ 2.5. Representative conformations are shown for each partition. Overlay of the computed RDCs for each of the three portions of the ensemble (black) and the average for the total ensemble (gray) are shown.

We calculate the RDCs assuming a common degree of alignment for all molecules. However, molecules with higher ARs should align more strongly. Accordingly, we apply an empirical weighting scheme, alignment ARⁿ, but find a negligible improvement between calculated and experimental RDCs (e.g., apoMB, R = 0.71 → 0.73 for n = 0 → 5).

The computed RDCs are of a single sign because of the prevalence of extended conformations in the coil library and the global alignment of the entire chain. Wright, Dyson, and coworkers (29) proposed a similar view for apoMb in that the RDCs originate from transient alignment of short segments composed of extended conformations, although no detailed calculations are presented. To test their assertion, we calculate RDCs by using the local alignment for each of the four major segments of unfolded apoMb identified in their study (results not shown) or alternatively by averaging over every possible seven residue window (the average persistence length of a polypeptide). The agreement with experiment is worse than when calculations assume alignment of the entire chain (see Fig. 8, which is published as supporting information on the PNAS web site). Therefore, the global chain alignment used our study is more probable.

Lack of Native-Topology in Unfolded State. For the 5,000 members of Ub's unfolded ensemble, the average contact matrix lacks the native topology (see Fig. 9, which is published as supporting information on the PNAS web site). Visual inspection of the Ub conformations highlights their lack of native topology (Fig. 5). Therefore, it is unlikely that native topology persists in the unfolded state for proteins whose experimental RDC pattern our model can recapitulate.

Furthermore, chain configurations with the highest ARs contribute most of the computed RDC signal. These extended configurations have more than twice the number of β plus PPII vs. α conformers. This argument probably applies to the experiments as well. In the presence of denaturant and confinement to the narrow channels of the aligning medium, extended conformations may be further favored. Hence, RDC values arise from conformations that are less likely to reflect the topology of a (compact) native protein.

The previously observed correlation between experimental RDCs in the native state and in the unfolded state is weak for elgin (10). More importantly, the RDCs in these two states represent contributions from completely different sets of backbone angles. The native protein yields both positive and negative RDCs because the helical and sheet elements do not necessarily align with the molecular axis. However, RDCs in the unfolded state are almost always of a single sign, originating from the preponderance of extended conformations that align along the molecular axis. Thus, it is difficult to conceive that the native and unfolded states could have similar topologies.

Shortle et al. (1, 10, 28) have analyzed RDCs to argue for the presence of a native-like organization of chain segments in unfolded proteins. Their original study (1) presents a correlation between RDCs of Δ131Δ in 8 M urea and in water. Although the correlation does not extend to the native state, Δ131Δ was deduced to have native topology based on independent distance constraints between numerous extrinsic spin labels (48, 49). Of the four proteins investigated, Δ131Δ exhibits the poorest agreement with our model. The deviation is greater for Δ131Δ in aqueous solutions (data not shown), suggesting that Δ131Δ deviates from statistical coil behavior. Hence, this molecule may have native topology. However, its RDCs are mostly negative, indicating the backbone predominantly is in either a β or PPII conformation, whereas the native structure contains both helices and sheets across this portion of the Snase sequence.

Implications for Computer Simulations. The two common initial conditions for folding simulations are a completely extended or thermally denatured chain. Because both initial choices are unphysical, significant amounts of computer time must be spent to thermalize the system. This issue is most relevant to distributed computing methods, where numerous trajectories must be individually equilibrated, taking up a large fraction of each trajectory. Furthermore, the initial configuration could even drive the protein down an otherwise unpopulated folding pathway. Thus, a physically realistic configuration for the unfolded state, such as our model, should save computational resources while increasing accuracy.

Conclusions

Various models agree with experimentally determined dimensions of the unfolded state. However, this criterion is insufficient to conclude that the unfolded state is a statistical coil. RDCs provide a local, and more sensitive, measure of structure and, therefore, a much more stringent test. Our statistical coil model using the backbone frequencies observed in a restricted coil library, along with excluded volume repulsions, reproduces both the known coil scaling behavior for the R_g and, more importantly, compares remarkably well with the experimental RDCs for chemically denatured proteins. The RDC values are dominated by high AR chain configurations, which are predominantly composed of PPII and β conformers. No evidence for native-like topology exists in this configuration or any subset of the ensemble. Hence, the model resolves the so-called “reconciliation problem,” because the model accurately accounts for the presence of local structure in unfolded states while retaining random coil scaling (14).

The statistical coil model implies that a Levinthal-like number of denatured conformations exists, although correlations between neighboring residues reduce this number to some extent (35, 36). Local sterics generally are too weak to generate persistent structure or native-like topology or to reduce significantly the conformational entropy in the unfolded state. Nevertheless, the locally encoded backbone can bias the conformational search toward native-like elements and thereby reduce the Levinthal paradox. In combination with tertiary context, local sterics determine the structure and stability of the native state.

Supplementary Material

Acknowledgments

Notes

Author contributions: A.K.J., K.F.F., and T.R.S. designed research; A.K.J., A.C., K.F.F., and T.R.S. performed research; A.K.J., A.C., K.F.F., and T.R.S. contributed new reagents/analytic tools; A.K.J., A.C., T.R.S., and K.F.F. analyzed data; and A.K.J., K.F.F., and T.R.S. wrote the paper.

Abbreviations: apoMb, apomyoglobin; AR, aspect ratio; NN, nearest neighbor; PDB, Protein Data Bank; PPII, polyproline II; R_g, radius of gyration; RDC, residual dipolar coupling; Ub, ubiquitin.

References