Abstract

Methods

Theory of Confinement-Induced α-Helix Formation. The thermodynamic equilibrium between the helix and the coil states of a polypeptide chain is determined by the difference in the Gibbs free energy between the two

[1]

where U_helix (U_coil) is the enthalpy of the helix (coil) state and S_helix (S_coil) is the entropy of the helix (coil) state. For simplicity, we normalize all quantities by a, the unit of length, which is set to the average C^α distance (≈3.8 Å), and calculate energy per residue. The difference between the two enthalpic terms is mainly due to the formation of hydrogen bonds between residues i and i + 4 in the helix state. If ΔG_hc < 0, the helical state is thermodynamically stable, whereas for ΔG_hc > 0 the coiled state is the more stable one. Confinement of the polypeptide within a cylinder with inert walls does not affect the enthalpic terms in Eq. 1. Thus, ΔG_hc changes upon confinement only because of changes in the entropy of the helix and coil states. As can be seen in Fig. 1, the confinement-induced reduction in the number of allowed conformations of the coil state is far larger than that of the (less flexible) helix state. We model the change in the coil-configurational entropy, ΔS_coil, using the energy cost per unit length of a confined self-avoiding random walk (SAW) (15)

[2]

where D is the cylinder diameter, α₀ is a constant on the order unity, and R is the universal gas constant. For the helical state we use the results of Lamura et al. (16), who showed that the entropy cost per unit length of a helical polymer with persistence length l_p, pitch p, and diameter d₀ is the same as that of a semiflexible chain with an effective persistence length , where , confined in a cylinder with effective diameter D_eff, D_eff D – d₀ for P « D and D_eff ≈ D for p » D

[3]

where A₀ 2.375 (17). In our model α-helix p ≈ 2.1 and d₀ ≈ 1.3, so that ξ ≈ 0.45. Because in our simulations p is neither much larger nor much smaller than D, we set D_eff D – f·d₀, where 0 ≤ f ≤ 1 is a free parameter.

Open in a separate window

Fig. 1.

Confinement effects on conformational entropy of a polypeptide chain. In the coiled state, confining the peptide to a cylinder of diameter D << R_F (where R_F is the Flory radius) excludes many configurations shown as gray lines. On the other hand, the rigid α-helix for which D « l_p (where l_p is the α-helix persistence length) loses only a few conformations, which makes the loss in entropy much smaller.

Using Eqs. 2 and 3 the confinement-induced change in the energy difference between helix and coil states, ΔΔG_hc, becomes

[4]

where α₀, f, and l_p are free parameters, and T is the temperature. For an infinitely rigid α-helix, l_p → ∞, we expect f → 1, and hence ΔΔG_hc/RT = –α₀D^–5/3 for D > d₀ and ΔΔG_hc/RT > 0 for D ≈ d₀. Thus, the helical state is entropically stabilized by confinement as long as D > D* ≈ d₀. For an α-helix with a large but finite persistence length, ΔΔG_hc < 0 for large D and increases sharply as D < D*. Therefore, for a peptide that is unstable in solution, cylindrical confinement may render the helix state thermodynamically stable.

The arguments given above ignore intermediates that must be included in light of the noncooperative nature of the helix–coil transition (18–20). To incorporate intermediates into our theory, we use a simple model (21) in which each residue has two possible states, helix or coil, with thermodynamic weights u and v, respectively. The overall weight (i.e., the unnormalized probability) for a particular conformation is given by the product of the individual weights. Because of the lack of interactions between residues in this model, the average helical content, i.e., the average fraction of helical residues, is just θ = u/(v + u) ≡ s/(1 + s) where s ≡ u/v. The Gibbs free energy of Eq. 4 is introduced into the model by writing s_c = s_bulk exp(–ΔΔG_hc/RT), with s_c and s_bulk the values of the parameter s in confinement and in bulk, respectively. Thus one gets for the confined peptide

[5]

Because θ is a monotonically increasing function of s_c, and since ΔΔG_hc < 0 for D > D*, it follows that the helical content should increase upon confinement.

Off-Lattice Simulations. We studied numerically the effect of confinement on α-helix formation by performing Langevin dynamics simulations. A coarse-grained representation of the polypeptide chain was used, in which only the positions of the C^α carbons are retained, and each residue is either hydrophobic (B) or hydrophilic (L) (22). Most simulations were conducted with an N = 16 residue sequence L(LBLLBBL)₂L, but we also performed simulations with N = 9 [LLBLLBBLL], N = 30 [L(LBLLBBL)₄L], and N = 47 [L(LBLLBBL)₆LBLL]. The hydrogen bonds between the backbone carbonyl oxygen CO and the amine hydrogen NH groups were mimicked by using virtual moieties located between backbone α-carbons (19). The potential energy of a conformation, represented by the set of α-carbons positions {} (i = 1, 2,..., N), was E({}) = V_BL + V_BA + V_DIH + V_HB + V_NON + V_CYL, where V_BL, V_BA, V_DIH, V_HB, and V_NON are bond-length potential, bond-angle potential, dihedral angle potential, hydrogen-bond potential, nonbonded long-range potential, and cylindrical-confinement potential, respectively. The forms of the potentials V_BL, V_BA, V_HB, and V_NON are given in ref. 19. We used the dihedral angle potential V_DIH

[6]

where A₁ = B₁ = C₁ = ε_h. The unit of energy in our simulations, ε_h, (≈1.2 kcal/mol), corresponds to the minimum of interaction potential of two B residues. This form of the dihedral angle potential leads to a stable four-helix bundle in the bulk (23), but an isolated α-helix is unstable (19). We chose this destabilized model to test whether confinement inside a cylinder can shift the thermodynamic equilibrium of this model polypeptide.

For all simulations in confined space, we used a confining potential with cylindrical symmetry, V_CYL,

[7]

where D is the cylinder diameter, and is the distance of residue i from the z axis. The strength of the confinement potential (ε_W) is taken as ε_W = 100ε_h. All simulation observables were normalized by the unit of length a (≈3.8 Å). Temperature was measured in units ofε_h/R.

We used simulated annealing to perform simulations in the bulk (i.e., without V_CYL) and in cylinders with varying D, carrying out 60 runs under each condition. Each annealing simulation was preceded by heating the polypeptide chain to T = 4 followed by a temperature quench to T = 1.2 to randomize the initial conditions. The temperature was then lowered by 0.02 every 1,000,000 time-steps, where each time-step (τ) is ≈3 ps (19). After each temperature change the system was equilibrated for 500,000 steps before collecting the averages of physical observables. Simulations were performed by using the velocity form of the Verlet algorithm at a value of friction coefficient ζ = 0.05τ^–1 and a time integration step h = 0.005τ. All thermodynamic averages were calculated by using the multiple histogram method (24).

Analysis. To evaluate the state of the polypeptide chain during the simulation we calculated the number of helical dihedral angles (n_HD) for each saved configuration. A dihedral angle was considered to be helical if it deviates by at most δ ≈ 10° from its value in the helix state. The helical content θ of a conformation was defined as θ = n_HD/(N – 3), where N – 3 is the total number of dihedral angles. The folding temperature T_f was determined by the condition θ _Tf, where ... _T is the thermodynamic average at temperature T, and θ is the average helical content.

Results

Cylindrical Confinement Induces α-Helix Formation. Comparison of the temperature dependence of θ for a peptide in the bulk and in cylinders with decreasing D shows a substantial increase in θ as D decreases (Fig. 2a Inset). At a fixed temperature T = 0.5, corresponding to ≈300 K, θ increases by as much as 17% when going from bulk to D = 1.3 (Fig. 2a), which is essentially the native α-helix diameter. It is surprising to find such a large increase, especially because the sequence is inherently unstable in the bulk. Below D = 1.3 the helix becomes too large to fit inside the cylinder, and θ decreases sharply. When D ≤ 1, α-helix formation does not occur even at very low temperatures. The folding temperature T_f exhibits a similar behavior, increasing from ≈285 K in the bulk to ≈360 K for D = 1.3 and decreasing abruptly as D decreases (Fig. 2b). Thus, our model α-helix, which does not fold in the bulk at ambient temperature (i.e., T ≈ 300 K), can readily fold when confined inside a cylinder with D > D* ≈ 1. Below D*, however, there is an abrupt destabilization of the helix as the polypeptide undergoes a helix-stretched coil transition. These results are in qualitative accord with the theoretical arguments presented above.

Open in a separate window

Fig. 2.

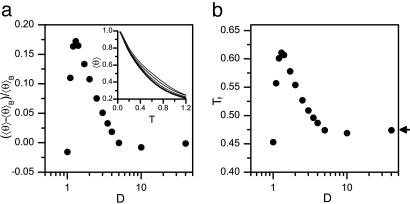
Confinement-induced α-helix formation. (a) Change of mean helical content θ of an N = 16 helix model relative to mean helical content in the bulk θ _B, as a function of cylinder diameter at T = 0.5 (≈300 K). For D > 1.3 θ is larger than in the bulk, i.e., the α-helix is stabilized by the cylinder. Below D ≈ 1.3, θ decreases sharply. (Inset) Temperature dependence of θ in the bulk (thick line) and in cylinders of diameter D = 3, 2, 1.4 (thin lines, bottom to top). (b) The folding temperature T_f as a function of D. T_f increases remarkably up to D ≈ 1.3. Arrow indicates folding temperature in the bulk.

Although thermodynamic stability increases upon confinement, the transition becomes less cooperative as D decreases, as observed in the more gentle decay of θ with increasing temperature. This finding is consistent with previous studies of protein folding in various confining geometries (25, 26), which showed that folding cooperatively decreases in restricted spaces.

To further investigate the origin of confinement-induced α-helix formation, we analyze our simulation results by using the theoretical model (see Methods). We calculate from the simulations the distribution of the number of helical dihedral angles n_HD at T = 0.5 in the bulk and for various values of D. We then fit this value to the distribution function P(n_HD) of our theoretical model

[8]

where N_D = N – 3 is the total number of dihedral angles. An example of such a fit is shown in Fig. 3 Inset. From the ratio between s_c for a peptide confined in a cylinder of diameter D and s_bulk calculated from a simulation in the bulk we compute the free energy difference ΔΔG_hc as a function of D (Fig. 3). We find that the D-dependence of ΔΔG_hc is well fitted using Eq. 4. The persistence length obtained from the fit is l_p = 230 ± 72. This value agrees well with a recent calculation of the elastic properties of long α-helices (27), which predicted l_p ≈ 263 (=100 nm), although other authors quote a somewhat smaller number (28). Thus, entropic interactions are sufficient to account for the thermodynamic stabilization of the helical state under cylindrical confinement observed in our simulations.

Open in a separate window

Fig. 3.

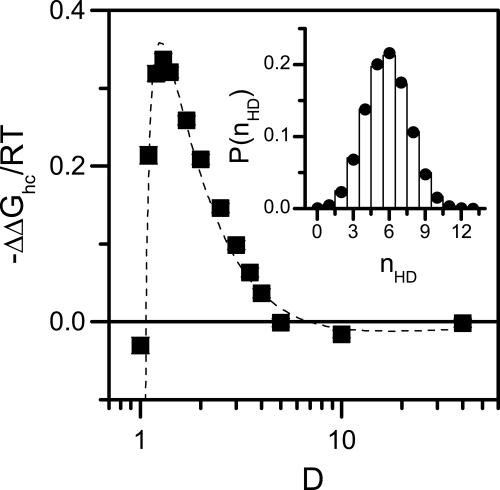
Helix stabilization is entropic in nature. The change in the Gibbs free energy difference between helix and coil states, ΔΔG_hc, as a function of D at T = 0.5. α-Helix formation is favored when D is larger than the diameter of the native helix (≈1.3). For smaller D the helix state cannot fit within the cylinder, and ΔG_hc increases sharply. For D < 1 helix does not form even at T = 0. Dashed line is a fit to Eq. 4 with fitted parameters α₀ = 3.9 ± 0.2, f = 0.778 ± 0.005, and l_p = 230 ± 72. (Inset) Comparison of measured (bars) and calculated (circles) probability distributions of helical dihedral angles P(n_HD) in a cylinder with D = 1.4. Circles are calculated by fitting Eq. 8 to the simulation data obtaining s = 1.28 ± 0.01.

Helix Stability in a Cylinder Depends on Sequence Length. Our analytical model ignores finite-length effects, such as the increased energetic cost of α-helix formation at the chain termini. It is likely that these effects play some role in short peptides. To evaluate the role of peptide length, we performed simulations with N varying from 9 to 47 residues. For all of the peptides in the bulk, there is no apparent effect of N on θ . On the other hand, upon confining the peptides to a cylinder with D = 1.4, θ increases with N (see Fig. 4a), indicating stronger stabilization of the helical state for longer peptides. In addition, the folding temperature T_f, which is the same for all peptides in the bulk, increases with N (Fig. 4b).

Open in a separate window

Fig. 4.

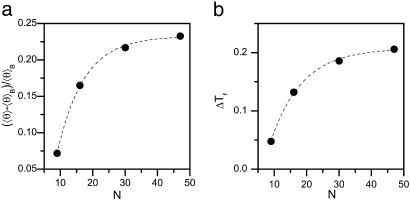
Confinement-induced α-helix formation is length-dependent. (a) The mean helical content θ , calculated for D = 1.4 and T = 0.5 relative to the bulk value, θ _B, increases with N. (b) Change of folding temperature ΔT_f upon confinement in a cylinder of D = 1.4 at T = 0.5. In the bulk T_f ≈ 0.48 for all peptides. Dashed lines are guides to the eye.

Coiled State Undergoes a Structural Transition upon Confinement. Plotting the root-mean-squared (rms) end-to-end distance as a function of temperature in the bulk (black line) and in cylinders of different sizes (Fig. 5), we observe a confinement-induced structural transition in the coiled state even at high T. For a peptide in the bulk, decreases the peptide unfolds. This when result is because for an α-helix scales with N, the number of residues, whereas in the coiled state it scales as N^ν with ν = 3/5. In contrast, increases upon unfolding in cylindrical confinement, because unlike in the bulk the coil state can adopt only extended conformations, such as the one shown in the upper right corner of Fig. 5. This increase is clearly observed in the distributions of R_ee plotted in Fig. 5 Inset. We also observe a significant decrease in the fluctuations of R_ee, manifested by a decrease in its standard deviation from 1.25 in the bulk to ≈0.5 in a cylinder with D = 1.3.

Open in a separate window

Fig. 5.

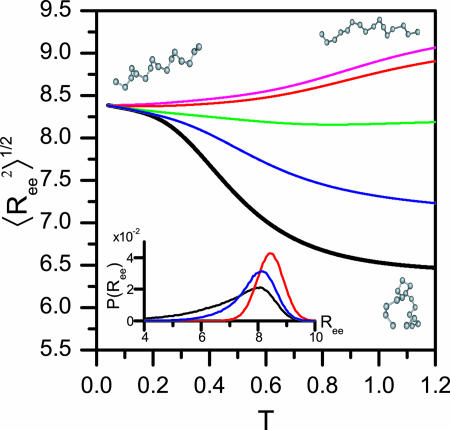
Structural transition upon confinement. The rms end-to-end distance in cylindrical confinement as a function of temperature in the bulk (black line) and in cylinders of diameter D = 3 (blue), 2 (green),1.4 (red), and 1.3 (magenta). At low temperature the peptide adopts a helical conformation (drawn in the left-hand side). At the high T limit in the bulk, the peptide samples many conformations, with either small (such as the conformation drawn in bottom right corner) or with ends far away (such as the conformation drawn in top right corner). For the confined peptide, only extended conformations are observed, signifying a random coil → stretch structural transition upon confinement. (Inset) The end-to-end distance distribution function, P(R_ee) in the bulk (black line) and in cylinders with diameter D = 3 (blue line) and D = 1.4 (red line). The fluctuations in the end-to-end distance are suppressed as D decreases, and the distributions sharpen.

Conformational Sampling Decreases upon Confinement. To evaluate the effects of confinement on the helix–coil transition kinetics, we calculate the “ergodic measure” Ω for the helical content (29). The ergodic measure corresponds to the time scale of diffusion on the conformational energy landscape, projected on the chosen reaction coordinate (in this case θ). To calculate Ω we first define

where θ_j(t) is the helical content of trajectory j at time t. By using this definition, an ergodic measure is calculated (29), and a energy-landscape diffusion coefficient d_E is obtained from the asymptotic behavior

where the averages are performed over all trajectories.

We calculated d_E for different size cylinders at T = 0.5 and normalized it by the respective quantity in the bulk, d_E,bulk. The resulting diffusion coefficients are d_E/d_E,bulk = 2 ± 0.05 for D = 1.4, d_E/d_E,bulk = 1.3 ± 0.03 for D = 1.7, and d_E/d_E,bulk ≈ 1 for larger cylinders. Thus, we observe an increase in the time needed to cover phase-space for small cylinders, which quickly approaches the bulk time scale for cylinders larger then D ≈ 2.

Discussion

In this work, we have proposed and theoretically validated the hypothesis that cotranslational α-helix formation within the ribosome exit tunnel is entropically driven. Both our analytical arguments and numerical simulations indicate that confinement within a cylindrical space can stabilize the helical states of polypeptide chains. This stabilization effect is purely entropic in nature and is a consequence of the severe restriction of the conformational space of the coil states inside the cylinder.

The simulation results are quantitatively explained by a model for the helix–coil transition, which takes into account only the relative reduction of entropy in the coil and helix states. Confinement not only stabilizes the helical state but also has an effect on the coil state. Coil conformations that cannot be accommodated within the cylinder are disallowed, which leaves only those that make the chain much more extended even at high temperatures compared with the bulk. This structural transition is accompanied by a significant reduction in chain dynamics. The latter is evidenced by a narrowing of the end-to-end distance distribution, as well as an increase in the time scales for navigation of conformational space. These findings are consistent with an intuitive picture of confined kinetics, where entropic barriers become larger as the confining dimensions become smaller.

The length dependence of the confinement-induced α-helix formation, found in the simulations, is somewhat surprising and cannot be understood within the framework of our simple analytical model. Previous experimental studies have shown a weak length dependence of the helix–coil transition in solution (30, 31). Compared with intrinsic helical propensity and entropic stabilization in confined spaces, we expect that the dependence of helix formation on N should be a secondary effect. In our model the probability of finding each residue in a helical conformation does not significantly depend on N. The interesting outcome of the simulations under confinement is that long peptides are more likely to adopt a helical conformation upon confinement than short peptides. Thus, the simulations indicate that additional finite-size effects become relevant in confined space. The confinement-induced α-helix stabilization also depends on the helix-forming propensity of the sequence that in our model is parameterized by the dihedral-angle potential V_DIH (Eq. 6); a model peptide that does not form an α-helix in bulk shows no helix formation upon confinement (data not shown). This finding may partially explain the origin of the experimental observation of sequence-dependent structure formation inside the ribosome exit tunnel.

We explore the implication of our work for the experimental results, especially those of Johnson and coworkers (8), who measured the FRET efficiency between probes attached to the two ends of an α-helix forming peptide. By using the probability distribution of the end-to-end distance P(R_ee), we calculated the average FRET efficiency (E )

[9]

where R₀ is the Förster distance, i.e., the distance at which E = 0.5. The FRET efficiency dependence on temperature is plotted in Fig. 6 for a peptide of N = 30, using R₀ = 15 (≈57 Å), which is similar to the parameter used by Woolhead et al. (8). In the bulk E grows with temperature. This assumption is understood based on arguments presented above. Indeed, we showed that the rms end-to-end distance decreases upon transition from helix to coil, and because conformations with short distance contribute significantly to E , the latter should increase strongly. On the other hand, upon confinement the coil state is more extended than the helix state, and therefore E shows a decrease at high temperatures.

Open in a separate window

Fig. 6.

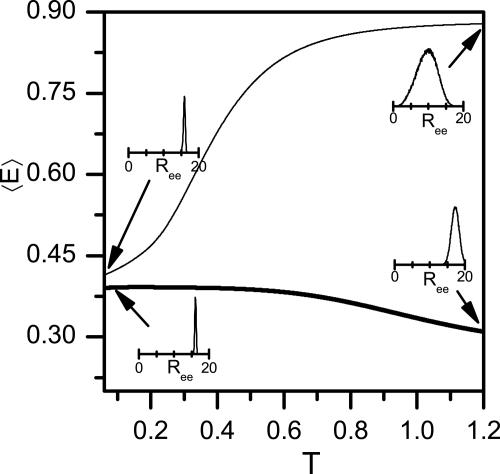
Förster energy transfer for a peptide with N = 30. The average FRET efficiency E , calculated from the simulations according to Eq. 10, and plotted as function of temperature in the bulk (thin line) and under confinement in a cylinder of D = 1.4 (thick line). Insets show P(R_ee) at the indicated points. At low temperatures both bulk and confined peptides are helical, whereas at high temperatures the bulk peptide is a random coil with a high E , but the confined peptide is relatively extended, with low E .

Our simulations also showed that short peptides are less affected by confinement. This finding implies that a peptide with a short TMS sequence (but with the same overall number of amino acids), will have a larger end-to-end distance and a lower FRET efficiency than a full TMS peptide. This conclusion is in qualitative agreement with the results of Woolhead et al. (8) for peptides within the ribosome exit tunnel. Surprisingly, however, they also found that the helical peptide, when released into solution, shows low FRET efficiency. However, our simulations, as well as simple arguments based on polymer theory, suggest that the FRET efficiency should increase in the bulk. This discrepancy calls for further experimental and theoretical work.

Although our simulations indicate that entropic stabilization can explain α-helix formation within the ribosome exit tunnel, we cannot entirely rule out a role for specific interactions, e.g., with ribosomal proteins forming part of the tunnel walls. Such interactions would explain the cross-linking experimental results of Woolhead et al. (8). Although possibly not contributing to the formation of secondary structure elements, these interactions may play a role in signaling events related to chain elongation and communication with the translocon (12–14). This interesting conjecture awaits experimental verification.

Coarse-grained model for the polypeptide chain used in this study have yielded qualitative insights into the folding of secondary and tertiary structure elements of proteins (32). For this model we find that α-helices are most stabilized in a cylindrical cavity with diameter of ≈8.3Å(= 1.3 × 3.8 Å + 2 × 1.7 Å, where we added two van der Waals radii of the C^αs), which is about the narrowest diameter found in the ribosome exit tunnel. Our coarse-grained model neglects side chains, which might change the results in two ways: First, the diameter of the α-helix will increase, but this increase is expected to only shift the curves of Figs. ​Figs.22 and ​and3,3, so that the maximum effect occurs at a larger D. Second, specific amino acid side chains might contribute to further stabilization or destabilization of the helical state. Another simplification of our simulations is the use of a straight, constant-diameter cylinder to represent the ribosome exit tunnel. The simulations show, however, that the helical state is stabilized over a range of tunnel diameters, so that even as the tunnel diameter changes along its length the helix-forming propensity would not change by much. Further, the natural flexibility of α-helices [leading to bent helices such as those appearing in coiled coils (33)] is likely to accommodate tunnel bending. We also have not included solvent effects explicitly. It is possible that preferential interactions of the polypeptide chains with water in confined space can influence helix stability. Indeed, a recent work (E. J. Sorin and V. S. Pande, private communication) suggests that a helix confined to carbon nanotubes, whose surface is apolar, is destabilized as a result of confinement-induced changes in solvent entropy. It is unclear whether similar arguments apply to folding in the exit tunnel of ribosome whose surface is polar.

Conclusions

We showed in this work, using simulations of coarse-grained off-lattice peptide models, that confinement within the ribosome exit tunnel can cause the formation of secondary structure in the nascent polypeptide chain. The diameter of the exit tunnel is very close to that of an α-helix, and our simulations showed that in this case the confinement effect is maximized. We also found that longer helix-forming peptides are more stabilized by confinement than shorter ones. This finding has implications for the possible timing of cotranslational secondary structure formation within the exit tunnel, which may only initiate after a long-enough peptide was synthesized.

Our findings are in accord with recent experimental work (5–9). Consequently, the simplest proposition that long helices can be entropically stabilized in the tunnel is sufficient to rationalize many of the available experimental data, without invoking specific interactions with the tunnel walls. It will be interesting to understand the possible implications of confinement-induced secondary structure formation for cotranslational folding of proteins within the ribosome exit tunnel.

Acknowledgments

Notes

Author contributions: G.H. and D.T. designed research; G.Z. performed research; G.Z. and D.T. analyzed data; and G.Z., G.H., and D.T. wrote the paper.

Conflict of interest statement: No conflicts declared.

This paper was submitted directly (Track II) to the PNAS office.

Abbreviation: TMS, transmembrane sequence.

References