Abstract
Free full text

Standardized Evaluation Methodology and Reference Database for Evaluating Coronary Artery Centerline Extraction Algorithms
Abstract
Efficiently obtaining a reliable coronary artery centerline from computed tomography angiography data is relevant in clinical practice. Whereas numerous methods have been presented for this purpose, up to now no standardized evaluation methodology has been published to reliably evaluate and compare the performance of the existing or newly developed coronary artery centerline extraction algorithms. This paper describes a standardized evaluation methodology and reference database for the quantitative evaluation of coronary artery centerline extraction algorithms. The contribution of this work is fourfold: 1) a method is described to create a consensus centerline with multiple observers, 2) well-defined measures are presented for the evaluation of coronary artery centerline extraction algorithms, 3) a database containing thirty-two cardiac CTA datasets with corresponding reference standard is described and made available, and 4) thirteen coronary artery centerline extraction algorithms, implemented by different research groups, are quantitatively evaluated and compared. The presented evaluation framework is made available to the medical imaging community for benchmarking existing or newly developed coronary centerline extraction algorithms.
1. Introduction
Coronary artery disease (CAD) is currently the primary cause of death among American males and females [1] and one of the main causes of death in the world [2]. The gold standard for the assessment of CAD is conventional coronary angiography (CCA) [3]. However, because of its invasive nature, CCA has a low, but non-negligible, risk of procedure related complications [4]. Moreover, it only provides information on the coronary lumen.
Computed Tomography Angiography (CTA) is a potential alternative for CCA [5]. CTA is a noninvasive technique that allows, next to the assessment of the coronary lumen, the evaluation of the presence, extent, and type (non-calcified or calcified) of coronary plaque [6]. Such non-invasive, comprehensive plaque assessment may be relevant for improving risk stratification when combined with current risk measures: the severity of stenosis and the amount of calcium [3]. A disadvantage of CTA is that the current imaging protocols are associated with a higher radiation dose exposure than CCA [7].
Several techniques to visualize CTA data are used in clinical practice for the diagnosis of CAD. Besides evaluating the axial slices, other visualization techniques such as maximum intensity projections (MIP), volume rendering techniques, multi-planar reformatting (MPR), and curved planar reformatting (CPR) are used to review CTA data [3]. CPR and MPR images of coronary arteries are based on the CTA image and a central lumen line (for convenience referred to as centerline) through the vessel of interest [8]. These reformatted images can also be used during procedure planning for, among other things, planning the type of intervention and size of stents [9]. Efficiently obtaining a reliable centerline is therefore relevant in clinical practice. Furthermore, centerlines can serve as a starting point for lumen segmentation, stenosis grading, and plaque quantification [10, 11, 12].
This paper introduces a framework for the evaluation of coronary artery centerline extraction methods. The framework encompasses a publicly available database of coronary CTA data with corresponding reference standard centerlines derived from manually annotated centerlines, a set of well-defined evaluation measures, and an on-line tool for the comparison of coronary CTA centerline extraction techniques. We demonstrate the potential of the proposed framework by comparing thirteen coronary artery centerline extraction methods, implemented by different authors as part of a segmentation challenge workshop at the Medical Image Computing and Computer-Assisted Intervention (MICCAI) conference [13].
In the next two sections we will respectively describe our motivation of the study presented in this paper and discuss previous work on the evaluation of coronary segmentation and centerline extraction techniques. The evaluation framework will then be outlined by discussing the data, reference standard, evaluation measures, evaluation categories, and web-based framework. The paper will be concluded by presenting the comparative results of the thirteen centerline extraction techniques, a discussion of these results, and a conclusion about the work presented.
2. Motivation
The value of a standardized evaluation methodology and a publicly available image repository has been shown in a number of medical image analysis and general computer vision applications, for example in the Retrospective Image Registration Evaluation Project [14], the Digital Retinal Images for Vessel Extraction database [15], the Lung Image Database project [16], the Middlebury Stereo Vision evaluation [17], the Range Image Segmentation Comparison [18], the Berkeley Segmentation Dataset and Benchmark [19], and a workshop and on-line evaluation framework for liver and caudate segmentation [20].
Similarly, standardized evaluation and comparison of coronary artery centerline extraction algorithms has scientific and practical benefits. A benchmark of state-of-the-art techniques is a prerequisite for continued progress in this field: it shows which of the popular methods are successful and researchers can quickly apprehend where methods can be improved.
It is also advantageous for the comparison of new methods with the state-of-the-art. Without a publicly available evaluation framework, such comparisons are difficult to perform: the software or source code of existing techniques is often not available, articles may not give enough information for re-implementation, and if enough information is provided, re-implementation of multiple algorithms is a laborious task.
The understanding of algorithm performance that results from the standardized evaluation also has practical benefits. It may, for example, steer the clinical implementation and utilization, as a system architect can use objective measures to choose the best algorithm for a specific task.
Furthermore, the evaluation could show under which conditions a particular technique is likely to succeed or fail, it may therefore be used to improve the acquisition methodology to better match the post-processing techniques.
It is therefore our goal to design and implement a standardized methodology for the evaluation and comparison of coronary artery centerline extraction algorithms and publish a cardiac CTA image repository with associated reference standard. To this end, we will discuss the following tasks below:
Collection of a representative set of cardiac CTA datasets, with a manually annotated reference standard, available for the entire medical imaging community;
Development of an appropriate set of evaluation measures for the evaluation of coronary artery centerline extraction methods;
Development of an accessible framework for easy comparison of different algorithms;
Application of this framework to compare several coronary CTA centerline extraction techniques;
Public dissemination of the results of the evaluation.
3. Previous work
Approximately thirty papers have appeared that present and/or evaluate (semi-)automatic techniques for the segmentation or centerline extraction of human coronary arteries in cardiac CTA datasets. The proposed algorithms have been evaluated by a wide variety of evaluation methodologies.
A large number of methods have been evaluated qualitatively [21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37]. In these articles detection, extraction, or segmentation correctness have been visually determined. An overview of these methods is given in Table 1.
Table 1
An overview of CTA coronary artery segmentation and centerline extraction algorithms that were qualitatively evaluated. The column ‘Time’ indicates if information is provided about the computational time of the algorithm.
| Article | Patients / observers | Vessels | Evaluation details | Time |
|---|---|---|---|---|
|
| ||||
| Bartz et al. [21] | 1/1 | Complete tree | Extraction was judged to be satisfactory. | Yes |
| Bouraoui et al. [22] | 40/1 | Complete tree | Extraction was scored satisfactory or not. | No |
| Carrillo et al. [23] | 12/1 | Complete tree | Extraction was scored with the number of ex tracted small branches. | Yes |
| Florin et al. [24] | 1/1 | Complete tree | Extraction was judged to be satisfactory. | Yes |
| Florin et al. [25] | 34/1 | 6 vessels | Scored with the number of correct extractions. | No |
| Hennemuth et al. [26] | 61/1 | RCA, LAD | Scored with the number of extracted vessels and categorized on the dataset difficulty. | Yes |
| Lavi et al. [27] | 34/1 | 3 vessels | Scored qualitatively with scores from 1 to 5 and categorized on the image quality. | Yes |
| Lorenz et al. [28] | 3/1 | Complete tree | Results were visually analyzed and criticized. | Yes |
| Luengo-Oroz et al. [29] | 9/1 | LAD & LCX | Scored with the number of correct vessel ex tractions. The results are categorized on the image quality and amount of disease. | Yes |
| Nain et al. [30] | 2/1 | Left tree | Results were visually analyzed and criticized. | No |
| Renard et al. [31] | 2/1 | Left tree | Extraction was judged to be satisfactory. | No |
| Schaap et al. [32] | 2/1 | RCA | Extraction was judged to be satisfactory. | No |
| Szymczak et al. [33] | 5/1 | Complete tree | Results were visually analyzed and criticized. | Yes |
| Wang et al. [34] | 33/1 | Complete tree | Scored with the number of correct extractions. | Yes |
| Wesarg et al. [35] | 12/1 | Complete tree | Scored with the number of correct extractions. | Yes |
| Yang et al. [36] | 2/1 | Left tree | Extraction was judged to be satisfactory. | Yes |
| Yang et al. [37] | 2/1 | 4 vessels | Scored satisfactory or not. Evaluated in ten ECG gated reconstructions per patient. | Yes |
Other articles include a quantitative evaluation of the performance of the proposed methods [38, 39, 40, 41, 42, 43, 12, 10, 44, 45, 11, 46]. See Table 2 for an overview of these methods.
Table 2
An overview of the quantitatively evaluated CTA coronary artery segmentation and centerline extraction algorithms. With ‘centerline’ and ‘reference’ we respectively denote the (semi-)automatically extracted centerline and the manually annotated centerline. The column ‘Time’ indicates if information is provided about the computational time of the algorithm. ‘Method eval.’ indicates that the article evaluates an existing technique and that no new technique has been proposed.
| Article | Patients / observers | Vessels | Used evaluation measures and details | Time | Method eval. |
|---|---|---|---|---|---|
|
| |||||
| Bulow et al. [38] | 9/1 | 3-5 vessels | Overlap: Percentage reference points having a centerline point within 2 mm. | No | |
| Busch et al. [39] | 23/2 | Complete tree | Stenoses grading: Compared to human per- formance with CCA as ground truth. | No | × |
| Dewey et al. [40] | 35/1 | 3 vessels | Length difference: Difference between ref- erence length and centerline length. Stenoses grading: Compared to human performance with CCA as ground truth. | Yes | × |
| Khan et al. [12] | 50/1 | 3 vessels | Stenoses grading: Compared to human per- formance with CCA as ground truth. | No | × |
| Larralde et al. [41] | 6/1 | Complete tree | Stenoses grading and calcium detection: Compared to human performance. | Yes | |
| Lesage et al. [42] | 19/1 | 3 vessels | Same as Metz et al. [44] | Yes | |
| Li et al. [43] | 5/1 | Complete tree | Segmentation: Voxel-wise similarity indices. | No | |
| Marquering et al. [10] | 1/1 | LAD | Accuracy: Distance from centerline to reference standard. | Yes | |
| Metz et al. [44] | 6/3 | 3 vessels | Overlap: Segments on the reference standard and centerline are marked as true positives, false positives or false negatives. This scoring was used to construct similarity indices. Accuracy: Average distance to the reference standard for true positive sections. | No | |
| Olabarriaga et al. [45] | 5/1 | 3 vessels | Accuracy: Mean distance from the centerline to the reference. | No | |
| Wesarg et al. [11] | 10/1 | 3 vessels | Calcium detection: Performance compared to human performance. | No | × |
| Yang et al. [46] | 2/1 | 3 vessels | Overlap: Percentage of the reference standard detected. Segmentation: Average distance to contours. | No | |
None of the abovementioned algorithms has been compared to another and only three methods were quantitatively evaluated on both the extraction ability (i.e. how much of the real centerline can be extracted by the method?) and the accuracy (i.e. how accurately can the method locate the centerline or wall of the vessel?). Moreover, only one method was evaluated using annotations from more than one observer [44].
Four methods were assessed on their ability to quantify clinically relevant measures, such as the degree of stenosis and the number of calcium spots in a vessel [36, 40, 12, 11]. These clinically oriented evaluation approaches are very appropriate for assessing the performance of a method for a possible clinical application, but the performance of these methods for other applications, such as describing the geometry of coronary arteries [47, 48], can not easily be judged.
Two of the articles (Dewey et al. [40] and Busch et al. [39]) evaluate a commercially available system (respectively Vitrea 2, Version 3.3, Vital Images and Syngo Circulation, Siemens). Several other commercial centerline extraction and stenosis grading packages have been introduced in the past years, but we are not aware of any scientific publication containing a clinical evaluation of these packages.
4. Evaluation framework
In this section we will describe our framework for the evaluation of coronary CTA centerline extraction techniques.
4.1. Cardiac CTA data
The CTA data was acquired in the Erasmus MC, University Medical Center Rotterdam, The Netherlands. Thirty-two datasets were randomly selected from a series of patients who underwent a cardiac CTA examination between June 2005 and June 2006. Twenty datasets were acquired with a 64-slice CT scanner and twelve datasets with a dual-source CT scanner (Sensation 64 and Somatom Definition, Siemens Medical Solutions, Forchheim, Germany).
A tube voltage of 120 kV was used for both scanners. All datasets were acquired with ECG-pulsing [49]. The maximum current (625 mA for the dual-source scanner and 900 mA for the 64-slice scanner) was used in the window from 25% to 70% of the RR-interval and outside this window the tube current was reduced to 20% of the maximum current.
Both scanners operated with a detector width of 0.6 mm. The image data was acquired with a table feed of 3.8 mm per rotation (64-slice datasets) or 3.8 mm to 10 mm, individually adapted to the patient’s heart rate (dual-source datasets).
Diastolic reconstructions were used, with reconstruction intervals varying from 250 ms to 400 ms before the R-peak. Three datasets were reconstructed using a sharp (B46f) kernel, all others were reconstructed using a medium-to-smooth (B30f) kernel. The mean voxel size of the datasets is 0.32 × 0.32 × 0.4mm3.
4.1.1. Training and test datasets
To ensure representative training and test sets, the image quality of and presence of calcium in each dataset was visually assessed by a radiologist with three years experience in cardiac CT.
Image quality was scored as poor (defined as presence of image-degrading artifacts and evaluation only possible with low confidence), moderate (presence of artifacts but evaluation possible with moderate confidence) or good (absence of any image-degrading artifacts related to motion and noise). Presence of calcium was scored as absent, modest or severe. Based on these scorings the data was distributed equally over a group of 8 and a group of 24 datasets. The patient and scan parameters were assessed by the radiologist to be representative for clinical practice. Table 3 and and44 describe the distribution of respectively the image quality and calcium scores in the datasets.
Table 3
Image quality of the training and test datasets.
| Poor | Moderate | Good | Total | |
|---|---|---|---|---|
| Training | 2 | 3 | 3 | 8 |
| Testing | 4 | 8 | 12 | 24 |
Table 4
Presence of calcium in the training and test datasets.
| Low | Moderate | Severe | Total | |
|---|---|---|---|---|
| Training | 3 | 4 | 1 | 8 |
| Testing | 9 | 12 | 3 | 24 |
The first group of 8 datasets can be used for training and the other 24 datasets are used for performance assessment of the algorithms. All the thirty-two cardiac CTA datasets and the corresponding reference standard centerlines for the training data are made publicly available.
4.2. Reference standard
In this work we define the centerline of a coronary artery in a CTA scan as the curve that passes through the center of gravity of the lumen in each cross-section. We define the start point of a centerline as the center of the coronary ostium (i.e. the point where the coronary artery originates from the aorta), and the end point as the most distal point where the artery is still distinguishable from the background. The centerline is smoothly interpolated if the artery is partly indistinguishable from the background, e.g. in case of a total occlusion or imaging artifacts.
This definition was used by three trained observers to annotate centerlines in the selected cardiac CTA datasets. Four vessels were selected for annotation by one of the observers in all 32 datasets, yielding 32 × 4 = 128 selected vessels. The first three vessels were always the right coronary artery (RCA), left anterior descending artery (LAD), and left circumflex artery (LCX). The fourth vessel was selected from the large side branches of these main coronary arteries and the selection was as follows: first diagonal branch (14x), second diagonal branch (6x), optional diagonal coronary artery (6x), first obtuse marginal branch (2x), posterior descending artery (2x), and acute marginal artery (2x). This observer annotated for all the four selected vessels points close to the selected vessels. These points (denoted with ‘point A’) unambiguously define the vessels, i.e. the vessel of interest is the vessel closest to the point and no side-branches can be observed after this point.
After the annotation of these 128 points, the three observers used these points to independently annotate the centerlines of the same four vessels in the 32 datasets. The observers also specified the radius of the lumen at least every 5 mm, where the radius was chosen such that the enclosed area of the annotated circle matched the area of the lumen. The radius was specified after the complete central lumen line was annotated (see Figure 4).

An example of the annotations of the three observers in black and the resulting reference standard in white. The crosses indicate the centers and the circles indicate the radii.
The paths of the three observers were combined to one centerline per vessel using a Mean Shift algorithm for open curves: The centerlines are averaged while taking into account the possibly spatially varying accuracy of the observers by iteratively estimating the reference standard and the accuracy of the observers. Each point of the resulting reference standard is a weighted average of the neighboring observer centerline points, with weights corresponding to the locally estimated accuracy of the observers [50].
After creating this first weighted average, a consensus centerline was created with the following procedure: The observers compared their centerlines with the average centerline to detect and subsequently correct any possible annotation errors. This comparison was performed utilizing curved planar reformatted images displaying the annotated centerline color-coded with the distance to the reference standard and vice-versa (see Figure 2). The three observers needed in total approximately 300 hours for the complete annotation and correction process.
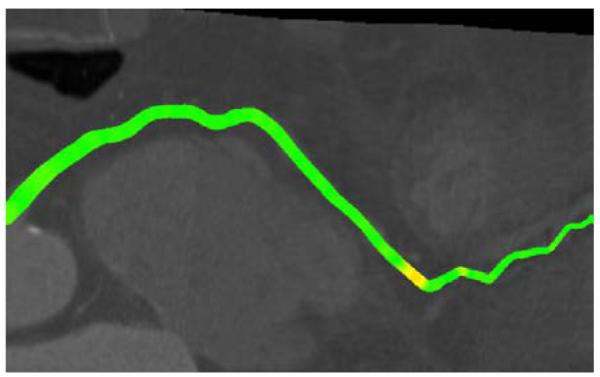
An example of one of the color-coded curved planar reformatted images used to detect possible annotation errors.
After the correction step the centerlines were used to create the reference standard, using the same Mean Shift algorithm. Note that the uncorrected centerlines were used to calculate the inter-observer variability and agreement measures (see section 4.5).
The points where for the first time the centerlines of two observers lie within the radius of the reference standard when traversing over this centerline from respectively the start to the end or vice versa were selected as the start- and end point of the reference standard. Because the observers used the abovementioned centerline definition it is assumed that the resulting start points of the reference standard centerlines lie within the coronary ostium.
The corrected centerlines contained on average 44 points and the average distance between two successive annotated points was 3.1 mm. The 128 resulting reference standard centerlines were on average 138 mm (std. dev. 41 mm, min. 34 mm, max. 249 mm) long.
The radius of the reference standard was based on the radii annotated by the observers and a point-to-point correspondence between the reference standard and the three annotated centerlines. The reference standard centerline and the corrected observer centerlines were first resampled equidistantly using a sampling distance of 0.03 mm. Dijkstra’s graph searching algorithm was then used to associate each point on the reference standard with one or more points on each annotated centerline and vice versa. Using this correspondence, the radius at each point of the reference standard was determined by averaging the radius of all the connected points on the three annotated centerlines (see also Figure 3 and Figure 4). An example of annotated data with corresponding reference standard is shown in Figure 1. Details about the connectivity algorithm are given in section 4.3.
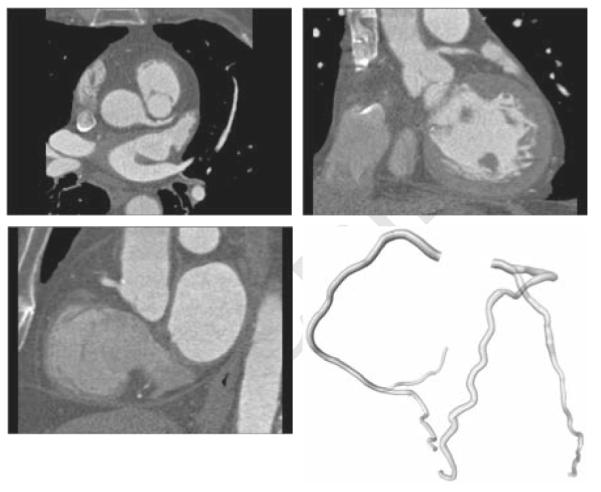
An example of the data with corresponding reference standard. Top-left: axial view of data. Top-right: coronal view. Bottom-left: sagittal view. Bottom-right: a 3D rendering of the reference standard.
4.3. Correspondence between centerlines
All the evaluation measures are based on a point-to-point correspondence between the reference standard and the evaluated centerline. This section explains the mechanism for determining this correspondence.
Before the correspondence is determined the centerlines are first sampled equidistantly using a sampling distance of 0.03 mm, enabling an accurate comparison. The evaluated centerline is then clipped with a disc that is positioned at the start of the reference standard centerline (i.e. in or very close to the coronary ostium). The centerlines are clipped because we define the start point of a coronary centerline at the coronary ostium and because for a variety of applications the centerline can start somewhere in the aorta. The radius of the disc is twice the annotated vessel radius and the disc normal is the tangential direction at the beginning of the reference standard centerline. Every point before the first intersection of a centerline and this disc is not taken into account during evaluation.
The correspondence is then determined by finding the minimum of the sum of the Euclidean lengths of all point-point connections that are connecting the two centerlines over all valid correspondences. A valid correspondence for centerline I, consisting of an ordered set of points pi (0 ≤ i < n, p0 is the most proximal point of the centerline), and centerline II, consisting of an ordered set of points qj (0 ≤ j < m, q0 is the most proximal point of the centerline), is defined as the ordered set of connections C = {c0, …, cn+m−1}, where ck is a tuple [pa, qb] that represents a connection from pa to qb, which satisfies the following conditions:
The first connection c0 connects the start points: c0 = [p0, q0].
The last connection cn+m−1 connects the end points: cn+m−1 = [pn−1, qm−1].
If connection ck = [pa, qb] then connection ck+1 equals either [pa+1, qb] or [pa, qb+1].
These conditions guarantee that each point of centerline I is connected to at least one point of centerline II and vice versa.
Dijkstra’s graph search algorithm is used on a matrix with connection lengths to determine the minimal Euclidean length correspondence. See Figure 3 for an example of a resulting correspondence.
4.4. Evaluation measures
Coronary artery centerline extraction may be used for different applications, and thus different evaluation measures may apply. We account for this by employing a number of evaluation measures. With these measures we discern between extraction capability and extraction accuracy. Accuracy can only be evaluated when extraction succeeded; in case of a tracking failure the magnitude of the distance to the reference centerline is no longer relevant and should not be included in the accuracy measure.
4.4.1. Definition of true positive, false positive and false negative points
All the evaluation measures are based on a labeling of points on the centerlines as true positive, false negative or false positive. This labeling, in its turn, is based on a correspondence between the points of the reference standard centerline and the points of the centerline to be evaluated. The correspondence is determined with the algorithm explained in section 4.3.
A point of the reference standard is marked as true positive TPRov if the distance to at least one of the connected points on the evaluated centerline is less than the annotated radius and false negative FNov otherwise.
A point on the centerline to be evaluated is marked as true positive TPMov if there is at least one connected point on the reference standard at a distance less than the radius defined at that reference point, and it is marked as false positive FPov otherwise. With 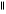 ·
· we denote the cardinality of a set of points, e.g.
we denote the cardinality of a set of points, e.g.  TPRov
TPRov denotes the number of reference points marked true positive. See also Figure 5 for a schematic explanation of these terms and the terms mentioned in the next section.
denotes the number of reference points marked true positive. See also Figure 5 for a schematic explanation of these terms and the terms mentioned in the next section.
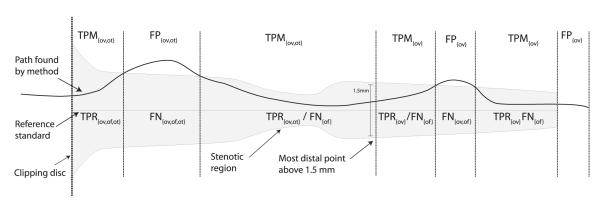
An illustration of the terms used in the evaluation measures (see section 4.4). The reference standard with annotated radius is depicted in gray. The terms on top of the figure are assigned to points on the centerline found by the evaluated method. The terms below the reference standard line are assigned to points on the reference standard.
4.4.2. Overlap measures
Three different overlap measures are used in our evaluation framework.
Overlap (OV) represents the ability to track the complete vessel annotated by the human observers and this measure is similar to the well-known Dice coefficient. It is defined as:
Overlap until first error (OF) determines how much of a coronary artery has been extracted before making an error. This measure can for example be of interest for image guided intravascular interventions in which guide wires are advanced based on pre-operatively extracted coronary geometry [51]. The measure is defined as the ratio of the number of true positive points on the reference before the first error (TPRof) and the total number of reference points (TPRof + FNof):
The first error is defined as the first FNov point when traversing from the start of the reference standard to its end while ignoring false negative points in the first 5 mm of the reference standard. Errors in the first 5 mm are not taken into account because of the strictness of this measure and the fact that the beginning of a coronary artery centerline is sometimes difficult to define and for some applications not of critical importance. The threshold of five millimeters is equal to the average diameter annotated at the beginning of all the reference standard centerlines.
Overlap with the clinically relevant part of the vessel (OT) gives an indication of how well the method is able to track the section of the vessel that is assumed to be clinically relevant. Vessel segments with a diameter of 1.5 mm or larger, or vessel segments that are distally from segments with a diameter of 1.5 mm or larger are assumed to be clinically relevant [52, 53].
The point closest to the end of the reference standard with a radius larger than or equal to 0.75 mm is determined. Only points on the reference standard between this point and the start of the reference standard and points on the (semi-)automatic centerline connected to these reference points are used when defining the true positives (TPMot and TPRot), false negatives (FNot) and false positives (FPot). The OT measure is calculated as follows:
4.4.3. Accuracy measure
In order to discern between tracking ability and tracking accuracy we only evaluate the accuracy within sections where tracking succeeded.
Average inside (AI) is the average distance of all the connections between the reference standard and the automatic centerline given that the connections have a length smaller than the annotated radius at the connected reference point. The measure represents the accuracy of centerline extraction, provided that the evaluated centerline is inside the vessel.
4.5. Observer performance and scores
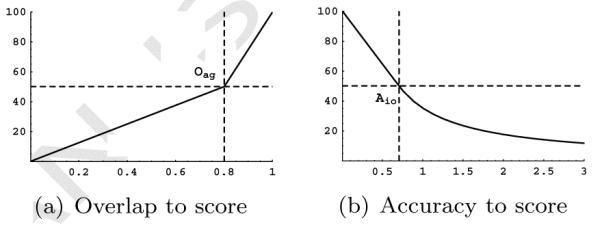
Each of the evaluation measures is related to the performance of the observers by a relative score. A score of 100 points implies that the result of the method is perfect, 50 points implies that the performance of the method is similar to the performance of the observers, and 0 points implies a complete failure. This section explains how the observer performance is quantified for each of the four evaluation measures and how scores are created from the evaluation measures by relating the measures to the observer performance.
4.5.1. Overlap measures
The inter-observer agreement for the overlap measures is calculated by comparing the uncorrected paths with the reference standard. The three overlap measures (OV, OF, OT) were calculated for each uncorrected path and the true positives, false positives and false negatives for each observer were combined into inter-observer agreement measures per centerline as follows:
where i = {0, 1, 2} indicates the observer.
After calculating the inter-observer agreement measures, the performance of the method is scored. For methods that perform better than the observers the OV, OF, and OT measures are converted to scores by linearly interpolating between 100 and 50 points, respectively corresponding to an overlap of 1.0 and an overlap similar to the inter-observer agreement value. If the method performs worse than the inter-observer agreement the score is obtained by linearly interpolating between 50 and 0 points, with 0 points corresponding to an overlap of 0.0:
where Om and Oag define the OV, OF, or OT performance of respectively the method and the observer. An example of this conversion is shown in Figure 6(a).
4.5.2. Accuracy measures
The inter-observer variability for the accuracy measure AI is defined at every point of the reference standard as the expected error that an observer locally makes while annotating the centerline. It is determined at each point as the root mean squared distance between the uncorrected annotated centerline and the reference standard:
where n = 3 (three observers), and d(p(x), pi) is the average distance from point p(x) on the reference standard to the connected points on the centerline annotated by observer i.
The extraction accuracy of the method is related per connection to the inter-observer variability. A connection is worth 100 points if the distance to the reference standard is 0 mm and it is worth 50 points if the distance is equal to the inter-observer variability at that point. Methods that perform worse than the inter-observer variability get a decreasing amount of points if the distance increases. They are rewarded per connection 50 points times the fraction of the inter-observer variability and the method accuracy:
where Am(x) and Aio(x) define the distance from the method centerline to the reference centerline and the inter-observer accuracy variability at point x. An example of this conversion is shown in Figure 6(b).
The average score over all connections that connect TPR and TPM points yields the AI observer performance score. Because the average accuracy score is a non-linear combination of all the distances, it can happen that a method has a lower average accuracy in millimeters and a higher score in points than another method, or vice versa.
Note that because the reference standard is constructed from the observer centerlines, the reference standard is slightly biased towards the observer centerlines, and thus a method that performs similar as an observer according to the scores probably performs slightly better. Although more sophisticated methods for calculating the observer performance and scores would have been possible, we decided because of simplicity and understandability for the approach explained above.
4.6. Ranking the algorithms
In order to rank the different coronary artery centerline extraction algorithms the evaluation measures have to be combined. We do this by ranking the resulting scores of all the methods for each measure and vessel. Each method receives for each vessel and measure a rank ranging from 1 (best) to the number of participating methods (worst). A user of the evaluation framework can manually mark a vessel as failed. In that case the method will be ranked last for the flagged vessel and the absolute measures and scores for this vessel will not be taken into account in any of the statistics.
The tracking capability of a method is defined as the average of all the 3(overlap measures) × 96 (vessels) = 288 related ranks. The average of all the 96 accuracy measure ranks defines the tracking accuracy of each method. The average overlap rank and the accuracy rank are averaged to obtain the overall quality of each of the methods and the method with the best (i.e. lowest) average rank is assumed to be the best.
5. Algorithm categories
We discern three different categories of coronary artery centerline extraction algorithms: automatic extraction methods, methods with minimal user interaction and interactive extraction methods.
5.1. Category 1: automatic extraction
Automatic extraction methods find the centerlines of coronary arteries without user interaction. In order to evaluate the performance of automatic coronary artery centerline extraction, two points per vessel are provided to extract the coronary artery of interest:
Point A: a point inside the distal part of the vessel; this point unambiguously defines the vessel to be tracked;
Point B: a point approximately 3 cm (measured along the centerline) distal of the start point of the centerline.
Point A should be used for selecting the appropriate centerline. If the automatic extraction result does not contain centerlines near point A, point B can be used. Point A and B are only meant for selecting the right centerline and it is not allowed to use them as input for the extraction algorithm.
5.2. Category 2: extraction with minimal user interaction
Extraction methods with minimal user interaction are allowed to use one point per vessel as input for the algorithm. This can be either one of the following points:
Point A or B, as defined above;
Point S: the start point of the centerline;
Point E: the end point of the centerline;
Point U: any manually defined point.
Points A, B, S and E are provided with the data. Furthermore, in case the method obtains a vessel tree from the initial point, point A or B may be used after the centerline determination to select the appropriate centerline.
5.3. Category 3: interactive extraction
All methods that require more user-interaction than one point per vessel as input are part of category 3. Methods can use e.g. both points S and E from category 2, a series of manually clicked positions, or one point and a user-defined threshold.
6. Web-based evaluation framework
The proposed framework for the evaluation of CTA coronary artery centerline extraction algorithms is made publicly available through a web-based interface (http://coronary.bigr.nl). The thirty-two cardiac CTA datasets, and the corresponding reference standard centerlines for the training data, are available for download for anyone who wishes to validate their algorithm. Extracted centerlines can be submitted and the obtained results can be used in a publication. Furthermore, the website provides several tools to inspect the results and compare the algorithms.
7. MICCAI 2008 workshop
This study started with the workshop ‘3D Segmentation in the Clinic: A Grand Challenge II’ at the 11th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) in September 2008 [13]. Approximately 100 authors of related publications, and the major medical imaging companies, were invited to submit their results on the 24 test datasets. Fifty-three groups showed their interest by registering for the challenge, 36 teams downloaded the training and test data, and 13 teams submitted results: five fully-automatic methods, three minimally interactive methods, and five interactive methods. A brief description of the thirteen methods is given below.
During the workshop we used two additional measures: the average distance of all the connections (AD) and the average distance of all the connections to the clinical relevant part of the vessel (AT). In retrospect we found that these accuracy measures were too much biased towards methods with high overlap and therefore we do not use them anymore in the evaluation framework. This resulted in a slightly different ranking than the ranking published during the MICCAI workshop [13]. Please note that the two measures that were removed are still calculated for all the evaluated methods and they can be inspected using the web-based interface.
7.1. Fully-automatic methods
AutoCoronaryTree [54, 55]: The full centerline tree of the coronary arteries is extracted via a multi-scale medialness-based vessel tree extraction algorithm which starts a tracking process from the ostia locations until all coronary branches are reached.
CocomoBeach [56]: This method starts by segmenting the ascending aorta and the heart. Candidate coronary regions are obtained using connected component analysis and the masking of large structures. Using these components a region growing scheme, starting in the aorta, segments the complete tree. Finally, centerlines within the pre-segmented tree are obtained using the WaveProp [10] method.
DepthFirstModelFit [57]: Coronary artery centerline extraction is accomplished by fitting models of shape and appearance. A large-scale model of the complete heart in combination with symmetry features is used for detecting coronary artery seeds. To fully extract the coronary artery tree, two small-scale cylinder-like models are matched via depth-first search.
GVFTube’n’Linkage [58]: This method uses a Gradient Vector Flow [59] based tube detection procedure for identification of vessels surrounded by arbitrary tissues [60, 61]. Vessel centerlines are extracted using ridge-traversal and linked to form complete tree structures. For selection of coronary arteries gray value information and centerline length are used.
VirtualContrast [62]: This method segments the coronary arteries based on the connectivity of the contrast agent in the vessel lumen, using a competing fuzzy connectedness tree algorithm [34]. Automatic rib cage removal and ascending aorta tracing are included to initialize the segmentation. Centerline extraction is based on the skeletonization of the tree structure.
7.2. Semi-automatic methods
AxialSymmetry [63]: This method finds a minimum cost path connecting the aorta to a user supplied distal endpoint. Firstly, the aorta surface is extracted. Then, a two-stage Hough-like election scheme detects the high axial symmetry points in the image. Via these, a sparse graph is constructed. This graph is used to determine the optimal path connecting the user supplied seed point and the aorta.
CoronaryTreeMorphoRec [64]: This method generates the coronary tree iteratively from point S. Pre-processing steps are performed in order to segment the aorta, remove unwanted structures in the background and detect calcium. Centerline points are chosen in each iteration depending on the previous vessel direction and a local gray scale morphological 3D reconstruction.
KnowledgeBasedMinPath [65]: For each voxel, the probability of belonging to a coronary vessel is estimated from a feature space and a vesselness measure is used to obtain a cost function. The vessel starting point is obtained automatically, while the end point is provided by the user. Finally, the centerline is obtained as the minimal cost path between both points.
7.3. Interactive methods
3DInteractiveTrack [66]: This method calculates a local cost for each voxel based on eigenvalue analysis of the Hessian matrix. When a user selects a point, the method calculates the cost linking this point to all other voxels. If a user then moves to any voxel, the path with minimum overall cost is displayed. The user is able to inspect and modify the tracking to improve performance.
ElasticModel [67]. After manual selection of a background-intensity threshold and one point per vessel, centerline points are added by prediction and refinement. Prediction uses the local vessel orientation, estimated by eigen-analysis of the inertia matrix. Refinement uses centroid information and is restricted by continuity and smoothness constraints of the model [68].
MHT [69]: Vessel branches are in this method found using a Multiple Hypothesis Tracking (MHT) framework. A feature of the MHT framework is that it can traverse difficult passages by evaluating several hypothetical paths. A minimal path algorithm based on Fast Marching is used to bridge gaps where the MHT terminates prematurely.
Tracer [70]: This method finds the set of core points (centers of intensity plateaus in 2D slices) that concentrate near vessel centerlines. A weighted graph is formed by connecting nearby core points. Low weights are given to edges of the graph that are likely to follow a vessel. The output is the shortest path connecting point S and point E.
TwoPointMinCost [71]: This method finds a minimum cost path between point S and point E using Dijkstra’s algorithm. The cost to travel through a voxel is based on Gaussian error functions of the image intensity and a Hessian-based vesselness measure [72], calculated on a single scale.
8. Results
The results of the thirteen methods are shown in Table 5, ,6,6, and and7.7. Table 6 shows the results for the three overlap measures, Table 7 shows the accuracy measures, and Table 5 shows the final ranking, the approximate processing time, and amount of user-interaction that is required to extract the four vessels. In total 10 extractions (< 1%) where marked as failed (see section 4.6).
Table 5
The overall ranking of the thirteen evaluated methods. The average overlap rank, accuracy rank and the average of these two is shown together with an indication of the computation time and the required user-interaction.
| Method | Challenge | Avg. Ov. rank | Avg. Acc. rank | Avg. rank | Computation time | User- interaction | ||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||||
| MHT [69] | × | 2.07 | 1.58 | 1.83 | 6 minutes | 2 to 5 points | ||
| Tracer [70] | × | 4.21 | 2.52 | 3.37 | 30 minutes | Point S and point E | ||
| DepthFirstModelFit [57] | × | 6.17 | 3.33 | 4.75 | 4-8 minutes | |||
| KnowledgeBasedMinPath [65] | × | 4.31 | 8.36 | 6.34 | 7 hours | Point E | ||
| AutoCoronaryTree [54] | × | 7.69 | 5.18 | 6.44 | < 30 seconds | |||
| GVFTube’n’Linkage [58] | × | 5.39 | 8.02 | 6.71 | 10 minutes | |||
| CocomoBeach [56] | × | 8.56 | 5.04 | 6.80 | 70 seconds | |||
| TwoPointMinCost [71] | × | 5.30 | 8.80 | 7.05 | 12 minutes | Point S and point E | ||
| VirtualContrast [62] | × | 8.71 | 7.74 | 8.23 | 5 minutes | |||
| AxialSymmetry [63] | × | 6.95 | 9.60 | 8.28 | 5 minutes | Point E | ||
| ElasticModel [67] | × | 9.05 | 8.29 | 8.67 | 2-6 minutes | Global intens. thresh. + 1 point per axis | ||
| 3DInteractiveTrack [66] | × | 7.52 | 10.91 | 9.22 | 3-6 minutes | 3 to 10 points | ||
| CoronaryTreeMorphoRec [64] | × | 10.42 | 11.59 | 11.01 | 30 minutes | Point S | ||
Table 6
The resulting overlap measures for the thirteen evaluated methods. The average overlap, score and rank is shown for each of the three overlap measures.
| Method | Challenge | OV | OF | OT | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | % | score | rank | % | score | rank | % | score | rank | |
| MHT [69] | × | 98.5 | 84.0 | 1.74 | 83.1 | 72.8 | 2.64 | 98.7 | 84.5 | 1.83 | ||
| Tracer [70] | × | 95.1 | 71.0 | 3.60 | 63.5 | 52.0 | 5.22 | 95.5 | 70.2 | 3.81 | ||
| DepthFirstModelFit [57] | × | 84.7 | 48.6 | 7.29 | 65.3 | 49.2 | 5.32 | 87.0 | 60.1 | 5.90 | ||
| KnowledgeBasedMinPath [65] | × | 88.0 | 67.4 | 4.46 | 74.2 | 61.1 | 4.27 | 88.5 | 70.0 | 4.21 | ||
| AutoCoronaryTree [54] | × | 84.7 | 46.5 | 8.13 | 59.5 | 36.1 | 7.26 | 86.2 | 50.3 | 7.69 | ||
| GVFTube’n’Linkage [58] | × | 92.7 | 52.3 | 6.20 | 71.9 | 51.4 | 5.32 | 95.3 | 67.0 | 4.66 | ||
| CocomoBeach [56] | × | 78.8 | 42.5 | 9.34 | 64.4 | 40.0 | 7.39 | 81.2 | 46.9 | 8.96 | ||
| TwoPointMinCost [71] | × | 91.9 | 64.5 | 4.70 | 56.4 | 45.6 | 6.22 | 92.5 | 64.5 | 4.97 | ||
| VirtualContrast [62] | × | 75.6 | 39.2 | 9.74 | 56.1 | 34.5 | 7.74 | 78.7 | 45.6 | 8.64 | ||
| AxialSymmetry [63] | × | 90.8 | 56.8 | 6.17 | 48.9 | 35.6 | 7.96 | 91.7 | 55.9 | 6.71 | ||
| ElasticModel [67] | × | 77.0 | 40.5 | 9.60 | 52.1 | 31.5 | 8.46 | 79.0 | 45.3 | 9.09 | ||
| 3DInteractiveTrack [66] | × | 89.6 | 51.1 | 7.04 | 49.9 | 30.5 | 8.36 | 90.6 | 52.4 | 7.15 | ||
| CoronaryTreeMorphoRec [64] | × | 67.0 | 34.5 | 11.00 | 36.3 | 20.5 | 9.53 | 69.1 | 36.7 | 10.74 | ||
Table 7
The accuracy of the thirteen evaluated methods. The average distance, score and rank of each is shown for the accuracy when inside (AI) measure.
| Method | Challenge | AI | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | mm | score | rank | |
| MHT [69] | × | 0.23 | 47.9 | 1.58 | ||
| Tracer [70] | × | 0.26 | 44.4 | 2.52 | ||
| DepthFirstModelFit [57] | × | 0.28 | 41.9 | 3.33 | ||
| KnowledgeBasedMinPath [65] | × | 0.39 | 29.2 | 8.36 | ||
| AutoCoronaryTree [54] | × | 0.34 | 35.3 | 5.18 | ||
| GVFTube’n’Linkage [58] | × | 0.37 | 29.8 | 8.02 | ||
| CocomoBeach [56] | × | 0.29 | 37.7 | 5.04 | ||
| TwoPointMinCost [71] | × | 0.46 | 28.0 | 8.80 | ||
| VirtualContrast [62] | × | 0.39 | 30.6 | 7.74 | ||
| AxialSymmetry [63] | × | 0.46 | 26.4 | 9.60 | ||
| ElasticModel [67] | × | 0.40 | 29.3 | 8.29 | ||
| 3DInteractiveTrack [66] | × | 0.51 | 24.2 | 10.91 | ||
| CoronaryTreeMorphoRec [64] | × | 0.59 | 20.7 | 11.59 | ||
We believe that the final ranking in Table 5 gives a good indication of the relative performance of the different methods, but one should be careful to judge the methods on their final rank. A method ranked first does not have to be the method of choice for a specific application. For example, if a completely automatic approximate extraction of the arteries is needed one could choose GVF-Tube’n’Linkage [58] because it has the highest overlap with the reference standard (best OV result). But if one wishes to have a more accurate automatic extraction of the proximal part of the coronaries the results point you toward DepthFirstModelFit [57] because this method is highly ranked in the OF measure and is ranked first in the automatic methods category with the AI measure.
The results show that on average the interactive methods perform better on the overlap measures than the automatic methods (average rank of 6.30 vs. 7.09) and vice versa for the accuracy measures (8.00 vs. 6.25). The better overlap performance of the interactive methods can possibly be explained by the fact that the interactive methods use the start- and/or end point of the vessel. Moreover, in two cases (MHT [69] and 3DInteractive-Track [66]) additional manually annotated points are used, which can help the method to bridge difficult regions.
When vessels are correctly extracted, the majority of the methods are accurate to within the image voxel size (AI < 0.4mm). The two methods that use a tubular shape model (MHT [69] and DepthFirst-ModelFit [57]) have the highest accuracy, followed by the multi-scale medialness-based AutoCoronary-Tree [54, 55] method and the CocomoBeach [56] method.
Overall it can be observed that some of the methods are highly accurate and some have great extraction capability (i.e. high overlap). Combining a fully-automatic method with high overlap (e.g. GVFTube’n’Linkage [58]) and a, not necessarily fully-automatic, method with high accuracy (e.g. MHT [69]) may result in an fully-automatic method with high overlap and high accuracy.
8.1. Results categorized on image quality, calcium score and vessel type
Separate rankings are made for each group of datasets with corresponding image quality and calcium rating to determine if the image quality or the amount of calcium has influence on the rankings. Separate rankings are also made for each of the four vessel types. These rankings are presented in Table 8. It can be seen that some of the methods perform relatively worse when the image quality is poor or an extensive amount of calcium is present (e.g. CocomoBeach [56] and DepthFirstModelFit [57]) and vice versa (e.g. KnowledgeBasedMinPath [65] and VirtualContrast [62]).
Table 8
Ranks per image quality; poor(P), moderate(M) or good(G), calcium score; low(L), moderate(M) or severe(S) and vessel type. The numbers indicate the rank of each team if only the specified datasets or vessels would have been taken into account.
| Method | Challenge | Image quality | Calcium score | Vessel | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | P | M | G | L | M | S | RCA | LAD | LCX | 4th | |
| MHT [69] | × | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| Tracer [70] | × | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | ||
| DepthFirstModelFit [57] | × | 5 | 4 | 3 | 4 | 3 | 5 | 5 | 4 | 5 | 3 | ||
| KnowledgeBasedMinPath [65] | × | 3 | 3 | 4 | 3 | 4 | 3 | 3 | 6 | 3 | 4 | ||
| AutoCoronaryTree [54] | × | 7 | 8 | 7 | 8 | 7 | 6 | 6 | 9 | 6 | 9 | ||
| GVFTube’n’Linkage [58] | × | 6 | 5 | 6 | 6 | 6 | 4 | 4 | 3 | 7 | 6 | ||
| CocomoBeach [56] | × | 12 | 7 | 9 | 9 | 8 | 8 | 8 | 8 | 10 | 8 | ||
| TwoPointMinCost [71] | × | 4 | 6 | 5 | 5 | 5 | 7 | 7 | 5 | 4 | 5 | ||
| VirtualContrast [62] | × | 9 | 11 | 12 | 12 | 10 | 9 | 11 | 10 | 12 | 10 | ||
| AxialSymmetry [63] | × | 8 | 9 | 8 | 7 | 9 | 12 | 10 | 11 | 8 | 7 | ||
| ElasticModel [67] | × | 11 | 12 | 10 | 10 | 12 | 11 | 9 | 12 | 11 | 12 | ||
| 3DInteractiveTrack [66] | × | 10 | 10 | 11 | 11 | 11 | 10 | 12 | 7 | 9 | 11 | ||
| CoronaryTreeMorphoRec [64] | × | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | ||
Table 8 also shows that on average the automatic methods perform relatively worse for datasets with poor image quality (i.e. the ranks of the automatic methods in the P-column are on average higher compared to the ranks in the M- and G-column). This is also true for the extraction of the LCX centerlines. Both effects can possibly be explained by the fact that centerline extraction from poor image quality datasets and centerline extraction of the (on average relatively thinner) LCX is more difficult to automate.
8.2. Algorithm performance with respect to distance from the ostium
For a number of coronary artery centerline extraction applications it is not important to extract the whole coronary artery; only extraction up to a certain distance from the coronary ostium is required (see e.g. [73, 74]).
In order to evaluate the performance of the methods with respect to the distance from the ostium, charts are generated that demonstrate the average performance over all 96 evaluated centerlines for each of the methods at a specific distance from the ostium (measured along the reference standard). Figure 7(a) shows these results for the automatic methods, Figure 7(b) shows the results for the methods with minimal user-interaction, and Figure 7(c) shows the results for the semi-automatic methods.
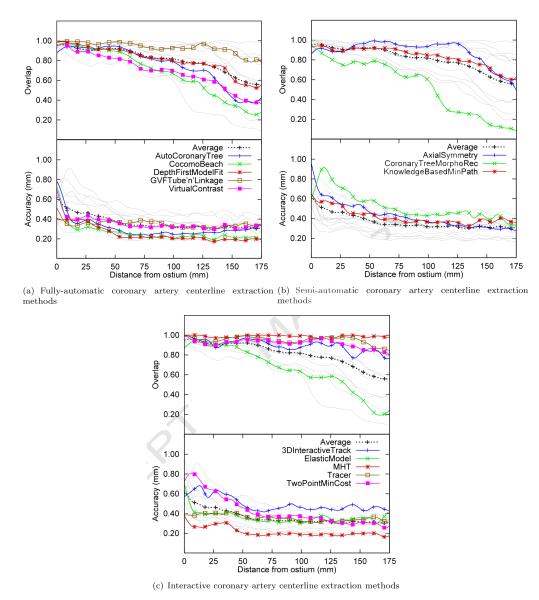
The algorithm performance of each method with respect to the distance from the ostium averaged over all 96 evaluated vessels over the first 175mm (only 10% of the vessels were longer than 175mm). Overlap: the fraction of points on the reference standard marked as true positive. Accuracy: the average distance to the centerline if the point is marked true positive. Each of the three graphs shows in light-gray the results of all the thirteen evaluated methods and in color the results of the respective algorithm category. The graphs also show in black the average accuracy and overlap for all thirteen evaluated methods.
The graphs show that all the evaluated methods are better able to extract the proximal part of the coronaries than the more distal part of the vessels.
They also show that after approximately 5 cm the accuracy of almost all the methods is relatively constant. Furthermore, the graphs again demonstrate the fact that the automatic methods are on average more accurate than the semi-automatic or interactive methods.
8.3. More statistics available online
Space limitations prevent us to incorporate more statistics here, but the on-line evaluation framework (http://coronary.bigr.nl) provides the possibilities to rank the methods based on different measures or scores, create statistics on a subset of the data and create overview tables for specific measures, categorized on image quality or score. It is for example possible to create Table 5, ,6,6, and and77 for a specific subset of the data or to create Table 8 with a measure or score of choice, instead of the overall ranks.
The website also contains the most recent version of the results. The on-line results may be different from the results reported in this paper because of recent improvements in implementation of the different methods.
9. Discussion
A framework for the evaluation of CTA coronary artery centerline extraction techniques has been developed and made available through a web-based interface (http://coronary.bigr.nl). Currently thirty-two cardiac CTA datasets with corresponding reference standard centerlines are available for anyone how wants to benchmark a coronary artery centerline extraction algorithm.
Although the benefits of a large-scale quantitative evaluation and comparison of coronary artery centerline extraction algorithms are clear, no previous initiatives have been taken towards such an evaluation. This is probably because creating a reference standard for many datasets is a laborious task. Moreover, in order to get a good reference standard, annotations are needed from multiple observers and combining annotations from multiple observers is known to be difficult [75] and until recently unexplored for three-dimensional curves [50]. Furthermore, an appropriate set of evaluation measures has to be developed and a representative set of clinical datasets have to be made available. By addressing these issues we were able to present and use the proposed framework.
A limitation of the current study is the point-based vessel selection step for fully-automatic methods. Because the coronary artery tree contains more vessels than the four annotated vessels this selection step had to be included, but it introduced the problem that fully-automatic methods can extract many false-positives but still obtain a good ranking. This fact combined with the presented results of the fully-automatic methods for the four evaluated vessels makes us believe that a future evaluation framework for coronary artery extraction methods should focus on the complete coronary tree. An obvious approach for such an evaluation would be to annotate the complete coronary artery tree in all the 32 datasets, but this is very labor intensive. An alternative approach would be to use the proposed framework for the quantitative evaluation of the four vessels and to qualitatively evaluate the complete tree. In this qualitative evaluation an observer should score if any vessels are falsely extracted and if all vessels of interest are extracted.
A further limitation of this study is that all the data have been acquired on two CT scanners of the same manufacturer in one medical center. We aim to extend the collection of datasets with datasets from different manufacturers and different medical centers. Further studies based on this framework could extend the framework with the evaluation of coronary lumen segmentation methods, coronary CTA calcium quantification methods or methods that quantify the degree of stenosis.
10. Conclusion
A publicly available standardized methodology for the evaluation and comparison of coronary centerline extraction algorithms is presented in this article. The potential of this framework has successfully been demonstrated by thoroughly comparing thirteen different coronary CTA centerline extraction techniques.
Acknowledgements
Michiel Schaap, Coert Metz, Theo van Walsum and Wiro Niessen are supported by the Stichting voor de Technische Wetenschappen (STW) of The Netherlands Organization for Scientific Research (NWO). Christian Bauer was supported by the Austrian Science Fund (FWF) under the doctoral program Confluence of Vision and Graphics W1209. The work of Hrvoje Bogunović has been partially funded by the Industrial and Technological Development Centre (CDTI) under the CENIT Programme (CDTEAM Project), the EC @neurIST (IST-FP6-2004-027703) project and the Networking Research Center on Bioengineering, Biomaterials and Nanomedicine (CIBER-BBN). Michel Frenay was supported by a research grant from Bio-Imaging Technologies. Marcela Hernández Hoyos and Maciej Orkisz were supported by ECOS-Nord #C07M04 and Region Rhone-Alpes PP3/I3M of cluster ISLE. Pieter Kitslaar was supported by innovation grant IS044070(ADVANCE) from the Dutch Ministry of Economic Affairs. Karl Krissian is funded by the Spanish government and the University of Las Palmas of Gran Canaria under the Ramon y Cajal program and he would like to acknowledge J. Pozo, M. Villa-Uriol, and A. Frangi for their contribution to this work. Luengo-Oroz and Carlos Castro would like to acknowledge Maria Jesus Ledesma-Carbayo for her supervision and the work of Luengo-Oroz and Carlos Castro was supported by the research projects TIN2007-68048-C02-01 from the Spanish Ministry of Education and Science and the CDTEAMproject from the Spanish Ministry of Industry (CDTI). Simon K. Warfield was supported in part by NIH grants R01 RR021885, R01 GM074068 and R01 EB008015. The work of Zambal et al. was in part funded by Agfa HealthCare and in part by the Austrian Kplus funding program.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
Full text links
Read article at publisher's site: https://doi.org/10.1016/j.media.2009.06.003
Read article for free, from open access legal sources, via Unpaywall:
https://cdr.lib.unc.edu/downloads/cn69mc016
Citations & impact
Impact metrics
Article citations
Graph neural networks for automatic extraction and labeling of the coronary artery tree in CT angiography.
J Med Imaging (Bellingham), 11(3):034001, 15 May 2024
Cited by: 0 articles | PMID: 38756439
Automated Coronary Artery Tracking with a Voronoi-Based 3D Centerline Extraction Algorithm.
J Imaging, 9(12):268, 01 Dec 2023
Cited by: 1 article | PMID: 38132686 | PMCID: PMC10743762
Using Deep Learning and B-Splines to Model Blood Vessel Lumen from 3D Images.
Sensors (Basel), 24(3):846, 28 Jan 2024
Cited by: 0 articles | PMID: 38339562 | PMCID: PMC10857344
A deep learning-based automated algorithm for labeling coronary arteries in computed tomography angiography images.
BMC Med Inform Decis Mak, 23(1):249, 06 Nov 2023
Cited by: 0 articles | PMID: 37932709 | PMCID: PMC10626726
Relationships between the coronary fat attenuation index for patients with heart-related disease measured automatically on coronary computed tomography angiography and coronary adverse events and degree of coronary stenosis.
Quant Imaging Med Surg, 13(12):8218-8229, 25 Sep 2023
Cited by: 1 article | PMID: 38106238 | PMCID: PMC10722073
Go to all (105) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Standardized evaluation framework for evaluating coronary artery stenosis detection, stenosis quantification and lumen segmentation algorithms in computed tomography angiography.
Med Image Anal, 17(8):859-876, 04 Jun 2013
Cited by: 45 articles | PMID: 23837963
Model-based automatic segmentation algorithm accurately assesses the whole cardiac volumetric parameters in patients with cardiac CT angiography: a validation study for evaluating the accuracy of the workstation software and establishing the reference values.
Acad Radiol, 21(5):639-647, 01 May 2014
Cited by: 7 articles | PMID: 24703477
Robust and accurate coronary artery centerline extraction in CTA by combining model-driven and data-driven approaches.
Med Image Comput Comput Assist Interv, 16(pt 3):74-81, 01 Jan 2013
Cited by: 13 articles | PMID: 24505746
Coronary CTA: stenosis classification and quantification, including automated measures.
J Cardiovasc Comput Tomogr, 3 Suppl 2:S109-15, 30 Oct 2009
Cited by: 2 articles | PMID: 20129518
Review
Funding
Funders who supported this work.
NCRR NIH HHS (1)
Grant ID: R01 RR021885
NIBIB NIH HHS (1)
Grant ID: R01 EB008015
NIGMS NIH HHS (1)
Grant ID: R01 GM074068