ODE, RDE and SDE models of cell cycle dynamics and clustering in yeast.

Boczko EM; Gedeon T; Stowers CC; Young TR

doi:10.1080/17513750903288003

ODE, RDE and SDE models of cell cycle dynamics and clustering in yeast.

Affiliations

1. Department of Biomedical Informatics, Vanderbilt University, Nashville, USA.
Authors
Boczko EM¹
(1 author)

Journal of Biological Dynamics, 01 Jul 2010, 4(4):328-345
https://doi.org/10.1080/17513750903288003 PMID: 20563236 PMCID: PMC2885793

Free full text in Europe PMC

Abstract

Biologists have long observed periodic-like oxygen consumption oscillations in yeast populations under certain conditions, and several unsatisfactory explanations for this phenomenon have been proposed. These ‘autonomous oscillations’ have often appeared with periods that are nearly integer divisors of the calculated doubling time of the culture. We hypothesize that these oscillations could be caused by a form of cell cycle synchronization that we call clustering. We develop some novel ordinary differential equation models of the cell cycle. For these models, and for random and stochastic perturbations, we give both rigorous proofs and simulations showing that both positive and negative growth rate feedback within the cell cycle are possible agents that can cause clustering of populations within the cell cycle. It occurs for a variety of models and for a broad selection of parameter values. These results suggest that the clustering phenomenon is robust and is likely to be observed in nature. Since there are necessarily an integer number of clusters, clustering would lead to periodic-like behaviour with periods that are nearly integer divisors of the period of the cell cycle. Related experiments have shown conclusively that cell cycle clustering occurs in some oscillating yeast cultures.

Free full text

J Biol Dyn. Author manuscript; available in PMC 2011 Jul 1.

Published in final edited form as:

J Biol Dyn. 2010 Jul 1; 4(4): 328–345.

https://doi.org/10.1080/17513750903288003

PMCID: PMC2885793

NIHMSID: NIHMS147352

PMID: 20563236

ODE, RDE and SDE Models of Cell Cycle Dynamics and Clustering in Yeast

Erik M. Boczko, Chris C. Stowers, Tomas Gedeon, and Todd R. Young^*

Author information Copyright and License information Disclaimer

See other articles in PMC that cite the published article.

Go to:

Abstract

Biologists have long observed periodic-like oxygen consumption oscillations in yeast populations under certain conditions and several unsatisfactory explanations for this phenomenon have been proposed. These “autonomous oscillations” have often appeared with periods that are nearly integer divisors of the calculated doubling time of the culture.

We hypothesize that these oscillations could be caused by a form of cell cycle synchronization that we call clustering. We develop some novel ordinary differential equation models of the cell cycle. For these models, and for random and stochastic perturbations, we give both rigorous proofs and simulations showing that both positive and negative growth rate feedback within the cell cycle are possible agents that can cause clustering of populations within the cell cycle. It occurs for a variety of models and for a broad selection of parameter values. These results suggest that the clustering phenomenon is robust and is likely to be observed in nature. Since there are necessarily an integer number of clusters, clustering would lead to periodic-like behavior with periods that are nearly integer divisors of the period of the cell cycle.

Related experiments have shown conclusively that cell cycle clustering occurs in some oscillating yeast cultures.

Keywords: Autonomous Oscillations, Cell Cycle, Budding Yeast

Go to:

1 The Yeast Cell Cycle and Experimental Observations

Klevecz [37], McKnight [48], and others have observed oscillations in the dissolved O₂ levels of various strains of budding yeast under certain conditions. For instance in Figure 1 we show data from such an experiment for the yeast strain Cen.PK 113 [44, 45, 40]. It is seen in this experiment that dissolved O₂ levels oscillate between about 5% to 55%, with a period of a little less than 4 hours. Since the doubling time (as calculated from the dilution rate) for this culture was 7.8 hours it is natural to suppose that the doubling time and O₂ oscillations are causally related.

An external file that holds a picture, illustration, etc.
Object name is nihms147352f1.jpg

Figure 1

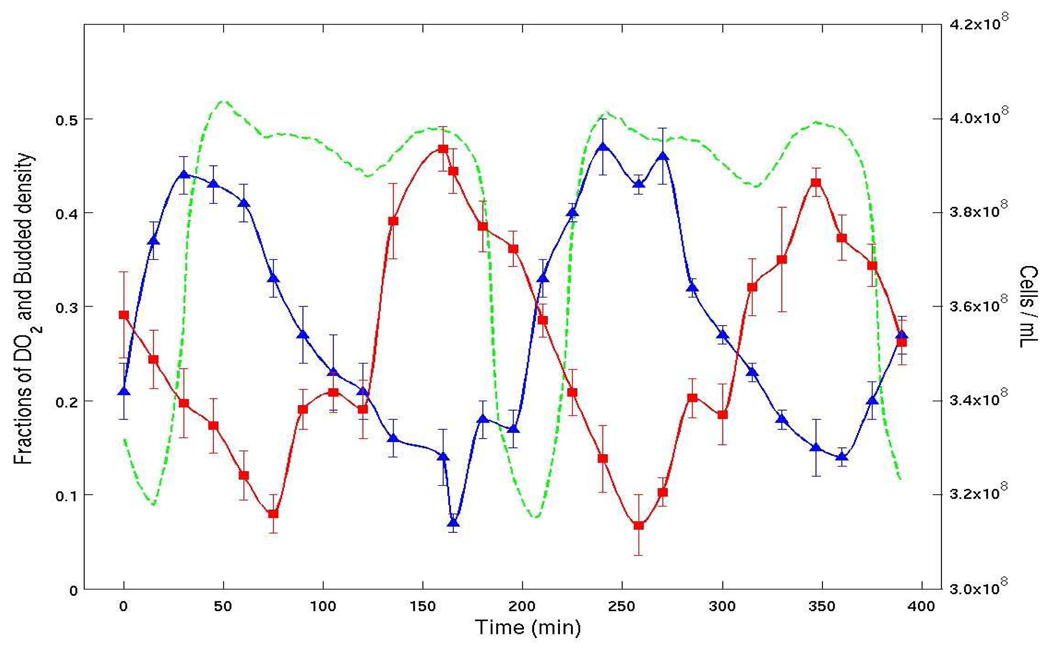
Percent Dissolved O₂ (green), bud index (blue) and cell density (red). The bud index (percentage of cells with buds) and cell density are both synchronized with the oscillation in the level of dissolved O₂. Moreover, time periods of sharp increases in bud index percentage show that a cluster of cell (consisting of almost 50% of the cells) is passing into S phase together. The doubling time of this culture is 7.8 hours. Two oscillations per 7.8 hour period also is consistent with two clusters of cells.

Autonomous oscillations been the subject of speculation and analysis [44, 8, 12, 21, 22, 23, 38, 40, 48, 52]. Cultures exhibiting O₂ oscillations, although planktonic, are dense; the average distance between cells has been reported to be on the order of 1 cell diameter [37]. Observations such as these suggest the involvement of quorum sensing. Indeed, Klevecz and others have suggested that signaling is responsible for the O₂ oscillations based on the observation that acetyaldehyde and H₂S pulses reset the phase of the oscillations [32, 37]. Alternative explanations involving signaling have been proposed. For instance [23] has suggested an elegant mechanism in which the periodic consumption of metabolites can stabilize population synchrony.

Because the mitotic cell cycle of budding yeast plays an important role as a coordinate in the ensuing analysis and theory we briefly describe some of the relevant facts and nomenclature.

Detailed reviews of the physiology and genetics of the budding yeast cell cycle abound [4, 19, 20, 30, 35], to list only a few. The mitotic cell cycle entails the process of DNA duplication, daughter cell growth and the subsequent cell division. The division processes in budding yeast is asymmetric in the sense that it results in a distinguishable mother and daughter cell. The daughter cell at division is typically smaller in volume than the mother cell [50]. Only the mother cell carries an observable and permanent chitanous bud scar at the site of daughter cell growth. The number of bud scars determines a yeast cell’s replicative age, to be distinguished from its chronological age. The bud scar equivalence classes are henceforth called generations. The emergence of a single bud, as opposed to multiple buds, per division cycle is tightly regulated.

As depicted in Figure 2, the mitotic cell cycle is typically partitioned into four phases, canonically enumerated in the sequence: G1, S, G2 and M. The DNA is replicated during the S-phase and its temporal duration is the least variable [2, 9, 42, 43]. The G1 phase duration is observed to be the most variable. During the G1 phase environmental cues are integrated and synthetic precursors are obtained. Volumetric growth of the mother-daughter pair is observed to be monotone along the cell cycle in single cells [28, 47, 51], with growth and division jointly regulated by an as yet incompletely understood genetic network [31]. A complete causal description of the transition from G1 to S remains open [6, 30]. This transition closely coincides with the phenomena of bud emergence.

An external file that holds a picture, illustration, etc.
Object name is nihms147352f2.jpg

Figure 2

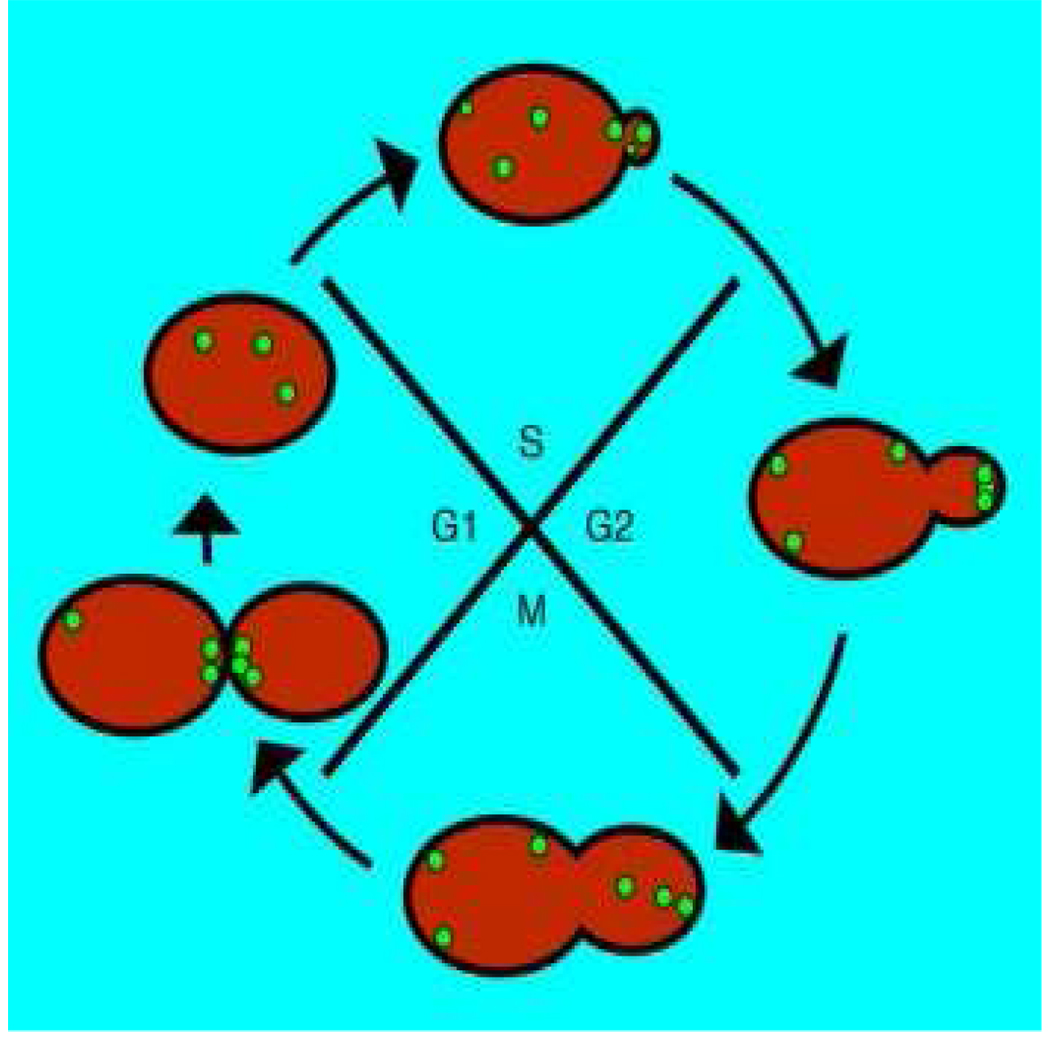
Phases of the yeast cell cycle. DNA is replicated in the synthetic or S-phase. DNA synthesis is preceded by the G1 phase, in which environmental cues are integrated and precursors are acquired. Our model explores the implications of the existence of a responsive R-phase, situated within the G1-phase, during which cells are can respond to signals by increasing or decreasing their growth rate. The M phase ends in cell division.

In this article we study the implications of the hypothesis that cells in the S-phase can effect the growth rate of cells in a responsive phase (denoted as R) situated in the G1 phase. The growth rate modulation can be either positive or negative. We show rigorously and numerically in simple models that various forms of signaling among cells, with either positive or negative feedback, robustly leads the population density to become multimodal or clustered within the cell cycle.

We propose here that dissolved O₂ oscillations in some strains could be due to a phenomenon that we will call clustering. In general we will define clustering loosely as significant groups of cells going through cell cycle milestones at approximately the same time, i.e. there is a form of temporal synchronization. The clustering could cause fluctuations in the O₂ dilution levels by clusters passing in and out of high oxygen metabolism phases of the cell cycle, i.e. G1 phase.

We will prove mathematically in idealized models that clustering occurs and that the number of clusters formed depends on the widths |S| and |R| of the S-phase and the hypothesized region R. Of key importance is the necessity that if clustering occurs, then there are an integer number of clusters. This can provide the basis for a periodic-looking behavior with a period which is approximately an integer divisor of the cell-cycle length. Models for which proofs are constructed include noisy or randomly perturbed models. We use simulations to demonstrate that the same type of behavior occurs in more detailed models.

In prior work [44, 45, 40] we have shown through an analysis of the bud index and cell density time-series (see Figure 1) that clustering occurs, and have proposed how the periodic population phenomena could be exploited to enhance bioprocess.

In this paper we focus on models that assume that the cell cycles of different generations are identical, or nearly so. Although this assumption is not justified in general yeast cultures, there is some evidence for it in the cultures under study. In conditions where the oscillations have been observed, the doubling time of the culture is extended significantly, by a factor of about 4. It is known, and confirmed in [44, 45, 40], that when the cell cycle is extended, most of the extension occurs in the G1 phase. Age dependent differences in cell cycle duration have been observed and quantified [50], and are attributed to differences in G1 duration, although this will require further quantization at the single cell level [47, 51]. Regardless, during autonomous oscillation the extending the doubling time effectively elongates the cycles of all the generations to such an extent that the relative differences become insignificant. The Age distribution provides further evidence that the assumption of equal cell cycle length for different generations is approximately true in the cited experiments.

In addition to models with the assumptions of identical or nearly identical cell cycles we also briefly treat models with relative differences across generations and cases where even larger differences could still lead to clustering. In [44, 45], we have explored a model with stratified generations under various assumptions and using biologically relevant values for all the parameters that can be determined. In all these models clustering emerges as a common and robust phenomenon.

Go to:

2 Models of Cell Cycle Dynamics and Clustering

2.1 A general model for the cell cycle of an individual cell

We will begin by defining a normalized logarithmic scale to represent the cell cycle. Customarily, the cell cycle is delineated by volume milestones. For a given cell, indexed by i, let υ_i(t) denote its volume. It is usually assumed that the volume growth of a cell in a culture is proportional to its volume, i.e.

\frac{d υ_{i}}{d t} = c_{i} (t) υ_{i}

where the relative growth rate c_i(t) may depend on many factors, such as available resources, chemical composition of the culture substrate, etc [11, 27, 29, 49]. We will allow that the growth rate may also be influenced by the state of the cell itself, thus the cell may react to environmental factors in differing ways at different stages of its cycle. The environmental factors in turn may be influenced by the cells in the culture and their history. Finally, the individual cells may have individual differences. Without any loss of generality, we may include all of these factors in the rate c_i(t).

Let V_b,i denote the volume of the cell at the beginning of it cell cycle and V_d,i its volume at division. In order to have x_i [set membership] [0, 1) we make the change of variables:

x_{i} = \frac{ln (υ_{i} / V_{b, i})}{ln (V_{d, i} / V_{b, i})} .

With this change birth has coordinate x_i = 0 and division occurs at x_i = 1. We have then that x_i satisfies

\frac{d x_{i}}{d t} = d_{i} (t) \equiv \frac{c_{i} (t)}{ln (V_{d, i} / V_{b, i})} .

Next we may rescale time so that the average time span of a cell cycle in the culture is normalized to 1, i.e. scale by a factor 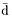(t) which is the average (over all cells) growth rate in a culture. In making this change of time we obtain

\frac{d x_{i}}{d t} = \frac{d_{i} (t)}{\bar{d} (x)} .

If the variation between individual cells is not too great then the right hand side of this equation is approximately 1. Next, we distinguish between those influences on the growth rate that are common to all the cells in the culture and those due to individual differences. The common features we allow to depend on the state, x_i of the cell itself, as well as the conglomerate history of the whole culture, which we denote by . Denote the common part of the growth rate as a and the individual part as g_i. We can thus write the equation as:

\frac{d x_{i}}{d t} = a (t, x_{i}, \bar{x}) + g_{i} (t) .

(2.1)

The part of the growth rate due solely to individual differences in cells is contained in the term g_i. In many applications this term will be relatively small and “random” in the sense that differences are due to details of the cell process that are far too minute and complex to model. It contains both variations in the growth rate and differences in V_b,i and V_d,i. Thus we may view (2.3) as a Random Differential Equation (RDE) [3]. A reasonable approximation of this equation in some circumstances is to replace g_i by a stochastic term:

d x_{i} = a (t, x_{i}, \bar{x}) d t + \sqrt{σ} d W_{i},

(2.2)

where dW_i represents an independent noise term. This Stochastic Differential Equation (SDE) must be interpreted in the usual way as an Ito integral equation. For other possible stochastic approximations see [1]. It is also reasonable under certain circumstances to consider (2.1) and (2.2) as perturbations of an Ordinary Differential Equation (ODE)

\frac{d x_{i}}{d t} = a (t, x_{i}, \bar{x}) .

(2.3)

This model allows for variation of the growth on state within the cell cycle and the overall state of the system, but ignores differences between individual cells. We will consider versions of this model in the rest of this section. In the next two sections we will consider (2.1) and (2.2) as perturbations of (2.3).

2.2 Model of the culture

First of all, we note that in a culture, cells are constantly dividing, dying and perhaps being harvested. Thus the equations above must be applied to a changing set of cells, indexed by a changing finite set of positive integers S(t) [subset or is implied by] . If the i-th cell dies or is harvested, then i is dropped from S. When a cell divides, one of the new cells could continue being denoted by i, with x_i resetting to 0 and the other (daughter cell) would be identified by a new index. This would be appropriate in budding yeast where the mother and daughter cells are distinguishable. The conglomerate history would contain each x_i over its respective lifespan.

Now suppose that we are considering the unperturbed equation (2.3). Since in this model there are no terms that differentiate the progression of different cells, when a cell divides its two descendants will both start at x_i = 0 and remain completely synchronized for the rest of their lifespans. Thus tracking the evolution of both cells is redundant in this model and we are inevitably led to consider a fixed set of cells. If the culture is in a steady or periodic state, then there is also a probabilistic interpretation of this simplification; given a living cell at time t, the expected number of cells descended from that cell at any later time t + n is exactly 1. Thus the original model with a changing index set S can be replaced by a fixed system, each variable x_i(t) representing the state of its expected descendant at time t. A PDE justification of considering a fixed index set appears in the appendix.

With a fixed index set, this model is easily amenable to numerical investigation with currently available computer speeds. For instance, one can easily investigate the behavior of a conglomeration of 10,000 or more cells over several cell cycles on a desktop workstation. Further, under some additional assumptions on the dependence of a and g_i, we can investigate properties of the solutions of (2.3) and (2.1) rigorously as we show below.

2.3 Modeling of the growth term a

The standard biological assumption on a is that it does not depend on x_i i.e. it is independent of the cell’s current state within the cycle. Rather it is assumed to depend mostly on the nutrients available and other environmental factors. With these assumptions a = a(t, ).

As already described above, we hypothesize a more sophisticated form for a, in which the location of cells in cell cycle may influence the growth rate of themselves and other cells, i.e.

a = a (t, x_{i}, \bar{x}) .

For example in budding yeast it has been hypothesized that cells in the S phase may influence the growth of cells in the pre-budded G1 phase through some (unspecified) signaling mechanism [7, 17, 24, 36].

In our models the population of cells in the S-phase will be assumed to effect the growth of cells in a preceding portion of the cell cycle which we denote by R = [r,s], i.e. a portion of the G1-phase. As explained in the previous section and in the appendix will consider a fixed finite population of N cells, each of them progressing via the following form of (2.3)

\frac{d x_{i}}{d t} = {\begin{array}{l} 1 & if & x_{i} \notin R \\ 1 + F (# {cells in S}) & if & x_{i} \in R . \end{array}

(2.4)

When a cell in the model reaches division at x = 1 it returns to the beginning of the cycle, x = 0. The phase space for each individual cell is thus the unit circle and the phase space of the entire culture is the N-torus. In this section we will consider two idealized (and discontinuous) forms of positive and negative F that we call the advancing and blocking. Our motivation for considering such models is that they are analytically tractable. Also, biologically it is known that the introduction of certain compounds has been shown to arrest or rapidly accelerate cell processes in budding yeast and other micro-organisms [37, 8, 16, 26]. Note that periodic blocking at division was considered by [41].

By the advancing model we will mean that if the fraction of cells in S exceeds some threshold τ, then all cells in R are instantaneously advanced to the beginning of S, from which they resume normal growth. This corresponds to a limit F → ∞ in (2.4) when #{cells in S} ≥ τ and F = 0 when #{cells in S} < τ.

By the blocking model we mean that if the fraction of cells in S equals or exceeds some threshold τ, then cells at s are blocked from proceeding into the S-phase, until the fraction of cells in S drops below the threshold. This corresponds to choice F = −1 when x_i = s and #{cells in S} ≥ τ and F = 0 when #{cells in S} < τ. If more than τ cells have accumulated at s, then all of those cells will enter S together when the fraction of cells drops below τ.

Note that the advancing and blocking models are defined in terms of their flow directly, thus the solution flow is unique. Since the phase space is compact the flow is global.

2.4 Clustering

Under either the advancing or blocking models, it is clear that some cells may become synchronized. Consider the advancing model; whenever the fraction of cells in S exceeds the threshold τ, then all cells in R are instantaneously synchronized at s. There being no mechanism in the model to subsequently differentiate them, they will remain synchronized from then on. Similarly, for the blockling model, during a period when the threshold is exceeded, all cells arriving at s will be thereafter synchronized. We will call a group of synchronized cells a cluster. If the number of cells in a cluster is large enough to exceed the threshold of the model, we call it a critical cluster.

Given an initial (discrete) distribution (0) or $w (s) = \sum_{i = 1}^{N} δ_{x_{i} (0)} (s)$ the evolution of such distribution under either model will be called a trajectory starting at w(s) and denoted by [var phi] (t, w(s)). It is clear that different trajectories can merge.

A trajectory is called an equilibrium if it is stationary in the coordinate frame moving with the speed 1. In other words, ϕ(t, w(s)) = w((x − t) mod 1) for all t ≥ 0. A periodic orbit is a trajectory which is periodic in the moving frame. In such a case there exists T with ϕ(T + t, w(x)) = ϕ(t, w((x))) for all t [set membership] [0, T]; if T is the smallest number with this property, it is called a period.

2.5 Advancing model

Denote by [left floor] x [right floor] the largest integer ≤ x and by [left ceiling] x [right ceiling] the smallest integer ≥ x.

Theorem 2.1

Consider the advancing model.

If the initial w(x) exceeds the threshold on all intervals of length |S|, except possibly inside the interval R, then the trajectory converges to a periodic orbit.
Any initial w(x) that is below threshold on all intervals of length |S|, is an equilibrium point.
Every other initial condition converges to an equilibrium e with a finite number of critical clusters, separated by voids of length at least |R| + |S|.

Proof

Let

q(t, x) = ∫_{[x,x+|S|] mod 1}ϕ(t, w(z))dz.

(2.5)

The function q(t, x) is a form of local density of the discrete distribution of cells. Observe that if q(0, x) < τ for all x then this is a fixed point of the dynamics. This corresponds to the case B above.

The case A corresponds to the case when q(0, x) ≥ τ for all x, except for x [set membership] R. At t = 0 all cells in R are advanced to the point s. Since the q(0, x) ≥ τ for all x the cells arriving at r, the start of the interval R, are immediately transferred to the point s. This continues indefinitely. This trajectory is a periodic orbit in the moving frame.

Now we do the analysis of the case C. Let q(i, x), i = 0, 1,… be the mass function after i passes though the cell cycle. We decompose the domain I = [0, 1] into intervals $I_{1}^{i} \cup J_{1}^{i} \cup \dots \cup J_{n - 1}^{i} \cup I_{k}^{i}$ where q(i, x) ≥ τ for all $x \in I_{j}^{i}$ and q(i, x) < τ for all $x \in J_{j}^{i}$ . Set $I_{j}^{i} ≔ [d_{j}^{i}, c_{j}^{i}]$ . We compare the intervals $I_{j}^{i}$ from iteration to iteration. There are several possibilities that can happen to $I_{j}^{i}$ after a passage through a cell cycle:

The interval $I_{j}^{i}$ will shorten by |R| and $I_{j}^{i + 1} = [d_{j}^{i} + | R |, C_{j}^{i}]$ .
The intervals $I_{j}^{i}, \dots, I_{j - k}^{i}$ may merge, if all intervals in between fall within distance |R| i.e. $c_{j}^{i} - c_{j - k}^{i} < | R |$ ;
If an interval $I_{j - 1}^{i}$ follows the interval $I_{j}^{i}$ by a distance closer then |R| + |S| i.e. $d_{j}^{i} - c_{j - 1}^{i} \leq | R | + | S |$ , then the interval $I_{j - 1}^{i}$ , or a portion of that interval, will be promoted across R. The resulting distance between the two new intervals will be less then |S|. After each subsequent pass the distance between these two intervals will shorten by |R| and in finite number of steps they will be within |R| of each other and they will merge. The number of steps this takes is uniformly bounded above by $l ≔ \frac{| S |}{| R |} + 1$ . This process may result in a split of an interval $I_{j}^{i}$ into two intervals with the total mass conserved in the transaction. Notice that even though temporarily the number of intervals $I_{j}^{i + 1}$ may increase over the number $I_{j}^{i}$ , after k subsequent passes through S the number of intervals $I_{j}^{i + k}$ is less or equal to number of intervals $I_{j}^{i}$ .
The interval $I_{j}^{i}$ may shorten, if the preceding interval $I_{j + 1}^{i}$ has critical mass in S and therefore promotes part of the mass ahead of $c_{j}^{i}$ across R. Since a mass ahead of $c_{j}^{i}$ is lost, $c_{j}^{i + 1} < c_{j}^{i}$ . The difference between this case and case (3.) is that here $| R | + | S | \leq d_{j}^{i} - c_{j - 1}^{i} \leq | R | + | S | + | S |$ . Observe, that the transferred cells will not form a new interval $I_{j}^{i + 1}$ , since they do not have a sufficient mass.

In summary, the number of intervals $I_{j}^{i}$ is greater or equal to the number of intervals $I_{j}^{i + k}$ for every i and the length of each intervals is a non-increasing function of i. Finally, it is easy to see that the only interval $I_{j}^{i}$ that will not change under the advance operator, is a singleton $I_{j}^{i} = [c_{j}^{i}, c_{j}^{i}]$ . Since the population is finite, after a finite number of passes through S, each I_j is a singleton. If two such singletons follow each other closer then |R| + |S|, by the step 3. above, they will merge in finite number of steps. Eventually all remaining singletons I_j are followed by a empty void of length |R| + |S|.

Corollary 2.2

In the advancing model no more than [left floor] (|R| + |S|)⁻¹ [right floor] critical clusters can persist.

Proof

By the previous Theorem each critical cluster has to be followed by gap of length at least |R| + |S|.

2.6 Blocking model

Theorem 2.3

In the blocking model no more than [left ceiling] |S|⁻¹ [right ceiling] critical clusters can persist.

Proof

When two consecutive critical clusters pass through S, the second cluster must wait at s until the first cluster has passed t. Thus the distance between them must then be at least |S| and will remain at least |S| until the first cluster hits r. Then the first cluster may have to wait to enter S, possibly decreasing the distance between the two clusters in question.

Assume that the number n of persistent clusters is constant along some trajectory. Then either all these clusters are separated by a distance at least |S|, or there are n − 1 clusters separated by a distance |S| and there is an additional cluster inside S whose distance to a waiting cluster at s is smaller than |S|.

This minimal spacing implies that

(n − 1)|S| ≤ 1.

The result then follows.

We have shown that a cluster cannot persistently follow a critical cluster closer than |S| (except while the critical cluster is being blocked at s). Also, it is clear that as many as [left ceiling] |S|⁻¹ [right ceiling] critical clusters may persist if the overall number N of cell satisfies:

N > τ ⌈|S|⁻¹⌉.

Recall the definition of q(t, x) in (2.5).

Theorem 2.4

In the blocking model, if the cells are initially distributed so that the density q(x, 0) everywhere exceeds twice the threshold, then exactly [left ceiling] |S|⁻¹ [right ceiling] clusters will develop and persist.

Proof

Cells at s are initially stopped from entering S until the fraction of cells in S drops below the threshold. Since d(|S| −t) = τ, this will occur at

t = | S | - \frac{τ}{d} .

At this time the cells that have clustered at s number dt or d|S| − τ. Since d|S| is assumed to be at least twice τ, the threshold is again exceeded as the cluster enters S. The threshold will continue to be exceeded until this cluster leaves S. At this time a new cluster will have formed at s with volume d|S| which is by assumption above τ. The second cluster is spaced exactly distance |S| behind the first cluster. At third cluster, etc. will form in the same way until the first cluster returns to s. At that time there is either a cluster in the interior of S or at t. In the former case the first cluster will wait less than time |S| to enter S, ahead of when the second cluster arrives. In the latter case it enters S immediately. This scenario will repeat itself indefinitely and the number of critical clusters thus produced is an easy calculation.

Go to:

3 Small Perturbations of the Advancing and Blocking Models

3.1 Small Perturbations

Next we consider small perturbations of the advancing and blocking models by which we mean that the progression of each individual cell is independently perturbed by a small term which is independent of the other cells.

\frac{d x_{i}}{d t} = {\begin{array}{l} 1 + ε ξ_{i} (x_{i}, t) & if & x_{i} \notin R \\ 1 + F (# {cells in S}) + ε ξ_{i} (x_{i}, t) & if & x_{i} \in R, \end{array}

(3.1)

where |ξ_i(x_i, t)| ≤ 1 and ε is small. We will take as our definition of small that ε is smaller than min(|S|, |R|)/6. The effect of the perturbation is to cause initially synchronized cells to drift from each other, but by no more than 2ε or min(|S|, |R|)/3 within a single cell cycle. Note that under these assumptions (3.1) can be considered as a random differential equation with bounded noise. For general results about RDE with bounded noise see [25].

Note that this model can viewed as a relaxation of the assumption that cells are indistinguishable. It also can be considered as incorporating random variations and noise.

With these perturbations, clusters will not remain precisely synchronized as in the unperturbed models, but rather will spread out as the cells proceed through the cell cycle. We now expand our definition of cluster to include any group of at least τ cells that are within |S|/3 of each other in the cell cycle.

Below we will assume that the small perturbations act like noise in the ways we define below. We say that perturbations satisfy the maximum principle if

max_{x} q (t_{1}, x) > max_{x} q (t_{2}, x)

and

min_{x} q (t_{1}, x) < min_{x} q (t_{2}, x)

for any t₁ < t₂ that are not separated by an activation or deactivation of blocking or advancing. We will say that the perturbations are diffusive if:

the perturbations satisfy the maximum principle.
synchronized cells will immediately de-synchronize.

3.2 Perturbed Blocking Model

Theorem 3.1

In the blocking model with small diffusive perturbations such that ε < |S|/6, and an initial distribution of cells that satisfies q(0, x) > 2τ + 2ε for all x, the system will form either [left floor] |S|⁻¹ [right floor] , [left ceiling] |S|⁻¹ [right ceiling] , or, |S|⁻¹ + 1 critical clusters within one cell-cycle period and these clusters will persist indefinitely.

Proof

Denote d = min q(0, x). Cells at s are initially blocked from entering S until the fraction of cells in S drops below the threshold. This will occur at time t₀ no smaller than

t_{0} = \frac{| S | - \frac{τ}{d}}{1 + ε} .

At this time the cells that have clustered at s number at least t₀d or (d|S| − τ)/(1 + ε). This group of cells we will call cluster 1. By the assumptions, the threshold is again exceeded as the cluster enters and crosses S. While crossing S the cluster will de-synchronize, but all the cells will remain in S for at least t₁ = |S|/(1 + ε) and no longer than |S|/(1 − ε). Thus while the first cluster crosses S at least t₁d or d|S|/(1 + ε) cell accumulate at s. This group we call the second cluster and from the assumption q(0, x) > 2τ + 2ε it is critical. Its crossing time t₂ will again be bounded below by |S|/(1 + ε) and above by |S|/(1 − ε) and so this process of cluster formation will continue for as long as a density of cells at least d is arriving at s.

By a straight-forward calculation, the gap between any two adjacent clusters formed in this process is bounded below by:

| S | \frac{1 - ε}{1 + ε}

and obviously the gap is bounded above by |S|. If the first of two adjacent clusters travel at the minimal speed 1 − ε while outside of S, all the cells in the first cluster must arrive again at s no later than:

t^{*} = \frac{1}{1 - ε} - \frac{| S |}{1 + ε},

after cluster 2 leaves S. During the same time period the second of the adjacent clusters can travel at a rate at most 1 + ε and thus can travel a distance of no more than

d^{*} = t^{*} (1 + ε) = \frac{1 + ε}{1 - ε} - | S | < 1 .

Therefore the entirety of the first cluster must reach s before any of the second cluster does so. The gap at that time is at least

1 - d^{*} = | S | - \frac{2 ε}{1 + ε} > \frac{2 | S |}{3} .

Next consider the relative motion between the cells that began in S and the cells in cluster 1. Note that the initial gap will be at least |S|/2. Since ε < |S|/4, the last of the cells will reach s before the first cluster returns.

When cluster 2 leaves S, it is easily shown that the gap between cluster 1 and 2 is no wider than

| S | \frac{1 + ε}{1 - ε} < | S | (1 + 2 ε) .

At the same time the gap between cluster 1 and 3 is no more than the gap between cluster 1 and 2 plus |S|. That is,

2|S|(1 + ε).

When cluster 3 reaches t, the gap between clusters 1 and 3 is no more than

2 | S | (1 + ε) + | S | \frac{1 + ε}{1 - ε} - | S | < 2 (1 + 2 ε) | S | .

By induction one can show that the first cluster can be no more that

(j − 1)(1 + 2ε)|S|

ahead of the j-th cluster when the j cluster is at t. From this we can show that at least [left floor] |S|⁻¹ [right floor] clusters will form.

On the other hand, when cluster 2 leaves |S| the gap between clusters 1 and 2 must be at least

\frac{2}{1 + ε} | S |

and cluster 1 must be at least

\frac{j - 1 - ε}{1 + ε} | S |

ahead of the j-cluster. It is clear then that j must be less than [left ceiling] |S|⁻¹ [right ceiling] + 1.

Now to show that the clusters persist. Clearly, while cluster 1 is passing through the cycle the first time, there is always a critical cluster in S, at least until the cells that began in S again reach S. Note that the cells which were inside S when the first cluster was released from s are critical in number. We will call this group of cells the tail. When the tail begins to arrive back at S, its leading edge can be no more than

\frac{| S | (1 - | S |)}{1 - ε}

ahead of cluster 1. At that moment there will either be (1) a critical in the interior of S, or, (2) there are critical clusters at both ends of S. Let us consider case (2) first. In this case the cluster at the beginning of S will be critical and as it enters S the cells from tail will be blocked at s. Since the original width of the tail is less than |S|/2, its width when it reaches S will be less than 2|S|/3 and it will all reach S before the cluster ahead of it leaves S. Now two things can happen, both of which continue the process, either all or part of cluster 1 reaches S while the tail is blocked there, or it will be blocked by the tail. In the former situation part or all of cluster 1 will merge with the tail and be blocked and in the later the entirely of cluster will be blocked by the tail. Either way cluster 1 is blocked and will be inside S when cluster 2 arrives back. Now in case (1) all or part of the tail will reach S and be blocked while the previous cluster clears S. It will merge with other cells blocked at S and they will be a critical cluster when they are released. Thus when cluster 1 arrives at S, the last cluster including part or all of the tail will still be in S. Again in this case cluster 1 is blocked before reentering S and will be inside S when cluster 2 arrives. Now in either case cluster 1 is not only blocked, but resynchronized as it is blocked. The same happens for the subsequent clusters and the process continues.

3.3 Perturbed Advancing Model

First we note the lack of rigorous results for this model. We are not able to prove anything similar to Theorem 3.1. This lack of results, however is suggestive that the advancing model does not form clusters as naturally as does the blocking model.

For this model we can make the following observation: In the advancing model with small random perturbations and |R| = |S|, an initial single critical cluster will have “forward leakage.” Wherever a cluster begins in the cell cycle, when its edge reaches s it will have positive width. As some of the cells enter S the threshold will be exceeded, and the rest of the cells will be promoted to s. The cluster will then proceed around the cell cycle. When its edge reaches S again, its width will be larger and the leading edge flatter than during the previous cycle. Thus the front edge will reach deeper into S before the advance takes place. Thus the front edge of the cluster will grow wider and wider on each pass until some of the cells are able to pass through S completely before advance occurs. At this point these cells have essentially escaped from the cluster.

Note that the cells which leak forward may eventually slow down and drop back into the cluster, or, if they continue at a faster rate than the cluster will eventually be caught in the next cluster (or into the original cluster if it is the only one.) This implies that there may be steady states which have persistent clustering, but the cells in the clusters may not actually be synchronized in the strict sense.

Go to:

4 Linear feedback models and simulations

4.1 Graduated but unstratified model

Next we consider more realistic models. Rather than strict advancing and blocking we consider the possibility that the number of cells in S either act to slow down or speed up cell growth in the preceding region R. The population of cells in the S-phase is hypothesized to effect the growth of cells in a preceding phase R = [r, s] via a continuous function. This influence will be assumed to be a function of the number of cells in the S phase. Thus we have the following equations of motion:

d x_{i} = {\begin{array}{l} d t + \sqrt{σ} d W_{i} & if & x_{i} \notin R \\ (1 + F (# {cells in S})) d t + \sqrt{σ} d W_{i} & if & x_{i} \in R . \end{array}

(4.1)

Note that this form is quite general since we might consider any functional dependence F and R could be large or small.

We report simulations of this model where we will assume F to be linear function F(x) = ax, with a < 0 for the negative feedback model and a > 0 for the positive model. For example a nonlinear model would be obtained if F was a sigmoidal Hill function $F (x) = \frac{A}{1 + {(x / τ)}^{n}}$ . In the negative case in the limit of Hill coefficient n → ∞ we obtain a strict blocking model described in section 2.

In the simulations we also incorporate a small diffusive term (white noise) with variation σ. The program tracked the trajectories of 5000 individual cells, initially uniformly distributed, through 20 unperturbed cell cycles (20 units of time in equation 4.1). The simulation used an Euler method to integrate the SDE. In each of Figure 3–Figure 6 we show (a) a histogram of the final distribution of cells within the cell cycle and (b) a time-series of the fraction of cells inside S over the final two periods.

An external file that holds a picture, illustration, etc.
Object name is nihms147352f3.jpg

Figure 3

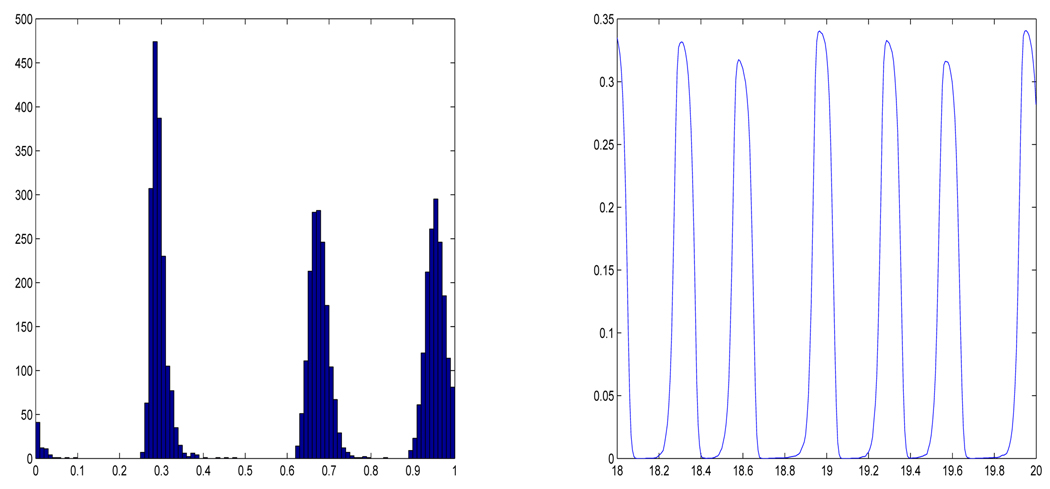
Simulations of the graduated model with positive feedback. Here R = [.1, .2], S = [.2, .3], σ = .02 and the linear factor was 5. (a) Histogram of the final distribution of cells within the cell cycles. (b) Time-series of the final two time frames. One unit of time corresponds to one unperturbed cell cycle.

An external file that holds a picture, illustration, etc.
Object name is nihms147352f6.jpg

Figure 6

Simulations of the graduated model with negative. Here R = [.15, .2], S = [.2, .25], σ = .01 and the linear factor was −10. (a) Histogram of the final distribution of cells. (b) Time-series of the final two time frames.

The figures clearly show clustering for all the specified parameter values.

We observe the following things from the simulations:

The negative feedback produces more clusters than positive.
The number of clusters formed is inversely proportional to the width of S or |R| + |S|.
Positive feedback causes sharper clustering, i.e. the clusters appear to be completely separated.
Too much noise can destroy the clustering effect. The amount of noise needed to do so was smaller for larger numbers of clusters.

The first two of these observations are consistent with the results concerning the idealized advancing and blocking models. The third observation is somewhat in contrast to the lack of rigorous results in section 3.3. The stochastically perturbed positive feedback model is seen to form clusters just as readily and even more markedly than the negative model. These simulations with more realistic models reinforce the hypothesis that clustering is a robust phenomenon in cell cycle dynamics with any form of feedback.

4.2 Stratified Model

When yeast cells divide, one is the mother and the other the daughter. The mother carries a scar from the bud and the daughter does not. The number of daughters a cell has had can be determined by counting the bud scars. We will refer to a cell’s generation as the number of daughters it has produced, starting the count from 0 for the daughters themselves in the first cell cycle.

It is known that after division the mother’s volume is slightly larger than that of a daughter. Further, the later generations have slightly shorter times to budding and slightly shorter cell cycle times.

Leslie proposed a general stratified population model that takes into account the differences in generations that we adapt to yeast in [46]. As before, we will simplify the model by considering logarithmic coordinates, normalized by the cell cycle length of the zero-th generation. In these coordinates the cell cycle of the 0 generation is the unit interval I₀ = [0, 1]. We will denote the S phase and R phases of the 0 generation by R = [r₀, s₀] and S = [s₀, t₀]. The successive generations in these coordinates are represented by the intervals I_k = [0, D_k] with R_k = [r_k, s_k] and S_k = [s_k, t_k].

Note first that if D_k = 1, R_k = R₀ and S_k = S₀ for all k ≥ 1, then this model reduces to the simplified model of the previous sections. Next we note that if these conditions approximately hold then the above analysis can be applied in the same way as the small random perturbations.

If there are marked differences in the parameters between generations, then we still might be able to repeat a rigorous analysis. For example, suppose that D_k = 2/3 for all k > 0. Then in the idealized models we could have 3 clusters in the 0-th generation and 2 clusters in the higher generations. In this scenario, at division parents would be synchronized with a cluster of daughters that was previously 1/3 of a cycle ahead of them. As another example, suppose that the ratio above is 3/4, then the system could support 4 daughter clusters and 3 parent clusters. In the same way, rational ratios of cell cycles could produce a variety of clustering combinations.

In real systems, first of all, ratios close to the above idealized “resonances” could still lead to clustering. Secondly, we may suppose that only the first few generations matter since higher generations are represented in numbers that decay approximately geometrically. Biologically, the successive generations beyond the second have not been found to exhibit marked differences anyway.

Go to:

5 Discussion

The main conclusion we wish to emphasize is that clustering seems to be a very robust phenomenon; it occurs in all the models studied and for a large spectrum of parameter values. This later point is quite important since the actual systems in question are so complex that many of the parameter values are difficult to accurately determine.

The observed synchronous behavior here is not driven by the cell cycle itself, but by feedback mechanisms acting on the cell cycle. However, the clusters must necessarily be an integer in number and so the oscillations produced by clustering would naturally appear with a period that is an integer fraction of the cell cycle period.

We observe two phenomena that possibly make negative feedback a more reasonable explanation of yeast cell-cycle synchrony. First, negative feedback allows for large numbers of clusters as in some experiments. Second, negative feedback is seen to initiate clustering more naturally, which we observe in analysis of the idealized models. However, either positive or negative feedback are possible agents of clustering and conclusive evidence of either cause would need extensive biological modeling confirmed by experiment. Currently there is a strong interest in modeling the details of the cell cycle.

Given the robustness of clustering, we suspect that it occurs in many other biological systems with cell cycles. Specifically it could play a role in many types of microbiological systems with cell cycles and some type of signaling, including bacteria [10, 13, 16, 33, 34]

An external file that holds a picture, illustration, etc.
Object name is nihms147352f4.jpg

Figure 4

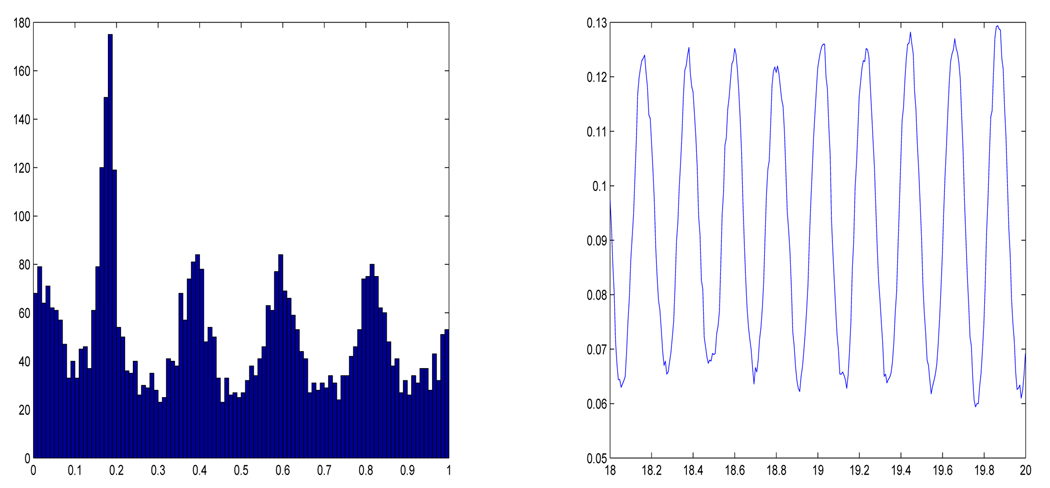
Simulations of the graduated model with negative feedback. Here R = [.1, .2], S = [.2, .3], σ = .02 and the linear inhibition factor was −5. (a) Histogram of the final distribution of cells. (b) Time-series of the final two time frames.

An external file that holds a picture, illustration, etc.
Object name is nihms147352f5.jpg

Figure 5

Simulations of the graduated model with positive feedback. Here R = [.15, .2], S = [.2, .25], σ = .01 and the linear factor was 10. (a) Histogram of the final distribution of cells. (b) Time-series of the final two time frames.

Go to:

Acknowledgment

E.M.B. and C.C.S. were partially supported through NSF-DMS 0443855, NSF-ECS 0601528 and the W.M. Keck Foundation Grant #062014. T.G. was partially supported by NSF/NIH grant 0443863, NIH-NCRR grant PR16445 and NSF-CRCNS grant 0515290.

We would like to acknowledge the input of the late Robert Klevecz in this manuscript. He is responsible for attracting our attention to this field, he generously opened his lab and shared his knowledge with us. Without his support and encouragement this manuscript would not be possible and we dedicate it to his memory.

Go to:

A PDE models of the cell cycle

In this appendix we turn our attention briefly to partial differential equation approximations of the models. The PDE models derived are presented to give some context to the ODE, RDE and SDE models that we consider in the rest of the paper. Also, there is some history of such models in the literature.

A.1 General PDE model

Let U (t, x) denote the distribution of cells within the cell cycle as represented by x [set membership] [0, 1), i.e.

U (t, x) = \frac{1}{N} \sum_{i \in S (t)} δ_{x_{i} (t)} (x)

where S(t) [subset or is implied by] S is the index set of cells that are living at time t and N might be taken as the average number of active cells. As is customary, we may approximate the point distribution by a more regular distribution u(t, x).

If there is no death or harvesting, then formally a distribution u(t, x) evolves locally under (2.2) by the Fokker-Planck equation, which takes the form:

\frac{\partial u}{\partial t} + \frac{\partial}{\partial t} (a (t, x, [u]) u) - σ \frac{\partial^{2} u}{\partial x^{2}} = 0 .

(A.1)

In this notation [u] denotes a functional dependence on u and possibly its history, for example via an integral operator. Note that this derivation is not standard since the cells in the distribution are not independent from each other, but coupled through the term a and the resulting equation is inherently nonlinear. Thus for rigour, equation (A.1) requires further justification.

If the culture is well mixed and harvesting is via removal of bulk material, as in a bio-reactor, then all cells are equally likely to be harvested, regardless of state and the effect of harvesting on the density will be proportional to u(t, x). Similarly, if death of a cell is equally likely at any stage of the cell cycle then the harvesting and death can be incorporated into the Fokker-Planck equation as a term −ku on the right hand side, i.e.:

\frac{\partial u}{\partial t} + \frac{\partial}{\partial x} (a (t, x, [u]) u) - σ \frac{\partial^{2} u}{\partial x^{2}} = - k u .

(A.2)

To take cell division into account in the PDE model, we need to require the boundary conditions:

\begin{matrix} u (t, 0) = 2 u (t, 1^{-}), & a (t, 0, [u]) u (t, 0) + σ u_{x} (t, 0) = 2 a (t, 1^{-}, [u]) u (t, 1^{-}) 2 σ u_{x} (t, 1^{- 1}) . \end{matrix}

(A.3)

Finally, in a PDE model we may represent a as an integral operator:

a (t, x, [u]) = b (t, x) + \int_{0}^{1} k (t, x, u (z), z) d z .

A.2 Periodic or Near Steady State

Next we suppose that the culture is growing in a bioreactor near a steady state or a periodic state so that the cell division is approximately balanced by harvesting. Suppose also that dependence of a on all variables besides x is small, or, that the dependence on t is averaged over one period, and that γ is small. Then equation (A.2) may be approximated by:

\frac{\partial u}{\partial t} + \frac{\partial}{\partial x} (a (x) u) = - k u .

(A.4)

If we make the change of variables:

u (t, x) = e^{- k \int_{0}^{x} \frac{1}{a (y)} d y} z (t, x),

then an easy calculation shows that z(t, x) satisfies:

\frac{\partial z}{\partial t} + \frac{\partial}{\partial x} (a z) = 0 .

(A.5)

Further, the balance between growth and harvesting implies $k = ln 2 / (\int_{0}^{1} \frac{1}{a})$ . This implies that the boundary conditions on z are

z(t, 0) = z(t, 1).

(A.6)

The ordinary differential equation that generates (A.5) is simply:

\frac{d x}{d t} = a (x),

on [0, 1). If we reincorporate the other influences on the growth rate then the unperturbed and pertubed equations become:

\frac{d x_{i}}{d t} = a (t, x_{i}, \bar{x}),

(A.7)

and

\frac{d x_{i}}{d t} = a (t, x_{i}, \bar{x}) + g_{i} (t) .

(A.8)

Note that (A.5) with (A.6) is a conservative equation in the sense that ∫ z dx is preserved, thus in the ODE (A.7) and RDE (A.8) the total number of cells considered should not change. It is thus reasonable to take S to be a fixed set {1,2,…, N} and let x_i(t) to be defined for all t [set membership] [0, T]. To accommodate division we may reset x_i(t) to 0 each time it reaches 1.

A.3 Notes the PDE models and related work

The importance of the cell cycle has been recognized in hematopoiesis [14, 15], as well as yeast growth [18], where PDE models similar to (A.4) are considered with a assumed constant. Thirty years ago Rotenberg [41] described the PDE model (A.4) for yeast growth, but with constant coefficients and an externally applied periodic blocking at cell division. He demonstrated numerically that clustering occurs in the model. Surprisingly, this article has received few citations and little attention. A trivial, but important step, common to our work and that of Rotenberg, is normalization of the cell cycle. This provides a standard domain on which to consider both ODE and PDE models.

In related recent work [52] Zhu et. al. have considered population balance models coupled with a substrate balance equation, where a = a(s) with s the effective substrate concentration. In [22] a = a(s, x) is admitted, but the focus is on a survey of possible numerical methods, not analysis of the model, and clustering solutions are not discussed. Note that the models considered in the current manuscript implicitly incorporate the substrate balance equation (and also the density of any other signaling compounds) into the term a via [u].

Go to:

Footnotes

AMS Subject Classification: 37N25, 34C25, 34F05, 92D25

Go to:

Contributor Information

Erik M. Boczko, Department of Biomedical Informatics, Vanderbilt University.

Chris C. Stowers, Dow Chemical, Indianapolis, IN.

Tomas Gedeon, Department of Mathematics, Montana State University.

Todd R. Young, Department of Mathematics, Ohio University.

Go to:

References

1. Allen EJ, Allen LJS, Schurz H. A Comparison of Persistence-Time Estimation for Discrete and Continuous Population Models that Include Demographic and Environmental Variability. Mathematical Biosciences. 2005;196:14–38. [Abstract] [Google Scholar]

2. Alvino GM, Collingwood D, Murphy JM, Delrow J, Brewer BJ, Raghuraman MK. Replication in Hydroxyurea: It’s a Matter of Time. Mol Cell Biol. 2007;27 63966406. [Europe PMC free article] [Abstract] [Google Scholar]

3. Arnold L. Random Dynamical Systems. Berlin: Springer Monographs in Mathematics. Springer-Verlag; 1998. [Google Scholar]

4. Bahler J. Cell-cycle control of gene expression in budding and fision yeast. Annu. Rev. Genet. 2004;39:69–94. [Abstract] [Google Scholar]

5. Ban H, Boczko E. Age distribution formulas for budding yeast. Vanderbilt Technical Report. 2008. http://hdl.handle.net/1803/1166.

6. Barberis M, Klipp E. Insights into the network controlling the G1/S transition in budding yeast. Genome Inform. 2007;18:85–99. [Abstract] [Google Scholar]

7. Beuse M, Bartling R, Kopmann A, Diekmann H, Thoma M. Effect of the dilution rate on the mode of oscillation in continuous cultures of Saccharomyces cerevisiae. J. Biotechnology. 1998;61(1):15–31. [Abstract] [Google Scholar]

8. Boye E, Stokke T, Kleckner N, Skarstad K. Coordinating DNA replication initiation with cell growth: Differential roles for DnaA and SeqA proteins. Proc. Natl. Acad. Sci. 1996;93:12206–12211. [Europe PMC free article] [Abstract] [Google Scholar]

9. Brewer BJ, Chlebowicz-Sledziewska E, Molo Pipo, Fangman WL. Cell cycle phases in the unequal mother/daughter cell cycles of Saccharomyces cerevisiae. Mol. Cell. Biol. 1984;4:2529–2531. [Europe PMC free article] [Abstract] [Google Scholar]

10. Chen H, Fujita M, Feng Q, Clardy J, Fink GR. Tyrosol is a quorum sensing molecule in Candida albicans. Proc. Natl. Acad. Sci. 2004;101:5048–5052. [Europe PMC free article] [Abstract] [Google Scholar]

11. Chen KC, Calzone L, Csikasz-Nagy A, Cross FR, Novak B, Tyson JJ. Integrative Analysis of Cell Cycle Control in Budding Yeast, Molecular Biology of the Cell. 2004;15(8):3841–3862. [Europe PMC free article] [Abstract] [Google Scholar]

12. Chen Z, Odstrcil EA, Tu BP, McKnight SL. Restriction of DNA replication to the reductive phase of the metabolic cycle protects genome integrity. Science. 2007;316:1916–1919. [Abstract] [Google Scholar]

13. Collier J, McAdams HH, Shapiro L. A DNA methylation ratchet governs cell cycle progression through a bacterial cell cycle. Proc. Natl. Acad. Sci. 2007;104:17111–17116. [Europe PMC free article] [Abstract] [Google Scholar]

14. Colijn C, Mackey MC. Bifurcation and bistability in a model of hematopoietic regulation. SIAM J. Appl. Dyn. Syst. 2007;6:378–394. [Google Scholar]

15. Drobnjak I, Fowler AC, Mackey MC. Oscillations in a Maturation Model of Blood Cell Production. SIAM J. Appl. Math. 2006;66:2027–2048. [Google Scholar]

16. Dunny GM, Leonard BAB. Cell cell communication in Gram Positive bacteria. Annu. Rev. Microbiol. 1997;51:527–564. [Abstract] [Google Scholar]

17. Futcher B. Metabolic cycle, cell cycle and the finishing kick to start. Genome Biology. 2006;7(4):107. [Europe PMC free article] [Abstract] [Google Scholar]

18. Gage TB, Williams FM, Horton JB. Division synchrony and the dynamics of microbial populations: a size-specific model. Theoret. Population Biol. 1984;26:296–314. [Abstract] [Google Scholar]

19. Hartwell LH. Cell division from a genetic prespective. J. Cell Biol. 1978;77:627–637. [Europe PMC free article] [Abstract] [Google Scholar]

20. Hartwell LH. Saccharomyces Cerevisiae cell cycle. Bacteriological Reviews. 1974;38:164–198. [Europe PMC free article] [Abstract] [Google Scholar]

21. Hense BA, Kuttler C, Muller J, Rothballer M, Hartmann A, Kreft J. Does efficiency sensing unify diffusion and quorum sensing? Nat. Rev. Microbiol. 2007;5:230–239. [Abstract] [Google Scholar]

22. Henson MA. Cell ensemble modeling of metabolic oscillations in continuous yeast cultures. Comput. Chem. Enginer. 2005;29:645–661. [Google Scholar]

23. Hjortsø M, Nielsen J. A conceptual model of autonomous oscillations in microbial cultures. Chemical Engineering Science. 1994;49:1083–1095. [Google Scholar]

24. Hjortso M, Nielsen J. Population balance models of autonomous microbial oscillations. J. Biotechnology. 1995;42:255–269. [Abstract] [Google Scholar]

25. Homburg AJ, Young T. Hard bifurcations in dynamical systems with bounded random perturbations. Regular & Chaotic Dynamics. 2006;11:247–258. [Google Scholar]

26. Hornby JM, Jensen EC, Lisec,… AD, Nickeron KW. Quorum sensing in the dimorphic fungus Candida albacans is mediated by farnesol. Appl. Environ. Microbiol. 2001;67:2982–2992. [Europe PMC free article] [Abstract] [Google Scholar]

27. Huls PG, Nanninga N, van Spronsen EA, Valkenburg JAC, Vishcer NOE, Woldringh CL. A computer-aided measuring system for the characterization of yeast populations combining 2D-image analysis, electronic particle counter, and flow cytometry. Biotechnology and Bioengineering. 2004;39(3):343–350. [Abstract] [Google Scholar]

28. Johnston GC, Pringle JR, Hartwell LH. Coordination of growth with cell division in the yeast Saccharomyces Cerevisiae. Exp. Cell. Res. 1977;105:79–98. [Abstract] [Google Scholar]

29. Jones KD, Kompala DS. Cybernetic model of growth dynamics of Saccharomyces Cerevisiae in batch and continuous culture. J. Biotechnology. 1999;71:105–131. [Abstract] [Google Scholar]

30. Jorgensen P, Tyers M. How cells coordinate growth and division. Curr. Biol. 2004;14:R1014–R1027. [Abstract] [Google Scholar]

31. Jorgensen P, Nishikawa JL, Breitkreutz B-J, Tyers M. Systematic identification of pathways that couple cell growth and division in yeast. Science. 2002;297:395–400. [Abstract] [Google Scholar]

32. Klevecz R, Murray D. Genome wide oscillations in expression. Molecular Biology Reports. 2001;28:73–82. [Abstract] [Google Scholar]

33. Lyon GJ, Novick RP. Peptide signaling in Staphylococcus aureus and other Gram positive bacteria. Peptides. 2004;25:1389–1403. [Abstract] [Google Scholar]

34. Macau EEN, Grebogi C. Driving trajectories in complex system. Phys. Rev. E. 1999;59:4062–4070. [Google Scholar]

35. Madden K, Snyder M. Cell polarity and morphogenesis in budding yeast. Annu. Rev. Microbiol. 1998;52:687–744. [Abstract] [Google Scholar]

36. Muller D, Exler S, Aguilera-Vzquez L, Guerrero-Martn E, Reuss M. Cyclic amp mediates the cell cycle dynamics of energy metabolism in Saccharomyces Cerevisiae. Yeast. 2003;20:351–367. [Abstract] [Google Scholar]

37. Murray D, Klevecz R, Lloyd D. Generation and maintenance of synchrony in Sac-charomyces cerevisiae continuous culture. Experimental Cell Research. 2003;287:10–15. [Abstract] [Google Scholar]

38. Palkova Z, Forstova J. Yeast colonies synchronize their growth and development. J. Cell Science. 2000;113:1923–1928. [Abstract] [Google Scholar]

39. Palkova Z, Vachova L. Life within a community: benefits to yeast long term survival. FEMS. Microbiol. Rev. 2006;30:806–824. [Abstract] [Google Scholar]

40. Robertson JB, Stowers C, Boczko EM, Johnson CH. Real-time luminescence monitoring of cell cycle and metabolic oscillations in yeast. Proc. Natl. Acad. Sci. 2008;105:17988–17993. [Europe PMC free article] [Abstract] [Google Scholar]

41. Rotenberg M. Selective synchrony of cells of differing cycle times. J. Theoret. Biol. 1977;66:389–398. [Abstract] [Google Scholar]

42. Singer RA, Johnston GC. Nature of the G₁ phase of the yeast Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. 1981;78:3030–3033. [Europe PMC free article] [Abstract] [Google Scholar]

43. Smith JA, Martin L. ”Do Cells Cycle?” PNAS. 1973;70(4):1263–1267. [Europe PMC free article] [Abstract] [Google Scholar]

44. Stowers C, Robertson JB, Ban H, Tanner RD, Boczko EM. Periodic Fermentor Yield and Enhanced Product Enrichment from Autonomous Oscillations. Applied Biochemistry and Biotechnology. 2009;156:59. [Abstract] [Google Scholar]

45. Stowers C, Ban H, Robertson B, Johnson C, Young T, Boczko E. Clustering, Communication and Environmental Oscillations in Populations of Budding Yeast, Preprint. 2008 [Google Scholar]

46. Stowers C, Hackworth D, Gedeon T, Mischaikow K, Boczko EM. Extending cell cycle synchrony and deconvolving population effects in budding yeast through an analysis of volume growth with a structured Leslie model. Theor. Pop. Biol. 2008 Submitted. [Google Scholar]

47. Sun J, Li D, Stowers C, Boczko EM. Proceedings of IMECE2008. Vol. 69098. Massachusetts, USA: Boston; 2008. Measurement of budding yeast growth rate with mosfet-based microfluidic coulter counters. [Google Scholar]

48. Tu BP, Kudlicki A, Rowicka M, McKnight SL. Logic of the yeast metabolic cycle: temporal compartmentation of cellular processes. Science. 2005;310:1152–1158. [Abstract] [Google Scholar]

49. Tyson JJ, Diekmann O. Sloppy size control of the cell division cycle. J. Theor Biol. 1986;118(4):405–426. [Abstract] [Google Scholar]

50. Woldringh CL, Huls PG, Vischer NOE. Volume growth of daughter and parent cells during the cell cycle of Saccharomyces cerevisiae a/α as determined by image cytometry. J. Bacteriology. 2003;175:3174–3181. [Europe PMC free article] [Abstract] [Google Scholar]

51. Zadrag R, Kwolek-Mirek M, Bartosz G, Bilinski T. Relationship between replicative age and cell volume in Saccharomyces cerevisiae. Acta. Biochem. Pol. 2006;53:747–751. [Abstract] [Google Scholar]

52. Zhu G, Zamamiri A, Henson MA, Hjortsø MA. Model predictive control of continuous yeast bioreactors using cell population balance models. Chemical Engineering Science. 2000;55:6155–6167. [Google Scholar]

Full text links

Read article at publisher's site: https://doi.org/10.1080/17513750903288003

Read article for free, from open access legal sources, via Unpaywall: https://scholarworks.montana.edu/xmlui/bitstream/1/9537/1/Gedeon_JBD_2010.pdf

Citations & impact

Impact metrics

Citations

Jump to Citations

Data citation

Jump to Data

Citations of article over time

Smart citations by scite.ai
Explore citation contexts and check if this article has been supported or disputed.
https://scite.ai/reports/10.1080/17513750903288003

Supporting

Mentioning

Contrasting

Article citations

Instability of the steady state solution in cell cycle population structure models with feedback.
Bárány B, Moses G, Young T
J Math Biol, 78(5):1365-1387, 06 Dec 2018
Cited by: 0 articles | PMID: 30523382
Evidence for internuclear signaling in drosophila embryogenesis.
Buckalew R, Finley K, Tanda S, Young T
Dev Dyn, 244(8):1014-1021, 02 Jul 2015
Cited by: 2 articles | PMID: 26033666
Cell cycle dynamics: clustering is universal in negative feedback systems.
Breitsch N, Moses G, Boczko E, Young T
J Math Biol, 70(5):1151-1175, 10 May 2014
Cited by: 1 article | PMID: 24816612
Cell cycle dynamics in a response/signalling feedback system with a gap.
Gong X, Buckalew R, Young T, Boczko E
J Biol Dyn, 8:79-98, 01 Jan 2014
Cited by: 2 articles | PMID: 24963979 | PMCID: PMC4241679
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC

Data

Data that cites the article

This data has been provided by curated databases and other sources that have cited the article.

Saccharomyces Genome Database

https://www.yeastgenome.org/reference/S000134541

Funding

Funders who supported this work.

NIGMS NIH HHS (1)

Grant ID: R01 GM090207
15 publications

OCPHP CDC HHS (1)

Grant ID: PR16445
7 publications

Search life-sciences literature (45,103,589 articles, preprints and more)

ODE, RDE and SDE models of cell cycle dynamics and clustering in yeast.

Author information

Affiliations

Authors

Abstract

Free full text

ODE, RDE and SDE Models of Cell Cycle Dynamics and Clustering in Yeast

Erik M. Boczko

Chris C. Stowers

Tomas Gedeon

Todd R. Young

Abstract

1 The Yeast Cell Cycle and Experimental Observations

2 Models of Cell Cycle Dynamics and Clustering

2.1 A general model for the cell cycle of an individual cell

2.2 Model of the culture

2.3 Modeling of the growth term a

2.4 Clustering

2.5 Advancing model

Theorem 2.1

Proof

Corollary 2.2

Proof

2.6 Blocking model

Theorem 2.3

Proof

Theorem 2.4

Proof

3 Small Perturbations of the Advancing and Blocking Models

3.1 Small Perturbations

3.2 Perturbed Blocking Model

Theorem 3.1

Proof

3.3 Perturbed Advancing Model

4 Linear feedback models and simulations

4.1 Graduated but unstratified model

4.2 Stratified Model

5 Discussion

Acknowledgment

A PDE models of the cell cycle

A.1 General PDE model

A.2 Periodic or Near Steady State

A.3 Notes the PDE models and related work

Footnotes

Contributor Information

References

Full text links

Citations & impact

Impact metrics

Citations of article over time

Article citations

Data

Data that cites the article

Saccharomyces Genome Database

Similar Articles

Funding

NIGMS NIH HHS (1)﻿

OCPHP CDC HHS (1)﻿

Partnerships & funding

NIGMS NIH HHS (1)

OCPHP CDC HHS (1)