Abstract
Free full text

FEBio: Finite Elements for Biomechanics
Short abstract
In the field of computational biomechanics, investigators have primarily used commercial software that is neither geared toward biological applications nor sufficiently flexible to follow the latest developments in the field. This lack of a tailored software environment has hampered research progress, as well as dissemination of models and results. To address these issues, we developed the FEBio software suite (http://mrl.sci.utah.edu/software/febio), a nonlinear implicit finite element (FE) framework, designed specifically for analysis in computational solid biomechanics. This paper provides an overview of the theoretical basis of FEBio and its main features. FEBio offers modeling scenarios, constitutive models, and boundary conditions, which are relevant to numerous applications in biomechanics. The open-source FEBio software is written in C++, with particular attention to scalar and parallel performance on modern computer architectures. Software verification is a large part of the development and maintenance of FEBio, and to demonstrate the general approach, the description and results of several problems from the FEBio Verification Suite are presented and compared to analytical solutions or results from other established and verified FE codes. An additional simulation is described that illustrates the application of FEBio to a research problem in biomechanics. Together with the pre- and postprocessing software PREVIEW and POSTVIEW, FEBio provides a tailored solution for research and development in computational biomechanics.
1. Introduction
Accurate, quantitative simulations of the biomechanics of living systems and their surrounding environment have the potential to facilitate advancements in nearly every aspect of medicine and biology. For instance, computational models can yield estimates of stress and strain data over the entire continuum of interest, which is especially advantageous for locations where it may be difficult or impossible to obtain experimental measurements. Computational modeling in biomechanics has already become a standard methodology, both for interpreting the biomechanical and biophysical basis of experimental results and as an investigative approach in its own right when experimental investigation is difficult or impossible. Applications span all fields of the biomedical sciences, including areas as diverse as molecular dynamics, cell motility and mechanics, cardiovascular mechanics, musculoskeletal biomechanics and tissue engineering. Advancements in imaging techniques and geometry reconstruction have opened the door to patient-specific modeling [1–6], which could revolutionize the way clinicians diagnose and treat certain pathologies. Continuing improvements in speed and availability of high performance computing hardware have allowed the use of finely discretized geometries (e.g., high resolution representations of vertebral bodies [7]) and sophisticated constitutive models (e.g., mixture theory [8,9]), with the hope that these added complexities will produce more realistic representations of biological materials.
The finite element (FE) method is by far the most common numerical discretization and solution technique that has been used in computational biosolid mechanics. The FE method provides a systematic approach for assembling the response of a complex system from individual contributions of elements, and thus it is ideal for the complex geometries often encountered in biomechanical systems. It also provides a consistent way to address material inhomogeneities and differences in constitutive models between disjoint or continuous parts of a model. The solution procedure involves the consideration of overall energy minimization and/or other fundamental physical balance laws to determine unknown field variables over the domain. The FE method has been applied to problems in biomechanics as early as the 1970s (see, e.g., Refs. [10–15].). The application of finite element analysis in biomechanics research and design has increased exponentially over the last 30 years as commercial software availability has improved and researchers obtained better access to appropriate computing platforms. Applications have spanned from the molecular to cellular, tissue, and organ levels.
However, the lack of a FE software environment that is tailored to the needs of the field has hampered research progress, dissemination of research, and sharing of models and results. Investigators have primarily used commercial software, but these packages are not specifically geared toward biological applications, are difficult to verify [16,17], preclude the easy addition and sharing of new features such as constitutive models, and are not sufficiently general to encompass the broad framework needed in biomechanics. To address these issues, we developed FEBio (an acronym for “Finite Elements for Biomechanics”), a nonlinear implicit finite element framework designed specifically for analysis in computational solid biomechanics [18].
Arguably the most important aspect of developing a new FE code is proper verification. The American Society of Mechanical Engineer's “Guide for Verification and Validation in Computational Solid Mechanics” [19] defines verification as: “The process of determining that a computational model accurately represents the underlying mathematical model and its solution. In essence, verification is the process of gathering evidence to establish that the computational implementation of the mathematical model and its associated solution are correct.”
In the case of computational solid biomechanics, the mathematical model is based on the governing equations of continuum mechanics (in particular the conservation of linear momentum), the associated boundary conditions, initial conditions, and constitutive equations. Development of a numerical method of analysis based on the mathematical model requires numerical discretization, solution algorithms, and convergence criteria [19,20]. To verify the numerical methods and computational implementation of the mathematical model in FEBio, it must be demonstrated that it gives the correct solution to a set of benchmark problems that consists of either analytical solutions or results from established FE codes.
Our long term goal is to develop a freely available, extensible finite element modeling framework for solid mechanics, fluid mechanics, solute transport, and electrokinetics in biological cells, tissues, and organs, based around the FEBio framework. To date, no such tools are available for general use in the public domain. The specific objectives of this paper are to introduce the theoretical framework of FEBio and to present results for a suite of verification problems that simultaneously illustrates some of its capabilities.
2. Overview
FEBio offers modeling scenarios, constitutive models and boundary conditions that are relevant to numerous applications in biomechanics. FEBio supports both quasi-static and dynamic analyses. In a quasi-static analysis, the equilibrium response of the system is sought and inertial terms are ignored. An incremental iterative solution is obtained by discretizing applied loads and other boundary conditions in quasi-time. For deformable porous media, a coupled solid–fluid problem is solved. In a dynamic analysis, the inertial terms are included to calculate the time-dependent response of the system. FEBio uses an implicit time integration scheme for both types of analyses.
Many different constitutive models are available to represent biological materials and synthetic biomaterials. Many of the materials are based on the framework of hyperelasticity. Both isotropic and anisotropic constitutive models are available. FEBio also contains a rigid body constitutive model. This model can be used to represent materials or structures whose deformation is negligible compared to that of other materials in the overall model.
FEBio supports a wide range of boundary conditions to model biological interactions. These include prescribed displacements, nodal forces, surface tractions, pressure forces, and body forces (e.g., gravity). For dynamic problems, initial conditions are available for prescribing the initial values for velocity, acceleration and, in the case of biphasic analysis, fluid pressure and fluid flux. Deformable models can be connected to rigid bodies. This allows the user to model prescribed rotations and torques for rigid segments, thereby allowing the coupling of rigid body mechanics with deformable continuum mechanics. FEBio offers several ways to represent contact between rigid and/or deformable materials. Using a sliding surface, the user can connect two surfaces that are allowed to separate and slide across each other but are not allowed to penetrate. If the contacting surfaces are poroelastic, the user can choose to allow fluid to flow through the contact interface in the presence of a fluid pressure gradient across the interface. The tied interface can be used to tie two possibly nonconforming surfaces together.
FEBio is open source, and both the executables and source code may be downloaded free of charge (http://www.febio.org). Each downloadable package contains the executable, verification and example problems, a user's manual and a theory manual. Precompiled executables are available for the Windows 7, Windows XP, Linux 64 bit, Linux 32 bit, and Mac OSX platforms. FEBio can be an excellent starting point for researchers who wish to implement new technologies. Although adding new functionality to FEBio requires some C++ programming skills, the modular structure of the code greatly facilitates this process. The source code is commented clearly and HTML documentation exists as well. To facilitate support, bug tracking and feature requests, a public forum has been created (http://mrl.sci.utah.edu/forums).
Two software packages that support the use of the FEBio software have also been created. PREVIEW is a finite element preprocessor that offers a graphical user interface that facilitates the process of defining finite element models. The user can import geometry, assign material parameters, define boundary and contact conditions, and export the final model as a FEBio input file. The results of a FEBio run can subsequently be analyzed and visualized in the finite element post-processor POSTVIEW. This environment offers tools to inspect and analyze the model results similar to those found in most commercial finite element software packages. Both PREVIEW and POSTVIEW may be downloaded for free from the same software website.
3. Theory and Implementation
The following section assumes knowledge of nonlinear continuum mechanics and finite element methods. The FEBio Theory Manual [21] and the references in the reference section can be consulted for more detailed explanations of the presented theory.
3.1. Weak Form, Linearization and Finite Element Discretization.
Generally, a finite element formulation is established by a variational statement, which represents the weak form of a physical law. In mechanics, this can either be written as the minimization of an energy function or, alternatively, the virtual work equation can serve as the starting point [22]. The spatial form of the virtual work equation, representing the weak form of conservation of linear momentum for a deformable body, can be written as
Here,
The directional derivative of Eq. (1) is needed for the linearization. In an iterative procedure, the deformation
where
In the finite element method, the domain is divided into connected subunits called finite elements. The discretization process is established by interpolating the position X of a point within a finite element in terms of the coordinates
where n is the number of nodes in a finite element. Quantities such as spatial coordinates, displacement, velocity, and their virtual equivalents can be interpolated similarly.
The discretization of Eq. (2) with Eq. (3) leads to the discrete form of the nonlinear finite element equations [24]:
Here, K is the stiffness matrix, which is mostly defined by the constitutive model, u is the vector of nodal displacements, and R is the residual vector, which measures the difference between internal and external forces. As the virtual velocities
Here,  +
+ 1, respectively. Ideally, Newton's method achieves a quadratic convergence rate in the neighborhood of a solution. However, it also requires the formation and factorization of the stiffness matrix at every iteration, which is the most costly part of nonlinear finite element analysis from a computational standpoint. Quasi-Newton methods offer an attractive alternative. For these methods, the true stiffness matrix K is replaced by an approximation that is relatively easy to calculate. FEBio uses the BFGS method [23], which is one of the more effective quasi-Newton methods for computational solid mechanics.
1, respectively. Ideally, Newton's method achieves a quadratic convergence rate in the neighborhood of a solution. However, it also requires the formation and factorization of the stiffness matrix at every iteration, which is the most costly part of nonlinear finite element analysis from a computational standpoint. Quasi-Newton methods offer an attractive alternative. For these methods, the true stiffness matrix K is replaced by an approximation that is relatively easy to calculate. FEBio uses the BFGS method [23], which is one of the more effective quasi-Newton methods for computational solid mechanics.
3.2. Element Technology.
The 3D solid elements in FEBio are isoparametric elements, meaning that the element geometry and displacement fields on the element are interpolated with the same shape functions. Currently available elements include the linear hexahedron, pentahedron, and tetrahedron. It is well-known that these elements tend to “lock” for nearly and fully incompressible material response when using a displacement-only formulation. FEBio deals with this problem by using a three-field element formulation (the mean dilatation method) for the hexahedral and pentahedral elements [25]. For tetrahedral elements, a nodally integrated tetrahedron provides enhanced performance for finite deformation and near-incompressibility compared to the standard constant strain tetrahedron [26].
Quadrilateral and triangular shell elements in FEBio use an extensible director formulation [27]. Six degrees of freedom are assigned to each shell node: three displacement degrees of freedom and three director degrees of freedom. A three-point Gaussian quadrature rule is used for integration through the thickness of the shell.
FEBio also solves porous media problems using the mixture framework known as the biphasic theory [28]. For such problems, a fluid phase exists along with the solid phase and therefore requires the solution of a separate fluid field problem. In FEBio, a u–p formulation is used to solve the coupled solid–fluid problem for the unknown displacements and fluid pressures [29]. Like the displacements, the fluid pressures are defined at the nodes and the biphasic elements are integrated using the same quadrature rule as the structural elements. In the formulation an additional equation is needed to satisfy the conservation of mass for the mixture. The weak formulation now requires the solution of a coupled displacement-pressure problem.
and
Equation (6) is recognized as the virtual work Equation (1). In Eq. (7),
3.3. Constitutive Models.
The material representations in FEBio span the range of elastic solids, viscoelastic solids, biphasic materials, biphasic-solid materials, and rigid bodies. Many of the constitutive models are based on the concept of hyperelasticity. Constitutive models with isotropic, transversely isotropic [30], and orthotropic material symmetries are available. For most materials, uncoupled formulations are used so that these materials can be used effectively in nearly incompressible analyses. Detailed descriptions of all of the materials in FEBio can be found in the FEBio Theory Manual [21].
3.3.1. Contact.
Several contact algorithms are available in FEBio. To enforce the contact constraint, a contact work contribution is added to the virtual work statement in Eq. (1). The contact integral is of the following form:
Here,
3.4. Rigid Bodies.
Rigid bodies are supported as a separate material type. For groups of elements, faces and/or nodes that are assigned the “rigid body” material type in FEBio, nodal degrees of freedom are condensed down to six degrees of freedom. The result is a vast reduction in the number of the total degrees of freedom and leads to a very efficient implementation of the rigid body constraint [33]. Rigid bodies can also be connected by rigid joints. The rigid joint constraints are enforced using an augmented Lagrangian method.
3.5. Linear Solvers.
As over 90% of the execution time of large problems in an implicitly integrated nonlinear FE code is spent in the linear solver (which is called repeatedly for the Newton or quasi-Newton solution method), the linear solver is typically the bottleneck for large computations. Consequently, an efficient and robust linear solver was needed. The linear solver must run on all supported platforms (Linux, Windows, Mac), take optimal advantage of the sparseness of the stiffness matrix, handle both symmetric and nonsymmetric matrices (necessary for biphasic problems), and support parallel execution. For this reason, FEBio includes support for PARDISO [34,35], SUPERLU [36], and WSMP [37]. These solvers take optimal advantage of the sparse stiffness matrix by storing only the nonzero matrix elements using the Harwell–Boeing matrix storage format. Further, they can handle nonsymmetric matrices and support parallel execution on multicore shared-memory architectures.
3.6. Software Implementation.
FEBio is written in C++. This programming language was chosen over FORTRAN—the more commonly used language in scientific computing—for two reasons. First, the performance penalties that once existed in object-oriented programming languages (compared to procedural languages such as FORTRAN) have been mostly overcome by modern compilers [38]. Second, C++ encourages the use of a modular code structure that simplifies the development and maintenance of a sophisticated software program. This modular structure also offers advantages for users who wish to customize FEBio for their own needs. For instance, it provides a simple yet elegant way to add new materials without the need to modify any of the existing code. By simply providing a new constitutive relation, the new material is automatically recognized in the input format and supported in restart analyses, the parameter optimization module, as well as all other features of FEBio that support different materials. To simplify the addition of custom materials further, a custom math library was designed that facilitates the implementation of tensor and matrix operations. This library allows the user to implement the material model using programming statements that closely resemble the analytical mathematical expressions. To verify the material implementation, several diagnostic tools are available for the developer to check the consistency between the stress tensor and the fourth-order elasticity tensor. The software is commented extensively to clarify the data flow of the code. Online documentation of the source code is available as well.
4. Verification Problems
Results produced by FEBio were compared to analytical solutions or the solutions from two established and verified FE codes, ABAQUS (Version 6.7, Simulia, Providence, RI) and NIKE3D (Version 3.4.1, Methods Development Group, Lawrence Livermore National Laboratory, Livermore, CA [39]). The problem description and results are presented together for each verification problem. The FEBio Verification Suite consists of over 140 test problems, and those described in the following are representative.
4.1. Uniaxial Tension-Compression Material Tests.
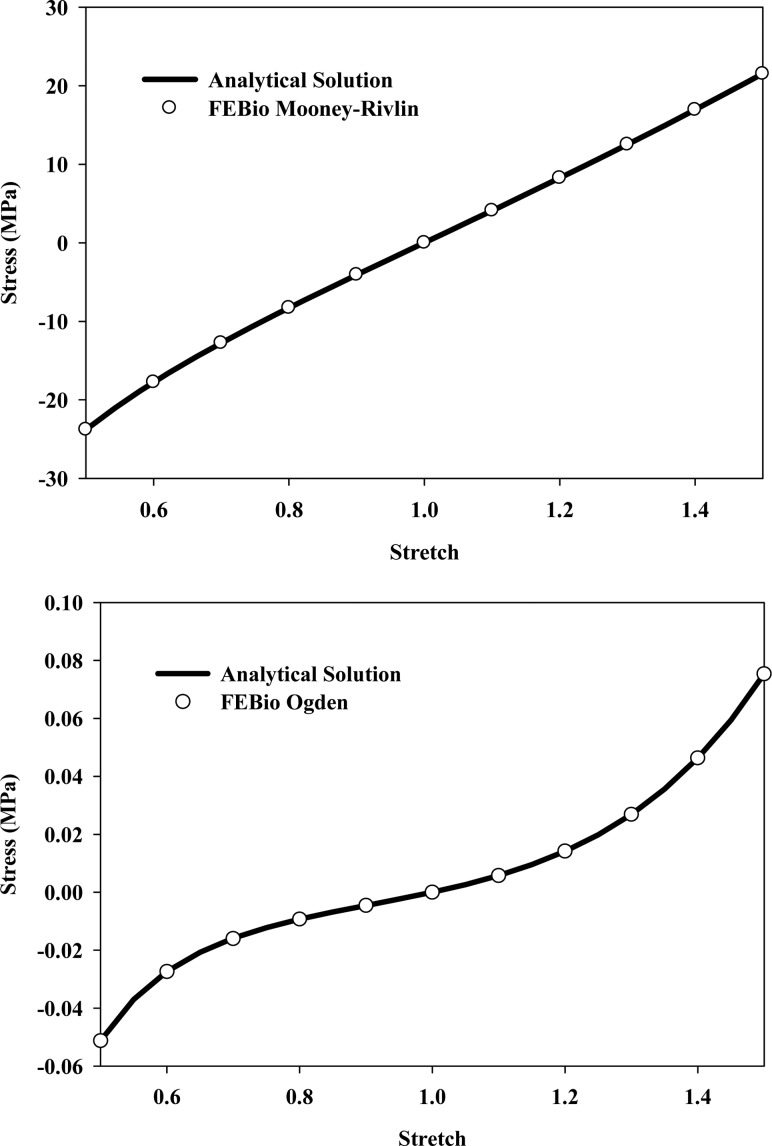
The single-element uniaxial stress test is a standard verification test for material models. As the deformation is homogeneous, the analytical solution can often be obtained in closed form. This allows for direct comparison of the FEBio results with the analytical solution. In this case study, results for the Mooney–Rivlin and Ogden hyperelastic constitutive models are presented. Both materials are often used to represent the matrix component of biological tissues. The Mooney–Rivlin constitutive model in FEBio has the following uncoupled strain-energy function:
where
The Ogden constitutive model with uncoupled deviatoric and dilatational response has the following strain-energy function [41]:
Here,  =
= 1,
1,
4.2. Confined Compression Creep.
The confined compression creep test is often used for material characterization of deformable porous media [28,43,44]. A cylindrical tissue sample is placed in a confining chamber with rigid impermeable bottom and side walls. The top of the tissue is compressed with a free-draining rigid porous indenter. If a constant applied load is used, a creep deformation is produced, increasing over time (Fig. (Fig.22).
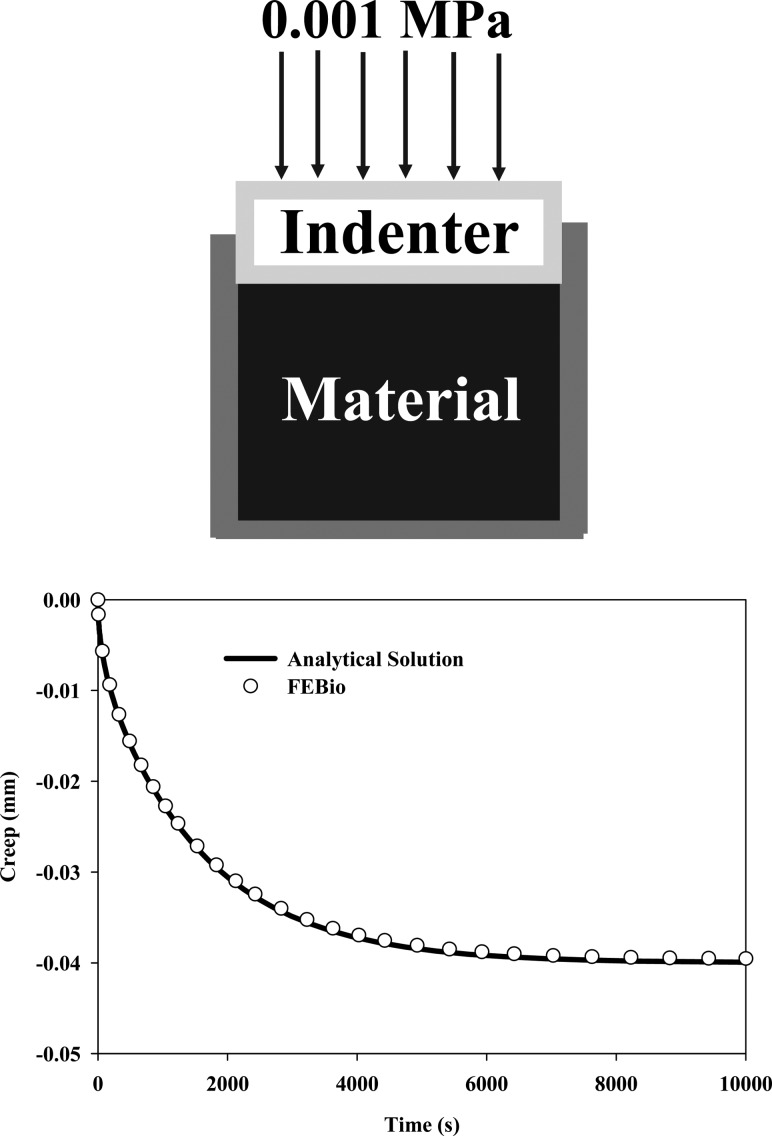
Confined compression creep testing of deformable porous media. (Top) Loading and boundary conditions for the confined compression creep simulation. (Bottom) Creep displacement as a function of time, calculated from the analytical solution and predicted by FEBio, showing the excellent agreement between the two results.
A unit cube was created and the nodes were constrained so that only the top surface could move along the normal direction. A pressure of 0.001 MPa was applied to the top surface. The material was assumed to be biphasic. The solid phase was modeled as a neo-Hookean material with strain energy given by
Here,
4.3. Unconfined Compression Stress Relaxation.
In this test, a cylindrical tissue sample is exposed to a prescribed displacement in the axial direction while left free to expand radially. After loading the tissue, the displacement is held constant while the tissue under the displacement relaxes in the radial direction due to interstitial fluid flow through the material. For porous media, the outer radial boundary is free-draining (Fig. (Fig.3,3, arrows).
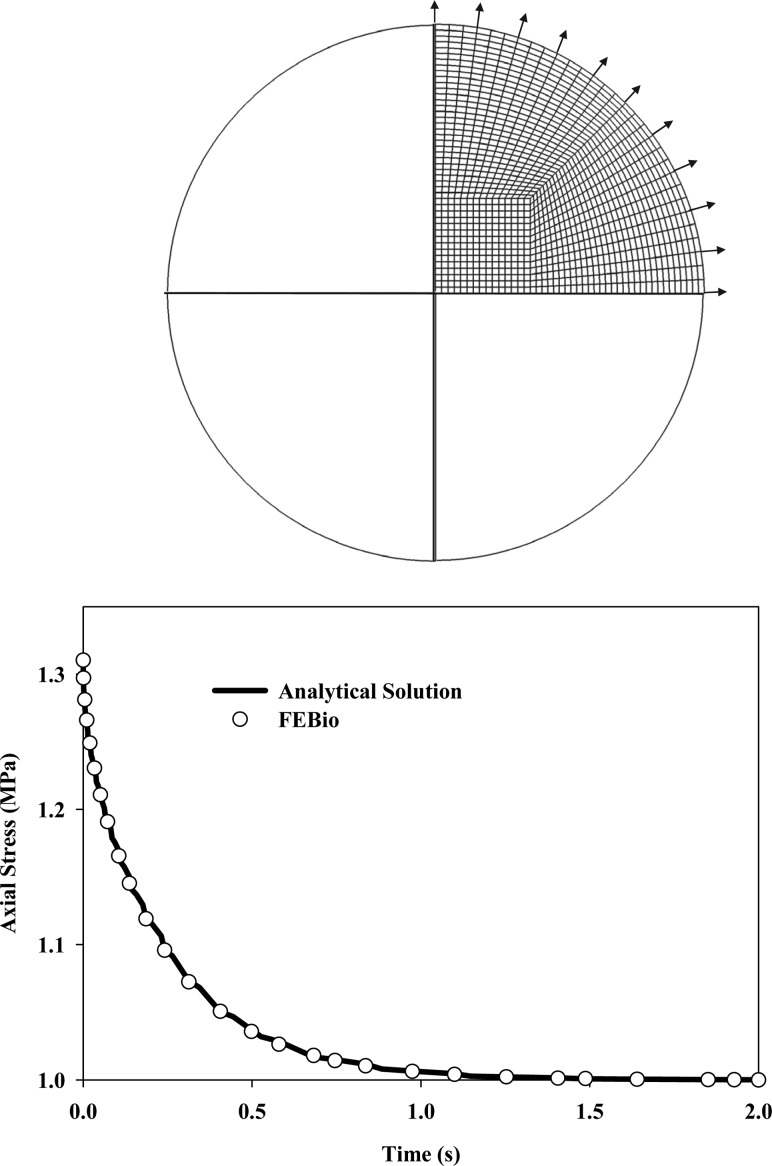
Unconfined compression stress relaxation. (Top) Quarter-symmetry model used for the simulation with the free fluid flow through the outer boundaries indicated with arrows. (Bottom) Axial stress versus time calculated from the analytical solution and predicted by FEBio, showing the excellent agreement between the two results.
A quarter-symmetry mesh was used to model the cylindrical tissue sample. The outer radius and height of the cylinder were 1 mm, whereas the axial compression was 0.01 mm. The bottom of the tissue was constrained and quarter-symmetry boundary conditions were applied. The fluid pressure was constrained to zero at the outer radial surface, whereas the fluid pressure throughout the rest of the body was determined by solution of the equilibrium equations for porous media. The solid phase was represented as a neo-Hookean material (Eq. (11),
The unconfined compression response can be modeled with the biphasic theory [28]. For the special case of a cylindrical geometry and assumptions regarding the direction of the fluid flow, Armstrong et al. [45] found a closed-form analytical solution for the average axial stress on the sample in response to a step loading function. The axial stress predicted by FEBio was nearly identical to the analytical solution provided by Armstrong et al. (Fig. (Fig.33).
4.4. Strip Biaxial Stretching of an Elastic Sheet with a Circular Hole.
This example demonstrates the use and verifies the results of a hyperelastic material in plane stress under large deformation. A thin, initially square sheet containing a centrally located circular hole was subjected to strip biaxial stretch. The undeformed square sheet was 165 ×
× 165
165 ×
× 2 mm, with a centrally located internal hole of radius 6.35 mm (Fig.
(Fig.4).4). The sheet was meshed with 32 hexahedral elements. This example is identical to the problem in Sec. 1.1.8 of the ABAQUS Benchmark Manual (Version 6.7).
2 mm, with a centrally located internal hole of radius 6.35 mm (Fig.
(Fig.4).4). The sheet was meshed with 32 hexahedral elements. This example is identical to the problem in Sec. 1.1.8 of the ABAQUS Benchmark Manual (Version 6.7).
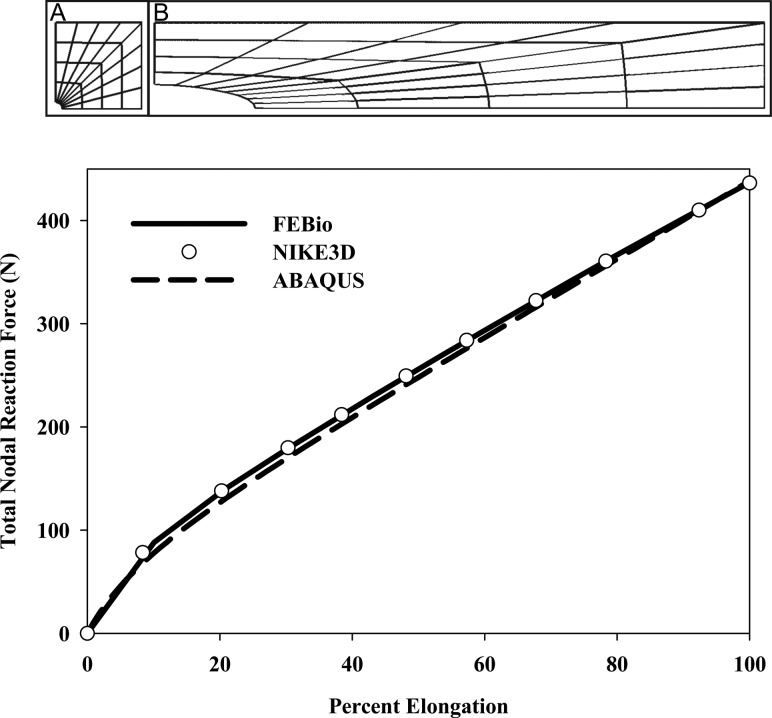
Strip biaxial stretching of an elastic sheet with a circular hole. (Top) Quarter-symmetry model used for this simulation (A) and deformed configuration after applied strain (B). (Bottom) Total nodal reaction force versus percent elongation for FEBio, NIKE3D, and ABAQUS. FEBio and NIKE3D predicted identical results that were slightly different than ABAQUS due to the different algorithms used to enforce the material incompressibility.
The sheet was stretched to a length of 1181 mm (615.76% strain), whereas the edges parallel to the displacement were restrained from contracting. The sheet was represented as a hyperelastic Mooney–Rivlin material with uncoupled deviatoric and volumetric behavior (Eq. (9)). The material coefficients were  =
= 100 MPa, as used by Oden [46] to match the experimental results for a rubber sheet first reported by Treloar [47]. The reaction force predicted by FEBio was compared to results from ABAQUS and NIKE3D as a function of percent elongation.
100 MPa, as used by Oden [46] to match the experimental results for a rubber sheet first reported by Treloar [47]. The reaction force predicted by FEBio was compared to results from ABAQUS and NIKE3D as a function of percent elongation.
The total nodal reaction force predicted by FEBio was identical to the results produced by NIKE3D, but was slightly higher than predictions from ABAQUS (Fig. (Fig.4).4). The small difference is likely due to the slightly different implementation of the Mooney–Rivlin material in ABAQUS. More specifically, ABAQUS uses a different function for the dilatational strain energy (that is, the last term in Eq. (9)) than FEBio and NIKE3D.
4.5. Geometrically Nonlinear Analysis of a Cantilever Beam.
A 10 m long cantilever beam was subjected to a tip load in the transverse direction to produce over 8 m of lateral deflection (Fig.
(Fig.5).5). The beam had a solid rectangular cross section (100 mm thick ×
× 150 mm height) and three different mesh densities were used (100, 200, and 400 elements along the length of the beam). One element was used through the thickness in all cases. One end of the beam was constrained using nodal constraints, whereas a vertical load of 269.35 N was applied at the opposite tip of the beam. The beam was represented as a hyperelastic St. Venant–Kirchhoff elastic material:
150 mm height) and three different mesh densities were used (100, 200, and 400 elements along the length of the beam). One element was used through the thickness in all cases. One end of the beam was constrained using nodal constraints, whereas a vertical load of 269.35 N was applied at the opposite tip of the beam. The beam was represented as a hyperelastic St. Venant–Kirchhoff elastic material:
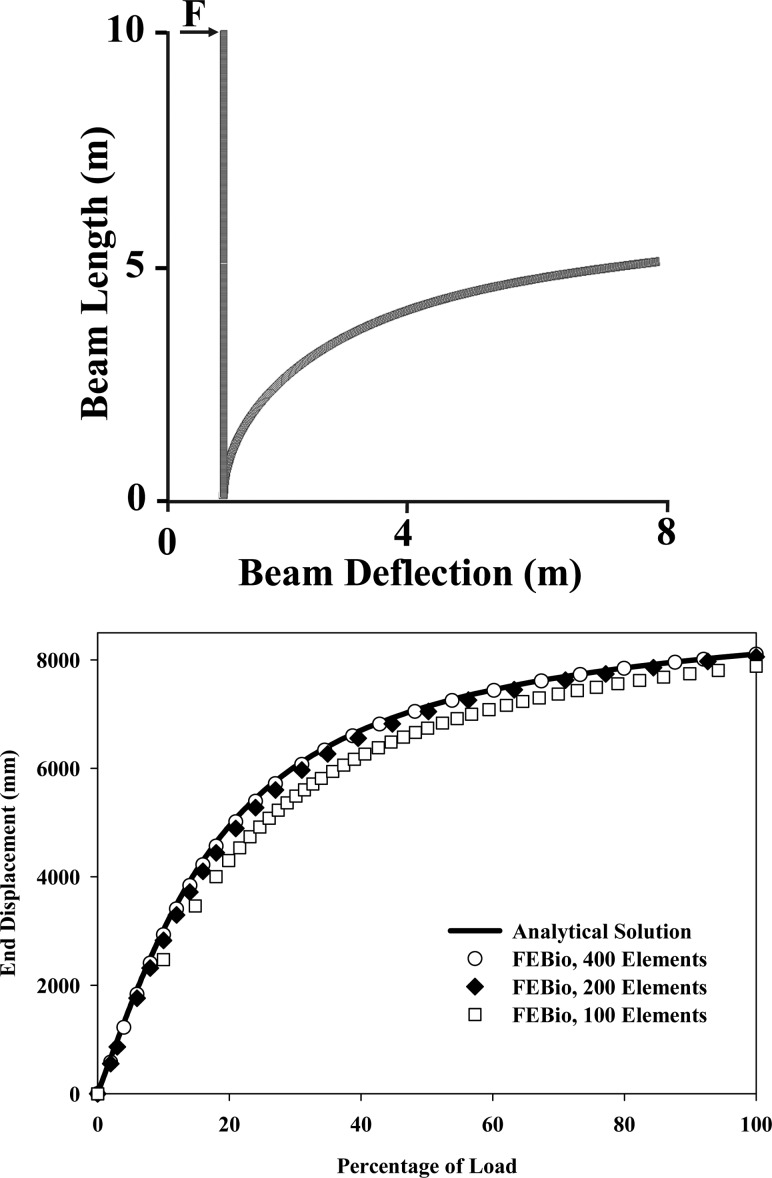
Geometrically nonlinear analysis of a cantilever beam. (Top) Cantilever beam in the undeformed and deformed configurations showing the beam length and deflection. (Bottom) End displacement versus percentage of applied load for the analytical solution and FEBio simulations using 100, 200, and 400 elements along the length of the beam. The beam deflection predicted by FEBio was nearly identical to the analytical solution when 400 elements were used to discretize the beam.
where  =
= 0 MPa, μ
0 MPa, μ =
= 50 MPa) and E is the Green–Lagrange strain tensor. The use of the Green–Lagrange strain tensor in the formulation of the St. Venant–Kirchhoff constitutive equation makes it appropriate for the large rotations and small strains in this problem. The cantilever tip deflection predicted by FEBio was compared to the analytical solution for the large deflection of a cantilever beam [48].
50 MPa) and E is the Green–Lagrange strain tensor. The use of the Green–Lagrange strain tensor in the formulation of the St. Venant–Kirchhoff constitutive equation makes it appropriate for the large rotations and small strains in this problem. The cantilever tip deflection predicted by FEBio was compared to the analytical solution for the large deflection of a cantilever beam [48].
The beam deflection predicted by FEBio was nearly identical to the analytical solution for the geometrically nonlinear analysis of a cantilever beam for a model with 400 elements along the length of the beam (Fig. (Fig.5).5). Models with 100 and 200 elements produced a slightly stiffer response.
4.6. Twisted Ribbon Test for Shells.
This is one of a number of verification problems that are used to verify the shell element formulation in FEBio. A plate discretized with shell elements was twisted by constraining one end and applying equal but opposite forces to the corners of the nonconstrained end (Fig.
(Fig.6).6). The problem description and analytical solution were originally presented by Batoz [49]. The plate dimensions were 1.00 ×
× 2.00
2.00 ×
× 0.05 mm and five models with mesh densities from 32 to 2048 elements were used for a convergence study. Nodes along one short edge were clamped using nodal constraints and the plate was twisted by applying equal but opposite forces of 1 N to the corners nodes of the opposite short edge. The St. Venant–Kirchhoff material was used (Eq. (12), λ
0.05 mm and five models with mesh densities from 32 to 2048 elements were used for a convergence study. Nodes along one short edge were clamped using nodal constraints and the plate was twisted by applying equal but opposite forces of 1 N to the corners nodes of the opposite short edge. The St. Venant–Kirchhoff material was used (Eq. (12), λ =
= 2.5
2.5 ×
× 107 MPa, μ
107 MPa, μ =
= 2
2 ×
× 106 MPa). The displacement of the corner node predicted by FEBio was compared to the analytical solution.
106 MPa). The displacement of the corner node predicted by FEBio was compared to the analytical solution.
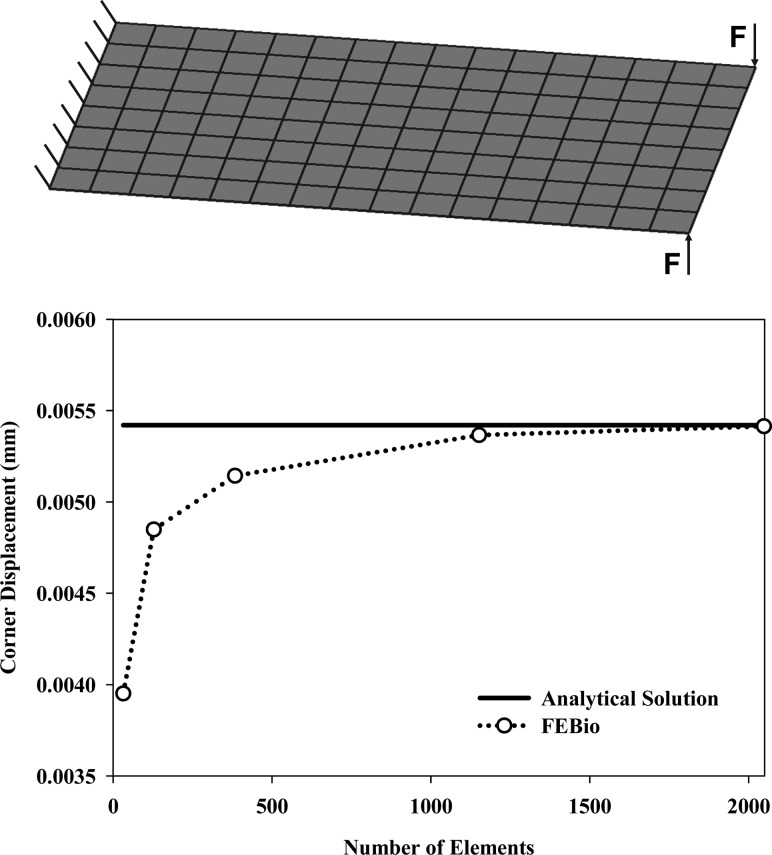
Twisted ribbon test for shells. (Top) Model in the undeformed configuration with loading and boundary conditions indicated. (Bottom) Displacement of the outside corner node versus number of elements used to discretize the model. 2048 elements were needed to exactly match the analytical solution, but there was <2% difference when only half that many elements were used to discretize the model.
The corner displacement predicted by FEBio was nearly identical to the analytical solution for the twisted ribbon test for shells when 2048 elements were used to mesh the plate (Fig. (Fig.6).6). To put this result in perspective, the corner displacement predicted by FEBio was <2% different when half that many elements were used and ~30% different when only 32 elements were used.
4.7. Upsetting of an Elastic Billet.
This problem is commonly used to test finite element approaches for enforcing near- and full-incompressibility, as the domain is highly constrained. A billet of material was compressed between two rigid flat surfaces (Fig. 7(A)). As the material was only compressed to the point when the material bulging from the middle of the billet makes contact with the flat surfaces (Fig. 7(B)), this problem is a simplification of the contact problem presented in the next example (Fig. 7(C)).
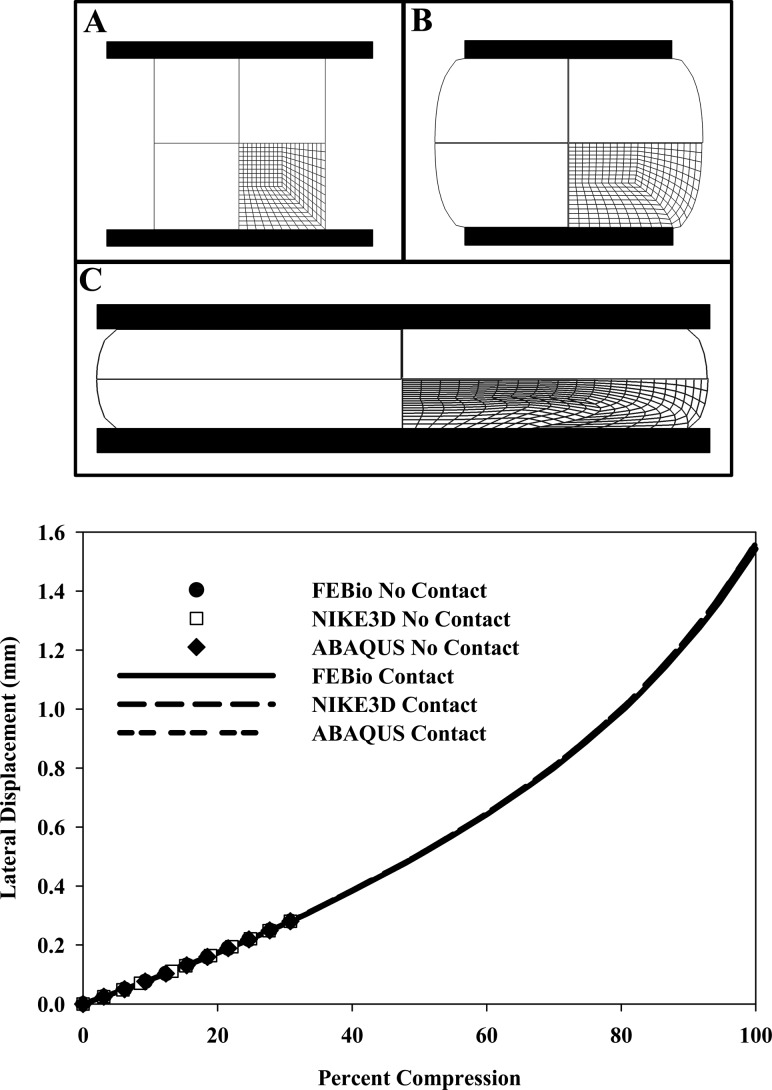
Upsetting of an elastic billet. (Top) Quarter-symmetry model in the initial configuration (A); billet deformed until there is contact between the inner material of the billet and the rigid planes (B); and deformed billet with contact between the inner material and the rigid planes (C). (Bottom) Lateral displacement (bulge) versus percent compression for FEBio, NIKE3D, and ABAQUS. There was excellent agreement in the predicted results from all three FE codes for both the contact and noncontact versions of this problem.
A quarter-symmetry, plane strain model was produced (Fig. 7(A)). The model dimensions were 1.0 ×
× 1.0
1.0 ×
× 0.1 mm, and a mesh of 10
0.1 mm, and a mesh of 10 ×
× 10
10 ×
× 1 elements produced converged results. Boundary and loading conditions were prescribed using nodal constraints and nodal loads, respectively. The billet was represented as an uncoupled Mooney–Rivlin material (Eq. (9), C
1
1 elements produced converged results. Boundary and loading conditions were prescribed using nodal constraints and nodal loads, respectively. The billet was represented as an uncoupled Mooney–Rivlin material (Eq. (9), C
1 =
= 1 MPa, C
2
1 MPa, C
2 =
= 10
10 MPa, K=10,000
MPa, K=10,000 MPa). The augmented Lagrangian method was used to enforce incompressibility [32]. The displacement of the top right node of the mesh (representing the amount of lateral bulging) was plotted versus the percent compression and the results from FEBio were compared to results from ABAQUS and NIKE3D.
MPa). The augmented Lagrangian method was used to enforce incompressibility [32]. The displacement of the top right node of the mesh (representing the amount of lateral bulging) was plotted versus the percent compression and the results from FEBio were compared to results from ABAQUS and NIKE3D.
The lateral displacement of the billet predicted by FEBio was nearly identical to the results produced by ABAQUS and NIKE3D (Fig. (Fig.7,7, right panel).
To verify the contact algorithm implemented in FEBio, contact between the incompressible material of the billet and the rigid plane was added to the problem. The billet was compressed 60% of its original height, causing extensive contact between the rigid plane and the material originally in the middle of the billet. The boundary conditions for this problem were the same as the previous problem, but here the compression of the billet was caused by frictionless contact between the billet and rigid plane. This contact was enforced using an augmented-Lagrangian method. Again, the lateral displacement of the billet predicted by FEBio was nearly identical to the results produced by ABAQUS and NIKE3D. The results from the noncontact and contact problems lined up through the smaller range of compression (Fig. (Fig.7,7, right panel).
4.8. Crushing of a Pipe.
This problem simulated the crushing of a long, straight pipe of cylindrical cross section between two flat, frictionless anvils. This benchmark problem includes large strains/rotations and contact between deformable and rigid materials. A quarter-symmetry, plane strain model of a 114.3 mm radius pipe with an 8.87 mm thickness was created for this problem (Fig.
(Fig.8).8). The model was meshed with 24 elements along the arc, four elements through the thickness, and one element through the length. Nodal constraints were used for the plane-strain and quarter-symmetry boundary conditions, and the problem was driven by prescribing a 50 mm displacement to the rigid body. Contact between the anvil and pipe was enforced using the augmented Lagrangian method. The St. Venant–Kirchhoff material was used for this problem (
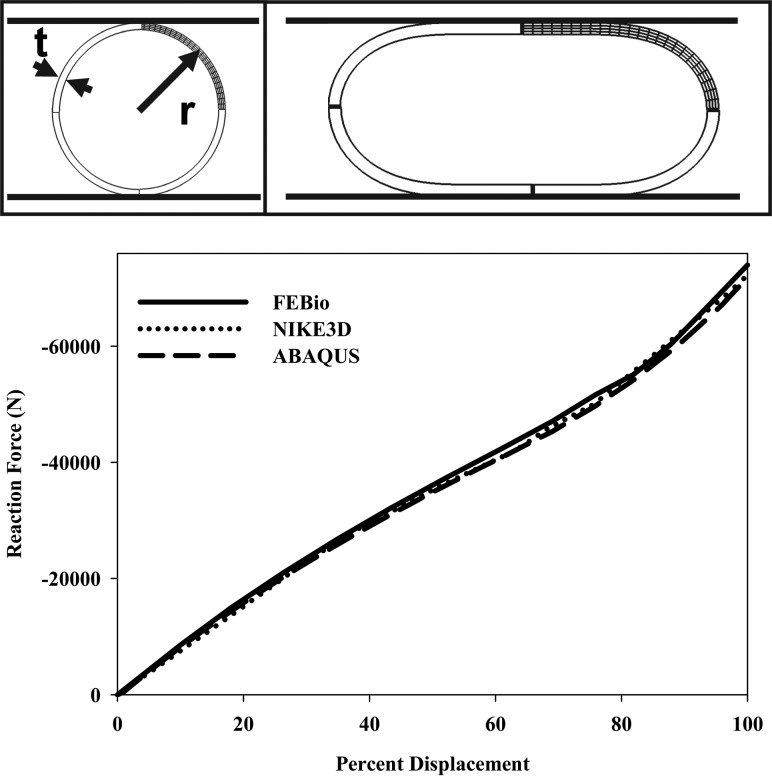
Crushing of a pipe. (Top, left) Quarter-symmetry model with rigid crushing planes and key dimensions shown. (Top, right) Pipe in the final crushed configuration. (Bottom) Rigid body reaction force versus percent applied displacement for the crushing planes. There was less than a 3% difference in the peak forces predicted by the three FE codes.
The results predicted by the three FE codes are shown in Fig. Fig.8,8, demonstrating good agreement among all three codes. Small observed differences were most likely due to the different algorithms to enforce contact. Still, at peak displacement there was less than 3% difference in the predicted forces.
4.9. Cartilage Layer Compressed by a Flat, Rigid, Impermeable Surface.
A half-symmetry finite element frictionless contact analysis was performed between a spherical elastic layer anchored to a rigid impermeable substrate and a flat impermeable rigid surface (Fig.
(Fig.9).9). The geometry was representative of the articular layer of an immature bovine humeral head, with a cartilage surface radius of 46.3 mm and a cartilage layer thickness of 0.8 mm. The converged mesh consisted of 20 tri-linear hexahedral elements through the thickness, 50 along the radial direction, and 14 along the circumferential direction. The top of the cartilage layer was constrained by defining the top layer of nodes as a rigid body with all 6 degrees of freedom constrained. The deformation at the center of the articular layer was set to 0.095 mm (~12% of the thickness) by displacing the bottom nodes using nodal prescribed displacements. The cartilage layer was represented by the Mooney–Rivlin constitutive model in Eq. (9) to approximate the short-time response of the tissue, again using
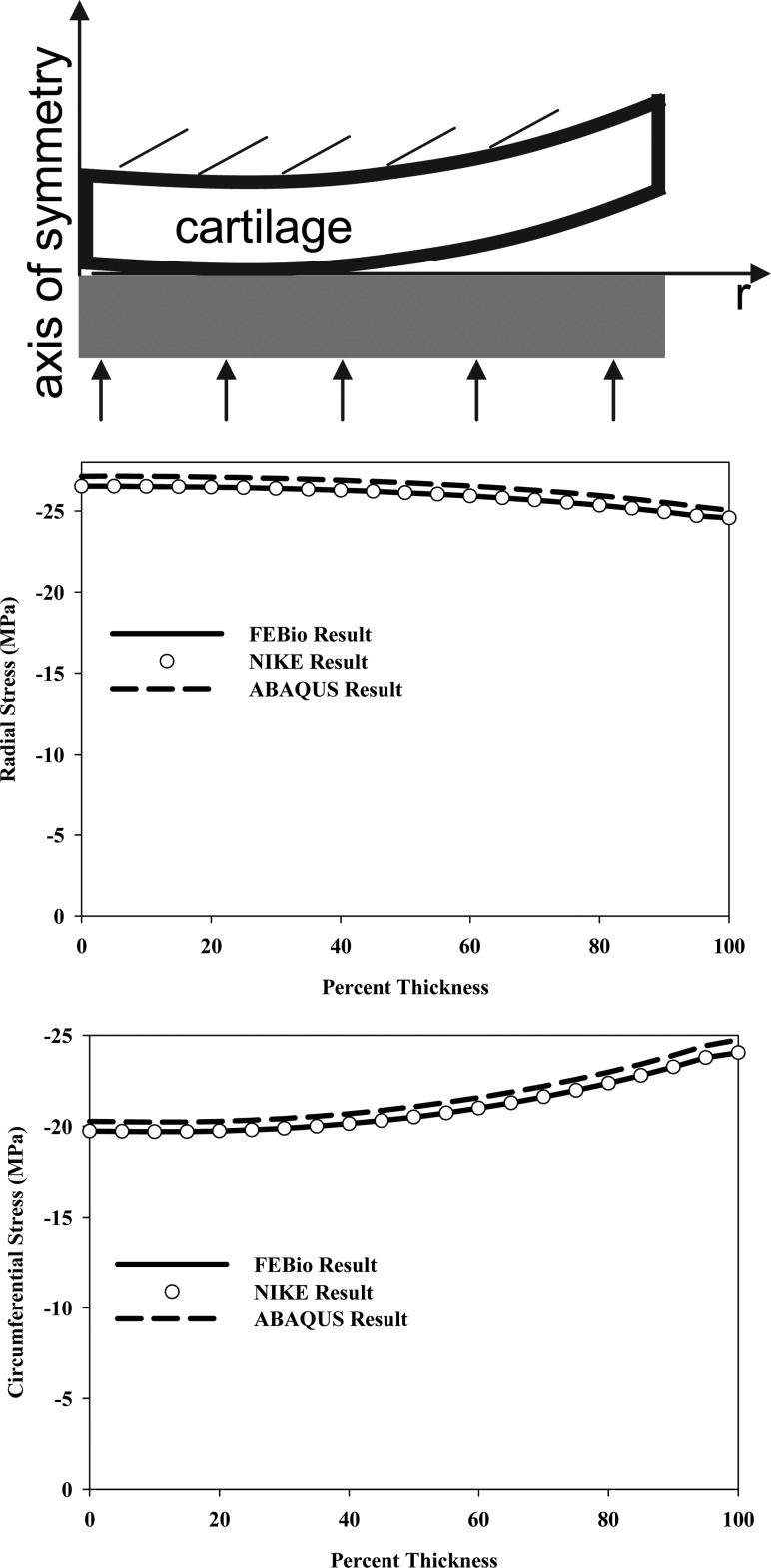
Cartilage layer compressed by a flat, rigid, impermeable surface. (Top) Schematic of the model illustrating the boundary and loading conditions. (Middle) Radial stress versus percent thickness through the middle of the cartilage layer predicted by FEBio, NIKE3D, and ABAQUS. (Bottom) Circumferential stress versus percent thickness predicted by the three FE codes. The stresses predicted by FEBio and NIKE3D were nearly identical and the stresses predicted by ABAQUS were less than 3% different than the other codes.
The predicted radial and circumferential stresses through the thickness of the middle of the cartilage layer were the same for FEBio and NIKE3D, but the stresses predicted by ABAQUS were consistently slightly larger (Fig. (Fig.9).9). The small differences (<3%) are most likely due to differences in the algorithms used to enforce the contact constraint: FEBio and NIKE3D use an augmented Lagrangian method to enforce contact, whereas ABAQUS uses a Lagrange multiplier method.
4.10. Validated Model of the Human Inferior Glenohumeral Ligament.
This problem illustrates the use of FEBio for a current research topic in computational biomechanics. The objective of the research was to develop and validate a model of the inferior glenohumeral ligament using experimental data. The subject-specific model incorporated experimental measurements of the geometry of capsular regions, humerus, and scapula, the mechanical properties of capsular regions; and joint kinematics during a simulated clinical exam. Strain distributions were measured experimentally and used to validate the FE model predictions. A full description of the model and its validation were reported by Moore et al. [50]. This original publication made use of NIKE3D for the finite element analysis. At the time, only hypoelastic materials could be used with shell elements in NIKE3D to represent the capsule. We re-analyzed this model in FEBio, which has allowed the use of a variety of more appropriate and accurate constitutive models for the capsule material (Fig. (Fig.10)10) [51].
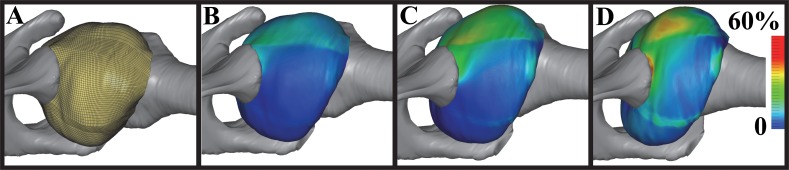
Validated model of the human inferior glenohumeral ligament, analyzed with FEBio. (A) Initial position of the model, showing the fine discretization of the shoulder capsule with shell elements. (B–D) First principal Green–Lagrange strains at 33%, 66%, and 100% through the applied kinematics that simulated a clinical exam.
5. Discussion
This paper presented FEBio, a new software tool for computational biomechanics. Some of the underlying theoretical aspects were discussed. In particular, the two most important areas of application were mentioned, namely large deformation and contact of solid and biphasic materials. FEBio provides analysis methods and constitutive models that are relevant for computational biomechanics and in this regard differs from many of the existing software tools that are currently in use for research. Although users must tailor their use of commercial applications around the limitations of the software, FEBio offers them a way to tailor the software to their specific needs.
A set of test problems was presented to illustrate our approach to verification of the presented algorithms. The results demonstrated very good to excellent agreement with either analytical solutions and/or results obtained from other finite element software. Small discrepancies were easily explained by differences in numerical algorithms between the different software packages. These results give researchers confidence that FEBio can provide accurate results for their computational research questions as well. Of course, problem-specific verification, mesh convergence studies and validation are still necessary to assure that the predictions from FEBio (or any other FE code) are accurate for a specific problem [16,17].
The development of FEBio is ongoing. New element formulations, contact algorithms, and constitutive equations are being implemented and will become available in future versions. Continued emphasis will be placed on support and dissemination of FEBio in the form of documentation of the software and its example problems, online manuals, and on our online forum. We hope that this open-source finite element framework using modern software design principles will not only provide a new and useful tool for computational biomechanics, but also set a new standard for computational simulation software in this field.
Acknowledgment
Financial support from the National Institutes of Health (1R01GM083925) is gratefully acknowledged. The authors thank Dr. Ahmet Erdemir (Cleveland Clinic Foundation) and Dr. Alexander Veress (University of Washington) for their feedback related to the FEBio software development.
Contributor Information
Benjamin J. Ellis, Department of Bioengineering,
Scientific Computing and Imaging Institute,
University of Utah,
Salt Lake City, UT 84112.
Gerard A. Ateshian, Department of Mechanical Engineering,
Department of Biomedical Engineering,
Columbia University,
New York, NY 10027.
Jeffrey A. Weiss, Department of Bioengineering,
Scientific Computing and Imaging Institute,
University of Utah,
Salt Lake City, UT 84112,
e-mail: [email protected].
[email protected].
References
Articles from Journal of Biomechanical Engineering are provided here courtesy of American Society of Mechanical Engineers
Full text links
Read article at publisher's site: https://doi.org/10.1115/1.4005694
Read article for free, from open access legal sources, via Unpaywall:
https://europepmc.org/articles/pmc3705975?pdf=render
Citations & impact
Impact metrics
Citations of article over time
Alternative metrics

Discover the attention surrounding your research
https://www.altmetric.com/details/137586236
Article citations
Modeling Fatigue Failure of Cartilage and Fibrous Biological Tissues Using Constrained Reactive Mixture Theory.
J Biomech Eng, 146(12):121001, 01 Dec 2024
Cited by: 0 articles | PMID: 39152721
Residual Strain and Joint Pressurization Maintain Collagen Tension for On-Joint Lumbar Facet Capsular Ligaments.
J Biomech Eng, 146(11):111005, 01 Nov 2024
Cited by: 0 articles | PMID: 39082759
A clinical comparison of a digital versus conventional design methodology for transtibial prosthetic interfaces.
Sci Rep, 14(1):25833, 28 Oct 2024
Cited by: 0 articles | PMID: 39468101 | PMCID: PMC11519600
Continuum Growth Mechanics: Reconciling Two Common Frameworks.
J Biomech Eng, 146(10):101003, 01 Oct 2024
Cited by: 1 article | PMID: 38607565
Influence of Contact Lens Parameters on Cornea: Biomechanical Analysis.
Bioengineering (Basel), 11(10):966, 27 Sep 2024
Cited by: 0 articles | PMID: 39451343 | PMCID: PMC11505363
Go to all (434) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
A Plugin Framework for Extending the Simulation Capabilities of FEBio.
Biophys J, 115(9):1630-1637, 26 Sep 2018
Cited by: 8 articles | PMID: 30297132 | PMCID: PMC6225080
A systematic comparison between FEBio and PolyFEM for biomechanical systems.
Comput Methods Programs Biomed, 244:107938, 29 Nov 2023
Cited by: 0 articles | PMID: 38056313
FEBio: History and Advances.
Annu Rev Biomed Eng, 19:279-299, 01 Jun 2017
Cited by: 28 articles | PMID: 28633565 | PMCID: PMC6141040
Review Free full text in Europe PMC
Finite element implementation of mechanochemical phenomena in neutral deformable porous media under finite deformation.
J Biomech Eng, 133(8):081005, 01 Aug 2011
Cited by: 18 articles | PMID: 21950898 | PMCID: PMC3431289
Funding
Funders who supported this work.
NIGMS NIH HHS (2)
Grant ID: 1R01GM083925
Grant ID: R01 GM083925