MR to CT Registration of Brains using Image Synthesis.

Roy S; Carass A; Jog A; Prince JL; Lee J

doi:10.1117/12.2043954

MR to CT Registration of Brains using Image Synthesis.

Affiliations

1. Center for Neuroscience and Regenerative Medicine, Henry M. Jackson Foundation.
Authors
Roy S¹
(1 author)
2. Image Analysis and Communications Laboratory, The Johns Hopkins University.
Authors
Carass A²
Jog A²
Prince JL²
(3 authors)
3. Radiation Oncology and Molecular Radiation Sciences, Johns Hopkins School of Medicine.
Authors
Lee J³
(1 author)

ORCIDs linked to this article

Proceedings of Spie--the International Society for Optical Engineering, 01 Mar 2014, 9034:spie.org/Publications/Proceedings/Paper/10.1117/12
https://doi.org/10.1117/12.2043954 PMID: 25057341 PMCID: PMC4104818

Free full text in Europe PMC

Abstract

Computed tomography (CT) is the standard imaging modality for patient dose calculation for radiation therapy. Magnetic resonance (MR) imaging (MRI) is used along with CT to identify brain structures due to its superior soft tissue contrast. Registration of MR and CT is necessary for accurate delineation of the tumor and other structures, and is critical in radiotherapy planning. Mutual information (MI) or its variants are typically used as a similarity metric to register MRI to CT. However, unlike CT, MRI intensity does not have an accepted calibrated intensity scale. Therefore, MI-based MR-CT registration may vary from scan to scan as MI depends on the joint histogram of the images. In this paper, we propose a fully automatic framework for MR-CT registration by synthesizing a synthetic CT image from MRI using a co-registered pair of MR and CT images as an atlas. Patches of the subject MRI are matched to the atlas and the synthetic CT patches are estimated in a probabilistic framework. The synthetic CT is registered to the original CT using a deformable registration and the computed deformation is applied to the MRI. In contrast to most existing methods, we do not need any manual intervention such as picking landmarks or regions of interests. The proposed method was validated on ten brain cancer patient cases, showing 25% improvement in MI and correlation between MR and CT images after registration compared to state-of-the-art registration methods.

Free full text

Proc SPIE. Author manuscript; available in PMC 2014 Jul 21.

Published in final edited form as:

Proc SPIE. 2014 Mar 21; 9034: spie.org/Publications/Proceedings/Paper/10.1117/12.2043954.

https://doi.org/10.1117/12.2043954

PMCID: PMC4104818

NIHMSID: NIHMS613560

PMID: 25057341

MR to CT Registration of Brains using Image Synthesis

Snehashis Roy,^* Aaron Carass,^† Amod Jog,^† Jerry L. Prince,^† and Junghoon Lee^§

Author information Copyright and License information Disclaimer

See other articles in PMC that cite the published article.

Abstract

Keywords: magnetic resonance imaging, MRI, CT, image synthesis, intensity normalization, histogram matching, brain, hallucination, patches

1. INTRODUCTION

CT is the primary imaging modality for radiation therapy planning and dose computation. Accurate segmentation of the target structures and tumors based on CT alone is challenging due to insu cient image contrast. To compensate, MRI is used in conjunction with CT for the target and tumor delineation. Although MRI shows excellent soft tissue contrast with high SNR, MR images show geometric image distortions and do not provide electron density information needed for dose computation. Therefore, an accurate registration between MRI and CT is crucial for accurate radiotherapy planning and delivering the prescribed dose to the patient.¹ This is particularly critical in areas such as the head and neck where the planning target volume must spare critical structures.

Several MR to CT registration techniques have been proposed in the past. Mutual information (MI) is a common cost function used to drive a registration.² MR to CT methods typically require users to input landmarks or draw region of interests on the CT and MR, and the MR is then deformably registered using the segmentations of the regions³ or landmarks.⁴ It has also been shown that the fully automatic methods perform comparably or worse than semi-automatic methods,⁵ although any manual intervention is likely to be prone to reproducibility error and is time consuming.

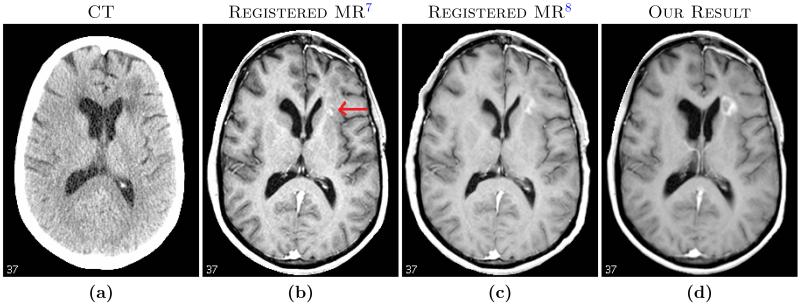
Unlike CT, MR intensities do not possess a calibrated intensity scale. Thus MR intensities obtained from di erent scanners or imaging sessions usually have di erent scales and probability distributions. As MI depends on the joint distribution of the images, it sometimes leads to local maxima,⁶ especially when the intensity scales are widely di erent. An example is shown in Fig. 1, where MR and CT images of the same subject were registered by rigid registration followed by a b-spline registration using commercial software (VelocityAI, Velocity Medical Solutions, Atlanta, GA).⁷ We also computed the registration using a state-of-the-art MI-based di eomorphic deformable registration algorithm SyN.⁸ Both methods did not properly register soft tissues such as ventricles (red arrow) while registering the skull reasonably well. The soft tissue registration was improved with the proposed method.

An external file that holds a picture, illustration, etc.
Object name is nihms-613560-f0001.jpg

Figure 1

(b) A real MR image is registered to its CT acquisition (shown in (a)) using an MI based commercial b-spine registration,⁷ (c) shows the registration using an MI based state-of-the-art deformable registration algorithm,⁸ (d) shows the result from the proposed framework.

In this paper, we propose a fully automated framework to register MR to CT via a synthetic CT (sCT) that contains the same intensity scale as a CT image. We use a registered MR and CT image pair as atlas which is often done in a semi-automated way. Note that the atlas and subject images are not registered. The atlas and subject images are first decomposed into patches, generating corresponding “patch clouds”. The subject patch cloud is matched to the atlas cloud using a number of Gaussian mixture models by incorporating the idea of coherent point drift.⁹ The sCT image is obtained as a maximum likelihood estimate from the model. The sCT is in the same space as the subject MR and contains CT-like intensities, it is deformably registered to the original subject CT by maximizing cross-correlation (CC) using SyN. The subject MRI is then registered to the CT by applying the corresponding deformation. We compare the proposed framework with two methods, a b-spline based registration (VelocityAI⁷) and SyN.⁸ In both cases, the MR is registered to the CT using MI as a similarity metric. Similar inter-modality analyses has been previously explored in a MR image registration context.^10–12 We emphasize that our sCT images are used for the sole purpose of registration improvement and are treated as an intermediate result. They are not meant to be used by radiologists for any diagnostic purposes.

2. METHOD

2.1 Atlas and patch description

We define the atlas as a pair of co-registered images {a₁, a₂} having the same resolution with contrasts C₁ and C₂, respectively. In this paper, C₁ is MR and C₂ is CT. The subject, also having the same resolution, is denoted by b₁ and is of contrast C₁. Both a₁ and b₁ are normalized such that their WM peak intensities are at unity. WM peak intensity is found from the corresponding histogram. At each voxel of an image, 3D patches—size p × q × r—are stacked into 1D vectors of size d × 1, with d = pqr. Atlas C₁ and C₂ contrast patches are denoted by y_j and v_j, respectively, where j = 1, … , M. Subject b₁ yields C₁ contrast patches which are denoted by x_i, i = 1, … , N. The unobserved C₂ contrast subject patches of b₁ are denoted by u_i. N and M are the number of non-zero voxels in the subject and the atlas, respectively. We combine the patch pairs as 2d × 1 vectors $p_{i} = {[x_{i}^{T} u_{i}^{T}]}^{T}$ and $q_{j} = {[y_{j}^{T} v_{j}^{T}]}^{T}$ . The patch clouds are defined as the collection of patches and patch-pairs X = {x_i}, P = {p_i}, and Q = {q_j}.

2.2 Contrast synthesis algorithm

The subject and atlas C₁ patches represent a pattern of intensities that are scaled to a similar intensity range. Therefore, an atlas patch that has a pattern of intensities that is similar to a given subject patch might arise from the same distribution of tissues. In that case, the C₂ patch in the atlas can be expected to represent an approximate C₂ contrast of the subject in that patch.¹³ One could naively find a single patch within the atlas that is close (or closest) to the subject patch and then use the corresponding C₂ atlas patch directly in synthesis. A slightly more complex way to use this is to find a sparse collection of atlas patches that can better reconstruct the subject patch, then use the same combination of C₂ patches to reconstruct a synthetic image.^14–16 Neither of these approaches uses the C₂ atlas patches in selecting the combination. A joint dictionary learning using both C₁ and C₂ contrast patches has been proposed in a registration framework.¹⁷ In this paper, we propose a synthesis framework where we want to combine a small number of patches and take advantage of the C₂ patches in the atlas while selecting the C₁ patches. This idea of pattern matching su ers if there are pathologies (e.g., tumors or lesions) in the subject which is not present in the atlas. Nevertheless, since the synthetic images are used to improve registration and treated as intermediary result, we synthesize C₂ contrast patches with matching atlas patches irrespective of their underlying biology.

We propose a probabilistic model that specifically relates subject C₁ patches to atlas C₁ patches. Since atlas patches may not be plentiful enough to closely resemble all subject patches, we consider all convex combinations of pairs of atlas patches. We then postulate that subject patches are random vectors whose probability densities are Gaussian with means given by an unknown convex combinations of pairs of atlas patches and with unknown covariance matrices. This framework captures the notion that a convex combination of a small number of atlas patches (just two in this paper) could be used to describe a subject patch. In order to tie the C₁ and C₂ contrasts together, we further assume that the subject’s unknown C₂ patch is a random vector whose mean is the same convex combination of the same two atlas patches associated with the C₁ contrast, with a covariance matrix that can be di erent, in principle.

This can be summarized succinctly by considering a subject patch p_i and two associated atlas patches q_j and q_k. Then p_i is assumed to arise from the Gaussian distribution,

p_{i} \sim N (α_{i t} q_{j} + (1 - α_{i t}) q_{k}, Σ_{t}), t \equiv {j, k}, α_{i t} \in (0, 1) .

(1)

Where Σ_t is a covariance matrix associated with the atlas patches and t [set membership] Ψ, where Ψ is the set of all pairs of atlas patch indices, and α_it (0, 1) is a mixing coe cient for the i^th subject patch to the t^th atlas patch-pairs. In essence, each subject patch follows an ( $\begin{matrix} M \\ 2 \end{matrix}$ )-class Gaussian mixture model (GMM). We assume the patches are i.i.d. and maximize the probability of observing the subject patches p_i using expectation-maximization (EM) to find the synthetic contrast patches u_i.

We define z_it as the indicator function that p_i comes from a GMM of the t = {j, k}^th atlas pair, Σ_tΨ z_it = 1 ∀i, z_it [set membership] {0, 1}. Then the probability of observing p_i can be written as,

P (p_{i} ∣ z_{i t} = 1, Σ_{t}, α_{i t}) = \frac{1}{\sqrt{2 π} ∣ Σ_{t} ∣} \exp {- \frac{1}{2} h_{i t}^{T} Σ_{t}^{- 1} h_{i t}},

(2)

where h_it = p_i − α_itq_j − (1 − α_it)q_k, t ≡ {j, k}. The prior probability of having p_i originating from the distribution of the t^th pair is P (z_it = 1 |Σt, α_it). Without any knowledge of x_i, this prior should ideally depend on a classification of the patch cloud Q. However, we avoid any classification of patches by assuming a uniform prior. We have experimentally found that a full-rank Σ_t is often less robust to estimate. Instead, we assume it to be separable and block diagonal,

Σ_{t} = [\begin{matrix} σ_{1 t}^{2} I & 0 \\ 0 & σ_{2 t}^{2} I \end{matrix}],

indicating that the variations of each voxel in a patch are the same around the means, although individual voxels can be of di erent tissue. Thus the joint probability becomes,

\begin{matrix} P (P, Z ∣ ϴ) & = D \prod_{t \in Ψ} \prod_{i = 1}^{N} {[\frac{1}{σ_{1 t} σ_{2 t}} \exp {- \frac{{∣ ∣ f_{i t} ∣ ∣}^{2}}{2 σ_{1 t}^{2}}} \exp {- \frac{{∣ ∣ g_{i t} ∣ ∣}^{2}}{2 σ_{2 t}^{2}}}]}^{z_{i t}}, \\ f_{i t} = x_{i} - & α_{i t} y_{j} - (1 - α_{i t}) y_{k}, g_{i t} = u_{i} - α_{i t} v_{j} - (1 - α_{i t}) v_{k} . \end{matrix}

(3)

The set of parameters are Θ = {σ_1t, σ_2t, α_it; i = 1, … , N, t [set membership] Ψ}, and the maximum likelihood estimators of Θ are found by maximizing Eqn. 3 using EM. The EM algorithm be outlined as,

E-step: to find new update Θ^(m+1) at the m^th iteration, compute the expectation Q(Θ^(m+1)|Θ^(m)) = E[log P(P, Z|Θ^(m+1))|X, Θ^(m)].
M-step: find new estimates Θ^(m+1) based on the previous estimates using the following equation Θ^(m+1) = arg max_Θ^(m+1) Q(Θ^(m+1)Θ^(m)).

The E-step requires the computation of E(z_it|P, Θ^(m)) = P (z_it|P, Θ^(m). Given that z_it is an indicator function, it can be shown that $E (z_{i t} ∣ P, ϴ^{(m)}) = w_{i t}^{(m)}$ , where

w_{i t}^{(m + 1)} = \frac{\frac{1}{σ_{1 t}^{(m)} σ_{2 t}^{(m)}} \exp {- \frac{{∣ ∣ f_{i t}^{(m)} ∣ ∣}^{2}}{2 σ_{1 t}^{{(m)}^{2}}}} \exp {- \frac{{∣ ∣ g_{i t}^{(m)} ∣ ∣}^{2}}{2 σ_{2 t}^{{(m)}^{2}}}}}{Σ_{ℓ \in Ψ} \frac{1}{σ_{1 ℓ}^{(m)} σ_{2 l}^{(m)}} \exp {- \frac{{∣ ∣ f_{i ℓ}^{(m)} ∣ ∣}^{2}}{2 σ_{1 ℓ}^{{(m)}^{2}}}} \exp {- \frac{{∣ ∣ g_{i ℓ}^{(m)} ∣ ∣}^{2}}{2 σ_{2 ℓ}^{{(m)}^{2}}}}},

(4)

$w_{i t}^{(m)}$ being the posterior probability of p_i originating from the Gaussian distribution of the t^th atlas patches q_j and q_k. $f_{i t}^{(m)}$ and $g_{i t}^{(m)}$ are the expressions defined in Eqn. 3 but with $α_{i t}^{(m)}$ . $f_{i ℓ}^{(m)}$ and $g_{i ℓ}^{(m)}$ denote the corresponding values with atlas patches belonging to the [ell] ^th pair, [ell] [set membership] Ψ, with $α_{i ℓ}^{(m)}$ . The synthetic patches are obtained by the following expectation,

E (u_{i} ∣ ϴ^{(m)}) = \sum_{t \in Ψ} w_{i t}^{(m)} (α_{i t}^{(m)} v_{j} + (1 - α_{i t}^{(m)}) v_{k}) .

(5)

At each iteration, we replace the value of u_i with its expectation. The M-step involves the maximization of the log of the expectation w.r.t. the parameters given the current $w_{i t}^{(m)}$ . The update equations are given by,

σ_{1 t}^{{(m + 1)}^{2}} = \frac{Σ_{i = 1}^{N} w_{i t}^{(m)} {∣ ∣ x_{i} - α_{i t}^{(m)} y_{j} - (1 - α_{i t}^{(m)}) y_{k} ∣ ∣}^{2}}{Σ_{i = 1}^{N} w_{i t}^{(m)}},

(6)

σ_{2 t}^{{(m + 1)}^{2}} = \frac{Σ_{i = 1}^{N} w_{i t}^{(m)} {∣ ∣ u_{i} - α_{i t}^{(m)} v_{j} - (1 - α_{i t}^{(m)}) v_{k} ∣ ∣}^{2}}{Σ_{i = 1}^{N} w_{i t}^{(m)}},

(7)

α_{i t}^{(m + 1)} : F (α_{i t}^{(m + 1)}) = 0, where F (x) = A x^{2} (1 - x) - B x (1 - x) + 2 x - 1, A = \frac{{∣ ∣ y_{k} - y_{j} ∣ ∣}^{2}}{σ_{1 t}^{{(m + 1)}^{2}}} + \frac{{∣ ∣ v_{k} - v_{j} ∣ ∣}^{2}}{σ_{2 t}^{{(m + 1)}^{2}}}, B = \frac{{(y_{k} - x_{i})}^{T} (y_{k} - y_{j})}{σ_{1 t}^{{(m + 1)}^{2}}} + \frac{{(v_{k} - u_{i})}^{T} (v_{k} - v_{j})}{σ_{2 t}^{{(m + 1)}^{2}}} .

It should be noted that F (0) = −1, F (1) = 1, ∀ A, B; thus, there is always a feasible $α_{i t}^{(m)} \in (0, 1)$ . Once EM converges, the expectation of the final u_i is considered the synthetic C₂ contrast, and the center voxel of u_i is used as the C₂ contrast replacement of the i^th voxel.

The imaging model is valid for those atlas and subject patches that are close in intensity. Using a non-local type of criterion,¹⁸ for every subject patch x_i, we choose a feasible set of L atlas patches such that they are the L nearest neighbors of x_i. Thus the i^th subject patch follows an $(\begin{matrix} L \\ 2 \end{matrix})$ -class GMM and the algorithm becomes O(NL²). In all our experiments, we used 3 × 3 × 3 patches with L = 40.

3. RESULTS

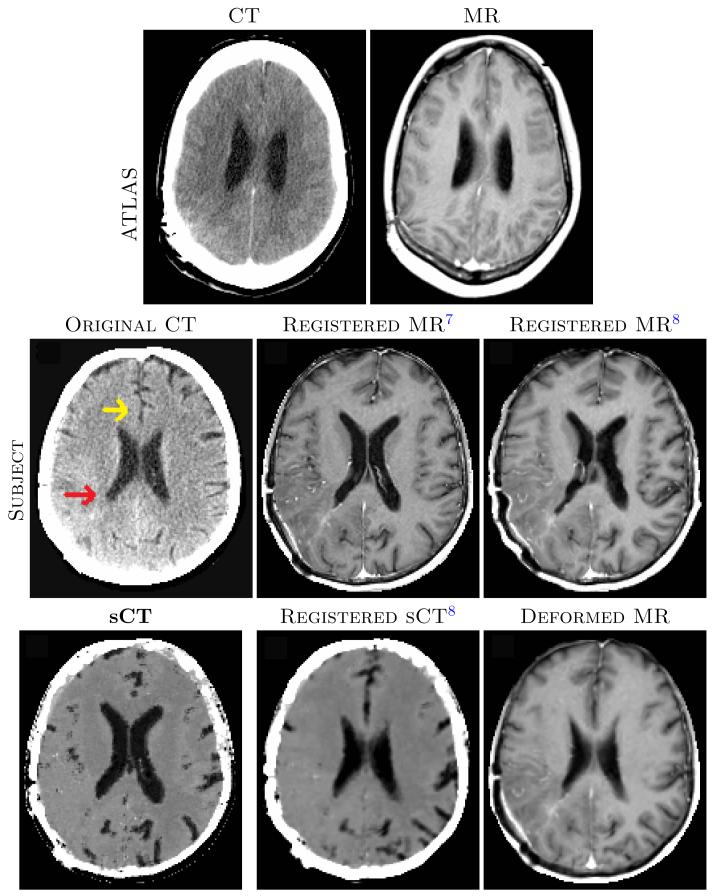
We experimented on images from ten brain cancer patients with various sizes and shapes of tumors, each having one MR and CT acquisition. A di erent subject was chosen as the atlas, for which the MRI was carefully registered to the CT using a commercial software.⁷ This registered MR-CT pair was used as the atlas {a₁, a₂}. For each of the ten subjects, we registered the MRI to CT using b-spline registration⁷ and SyN.⁸ We also generated the sCT image from the MRI (b₁), registered (SyN) sCT to the original CT and applied the deformation to the MRI to get registered MRI. An example of the atlas {a₁, a₂}, subject MR b₁, registration results from b-spline, SyN, sCT, and the corresponding deformed MR images from their registrations are shown in Fig. 2.

An external file that holds a picture, illustration, etc.
Object name is nihms-613560-f0002.jpg

Figure 2

Top row shows a registered pair of MR-CT images used as atlas. Middle row shows the original subject CT image, and the registered MRIs by b-spline⁷ and SyN.⁸ Bottom row shows the sCT, SyN registered sCT, and the corresponding deformed MR with the deformation from sCT to original CT via SyN.

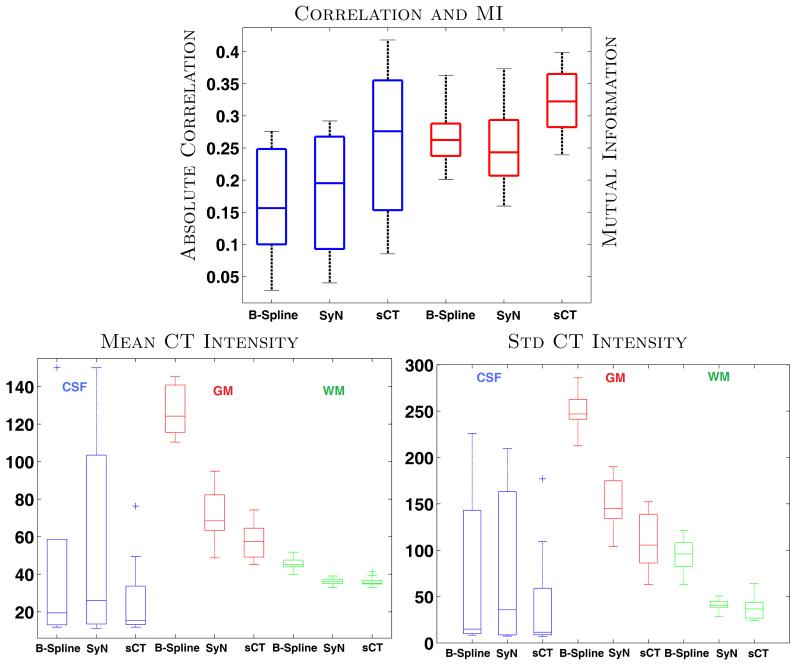
Fig. 3 top image shows absolute values of correlation and MI between CT and the registered MR brain volumes of ten subjects. The brain volumes are obtained from skull-stripping¹⁹ masks of the MR images. Both MI and correlations increase significantly (p-value < 0.05) after registration via sCT, indicating significant improvement in MR-CT registration of the brains. Another registration metric is the variability of CT intensities for di erent tissue classes. For each subject, we segmented the registered MRI into three classes, cerebro-spinal fluid (CSF), gray matter (GM) and white matter (WM), using an atlas based method.²⁰ The mean and standard deviations of CT intensities for each of the classes are plotted in Fig. 3 bottom row. For every tissue, standard deviations from sCT deformed MRI reduce significantly (p-value < 0.05) in comparison to both the b-spline and SyN registered MRIs. Misregistration causes the inclusion of other structures with di erent intensities in the segmentation, which leads to higher variability. The sCT registration also gives the closest mean CT intensities to the truth, 15, 40, and 25 Hounsfield units for CSF, GM, and WM, respectively.²¹ A visual inspection in Fig. 2 of the subject MRI shows the registration improvement near the ventricles (red arrow) and frontal gray matter (yellow arrow).

An external file that holds a picture, illustration, etc.
Object name is nihms-613560-f0003.jpg

Figure 3

Top image shows absolute values of correlation (blue) and MI (red) between original CT and b-spline,⁷ SyN⁸ and sCT registered MRIs. Bottom row shows mean and standard deviations of CT intensities from segmentations of the three registered MR images.

4. DISCUSSION AND CONCLUSION

We have proposed a novel framework for registering MRI to CT using CT synthesis as an intermediate step. Since the sCT has the same intensity scale as CT, we register sCT to the subject CT using CC as a similarity metric instead of directly registering MRI to CT based on MI. For the current work, we created the atlas by registering MR and CT using a semi-automatic method. We note that this atlas MR-CT registration can be improved using the proposed framework (i.e., synthesize and register). However, for the current work, we visually checked the atlas and found little registration error. Although the sCT is only used for improving registration in this study, the synthesis quality can be improved by using multiple atlases and di erent patch sizes or shapes. The capability of accurately synthesizing CT from MRI will allow us to directly compute dose on sCT and enable solely MRI-based radiotherapy planning.

Acknowledgments

This work was supported by the NIH/NIBIB under grants 1R01EB017743 and 1R21EB012765.

REFERENCES

[1] Rosenman JG, Miller EP, Tracton G, Cullip TJ. Image Registration: An Essential Part of Radiation Therapy Treatment Planning. Intl. Journal of Rad. Oncology. 1998;40(1):197–205. [Abstract] [Google Scholar]

[2] Chen HM, Varshney PK. Mutual information-based CT-MR brain image registration using generalized partial volume joint histogram estimation. IEEE Trans. Medical Imag. 2003;22(9):1111–1119. [Abstract] [Google Scholar]

[3] Noble JH, Dawant BM. An atlas-navigated optimal medial axis and deformable model algorithm (NOMAD) for the segmentation of the optic nerves and chiasm in MR and CT images. Medical Image Analysis. 2011;15(6):877–884. [Europe PMC free article] [Abstract] [Google Scholar]

[4] McLaughlin PW, Narayana V, Kessler M, McShan D, Troyer S, Marsh L, Hixson G, Roberson PL. The use of mutual information in registration of CT and MRI datasets post permanent implant. Brachytherapy. 2004;3(2):61–70. [Abstract] [Google Scholar]

[5] Dean CJ, Sykes JR, Cooper RA, Hatfield P, Carey B, Swift S, Bacon SE, Thwaites D, Sebag-Montefiore D, Morgan AM. An evaluation of four CTMRI co-registration techniques for radiotherapy treatment planning of prone rectal cancer patients. British Journal of Radiology. 2012;85(1009):61–68. [Europe PMC free article] [Abstract] [Google Scholar]

[6] Loeckx D, Slagmolen P, Maes F, Vandermeulen D, Suetens P. Nonrigid Image Registration Using Conditional Mutual Information. IEEE Trans. Medical Imag. 2010;29(1):19–29. [Abstract] [Google Scholar]

[7] Lawson JD, Schreibmann E, Jani AB, Fox T. Quantitative Evaluation of a Cone Beam Computed Tomography (CBCT)-CT Deformable Image Registration Method for Adaptive Radiation Therapy. Journal of Appl. Clin. Med. Phys. 2007;8(4):96–113. [Europe PMC free article] [Abstract] [Google Scholar]

[8] Avants BB, Epstein CL, Grossman M, G. JC. Symmetric di eomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12(1):26–41. [Europe PMC free article] [Abstract] [Google Scholar]

[9] Myronenko A, Song X. Point-Set Registration: Coherent Point Drift. IEEE Trans. Patt. Anal. and Machine Intell. 2010;32(12):2262–2275. [Abstract] [Google Scholar]

[10] Ye DH, Zikic D, Glocker B, Criminisi A, Konukoglu E. Modality Propagation: Coherent Synthesis of Subject-Specific Scans with Data-Driven Regularization. Med. Image Comp. and Comp.-Asst. Intervention (MICCAI) 2013;8149:606–613. [Abstract] [Google Scholar]

[11] Iglesias JE, Konukoglu E, Zikic D, Glocker B, Leemput KV, Fischl B. Is Synthesizing MRI Contrast Useful for Inter-modality Analysis? Med. Image Comp. and Comp.-Asst. Intervention (MICCAI) 2013;8149:631–638. [Europe PMC free article] [Abstract] [Google Scholar]

[12] Roy S, Jog A, Carass A, Prince JL. Atlas Based Intensity Transformation of Brain MR Images. Multimodal Brain Image Analysis (MBIA) 2013;8159:51–62. [Google Scholar]

[13] Hertzmann A, Jacobs CE, Oliver N, Curless B, Salesin DH. Image analogies; Conf. on Comp. Graphics and Interactive Techniques (SIGGRAPH); 2001.pp. 327–340. [Google Scholar]

[14] Roy S, Carass A, Prince JL. Synthesizing MR contrast and resolution through a patch matching technique. Proc. of SPIE Med. Imaging. 2010 Mar;7623:76230J. [Europe PMC free article] [Abstract] [Google Scholar]

[15] Roy S, Carass A, Prince JL. A compressed sensing approach for MR tissue contrast synthesis. Inf. Proc. in Medical Imaging. 2011:371–383. [Europe PMC free article] [Abstract] [Google Scholar]

[16] Roy S, Carass A, Prince JL. Magnetic Resonance Image Example-Based Contrast Synthesis. IEEE Trans. on Med. Imag. 2013;32(12):2348–2363. [Europe PMC free article] [Abstract] [Google Scholar]

[17] Cao T, Zach C, Modla S, Powell D, Czymmek K, Niethammer M. Registration for correlative microscopy using image analogies. Workshop on Biomedical Image Registration (WBIR) 2012:296–306. [Europe PMC free article] [Abstract] [Google Scholar]

[18] Mairal J, Bach F, Ponce J, Sapiro G, Zisserman A. Non-local sparse models for image restoration. IEEE Intl. Conf. on Comp. Vision. 2009:2272–2279. [Google Scholar]

[19] Carass A, Cuzzocreo J, Wheeler MB, Bazin P-L, Resnick SM, Prince JL. Simple paradigm for extra-cerebral tissue removal: Algorithm and analysis. NeuroImage. 2011;56(4):1982–1992. [Europe PMC free article] [Abstract] [Google Scholar]

[20] Shiee N, Bazin P-L, Cuzzocreo J, Blitz A, Pham D. Segmentation of brain images using adaptive atlases with application to ventriculomegaly. Inf. Proc. in Medical Imaging. 2011:1–12. [Europe PMC free article] [Abstract] [Google Scholar]

[21] Toennies KD. Guide to Medical Image Analysis: Methods and Algorithms. Springer; 2012. ch. 2. [Google Scholar]

Full text links

Read article at publisher's site: https://doi.org/10.1117/12.2043954

Read article for free, from open access legal sources, via Unpaywall: https://europepmc.org/articles/pmc4104818?pdf=render

Citations & impact

Impact metrics

Citations

Jump to Citations

Citations of article over time

Smart citations by scite.ai
Explore citation contexts and check if this article has been supported or disputed.
https://scite.ai/reports/10.1117/12.2043954

Supporting

Mentioning

Contrasting

Article citations

TAI-GAN: A Temporally and Anatomically Informed Generative Adversarial Network for early-to-late frame conversion in dynamic cardiac PET inter-frame motion correction.
Guo X, Shi L, Chen X, Liu Q, Zhou B, Xie H, Liu YH, Palyo R, Miller EJ, Sinusas AJ, Staib L, Spottiswoode B, Liu C, Dvornek NC
Med Image Anal, 96:103190, 07 May 2024
Cited by: 0 articles | PMID: 38820677
TCGAN: a transformer-enhanced GAN for PET synthetic CT.
Li J, Qu Z, Yang Y, Zhang F, Li M, Hu S
Biomed Opt Express, 13(11):6003-6018, 24 Oct 2022
Cited by: 2 articles | PMID: 36733758 | PMCID: PMC9872870
Free full text in Europe PMC
MR-CT multi-atlas registration guided by fully automated brain structure segmentation with CNNs.
Walluscheck S, Canalini L, Strohm H, Diekmann S, Klein J, Heldmann S
Int J Comput Assist Radiol Surg, 18(3):483-491, 05 Nov 2022
Cited by: 1 article | PMID: 36334164 | PMCID: PMC9939492
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
Virtual contrast enhancement for CT scans of abdomen and pelvis.
Liu J, Tian Y, Duzgol C, Akin O, Ağıldere AM, Haberal KM, Coşkun M
Comput Med Imaging Graph, 100:102094, 26 Jul 2022
Cited by: 0 articles | PMID: 35914340 | PMCID: PMC10227907
Free full text in Europe PMC
Abdominopelvic MR to CT registration using a synthetic CT intermediate.
Heo JU, Zhou F, Jones R, Zheng J, Song X, Qian P, Baydoun A, Traughber MS, Kuo JW, Helo RA, Thompson C, Avril N, DeVincent D, Hunt H, Gupta A, Faraji N, Kharouta MZ, Kardan A, Bitonte D, [...] Muzic RF
J Appl Clin Med Phys, 23(9):e13731, 03 Aug 2022
Cited by: 1 article | PMID: 35920116 | PMCID: PMC9512351
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC

Go to all (23) article citations

Funding

Funders who supported this work.

NIBIB NIH HHS (2)

Grant ID: R21 EB012765
23 publications
Grant ID: R01 EB017743
21 publications

Search life-sciences literature (45,103,589 articles, preprints and more)

MR to CT Registration of Brains using Image Synthesis.

Author information

Affiliations

Authors

Authors

Authors

ORCIDs linked to this article

Abstract

Free full text

MR to CT Registration of Brains using Image Synthesis

Snehashis Roy

Aaron Carass

Amod Jog

Jerry L. Prince

Junghoon Lee

Abstract

1. INTRODUCTION

2. METHOD

2.1 Atlas and patch description

2.2 Contrast synthesis algorithm

3. RESULTS

4. DISCUSSION AND CONCLUSION

Acknowledgments

REFERENCES

Full text links

Citations & impact

Impact metrics

Citations of article over time

Article citations

Similar Articles

Funding

NIBIB NIH HHS (2)﻿

Partnerships & funding

NIBIB NIH HHS (2)