Abstract
Free full text

Neural Correlates of Expected Risks and Returns in Risky Choice across Development
Abstract
Adolescence is often described as a period of increased risk taking relative to both childhood and adulthood. This inflection in risky choice behavior has been attributed to a neurobiological imbalance between earlier developing motivational systems and later developing top-down control regions. Yet few studies have decomposed risky choice to investigate the underlying mechanisms or tracked their differential developmental trajectory. The current study uses a risk–return decomposition to more precisely assess the development of processes underlying risky choice and to link them more directly to specific neural mechanisms. This decomposition specifies the influence of changing risks (outcome variability) and changing returns (expected value) on the choices of children, adolescents, and adults in a dynamic risky choice task, the Columbia Card Task. Behaviorally, risk aversion increased across age groups, with adults uniformly risk averse and adolescents showing substantial individual differences in risk sensitivity, ranging from risk seeking to risk averse. Neurally, we observed an adolescent peak in risk-related activation in the anterior insula and dorsal medial PFC. Return sensitivity, on the other hand, increased monotonically across age groups and was associated with increased activation in the ventral medial PFC and posterior cingulate cortex with age. Our results implicate adolescence as a developmental phase of increased neural risk sensitivity. Importantly, this work shows that using a behaviorally validated decision-making framework allows a precise operationalization of key constructs underlying risky choice that inform the interpretation of results.
Introduction
Adolescence is a period of changing cognitive, social, sexual, and physical demands with significant changes in brain circuitry. That is, during adolescence there are ongoing increases in myelination and a gradual decrease in synaptic density (Huttenlocher, 1990; Huttenlocher and Dabholkar, 1997; Gogtay et al., 2004; Tamnes et al., 2010), with prefrontal regions—implicated in top-down control processes—developing later than subcortical regions implicated in affective-motivational processes. These different maturational trajectories have been linked to a potential imbalance during adolescence (Casey et al., 2008), hypothesized to result in heightened emotional responding, poor choice, and an increased propensity to engage in risky behaviors (Somerville et al., 2010; Gladwin et al., 2011).
However, to date, few studies have focused on the mechanisms underlying risky choice across development. That is, most developmental imaging studies focused on adolescents' neural responses to rewards. Of these studies, some observed hypersensitive striatal responses to reward in adolescents (Galvan et al., 2006; Van Leijenhorst et al., 2010; Padmanabhan et al., 2011; Smith et al., 2011), while others observed hyposensitivity (Bjork et al., 2004, 2010), or minimal developmental changes (May et al., 2004; Paulsen et al., 2011; Teslovich et al., 2014). These conflicting results may be explained partly by methodological differences (Galvan, 2010), with some studies confounding reward and risk, and many studies not studying risky choice (for review, see Richards et al., 2013). In the current study we use a model-based approach to operationalize central constructs of risky choice.
In behavioral decision sciences and neuroeconomics, risky choices are typically analyzed within formal frameworks. A specific class of models—risk–return models (Weber, 2010)—decompose risky choice into a return component (i.e., the mean or expected value of a decision's outcome) and a risk component (the outcome variability, typically the variance or SD of the distribution of possible outcomes). In contrast to utility-based models such as prospect theory (Kahneman and Tversky, 1979), risk–return models explicitly model a component of risk in choice behavior. Adult neuroimaging studies using risk–return frameworks showed greater returns to be associated with increased striatal and ventromedial (vm) PFC activation, and greater risks to be associated with increased activations in dorsomedial (dm) PFC, thalamus, and the anterior insula (Tobler et al., 2009; Mohr et al., 2010a, b).
To investigate the processes that underlie and drive risky choice across development, we applied a risk–return model to the dynamic risky choices of children, adolescents, and adults in a modified, fMRI-compatible version of the “hot” Columbia Card Task (CCT). The hot CCT is a dynamic risky choice task sensitive to individual and developmental differences in risk taking (Figner et al., 2009; Figner and Weber, 2011). Using parametric fMRI analyses, we identified brain regions that were modulated by expected risks, expected returns, and/or the outcomes of participants' choices (i.e., gains and losses). Specifically we were interested in how these responses changed across age groups. Therefore, we examined both linear effects (reflecting monotonic developmental differences) and quadratic effects (reflecting adolescent-specific differences).
Materials and Methods
Participants
To be able to study developmental changes in and out of adolescence, we included children, mid-to-late adolescents, and adults in our sample: 85 participants between ages 8 and 35 years were scanned for this study. Data from five participants were excluded due to their inability to complete the task and/or technical problems; data from eight participants were excluded due to excessive head motion (a root mean square difference between consecutive volumes of >3 mm in >5% of the volumes of a run). For some participants, head movement or technical problems led to the exclusion of one run (n = 6; two adolescents, four children) or two runs (n = 1; one child) out of the total four runs, leaving, however, sufficient trials to estimate effects (e.g., >100 decision trials). For occasionally occurring head motions (≤5% of the volumes of a run), volumes with motion—and an additional +1/−1 volumes to account for spin-history effects—were not included in regressors of interest and were modeled by nuisance regressors (i.e., censored). All participants provided written informed consent for the study (parental consent and participant assent for children and adolescents). All procedures were approved by local institutional review boards.
Our final sample consisted of 23 children (8–11 years, mean age = 10, SD = 1.25, 14 females), 25 adolescents (16–19 years, mean age = 17.9, SD = 1.51, 14 females), and 24 adults (25–34 years, mean age = 28.3, SD = 2.5, 12 females). Participants were recruited through local advertisements and received a reimbursement of $30 for the first (behavioral) session and $50 for the second (fMRI) session (see below, Procedure). Additionally, a $10 endowment was given in each session: participants were explicitly instructed that three game rounds of the CCT would be randomly drawn from the set of played game rounds and the outcomes of these game rounds would be totaled and added to (in case of a positive total) or subtracted from (in case of a negative total) the $10 endowment (with 1 point worth 1 cent). Participants could not lose more than the $10 endowment.
All participants were right-handed, reported normal or corrected-to-normal vision, and had an absence of neurological or psychiatric impairments. Estimated intelligence scores were obtained using the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999). Estimated mean IQs were 112.8 for children [one child (male) did not provide WASI scores], 115.2 for adolescents, and 118.0 for adults; IQ did not differ between age groups (p = 0.43).
Materials
Task.
In this study, we developed and administered an fMRI-adjusted version of the hot CCT (referred to as the fMRI-CCT; Fig. 1). The original behavioral version of this task has been used frequently to assess risk taking in an affective-motivational context (Figner et al., 2009; Figner and Weber, 2011; Baumann and DeSteno, 2012; Penolazzi et al., 2012; Panno et al., 2013).
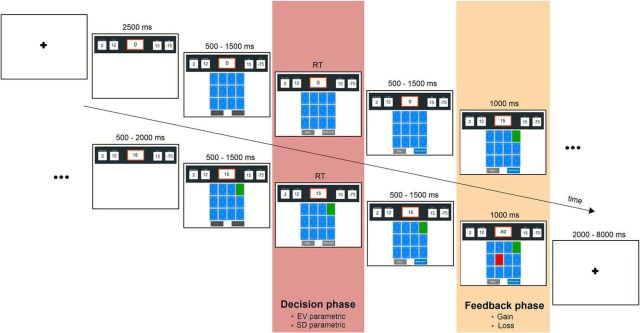
Example of a game round in the fMRI-CCT (with two turned cards) ending because a loss card is drawn. Within each game round, we modeled the decision and the feedback phase.
The fMRI-CCT consists of several game rounds, each of which starts with a specified number of cards shown face down (ranging from 6 to 16). Explicit information is given about (1) the total number of cards, (2) the number of loss cards (ranging from 1 to 8) hidden among them, (3) the gain amount for each turned over gain card (ranging from 1 to 30), and (4) the loss amount if a loss card is turned over (ranging from −5 to −100). In addition, a running total of the points accumulated in the current game round is shown and updated with each card turned over. Each new game round starts with a score of 0. Within each game round, participants make a series of binary decisions whether to turn over a(nother) card or to stop turning over cards. A game round continues, with points accumulating, until the participant decides to stop turning over cards or until he or she turns over a loss card, which leads to the subtraction of the stated loss amount from the running score and ends the current game round. In different game rounds, the decision process is always the same, but the probability and amounts of gain and loss vary.
For fMRI purposes, the CCT was adapted as follows (see Fig. 1). First, the start of a new game round was indicated by a fixation cross displayed on the screen for 2–8 s (jittered in steps of 2 s). Then, the game round information (total number of cards, number of loss cards, gain amount, and loss amount) was presented for 2.5 s. This information, along with the running score, continued to be displayed at the top of the screen throughout the game round. After 2.5 s, the cards (face down) and the two response buttons (take card/stop taking cards) were presented. After 0.5–1.5 s (jittered) the buttons were “activated” (a change in color from pale to bright gray) indicating to the participants that they now could choose whether to take a card or stop taking cards (i.e., end the current game round). Placement of the “take card” button and the “stop” button (and respective finger responses of index vs middle finger) was counterbalanced across participants. Participants were allowed a maximum of 10 s to respond; if they did not respond within this time window, a screen was presented indicating a missed response (Too Late!) after which the current game round ended and a new game round started. In case of a missed response, no points were won or lost in this game round. After the participant made a decision (take card/stop), the pressed button changed color to blue for 0.5–1.5 s (jittered), then one card (randomly chosen by the computer among the remaining face-down cards) was turned over and the running score was updated. This outcome display stayed on the screen for 1 s. If the turned card was a gain card, the game round continued after a 0.5–2 s blank screen (jittered). The game round ended if the participant turned over a loss card or if the participant decided to stop taking cards. In both cases, the feedback (loss card) or choice (highlighted stop taking cards button) stayed on screen for 1 s before a new game round started. Game rounds with missed responses were not repeated and were not included in the pool of game rounds relevant for the final outcome. Missed responses were rare, in 1.42, 0.84, and 0.71% of game rounds in children, adolescents, and adults, respectively. The average amount of points earned across game rounds (i.e., final score per game round divided by the number of game rounds) did show a significant positive correlation with age (r = 0.27, p = 0.02), indicating that older participants had a higher average score in the task; this is consistent with the results of the risk–return analysis reported below (see Results).
To be able to estimate the effects of the predictors of main interest (i.e., risk, return, gain), we aimed to choose the task characteristics (total number of cards, number of loss cards, gain amount, and loss amount) in a way that minimized potential collinearity between, and maximized variances within, these predictors. To achieve this goal, we used a formal design optimization approach to determine the required characteristics of game rounds. In brief, a space of possible game rounds was specified (6–16 cards, 1–8 loss cards, gain amount 1–30, and loss amount −5 to −100), from which we eliminated impossible combinations and further eliminated combinations that we expected to lead to uniform behavior across participants (e.g., if the gain amount was larger than the loss amount). We optimized D-optimality by the Fedorov exchange algorithm (Atkinson and Donev, 1992) to generate a set of game rounds. Note that risk and return vary not only between, but also within game rounds across binary take card/stop decisions. Accordingly, a participant who turned over more cards might not have encountered exactly the same values of risk and return as a participant who turned over fewer cards. However, our task design ensured that all participants encountered a wide range or risk and return values.
Procedure
Data were collected at the Sackler Institute of the Weill Cornell Medical College. Participants came in for two separate sessions. On the first visit, they were familiarized with the scanning environment using a mock scanner and played a behavioral version of the fMRI-CCT with a set of 51 game rounds divided over three runs. Half were unique game rounds, and half were also included in the imaging session. Task parameters and payment were identical to the imaging version of the task except that the interval between game rounds was constant (1 s) instead of jittered. Before the task started, all participants received explicit instructions on the information presented in the task and played five practice game rounds in which the experimenter verbally explained the ongoing changes in the screen. Also, the WASI was administered in the first session (before the fMRI-CCT), as were other assessments, not specific to the current experiment.
On their second visit, participants performed the fMRI-CCT inside the MRI scanner. Before the start of the experiment, participants were shown a screenshot of the fMRI-CCT and asked to explain to the experimenter the numerically displayed information on the screen (total number of cards and number of loss cards (i.e., probability), gain amount, loss amount, and running score). If a participant did not remember, the explanation of all information was repeated until she or he correctly explained all information to the experimenter to achieve full understanding in all participants.
Game rounds were divided into four fMRI runs, each lasting 7.5 min. Depending on the average number of cards turned over, participants differed in the number of game rounds completed, with a minimum of 11 and a maximum of 22 game rounds per run. Participants completed on average 75.5 game rounds in total, which did not differ significantly between age groups (p = 0.9). Participants' mean response times were not related to the number of rounds participants played (r = −0.13, p = 0.27), suggesting that there were no speed-accuracy tradeoffs present.
A high-resolution T1 scan was collected for registration purposes. After scanning, participants were given a short questionnaire asking about their decision strategies and understanding of the game.
Behavioral risk–return decomposition.
The risk–return decomposition of the CCT estimated the effect of return (operationalized as the expected value, EV) and the effect of risk (operationalized as the SD) on the likelihood to take a card versus to stop taking cards. Return (EV) was defined as follows:

Risk (SD) was defined as follows:
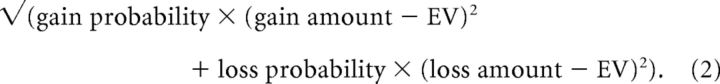
As the SD for stopping is zero, taking a card always entails a greater (nonzero) risk, compared with not taking a card. Similarly, as the EV of stopping is zero, a positive return value indicates greater return for taking compared with not taking a card, while a negative return value indicates the opposite. These two variables, risk and return, served as the key independent variables in our behavioral analysis, with the binary choices to take a card/stop taking cards as the dependent variable.
To assess the effects of risk and return on choice, and to assess whether these effects differed between age groups, the behavioral data from the fMRI session and the behavioral session were analyzed with a generalized linear mixed-effects model approach using the lme4 package in R (Bates et al., 2013). Risk and return variables were grand mean centered. P values were determined using Likelihood Ratio Tests as implemented in the mixed function in the afex package (Singmann, 2013). The unit of analysis was the binary decision level (take card/stop taking cards). The fitted mixed-effect model reads in formal notation:
First level:
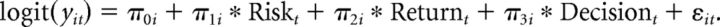
Second level:
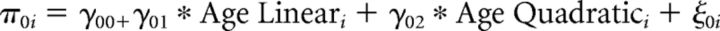

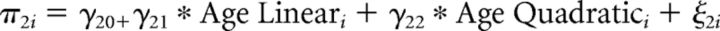
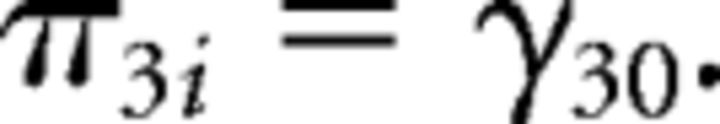
In which yit indicates the response of the ith individual at the tth trial, with yit = 0 denoting stopping and yit = 1 denoting taking a card. Substitution of the second level model into the first level model gives the integrated model that was fitted to the data. Parameters in this model are the fixed effects (γs) and the random effects (variance of ε term and ξ terms), the latter terms model between-participant variance, required to account for the repeated-measures nature of the data and to avoid inflated type 1 errors (Baayen et al., 2008; Barr et al., 2013). Covariances between random effects were explicitly estimated.
As risk and return were centered, the fixed intercept, γ00, denotes the tendency to take a card for average risk and return. The model includes in addition polynomial linear and quadratic main effects of age group (γ01 and γ02), main effects of risk and return (γ10 and γ20), as well as interactions of age group (linear and quadratic) with risk and return (γ11, γ12, γ21, and γ22). Similar to the fMRI analysis, we included as predictor of no interest a variable (effect denoted by γ30) that indicates which decision within a game round it was (first, second, etc.), to account for changes in the likelihood to take a card within a game round independent of risk and return. Participant-specific random slopes for risk and for return captured individual differences in sensitivity to risks and returns. That is, the variance of ξ0i denotes between-participant variance in the tendency to take a card for average risk and return, and the variance of ξ1i and ξ2i denote between-participant variance in the effect of risk and return, respectively. Finally, the variance of εit denotes within-participant variance.
This model allows us to decompose overt choices into three components: (1) risk taking (i.e., defined by the intercept); (2) risk sensitivity, this coefficient could either be approach related (i.e., a positive coefficient indicates an increased likelihood to take a card with increasing risk) or avoidance related (i.e., a negative coefficient indicates a decreased likelihood to take a card with increasing risk; note that greater risk sensitivity can refer to both directions, approach or avoidance); and (3) return sensitivity. Note that return sensitivity could also refer to both approach- and avoidance-related behaviors. Although the decisions in the fMRI session were of main interest, we analyzed the behavioral session as well with the same model to (1) check for consistency in risk taking and risk sensitivity and return sensitivity and (2) to relate neural activation to behaviorally estimated risk sensitivity and return sensitivity in both the behavioral and fMRI sessions.
Imaging acquisition.
fMRI data were acquired with a standard whole-head coil using a 3 tesla Siemens Magnetom scanner. T2*-weighted EPIs were acquired during four functional runs. The first four volumes were discarded to allow for equilibration of T1 saturation effects. Volumes covered the whole brain (33 slices; voxel size 3.4 × 3.4 × 4 mm, 4 mm slice thickness; 220 × 220 mm FOV; interleaved acquisition) and were acquired every 2000 ms (TE = 30 ms). A high-resolution T1-weighted anatomical scan (160 slices; voxel size 1 × 1 × 1.2 mm, 1.20 mm slice thickness; 256 × 256 mm FOV; TR = 2170 ms, TE = 4.33 ms) was obtained from each participant before the functional runs.
Imaging analysis was performed using the FMRI Expert Analysis Tool (FEAT. v5.98) part of FSL v4.1 (FMRIB's Software Library; www.fmrib.ox.ac.uk/fsl). The data were high-pass filtered with a cutoff frequency of 100 s to remove baseline drift in the signal. Preprocessing of functional volumes included spatial smoothing with a 6 mm FWHM isotropic Gaussian kernel, motion-corrected (MCFLIRT; Jenkinson et al., 2002), removal of nonbrain tissue (Smith, 2002), and grand mean intensity normalization of the entire 4D dataset by a single multiplicative factor. All functional datasets were registered into 3D space using the participant's individual high-resolution anatomical images. The individual 3D image was then used to normalize the functional data into MNI standard space. Registration to high-resolution structural and standard space images was performed using FLIRT (Jenkinson and Smith, 2001; Jenkinson et al., 2002). Registration from high-resolution structural to standard space was further refined using FNIRT nonlinear registration (Andersson et al., 2007a, b).
fMRI analyses.
Statistical analyses were performed using the GLM. The design matrix of the GLM was convolved with a double-gamma hemodynamic response function and its first derivative. In the GLM, we included an intercept, parametric regressors of return and risk, and discrete regressors for gain and loss outcomes (Figure 1). The intercept regressor was orthogonalized with respect to the parametric return and risk regressors. The onset of the intercept, return, and risk regressor was modeled at the moment participants could make a decision (activation of choice buttons); their duration was modeled by the respective response time of that choice. Note that response times (RT) did not show differences between children, adolescents, and adults (mean RT = 1.33 s, mean RT = 1.29 s, mean RT = 1.40 s, respectively; p = 0.68). The onset of the gain and loss regressors was modeled with zero-duration regressors at the start of the feedback presentation screen. Additionally, we included a parametric regressor of no interest coding the decision within a game round (first, second, etc.) to account for changes in the likelihood to take a card within a game round independent of return and risk. Finally, motion regressors for occasional volumes with high motion and too slow responses were included as regressors of no interest.
An additional lower level model was fitted to test for age-related changes in neural activation related to parametric gains. This additional model focusing on gains was tested because (1) adolescence often has been associated with increased gain sensitivity compared with childhood and adulthood (Galvan et al., 2006; Van Leijenhorst et al., 2010; Padmanabhan et al., 2011; Smith et al., 2011) and (2) gains, in contrast to losses, could be analyzed parametrically since they were encountered frequently in varying sizes. That is, gains were present at each choice turning a gain card and gain amounts (2–20) varied substantially between game rounds. In contrast, losses were encountered only when a game round ended because of a loss card. This GLM was identical as the model outlined before, with an additional parametric regressor coding the gain amount of each choice outcome, modeled at the start of the feedback screen. Note that one adolescent (female) was not included in this parametric gain model, due to a low number of gains across trials (<10 in total).
Higher level analyses were performed using FMRIB's Local Analysis of Mixed Effects (FLAME) stage 1 with automatic outlier detection and included linear and quadratic effects of age group. Linear age effects were modeled as follows: children, adolescents, adults [−1 0 1] for age-increasing effects and [1 0 −1] for age-decreasing effects. Quadratic age effects were modeled as follows: children, adolescents, adults [−1 2 −1] for an adolescent-specific increase of activation and [1 −2 1] for an adolescent-specific decrease of activation.
For whole-brain analyses, Z statistic images were thresholded with Gaussian Random Field Theory cluster-wise correction, Z > 2.3 and FWE corrected with p < 0.05. Note that this default Z-threshold of 2.3 is more sensitive to larger clusters compared with a higher Z-threshold (Smith and Nichols, 2009). Recent developmental neuroimaging studies used the same threshold, improving comparability across studies in this field (Paulsen et al., 2011; Galván and McGlennen, 2013; Telzer et al., 2013). However, to additionally inspect more peaked cluster activation, we reran our whole-brain analyses with a cluster-thresholding criterion of Z > 2.6, p < 0.05, and report the respective results in addition to the results from our standard thresholding criterion.
To visualize whole-brain effects, we extracted the mean percentage of signal change from clusters of activation. If a whole-brain cluster spanned several anatomical regions we extracted the overlap of the functional activation with an anatomical image from the Harvard-Oxford atlas implemented in FSL.
Results
Choice fMRI session
Our analysis showed significant main effects of both risk and return. A higher risk led to a decreased likelihood to take a card (i.e., participants on average avoided risks; B = −0.021, p = 0.014), while a higher return led to an increased likelihood to take a card (i.e., participants on average approached returns; B = 0.184, p < 0.001). Results did not show a main linear or quadratic effect of Age Group, indicating that all age groups had a similar risk-taking tendency (Figure 2A). Risk showed a significant interaction with Age Group (linear; B = −0.0192, p = 0.048), indicating that risk aversion increased with age (Figure 2B). There was a significant Age Group (linear) × Return interaction (B = 0.063, p < 0.001), indicating that return sensitivity (i.e., approaching returns) increased with age (Figure 2C). Interactions with quadratic age terms were not significant (all ps > 0.2).
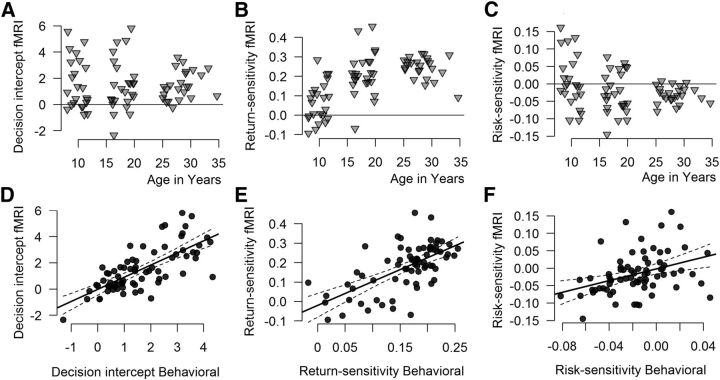
Top, Participant-specific random effects (fixed effect plus participant-specific random adjustment). Each dot represents one participant, x-axis shows age in years. A, Risk taking (intercept). B, Return sensitivity (random EV slope). C, Risk sensitivity (random SD slope). Bottom, Correlations (including 95% confidence intervals) between the participant-specific random effects estimated in the behavioral and the fMRI sessions. D, Risk taking (intercept). E, Return sensitivity (random EV slope). F, Risk sensitivity (random SD slope).
Follow-up tests per Age Group, using the same mixed-effects model approach, showed that risk did not significantly influence the tendency to take a card in children (p = 0.68). In contrast, increasing risk showed a marginally significant trend toward a decreased tendency to take a card in adolescents (B = −0.027, p = 0.095). Adults showed a negative effect of risk on choice (B = −0.031, p = 0.004), indicating risk aversion. In contrast, increasing return significantly increased the tendency to take a card in children (B = 0.068, p = 0.014), in adolescents (B = 0.218, p < 0.001), and in adults, (B = 0.248, p < 0.001).
There were substantial individual differences in participants' tendencies to take a card, their sensitivity to risk, and their sensitivity to return (see Fig. 2). Note that increasing returns generally increased risk taking across participants in all age groups (although to different extents), whereas increasing risks decrease risk taking uniformly only in adults. In the adolescent age group, individuals differed substantially, some “approaching” risk (increased tendency to take a card with increasing risk, i.e., risk seeking), and some most strongly “avoiding” risk (decreased tendency to take a card with increasing risk, i.e., risk aversion). In children, large individual variability was also observed, with, however, the main effect straddling zero. This may indicate that children show individual choice strategies that are consistent with a wide range of possible risk sensitivities, but that their choice behavior is not strongly and consistently influenced by changes in risk (i.e., children appear to be risk insensitive).
To further investigate age effects, we correlated participants' risk-sensitivity estimates with age (in years) for children, adolescents, and adults separately. In adults and adolescents, no significant correlations were observed (ps > 0.8). However, in children, age correlated negatively with risk-sensitivity (r = −0.43, p = 0.043), indicating that older children exhibited increased risk aversion. No significant correlations were observed for return sensitivity in children (p = 0.12) or in the other age groups (ps > 0.07). These within-age group results are consistent with our between-age group results of an age-related increase in risk sensitivity (in particular, risk aversion), though at a more fine-grained age level during childhood. We additionally investigated the relation between IQ and estimated risk (and return) sensitivity: IQ did not correlate significantly with either risk sensitivity or return sensitivity or across age groups or within any of the age groups (ps > 0.1).
We ran a set of supplemental behavioral analyses, to investigate potential effects of gender, time, and choice strategy across age groups. First, given reported gender differences in risky choice behavior (Byrnes et al., 1999; Figner and Weber, 2011; Jansen et al., 2014), we ran a similar mixed model, but with Gender as an additional fixed effect, as well as an interaction between Gender and Age Group (linear) and Gender and Age Group (quadratic). This model showed no effect of Gender on choice (p = 0.88) or any interactions between Gender and Age Group (all ps > 0.1).
Second, we tested possible effects of time on risky choice, as age groups might differ in, for example, whether they grow tired during the task, or take longer (i.e., more game rounds) to optimize their decision strategies. Accordingly, we ran a similar mixed model, with a fixed effect of time added (i.e., run: ranging from 1 to 4, according to the four fMRI runs of our design), as well as the interaction between Time × Age Group (linear) and Time × Age Group (quadratic). In addition to a participant-specific random intercept, and participant-specific random slopes for risk and return, a participant-specific random slope for Time was added to the model. The results show no effect of Time on choice (p = 0.32) or any interactions between Time and Age Group (linear: p = 0.38; quadratic: p = 0.84). These results suggest (1) that overall there was little change in decisions over time and (2) that there were no age differences in any potential time-dependent effects.
Third, we assessed participants' understanding of the task by running a mixed model on choice behavior that included all the information presented on the screen (number of cards/amount of loss cards, i.e., loss probability, loss amount, and gain amount). We observed in all age groups significant effects of loss probability, loss amount, and gain amount (all ps < 0.001), all in the expected directions. That is, lower loss probability, lower loss amount, and higher gain amount increased the tendency to take another card in all age groups. These results suggest that all age groups understood the task information and were able to use it appropriately.
Fourth, participants' decision strategies and goals when performing the fMRI-CCT were assessed with self-report items administered after the fMRI-CCT was completed: The first set of questions focused on participants' use of the information presented in the CCT. Questions included: “I mainly focused on the number of loss cards,” “I mainly focused on the amount of loss,” and “I mainly focused on the amount of gain,” answered on seven-point Likert scales ranging from “doesn't apply at all” (1) to “strongly applies” (7). We observed no significant differences between the three age groups on (1) focus on number of loss cards (Children: M = 4.5, SD = 1.5; Adolescents: M = 4.6, SD = 1.3; Adults M = 4.4, SD = 1.2; p = 0.85) and (2) focus on loss amount (Children: M = 4.3, SD = 1.9; Adolescents M = 4.3, SD = 1.3; Adults M = 4.3, SD = 1.5; p = 0.99). These results suggest that participants in all three age groups were equally aware that they used that information in making their decisions. However, gain amount ratings showed a significant difference between age groups (F(2,69) = 5.14, p = 0.008), with children reporting a stronger focus on gains than adolescents (Children: M = 4.9; SD = 1.5; Adolescents: M = 3.6; SD = 1.4; Adults: M = 4.3; SD = 1.3; Bonferroni-corrected pairwise comparison, p = 0.007; all other pairwise comparisons were not significant, ps > 0.1).
The second set of questions concerned participants' strategies, formulated as the goals they may have had: “My goal was to test my luck and see how many cards I could turn over before I get busted,” “My goal was to make as much money as possible,” “My goal was to avoid turning over a loss card,” and “My goal was to have fun playing the game.” (For one adolescent and six adults, these data are missing.) None of these questions showed a significant difference between age groups, again suggesting no differences in goals/strategies across age groups (all ps > 0.3).
Choice behavioral session
To investigate the consistency of individuals' risk taking, risk sensitivity, and return sensitivity, we estimated participant-specific effects in choice behavior in the behavioral session. These data from the behavioral session were analyzed with a similar risk–return mixed-effects model as stated in the Materials and Methods section, to extract individual estimates, i.e., participant-specific tendencies to take a card (intercepts) and participant-specific sensitivities to risk and return (slopes). To investigate consistency across sessions, we correlated the estimates from the behavioral and the estimates from the fMRI session. High correlations across sessions were observed particularly for participants' risk-taking tendency (r = 0.721, p < 0.001; Fig. 2D) and for their return sensitivity (r = 0.635, p < 0.001; Fig. 2E). Participants' risk sensitivity (r = 0.382, p = 0.001; Fig. 2F) showed a lower, but still considerable consistency between sessions.
To investigate whether age groups differed in the stability of the estimated risk and return sensitivity parameters across sessions, we regressed the estimated risk (and return) sensitivity from the behavioral session, age, and the interaction of these terms, on the estimated risk (and return) sensitivity in the fMRI session. The results showed no significant interaction effect between age and risk sensitivity (p = 0.27), or between age and return sensitivity (p = 0.1). These results indicate a relative stability across sessions in individual differences in risk taking, risk sensitivity, and return sensitivity, and this stability in return sensitivity and risk sensitivity did not differ significantly between age groups.
Whole-brain results
Risk
First, we tested age-related changes in neural activation associated with risk. A whole-brain analysis showed that the quadratic age contrast—testing for an adolescent peak in neural activation—showed a cluster of heightened adolescent activation encompassing the right anterior insula extending into inferior frontal gyrus and the dmPFC; a second cluster showed heightened adolescent activation in the bilateral caudate (see Figure 3A, Table 1 for a complete list). No significant results were found for the reversed quadratic or the linear age contrasts. Thus, neural activation associated with risk peaked in adolescents in regions that have been previously implicated in risk processing (Preuschoff et al., 2008; Mohr et al., 2010a, b).
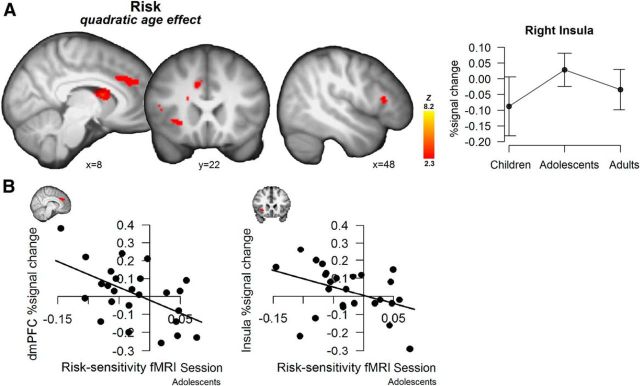
A, Whole-brain maps for the risk regressor, showing regions with peak activation in adolescents ∩. Displays thresholded at Z > 2.3, p < 0.05 (FWE cluster-corrected). The line graph is only for visualization purposes and displays extracted percentage signal change per age group for the risk-related activation in the anterior insula (functional activation is anatomically masked), including 95% confidence intervals. B, Scatterplots showing the correlation between adolescents' behaviorally estimated risk sensitivity in the fMRI session and neural activation in response to risk in anterior insula and dmPFC.
Table 1.
Clusters showing age-related differences in risk coding
| Region | MNI coordinates (mm) | ||||
|---|---|---|---|---|---|
| x | y | z | Vox | Max Z | |
| Quadratic risk ∩ | |||||
    R insula/R inferior frontal gyrus R insula/R inferior frontal gyrus | 32 | 32 | 10 | 1602 | 3.74 |
    R insula/R inferior frontal gyrus R insula/R inferior frontal gyrus | 38 | 32 | 6 | 3.71 | |
    R medial frontal gyrus R medial frontal gyrus | 18 | 40 | 24 | 3.42 | |
    R paracingulate R paracingulate | 10 | 38 | 28 | 3.28 | |
    L caudate L caudate | −6 | 8 | 14 | 3.72 | |
    R caudate R caudate | 8 | 6 | 12 | 3.68 | |
| Positive main effect risk | |||||
    Thalamus Thalamus | 0 | −24 | 10 | 6555a | 4.77 |
    R superior frontal gyrus R superior frontal gyrus | 26 | −4 | 70 | 4.03 | |
    R superior frontal gyrus R superior frontal gyrus | 22 | −2 | 68 | 4.01 | |
| Negative main effect risk | |||||
    L frontal pole/inferior frontal gyrus L frontal pole/inferior frontal gyrus | −46 | 42 | 2 | 2670a | 5.33 |
    L inferior frontal gyrus L inferior frontal gyrus | −42 | 8 | 22 | 4.35 | |
    L middle frontal gyrus L middle frontal gyrus | −44 | 26 | 28 | 3.72 | |
    L precentral gyrus L precentral gyrus | −42 | 0 | 28 | 3.43 | |
    L superior parietal cortex L superior parietal cortex | −36 | −70 | 50 | 1930a | 3.75 |
In the case of large clusters, local peaks in encompassing regions are reported.
aIndicates clusters also observed at the more peaked cluster-thresholding criterion Z > 2.6, p < 0.05; FWE cluster-corrected. R, right; L, left.
Additionally, we performed a whole-brain analysis to investigate whether some brain regions uniformly track risk over all age groups. This analysis yielded risk-related activation in thalamus and superior frontal gyrus. Similarly, we tested which regions uniformly decreased activation with increasing risk. This analysis revealed relatively large left prefrontal and bilateral parietal clusters of activation (Table 1).
To investigate the correspondence between behavioral and neural risk sensitivity, we correlated individuals' estimated risk sensitivity from the behavioral analysis with individuals' neural activation in the dmPFC and the right anterior insula, two regions that were identified in our age-differences analysis and that have been previously implicated as central in risk processing. Both functional regions of interest were masked with a corresponding anatomical mask to extract percentage signal change to parametric changes in risk.
No significant correlations were observed between neural activation and behavior from the fMRI session when pooling participants across all age groups. Follow-up tests per age group, however, showed that adolescents' behaviorally estimated risk sensitivity was significantly related to neural risk activation in both regions: smaller values of the random slope for risk correlated with greater dmPFC activation (r = −0.536, p = 0.006; i.e., individuals that more strongly avoided risks, showed greater neural activation in response to risk; Fig. 3B). A similar correlation, also in adolescents, was observed for the right anterior insula (r = −0.399, p = 0.048; Fig. 3B). The same analyses for children and adults did not reveal any significant correlations (ps > 0.2). Finally, we also tested for associations between behaviorally estimated risk sensitivity and activation in the caudate, which revealed no significant correlations across or within age groups (ps > 0.2).
Additionally, we correlated these neural activations with behaviorally estimated risk sensitivity from the behavioral session. Similar correlations between adolescents' neural activation and risk sensitivity estimated from the behavioral session were, however, not significant (all ps > 0.9).
Return
Next, we tested age-related changes in neural activation associated with return (see Figure 4A, Table 2 for a complete list. A whole-brain analysis showed that return-related activation increased linearly with age in the vmPFC, including a cluster in the medial orbital frontal cortex and subcallosal ACC, and in a cluster encompassing the posterior cingulate cortex (PCC). The contrast testing for an adolescent peak in return-related neural activation resulted in a cluster in the visual cortex extending into right superior parietal cortex. No significant results were found for the reversed linear and quadratic contrast.
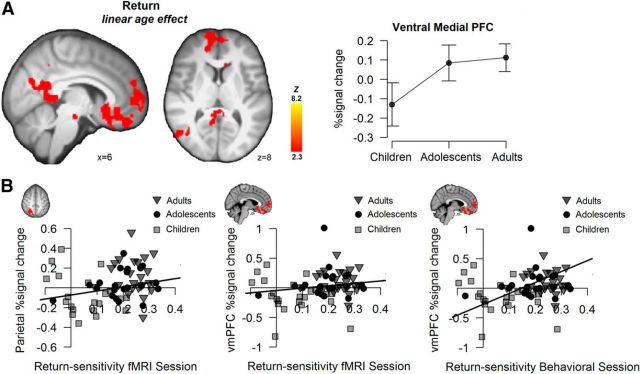
A, Whole-brain maps for the return regressor, showing regions with significant activation for a linear age contrast. Displays thresholded at Z > 2.3, p < 0.05 (FWE cluster-corrected). The line graph is only for visualization purposes and displays extracted percentage signal change per age group for the return-related activation in vmPFC, including 95% confidence intervals. B, Scatterplots showing the correlation between individuals' behaviorally estimated return sensitivity and neural activation in response to return in the superior parietal cortex (fMRI session) and vmPFC (fMRI session and behavioral session).
Table 2.
Clusters showing age-related differences in return coding
| Region | MNI coordinates (mm) | ||||
|---|---|---|---|---|---|
| x | y | Z | Vox | Max Z | |
| Positive linear return | |||||
    L vmPFC L vmPFC | −10 | 26 | −12 | 2414 | 3.52 |
    R vmPFC R vmPFC | 14 | 38 | −16 | 3.43 | |
    L inferior temporal gyrus L inferior temporal gyrus | −48 | −48 | −14 | 1725a | 4.08 |
    R middle temporal gyrus R middle temporal gyrus | 52 | −6 | −20 | 1305a | 3.59 |
    R midbrain R midbrain | −10 | −24 | −20 | 1237 | 3.85 |
    L midbrain L midbrain | 12 | −28 | −10 | 3.39 | |
    L parahippocampal gyrus L parahippocampal gyrus | −12 | 40 | −2 | 3.06 | |
    R posterior cingulate R posterior cingulate | 8 | −42 | 6 | 3.19 | |
    R posterior cingulate R posterior cingulate | 4 | −50 | 20 | 3.03 | |
    Lateral occipital cortex Lateral occipital cortex | 52 | −64 | 18 | 871 | 3.75 |
| Quadratic return ∩ | |||||
    L occipital cortex/R superior parietal lobe L occipital cortex/R superior parietal lobe | −46 | −66 | −8 | 8246a | 4.03 |
In the case of large clusters, local peaks in encompassing regions are reported.
aIndicates clusters also observed at the more peaked cluster-thresholding criterion Z > 2.6, p < 0.05; FWE cluster-corrected. R, right; L, left.
As for risk, we also tested which regions increased activation with increasing return uniformly across age groups. This analysis showed no additional neural activation compared with the neural regions sensitive to age-related changes. Finally, no regions showed decreased activation with increasing return. Thus, consistent with the behavioral effects, neural activation to return increased linearly across age groups. This age-related linear increase was predominantly observed in the vmPFC and PCC, key regions implicated in the processing of (expected and subjective) value (Sescousse et al., 2013).
Pooled across age groups, vmPFC and PCC activation to parametric returns correlated with behaviorally estimated return sensitivity in the fMRI session in the expected direction, but not significantly so (vmPFC: r = 0.189, p = 0.113; PCC: r = 0.197; p = 0.097; Fig. 4B). The return-sensitivity estimates from the behavioral session showed the same positive correlations, and were significant: across age groups, higher return sensitivity correlated with greater vmPFC (r = 0.449, p < 0.001, and PCC activation, r = 0.462, p < 0.001; Figure 4B; i.e., individuals that more strongly approached return showed greater neural activation in response to return).
A similar association as in vmPFC and PCC was observed in the superior parietal cortex. That is, individually extracted percentage signal change in response to returns in the superior parietal cortex (anatomically masked functional activation) correlated positively with individuals' estimated behavioral return sensitivity in both the fMRI session (r = 0.282, p = 0.016) and the behavioral session (r = 0.367, p = 0.002; Figure 4B).
Gains and losses
Third, we tested age-related changes in neural activation related to gain and loss outcomes. Figure 5 displays activation maps per age group for the gain > baseline (i.e., fixation) and the loss > baseline contrasts. As shown, neural activation in all three age groups widely overlaps and includes cortical (frontoparietal and insula) and subcortical (thalamus, striatal, and brainstem) regions.
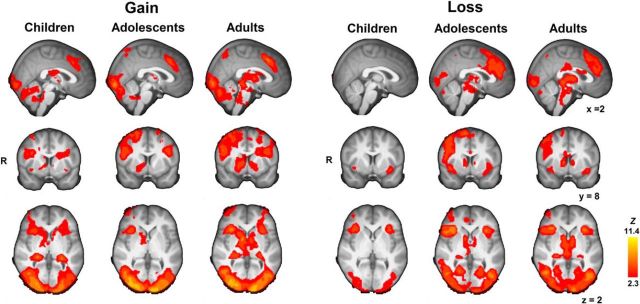
Whole-brain maps display per age group Gain > Baseline and Loss> Baseline contrasts, thresholded at Z > 2.3, p < 0.05 (FWE cluster-corrected). Note that whole-brain maps are highly similar at the more peaked thresholding criterion of Z > 2.6, p < 0.05; FWE cluster-corrected.
The [gain > baseline] and [loss > baseline] contrasts were subjected to similar analyses to test for age-related changes, masked for regions that were more active for gain > baseline or for regions that were more active for loss > baseline effects, respectively. Gain-related activation did not show any linear or quadratic age changes, suggesting uniform processing of gains throughout our studied age range. Loss-related activation also showed little significant age changes. Linear developmental increases were observed only within bilateral thalamus and caudate (cluster size = 559 voxels, peak activation xyz = −8, −2, 0), the right precuneus (cluster size = 635 voxels, peak activation xyz = 22, −68, 46), and the visual cortex (cluster size = 1340, peak activation xyz = −12, −96, 4). The reversed linear and quadratic age contrasts showed no significant effects. With the more peaked cluster-threshold criterion (Z > 2.6, p < 0.05) only the visual cortex cluster was identified.
Finally, we tested the parametric effects of gain for age-related differences. Testing for regions that uniformly tracked changes in gains across age groups revealed a large cluster of thalamus and striatal activation (voxel size = 4607, peak activation xyz = 8, 4, −2) that increased activation with increasing gains (Fig. 6). Moreover, a cluster of heightened adolescent activation was observed in right lateral prefrontal cortex (voxel size = 1108, peak activation xyz = 40, 6, 26). No linear increases were observed with age. These results indicate more cortical prefrontal recruitment of adolescents in relation to increasing gains.
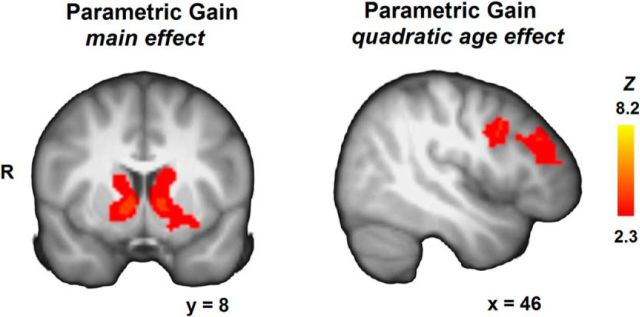
Whole-brain maps for the parametric gain regressors, showing regions with significant activation across age groups (left; also significant at the more peaked thresholding criterion of Z > 2.6, p < 0.05; FWE cluster-corrected), and regions with significant activation for a quadratic age contrast ∩ (right). Displays thresholded at Z > 2.3, p < 0.05 (FWE cluster-corrected).
Discussion
This study focused on age-related changes in behavioral and neural processes related to risk sensitivity and return sensitivity in risky choice. Though evidence has accumulated using simple reward paradigms, the current study takes a computational approach to break down complex, dynamic risky decisions into constituent features to isolate what, in particular, drives unique features of decisions of children and adolescents at the behavioral level, and asks how the developing brain might carry out such unique decision calculations. A risk–return approach has been applied and validated across many behavioral (Weber, 2010) and neuroeconomic studies in adults (Preuschoff et al., 2008; Tobler et al., 2009; Mohr et al., 2010a, b; Rudorf et al., 2012), but is new to developmental neuroimaging studies. By applying this risk–return decomposition we were able to study the development of behavior and underlying brain processes in a dynamic risky choice task, and additionally differentiate decision processes (risk and return processing) from outcome processes (gain and loss processing). Using behavioral and parametric fMRI analyses, we focused on examining monotonic developmental differences (linear effects) and adolescent-specific developmental differences (quadratic effects).
Risk
Risk (i.e., outcome variability) has been linked to neural activation in the thalamus, anterior insula, the dmPFC, and the lateral PFC (Preuschoff et al., 2008; Tobler et al., 2009; Mohr et al., 2010a, b). The current study identified these regions as responsive to changes in risk as well and—more importantly in the context of the current paper—observed that adolescents showed heightened activation in insula and dmPFC compared with children and adults in response to increasing risk. Further, adolescents' individual activations in these regions were significantly correlated with their behaviorally determined individual risk-sensitivity estimates.
Previous studies have linked the insula and dmPFC to an emotional and a cognitive component of risk, respectively (Mohr et al., 2010a). In this view, insula-related processes would reflect the negative emotional evaluation associated with greater uncertainty about the outcome one would obtain, whereas the dmPFC would reflect a more cognitive-computational process of risk. Following these lines of reasoning, our results suggest that adolescents may have a heightened emotional response to risks relative to children and adults and—at the same time (and perhaps therefore)—may engage more cognitive-regulatory processes in response to risk.
Following Holper et al. (2014) the interpretation of the role of the insula in risk activation might be related to at least four different mechanisms: in addition to affect, risk activation could indicate subjective valuations of risk, perceptions of risk, or objective risk processing. Our study was not designed to decide between these different roles, but given that insula activation tracked increasing risks and greater activation was related to greater risk aversion (at least in adolescents), our results may be consistent with an (aversive) valuation of risk or increased perception of risk in adolescence (Rudorf et al., 2012). Subjective risk (and return) ratings in future studies may help to disentangle these accounts.
Lateral PFC (as part of a large cluster also encompassing parts of the frontal pole and inferior frontal gyrus) and parietal cortex decreased with increasing risk uniformly across age groups. In adults, specifically the lateral PFC has been implicated in self-control processes in risky and intertemporal choice (Knoch et al., 2006; Figner et al., 2010) and in integrating choice information to arrive at a decision (Mohr et al., 2010a). In the current study risk and return varied relatively independently. Thus, given the same return levels, decisions with higher, compared with lower, risk were for most participants less attractive. Accordingly, one could speculate that there was reduced need for self-control in such high-risk situations, leading to the observed negative correlation between risk and lateral PFC activation.
Return
There is wide agreement in the literature about a value-coding network that responds positively to increasing returns and includes the vmPFC and the posterior cingulate cortex (Knutson et al., 2005; Tobler et al., 2009; Carter et al., 2010; Levy et al., 2010; Levy and Glimcher, 2012). In our study, return-related activations in these regions increased linearly across age groups and correlated positively with behavioral return sensitivity (from the behavioral session) across age groups. A number of other brain regions have also been related to the coding and calculation of return. A recent study observed specifically heightened reward-related signals in the ventral striatum in adolescents (Cohen et al., 2010), a region related to learning signals (van Duijvenvoorde and Crone, 2013) and basic reward processing. Also regions such as the parietal cortex have been implicated in the coding and calculation of return (i.e., expected value; Kable and Glimcher, 2009; Louie and Glimcher, 2012). Unexpectedly, the current study identified a cluster in the parietal cortex that exhibited an adolescent peak in return-related activation. Exactly how vmPFC, striatum, and the parietal cortex differently contribute to return sensitivity across development remains to be determined.
When studying respondents in different age groups, one possible concern is that the meaning of a given monetary amount might change with age, which in turn might affect behavior. Typically, studies in adults indicate that a larger (subjective) value for money leads to less risk taking (Markowitz, 1952; Prelec and Loewenstein, 1991). Thus, if it would be the case that one of the age groups (e.g., children) would subjectively value money differently, their true risk-taking levels might deviate from that of other age groups. Although we observed developmental differences in behavioral risk sensitivity and return sensitivity, the tendency to take a card (i.e., an index of “risk taking”) did not differ significantly between age groups. Separate studies are necessary to thoroughly study age-related differences in subjective representations (Harbaugh et al., 2002).
The current study contributes to the diverse range of reported age-related changes in risk taking. That is, some laboratory risk tasks find a peak in early or late adolescent risk taking (Figner et al., 2009; Burnett et al., 2010), while others observe decreasing risk-taking levels from childhood to adulthood (Levin and Hart, 2003; Levin et al., 2007; for a meta-analysis, see Defoe et al., 2014). In the current study, the general tendency to take a card was found to differ substantially between individuals, particularly in children and adolescents. We therefore believe that our approach of decomposing overt risk-taking levels into underlying processes and the individual differences therein is informative and promising for future studies (Figner and Weber, 2011).
Gain and loss
The current paradigm allowed us to not only study decision-related processes (risks and returns), but also outcome-related processes such as age-related changes in gain and loss processing. Prior studies have reported mixed findings of developmental differences in response to gains (Richards et al., 2013). Here, we did not observe significant developmental changes in neural processing of gains. Similarly for loss, we observed little, but if anything linear, developmental changes. A loss (or more generally negative feedback) often is a signal that behavior should be adjusted. Consistent with this view, particularly loss processing is typically related to a prefrontal-parietal network involved in the maturing ability to execute control and update behavior in accordance with internal goals (Miller and Cohen, 2001; van Duijvenvoorde et al., 2008; Peters et al., 2014). Speculatively, it may be that the relatively minor developmental changes in outcome processing may be related to the fact that in the current task gains do not indicate a strong learning signal.
Parametric analyses for gain, however, showed neural activation in subcortical structures including the striatum and thalamus that increased with increasing gains. Additionally, adolescents recruited the right lateral PFC more than other age groups in response to increasing gains. Tentatively, these results may indicate a heightened adolescent tendency to execute control in response to increasing gain to guide further choice behavior. These results also suggest that it may not be reward per se, but the differences in reward magnitude to which adolescents might be particularly sensitive, which is an important insight for future studies on adolescent reward sensitivity.
Conclusions
In conclusion, the current study highlights the potential of a model-based approach combined with an algorithmically optimized task design to decompose overt risk-taking levels into the underlying psychological and neural mechanisms related to the processing of risk and return in the risky choices of children, adolescents, and adults. The risk–return framework has the advantage over other, utility-based models such as Prospect Theory (Kahneman and Tversky, 1979) of including an explicit component of risk. Overall, children were insensitive to changing levels of risk, but showed significant sensitivity to changing levels of return. In contrast, both adolescents and adults showed sensitivity to risk and return, on average seeming to avoid increasing risk and to approach increasing return. However, adolescents' individual differences in risk sensitivity were clearly more pronounced than those of adults. Neural responses to risk also showed pronounced adolescent-specific changes (i.e., non-monotonic, quadratic age effects in neural responses). Return sensitivity, on the other hand, showed predominantly monotonic age-related changes in behavior and underlying neural activation. This novel approach provides important targets for future studies into the development of risky decision making.
Notes
Supplemental material for this article is available at www.columbiacardtask.org. The actual parameters per game round in the fMRI-CCT (number of cards, gain amount, loss amount, probability of loss, risk, and return) can be found on this website as an external file. This material has not been peer reviewed.
Footnotes
This work was supported by Grant SNF-PA001-15327 awarded to B.F., Grant NSF-SES-0922743 awarded to E.U.W. and B.F., a VIDI grant awarded to H.M.H., and a Ter Meulen Fonds stipend awarded to A.C.K.v.D. We thank Eveline Crone for helpful discussions.
The authors declare no competing financial interests.
References
- Andersson J, Jenkinson M, Smith S. Non-linear optimization. FMRIB Technical Report TR07JA1. 2007a [Google Scholar]
- Andersson J, Jenkinson M, Smith S. Non-linear registration, aka spatial normalization. FMRIB Technical Report TR07JA2. 2007b [Google Scholar]
- Atkinson AC, Donev AN. Optimum experimental designs. Oxford: Clarendon; 1992. [Google Scholar]
- Baayen R, Davidson D, Bates D. Mixed-effects modeling with crossed random effects for subjects and items. J Mem Lang. 2008;59:390–412. 10.1016/j.jml.2007.12.005. [CrossRef] [Google Scholar]
- Barr DJ, Levy R, Scheepers C, Tily HJ. Random effects structure for confirmatory hypothesis testing: keep it maximal. J Mem Lang. 2013;68:255–278. 10.1016/j.jml.2012.11.001. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Bates D, Maechler M, Bolker B, Walker S. lme4:linear mixed-effects models using Eigen and S4. R package version 1.0–5. 2013. http://CRAN.R-project.org/package=lme4.
- Baumann J, DeSteno D. Context explains divergent effects of anger on risk taking. Emotion. 2012;12:1169–1199. 10.1037/a0029788. [Abstract] [CrossRef] [Google Scholar]
- Bjork JM, Knutson B, Fong GW, Caggiano DM, Bennett SM, Hommer DW. Incentive-elicited brain activation in adolescents: similarities and differences from young adults. J Neurosci. 2004;24:1793–1802. 10.1523/JNEUROSCI.4862-03.2004. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Bjork JM, Smith AR, Chen G, Hommer DW. Adolescents, adults and rewards: comparing motivational neurocircuitry recruitment using fMRI. PLoS One. 2010;5:e11440. 10.1371/journal.pone.0011440. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Burnett S, Bault N, Coricelli G, Blakemore SJ. Adolescents' heightened risk-seeking in a probabilistic gambling task. Cogn Dev. 2010;25:183–196. 10.1016/j.cogdev.2009.11.003. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Byrnes JP, Miller DC, Schafer WD. Gender differences in risk taking: a meta-analysis. Psychol Bull. 1999;125:367–383. 10.1037/0033-2909.125.3.367. [CrossRef] [Google Scholar]
- Carter RM, Meyer JR, Heuttel SA. Functional neuroimaging of intertemporal choice models: a review. J Neurosci, Psychol Econ. 2010;3:27–45. 10.1037/a0018046. [CrossRef] [Google Scholar]
- Casey BJ, Getz S, Galvan A. The adolescent brain. Dev Rev. 2008;28:62–77. 10.1016/j.dr.2007.08.003. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Cohen JR, Asarnow RF, Sabb FW, Bilder RM, Bookheimer SY, Knowlton BJ, Poldrack RA. A unique adolescent response to reward prediction errors. Nat Neurosci. 2010;13:669–671. 10.1038/nn.2558. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Defoe IN, Dubas JS, Figner B, van Aken MA. A meta-analysis on age differences in risky decision making: adolescents versus children and adults. Psychol Bull. 2014 10.1037/a0038088. Advance online publication. [Abstract] [CrossRef] [Google Scholar]
- Figner B, Weber E. Who takes risk when and why? Determinants of risk taking. Curr Dir Psychol Sci. 2011;20:211–216. 10.1177/0963721411415790. [CrossRef] [Google Scholar]
- Figner B, Mackinlay RJ, Wilkening F, Weber EU. Affective and deliberative processes in risky choice: age differences in risk taking in the Columbia Card Task. J Exp Psychol Learn Mem Cogn. 2009;35:709–730. 10.1037/a0014983. [Abstract] [CrossRef] [Google Scholar]
- Figner B, Knoch D, Johnson EJ, Krosch AR, Lisanby SH, Fehr E, Weber EU. Lateral prefrontal cortex and self-control in intertemporal choice. Nat Neurosci. 2010;13:538–539. 10.1038/nn.2516. [Abstract] [CrossRef] [Google Scholar]
- Galvan A. Adolescent development of the reward system. Front Hum Neurosci. 2010;4:6. 10.3389/neuro.09.006.2010. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Galván A, McGlennen KM. Enhanced striatal sensitivity to aversive reinforcement in adolescents versus adults. J Cogn Neurosci. 2013;25:284–296. 10.1162/jocn_a_00326. [Abstract] [CrossRef] [Google Scholar]
- Galvan A, Hare TA, Parra CE, Penn J, Voss H, Glover G, Casey BJ. Earlier development of the accumbens relative to orbitofrontal cortex might underlie risk-taking behavior in adolescents. J Neurosci. 2006;26:6885–6892. 10.1523/JNEUROSCI.1062-06.2006. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Gladwin TE, Figner B, Crone EA, Wiers RW. Addiction, adolescence, and the integration of control and motivation. Dev Cogn Neurosci. 2011;1:364–376. 10.1016/j.dcn.2011.06.008. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Gogtay N, Giedd JN, Lusk L, Hayashi KM, Greenstein D, Vaituzis AC, Nugent TF, 3rd, Herman DH, Clasen LS, Toga AW, Rapoport JL, Thompson PM. Dynamic mapping of human cortical development during childhood through early adulthood. Proc Natl Acad Sci U S A. 2004;101:8174–8179. 10.1073/pnas.0402680101. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Harbaugh W, Krause K, Vesterlund L. Risk attitudes of children and adults: choices over small and large probability gains and losses. Exp Econ. 2002;5:53–84. 10.1023/A:1016316725855. [CrossRef] [Google Scholar]
- Holper L, Wolf M, Tobler PN. Comparison of functional near-infrared spectroscopy and electrodermal activity in assessing objective versus subjective risk during risky financial decisions. Neuroimage. 2014;84:833–842. 10.1016/j.neuroimage.2013.09.047. [Abstract] [CrossRef] [Google Scholar]
- Huttenlocher PR. Morphometric study of human cerebral cortex development. Neuropsychologia. 1990;28:517–527. 10.1016/0028-3932(90)90031-I. [Abstract] [CrossRef] [Google Scholar]
- Huttenlocher PR, Dabholkar AS. Regional differences in synaptogenesis in human cerebral cortex. J Comp Neurol. 1997;387:167–178. 10.1002/(SICI)1096-9861(19971020)387:2<167::AID-CNE1>3.0.CO;2-Z. [Abstract] [CrossRef] [Google Scholar]
- Jansen BR, Van Duijvenvoorde AC, Huizenga HM. Developmental and gender related differences in response switches after nonrepresentative negative feedback. Dev Psychol. 2014;50:237–246. 10.1037/a0032493. [Abstract] [CrossRef] [Google Scholar]
- Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5:143–156. 10.1016/S1361-8415(01)00036-6. [Abstract] [CrossRef] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S. Improved optimisation for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. 10.1006/nimg.2002.1132. [Abstract] [CrossRef] [Google Scholar]
- Kable JW, Glimcher PW. The neurobiology of decision: consensus and controversy. Neuron. 2009;63:733–745. 10.1016/j.neuron.2009.09.003. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk Econometria. 1979;47:263–292. 10.2307/1914185. [CrossRef] [Google Scholar]
- Knoch D, Gianotti LR, Pascual-Leone A, Treyer V, Regard M, Hohmann M, Brugger P. Disruption of right prefrontal cortex by low-frequency repetitive transcranial magnetic stimulation induces risk-taking behavior. J Neurosci. 2006;26:6469–6472. 10.1523/JNEUROSCI.0804-06.2006. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Knutson B, Taylor J, Kaufman M, Peterson R, Glover G. Distributed neural representation of expected value. J Neurosci. 2005;25:4806–4812. 10.1523/JNEUROSCI.0642-05.2005. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Levin I, Hart S. Risk preferences in young children: early evidence of individual differences in reaction to potential gains and losses. J Behav Decision Making. 2003;16:397–413. 10.1002/bdm.453. [CrossRef] [Google Scholar]
- Levin I, Hart S, Weller J, Harshman L. Stability of choices in a risky decision-making task: a 3-year longitudinal study with children and adults. J Behav Decision Making. 2007;20:241–252. 10.1002/bdm.552. [CrossRef] [Google Scholar]
- Levy DJ, Glimcher PW. The root of all value: a neural common currency for choice. Curr Opin Neurobiol. 2012;22:1027–1038. 10.1016/j.conb.2012.06.001. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Levy I, Snell J, Nelson AJ, Rustichini A, Glimcher PW. Neural representation of subjective value under risk and ambiguity. J Neurophysiol. 2010;103:1036–1047. 10.1152/jn.00853.2009. [Abstract] [CrossRef] [Google Scholar]
- Louie K, Glimcher PW. Efficient coding and the neural representation of value. Ann N Y Acad Sci. 2012;1251:13–32. 10.1111/j.1749-6632.2012.06496.x. [Abstract] [CrossRef] [Google Scholar]
- Markowitz H. The utility of wealth. J Political Econ. 1952;60:151–158. 10.1086/257177. [CrossRef] [Google Scholar]
- May JC, Delgado MR, Dahl RE, Stenger VA, Ryan ND, Fiez JA, Carter CS. Event-related functional magnetic resonance imaging of reward-related brain circuitry in children and adolescents. Biol Psychiatry. 2004;55:359–366. 10.1016/j.biopsych.2003.11.008. [Abstract] [CrossRef] [Google Scholar]
- Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Annu Rev Neurosci. 2001;24:167–202. 10.1146/annurev.neuro.24.1.167. [Abstract] [CrossRef] [Google Scholar]
- Mohr PN, Biele G, Heekeren HR. Neural processing of risk. J Neurosci. 2010a;30:6613–6619. 10.1523/JNEUROSCI.0003-10.2010. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Mohr PN, Biele G, Krugel LK, Li SC, Heekeren HR. Neural foundations of risk-return trade-off in investment decisions. Neuroimage. 2010b;49:2556–2563. 10.1016/j.neuroimage.2009.10.060. [Abstract] [CrossRef] [Google Scholar]
- Padmanabhan A, Geier CF, Ordaz SJ, Teslovich T, Luna B. Developmental changes in brain function underlying the influence of reward processing on inhibitory control. Dev Cogn Neurosci. 2011;1:517–529. 10.1016/j.dcn.2011.06.004. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Panno A, Lauriola M, Figner B. Emotion regulation and risk taking: predicting risky choice in deliberative decision making. Cogn Emot. 2013;27:326–334. 10.1080/02699931.2012.707642. [Abstract] [CrossRef] [Google Scholar]
- Paulsen DJ, Carter RM, Platt ML, Huettel SA, Brannon EM. Neurocognitive development of risk aversion from early childhood to adulthood. Front Hum Neurosci. 2011;5:178. 10.3389/fnhum.2011.00178. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Penolazzi B, Gremigni P, Russo PM. Impulsivity and reward sensitivity differentially influence affective and deliberative risky decision making. Personality Indiv Diff. 2012;53:655–659. 10.1016/j.paid.2012.05.018. [CrossRef] [Google Scholar]
- Peters S, Braams BR, Raijmakers ME, Koolschijn PC, Crone EA. The neural coding of feedback learning across child and adolescent development. J Cogn Neurosci. 2014;26:1705–1720. 10.1162/jocn_a_00594. [Abstract] [CrossRef] [Google Scholar]
- Prelec D, Loewenstein L. Decision making over time and under uncertainty: a common approach. Management Sci. 1991;37:770–786. 10.1287/mnsc.37.7.770. [CrossRef] [Google Scholar]
- Preuschoff K, Quartz SR, Bossaerts P. Human insula activation reflects risk prediction errors as well as risk. J Neurosci. 2008;28:2745–2752. 10.1523/JNEUROSCI.4286-07.2008. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Richards JM, Plate RC, Ernst M. A systematic review of fMRI reward paradigms used in studies of adolescents vs. adults: the impact of task design and implications for understanding neurodevelopment. Neurosci Biobehav Rev. 2013;37:976–991. 10.1016/j.neubiorev.2013.03.004. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Rudorf S, Preuschoff K, Weber B. Neural correlates of anticipation risk reflect risk preferences. J Neurosci. 2012;32:16683–16692. 10.1523/JNEUROSCI.4235-11.2012. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Sescousse G, Caldú X, Segura B, Dreher JC. Processing of primary and secondary rewards: a quantitative meta-analyses and review of human functional neuroimaging studies. Neurosci Biobehav Rev. 2013;37:681–696. 10.1016/j.neubiorev.2013.02.002. [Abstract] [CrossRef] [Google Scholar]
- Singmann H. afex: analysis of Factorial Experiments. R package version 0.7-90. 2013. http://CRAN.R-project.org/package=afex.
- Smith AB, Halari R, Giampetro V, Brammer M, Rubia K. Developmental effects of reward on sustained attention networks. Neuroimage. 2011;56:1693–1704. 10.1016/j.neuroimage.2011.01.072. [Abstract] [CrossRef] [Google Scholar]
- Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17:143–155. 10.1002/hbm.10062. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Smith SM, Nichols TE. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localization in cluster inference. Neuroimage. 2009;44:83–98. 10.1016/j.neuroimage.2008.03.061. [Abstract] [CrossRef] [Google Scholar]
- Somerville LH, Jones RM, Casey BJ. A time of change: behavioral and neural correlates of adolescent sensitivity to appetitive and aversive environmental cues. Brain Cogn. 2010;72:124–133. 10.1016/j.bandc.2009.07.003. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Tamnes CK, Ostby Y, Fjell AM, Westlye LT, Due-Tønnessen P, Walhovd KB. Brain maturation in adolescence and young adulthood: regional age-related changes in cortical thickness and white matter volume and microstructure. Cereb Cortex. 2010;20:534–548. 10.1093/cercor/bhp118. [Abstract] [CrossRef] [Google Scholar]
- Telzer EH, Fuligni AJ, Lieberman MD, Galván A. Meaningful family relationships: neurocognitive buffers of adolescent risk taking. J Cogn Neurosci. 2013;25:374–387. 10.1162/jocn_a_00331. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- Teslovich T, Mulder M, Franklin NT, Ruberry EJ, Millner A, Somerville LH, Simen P, Durston S, Casey BJ. Adolescents let sufficient evidence accumulate before making a decision when large incentives are at stake. Dev Sci. 2014;17:59–70. 10.1111/desc.12092. [Abstract] [CrossRef] [Google Scholar]
- Tobler PN, Christopoulos GI, O'Doherty JP, Dolan RJ, Schultz W. Risk-dependent reward value signal in human prefrontal cortex. Proc Natl Acad Sci U S A. 2009;106:7185–7190. 10.1073/pnas.0809599106. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- van Duijvenvoorde ACK, Crone EA. The teenage brain: a neuroeconomic approach to adolescent decision making. Curr Dir Psychol Sci. 2013;22:108–113. 10.1177/0963721413475446. [CrossRef] [Google Scholar]
- van Duijvenvoorde AC, Zanolie K, Rombouts SA, Raijmakers ME, Crone EA. Evaluating the negative or valuing the positive? Neural mechanisms supporting feedback-based learning across development. J Neurosci. 2008;28:9495–9503. 10.1523/JNEUROSCI.1485-08.2008. [Europe PMC free article] [Abstract] [CrossRef] [Google Scholar]
- van Leijenhorst L, Zanolie K, Van Meel CS, Westenberg PM, Rombouts SA, Crone EA. What motivates the adolescent? Brain regions mediating reward sensitivity across adolescence. Cereb Cortex. 2010;20:61–69. 10.1093/cercor/bhp078. [Abstract] [CrossRef] [Google Scholar]
- Weber EU. Risk attitude and preference. Wiley Interdiscip Rev Cogn Sci. 2010;1:79–88. 10.1002/wcs.5. [Abstract] [CrossRef] [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. New York: The Psychological Corporation; 1999. [Google Scholar]
Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience
Full text links
Read article at publisher's site: https://doi.org/10.1523/jneurosci.1924-14.2015
Read article for free, from open access legal sources, via Unpaywall:
https://www.jneurosci.org/content/jneuro/35/4/1549.full.pdf
Citations & impact
Impact metrics
Article citations
Combined Effects of Social Exclusion and Social Rank Feedback on Risky Decision-Making Across Adolescence.
J Youth Adolesc, 28 Aug 2024
Cited by: 0 articles | PMID: 39198345
Risk-Taking Is Associated with Decreased Subjective Value Signals and Increased Prediction Error Signals in the Hot Columbia Card Task.
J Neurosci, 44(21):e1337232024, 22 May 2024
Cited by: 0 articles | PMID: 38561225
The neurocomputational link between defensive cardiac states and approach-avoidance arbitration under threat.
Commun Biol, 7(1):576, 16 May 2024
Cited by: 1 article | PMID: 38755409 | PMCID: PMC11099143
Decoding the dynamic perception of risk and speed using naturalistic stimuli: A multivariate, whole-brain analysis.
Hum Brain Mapp, 45(4):e26652, 01 Mar 2024
Cited by: 1 article | PMID: 38488473 | PMCID: PMC10941534
Friendship changes differentially predict neural correlates of decision-making for friends across adolescence.
Dev Cogn Neurosci, 65:101342, 11 Jan 2024
Cited by: 0 articles | PMID: 38219708 | PMCID: PMC10825619
Go to all (69) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Differential neurobiological effects of expert advice on risky choice in adolescents and adults.
Soc Cogn Affect Neurosci, 7(5):557-567, 03 May 2012
Cited by: 26 articles | PMID: 22563008 | PMCID: PMC3375892
Adolescent risky decision-making: neurocognitive development of reward and control regions.
Neuroimage, 51(1):345-355, 24 Feb 2010
Cited by: 238 articles | PMID: 20188198
Individual differences in risk preference predict neural responses during financial decision-making.
Brain Res, 1290:28-51, 02 Jul 2009
Cited by: 43 articles | PMID: 19576868 | PMCID: PMC4353645
[Risk-taking in adolescence: A neuroeconomics approach].
Encephale, 36(2):147-154, 22 Sep 2009
Cited by: 8 articles | PMID: 20434632
Review
 1,2,3
1,2,3 




