Using image synthesis for multi-channel registration of different image modalities.

Chen M; Jog A; Carass A; Prince JL

doi:10.1117/12.2082373

Using image synthesis for multi-channel registration of different image modalities.

Affiliations

1. Image Analysis and Communications Laboratory, Dept. of ECE, The Johns Hopkins University ; Translational Neuroradiology Unit, National Institute of Neurological Disorders and Stroke.
Authors
Chen M¹
(1 author)
2. Image Analysis and Communications Laboratory, Dept. of ECE, The Johns Hopkins University.
Authors
Jog A²
Prince JL²
(2 authors)
3. Image Analysis and Communications Laboratory, Dept. of ECE, The Johns Hopkins University ; Department of Computer Science, The Johns Hopkins University.
Authors
Carass A³
(1 author)

ORCIDs linked to this article

Carass A | 0000-0003-4939-5085

Proceedings of Spie--the International Society for Optical Engineering, 01 Feb 2015, 9413:94131Q
https://doi.org/10.1117/12.2082373 PMID: 26246653 PMCID: PMC4523226

Free full text in Europe PMC

Abstract

This paper presents a multi-channel approach for performing registration between magnetic resonance (MR) images with different modalities. In general, a multi-channel registration cannot be used when the moving and target images do not have analogous modalities. In this work, we address this limitation by using a random forest regression technique to synthesize the missing modalities from the available ones. This allows a single channel registration between two different modalities to be converted into a multi-channel registration with two mono-modal channels. To validate our approach, two openly available registration algorithms and five cost functions were used to compare the label transfer accuracy of the registration with (and without) our multi-channel synthesis approach. Our results show that the proposed method produced statistically significant improvements in registration accuracy (at an α level of 0.001) for both algorithms and all cost functions when compared to a standard multi-modal registration using the same algorithms with mutual information.

Free full text

Proc SPIE Int Soc Opt Eng. Author manuscript; available in PMC 2015 Aug 3.

Published in final edited form as:

Proc SPIE Int Soc Opt Eng. 2015 Feb 21; 9413: 94131Q.

Published online 2015 Mar 20. https://doi.org/10.1117/12.2082373

PMCID: PMC4523226

NIHMSID: NIHMS710422

PMID: 26246653

Using image synthesis for multi-channel registration of different image modalities

Min Chen,^1,² Amod Jog,¹ Aaron Carass,^1,³ and Jerry L. Prince¹

Author information Copyright and License information Disclaimer

See other articles in PMC that cite the published article.

Abstract

Keywords: Multi-modal image registration, Multi-channel image registration, Magnetic resonance imaging, Image synthesis

1. DESCRIPTION OF PURPOSE

Image registration, the alignment of different image spaces, is a fundamental tool in medical image processing. It is used in a number of applications, include atlasing, population analysis, classification, and segmentation.¹ In general, registration is performed between a single pair of moving and target images. However, if additional modalities exist for both the moving and target subjects, a “multi-channel” or “multivariate” framework^2-5 can be used to improve the registration accuracy and robustness. In such frameworks, the extra modalities for the moving and target images are used to evaluate a combined cost function that optimizes a single deformation field to best align all the image modalities.

One primary restriction of multi-channel registration is that analogous modalities must be available for both the moving and target image. This prevents such algorithms from being used in cases where the data is missing modalities for specific subjects, or the modalities do not match between the moving and target images (i.e., in the case of multi-modal registration). In this work, we address this limitation by applying an image synthesis technique⁶ to provide the missing modality for the multi-channel registration. The method is able to synthesize an image of one modality from another by using aligned atlases of both modalities to learn the intensity and structural transform between the modalities.

Our proposed method is related to existing registration approaches that rely on modality reduction,^7,8 where both the moving and target images are converted into a single modality before registration. In particular, the use of image synthesis has recently been shown to be successful for performing such conversions.⁹ However, our approach has an advantage over these methods in that information is not lost during the conversion. By using a multi-channel registration, the algorithm can take advantage of the features and properties of both modalities to improve its performance.

2. NEW WORK PRESENTED

The main contribution of this work is in the application of image synthesis techniques to account for limitations in multi-channel techniques when facing a multi-modal registration problem, where not all channels are available. The image synthesis allows the single channel multi-modal registration problem to be converted into a multi-channel registration with mono-modal channels. This provides two main advantages: first, it allows the algorithm to use mono-modal cost functions in the registration, which are generally more accurate than multi-modal measures, particularly in regions of the images that are lacking information.¹⁰ Second, it allows the algorithm to use information from multiple modalities in the registration, which has been shown to provide more accurate and robust registrations.⁴

3. METHODS AND MATERIALS

3.1 Data

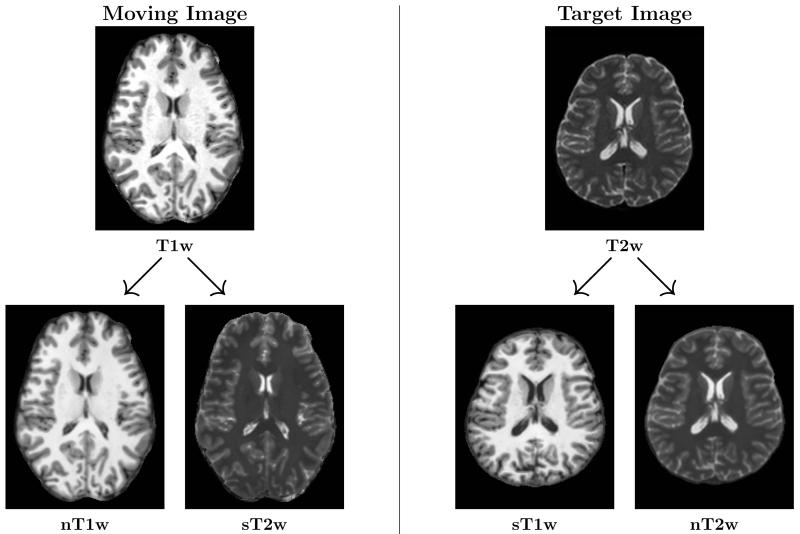
The Multi-modal MRI Reproducibility (MMR) dataset¹¹ was used for the evaluation of our algorithm. The dataset consist of magnetic resonance (MR) images from 21 healthy volunteers, with 16 MR image modalities for each subject. T1-weighted MPRAGE (T1w) images from 10 randomly chosen subjects from the dataset were designated as the “Moving” cohort, and T2-weighted dual echoes (T2w) images from 10 of the remaining subjects were designated as the “Target” cohort. The T1w and T2w image from the remaining unassigned subject was used as the training atlas for the image synthesis method (described in Section 3.3).

3.2 Multi-Channel Cost Function

Given a moving image S(x) and target image T (x), the general goal of a single channel image registration is to find a transformation $v : ℝ^{3} \to ℝ^{3}$ , such that the transformed moving image, S ○ v(x), is in the same space as T (x). This is generally performed by modeling v as a regularized transformation, and optimizing the model according to an energy cost function,

E_{Single Channel} = C (S \circ v, T),

(1)

where C is a similarity metric that describes how alike the two images are. Commonly used metrics include mutual information (MI), cross correlation (CC), and sum of square differences (SSD).¹

In multi-channel registration, additional modalities of the moving and target images are used together in the registration. A common implementation is to set each modality as a separate channel, and use a weighted sum of the similarity function of each channel for the total energy function. Suppose we have a moving image set with N modalities of the same subject, {S₁, S₂,…, S_N}, and a target image set with analogous modalities for another subject, {T₁, T₂,… T_N}, then the multi-channel energy function can be described by,

E_{Multi-Channel} = w_{1} C (S_{1} \circ v, T_{1}) + w_{2} C (S_{2} \circ v, T_{2}) + \dots + w_{N} C (S_{N} \circ v, T_{N}),

(2)

where w₁, w₂, …, w_N are weights that determine the contribution of each modality to the final energy function. This allows the final deformation to be optimized using the information from every image modality, thus combining and detecting features with different contrast that may not have been present in any given single channel.

3.3 MR Contrast Synthesis

From Equation 2, we see that if C is a mono-modal cost function then the multi-channel framework requires S_n and T_n to have the same modality at each channel n. This is a limitation for multi-modal registration problems, since the moving and target images have different modalities by definition. In order to use the multi-channel framework to solve such problems, we must first complete the channels by filling in the missing modalities. To perform this, we use a patch-based random forest regression approach.⁶

In our data the Moving cohort contained only T1w images and the Target cohort only contained T2w images, hence the goal is to create synthetic T2w (sT2w) images for the Moving cohort and synthetic T1w (sT1w) images for the Target cohort. To generate the sT2w image from the T1w image, the synthesis method extracts 3D patches from the T1w image as features which are used to predict the corresponding T2w voxel intensity. This is formulated as a nonlinear regression problem, where a mapping is learned from a training atlas using random forests classifiers. The mapping can then be applied to patches at each voxel in a T1w image, allowing the algorithm to predict a T2w value for each voxel, creating the sT2w image. Using the same approach, synthetic T1w (sT1w) images are created from the T2w image for each Target subject. In our experiments, the training atlas for the algorithm was constructed from the T1w and T2w images from the single unassigned subject in the MMR dataset. Figure 1 shows sT1w and sT2w images created using this approach.

An external file that holds a picture, illustration, etc.
Object name is nihms-710422-f0001.jpg

Figure 1

Shown is an example of a pair of Moving (T1w) and Target (T2w) images, and the normalized (nT1w, nT2w) and synthetic (sT2w, sT1w) images that are created from each image for the multi-channel registration.

3.4 Intensity Normalization Using Image Synthesis

Another application of the synthesis approach presented in Section 3.3 is to perform intra-modality synthesis to create “normalized” T1w (nT1w) images by learning the mapping between T1w and sT1w images (and similarly to create normalized T2w (nT2w) images). The advantage of these normalized images is that they are created from the same atlas as the synthetic images, which gives them intensities that are comparable to the synthetic images. Using these normalized images in place of the original images allows mono-modal cost functions, such as SSD, to perform better when registered with the synthetic images. Figure 1 shows nT1w and nT2w images created using this approach. We see that the contrast in the normalized images better match the synthesized images, particularly in the ventricles and subcortical regions.

3.5 Using synthesized images for multi-modal registrations

Once the synthesized and normalized images are created, they can be used to replace the missing modalities in the multi-channel framework. This allows us to fully represent multi-modal problems within a multi-channel framework. Using Equation 1, we can represent a standard MI-based multi-modal registration between a moving T1w image and a target T2w image as,

E_{Single Channel} = M I (S_{T 1 w} \circ v, T_{T 2 w}) .

(3)

By using image synthesis to create a nT1w and sT2w from the T1w image, and a sT1w and nT2w from the T2w image, we can complete the channels in Equation 2, which allows the energy function to be converted to,

E_{Multi-Channel} = w_{1} C (S_{n T 1 w} \circ v, T_{s T 1 w}) + w_{2} C (S_{s T 2 w} \circ v, T_{n T 2 w}) .

(4)

Since the channels are mono-modal, C is no longer restricted to MI after the conversion, and can be replaced with a mono-modal similarity metric such as SSD. For our experiments the channel weights, w₁ and w₂ are both set to be equal.

3.6 Registration Algorithms

From Equation 4, we see that the proposed technique is independent of the registration algorithm. Our method operates solely on the images entering the registration algorithm, and therefore, it functions as a pre-processing step that fills all the incomplete channels in the multi-channel algorithm. To demonstrate this, we validated our method with two distinct registration algorithms with very different transformation models. The first algorithm is a multi-channel enhancement¹² of the adaptive bases algorithm (ABA),¹³ which is available as part of the JIST software package (http://www.nitrc.org/projects/jist).¹⁴ ABA is a parametric registration approach that optimizes radial basis functions to model the deformation field. The second algorithm we used is a symmetric diffeomorphic algorithm (SyN),¹⁵ available as part of the ANTS software package (http://stnava.github.io/ANTs/). Both algorithms have multi-channel implementations similar to that described by Equation 2.

4. EXPERIMENTS

4.1 Label Transfer Validation

To evaluate the advantages of using image synthesis to aid multi-modal registration, the Moving and Target cohorts were used in several label transfer experiments. Each experiment evaluated a registration algorithm’s ability to accurately transform anatomical segmentations between different subject images using the learned deformation field. Cross-validation registrations were performed between each Moving subject and each Target subject, producing a total of 100 registrations for each experiment. The two label sets used for the evaluation were the Mindboggle (http://www.mindboggle.info/) manual cortical labels available for each subject in the MMR dataset,¹⁶ and tissue classifications of cerebrum structures for each subject, generated automatically using the TOADS¹⁷ algorithm. For each registration algorithm, and for each label set, Dice coefficients were calculated between the transformed Moving image labels and the labels for the Target image, individually for each label. The Dice scores are then averaged across all labels within each label set, creating two average Dice scores for each of the 100 Moving/Target registration pairs in each experimental setup.

The baseline registration setup, which we compared our method to, was a standard single-channel multi-modal registration between a Moving T1w image and a Target T2w image using mutual information. We compared this against multi-channel registrations using the synthesized images with and without the normalized images. Since our approach expands the multi-modal setup into two separate mono-modal channels, we also evaluated different mono-modal similarity metrics for the multi-channel experiments. The metrics evaluated were normalized mutual information (NMI) and sum of square difference (SSD) for ABA, and mutual information (MI), cross correlation (CC), and mean square error (MSE) for SyN. Tables 1 and and22 show the mean and standard deviation of the Dice for each registration algorithm.

Table 1

Mean (and standard deviation) of Mindboggle and TOADS label transfer Dice results, when using ABA with normalized mutual information (NMI) and sum of squared differences (SSD) as similarity metrics. The three experiments show results when using a single channel multi-modal registration (“T1→T2”), and multi-channel registrations using the synthesized images with (“[nT1, sT2] [implies] [sT1, nT2]”) and without (“[T1, sT2][sT1, T2]”) the normalized images. The bolded values show the best results for each label set.

		ABA
		NMI	SSD

MindBoggle	T1 → T2	0.312 (0.02)	–
	[T1, sT2][sT1, T2]	0.325 (0.02)	0.344 (0.01)
	[nT1, sT2][sT1, nT2]	0.335 (0.01)	0.350 (0.01)

TOADS	T1 → T2	0.702 (0.05)	–
	[T1, sT2][sT1, T2]	0.726 (0.03)	0.743 (0.03)
	[nT1, sT2][sT1, nT2]	0.743 (0.03)	0.752 (0.03)

Table 2

Mean (and standard deviation) of Mindboggle and TOADS label transfer Dice results, when using SyN with mutual information (MI), cross correlation (CC) and mean squared error (MSE) as similarity metrics. The three experiments show results when using a single channel multi-modal registration (“T1→T2”), and multi-channel registrations using the synthesized images with (“[nT1, sT2] [implies] [sT1, nT2]”) and without (“[T1, sT2][sT1, T2]”) the normalized images. The bolded values show the best results for each label set.

		SyN
		MI	CC	MSE

MindBoggle	T1 → T2	0.266 (0.06)	0.181 (0.06)	–
	[T1, sT2][sT1, T2]	0.276 (0.07)	0.308 (0.08)	0.299 (0.08)
	[nT1, sT2][sT1, nT2]	0.278 (0.07)	0.311 (0.07)	0.298 (0.07)

TOADS	T1 → T2	0.674 (0.04)	0.601 (0.07)	–
	[T1, sT2][sT1, T2]	0.705 (0.04)	0.730 (0.03)	0.733 (0.03)
	[nT1, sT2][sT1, nT2]	0.708 (0.04)	0.732 (0.04)	0.734 (0.03)

4.2 Results and Discussion

We see from the results that regardless of the registration algorithm or cost function used, both the normalized and non-normalized synthesized multi-channel registration performed better than the single channel multi-modal registration using mutual information. Standard single-tail, paired Students t-tests performed on these Dice results showed statistically significant improvements (at an α level of 0.001) when comparing any of the multi-channel results against the single channel mutual information results. This remained true for both the MindBoggle cortical labels and the cerebrum structural labels from TOADS.

From the bold values in the tables, we see that switching to a mono-modal cost function and using the normalized images for the multi-channel setup provided the best results for a given algorithm and label set. For ABA, using multi-channel with SDD produced the best result for both label sets. While for SyN, using multi-channel with CC gave the best result for the Mindboggle labels, and multi-channel with MSE gave the best result for the TOADS labels. However, the differences between the CC and MSE results were marginal relative to their improvement on using MI.

These results suggest that using a mono-modal cost function can greatly improve the registration accuracy. For both registration algorithms, switching to a mono-modal cost function in the multi-channel experiments produced a larger increase in average Dice than switching between single-channel and multi-channel registrations. Using the normalized images also improved the overall registration accuracy. However, the improvement was much smaller and mainly only benefited the ABA registration algorithm. One possible explanation for why using normalized images had little effect on the SyN results may be due to potential intensity normalization preprocessing that is already built into the algorithm.

5. CONCLUSION

In this work we have demonstrated an approach for multi-modal registration using image synthesis with multi-channel registration. Our validation showed that, independent of the registration algorithm used, our approach produced more accurate registrations relative to the standard multi-modal registration using mutual information. This suggests that our approach can be applied as a general preprocessing step to improve the accuracy of multi-channel registration algorithms. In addition, our approach has helped generalize the multi-channel registration framework by allowing such algorithms to be applicable in situations where image modalities are not analogous between the moving and target images.

There are several future directions for this work. First, the impact of the image normalization should be further evaluated, particularly within the context of mono-modal image registration. Although our results showed some improvements when using the normalize images, it is unclear under what situations it is beneficial for the registration. Second, our approach can potentially be used to synthesize additional channels that use modalities that are not available in either the moving or target image sets. This can further improve the registration by introducing additional information from the atlas. Finally, the multi-channel framework is only one of many multivariate registration frameworks. The application of synthetic images in other frameworks should also be explored.

ACKNOWLEDGMENTS

This work was supported in part by NIH/NIBIB grants R01-EB017743 and R21-EB012765, and the Intramural Research Program of NINDS.

REFERENCES

[1] Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: A survey. IEEE Trans. Med. Imag. 2013;32(7):1153–1190. [Europe PMC free article] [Abstract] [Google Scholar]

[2] Park H-J, Kubicki M, Shenton ME, Guimond A, McCarley RW, Maier SE, Kikinis R, Jolesz FA, Westin C-F. Spatial normalization of diffusion tensor MRI using multiple channels. Neuroimage. 2003;20(4):1995–2009. [Europe PMC free article] [Abstract] [Google Scholar]

[3] Rohde GK, Pajevic S, Pierpaoli C, Basser PJ. A comprehensive approach for multi-channel image registration; 2nd International Workshop on Biomedical Image Registration; 2003.pp. 214–223. [Google Scholar]

[4] Avants B, Duda JT, Zhang H, Gee JC. Multivariate normalization with symmetric diffeomorphisms for multivariate studies; Medical Image Computing and Computer-Assisted Intervention-MICCAI 2007; 2007.pp. 359–366. [Abstract] [Google Scholar]

[5] Forsberg D, Rathi Y, Bouix S, Wassermann D, Knutsson H, Westin C-F. Multimodal Brain Image Analysis. 2011. Improving registration using multi-channel diffeomorphic demons combined with certainty maps; pp. 19–26. [Google Scholar]

[6] Jog A, Roy S, Carass A, Prince JL. Magnetic resonance image synthesis through patch regression; 2013 IEEE 10th International Symposium on Biomedical Imaging: From Nano to Macro; 2013.pp. 350–353. [Europe PMC free article] [Abstract] [Google Scholar]

[7] Wein W, Brunke S, Khamene A, Callstrom MR, Navab N. Automatic CT-ultrasound registration for diagnostic imaging and image-guided intervention. Medical Image Analysis. 2008;12(5):577–585. [Abstract] [Google Scholar]

[8] Michel F, Paragios N. Image transport regression using mixture of experts and discrete Markov random fields; 2010 IEEE International Symposium on Biomedical Imaging: From Nano to Macro; 2010.pp. 1229–1232. [Google Scholar]

[9] Iglesias JE, Konukoglu E, Zikic D, Glocker B, Van Leemput K, Fischl B. Is Synthesizing MRI Contrast Useful for Inter-modality Analysis?; 16th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2013); 2013.pp. 631–638. [Europe PMC free article] [Abstract] [Google Scholar]

[10] Andronache A, von Siebenthal M, Székely G, Cattin P. Non-rigid registration of multi-modal images using both mutual information and cross-correlation. Medical Image Analysis. 2008;12(1):3–15. [Abstract] [Google Scholar]

[11] Landman BA, Huang AJ, Gifford A, Vikram DS, Lim IAL, Farrell JA, Bogovic JA, Hua J, Chen M, Jarso S, Smith SA, Joel S, Mori S, Pekar JJ, Barker PB, Prince JL, van Zijl PCM. Multi-parametric neuroimaging reproducibility: A 3-T resource study. Neuroimage. 2011;54(4):2854–2866. [Europe PMC free article] [Abstract] [Google Scholar]

[12] Chen M, Carass A, Wheeler MB, Liu X, Prince JL. Multi-channel enhancement of the adaptive bases algorithm; 16th Annual Meeting of the Organization for Human Brain Mapping; 2010. [Google Scholar]

[13] Rohde GK, Aldroubi A, Dawant BM. The adaptive bases algorithm for intensity based nonrigid image registration. IEEE Trans. Med. Imag. 2003;22(11):1470–1479. [Abstract] [Google Scholar]

[14] Lucas BC, Bogovic JA, Carass A, Bazin P-L, Prince JL, Pham DL, Landman BA. The Java Image Science Toolkit (JIST) for rapid prototyping and publishing of neuroimaging software. Neuroinformatics. 2010;8(1):5–17. [Europe PMC free article] [Abstract] [Google Scholar]

[15] Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Medical Image Analysis. 2008;12(1):26–41. [Europe PMC free article] [Abstract] [Google Scholar]

[16] Klein A, Tourville J. 101 labeled brain images and a consistent human cortical labeling protocol. Frontiers in Neuroscience. 2012;6:171. [Europe PMC free article] [Abstract] [Google Scholar]

[17] Bazin P-L, Pham DL. Topology-preserving tissue classification of magnetic resonance brain images. IEEE Trans. Med. Imag. 2007;26(4):487–496. [Abstract] [Google Scholar]

Full text links

Read article at publisher's site: https://doi.org/10.1117/12.2082373

Read article for free, from open access legal sources, via Unpaywall: https://europepmc.org/articles/pmc4523226?pdf=render

Citations & impact

Impact metrics

Citations

Jump to Citations

Citations of article over time

Article citations

Multimodal MRI synthesis using unified generative adversarial networks.
Dai X, Lei Y, Fu Y, Curran WJ, Liu T, Mao H, Yang X
Med Phys, 47(12):6343-6354, 27 Oct 2020
Cited by: 13 articles | PMID: 33053202 | PMCID: PMC7796974
Free full text in Europe PMC
Image synthesis-based multi-modal image registration framework by using deep fully convolutional networks.
Liu X, Jiang D, Wang M, Song Z
Med Biol Eng Comput, 57(5):1037-1048, 07 Dec 2018
Cited by: 10 articles | PMID: 30523534
Brain lesion segmentation through image synthesis and outlier detection.
Bowles C, Qin C, Guerrero R, Gunn R, Hammers A, Dickie DA, Valdés Hernández M, Wardlaw J, Rueckert D
Neuroimage Clin, 16:643-658, 08 Sep 2017
Cited by: 12 articles | PMID: 29868438 | PMCID: PMC5984574
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
Iterative framework for the joint segmentation and CT synthesis of MR images: application to MRI-only radiotherapy treatment planning.
Burgos N, Guerreiro F, McClelland J, Presles B, Modat M, Nill S, Dearnaley D, deSouza N, Oelfke U, Knopf AC, Ourselin S, Jorge Cardoso M
Phys Med Biol, 62(11):4237-4253, 14 Mar 2017
Cited by: 8 articles | PMID: 28291745 | PMCID: PMC5423555
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
Patch Based Synthesis of Whole Head MR Images: Application to EPI Distortion Correction.
Roy S, Chou YY, Jog A, Butman JA, Pham DL
Simul Synth Med Imaging, 9968:146-156, 23 Sep 2016
Cited by: 4 articles | PMID: 28367541 | PMCID: PMC5375117
Free full text in Europe PMC

Go to all (6) article citations

Funding

Funders who supported this work.

NIBIB NIH HHS (2)

Grant ID: R01 EB017743
21 publications
Grant ID: R21 EB012765
23 publications

Search life-sciences literature (45,103,589 articles, preprints and more)

Using image synthesis for multi-channel registration of different image modalities.

Author information

Affiliations

Authors

Authors

Authors

ORCIDs linked to this article

Abstract

Free full text

Using image synthesis for multi-channel registration of different image modalities

Min Chen

Amod Jog

Aaron Carass

Jerry L. Prince

Abstract

1. DESCRIPTION OF PURPOSE

2. NEW WORK PRESENTED

3. METHODS AND MATERIALS

3.1 Data

3.2 Multi-Channel Cost Function

3.3 MR Contrast Synthesis

3.4 Intensity Normalization Using Image Synthesis

3.5 Using synthesized images for multi-modal registrations

3.6 Registration Algorithms

4. EXPERIMENTS

4.1 Label Transfer Validation

Table 1

Table 2

4.2 Results and Discussion

5. CONCLUSION

ACKNOWLEDGMENTS

REFERENCES

Full text links

Citations & impact

Impact metrics

Citations of article over time

Article citations

Similar Articles

Funding

NIBIB NIH HHS (2)﻿

Partnerships & funding

NIBIB NIH HHS (2)