Europe PMC

This website requires cookies, and the limited processing of your personal data in order to function. By using the site you are agreeing to this as outlined in our privacy notice and cookie policy.

Multiscale Modeling of Antibody-Drug Conjugates: Connecting Tissue and Cellular Distribution to Whole Animal Pharmacokinetics and Potential Implications for Efficacy.

Author information

Affiliations

  • 1. Department of Chemical Engineering, University of Michigan, 2800 Plymouth Rd., Ann Arbor, Michigan, 48109, USA.
      Authors
    • Cilliers C 1
    • Guo H 1
    • Liao J 1
    • Christodolu N 1
    • Thurber GM 1
    (5 authors)

ORCIDs linked to this article

The AAPS Journal, 10 Jun 2016, 18(5):1117-1130
https://doi.org/10.1208/s12248-016-9940-z PMID: 27287046 PMCID: PMC4996726

Free full text in Europe PMC

Abstract 

Antibody-drug conjugates exhibit complex pharmacokinetics due to their combination of macromolecular and small molecule properties. These issues range from systemic concerns, such as deconjugation of the small molecule drug during the long antibody circulation time or rapid clearance from nonspecific interactions, to local tumor tissue heterogeneity, cell bystander effects, and endosomal escape. Mathematical models can be used to study the impact of these processes on overall distribution in an efficient manner, and several types of models have been used to analyze varying aspects of antibody distribution including physiologically based pharmacokinetic (PBPK) models and tissue-level simulations. However, these processes are quantitative in nature and cannot be handled qualitatively in isolation. For example, free antibody from deconjugation of the small molecule will impact the distribution of conjugated antibodies within the tumor. To incorporate these effects into a unified framework, we have coupled the systemic and organ-level distribution of a PBPK model with the tissue-level detail of a distributed parameter tumor model. We used this mathematical model to analyze new experimental results on the distribution of the clinical antibody-drug conjugate Kadcyla in HER2-positive mouse xenografts. This model is able to capture the impact of the drug-antibody ratio (DAR) on tumor penetration, the net result of drug deconjugation, and the effect of using unconjugated antibody to drive ADC penetration deeper into the tumor tissue. This modeling approach will provide quantitative and mechanistic support to experimental studies trying to parse the impact of multiple mechanisms of action for these complex drugs.

Free full text 

Logo of nihpaLink to Publisher's site
AAPS J. Author manuscript; available in PMC 2017 Sep 1.
Published in final edited form as:
PMCID: PMC4996726
NIHMSID: NIHMS798086
PMID: 27287046

Multiscale Modeling of Antibody Drug Conjugates: Connecting tissue and cellular distribution to whole animal pharmacokinetics and potential implications for efficacy

Cornelius Cilliers,* Hans Guo,* Jianshan Liao,* Nikolas Christodolu,* and Greg M. Thurber*#
Author information Copyright and License information Disclaimer

Abstract

Antibody drug conjugates exhibit complex pharmacokinetics due to their combination of macromolecular and small molecule properties. These issues range from systemic concerns, such as deconjugation of the small molecule drug during the long antibody circulation time or rapid clearance from non-specific interactions, to local tumor tissue heterogeneity, cell bystander effects, and endosomal escape. Mathematical models can be used to study the impact of these processes on overall distribution in an efficient manner, and several types of models have been used to analyze varying aspects of antibody distribution including physiologically based pharmacokinetic (PBPK) models and tissue-level simulations. However, these processes are quantitative in nature and cannot be handled qualitatively in isolation. For example, free antibody from deconjugation of the small molecule will impact the distribution of conjugated antibodies within the tumor. To incorporate these effects into a unified framework, we have coupled the systemic and organ-level distribution of a PBPK model with the tissue-level detail of a distributed parameter tumor model. We used this mathematical model to analyze new experimental results on the distribution of the clinical antibody drug conjugate Kadcyla in HER2 positive mouse xenografts. This model is able to capture the impact of the drug antibody ratio (DAR) on tumor penetration, the net result of drug deconjugation, and the effect of using unconjugated antibody to drive ADC penetration deeper into the tumor tissue. This modeling approach will provide quantitative and mechanistic support to experimental studies trying to parse the impact of multiple mechanisms of action for these complex drugs.

Keywords: antibody tissue penetration, drug antibody ratio (DAR), Kadcyla, Herceptin, Krogh cylinder, ado-trastuzumab emtansine

Introduction

Antibody-drug conjugates (ADCs) provide a powerful method to selectively deliver toxic small molecules to cancer cells while reducing non-specific uptake in healthy tissue. Significant effort has gone into designing the multiple aspects of these complex prodrugs, including the target selection, antibody structure and conjugation site, small molecule drug, linker design, and ratio of small molecule to antibody (drug antibody ratio, DAR)(1-5). Currently there are two FDA approved ADCs, with Kadcyla (ado-trastuzumab emtansine, T-DM1) being the only ADC approved for solid tumors, and there are over 30 ADCs in various stages of the clinical pipeline(6, 7). Although the mechanism of individual cell death by the cytotoxic small molecule is well documented, the multiple and complex steps in delivery involving both tumor uptake of the macromolecule, local metabolism, and distribution of the small molecule effector make it challenging to design an optimal drug. Mathematical simulations provide an efficient method for exploring the vast parameter space and selecting agents with an increased likelihood of success, reducing the thousands of possible combinations of these complex drugs to a few testable approaches.

Physiologically based pharmacokinetic (PBPK) models have become ubiquitous in translational research for evaluating the behavior of lead compounds in dosing regimens and providing valuable information into reaction kinetics and transport phenomena in vivo. PBPK models have been used extensively to data fit dosing curves for more accurate interspecies dose scaling(8-14) and in predictive methods for first in animal studies(15-19). Because these models are arranged anatomically they often provide better dosing estimations than simple one- or two-compartment models or allometric scaling. Also, these models provide a framework to estimate unknown parameters or rates that might be difficult to measure accurately in vivo. However, there is strong motivation within this framework to develop more predictive models (versus data fitting) so that the pharmacokinetic behavior of lead compounds can be simulated and used to streamline preclinical and clinical studies.

Current PBPK models for antibodies vary in how the organ compartments are structured. For example, a model by Baxter uses two-pore formalism to estimate the extravasation of the antibody into the surrounding tissues(9). Models by Ferl and Davda also used two-pore formalism but added FcRn recycling into select organ compartments to capture this important antibody metabolism pathway(10, 20). Another model from Garg et al. incorporated FcRn recycling into all tissues and used one-pore formalism to model antibody extravasation(11). Recently, Shah et al. developed a platform PBPK model that incorporates up to 18 compartments, each with detailed mechanistic behavior that subdivides each organ into plasma, blood cell, endothelial, interstitial, and cellular sub-compartments and uses FcRn interactions(14). While all these models share a similar framework, there is not a general consensus on the optimal way to describe the organ compartments(21). This likely results from the trade-offs of more detailed models being able to capture more complex behavior at the cost of additional parameters that could result in an underspecified system or one where it is difficult to independently measure values for predictions.

Although organ-level PBPK models can simulate systemic and individual organ concentrations over time, they lack detailed tissue level distribution and do not provide a framework for predicting the heterogeneous tumor distribution associated with antibodies. The most common method for capturing these tissue scale dynamics is through a Krogh cylinder or tumor cord geometry(22-26). Using this geometry along with mixed boundary conditions to capture permeability limitations, explicit blood flow and axial gradients to measure blood flow limitations, and diffusion with non-linear binding kinetics to quantify diffusion limitations, tissue level models are useful for determining the uptake and distribution of a diverse range of drugs, including small molecules, therapeutic proteins, and antibodies(27-31). For antibodies, the tumor cord geometry has been validated by multiple groups and has been used to estimate whole organ distribution and uptake(27, 32-36). The lack of functional lymphatics in tumors(37) also lends itself to this geometry focused on transcapillary exchange and distribution. However, the Krogh geometry requires the systemic (plasma) concentration as an input, therefore limiting its ability for purely predictive studies. Combining the Krogh cylinder to describe the tumor compartment with a general PBPK model for systemic distribution would give an accurate, multi-scale depiction of antibody distribution. Additionally, since self-consistent therapeutic parameters are available for a wide range of molecules including antibodies and small molecule drugs(19, 36, 38), the Krogh cylinder simulations are able to simultaneously capture multiple different species within the tumor.

Here we present a multi-scale model integrating two previously published and validated models: a PBPK model for organ and whole body distribution and a tumor tissue Krogh cylinder to simulate the distribution of the clinically used ADC T-DM1. This model combines the strength of PBPK models by simulating the systemic distribution while accurately capturing the heterogeneous antibody distribution in the tumor. To highlight the importance of systemic and tumor concentrations, we use two clinically relevant therapeutics: the monoclonal antibody Herceptin (trastuzumab) and the ADC T-DM1. Through simulation and experiment we show that at the clinical dose of T-DM1 (3.6 mg/kg) the tumor distribution is highly heterogeneous, resulting in a typical perivascular tumor distribution. Additionally we show that co-administration of trastuzumab with a constant T-DM1 dose results in a significantly more homogeneous tumor distribution, thereby targeting more tumor cells with the potent cytotoxic small molecule drug. Importantly, the total tumor uptake of the ADC does not change significantly, but in vivo experimental data shows a drastically different tumor distribution. The combined PBPK-Krogh cylinder model accurately captures the systemic organ concentrations and the considerably different tumor distribution, something that neither model can do alone. The interplay between systemic level pharmacokinetics and tumor distribution is important for ADCs, and several literature examples are shown in the context of tissue penetration. The impact of dose, DAR, deconjugation, receptor expression, and trafficking all strongly impact the distribution. This model is therefore useful in accurately capturing the complex distribution resulting from varying the DAR, linker stability, and antibody distribution on tumor efficacy.

Materials and Methods

In Vivo Experimental Work

T-DM1 and trastuzumab were obtained through the University of Michigan Pharmacy. Alexa Fluor 680 (AF680) was conjugated to T-DM1 following the manufacturer's instructions and as previously described(39). For reactions, a molar ratio of 0.7 was used that resulted in an overall degree of labeling of 0.3 to mitigate any potential physicochemical effects from the dye on the antibody. Conjugates were run on SDS-PAGE and scanned on an Odyssey CLx NIR scanner to ensure free dye was removed.

Animal studies were approved and conducted in accordance with University of Michigan University Committee on Use and Care of Animals (UCUCA). NCI-N87 cells were obtained from ATCC and were grown in RPMI-1640 containing 10 % (v/v) FBS, 50 U/ml penicillin, and 50 μg/ml streptomycin. Tumor xenograft studies consisted of 5×106 NCI-N87 cells inoculated in the rear flanks of nude mice. Tail vein injections were done approximately 4 weeks after inoculation when the longest axis of the tumor was approximately 10-12mm. Tail vein injections consisted of 3.6 mg/kg of T-DM1-AF680 and either 0, 10.8, or 28.8 mg/kg of unlabeled trastuzumab.

Plasma clearance was measured via retroorbital sampling, mixed with 15 μL of 10mM EDTA in PBS per 10 μL of whole blood, centrifuged (1 min, 3000xg), and scanned in a 384 well plate with the Odyssey CLx. Signal intensity was converted to absolute concentration using calibration curves of known concentrations of each agent in plasma and fit using a biexponential decay in PRISM. Animals were euthanized after 24 hours (the time of maximum tumor uptake, data not shown and (40)) for biodistribution and histology measurements.

The biodistribution protocol was adapted from previously published protocols(41, 42). Briefly, after the animals were euthanized, organs were resected, weighed, and homogenized. Homogenization consisted of incubating with a RIPA buffer/PBS mixture supplemented with 6mg/mL collagenase IV solution, cell disruption using FB-120 Sonic Dismembrator, and further incubation with a RIPA buffer/0.05% trypsin-EDTA solution. After homogenization, each organ was serially diluted in a 96 well plate and scanned using the Odyssey CLx scanner. The percent-injected dose per gram (%ID/g) was determined by comparing signal from the Odyssey CLx scanner to a calibration curve and then normalizing by organ weight and homogenate volume. A density of 1g/mL was assumed for each tissue.

To quantify the tumor distribution of the antibodies, nude mice bearing NCI-N87 xenografts were euthanized 24 hours after tail vein injection of antibody, and the tumors were resected and flash frozen in OCT using isopentane chilled on dry ice. Histology slices (16 micron) were imaged with an upright Olympus FV1200 confocal microscope using 405, 542, and 635 lasers, and a 20× objective. Sixteen micron sections were used relative to the more typical 5 micron slices to improve signal-to-noise from the NIR fluorescence imaging. High-resolution images of organs were obtained using a series of stitched smaller images and the Olympus software. Immunofluorescence staining was done using CD31 conjugated with Alexa Fluor 555. All confocal images were exported and analyzed using ImageJ image analysis software.

PBPK Model

For this study, the PBPK model was adapted from Ferl et al.(43). A graphical depiction of the model is shown in Fig. 1A. Changes from this previously published and validated model were as follows. Heart and lung compartments were added and follow the general structure of the other organ compartments. Physiologic parameters for the heart and lung were taken from Baxter et al. (9). The PBPK tumor compartment was removed and instead represented using a distributed parameter model with Krogh cylinder geometry (described below). Each organ compartment was divided into vascular, interstitial, and metabolite subcompartments, and the carcass contained an endothelial subcompartment for FcRn kinetics (Fig. 1B). All model equations and parameter values can be found in the supplemental data (Table S1). Other changes from the original PBPK model include changing the permeability surface area product for large and small pores to values for intact IgG. The model was constructed for both unconjugated antibodies and ADCs to simulate the distribution of each individually.

An external file that holds a picture, illustration, etc. Object name is nihms798086f1.jpg

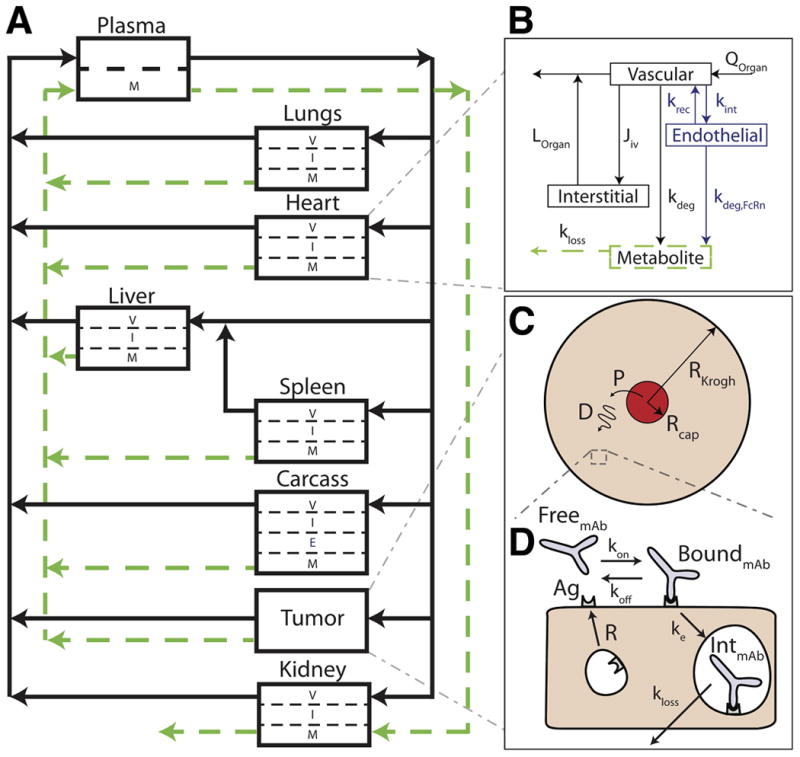
Multi-scale PBPK-Krogh cylinder model diagram. A, PBPK model tracks systemic distribution of both antibody and ADC. Solid black lines correspond to antibody/ADC flow and green dotted lines correspond to metabolite flow. B, representative organ compartment model. All organs except the tumor and carcass are divided into vascular, interstitial, and metabolite compartments. The endothelial compartment is added in the carcass to account for FcRn recycling. C, the tumor compartment is modeled by a 1-D Krogh cylinder tissue model with permeability (P) across the endothelium (extravasation) and diffusion (D) through the surrounding tissue. D, cellular-scale model showing binding, internalization, and degradation rates of both antibody and ADC.

Robust predictions of the whole animal distribution of biologics are not yet possible, so several agent specific parameters not found in the literature were fit to experimental data using Matlab as shown in Table 1. These parameters are the degradation rates for the liver (kdeg,liver), degradation rate in all other organs (kdeg,organ), the metabolite urinary excretion rate (U) and metabolite loss rate (kloss). Percent coefficient of variation (%CV) values and 95% confidence intervals (95% C.I.) for these fitted parameters are listed in Table 1.

Table 1

Fitted PBPK model parameters
ParameterValueUnits%CV95% C.I.Description
kdeg,liver7.4 × 10-6mL/s34.53.1 × 10-6 to 1.2 × 10-5Liver degradation rate
kdeg,organ3.2 × 10-7mL/s72.10* to 7.0 × 10-7Organ degradation rate
U6.9 × 10-4s-165.80* to 1.5 × 10-3Metabolite urinary excretion rate
kloss5.2 × 10-5s-120.93.4 × 10-5 to 7.1 × 10-5Metabolite loss rate
*Confidence interval was constrained to zero because lower bound was negative.

Tissue Disposition Model

A tissue distribution model based on previously published work(27, 28, 36) was incorporated into the PBPK model (Fig. 1C, 1D). This modeling approach has been validated for the tissue distribution of antibodies and ADCs by our group and others(27, 28, 32, 33, 35). Briefly, this model is based on the Krogh cylinder geometry of tumor blood vessels. Because antibodies are permeability limited, a one-dimensional model with only radial gradients was used. The model consisted of free antibody, free ADC, free target, bound antibody, bound ADC, internalized antibody, and internalized ADC. Detailed equations and parameter values can be found in the supplemental material and Table 2, but briefly, trastuzumab and T-DM1 extravasate from a blood vessel and are free to diffuse and bind to HER2 receptor in the tissue, upon which they are internalized and degraded. These molecules compete for the same pool of HER2, and after internalization, HER2 recycles back to the cell surface, consistent with experimental studies(44). The tissue disposition model is connected to the PBPK model by the entering and exiting plasma concentrations adjusted by the efflux into the tumor to capture any target-mediated drug disposition effects(45-47). Importantly, all parameters in the Krogh cylinder were taken from the literature and were not changed or fit to data.

Table 2

Krogh cylinder simulation parameters from literature
ParameterValueUnitsReferenceDescription
D10μm2/s(27)Antibody diffusivity
P3 × 10-9m/s(85)Antibody permeability
kon7.1 × 105M-1 s-1(86)Trastuzumab binding rate
Kd0.5nM(86)Trastuzumab dissociation constant
koff3.5 × 10-4s-1(86)Trastuzumab dissociation rate
RKrogh75μm(40, 87)Krogh cylinder radius
Rcapillary8μm(88)Capillary radius
[Ag]00.83μM(28, 62, 89)Initial Antigen concentration (106 HER2/cell, 5×108 cells/mL)
ε0.24Dimensionless(19)void fraction
H0.45Dimensionless(90)Hematocrit
ke3.3 × 10-5s-1(44)Trastuzumab internalization rate
Q0.0015mL/g/s(43)Blood flow rate to tumor
Rs3.3 × 10-5s-1(44)Antigen recycle rate

Results

A graphic depiction of the combined PBPK and Krogh cylinder model is shown in Fig. 1. This multi-scale model captures the systemic and organ level concentrations (PBPK model, Fig. 1A, 1B) along with the heterogeneous tissue distribution in the tumor and cellular metabolism of the ADC (Krogh cylinder model, Fig. 1C, 1D). Currently, the endosomal processing and escape of the metabolite are not included but could be added to the modeling framework as others have done(33, 48). The higher vascular density in healthy tissue (resulting in shorter diffusion distances between vessels) and lack of specific binding in most tissue results in a homogeneous antibody distribution(49). Therefore, only the tumor compartment is represented explicitly with a Krogh cylinder model. The small molecule metabolite for T-DM1 is relatively hydrophilic, resulting in little bystander effect within the tissue(3), so the diffusion of the metabolite was not simulated. The metabolite is represented by the green arrows.

The tumor distribution of antibody and small molecule drug is a function of the dose, DAR, systemic clearance, and in vivo kinetics (such as deconjugation depending on the linker(50, 51)). To capture the impact of the antibody dose relative to small molecule delivery, a constant dose of T-DM1-AF680 was given with increasing doses of trastuzumab. This could represent a constant small molecule dose while decreasing the DAR (assuming both free antibody and ADC behave similarly as seen with T-DM1(51)), the impact of deconjugation and free antibody accumulation in the plasma, or an intentional effort to increase antibody tissue penetration by competing for available antigen. Figure 2 shows that the clinical dose of T-DM1-AF680 (3.6 mg/kg) is highly heterogeneous in NCI-N87 tumor xenografts. Supplemental figures S7 and S8 show that the plasma clearance and tumor distribution of unlabeled T-DM1 and T-DM1-AF680 are similar. Co-administration of trastuzumab at a 3:1 or 8:1 ratio dramatically increases penetration of T-DM1 by competing for receptor sites within the tissue. These results also agree with literature reports where increasing the antibody dose results in more homogeneous distribution throughout the tumor(34, 40, 52).

An external file that holds a picture, illustration, etc. Object name is nihms798086f2.jpg

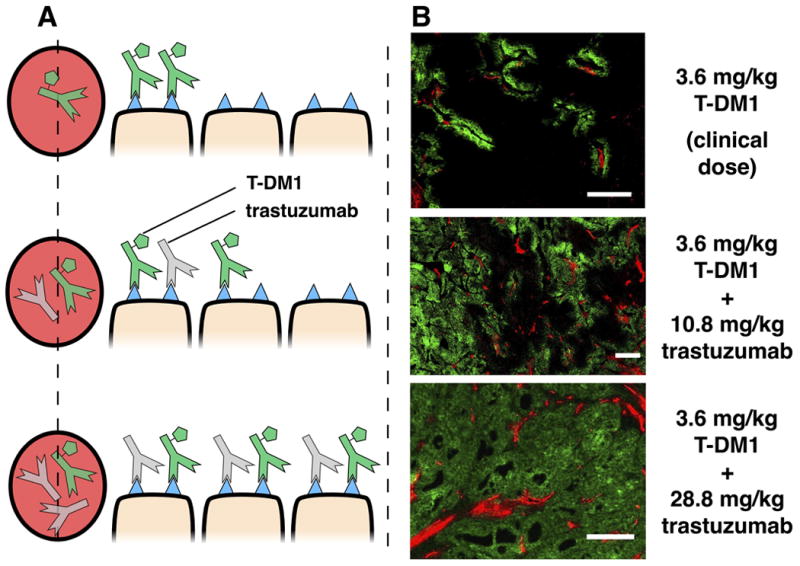
Heterogeneous ADC distribution. A, graphic depiction of T-DM1 tumor distribution with co-administration of trastuzumab. Without a carrier dose of trastuzumab, tumor distribution of T-DM1 is perivascular. Co-administration of T-DM1 with ‘carrier’ doses of trastuzumab (at constant T-DM1 doses) results in significantly more T-DM1 tumor penetration. B, immunofluorescence imaging following co-administration of 3.6 mg/kg of AlexaFluor 680 tagged T-DM1 (green) with trastuzumab at 0:1, 3:1, and 8:1 ratios (0 mg/kg, 10.8 mg/kg, and 28.8 mg/kg unlabeled trastuzumab, respectively). Immunofluorescence staining with CD31-AF555 (red) shows tumor vasculature. Window leveling of images is different. Scale bar = 200 μm.

A PBPK model using a compartmental model for the tumor can accurately capture the average tissue concentration(53), but does not describe the tumoral distribution. The increasing doses of trastuzumab do not significantly impact the average concentration of T-DM1 in the tumor or other organs prior to saturation (Fig. 3), but it dramatically changes the ADC tissue distribution (Fig. 2). The increased penetration lowered the concentration of T-DM1 on each cell (resulting in lower fluorescence intensity per cell) but did not lower the total tumor uptake. The lack of significant binding in other organs results in a minor difference in non-specific distribution (Fig. 3). The molecules co-exist in these tissues but do not interact/compete for binding sites. Because the PBPK portion of the simulation was adapted from a previously published model, the organ concentrations were fit to biodistribution data and plasma clearance (Fig. 3 and S6) using a minimal number of fitted agent-specific parameters for n = 3 mice per dose level, and the fitted parameters are shown in Table 1. For parameter estimates, the 24-hour time point was used for biodistribution studies because this is the approximate time for maximum uptake of trastuzumab and other antibodies(40, 43, 53) along with plasma clearance data out to 72 hours.

An external file that holds a picture, illustration, etc. Object name is nihms798086f3.jpg

PBPK model results and experimental biodistribution data. PBPK model shows systemic distribution of 3.6 mg/kg T-DM1 with trastuzumab at 0:1 (black), 3:1 (red), and 8:1 (blue) ratios (trastuzumab:T-DM1, N=3 mice for each). 0:1 and 3:1 distributions overlap since the tumor is below saturation at these dosing levels. At 8:1 ratio, the dose is slightly above tumor saturation resulting in lower tumor %ID/g and slower clearance. Experimental data shows T-DM1 distribution at 24 hours for the respective ratios; data points were shifted slightly for visibility. The PBPK results are similar despite widely differing distribution seen within the tumors in Fig. 2.

The Krogh cylinder portion of the model was used to predict the tumor tissue distribution following co-administration of trastuzumab and T-DM1 at 0:1, 3:1, and 8:1 ratios (0 mg/kg, 10.8 mg/kg, and 28.8 mg/kg unlabeled trastuzumab, and 3.6 mg/kg T-DM1, respectively)(Fig. 4A). It should be noted that none of the parameters used in this portion of the model were fit to new experimental data but were all taken from literature. The penetration distance increases from strongly perivascular distribution with the 0:1 ratio to homogeneous distribution with the 8:1 ratio while the T-DM1 concentration per cell is reduced. These results agree favorably with all tumors tested (SI Fig. S2-S4). Macroscopic images of a larger tumor region are shown (Fig. 4B) along with a higher magnification of the boxed region. The Krogh cylinder parameters used for all simulations are shown in Table 2.

An external file that holds a picture, illustration, etc. Object name is nihms798086f4.jpg

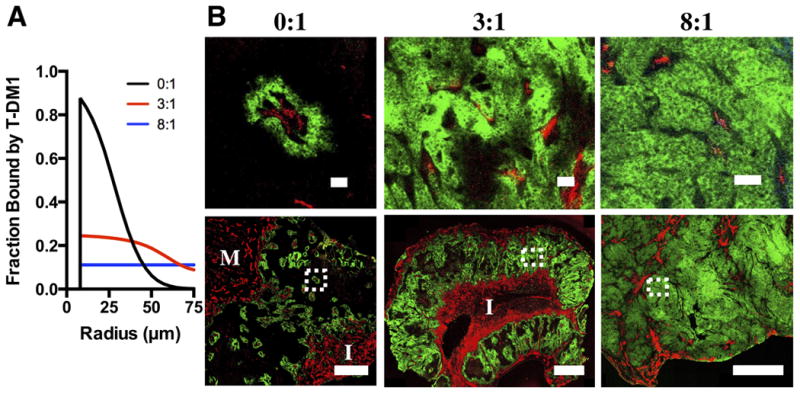
Quantitative Krogh cylinder simulation results and immunofluorescence imaging results. A, model predictions of bound T-DM1 with co-administration of trastuzumab at 0:1, 3:1, and 8:1 ratios 24 hours post injection. B, experimental validation of model predictions. Whole tumor (bottom) and inset (top) T-DM1 (green) distribution following injection of 3.6mg/kg T-DM1 with trastuzumab at 0:1, 3:1, and 8:1 ratios. Immunofluorescence staining with CD31-AF555 (red) shows tumor vasculature. I and M show regions of inflammatory cells and muscle, respectively. Window leveling between different carrier dose images is different. Scale bar = 50 μm (top) and 1 mm (bottom).

The penetration depth of antibodies is a complex function of dose, receptor expression and trafficking, and tumor physiology (permeability, vascular density, etc.). Figure 5 shows the predicted T-DM1 radial distribution as the competitor trastuzumab “carrier” dose is increased. When no carrier dose is added (only T-DM1 from 0 to 3.6 mg/kg total ADC dose), T-DM1 exhibits a perivascular distribution where cells immediately outside the blood vessel are saturated and cells farther away receive almost no ADC. As carrier trastuzumab is added, however, it competes for receptors, allowing T-DM1 to penetrate farther into the tumor, albeit with lower T-DM1 concentration per cell. (Note that higher doses of T-DM1 would also achieve additional penetration, but TDM-1 is limited by toxicity at 4.8 mg/kg(54).) As more carrier dose is added, the carrier dose continues to spread out the ADC distribution until all the binding sites are occupied by trastuzumab or TDM-1. At the theoretical receptor saturating concentration for total antibody, T-DM1 (and trastuzumab) penetrates evenly throughout the tumor. Above this total antibody saturating concentration, the T-DM1 concentration remains homogeneous throughout the tumor. However, the average intra-tumoral T-DM1 concentration starts to drop because the increasing amount of trastuzumab competes for receptors, and there are no additional binding sites deeper in the tissue once saturation is achieved. Importantly, receptor expression (and therefore the saturation dose) can vary significantly between patients and within tumors/metastases. To highlight the relationship between receptor expression, penetration depth, and total antibody dose (ADC plus free antibody), three-dimensional plots of radial concentration versus total dose with different receptor expression are shown in Fig. 5. These simulations were done using a high (1×106 receptors per cell) and moderate (3×105 receptors per cell) HER2 expression level (Fig. 5B and S5), which roughly corresponds to 3+ and 2+ IHC staining(55).

An external file that holds a picture, illustration, etc. Object name is nihms798086f5.jpg

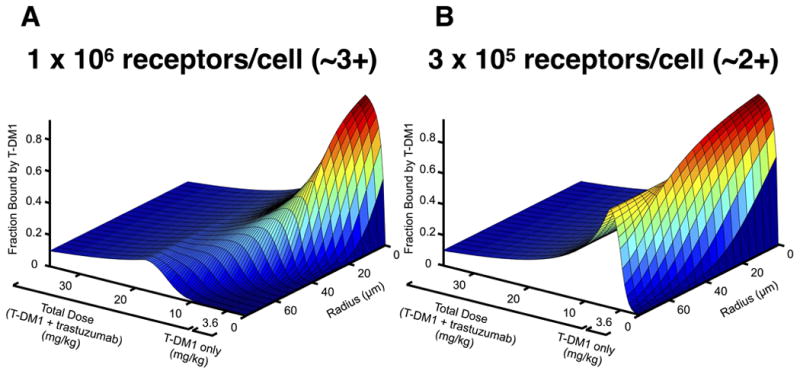
Prediction of T-DM1 distribution versus trastuzumab carrier dose. Predicted perivascular tumor distribution following dosage with T-DM1 and trastuzumab for tumor cells expressing 1 × 106 receptors per cell, A, and 3 × 105 receptors per cell, B, corresponding to ~3+ and ~2+ IHC staining, respectively. From 0 to 3.6 mg/kg total dose only T-DM1 is dosed. After 3.6 mg/kg the T-DM1 dose is kept constant (3.6 mg/kg) and trastuzumab carrier dose is increased.

The antibody penetration depth is also a function of time. Figure S1 shows the radial profile of 3.6 mg/kg T-DM1 along with a 3:1 and 8:1 trastuzumab co-administration. The penetration depth quickly reaches the maximum distance at 24 hrs and then stalls. This is caused by continuous internalization preventing further penetration even as the antibodies continue to extravasate. The longer circulation time of antibodies does not increase the penetration depth due to this constant internalization, making Cmax a critical factor in determining tissue penetration depth(28, 49).

Co-administration of trastuzumab with T-DM1 lowers the average effective DAR since the same amount of small molecule payload is administered with more antibodies. Multiple groups have examined the impact of DAR on plasma clearance and efficacy. Figure 6 highlights the results of several groups (using different ADCs against different targets) where the overall small molecule dose was similar but the DAR and ADC dose was varied. For clarity, only tumor growth curves where there is an equivalent small molecule dose spread over a different ADC dose (and different DAR) are shown. Previous work by several groups has demonstrated the importance of DAR on systemic clearance(56). Two important mechanisms include DAR-dependent clearance and DAR-dependent deconjugation. In DAR-dependent clearance, a high number of small molecule drugs per antibody can increase systemic clearance of the entire antibody-drug conjugate. With DAR-dependent deconjugation, a larger number of small molecule drugs can result in faster loss of the small molecule while the antibody (with a lower DAR or without a payload, i.e. DAR0) remains in circulation. Only a few informative studies have measured the dynamic change of individual DAR species in vivo. Using these studies, we modeled the effective difference in small molecule AUC and divided the results into cases where the antibody exposure, and therefore penetration distance into the tumor, was much higher than the difference in payload exposure (Fig. 6A), and cases where DAR-dependent clearance and/or deconjugation dominated over differences in antibody AUC. Vertical red lines and boxes show the approximate percentage difference between the small molecule payload AUC, typically chosen at a time point when the tumor growth curves begin to diverge. A more detailed description of this analysis can be found in the supplementary data. The results in Figure 6A highlight the fact that at a similar small molecule exposure,/AUC a higher antibody concentration (corresponding to increased tumor penetration) generally has higher efficacy. Individual cells receive less small molecule drug, but the IC50 is lower than the Kd for these agents, so cells within the saturated perivascular region still receive a toxic dose. The lone exception is a paper using a less toxic small molecule, and this is also the only paper where the IC50 is greater than the Kd (see Discussion). These studies provide preliminary (but indirect) evidence that a more homogeneous distribution may result in better ADC efficacy. Caveats are mentioned in the discussion and supplementary data. The studies shown in Figure 6B highlight the importance of DAR-dependent clearance. In Lyon et al. the linker was varied, and significant differences in the clearance were seen with the DAR8 conjugates. The faster clearance ultimately resulted in worse efficacy. Similarly, in Hamblett et al. the higher small molecule exposure resulted in better efficacy; however, the higher antibody dose at the time of maximum uptake in the tumor (predicted to occur approximately 1 day after the ADC was dosed) would result in higher tumor penetration, thereby complicating the interpretation.

An external file that holds a picture, illustration, etc. Object name is nihms798086f6.jpg

Literature review of efficacy with constant small molecule dose but differing DAR and antibody doses. A, at a constant small molecule dose, ADCs with a higher DAR and lower antibody dose (black) are generally less efficacious than ADCs with a lower DAR and higher antibody dose (gray). Blue arrows correspond to six cases where a constant small molecule dose delivered with a higher antibody dose improved efficacy and is predicted to have increased tissue penetration. In one case the reverse was true (green arrow); however, here the small molecule had an IC50 reported to be greater than the KD of the antibody due to a less toxic payload. This would require saturation of cells with a high DAR antibody for efficacy. Red lines and boxes correspond to the estimated difference in small molecule AUC between different DAR/antibody doses using literature reports of DAR-dependent deconjugation and clearance rates in a pharmacokinetic model. The pharmacokinetic analysis is outlined in the supplementary data. B, DAR-dependent clearance can significantly affect the efficacy, making it difficult to parse tumor penetration effects from small molecule AUC.

The increasing trastuzumab doses do not appreciably lower the tumor uptake of T-DM1 (Fig. 7). Because extravasation is the rate-limiting step in antibody uptake(49), T-DM1 molecules that extravasate but are blocked from binding perivascular cells will continue to diffuse deeper in the tissue rather than intravasate and wash out. Eventually they bind to a cell with free receptor. Similar to radiolabelled antibodies(57), only after the tumor is saturated will the %ID/g start to decrease (Fig. 7A).

An external file that holds a picture, illustration, etc. Object name is nihms798086f7.jpg

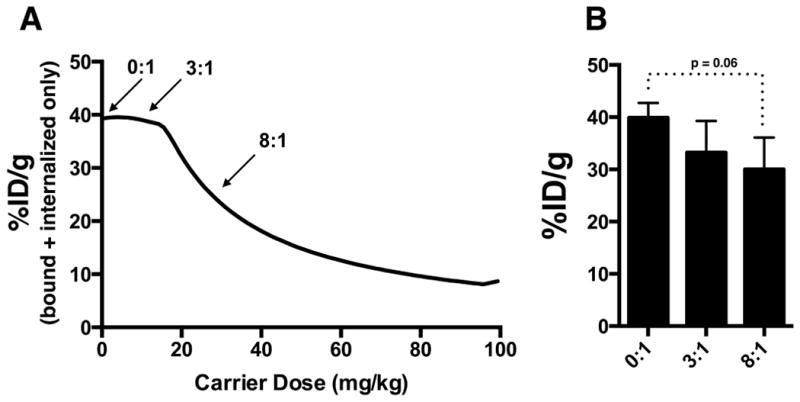
Predicted and experimental impact of carrier dose on total tumor uptake. A, bound and internalized uptake of T-DM1 in tumor with increasing trastuzumab carrier dose. Prior to saturation, the addition of a carrier dose (or equivalently, delivering a constant small molecule dose while lowering the DAR) does not lower total tumor uptake of a constant T-DM1 dose (3.6 mg/kg). It only changes the distribution. B, experimentally measured %ID/g of T-DM1 at respective ratios. Differences of %ID/g were not statistically significant between the 0:1 to 8:1.

In addition to the tumor site, some antigens are expressed in healthy tissue, and this is an important aspect of target-mediated toxicity. The higher vascular density results in homogeneous ADC distribution that can be accurately represented with a compartmental model. If the healthy tissue is saturated with ADC (which is likely given higher vascularization and often lower receptor expression), the co-administration of free antibody will lower the ADC uptake in this healthy tissue (Fig. 8) while having insignificant (p = 0.06) impact on tumor uptake (Fig. 7). This could potentially increase the therapeutic window provided the carrier dose has a neutral or positive impact on tumor efficacy due to increased drug penetration.

An external file that holds a picture, illustration, etc. Object name is nihms798086f8.jpg

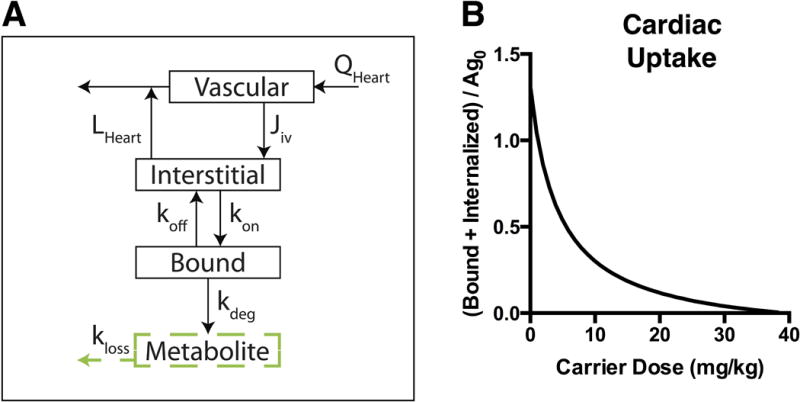
Impact of carrier dose/DAR on healthy tissue targeting. A, graphic depiction of specific binding added to the heart organ compartment. A bound compartment was added to represent the low levels of HER2 antigen expressed in the heart. B, Bound and internalized T-DM1 (constant 3.6 mg/kg dose) in heart compartment with increasing trastuzumab carrier dose shows lower healthy tissue uptake with a carrier dose or lower DAR. The y-axis is normalized to initial unbound antigen in heart.

Discussion

Antibody drug conjugates display complex pharmacokinetics at multiple scales: systemic clearance as a function of DAR and deconjugation, organ heterogeneity from specific and non-specific processes, tumor tissue heterogeneity due to target binding, and cellular/subcellular kinetics of endosomal escape and bystander effects. Here we present a novel pharmacokinetic model for antibody biodistribution where a mechanistic Krogh cylinder geometry tissue based model is integrated into a PBPK framework (Fig. 1). We show theoretically and experimentally that the tumor distribution of T-DM1 in NCI-N87 xenografts at clinical doses is highly heterogeneous, and that co-administration of trastuzumab effectively spreads out T-DM1 homogeneously throughout the tumor (Fig. 2, ​,4).4). Importantly, a compartmental treatment of the tumor would show similar average uptake of the ADC with and without the co-administration of trastuzumab but would not be able to discern any impact on distribution. The combined model accurately captures the similar average organ uptake but drastic differences in tumor heterogeneity (Fig. 2, ​,3,3, and ​and44).

To highlight the importance of the integrated tissue distribution model, we showed how co-administration of T-DM1 with trastuzumab results in a significantly different tumor distribution with a similar systemic distribution. At the clinical dosage level of T-DM1 (3.6 mg/kg), the tumor distribution was perivascular with limited penetration, similar to trastuzumab(40). Adding a carrier dose of trastuzumab at a 3:1 ratio considerably increased the tumor penetration with limited changes in the overall uptake. The total ADC per cell is lower, but more tumor cells are receiving the therapeutic. Similarly with the 8:1 ratio, although the overall concentration received by the cells is less than the 3:1 ratio, the distribution in the tumor is even more homogeneous. Since the 8:1 dose is close to the theoretical receptor-saturating dose, this resulted in a slight (but not statistically significant, p = 0.06) reduction in total uptake.

Compartmental PBPK models do not take into account the tissue-scale distribution of antibodies or ADCs. The integrated tissue model based on the Krogh cylinder, however, uses a systems approach based on the physicochemical properties of the ADC to predict tissue distribution. Although the combined model presented here is not purely predictive because several agent-specific PBPK parameters were fit to experimental data, the Krogh cylinder portion of the model only requires the systemic concentration as input since published parameter correlations are available for the other values(19, 27, 36). Importantly, the mechanistic tissue model gives the ability to easily change simulation parameters based on the specific therapeutic or target (Fig. 5). These simulations were based on literature parameters for trastuzumab/T-DM1 binding affinity, antibody diffusivity/permeability, NCI-N87 receptor expression, and HER2 receptor kinetics. However, these parameters are often measured for other therapeutics and targets, giving the model broad applicability.

It has been known for some time that antibody distribution in tumors is heterogeneous(58), saturating doses are required to obtain even distribution(34), and very high doses are required to saturate tumors in the clinic(59, 60). Many monoclonal antibodies for solid tumors are given frequently (often weekly) at relatively high doses (2-15 mg/kg), making it possible to approach tumor saturation. However, the potency of the small molecule payload often limits the dose and frequency of administration with ADCs. This limitation on dose and frequency, combined with current ADCs that often use high affinity antibodies, potent payloads, and highly expressed targets, can result in subsaturating (and therefore heterogeneous) distribution as we have shown when dosing T-DM1 at the clinical dosage (Fig. 2, ​,4,4, and S2). The importance of heterogeneity on therapeutic efficacy of antibodies and ADCs is still debated. The choice of model could implicitly bias the data interpretation (popularly phrased by Maslov's hammer). Examining the systemic clearance or deconjugation will focus on the impact these mechanisms have on efficacy. Likewise, measuring the tissue level heterogeneity will center the discussion on the impact of tumor distribution. By including both systemic and tissue level effects, the relative contribution of each can be quantified with this model and corresponding experiments.

We conducted an extensive literature search to determine if there is potential evidence of heterogeneity impacting ADC efficacy. Importantly, it depends on the toxicity of the payload. If receptor saturation with an ADC is required for cell death, then spreading out the ADC using a carrier dose may lower efficacy due to a subsaturating number of ADCs delivered per cell (a potency limitation). Conversely, if the ADC is toxic to cells at subsaturating concentrations, then heterogeneous delivery results in more drug being delivered to perivascular cells (“overkill”) while other cells receive no treatment (a delivery limitation). In this case, a more uniform distribution would benefit efficacy by using the ‘excess’ ADC to reach and kill more cells. This is counter-intuitive, where the most potent drug is often pursued during development, but considering the tumor heterogeneity and high toxicity of the payloads, is possible. Looking at in vitro cell killing curves, the toxic payloads, high expression levels, and efficient internalization often result in IC50 values well below the antibody Kd, indicating they are toxic at subsaturating concentrations(61, 62). To demonstrate that heterogeneity is having an impact on efficacy, the same payload must be delivered with varying heterogeneity to isolate and quantify the influence of heterogeneity on efficacy. One set of data available for this analysis are studies manipulating the DAR and dose. For example, an antibody with half the DAR but twice the antibody dose will deliver approximately the same small molecule payload to the tumor but spread out over twice the number of cells (assuming the plasma clearance and/or deconjugation of different DAR ADCs are similar). Several studies were identified that fit these criteria.

In the study by Hamblett et al. the effects of differing DAR and ADC dose to tumor killing was examined(63). When keeping the overall small molecule dosage the same (e.g. antibodies with a DAR of 2, and 4 dosed at 1, and 0.5 mg/kg, respectively), they found the best clinical response with the highest antibody dose, or the dosage that would penetrate into the tumor the farthest. Similarly, Junutula et al. examined the efficacy of ADCs with DARs of 1.6 and 3.1(64) and found the same pattern. They also showed that for the same antibody dose (but different DAR) the outcome was not significantly different, despite having different small molecule exposure. (Simulations show that this would deliver more small molecule to cells that are already receiving a toxic dose.) In another study with a different ADC and target Junutula and colleagues again showed that when keeping the small molecule dose the same, a significantly better outcome was seen with higher antibody doses(65). Jackson et al. did not find a difference in efficacy between DAR2 and DAR3.8 when the antibody dose was the same (which would reach the same number of cells) but observed much higher efficacy when the same small molecule dose was delivered with a higher antibody dose(62). A recent study by Pillow et al. (66) examined the efficacy of different DARs of THIOMAB conjugates, and they found that DAR2 conjugates dosed at 10mg/kg were more efficacious than DAR4 conjugates dosed at 5mg/kg. In other words, having higher drug loading per antibody did not improve efficacy, and correspondingly, when injecting the same dose of small molecule, the drug spread out over more antibodies is more efficacious. In contrast to these other 6 examples (blue arrows, Fig. 6), Goldenberg et al. found that with a low potency payload, a high DAR was needed.

To summarize the above results, we identified 6 publications with data suitable for analysis(62-67). Intriguingly, 5 of the 6 results showed higher efficacy with a lower DAR, where the same small molecule drug delivered with a larger antibody dose (due to lower DAR) resulted in reduced tumor growth (Fig. 6). Most of the cell lines used in these studies were also resistant to the free antibody therapy, indicating the higher antibody dose alone is not responsible for the effect. Upon closer inspection, the sole exception (Goldenberg et al. (67)) used a lower potency drug (SN-38 versus maytansinoids) with moderately lower expression (~105 receptors/cell versus ~106). Notably, the IC50 values for this ADC (range 1-33 nM, median 2 nM) were higher than the Kd of the antibody (0.564 nM). This is also consistent with the “overkill” hypothesis, where agents that require saturation for cell killing would not significantly benefit from a more even distribution, as this lowers the efficacy of all targeted cells. From a tissue penetration standpoint, matching the IC50 to the Kd of the ADC by lowering the DAR would be ideal. If the small molecule drug is dose-limiting, this maximizes the antibody dose to achieve maximum penetration while maintaining a toxic dose for the targeted cells. This also maximizes other mechanisms of action, such as cell-signaling disruption(68) and Fc-effector functions(69) compared to other strategies for increased penetration (such as lower affinity(70-72)). The model described here can help design experiments to determine if this strategy is effective in preclinical models.

DAR-dependent clearance and/or DAR-dependent deconjugation that significantly lowered the payload AUC/delivery could potentially explain the higher efficacy of lower DAR molecules. To quantify any impact of DAR-dependent clearance or DAR-dependent deconjugation, we modeled the small molecule exposure for each case. Details are located in the supplementary data, but pharmacokinetic measurements from each study were used to estimate the small molecule exposure. Since a detailed study of deconjugation or DAR-dependent clearance was not performed in all cases, we combined data from related studies to model the impact on small molecule AUC from deconjugation (unless data were presented showing deconjugation was negligible) or DAR-dependent clearance. The studies in Fig. 6A had a small difference in small molecule AUC (<25% and in most cases, <10%) relative to the large difference in antibody exposure (~100% or greater). On the contrary, the results in 6B showed a much larger difference in small molecule AUC (200-300%) relative to antibody exposure. Compared to the Lyon et al. paper, the studies in 6A showed a larger difference in tumor efficacy despite drastically lower differences in payload AUC, indicating systemic clearance is unlikely to explain the differences in efficacy in 6A. It is also worth noting that the Goldenberg et al. paper shows the exact opposite trend that one would expect if DAR-dependent clearance or deconjugation were playing a role but is consistent with a potency-limited (versus a distribution-limited) ADC.

This analysis is not proof that antibody penetration is the only element (or even a dominant factor) in determining efficacy. For example, the relative contribution between more efficient small molecule distribution versus higher tumor antibody levels is unknown, although most cell lines were resistant to unconjugated antibody. However, the lack of quantitative models in the literature between DAR-dependent clearance/deconjugation versus tumor tissue heterogeneity makes it difficult to draw strong conclusions about the relative contributions of these phenomena. Clearly, DAR-dependent clearance and deconjugation are important, both for tumor exposure and potential toxicity. Lyon et al. showed ADCs having the same DAR but different clearance rates have proven the importance of plasma clearance on efficacy(56). While not proof, these 6 papers are consistent with heterogeneity impacting efficacy. A more detailed discussion on the impact of heterogeneity impacting efficacy is provided with the supplemental data. The effect of individual tumor cell death on the eradication of the tumor is complex(73-75). The model developed here, by accounting for both systemic factors (like plasma clearance and linker stability) and tumor tissue heterogeneity, will be able to quantitatively examine the impact of both to design more efficient clinical agents.

Besides ADC distribution, the PBPK model can help track secondary tissue toxicity. Because ADCs have higher toxicity caused by the small molecule drug, it is important to track their accumulation in healthy tissue. For example, trastuzumab and T-DM1 are both known to exhibit some cardiac toxicity because of low HER2 expression in the heart(76). By increasing the trastuzumab carrier dose in these simulations the overall cardiac uptake of the ADC is lowered. In this case both the antibody and ADC show toxicity but for other possible targets, co-dosing with the unconjugated antibody could result in less overall toxicity to healthy tissue. Similarly, Boswell et al. showed that the intestines were acting as an antigen sink when dosing the ADC anti-TENB2-MMAE; however, co-administration of an anti-TENB2 antibody with the anti-TENB2-MMAE ADC significantly reduced ADC uptake in the intestines(77). These approaches are analogous to ‘cold’ dosing prior to radiolabelled antibody distribution(78). Although some unconjugated antibodies in the clinic are given at high doses, such as bevacizumab (15 mg/kg) or IVIG (multiple grams per kg), it is important to consider that co-administration of the naked antibody at 3 to 8 times the ADC dose could reach dose-limiting toxicities in the clinic. However, antibodies such as trastuzumab are well-tolerated even when delivering 18 mg/kg over a 3 week period(79).

There are a couple important model limitations. First, the pharmacodynamics of the therapeutic can affect the pharmacokinetics of delivery in the tumor. This coupling of PK and PD makes simulations of efficacy very challenging. For example, it has been reported that trastuzumab may result in vascular normalization(73), which can increase the functional vascular density in the tumor and lower the permeability of the vessels by making them less ‘leaky.’ Increasing the vascular density would result in a smaller Krogh cylinder radius in the model resulting in less carrier antibody needed for saturation. Since antibodies are extravasation/permeability limited, a decrease in the membrane permeability would result in less antibody extravasating out of the vessel(74). Additionally, vascular collapse and/or revascularization of areas (particularly during the 3 weeks between clinical treatment with T-DM1, for example) are difficult to predict. The second limitation is the impact of bystander effects. For T-DM1, the more hydrophilic nature of the metabolite results in few bystander effects (relative to more lipophilic conjugates that can diffuse out of the original targeted cell(80) or from the interstitium(81) and into a local cell(3)). Cytosolic access of hydrophilic metabolites may even require transporters within the target cell for toxicity(82). Bystander effects from more lipophilic payloads such as MMAE may explain why higher DAR can improve efficacy with the same antibody dose (e.g. (83)), while in the examples above with a hydrophilic payload, it had little benefit. The diffusion of the metabolite in the tissue could be incorporated into this model to predict the additional penetration of the metabolite into tumor tissue as a function of lipophilicity(36) and whether this reaches therapeutic concentrations far from the original site of antibody degradation. Finally, a recent study by Müller et al. showed that effector functions of T-DM1 (and not trastuzumab) could activate the immune system, where T-DM1 increased tumor vulnerability to immune attack(84). Modeling these complex immune interactions is difficult, but the simulations can help design experiments to test the overall impact on efficacy.

Conclusion

In conclusion, the multi-scale PBPK-Krogh cylinder model is able to track both the systemic and tissue scale distributions of antibodies and ADCs. We show that at clinical doses T-DM1 exhibits a heterogeneous perivascular distribution and through co-administration of trastuzumab the effective DAR is lowered and a homogeneous distribution is achieved. Modeling both the systemic and tissue level distribution can provide a facile method to facilitate ADC development by quantitatively combining complex factors such as target, linker stability, DAR, small molecule, and antibody backbone and their impact on efficacy.

Supplementary Material

Supplementary Information

Acknowledgments

The authors wish to thank John Rhoden, PhD, for helpful comments in the preparation of the manuscript. Funding for this work was provided by Eli Lilly and Company. Additional support was provided by the National Cancer Institute of the National Institutes of Health under award number P30CA046592.

References

1. Shen BQ, Xu K, Liu L, Raab H, Bhakta S, Kenrick M, et al. Conjugation site modulates the in vivo stability and therapeutic activity of antibody-drug conjugates. Nat Biotechnol. 2012 Feb;30(2):184–9. [Abstract] [Google Scholar]
2. Lyon RP, Setter JR, Bovee TD, Doronina SO, Hunter JH, Anderson ME, et al. Self-hydrolyzing maleimides improve the stability and pharmacological properties of antibody-drug conjugates. Nat Biotechnol. 2014 Oct;32(10):1059–62. [Abstract] [Google Scholar]
3. Erickson HK, Park PU, Widdison WC, Kovtun YV, Garrett LM, Hoffman K, et al. Antibody-maytansinoid conjugates are activated in targeted cancer cells by lysosomal degradation and linker-dependent intracellular processing. Cancer Res. 2006 Apr 15;66(8):4426–33. [Abstract] [Google Scholar]
4. Wu AM, Senter PD. Arming antibodies: prospects and challenges for immunoconjugates. Nature Biotechnology. 2005 Sep;23(9):1137–46. [Abstract] [Google Scholar]
5. Panowksi S, Bhakta S, Raab H, Polakis P, Junutula JR. Site-specific antibody drug conjugates for cancer therapy. MAbs. 2014 Jan-Feb;6(1):34–45. [Europe PMC free article] [Abstract] [Google Scholar]
6. Beck A, Reichert JM. Antibody-drug conjugates present and future. mAbs. 2014;6:15–7. [Europe PMC free article] [Abstract] [Google Scholar]
7. Mullard A. Maturing antibody-drug conjugate pipeline hits 30. Nature reviews Drug discovery. 2013;12:329–32. [Abstract] [Google Scholar]
8. Baxter L, Zhu H, Mackensen D, Butler W, Jain RK. Biodistribution of Monoclonal Antibodies: Scale-up from Mouse to Human Using a Physiologically Based Pharmacokinetic Model. Cancer Research. 1995;55:4611–22. [Abstract] [Google Scholar]
9. Baxter L, Zhu H, Mackensen D, Jain RK. Physiologically Based Pharmacokinetic Model for Specific and Nonspecific Monoclonal Antibodies and Fragments in Normal Tissues and Human Tumor Xenografts in Nude Mice. Cancer Research. 1994;54:1517–28. [Abstract] [Google Scholar]
10. Davda JP, Jain M, Batra SK, Gwilt PR, Robinson DH. A physiologically based pharmacokinetic (PBPK) model to characterize and predict the disposition of monoclonal antibody CC49 and its single chain Fv constructs. Int Immunopharmacol. 2008 Mar;8(3):401–13. [Abstract] [Google Scholar]
11. Garg A, Balthasar JP. Physiologically-based pharmacokinetic (PBPK) model to predict IgG tissue kinetics in wild-type and FcRn-knockout mice. J Pharmacokinet Pharmacodyn. 2007 Oct;34(5):687–709. English. [Abstract] [Google Scholar]
12. Nestorov I. Whole Body Pharmacokinetic Models. Clin Pharmacokinet. 2003;42(10):883–908. [Abstract] [Google Scholar]
13. Rowland M, Peck C, Tucker G. Physiologically-Based Pharmacokinetics in Drug Development and Regulatory Science. In: Cho AK, editor. Annual Review of Pharmacology and Toxicology. 2011;51:45–73. Annual Review of Pharmacology and Toxicology. 51. Palo Alto: Annual Reviews; 2011. [Abstract] [Google Scholar]
14. Shah DK, Betts AM. Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. J Pharmacokinet Pharmacodyn. 2012 Feb;39(1):67–86. [Abstract] [Google Scholar]
15. Germani M, Crivori P, Rocchetti M, Burton PS, Wilson AGE, Smith ME, et al. Evaluation of a basic physiologically based pharmacokinetic model for simulating the first-time-in-animal study. Eur J Pharm Sci. 2007 Jul;31(3-4):190–201. English. [Abstract] [Google Scholar]
16. Poulin P, Chen YH, Ding X, Gould SE, Hop CE, Messick K, et al. Prediction of drug distribution in subcutaneous xenografts of human tumor cell lines and healthy tissues in mouse: application of the tissue composition-based model to antineoplastic drugs. J Pharm Sci. 2015 Apr;104(4):1508–21. [Abstract] [Google Scholar]
17. Poulin P, Theil FP. Prediction of pharmacokinetics prior to in vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. Journal of Pharmaceutical Sciences. 2002 May;91(5):1358–70. English. [Abstract] [Google Scholar]
18. Li Z, Krippendorff BF, Sharma S, Walz AC, Lave T, Shah DK. Influence of molecular size on tissue distribution of antibody fragments. MAbs. 2016 Jan 2;8(1):113–9. [Europe PMC free article] [Abstract] [Google Scholar]
19. Schmidt MM, Wittrup KD. A modeling analysis of the effects of molecular size and binding affinity on tumor targeting. Molecular Cancer Therapeutics. 2009;8(10):2861. [Europe PMC free article] [Abstract] [Google Scholar]
20. Ferl GZ, Wu AM, DiStefano JJ. A predictive model of therapeutic monoclonal antibody dynamics and regulation by the neonatal Fc receptor (FcRn) Ann Biomed Eng. 2005;33(11):1640–52. [Abstract] [Google Scholar]
21. Fronton L, Pilari S, Huisinga W. Monoclonal antibody disposition: a simplified PBPK model and its implications for the derivation and interpretation of classical compartment models. J Pharmacokinet Pharmacodyn. 2014 Apr;41(2):87–107. [Abstract] [Google Scholar]
22. Krogh A. The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. Journal of Physiology. 1919;52(6):409–15. [Abstract] [Google Scholar]
23. Levitt DG. Capillary-Tissue Exchange Kinetics - Analysis of Krogh Cylinder Model. Journal of Theoretical Biology. 1972;34(1):103. &. English. [Abstract] [Google Scholar]
24. Tepper RS, Lee HL, Lightfoot EN. TRANSIENT CONVECTIVE MASS-TRANSFER IN KROGH TISSUE CYLINDERS. Annals of Biomedical Engineering. 1978;6(4):506–30. English. [Abstract] [Google Scholar]
25. Baxter LT, Jain RK. Transport of Fluid and Macromolecules in Tumors: 4. A Microscopic Model of the Perivascular Distribution. Microvasc Res. 1991 Mar;41(2):252–72. [Abstract] [Google Scholar]
26. Shorten PR, McMahon CD, Soboleva TK. Insulin transport within skeletal muscle transverse tubule networks. Biophys J. 2007 Nov;93(9):3001–7. English. [Europe PMC free article] [Abstract] [Google Scholar]
27. Thurber GM, Weissleder R. A Systems Approach for Tumor Pharmacokinetics. PLoS One. 2011;6(9):e24696. [Europe PMC free article] [Abstract] [Google Scholar]
28. Thurber GM, Zajic SC, Wittrup KD. Theoretic criteria for antibody penetration into solid tumors and micrometastases. J Nucl Med. 2007 Jun;48(6):995–9. [Abstract] [Google Scholar]
29. Venkatasubramanian R, Arenas RB, Henson MA, Forbes NS. Mechanistic modelling of dynamic MRI data predicts that tumour heterogeneity decreases therapeutic response. British Journal of Cancer. 2010 Aug;103(4):486–97. [Europe PMC free article] [Abstract] [Google Scholar]
30. Eikenberry S. A tumor cord model for Doxorubicin delivery and dose optimization in solid tumors. Theoretical Biology and Medical Modelling. 2009 Aug;6:20. English. [Europe PMC free article] [Abstract] [Google Scholar]
31. Bertuzzi A, Fasano A, Gandolfi A, Sinisgalli C. In: Tumour Cords and Their Response to Anticancer Agents. Bellomo N, Chaplain M, DeAngelis E, editors. Birkhauser Boston, 675 Massachusetts Ave, Cambridge, Ma 02139-2333 USA: 2008. pp. 183–206. [Google Scholar]
32. Shah DK, Haddish-Berhane N, Betts A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model: a case study with brentuximab-vedotin. J Pharmacokinet Pharmacodyn. 2012 Dec;39(6):643–59. [Abstract] [Google Scholar]
33. Vasalou C, Helmlinger G, Gomes B. A mechanistic tumor penetration model to guide antibody drug conjugate design. PLoS One. 2015;10(3):e0118977. [Europe PMC free article] [Abstract] [Google Scholar]
34. Blumenthal RD, Fand I, Sharkey RM, Boerman OC, Kashi R, Goldenberg DM. The Effect of Antibody Protein Dose on the Uniformity of Tumor Distribution of Radioantibodies - an Autoradiographic Study. Cancer Immunol Immunother. 1991 Aug;33(6):351–8. [Europe PMC free article] [Abstract] [Google Scholar]
35. Fujimori K, Covell DG, Fletcher JE, Weinstein JN. A modeling analysis of monoclonal antibody percolation through tumors: a binding-site barrier. Journal of nuclear medicine : official publication, Society of Nuclear Medicine. 1990 Jul;31(7):1191–8. eng. [Abstract] [Google Scholar]
36. Bhatnagar S, Deschenes E, Liao J, Cilliers C, Thurber GM. Multichannel Imaging to Quantify Four Classes of Pharmacokinetic Distribution in Tumors. J Pharm Sci. 2014 Jul 21;103(10):3276–86. [Europe PMC free article] [Abstract] [Google Scholar]
37. Baxter LT, Jain RK. Transport of Fluid and Macromolecules in Tumors: 2. Role of Heterogeneous Perfusion and Lymphatics. Microvasc Res. 1990;40(2):246–63. [Abstract] [Google Scholar]
38. Wittrup KD, Thurber GM, Schmidt MM, Rhoden JJ. Practical Theoretic Guidance for the Design of Tumor-Targeting Agents. Methods in Enzymology: Protein Engineering for Therapeutics, Vol 203, Pt B. 2012;503:255–68. [Europe PMC free article] [Abstract] [Google Scholar]
39. Cilliers C, Liao J, Atangcho L, Thurber GM. Residualization Rates of Near-Infrared Dyes for the Rational Design of Molecular Imaging Agents. Molecular imaging and biology : MIB : the official publication of the Academy of Molecular Imaging. 2015 Apr 14; [Europe PMC free article] [Abstract] [Google Scholar]
40. Baker J, Lindquist K, Huxham L, Kyle A, Sy J, Minchinton A. Direct Visualization of Heterogeneous Extravascular Distribution of Trastuzumab in Human Epidermal Growth Factor Receptor Type 2 Overexpressing Xenografts. Clinical Cancer Research. 2008;14(7):2171–9. [Abstract] [Google Scholar]
41. Oliveira S, Cohen R, Walsum MS, van Dongen GA, Elias SG, van Diest PJ, et al. A novel method to quantify IRDye800CW fluorescent antibody probes ex vivo in tissue distribution studies. EJNMMI research. 2012;2(1):50. [Europe PMC free article] [Abstract] [Google Scholar]
42. Zhang L, Thurber GM. Quantitative Impact of Plasma Clearance and Down-regulation on GLP-1 Receptor Molecular Imaging. Molecular imaging and biology : MIB : the official publication of the Academy of Molecular Imaging. 2015 Jul 21; [Europe PMC free article] [Abstract] [Google Scholar]
43. Ferl GZ, Kenanova V, Wu AM, DiStefano JJ. A two-tiered physiologically based model for dually labeled single-chain Fv-Fc antibody fragments. 2006 Jun;5(6):1550–8. [Abstract] [Google Scholar]
44. Austin CD, De Maziere AM, Pisacane PI, van Dijk SM, Eigenbrot C, Sliwkowski MX, et al. Endocytosis and sorting of ErbB2 and the site of action of cancer therapeutics trastuzumab and geldanamycin. Mol Biol Cell. 2004 Dec;15(12):5268–82. eng. [Europe PMC free article] [Abstract] [Google Scholar]
45. Levy G. Pharmacologic target-mediated drug disposition. Clinical pharmacology and therapeutics. 1994 Sep;56(3):248–52. eng. [Abstract] [Google Scholar]
46. Mager DE, Jusko WJ. General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J Pharmacokinet Pharmacodyn. 2001 Dec;28(6):507–32. eng. [Abstract] [Google Scholar]
47. Mager DE. Target-mediated drug disposition and dynamics. Biochemical Pharmacology. 2006 Jun 28;72(1):1–10. [Abstract] [Google Scholar]
48. Singh AP, Shin YG, Shah DK. Application of Pharmacokinetic-Pharmacodynamic Modeling and Simulation for Antibody-Drug Conjugate Development. Pharm Res. 2015 Feb 11; [Abstract] [Google Scholar]
49. Thurber GM, Schmidt MM, Wittrup KD. Antibody tumor penetration: Transport opposed by systemic and antigen-mediated clearance. Adv Drug Deliv Rev. 2008 Sep;60(12):1421–34. English. [Europe PMC free article] [Abstract] [Google Scholar]
50. Sukumaran S, Gadkar K, Zhang C, Bhakta S, Liu L, Xu K, et al. Mechanism-Based Pharmacokinetic/Pharmacodynamic Model for THIOMAB Drug Conjugates. Pharm Res. 2015 Jun;32(6):1884–93. [Abstract] [Google Scholar]
51. Bender B, Leipold DD, Xu K, Shen BQ, Tibbitts J, Friberg LE. A mechanistic pharmacokinetic model elucidating the disposition of trastuzumab emtansine (T-DM1), an antibody-drug conjugate (ADC) for treatment of metastatic breast cancer. The AAPS journal. 2014 Sep;16(5):994–1008. [Europe PMC free article] [Abstract] [Google Scholar]
52. Rhoden JJ, Wittrup KD. Dose dependence of intratumoral perivascular distribution of monoclonal antibodies. J Pharm Sci. 2012 Feb;101(2):860–7. [Europe PMC free article] [Abstract] [Google Scholar]
53. Thurber GM, Wittrup KD. A mechanistic compartmental model for total antibody uptake in tumors. Journal of Theoretical Biology. 2012 Dec;314:57–68. English. [Europe PMC free article] [Abstract] [Google Scholar]
54. Krop IE, Beeram M, Modi S, Jones SF, Holden SN, Yu W, et al. Phase I study of trastuzumab-DM1, an HER2 antibody-drug conjugate, given every 3 weeks to patients with HER2-positive metastatic breast cancer. Journal of clinical oncology : official journal of the American Society of Clinical Oncology. 2010 Jun 1;28(16):2698–704. [Abstract] [Google Scholar]
55. McLarty K, Cornelissen B, Scollard DA, Done SJ, Chun K, Reilly RM. Associations between the uptake of In-111-DTPA-trastuzumab, HER2 density and response to trastuzumab (Herceptin) in athymic mice bearing subcutaneous human tumour xenografts. Eur J Nucl Med Mol Imaging. 2009 Jan;36(1):81–93. English. [Abstract] [Google Scholar]
56. Lyon RP, Bovee TD, Doronina SO, Burke PJ, Hunter JH, Neff-LaFord HD, et al. Reducing hydrophobicity of homogeneous antibody-drug conjugates improves pharmacokinetics and therapeutic index. Nat Biotechnol. 2015 Jul;33(7):733–5. [Abstract] [Google Scholar]
57. Koppe E, Soede AC, Pels W, Oyen WJG, Goldenberg DM, Bleichrodt RP, et al. Experimental radioimmunotherapy of small peritoneal metastases of colorectal origin. Int J Cancer. 2003 Oct 10;106(6):965–72. [Abstract] [Google Scholar]
58. Fujimori K, Covell D, Fletcher J, Weinstein J. Modeling Analysis of the Global and Microscopic Distribution of Immunoglobulin G, F(ab')2, and Fab in Tumors. Cancer Research. 1989;49:5656–63. [Abstract] [Google Scholar]
59. Fenwick J, Philpott G, Connett J. Biodistribution and histological localization of anti-human colon cancer monoclonal antibody (MAb) 1A3: the influence of administered MAb dose on tumor uptake. Int J Cancer. 1989;44:1017–27. [Abstract] [Google Scholar]
60. Schroff R, Morgan A, Woodhouse C, Abrams P, Farrell M, Carpenter B, et al. Monoclonal Antibody Therapy in Malignant Melanoma: Factors Effecting In Vivo Localization. Journal of Biological Response Modifiers. 1987;6:457–72. [Abstract] [Google Scholar]
61. Lewis Phillips GD, Li G, Dugger DL, Crocker LM, Parsons KL, Mai E, et al. Targeting HER2-positive breast cancer with trastuzumab-DM1, an antibody-cytotoxic drug conjugate. Cancer Res. 2008 Nov 15;68(22):9280–90. [Abstract] [Google Scholar]
62. Jackson D, Atkinson J, Guevara CI, Zhang C, Kery V, Moon SJ, et al. In vitro and in vivo evaluation of cysteine and site specific conjugated herceptin antibody-drug conjugates. PLoS One. 2014;9(1):e83865. [Europe PMC free article] [Abstract] [Google Scholar]
63. Hamblett KJ, Senter PD, Chace DF, Sun MMC, Lenox J, Cerveny CG, et al. Effects of Drug Loading on the Antitumor Activity of a Monoclonal Antibody Drug Conjugate. Clin Cancer Res. 2004;10(20):7063–70. 2004 October 15. [Abstract] [Google Scholar]
64. Junutula JRJR, Raab H, Clark S, Bhakta S, Leipold DDD, Weir S, et al. Site-specific conjugation of a cytotoxic drug to an antibody improves the therapeutic index. Nat Biotechnol. 2008;26:925–32. [Abstract] [Google Scholar]
65. Junutula JR, Flagella KM, Graham RA, Parsons KL, Ha E, Raab H, et al. Engineered thio-trastuzumab-DM1 conjugate with an improved therapeutic index to target human epidermal growth factor receptor 2-positive breast cancer. Clin Cancer Res. 2010;16:4769–78. [Abstract] [Google Scholar]
66. Pillow TH, Tien J, Parsons-Reponte KL, Bhakta S, Li H, Staben LR, et al. Site-specific trastuzumab maytansinoid antibody-drug conjugates with improved therapeutic activity through linker and antibody engineering. J Med Chem. 2014 Oct 9;57(19):7890–9. [Abstract] [Google Scholar]
67. Goldenberg DM, Cardillo TM, Govindan SV, Rossi EA, Sharkey RM. Trop-2 is a novel target for solid cancer therapy with sacituzumab govitecan (IMMU-132), an antibody-drug conjugate (ADC) Oncotarget. 2015 Sep 8;6(26):22496–512. [Europe PMC free article] [Abstract] [Google Scholar]
68. Schoeberl B, Eichler-Jonsson C, Gilles ED, Muller G. Computational modeling of the dynamics of the MAP kinase cascade activated by surface and internalized EGF receptors. Nature Biotechnology. 2002 Apr;20(4):370–5. [Abstract] [Google Scholar]
69. Tang Y, Lou J, Alpaugh RK, Robinson MK, Marks JD, Weiner LM. Regulation of antibody-dependent cellular cytotoxicity by IgG intrinsic and apparent affinity for target antigen. 2007 Sep 1;179(5):2815–23. [Abstract] [Google Scholar]
70. Adams G, Schier R, McCall A, Simmons H, Horak E, Alpaugh K, et al. High Affinity Restricts the Localization and Tumor Penetration of Single-Chain Fv Antibody Molecules. Cancer Research. 2001;61:4750–5. [Abstract] [Google Scholar]
71. Rudnick SI, Lou JL, Shaller CC, Tang Y, Klein-Szanto AJP, Weiner LM, et al. Influence of Affinity and Antigen Internalization on the Uptake and Penetration of Anti-HER2 Antibodies in Solid Tumors. Cancer Research. 2011 Mar;71(6):2250–9. English. [Europe PMC free article] [Abstract] [Google Scholar]
72. Thurber GM, Wittrup KD. Quantitative spatiotemporal analysis of antibody fragment diffusion and endocytic consumption in tumor spheroids. Cancer Research. 2008;68:3334–41. [Europe PMC free article] [Abstract] [Google Scholar]
73. Izumi Y, Xu L, di Tomaso E, Fukumura D, Jain RK. Tumour biology: herceptin acts as an anti-angiogenic cocktail. Nature. 2002 Mar 21;416(6878):279–80. [Abstract] [Google Scholar]
74. Pastuskovas CV, Mundo EE, Williams SP, Nayak TK, Ho J, Ulufatu S, et al. Effects of anti-VEGF on pharmacokinetics, biodistribution, and tumor penetration of trastuzumab in a preclinical breast cancer model. Mol Cancer Ther. 2012 Mar;11(3):752–62. [Abstract] [Google Scholar]
75. Spector NL, Blackwell KL. Understanding the mechanisms behind trastuzumab therapy for human epidermal growth factor receptor 2-positive breast cancer. Journal of clinical oncology : official journal of the American Society of Clinical Oncology. 2009 Dec 1;27(34):5838–47. [Abstract] [Google Scholar]
76. Ozcelik C, Erdmann B, Pilz B, Wettschureck N, Britsch S, Hubner N, et al. Conditional mutation of the ErbB2 (HER2) receptor in cardiomyocytes leads to dilated cardiomyopathy. Proc Natl Acad Sci U S A. 2002 Jun 25;99(13):8880–5. [Europe PMC free article] [Abstract] [Google Scholar]
77. Boswell CA, Mundo EE, Firestein R, Zhang C, Mao W, Gill H, et al. An integrated approach to identify normal tissue expression of targets for antibody-drug conjugates: case study of TENB2. Br J Pharmacol. 2013 Jan;168(2):445–57. [Europe PMC free article] [Abstract] [Google Scholar]
78. Hernandez M, Knox S. Radiobiology of radioimmunotherapy: targeting CD20 B-cell antigen in non-Hodgkin's lymphoma. Int J Radiat Oncol Biol Phys. 2004;59(5):1274–87. [Abstract] [Google Scholar]
79. Leyland-Jones B, Colomer R, Trudeau ME, Wardley A, Latreille J, Cameron D, et al. Intensive loading dose of trastuzumab achieves higher-than-steady-state serum concentrations and is well tolerated. Journal of clinical oncology : official journal of the American Society of Clinical Oncology. 2010 Feb 20;28(6):960–6. [Abstract] [Google Scholar]
80. Li F, Emmerton KK, Jonas M, Zhang X, Miyamoto JB, Setter JR, et al. Intracellular Released Payload Influences Potency and Bystander-Killing Effects of Antibody-Drug Conjugates in Preclinical Models. Cancer Res. 2016 May 1;76(9):2710–9. [Abstract] [Google Scholar]
81. Perrino E, Steiner M, Krall N, Bernardes GJ, Pretto F, Casi G, et al. Curative properties of noninternalizing antibody-drug conjugates based on maytansinoids. Cancer Res. 2014 May 1;74(9):2569–78. [Abstract] [Google Scholar]
82. Hamblett KJ, Jacob AP, Gurgel JL, Tometsko ME, Rock BM, Patel SK, et al. SLC46A3 Is Required to Transport Catabolites of Noncleavable Antibody Maytansine Conjugates from the Lysosome to the Cytoplasm. Cancer Res. 2015 Dec 15;75(24):5329–40. [Abstract] [Google Scholar]
83. Bryant P, Pabst M, Badescu G, Bird M, McDowell W, Jamieson E, et al. In Vitro and In Vivo Evaluation of Cysteine Rebridged Trastuzumab-MMAE Antibody Drug Conjugates with Defined Drug-to-Antibody Ratios. Mol Pharm. 2015 Jun 1;12(6):1872–9. [Abstract] [Google Scholar]
84. Müller P, Kreuzaler M, Khan T, Thommen DS, Martin K, Glatz K, et al. Trastuzumab emtansine (T-DM1) renders HER2+ breast cancer highly susceptible to CTLA-4/PD-1 blockade. Sci Transl Med. 2015;7:315ra188–315ra188. [Abstract] [Google Scholar]
85. Yuan F, Dellian M, Fukumura D, Leunig M, Berk DA, Torchilin VP, et al. Vascular Permeability in a Human Tumor Xenograft: Molecular Size Dependence and Cutoff Size. Cancer Res 1995 September 1. 1995;55(17):3752–6. [Abstract] [Google Scholar]
86. Bostrom J, Haber L, Koenig P, Kelley RF, Fuh G. High affinity antigen recognition of the dual specific variants of herceptin is entropy-driven in spite of structural plasticity. PLoS One. 2011;6(4):e17887. [Europe PMC free article] [Abstract] [Google Scholar]
87. Jackson TL, Lubkin SR, Siemers NO, Kerr DE, Senter PD, Murray JD. Mathematical and experimental analysis of localization of anti-tumour antibody-enzyme conjugates. Br J Cancer. 1999 Aug;80(11):1747–53. [Europe PMC free article] [Abstract] [Google Scholar]
88. Hilmas D, Gillette E. Morphometric Analyses of the Microvasculature of Tumors During Growth and After X-Irradiation. Cancer. 1974;33:103–10. [Abstract] [Google Scholar]
89. Yamashita-Kashima Y, Shu S, Harada N, Fujimoto-Ouchi K. Enhanced antitumor activity of trastuzumab emtansine (T-DM1) in combination with pertuzumab in a HER2-positive gastric cancer model. Oncology reports. 2013 Sep;30(3):1087–93. [Abstract] [Google Scholar]
90. Green E. Biology of the Laboratory Mouse. New York: Dover Publications & The Jackson Laboratory; 1966. [Google Scholar]

Full text links 

Read article at publisher's site: https://doi.org/10.1208/s12248-016-9940-z

Read article for free, from open access legal sources, via Unpaywall: https://europepmc.org/articles/pmc4996726?pdf=renderUnpaywall

Citations & impact 

Impact metrics

59
Citations
Jump to Citations

Citations of article over time

Alternative metrics

Altmetric item for https://www.altmetric.com/details/8670734
Altmetric
Discover the attention surrounding your research
https://www.altmetric.com/details/8670734

Smart citations by scite.ai
Smart citations by scite.ai include citation statements extracted from the full text of the citing article. The number of the statements may be higher than the number of citations provided by EuropePMC if one paper cites another multiple times or lower if scite has not yet processed some of the citing articles.
Explore citation contexts and check if this article has been supported or disputed.
https://scite.ai/reports/10.1208/s12248-016-9940-z

Supporting
Mentioning
Contrasting
7
100
0

Article citations

Go to all (59) article citations

Data 

Data behind the article

This data has been text mined from the article, or deposited into data resources.

BioStudies: supplemental material and supporting data

Similar Articles 

To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.

Funding 

Funders who supported this work.

NCI NIH HHS (1)