Abstract
Free full text

Ecological metrics and methods for GPS movement data
Abstract
The growing field of movement ecology uses high resolution movement data to analyze animal behavior across multiple scales: from individual foraging decisions to population-level space-use patterns. These analyses contribute to various subfields of ecology—inter alia behavioral, disease, landscape, resource, and wildlife—and facilitate facilitate novel exploration in fields ranging from conservation planning to public health. Despite the growing availability and general accessibility of animal movement data, much potential remains for the analytical methods of movement ecology to be incorporated in all types of geographic analyses. This review provides for the Geographical Information Sciences (GIS) community an overview of the most common movement metrics and methods of analysis employed by animal ecologists. Through illustrative applications, we emphasize the potential for movement analyses to promote transdisciplinary GIS/wildlife-ecology research.
1. Introduction
The study of movement as a sub-discipline within the geographic information sciences is developing rapidly, driven by advances in localization technologies used to collect movement data (Dodge et al. 2016, Yuan 2017). Parallel to this expansion is the emergence of the field of movement ecology, which seeks to answer questions regarding where, how, and why individual animals move, placed within the context of diverse and varying natural environments (Nathan et al. 2008). In movement ecology, the movement pathway of an individual (or a group of individuals) is often the central feature studied.These pathways, considered within the heterogeneous landscapes they cross, expose individuals to various environmental elements that may positively or negatively impact long-term processes like reproduction and survival (Edelhoff et al. 2016). For example, an individual’s movement decisions, moving them toward or away from a resource-rich area, will directly impact their foraging success and, hence, fitness (Getz et al. 2015, 2016). At a broader scale, emergent spatial processes and patterns (e.g. the distribution of resources, disease transmission, and human-wildlife conflict) are all influenced by the movement decisions of animals. In this sub-field of ecology, the rapid technological advances driving data collection are facilitated by a conceptual framework for considering animal movements (the movement ecology paradigm of Nathan et al. 2008) and catalyzed by the development of new metrics and analytical tools.
Where movement ecology has a limited focus and specific ecological applications, research within the GIScience community into the quantitative analysis of movement takes a broader view, and in many cases has developed or adapted similarly powerful methods for the exploration of movement, both with and without specific ecological application. In movement ecology, multiple recent reviews have been written that explore the development of individual analyses or metrics of space use (e.g., home ranges, proximity/social networks, selection functions; see Cumming and Cornélis 2012, Pinter-Wollman et al. 2013, and Lele et al. 2013, respectively). In the same period, several special issues in the GIS community have been published on the topic of quantitative movement analysis and spatial ecology (Skidmore et al. 2011, Laffan et al. 2012, 2014, 2016, Dodge et al. 2016). Despite these domain-specific reviews and broader special issues, an exposition that provides an broad overview of metrics and tools used to analyze animal movement data is still needed. Our intention here is to provide such an exposition by reviewing metrics and methods of analysis that are widely used in the movement ecology field, emphasizing their applications beyond animal ecology into more general geospatial analysis. Throughout, we attempt to highlight similar metrics already adopted or developed by researchers in GISscience and the advances made in the field of movement research more broadly. For the most part, our review will emphasize methods most useful for analyzing high-resolution (also referred to as fine-scale) spatio-temporal location data from GPS tags (on collars, harnesses, or secured by other means), often paired with data from accelerometer, proximity, and physiological (e.g., temperature) sensors. While we acknowledge the significant contribution of additional localization technologies (e.g. acoustic arrays, light-based geolocators, VHF/radio data, ARGOS, and the upcoming ICARUS initiative, as in Pennisi 2011) to the recent expansion of movement research, the metrics developed for these pipelines are, for the most part, outside the scope of this review.
We begin our exposition by organizing movement ecology metrics according to whether they summarize one- (i.e. having only the dimension of length) or two-dimensional (i.e. having the dimensions of area) objects. This approach reflects Smouse et al.’s (2010) dichotomy of statistical analyses of relocation data in terms of Lagrangian methods focusing on discrete-step, time-interval, and turning-angle constructs (i.e., a one-dimensional view of movement pathways) and Eulerian methods focusing on emergent space-use constructs (i.e. a two-dimensional view of movement pathways). Within this dichotomy, we distinguish metrics by whether or not they have an environmental covariate context and whether they pertain to individuals or groups of individuals. The methods we discuss represent the range of questions movement ecologists generally address, from inferring animal behavior to understanding the structure and characteristics of the landscape. The first set of metrics is associated with one-dimensional objects: those metrics intended to derive descriptive statistics from individual movement trajectories and to investigate individual behavioral states across a trajectory. The second set are applied to two-dimensional objects: those meant to describe the frequency with which an individual or multiple individuals occur in a given area or to predict spatial usage patterns for an entire population of a particular species, rather than a single individual. These latter analyses inform researchers about the relationship between landscape structure and animal behavior. Throughout the review, we use data from a single zebra to demonstrate reproducible examples of selected metrics across scales. See Zidon et al. (2017) for details on the zebra population from which these data were collected, as well as Appendix A for specific details on individual AG256, the zebra data used here.
2. Trajectory Analyses
The improvement of modern tracking devices has led to a considerable increase in the amount of movement data available for analysis, specifically in the form of lengthy timeseries of discrete relocations in two or three dimensional space (Tomkiewicz et al. 2010). The level of correspondence between these relocations and the actual movement of the animal will vary, depending on the spatial and temporal resolution of the trajectory, but several metrics can be derived from the path to describe the general, usually statistical, tendencies of individual animals (Table 1).
Table 1.
Path Metrics & Ensuing Methods
| Metrics | Description | Suggested References |
|---|---|---|
| Step size (length) | The displacement between two consecutive coordinate fixes | Calenge et al. 2009, Turchin 1998 |
| Heading (or absolute angle) | The direction of heading relative to some standard (e.g., initial direction, compass North) | Calenge et al. 2009, Turchin 1998 |
| Turning angle | The change in heading from one step to the next | Calenge et al. 2009, Turchin 1998 |
| Displacement | The straight-line distance from the beginning to the end point of a path | Calenge et al. 2009, Turchin 1998 |
| Net squared displacement (NSD) | The square of the straight-line distance between the start of the trajectory and the current location | Calenge et al. 2009, Turchin 1998 |
| Persistence velocity | The speed of movement in the direction of heading | Gurarie et al. 2009 |
| First passage time | The time taken to exit a circle of prescribed radius r from a relocation point at the center of this circle | Fauchald and Tveraa 2003, McKenzie et al. 2009 |
| Straightness index | The ratio of | Benhamou 2004 |
| Tortuosity | The level of convolution in a movement path relative to a straight line | Benhamou 2004 |
| Residence time | The amount of time spent within a selected area | Barraquand and Benhamou 2008 |
| Return time (inter-visit gap) | The amount of time it takes an individual to return to a particular area after its last departure | Lyons et al. 2013 |
| Revisitation (or return) rate | The rate at which an individual returns to a particular area, where distinct visits are based on a minimum return time tr | Lyons et al. 2013, Van Moorter et al. 2016 |
| Mean duration | The average amount of time spent per visit over a number of visits to a selected area | Lyons et al. 2013 |
| Time to return | The duration of time between consecutive visits to a selected area | Bar-David et al. 2009 |
| Overall dynamic body acceleration (ODBA) | The sum of the absolute values of three orthogonal locally time-averaged accelerations | Gleiss et al. 2011, Qasem et al. 2012 |
| Behavioral state | Association of one of several discrete modes of behavior with each point on the trajectory | Getz and Saltz 2008 |
| Methods (in the context of movement ecology) | ||
| Cluster analyses | Methods for grouping trajectory points (or segments) that represent the same behavioral state (or syndrome) | Van Moorter et al. 2010 (or Abrahms et al. 2017) |
| Change-point analyses | Methods for detecting points on a trajectory where switches in behavioral states occur | Gurarie et al. 2009 |
| State-space analyses (hidden Markov models) | Methods for detecting underlying behavioral states and estimating state transition probabilities | Patterson et al. 2009 |
| Accelerometry visualization | Using tri-axial accelerometer data (e.g., OBDA) to evaluate behavioral states | Shepard et al. 2008 |
| Wavelet analysis | Method for detecting periodically varying movement and behavior patterns across all temporal scales | Polansky et al. 2010 |
| Recursion analyses | Methods for detecting movement trajectory recursions (returns to prior locations) | Berger-Tal and Bar-David 2015 |
2.1. Path-level analyses
Path-level analyses rely on several straightforward metrics that can be easily extracted from consecutive relocations in a time series of geographical points. These metrics are broadly referred to to as stepwise characteristics and can be split into primary and secondary metrics. Primary metrics, such as step length and turning angle (Table 1) are directly derived from relocations at each time step. However, they are highly sensitive to the spatial and temporal resolution at which the data were collected (Codling and Hill 2005, Gautestad 2012). Secondary metrics may be summary statistics derived from primary metrics (Edelhoff et al. 2016) or they may be computed from the trajectory at coarser spatio-temporal scales than represented by the raw data. These coarser scale metrics include net squared displacement (NSD) (Bunnefeld et al. 2011), which under a pure diffusive movement process scales linearly with time (Börger and Fryxell 2012), and residence time (Table 1). They may used, as in the case of NSD, to characterize the functional mode of a movement path (i.e., migratory vs. territorial; Bastille-Rousseau et al. 2016). The coarser-scale at which they are calculated makes them less sensitive to the spatio-temporal resolution of the data, provided the scale of the raw data is sufficiently fine (i.e., an order of magnitude finer than these secondary measures).
Metrics have been developed to describe structural aspects of movement trajectories that include many twists and turns. Two of these are the straightness index and tortuosity: both measure the degree to which movement trajectories deviate from straight lines (Table 1). A third is a trajectory’s fractal dimension: informally, it has a value between one and two, and is a measure of the extent to which a one-dimensional trajectory fills two-dimensional space, as an individual meanders around the landscape (values close to 2 represent trajectories that are more “space filling” than those with dimensions close to 1). These three structure-characterizing metrics are calculated across a series of steps (i.e. consecutive locations in space), typically using computer algorithms, although the fractal dimensions of earthworms moving in vegetated versus unvegetated landscapes have been computed by hand (Rice et al. 1998)!
2.2. Path Segmentation Analyses
One of the most active areas of research within movement ecology (see Edelhoff et al. 2016) is the development of methods to infer the behavioral state of individuals from relocation data. Some of these methods seek to segment movement paths into different behavioral phases (also known as canonical activity modes—see Getz and Saltz 2008), such as distinguishing between active and resting phases (van Beest and Milner 2013) or between foraging and traveling phases (Dzialak et al. 2015). Segmentation methods may be based on threshold concepts (Gutenkunst et al. 2007, Sur et al. 2014) or clustering methods (Van Moorter et al. 2010); or they may be based on geometric or periodic properties of the trajectory, as in recursion (Bar-David et al. 2009) and wavelet (Wittemyer et al. 2008) analyses, respectively (Table 1).
One set of methods—change point analyses (Table 1)—are designed to detect changes in the movement behavior of individuals, and then relate these to environmental covariates (Garstang et al. 2014) as possible causes for the behavioral shifts. These methods frequently use time-series analyses to identify notable shifts in the autocorrelations of the sequential values of primary or secondary metrics (Gurarie et al. 2009, 2016). Another set of methods—state space modeling approaches (Table 1)—are designed to identify a set of states (hopefully with a behavioral interpretation) underlying variations in movement behavior and, within the same analysis, determine the probabilities of switching among states. These methods attempt to assign “hidden behavioral states” to each location point, as well as a probability transition matrix that specifies the probability of an individual switching from one state to any other as the individual moves to the next location point. Essentially, the method produces a stochastic walk model, called a Hidden Markov Model (HMM; Patterson et al. 2009). HMM movement trajectory models are complicated generalizations of random walks (Morales et al. 2004), where movement elements (step size and turning angle) depend on the current behavioral state, as does the probability of changing behavioral state when reaching the next location. To demonstrate the HMM method, we have analyzed the trajectory of a zebra using the moveHMM package (Michelot et al. 2016) in the statistical analysis program R (version 3.4.3; R Core Team 2017). The results obtained constitute the most probable decomposition of all of the 10,600 steps into a “two-state no-covariate model”. The distributions of step lengths and turning angles associated with this model are depicted in Fig. 1.
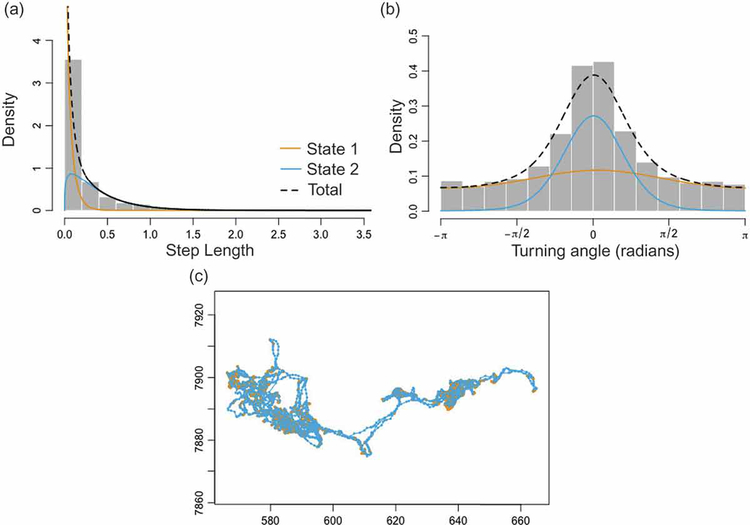
Results of a “2-state, no-covariate” behavioral model of zebra “AG256” using the moveHMM package in R (see supplementary files for data and code). This analysis assumed 2 distinct behavioral states and included only an intercept term, no environmental or other physiological covariates were included. Panels (a) & (b) show the empirical distributions of step lengths and turning angles respectively, using yellow and blue lines to depict the estimated distributions in each behavioral state. Panel (c) displays the particular trajectory used to produce distributions (a) and (b), with each color-coded with respect to their predicted behavioral state: yellow for state 1 and blue for state 2. Data exploration and biological knowledge of the observed individual is necessary to determine whether a model with more than two states clarifies or muddies interpretation of what each state is likely to represent. In our example, it seems probable, given the relatively uniform distribution of turning angles and the high density of short steps, that State 1 represents bouts of foraging while State 2 represents more directed movement behavior (e.g., travel; notice the apparently unbiased distribution of turning angles and larger step sizes).
Path or trajectory segmentation methods are one area of research common to both GIScience and movement ecology, with the GIS community supporting significant research on pattern-oriented, cross-scale, and cross-type segmentation methods (Dodge et al. 2009, Ahearn and Dodge 2018). In a study designed to explore the role of uncertainty in trajectory and segmentation analyses, Laube and Purves (2011) fitted 10 cows with GPS collars taking sub-second fixes to investigate questions of scale, granularity, and uncertainty when working with GPS data to assess movement parameters. The results of this work should be of great interest to ecologists, who typically collect much coarser fix data and then either invoke a straight-line assumption about the nature of paths between any two consecutive points in their data or assume Gaussian diffusion, often relying on a Brownian Bridge method for constructing likely trajectories between such points (Horne et al. 2007).
Often limitations regarding the temporal resolution of movement data may require analysis at somewhat broader scales. Even at this higher level of abstraction, however, behavioral classification may still be powerful. Indeed, Abrahms et al. (2017) identified “movement syndromes” across 13 diverse taxa (marine and terrestrial) using five standard metrics (mean turning angle correlation, mean residence time, mean time-to-return, volume of intersection, and mean net squared displacement) and a principle components analysis. Although the trajectories studied varied in movement mode (e.g. flying, walking, swimming) and taxon, the analysis successfully differentiated among migratory, nomadic, central place foraging, and territorial behaviors from GPS data alone.
Alongside the development of analyses to derive behavioral states from GPS data, new tags and collars fitted with tri-axial accelerometers (and, often, additional sensors for light, barometric pressure, temperature, etc.—see Wilson et al. 2008) increasingly allow for direct observation of the dynamic behavioral states of free-ranging animals (Shepard et al. 2008, Wang et al. 2015). Using various machine learning algorithms, accelerometer data (in the form of three-dimensional movement generally at a 20–40Hz resolution) can be processed to classify basic behaviors (e.g. sitting, walking, diving, running, resting, foraging) across multiple taxa with high accuracy (Nathan et al. 2012, Bidder et al. 2014, Fehlmann et al. 2017). Although these algorithms require high resolution training data, often relying upon intensive observation of captive animals, this technology used in combination with GPS relocations can aid in the exploration of links among the biomechanical, behavioral, and ecological processes that influence whole-animal movement and contribute to a unified field of movement ecology (Nathan et al. 2012).
2.3. Interactions
Although the majority of path trajectory analyses do not rely upon environmental covariates, often the results and interpretation of these metrics can be enhanced by assessing their environmental context. For example, taking account of the environmental context at a behavioral change-point can help researchers infer why an animal is changing behavior or what behaviors are being exhibited. Similarly, examining the environmental context alongside measures of first-passage time or residence time can be useful for understanding how animals relate to and behave in different environments. Inherently, the one-dimensional metrics we have highlighted here are applied only to individuals’ trajectories. However, when aggregated across a group of animals, their results can be useful in distinguishing individual heterogeneity in a population or variation across species, just as done by Abrahms et al. (2017) in their study of movement syndromes.
Emerging technologies, such as proximity collars, are advancing the study of conspecific interactions (and those among heterospecifics as well) along movement trajectories. The consideration of contacts among individuals moving across a given landscape can be vital for understanding the implications for resource use, competition, and disease transmission. Often interaction between two animals is assessed using point-based measures rather than integrating proximity across path segments, as in assessments of association coefficients or proximity analyses (Long et al. 2014). Recent advances in the GIS community, however, have led to improved methods for analyzing dynamic interactions (i.e. interactions that occur both in space and time using path-based metrics Long and Nelson 2013a). Often these interactions are translated into and analyzed as contact networks (an application of graph theory). However, since the majority of network analyses do not ask questions explicit to movement, we direct readers to alternative reviews of this growing area of research (e.g Croft et al. 2008, 2011, Pinter-Wollman et al. 2013, Silk et al. 2017).
3. Space-Use Analyses
When scaling up from path-level to space-use analyses, movement ecologists employ a variety of metrics designed to evaluate how an individuals’ movements, when viewed in the aggregate, partition the landscape in meaningful ways. Such two-dimensional constructions can explore how and when individuals use or share a given area or habitat in space or time with or without the consideration of the underlying environment. Below we explore these methods in two sections. First, we highlight methods based purely on movement metrics, irrespective of environmental context. These are generally used for characterizing the size and shape of animal home ranges. Second, we describe a suite of methods that combine movement locations with environmental covariates to make inference about habitat selection and the influence of landscape factors on space use.
3.1. Feature-independent analyses
Metrics analyzing the frequency of relocations across space regardless of environmental covariates broadly include the various methods for home-range estimation. These simple measures of animal space use (see Table 2) are applied widely, even with low-resolution data: though daily fix rates may prohibit fine-scale analyses such as behavioral state extraction, the aggregation of points at this resolution (over appropriate temporal spans) can easily inform the general size and shape of an animal’s home range (Worton 1989, Fieberg and Kochanny 2005, Fieberg and Börger 2012).
Table 2.
Space-Use Metrics & Methods (in the context of movement ecology)
| Featureless Landscapes | Description | Suggested References |
|---|---|---|
| Home range estimation | The estimation of habitually-used areas with function-dependent boundaries (e.g. summer range, defended territory, core territory). Most commonly accomplished using densities of use calculated from estimates of the animals’ locations across a landscape | Powell and Mitchell 2012, Fieberg and Borger 2012 |
| Utilization distribution | Relative frequency distributions of an animal’s location over space for a specified period of time | Worton 1989 |
| Home range fidelity | Measures of home-range overlap among individuals (e.g., volumes of intersection) and home-range stability over time | Fieberg and Kochanny 2005, Millspaugh et al. 2004 |
| Core area methods | Analyses for identifying areas of most consistent use/selection from individuals’ relocation histories | Vander Wal and Rodgers 2012 |
| Conspecific proximity methods | Methods for estimating and characterizing the interactions among and impact of conspecifics on movement trajectories | Delgado et al. 2014 |
| Featured Landscapes | ||
| Resource selection functions (RSFs) | Statistical models producing values proportional to the probability of use of a resource unit. RSFs are often constructed using a logistic regression framework comparing points used by an animal to those “available” to it within its home range | Manly et al. 2002, Boyce and McDonald 1999 |
| Step selection functions (SSF) | A model of resource selection that includes movement behavior to constrain selection and availability. In an SSF, each step at time t is paired with one or more random steps with the same starting point drawn at random from a distribution of step lengths and turning angles. | Thurfjell et al. 2014 |
| Landscape resistance | Measure of the relative difficulty (e.g., energy used per unit distance moved) for individuals to move as a function of topography and environmental features | Zeller et al. 2012 |
| Least cost methods | Analyses for finding the least difficult (least energy expended) path between two points. May be extended to avoid risks of encountering competitors, predators, etc. | Walker and Craighead 1997, Adriaensen et al. 2003 |
| Circuit theory | An application of electrical circuit theory to model landscape connectivity and resistance through graph and random walk theories | McRae et al. 2008 |
Several alternative methods for describing the home range of an animal exist, ranging in complexity from the construction of the minimum convex polygon containing the movement trajectory to a construction of a utilization distribution (Van Winkle 1975) that can be used to estimate the probability of finding an individual in selected areas inside the home range; see Fig. 2 for a comparison across three common methods for home-range construction. Most commonly, utilization distributions (UDs) are derived using kernel density estimators, now widely incorporated in many spatial analysis packages (Worton 1989). Subsequent development of other methods, based on Brownian movement models (Horne et al. 2007) and Local Convex Hull unions (Getz and Wilmers 2004, Getz et al. 2007, Lyons et al. 2013, Dougherty et al. 2017), as well as autocorrelated kernel methods (Fleming and Calabrese 2017) have enabled more realistic or robust estimates of the utilization distribution. In order to delineate areas of most consistent use or offer conservative estimates of an animal’s typical home range, researchers often include isopleths on maps of utilization distributions to identify the areas associated with a given percentage of relocations (e.g., 50%, 80%, or 95%). Utilization distributions can be calculated over any time interval of interest to delineate the space use of an animal over that time (e.g. a single month, a particular season, an entire year, etc.). By assessing the volume of intersection or overlap of successive short-term UDs for a particular individual, researchers can evaluate broad-scale site fidelity and ultimately the stability of an animal’s home range (Fieberg and Kochanny 2005, Millspaugh et al. 2004, Clapp and Beck 2015; Table 2). Additionally, these same metrics can be used across individuals to estimate concurrent or shared space use, which can be important for understanding social structure, disease transmission, or competition for resources.

Comparative home range estimates for zebra “AG256” (using only the data that pertains to the western part of its total range—cf. Panel (c) in Fig. 1) across 3 static (i.e., time-integrated) techniques. The simplest technique, a minimum convex polygon (MCP), displayed in Panel (a), defines the extent of a home range as the smallest convex polygon fitting a given percentage of points. Though still used widely, MCPs are criticized as poor estimators of an animal’s true home range because they often contain large areas unused, and potentially unavailable, to the observed individual, as evident in the upper-center of our trajectory. Panel (b) displays a common alternative: the 95% kernel utilization distribution. This method was developed to more rigorously quantify an animals actual space use and ultimately defines an animal’s home range as a bivariate probability density function, calculating the probability of relocating an animal in any given location (Worton 1989). Panel (c) offers a non-parametric approach, calculating the home range of the zebra using a-LoCoH, the adaptive local convex hull method developed by Getz et al. (2007) that constructs kernels at each relocation using all points within a total distance a such that the distances of all neighboring points to the reference point sum to a value less than or equal to a. In our example, we used a = 75000 m, which provided a contiguous range that trades-off fewer false positives at the expense of more false negatives than the other two methods. There is much debate and continued development in the area of home-range estimation and researchers must be conscious of the differences across metrics, because results often vary widely and may offer different biological interpretations (e.g., defining the extent of the habitat available to the animal for selection versus the area traversed in daily activity; see Fieberg and B¨orger 2012). For more detail on the construction of these three home range measures, see Appendix B.
Within the utilization distribution, ecologists often define a “core area” of use. Core area methods refer to any one of a group of analyses that seek to identify the most intensely used areas from individuals’ relocations histories. In their simplest form, these areas are defined as the smallest area incorporating some subjective percentage of relocations, generally 30–50%. Although widely used, the selection of the 30% or 50% isopleth is ad-hoc. In an attempt to make this selection more rigorous, Vander Wal and Rodgers (2012) propose researchers fit an exponential model to the rate at which home-range area increases for each percent increase in isopleth value; they define the core area as the point at which the slope of this exponential curve is 1. Other approaches involve integrating time-use patterns into the spatial analysis of movement data. In the simplest time-use metrics, researchers evaluate the time to return and the return rate (frequency of returns) to pre-defined areas in the home range, given some prescribed minimum time between “returns” (Seidel and Boyce 2015, Van Moorter et al.2016). More elaborate methods incorporate time-use into the construction of the utilization distributions themselves (Benhamou and Riotte-Lambert 2012). The T-LoCoH method (implemented in R through the tlocoh package; (Lyons et al. 2013)), for example, allows users to evaluate revisitation (a measure of separate visits) and average duration of visits (Table 1) to all local hulls within an animal’s home range. These analyses can help elucidate spatial patterns in time strategies: teasing out not only what habitats animals are using, but also separating those they used in repeated short visits from those used for infrequent but extended visits.
In the GIS community, the competition in and for space and time that ecologists study as habitat selection or home range analysis, has often been considered as an extension of classic time geography (Demšar et al. 2015, Long 2016). Various methods for illuminating space-time prisms, which map the potential movements of an object in both geographic space and time given information about its movement capabilities (e.g. travel velocity), can account for the time and sequentiality of measurements along movement paths. Extensions of these space-time prisms has resulted in methods for constructing 3-dimensional elements used to estimate the probability that an object was located at some location at some particular time. This approach offers a sophisticated technique for understanding the movements and activities (and potentially interactions) of animals at fine temporal and spatial scales (Downs et al. 2014).
All simple home-range estimators that ignore the temporal autocorrelation inherent in movement trajectories may be applied either to a single animal’s trajectory or to a combined dataset across multiple individuals. Estimation methods that use the temporal nature of movement trajectories (e.g., autocorrelated kernel density methods, Brownian bridges, T-LoCoH), however, must be applied first to individual trajectories independently and subsequently combined if population space use is of interest.
3.2. Feature-dependent analyses
Methods used to construct resource selection functions (RSFs; Boyce and McDonald 1999) are arguably the most utilized among spatially-explicit methods that incorporate environmental covariates (see Table 2). RSFs are typically employed to infer the probability of use of any given resource unit within the range of an individual or population, and thereby, represents the primary procedure for evaluating the selection of resources by both individuals and populations (Boyce and McDonald 1999, Manly et al. 2002). Within the genre of habitat selection analysis, step selection functions (SSFs) function in a similar manner to RSFs, but are constructed at a much finer scale. These models compare habitat attributes at points along a given trajectory and estimate resource selection by comparing the environmental structure of the next point along the trajectory to other possible points available to the animal (taking into account step length and turning angle distributional structure). Thus, in short, SSFs offer a finer-scale approximation of habitat selection along movement paths rather than the aggregate assessment yielded by a traditional RSF (Thurfjell et al. 2014; see Fig. 3); however, we note that SSFs are sensitive to the frequency at which data are collected (Gautestad 2012). In fact, consideration of behavioral state, data collection, and fix interval (i.e., sampling frequency) is crucial to accurate representation of both habitat selection and connectivity (Abrahms et al. 2016a, 2017). For example, when considering behavioral state in the evaluation of resource selection by African wild dogs, Abrahms et al. (2016a) demonstrated that the response of wild dogs to roads varied significantly depending on both the behavioral and landscape context in which roads were encountered.
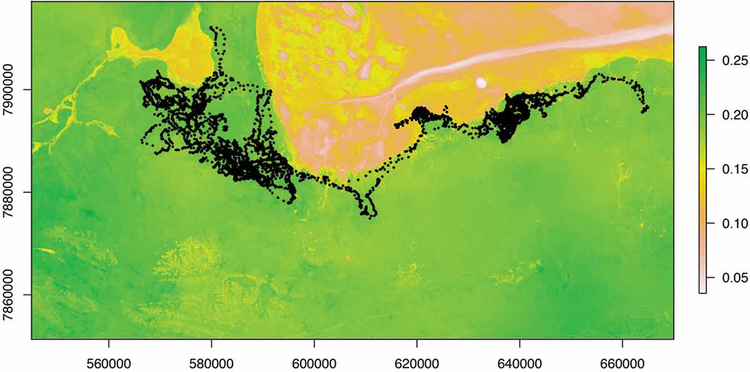
Predicted habitat selection using a step-selection function for zebra “AG256”. Fundamentally, selection functions calculate the selection ratio of any given resource unit by comparing characteristics of “used” units to those “available” to the animal, typically using a logistic regression framework. Step-selection functions differ from traditional RSFs by defining what is “available” according to randomly drawn steps from each point rather than a simple random sample of the home range as a whole. Here we display AG256’s predicted selection ratio for a portion of Etosha National Park according to 4 environmental layers: distance to primary roads, distance to functional water sources, mean greenness, and mean wetness. On top of the predicted selection layer, the original trajectory is plotted in black. Note that only the western part of the trajectory, which occurs during the wet season (Zidon et al. 2017), is used to construct the home ranges depicted in Fig. 2). For a complete discussion of the regression and details regarding the selection of available steps and the environmental layers used, please see Appendix B.
Beyond estimating the probability of use of any given resource in space, ecologists and conservation biologists often want to evaluate the connectivity of a landscape for movement, both within and between populations. Metrics for assessing landscape connectivity are expansive, but the most common approaches involve various landscape pattern indices which serve to evaluate structural connectivity, a characteristic inherent to the landscape (see Tischendorf and Fahrig 2000, Calabrese and Fagan 2004, Fagan and Calabrese 2006). Functional connectivity can be calculated directly using movement trajectories (Abrahms et al. 2016b,a) or estimated indirectly using capture-recapture data (Royle et al. 2013). For example, least-cost modeling, a popular analytical approach familiar to movement ecology and GIS alike, generates simulated paths based on estimates of the efficiency with which an individual could move between two points. Efficiency can be a function of distance, time, or any other weighted resistance layer. Traditionally, maps of landscape resistance have been generated from a mix of expert opinion, previous studies, species presence locations, habitat suitability indices (often also derived by expert opinion), and radio-telemetry points (Sawyer et al. 2011). More recently, these maps have been generated using circuit theory (McRae et al. 2008) or by using the inverse of selection functions, thereby integrating actual movement paths into the assessment of landscape permeability (Chetkiewicz and Boyce 2009, Zeller et al. 2016).
Often in the study of movement, dynamics within a population of animals, rather than those of a single individual, are of primary interest. As such, although both landscape connectivity and habitat selection analyses can be run on single trajectories, it is most common to run these analyses on groups of individuals to infer population-wide behaviors. Of course, without comprehensive tracking of all individuals in a population, general conclusions can be difficult to draw or, when formed from empirical observation on a subset of the population, biased due to individual and environmental heterogeneity (especially with small sample sizes). However, as GPS technology has become more costeffective and widely available, researchers with appropriate sampling schemes and investigating data from multiple individuals within a population can begin to draw conclusions about general space use and effectiveness of management strategies for a population or species.
4. Bridging Perspectives
4.1. In Ecology at Large
As a sub-discipline within ecology, movement ecology often has a somewhat narrow focus, considering foundational questions such as when, where, how, and why animals move (Nathan et al. 2008). Indeed, despite its interdisciplinary origins, movement ecology tools are often used for ‘basic’ science (i.e., addressing research questions without specific applications beyond the creation of new knowledge about a system) in contrast to GIScience’s often more applied focus. But the methods of movement ecology draw on several disciplines, including physics, biomechanics, behavioral ecology, landscape ecology, and GIScience. Moreover, at its core, movement ecology is a means of cutting across scales, linking the mechanical and physiological basis of behavior to continental-level patterns in animal distributions. That cross-scale nature allows movement ecology to be adaptable and flexible for solving real-world problems in human-dominated landscapes.
In conservation biology, movement tools have clear and well-tested applications for both policy making and wildlife management. In particular, movement ecology provides an invaluable framework for understanding, measuring, and predicting human-wildlife conflict. For instance, Mountrakis and Gunson (2009) used kernel density estimation to evaluate spatiotemporal hotspots where the risk of moose-vehicle collisions may be high. Further, in a study investigating the space-use behavior of leopards in human-dominated landscapes, Odden et al. (2014) found that home-range size was markedly smaller and movement patterns (as defined by step-length distributions) more nocturnal for leopards ranging closer to human settlements, results that reflect a behavioral shift that may reduce conflict. Movement tools can also be used to plan and optimize mitigation efforts, like highway overpasses and conservation corridors, and provide a means to evaluate the success of management decisions. Indeed, policy for dealing with conflict can be expensive and retaliatory (McManus et al. 2015), resulting in the death of endangered animals in an often misguided attempt to prevent future conflict. In the case of leopards in India, for example, the common management practice of haphazard capture and relocation of problem animals has been shown to be counterproductive; although translocations may provide temporary local relief, they were found to increase the subsequent overall level of conflict (Athreya et al. 2011, Odden et al. 2014).
Movement research also has tremendous potential for addressing complex challenges where movement is only an implicit part of the problem. In recent years, movement data has become an increasingly valuable asset in disease ecology, with the vast majority of emerging human health threats connected in some way to the human-wildlife-livestock interface (Jones et al. 2008). Movement already plays a key role in disease ecology, with many researchers interested in answering clear-cut questions like whether host movement behavior changes their risk of disease, or whether infection alters host movements. Movement tools are particularly useful for illuminating aspects of individual heterogeneity that may directly influence exposure and transmission processes; effective incorporation of such knowledge into existing (or adapted) epidemiological models may result in a framework that offers more accurate predictions of spatiotemporal disease dynamics (Dougherty et al. 2018). In an example of this, research into the spatial organization of badgers (Meles meles) has demonstrated that culling, a widespread government control method for tuberculosis, can have an adverse effect—and actually increases contact between badgers and cattle (Woodroffe et al. 2006). In the future, more real-time applications may become increasingly prevalent not only in forecasting but also in surveillance, for example, in efforts to prevent spillover of bat-borne viruses like Ebola and Nipah.
Further, although our focus here has been on analyses for GPS relocation data, in most cases the metrics and methods presented may be used to assess other kinds of geospatial data. In fact, many of the tools explored here have applications outside movement ecology and beyond the conservation and disease ecology considered here. These tools have considerable potential for facilitating cross-disciplinary research. For example, cluster analyses used in movement ecology to identify, inter alia, kill sites and foraging patches (Tambling et al. 2010, Seidel and Boyce 2015, Webb et al. 2008) were originally developed by researchers to identify disease hotspots from disease-incidence records (Kulldorff et al. 1998). In the same vein, resistance mapping and network analyses have clear implications for assessing transportation and traffic flow.
4.2. Outside Ecology
Many of the questions and methods used in movement ecology are not unique to animal behavior. As the digital traces on human lives have multiplied (e.g., via mobile phones, geo-tagged social media), the field of human mobility analysis (HMA) has become an increasingly important part of sociology and human geography (Chen et al. 2016). Movement ecology may be able to learn from the experience of GIS and HMA communities, as the streams of passive data available from mobile phone records and social media have already eclipsed those available to ecologists by several orders of magnitude. Models and techniques used in HMA and movement ecology often ask similar questions (e.g. can we infer activity or behavior from movement patterns?) and are motivated by a shared foundation in physics and mathematics (e.g. diffusion models and stochastic processes; Gonzalez et al. 2008).
Although the two fields often approach these questions at different scales, with different applications and impact, and using different nomenclature, movement ecologists can learn as much from this realm as geographers may take from movement ecology, especially as the resolution of available animal movement data increases to match that of HMA. In the future, both of these fields will face challenges to develop new methods and metrics to handle the proliferation of “big data” as movement tracking becomes lighter, easier, and cheaper to implement, and involuntary data collection becomes more ubiquitous for human mobility (Kitchin 2013). Further, the historical frameworks in transportation research for active data collection, using surveys and GPS loggers, can offer powerful means for validating new models and methods that would be unavailable in wildlife research (Chen et al. 2010).
It is worth noting in this context that quantitative models and approaches can only go so far, and behavior—human or animal—has limited predictability (Song et al. 2010a,b). Qualitative data and systems to collect and analyze them—a realm that has been advanced by human geographers and political ecologists who seek to document and understand the spatial nature of institutions and policy—can help to fill in some of the gaps and bring greater understanding to the motivations and patterns behind movement and human behavior more generally. In this vein, the application of qualitative data is yet another area where movement ecology can benefit from an integration with GIS. As there are no landscapes that remain untouched by humans, qualitative data and perspectives should be considered crucial not only to human research but also to the understanding of ecological systems. Research at the interface of ecology and human geography has the potential to enhance our understanding of both the social and ecological impacts of global change (e.g. Hardy and Hauer 2018).
The shared questions and challenges facing GIS and movement ecology may help facilitate fruitful collaboration in the future, especially if undertaken with a shared commitment to open science and its infrastructure, open data, and the development of open source tools on both sides. Though proprietary software, such as ESRI ArcGIS, is regularly used by ecologists, the community is moving toward open source solutions. Many of these tools are developed and maintained by the GIS community’s own open geography advocates and organizations (OsGeo); open source GIS software packages like GRASS and QGIS and spatial libraries in R and Python are becoming more developed and widely used. However, open data sharing is often a bottleneck in both fields. Political, legal, and privacy issues with sharing data, especially when human subjects are involved, generally limits open data availability (DeLyser and Sui 2014, Sui 2014). However even in movement ecology, data archival or sharing has been slow to take hold, even with the existence of community-specific infrastructures, such as Movebank, developed for the purpose (Wikelski and Kays 2018). Continued investment on both sides of GIScience and movement ecology can help guide wider dissemination of these tools and the successful integration of the two fields.
5. Discussion
Today, movement data are collected at increasingly high resolutions of time and space. This explosion of data demands new methods and techniques to analyze them efficiently (Long and Nelson 2013b). Likewise, improvements in technology for tracking animal movements has increased demand for toolkits able to extract the behavioral and ecological factors behind animal movement and space use. Here we have outlined a selection of methods for exploring movement data of free-ranging animals that can answer animal behavior questions across scales, particularly as they may relate to conservation and wildlife disease issues.
As has been noted, GIS is fundamentally based on the study of geographic information in the context of processes that enhance spatial knowledge and support decision making, often on a global scale (Yuan 2017). It thus follows that GIS and movement ecology overlap where environmental and landscape factors are considered in the context of space use by individuals and populations. Although we have limited our review to applications of single population or community analyses, studies of whole species distributions or long term range shifts (Elith et al. 2010; Araújo and Peterson 2012) are representative of active areas of research in ecology. These distributions are rarely linked to movement ecology even though they naturally emerge from animals’ individual movement decisions (Jønsson et al. 2016). No matter how climate suitability shifts over time, the ability of species to track changing climates ultimately depends on their dispersal ability—but in global change biology, this is most commonly reduced to a single maximum upper rate (Trisos et al. 2018). Movement ecology is on track to play an increasingly important role, not just in refining those predictions, but also in tracking species’ actual responses in real time.
In short, many of the questions addressed in movement ecology overlap with those being asked throughout the broader GIS community: questions relating to geospatial data analyses that address the behavior of individuals, the demography of populations, and the structure of landscapes in the face of global change. Given this overlap, we are confident this review will help stimulate further transdisciplinary and interdisciplinary research among ecologists and geographers.
Supplementary Material
Supp1
Supp2
Supp3
Acknowledgements
The authors wish to thank the Getz and Brashares labs at UC Berkeley for their careful consideration of early manuscript drafts and helpful comments towards the shaping of this review. This research was supported by grants NIH-GM 083863 and NSF-EEID 1617982. The impetus for this review arose from a presentation given by WMG at Ohio State University, at an NSF Workshop on Advancing Movement and Mobility Science by Bridging Research on Human Mobility and Animal Movement Ecology, organized by Harvey J. Miller, Jennifer A. Miller and Gil Bohrer.
Footnotes
Declaration of Interest Statement
The authors declare no potential conflicts of interest.
Data Availability Statement The data and code that support the examples within this review are openly available on GitHub and archived with Zenodo at http://doi.org/10.5281/zenodo.1185383.
References
- Abrahms B, et al., 2016a. Lessons from integrating behaviour and resource selection: activity-specific responses of African wild dogs to roads. Animal Conservation, 19 (3), 247–255. [Google Scholar]
- Abrahms B, et al., 2016b. Does wildlife resource selection accurately inform corridor conservation?. Journal of Applied Ecology. [Google Scholar]
- Abrahms B, et al., 2017. Suite of simple metrics reveals common movement syndromes across vertebrate taxa. Movement ecology, 5 (1), 12. [Europe PMC free article] [Abstract] [Google Scholar]
- Adriaensen F, et al., 2003. The application of least-cost modelling as a functional landscape model. Landscape and Urban Planning, 64 (4), 233–247. [Google Scholar]
- Ahearn SC and Dodge S, 2018. Recursive multi-frequency segmentation of movement trajectories (ReMuS). Methods in Ecology and Evolution, 9 (4), 1075–1087. [Google Scholar]
- Araújo MB and Peterson AT, 2012. Uses and misuses of bioclimatic envelope modeling. Ecology, 93 (7), 1527–1539. [Abstract] [Google Scholar]
- Athreya V, et al., 2011. Translocation as a tool for mitigating conflict with leopards in human-dominated landscapes of India. Conservation Biology, 25 (1), 133–141. [Abstract] [Google Scholar]
- Bar-David S, et al., 2009. Methods for assessing movement path recursion with application to African buffalo in South Africa. Ecology, 90 (9), 2467–2479. [Europe PMC free article] [Abstract] [Google Scholar]
- Barraquand F and Benhamou S, 2008. Animal movements in heterogeneous landscapes: identifying profitable places and homogeneous movement bouts. Ecology, 89 (12), 3336–3348. [Abstract] [Google Scholar]
- Bastille-Rousseau G, et al., 2016. Flexible characterization of animal movement pattern using net squared displacement and a latent state model. Movement Ecology, 4 (1), 15. [Europe PMC free article] [Abstract] [Google Scholar]
- Benhamou S, 2004. How to reliably estimate the tortuosity of an animal’s path: straightness, sinuosity, or fractal dimension?. Journal of Theoretical Biology, 229 (2), 209–220. [Abstract] [Google Scholar]
- Benhamou S and Riotte-Lambert L, 2012. Beyond the Utilization Distribution: Identifying home range areas that are intensively exploited or repeatedly visited. Ecological Modelling, 227, 112–116. [Google Scholar]
- Berger-Tal O and Bar-David S, 2015. Recursive movement patterns: review and synthesis across species. Ecosphere, 6 (9), 1–12. [Google Scholar]
- Bidder OR, et al., 2014. Love thy neighbour: automatic animal behavioural classification of acceleration data using the k-nearest neighbour algorithm. PloS one, 9 (2), e88609. [Europe PMC free article] [Abstract] [Google Scholar]
- Börger L and Fryxell J, 2012. Quantifying individual differences in dispersal using net squared displacement. Dispersal ecology and evolution, 222–230. [Google Scholar]
- Boyce MS and McDonald LL, 1999. Relating populations to habitats using resource selection functions. Trends in Ecology & Evolution, 14 (7), 268–272. [Abstract] [Google Scholar]
- Bunnefeld N, et al., 2011. A model-driven approach to quantify migration patterns: individual, regional and yearly differences. Journal of Animal Ecology, 80 (2), 466–476. [Abstract] [Google Scholar]
- Calabrese JM and Fagan WF, 2004. A comparison-shopper’s guide to connectivity metrics. Frontiers in Ecology and the Environment, 2 (10), 529–536. [Google Scholar]
- Calenge C, Dray S, and Royer-Carenzi M, 2009. The concept of animals’ trajectories from a data analysis perspective. Ecological Informatics, 4 (1), 34–41. [Google Scholar]
- Chen C, et al., 2010. Evaluating the feasibility of a passive travel survey collection in a complex urban environment: Lessons learned from the New York City case study. Transportation Research Part A: Policy and Practice, 44 (10), 830–840. [Google Scholar]
- Chen C, et al., 2016. The promises of big data and small data for travel behavior (aka human mobility) analysis. Transportation research part C: emerging technologies, 68, 285–299. [Europe PMC free article] [Abstract] [Google Scholar]
- Chetkiewicz CLB and Boyce MS, 2009. Use of resource selection functions to identify conservation corridors. Journal of Applied Ecology, 46 (5), 1036–1047. [Google Scholar]
- Clapp JG and Beck JL, 2015. Evaluating distributional shifts in home range estimates. Ecology and Evolution, 5 (18), 3869–3878. [Europe PMC free article] [Abstract] [Google Scholar]
- Codling E and Hill N, 2005. Sampling rate effects on measurements of correlated and biased random walks. Journal of Theoretical Biology, 233 (4), 573–588. [Abstract] [Google Scholar]
- Croft DP, James R, and Krause J, 2008. Exploring animal social networks. Princeton University Press. [Google Scholar]
- Croft DP, et al., 2011. Hypothesis testing in animal social networks. Trends in Ecology & Evolution, 26 (10), 502–507. [Abstract] [Google Scholar]
- Cumming GS and Corn´elis D, 2012. Quantitative comparison and selection of home range metrics for telemetry data. Diversity and Distributions, 18 (11), 1057–1065. [Google Scholar]
- Delgado M.d.M., et al., 2014. A statistical framework for inferring the influence of conspecifics on movement behaviour. Methods in Ecology and Evolution, 5 (2), 183–189. [Google Scholar]
- DeLyser D and Sui D, 2014. Crossing the qualitative-quantitative chasm III: Enduring methods, open geography, participatory research, and the fourth paradigm. Progress in Human Geography, 38 (2), 294–307. [Google Scholar]
- Demšar U, et al., 2015. Stacked space-time densities: a geovisualisation approach to explore dynamics of space use over time. GeoInformatica, 19 (1), 85–115. [Google Scholar]
- Dodge S, et al., 2016. Analysis of movement data. International Journal of Geographical Information Science, 30 (5), 825–834. [Europe PMC free article] [Abstract] [Google Scholar]
- Dodge S, Weibel R, and Forootan E, 2009. Revealing the physics of movement: Comparing the similarity of movement characteristics of different types of moving objects. Computers, Environment and Urban Systems, 33 (6), 419–434. [Google Scholar]
- Dougherty ER, et al., 2017. A cross-validation-based approach for delimiting reliable home range estimates. Movement ecology, 5 (1), 19. [Europe PMC free article] [Abstract] [Google Scholar]
- Dougherty ER, et al., 2018. Going through the motions: incorporating movement analyses into disease research. Ecology Letters, n/a–n/a. [Abstract] [Google Scholar]
- Downs JA, et al., 2014. Voxel-based probabilistic space-time prisms for analysing animal movements and habitat use. International Journal of Geographical Information Science, 28 (5), 875–890. [Google Scholar]
- Dzialak MR, et al., 2015. Incorporating within-and between-patch resource selection in identification of critical habitat for brood-rearing greater sage-grouse. Ecological Processes, 4 (1), 5. [Google Scholar]
- Edelhoff H, Signer J, and Balkenhol N, 2016. Path segmentation for beginners: an overview of current methods for detecting changes in animal movement patterns. Movement Ecology, 4 (1), 21. [Europe PMC free article] [Abstract] [Google Scholar]
- Elith J, Kearney M, and Phillips S, 2010. The art of modelling range-shifting species. Methods in ecology and evolution, 1 (4), 330–342. [Google Scholar]
- Fagan WF and Calabrese JM, 2006. Quantifying connectivity: balancing metric performance with data requirements In: Crooks KR and Sanjayan M, eds. Connectivity Conservation Cambridge University Press. [Google Scholar]
- Fauchald P and Tveraa T, 2003. Using First-Passage Time in the Analysis of AreaRestricted Search and Habitat Selection. Ecology, 84 (2), 282–288. [Google Scholar]
- Fehlmann G, et al., 2017. Identification of behaviours from accelerometer data in a wild social primate. Animal Biotelemetry, 5 (1), 6. [Google Scholar]
- Fieberg J and Börger L, 2012. Could you please phrase home range as a question?. Journal of Mammalogy, 93 (4), 890–902. [Google Scholar]
- Fieberg J and Kochanny CO, 2005. Quantifying home-range overlap: the importance of the utilization distribution. Journal of Wildlife Management, 69 (4), 1346–1359. [Google Scholar]
- Fleming CH and Calabrese JM, 2017. A new kernel density estimator for accurate home-range and species-range area estimation. Methods in Ecology and Evolution, 8 (5), 571–579. [Google Scholar]
- Garstang M, et al., 2014. Response of African elephants (Loxodonta africana) to seasonal changes in rainfall. PLoS One, 9 (10), e108736. [Europe PMC free article] [Abstract] [Google Scholar]
- Gautestad AO, 2012. Brownian motion or Lévy walk? Stepping towards an extended statistical mechanics for animal locomotion. Journal of the Royal Society Interface, 9 (74), 2332–2340. [Europe PMC free article] [Abstract] [Google Scholar]
- Getz WM, et al., 2007. LoCoH: nonparameteric kernel methods for constructing home ranges and utilization distributions. PLoS One, 2 (2), e207. [Europe PMC free article] [Abstract] [Google Scholar]
- Getz WM, et al., 2015. Panmictic and clonal evolution on a single patchy resource produces polymorphic foraging guilds. PloS one, 10 (8), e0133732. [Europe PMC free article] [Abstract] [Google Scholar]
- Getz WM, et al., 2016. Sympatric speciation in structureless environments. BMC evolutionary biology, 16 (1), 50. [Europe PMC free article] [Abstract] [Google Scholar]
- Getz WM and Saltz D, 2008. A framework for generating and analyzing movement paths on ecological landscapes. Proceedings of the National Academy of Sciences, 105 (49), 19066–19071. [Europe PMC free article] [Abstract] [Google Scholar]
- Getz WM and Wilmers CC, 2004. A local nearest-neighbor convex-hull construction of home ranges and utilization distributions. Ecography, 27 (4), 489–505. [Google Scholar]
- Gleiss AC, Wilson RP, and Shepard EL, 2011. Making overall dynamic body acceleration work: on the theory of acceleration as a proxy for energy expenditure. Methods in Ecology and Evolution, 2 (1), 23–33. [Google Scholar]
- Gonzalez MC, Hidalgo CA, and Barabasi AL, 2008. Understanding individual human mobility patterns. nature, 453 (7196), 779. [Abstract] [Google Scholar]
- Gurarie E, Andrews RD, and Laidre KL, 2009. A novel method for identifying behavioural changes in animal movement data. Ecology Letters, 12 (5), 395–408. [Abstract] [Google Scholar]
- Gurarie E, et al., 2016. What is the animal doing? Tools for exploring behavioural structure in animal movements. Journal of Animal Ecology, 85 (1), 69–84. [Abstract] [Google Scholar]
- Gutenkunst R, et al., 2007. Inferring resource distributions from Atlantic bluefin tuna movements: An analysis based on net displacement and length of track. Journal of Theoretical Biology, 245 (2), 243–257. [Abstract] [Google Scholar]
- Hardy RD and Hauer ME, 2018. Social vulnerability projections improve sea-level rise risk assessments. Applied Geography, 91, 10–20. [Google Scholar]
- Horne JS, et al., 2007. Analyzing animal movements using Brownian bridges. Ecology, 88 (9), 2354–2363. [Abstract] [Google Scholar]
- Jones KE, et al., 2008. Global trends in emerging infectious diseases. Nature, 451 (7181), 990–993. [Europe PMC free article] [Abstract] [Google Scholar]
- Jønsson KA, et al., 2016. Tracking animal dispersal: from individual movement to community assembly and global range dynamics. Trends in ecology & evolution, 31 (3), 204–214. [Abstract] [Google Scholar]
- Kitchin R, 2013. Big data and human geography: Opportunities, challenges and risks. Dialogues in human geography, 3 (3), 262–267. [Google Scholar]
- Kulldorff M, et al., 1998. Evaluating cluster alarms: a space-time scan statistic and brain cancer in Los Alamos, New Mexico.. American journal of public health, 88 (9), 1377–1380. [Abstract] [Google Scholar]
- Laffan SW, Skidmore AK, and Franklin J, 2012. Geospatial analysis of species, biodiversity and landscapes: introduction to the second special issue on spatial ecology. International journal of geographical information science, 26 (11), 2003–2007. [Google Scholar]
- Laffan SW, Skidmore AK, and Franklin J, 2014. Species distribution and diversity, habitat selection and connectivity: introduction to the Third Special Issue on Spatial Ecology. International Journal of Geographical Information Science, 28 (8), 1527–1530. [Google Scholar]
- Laffan SW, Skidmore AK, and Franklin J, 2016. Space, time, connectivity and conflict in biological landscapes: the fourth special issue on spatial ecology. International journal of geographical information science, 30 (1), 1–4. [Google Scholar]
- Laube P and Purves RS, 2011. How fast is a cow? cross-scale analysis of movement data. Transactions in GIS, 15 (3), 401–418. [Google Scholar]
- Lele SR, et al., 2013. Selection, use, choice and occupancy: clarifying concepts in resource selection studies. Journal of Animal Ecology, 82 (6), 1183–1191. [Abstract] [Google Scholar]
- Long J, 2016. A Field-Based Time Geography for Wildlife Movement Analysis. In: International Conference on GIScience Short Paper Proceedings, Vol. 1. [Google Scholar]
- Long JA and Nelson TA, 2013a. Measuring dynamic interaction in movement data. Transactions in GIS, 17 (1), 62–77. [Google Scholar]
- Long JA and Nelson TA, 2013b. A review of quantitative methods for movement data. International Journal of Geographical Information Science, 27 (2), 292–318. [Google Scholar]
- Long JA, et al., 2014. A critical examination of indices of dynamic interaction for wildlife telemetry studies. Journal of Animal Ecology, 83 (5), 1216–1233. [Abstract] [Google Scholar]
- Lyons AJ, Turner WC, and Getz WM, 2013. Home range plus: a space-time characterization of movement over real landscapes. Movement Ecology, 1 (1), 2. [Europe PMC free article] [Abstract] [Google Scholar]
- Manly B, et al., 2002. Resource selection by animals: statistical design and analysis for field studies. Kluwer. [Google Scholar]
- McKenzie HW, Lewis MA, and Merrill EH, 2009. First Passage Time Analysis of Animal Movement and Insights into the Functional Response. Bulletin of Mathematical Biology, 71 (1), 107–129. [Abstract] [Google Scholar]
- McManus J, et al., 2015. Dead or alive? Comparing costs and benefits of lethal and non-lethal human–wildlife conflict mitigation on livestock farms. Oryx, 49 (4), 687–695. [Google Scholar]
- McRae BH, et al., 2008. Using circuit theory to model connectivity in ecology, evolution, and conservation. Ecology, 89 (10), 2712–2724. [Abstract] [Google Scholar]
- Michelot T, Langrock R, and Patterson TA, 2016. moveHMM: an R package for the statistical modelling of animal movement data using hidden Markov models. Methods in Ecology and Evolution, 7 (11), 1308–1315. [Google Scholar]
- Millspaugh JJ, et al., 2004. Comparability of three analytical techniques to assess joint space use. Wildlife Society Bulletin, 32 (1), 148–157. [Google Scholar]
- Morales JM, et al., 2004. Extracting more out of relocation data: building movement models as mixtures of random walks. Ecology, 85 (9), 2436–2445. [Google Scholar]
- Mountrakis G and Gunson K, 2009. Multi-scale spatiotemporal analyses of moose–vehicle collisions: a case study in northern Vermont. International Journal of Geographical Information Science, 23 (11), 1389–1412. [Google Scholar]
- Nathan R, et al., 2008. A movement ecology paradigm for unifying organismal movement research. Proceedings of the National Academy of Sciences, 105 (49), 19052–19059. [Europe PMC free article] [Abstract] [Google Scholar]
- Nathan R, et al., 2012. Using tri-axial acceleration data to identify behavioral modes of free-ranging animals: general concepts and tools illustrated for griffon vultures. Journal of Experimental Biology, 215 (6), 986–996. [Europe PMC free article] [Abstract] [Google Scholar]
- Odden M, et al., 2014. Adaptable neighbours: movement patterns of GPS-collared leopards in human dominated landscapes in India. PLoS One, 9 (11), e112044. [Europe PMC free article] [Abstract] [Google Scholar]
- Patterson TA, et al., 2009. Classifying movement behaviour in relation to environmental conditions using hidden Markov models. Journal of Animal Ecology, 78 (6), 1113–1123. [Abstract] [Google Scholar]
- Pennisi E, 2011. Global tracking of small animals gains momentum. Science, 334. [Abstract] [Google Scholar]
- Pinter-Wollman N, et al., 2013. The dynamics of animal social networks: analytical, conceptual, and theoretical advances. Behavioral Ecology, p. art047. [Google Scholar]
- Polansky L, et al., 2010. From moonlight to movement and synchronized randomness: Fourier and wavelet analyses of animal location time series data. Ecology, 91 (5), 1506–1518. [Europe PMC free article] [Abstract] [Google Scholar]
- Powell RA and Mitchell MS, 2012. What is a home range?. Journal of Mammalogy, 93 (4), 948–958. [Google Scholar]
- Qasem L, et al., 2012. Tri-axial dynamic acceleration as a proxy for animal energy expenditure; should we be summing values or calculating the vector?. PloS one, 7 (2), e31187. [Europe PMC free article] [Abstract] [Google Scholar]
- R Core Team, 2017. R: A Language and Environment for Statistical Computing. Vienna, Austria: https://www.R-project.org/. [Google Scholar]
- Rice MR, Middleton BA, and Gibson DJ, 1998. Fractal analysis of movement pathways of earthworms in vegetated and unvegetated landscapes. Bios, 176–184. [Google Scholar]
- Royle JA, et al., 2013. Spatial capture–recapture models for jointly estimating population density and landscape connectivity. Ecology, 94 (2), 287–294. [Abstract] [Google Scholar]
- Sawyer SC, Epps CW, and Brashares JS, 2011. Placing linkages among fragmented habitats: do least-cost models reflect how animals use landscapes?. Journal of Applied Ecology, 48 (3), 668–678. [Google Scholar]
- Seidel DP and Boyce MS, 2015. Patch-use dynamics by a large herbivore. Movement Ecology, 3 (1), 7. [Europe PMC free article] [Abstract] [Google Scholar]
- Shepard EL, et al., 2008. Identification of animal movement patterns using tri-axial accelerometry. Endangered Species Research, 10, 47–60. [Google Scholar]
- Silk M, et al., 2017. Using social network metrics in wildlife disease ecology, epidemiology and management. BioScience, 67 (3), 245–257. [Europe PMC free article] [Abstract] [Google Scholar]
- Skidmore AK, et al., 2011. Geospatial tools address emerging issues in spatial ecology: a review and commentary on the Special Issue. International Journal of Geographical Information Science, 25 (3), 337–365. [Google Scholar]
- Smouse PE, et al., 2010. Stochastic modelling of animal movement. Philosophical Transactions of the Royal Society B: Biological Sciences, 365 (1550), 2201–2211. [Europe PMC free article] [Abstract] [Google Scholar]
- Song C, et al., 2010a. Modelling the scaling properties of human mobility. Nature Physics, 6 (10), 818. [Google Scholar]
- Song C, et al., 2010b. Limits of predictability in human mobility. Science, 327 (5968), 1018–1021. [Abstract] [Google Scholar]
- Sui D, 2014. Opportunities and impediments for open GIS. Transactions in GIS, 18 (1), 1–24. [Google Scholar]
- Sur M, et al., 2014. Change detection in animal movement using discrete wavelet analysis. Ecological Informatics, 20, 47–57. [Google Scholar]
- Tambling CJ, et al., 2010. Methods for locating African lion kills using global positioning system movement data. Journal of Wildlife Management, 74 (3), 549–556. [Google Scholar]
- Thurfjell H, Ciuti S, and Boyce MS, 2014. Applications of step-selection functions in ecology and conservation. Movement Ecology, 2 (1), 4. [Europe PMC free article] [Abstract] [Google Scholar]
- Tischendorf L and Fahrig L, 2000. On the usage and measurement of landscape connectivity. Oikos, 90 (1), 7–19. [Google Scholar]
- Tomkiewicz SM, et al., 2010. Global positioning system and associated technologies in animal behaviour and ecological research. Philosophical Transactions of the Royal Society B, 365 (1550), 2163–2176. [Europe PMC free article] [Abstract] [Google Scholar]
- Trisos CH, et al., 2018. Potentially dangerous consequences for biodiversity of solar geoengineering implementation and termination. Nature Ecology e& Evolution, p. 1. [Abstract] [Google Scholar]
- Turchin P, 1998. Quantitative analysis of movement. Sinauer Associates, Inc.). [Google Scholar]
- van Beest FM and Milner JM, 2013. Behavioural responses to thermal conditions affect seasonal mass change in a heat-sensitive northern ungulate. PLoS One, 8 (6), e65972. [Europe PMC free article] [Abstract] [Google Scholar]
- Van Moorter B, et al., 2016. Movement is the glue connecting home ranges and habitat selection. Journal of Animal Ecology, 85 (1), 21–31. [Abstract] [Google Scholar]
- Van Moorter B, et al., 2010. Identifying movement states from location data using cluster analysis. Journal of Wildlife Management, 74 (3), 588–594. [Google Scholar]
- Van Winkle W, 1975. Comparison of several probabilistic home-range models. Journal of Wildlife Management, 118–123. [Google Scholar]
- Vander Wal E and Rodgers A, 2012. An individual-based quantitative approach for delineating core areas of animal space use. Ecological Modelling, 224 (1), 48–53. [Google Scholar]
- Walker R and Craighead L, 1997. Analyzing wildlife movement corridors in Montana using GIS. In: Proceedings of the 1997 ESRI user conference. [Google Scholar]
- Wang Y, et al., 2015. Movement, resting, and attack behaviors of wild pumas are revealed by tri-axial accelerometer measurements. Movement ecology, 3 (1), 2. [Europe PMC free article] [Abstract] [Google Scholar]
- Webb NF, Hebblewhite M, and Merrill EH, 2008. Statistical methods for identifying wolf kill sites using Global Positioning System locations. Journal of Wildlife Management, 72 (3), 798–807. [Google Scholar]
- Wikelski M and Kays R, 2018. Movebank: archive, analysis and sharing of animal movement data. Hosted by the Max Planck Institute for Ornithology. www.movebank.org, accessed on 05-01-2018.
- Wilson RP, Shepard E, and Liebsch N, 2008. Prying into the intimate details of animal lives: use of a daily diary on animals. Endangered Species Research, 4 (1–2), 123–137. [Google Scholar]
- Wittemyer G, et al., 2008. Disentangling the effects of forage, social rank, and risk on movement autocorrelation of elephants using Fourier and wavelet analyses. Proceedings of the National Academy of Sciences, 105 (49), 19108–19113. [Europe PMC free article] [Abstract] [Google Scholar]
- Woodroffe R, et al., 2006. Effects of culling on badger Meles meles spatial organization: implications for the control of bovine tuberculosis. Journal of Applied Ecology, 43 (1), 1–10. [Google Scholar]
- Worton BJ, 1989. Kernel methods for estimating the utilization distribution in homerange studies. Ecology, 70 (1), 164–168. [Google Scholar]
- Yuan M, 2017. 30 years of IJGIS: the changing landscape of geographical information science and the road ahead. International Journal of Geographical Information Science, 31 (3), 425–434. [Google Scholar]
- Zeller KA, et al., 2016. Using step and path selection functions for estimating resistance to movement: pumas as a case study. Landscape Ecology, 31 (6), 1319–1335. [Google Scholar]
- Zeller KA, McGarigal K, and Whiteley AR, 2012. Estimating landscape resistance to movement: a review. Landscape Ecology, 27 (6), 777–797. [Google Scholar]
- Zidon R, et al., 2017. Zebra migration strategies and anthrax in Etosha National Park, Namibia. Ecosphere, 8 (8). [Europe PMC free article] [Abstract] [Google Scholar]
Full text links
Read article at publisher's site: https://doi.org/10.1080/13658816.2018.1498097
Read article for free, from open access legal sources, via Unpaywall:
https://escholarship.org/content/qt32h1v2q2/qt32h1v2q2.pdf?t=pnw0tb
Citations & impact
Impact metrics
Article citations
Voronoi diagrams and Delaunay triangulation for modelling animal territorial behaviour.
Ecol Evol, 14(7):e11715, 23 Jul 2024
Cited by: 0 articles | PMID: 39045500 | PMCID: PMC11263813
Landscape use by large grazers in a grassland is restructured by wildfire.
PLoS One, 19(2):e0297290, 13 Feb 2024
Cited by: 0 articles | PMID: 38349917 | PMCID: PMC10863880
Where did my dog go? A pilot study exploring the movement ecology of farm dogs.
Front Vet Sci, 10:1325609, 08 Jan 2024
Cited by: 0 articles | PMID: 38260201 | PMCID: PMC10800614
Beyond the horizon: immersive developments for animal ecology research.
Vis Comput Ind Biomed Art, 6(1):11, 20 Jun 2023
Cited by: 0 articles | PMID: 37338732 | PMCID: PMC10281911
Ants combine systematic meandering and correlated random walks when searching for unknown resources.
iScience, 26(2):105916, 30 Jan 2023
Cited by: 4 articles | PMID: 36866038 | PMCID: PMC9971824
Go to all (16) article citations
Data
Data behind the article
This data has been text mined from the article, or deposited into data resources.
BioStudies: supplemental material and supporting data
Data Citations
- (1 citation) DOI - 10.5281/zenodo.1185383
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Animal tracking moves community ecology: Opportunities and challenges.
J Anim Ecol, 91(7):1334-1344, 18 Apr 2022
Cited by: 11 articles | PMID: 35388473 | PMCID: PMC10286655
Characterizing the landscape of movement to identify critical wildlife habitat and corridors.
Conserv Biol, 35(1):346-359, 29 Jun 2020
Cited by: 7 articles | PMID: 32323365
Applying network theory to animal movements to identify properties of landscape space use.
Ecol Appl, 28(3):854-864, 01 Apr 2018
Cited by: 9 articles | PMID: 29420867
Emerging Perspectives on Resource Tracking and Animal Movement Ecology.
Trends Ecol Evol, 36(4):308-320, 20 Nov 2020
Cited by: 39 articles | PMID: 33229137
Review
Funding
Funders who supported this work.
NIGMS NIH HHS (1)
Grant ID: R01 GM083863
NIH-GM (1)
Grant ID: 083863
NSF-EEID (1)
Grant ID: 1617982





