Abstract
Objective
The aim of this study is to compare the performance of three strategies in determining the global innervation zone (IZ) distribution.Methods
High-density surface electromyography was recorded from the biceps brachii muscle of seven healthy subjects under isometric voluntary contractions at 20%, 50%, and 100% of the maximal voluntary contraction and supramaximal musculocutaneous nerve stimulations. IZs were detected: first, by visual identification in a column-specific manner (IZ-1D); second, based on decomposed bipolar mapping of motor unit action potentials (IZ-2D); and third, by source imaging in the three-dimensional muscle space (IZ-3D).Results
All three IZ detection approaches have exhibited excellent trial-to-trial repeatability. Consistent IZ results were found in the axial direction of the arm across all three approaches, yet a difference was observed in the mediolateral direction.Conclusions
Among all three approaches, IZ-3D is capable of providing the most comprehensive information regarding the global IZ distribution, while maintaining high consistency with IZ-1D and IZ-2D results.Significance
IZ-3D approach can be a potential tool for global IZ imaging, which is critical to the clinical diagnosis and treatment of neuromuscular disorders.Free full text

Global Innervation Zone Identification with High-Density Surface Electromyography
Abstract
Objective:
The aim of this study is compare the performance of three strategies in determining the global innervation zone (IZ) distribution.
Methods:
High-density surface electromyography was recorded from the biceps brachii muscle of seven healthy subjects under isometric voluntary contractions at 20%, 50%, 100% of the maximal voluntary contraction (MVC) and supramaximal musculocutaneous nerve stimulations. IZ were detected: 1) by visual identification in a column-specific manner (IZ-1D), 2) based on decomposed bipolar mapping of motor unit action potentials (IZ-2D), 3) source imaging in the three-dimensional muscle space (IZ-3D).
Results:
All three IZ detection approaches have exhibited excellent trial-to-trial repeatability. Consistent IZ results were found in the axial direction of the arm across all three approaches, yet a difference was observed in the mediolateral direction.
Conclusions:
Among all three approaches, IZ-3D is capable of providing the most comprehensive information regarding the global IZ distribution, while maintaining high consistency with IZ-1D and IZ-2D results.
Significance:
IZ-3D approach can be a potential tool for global IZ imaging, which is critical to the clinical diagnosis and treatment of neuromuscular disorders.
I. Introduction
Innervation zone (IZ) has frequently been used as a myoelectric term that indicates the physical territory of the neuromuscular junctions corresponding to one or multiple motor units (MUs) [1]. Accurate identification of IZs is critical to the reliability of amplitude, spectrum, and conduction velocity analyses of bipolar electromyography (EMG) recordings [2]. Additionally, the knowledge of the global IZ distribution can be beneficial to clinical diagnoses [3–6] and the treatment of neuromuscular diseases [7, 8]. Specifically, the targeted injection of botulinum toxin (BTX) to the IZ can improve treatment efficacy of muscle spasticity, while minimizing side effects and cost [7, 9]. Similarly, the IZ is considered to be a valuable biomarker for guiding BTX injection in patients with myofascial pain [8].
The symmetrical propagation of motor unit action potentials (MUAPs), from the neuromuscular junction towards the two ends of the muscle fibers, provides the basis for IZ detection [1]. Multi-channel surface electromyography (sEMG) has been widely employed to capture this symmetrical propagation with evenly spaced sEMG sensors along the muscle fiber direction over the skin. The IZ can then be identified as the point of signal symmetry by a human observer [10]. This strategy, where IZs are identified from a linear sEMG array, is categorized in this manuscript as one-dimensional (1D) IZ detection strategies (IZ-1D). Various other algorithms have also been implemented, including template matching [11], linear regression [1], Hermite shape function [12] and Radon Transform [13], to improve the automation, detection resolution, and noise-robustness of IZ detection with linear arrays. Additional criteria such as lowest signal amplitude, highest mean frequency, conduction velocity, and cross-correlation between differential sEMG channels have also been utilized to locate IZs [14], yet recent research has questioned the applicability of the first two criteria because of their relatively low detection accuracy [15].
High-density sEMG recording approaches have significantly extended the amount of spatiotemporal information obtained during a recording session, which further broadens the surface view of the global IZ distribution and enables the implementation of advanced IZ detection methods. This strategy, where IZs are identified from a two-dimensional (2D) sEMG grid to form a surface view of the IZ distribution over the skin, is categorized herein as 2D IZ detection strategy (IZ-2D). Piitulainen et al. have utilized 2D mapping of sEMG amplitude, mean frequency, and conduction velocity to identify IZs at different contraction levels [16]. Östlund et al. have presented an optic-flow-based IZ detection approach and demonstrated its superior performance over the lowest amplitude method [17]. Enck et al., and Peng et al., studied the IZ distribution symmetry in the pelvic muscles with decomposition-based methods, demonstrating potential applications of IZ localization for the diagnosis of pelvic neuromuscular disorders [4, 18].
Bioelectric source imaging techniques, which were widely employed in electroencephalography studies, have been utilized to extend the dimensionality of IZ detection in the muscle. Our prior work presented this novel IZ imaging approach with high-density sEMG recordings in the biceps brachii muscle [7, 19], and the imaging performance, especially the reconstructed depth, was validated using intramuscular EMG and ultrasonography in a three-dimensional (3D) muscle space [7]. This strategy, where IZs are identified in the 3D muscle space from high-density sEMG grids, is categorized in this manuscript as the 3D IZ detection strategy (IZ-3D).
There lacks a currently available approach for globally validating the motor IZ distribution in vivo, which highlights the importance of a study that compares existing IZ detection strategies. Results are expected to provide additional information regarding the accuracy, reliability and physiological meaning of the available IZ detection strategies. In this study, the performance of three IZ detection strategies, referred to herein as, IZ-1D, IZ-2D, and IZ-3D, were evaluated and compared using high-density sEMG recordings from the biceps brachii muscle in healthy subjects. Resultant intra-approach and inter-approach differences are expected to assess the detection performance of each strategy, as well as reveal the advantages and disadvantages of each approach in studying global IZ distributions.
II. MATERIALS AND METHODS
A. Participants and consent
Seven healthy subjects (six male, one female, mean age 29± 4 years) participated in this study. Before each experiment, every subject was informed of the procedure, any potential risks of the study, and gave written informed consent. The experimental protocol was approved by the University of Houston institutional review board. The biceps brachii muscle of the dominant arm (the right arm in all seven cases) was investigated.
B. Study protocol
The experimental setup was configured as established in previous studies [20, 21]. Briefly, the subjects were seated in an experimental chair with their right arm fixed in a 6 degree-of-freedom load cell (ATI Inc, Apex, NC) for isometric contraction with force feedback. After skin preparation, two high-density (8 by 8 sensors) sEMG grids (TMSi, Enschede, The Netherlands) were placed adjacently along the muscle fiber direction (Fig. 1(a)) to give 8 axial columns and 16 rows of EMG sensors. The adjacent border of two sEMG grids was located over the muscle belly. Each sEMG sensor was 4.5mm in diameter, and the inter-sensor spacing was 8.5 mm. A reference electrode was affixed near the lateral epicondyle of the humerus, and a ground electrode was affixed to the wrist of the idle arm with a thoroughly soaked Velcro strap (TMSi, Enschede, The Netherlands). The distance of the electrode grid to the medial epicondyle of the humerus was noted. All signals were recorded via a Refa-136 amplifier (TMSi, Enschede, The Netherlands) at a sampling frequency of 2,048 Hz, and were stored for offline signal processing.
Subjects were instructed to perform three isometric maximal voluntary contractions (MVCs) of the bicep brachii. Then three isometric contractions at 20% and 50% MVC were performed for 10 s, guided by the feedback of a virtual target representing force level, direction, and stability. Contraction levels of 20%, 50%, and 100% MVC were selected to study the IZ at mild, moderate, and full muscle activation, respectively. Each qualified contraction contained a stable contraction epoch of at least 5 s, and an adequate rest interval was given between trials to avoid muscle fatigue. For 100% MVC, stable contraction epochs of 2–3 s were acquired for each subject. After voluntary contraction, supramaximal compound muscle action potentials (or M-wave) of the biceps brachii muscle were obtained by transcutaneous stimulation of the musculocutaneous nerve via a DS7A constant current stimulator (Digitimer Ltd., Hertfordshire, UK) [20, 22]. M-wave was identified when a further increase of stimulation intensity did not increase the amplitude of muscle response. Stimulation was repeated three times at the supramaximal intensity.
C. IZ Detection
sEMG data were notch filtered at 60 Hz and bandpass filtered at 10–500 Hz with second-order Butterworth filters. Channels which failed to record physiological signals were manually identified by the observation of a flat line at zero and were removed from data analysis. The bipolar sEMG mapping (15 rows by 8 longitudinal columns) was then obtained by subtracting signals of each channel from its distal neighbor. M-wave recordings were notch filtered at 60 Hz and high pass filtered at 1 Hz with second-order Butterworth filters. The stimulation artifacts were identified and replaced with a cubic spline interpolation [19, 23]. The bipolar mappings of M-wave responses were further calculated. Three global IZ detection strategies were employed in this study: identifying IZs on a column-basis (IZ-1D), IZ detection based on sEMG decomposition (IZ-2D) and three-dimensional IZ imaging (IZ-3D).
1) IZ detection on a column-basis (IZ-1D)
Visual IZ assessment with linear electrode arrays is the most common approach with well-proven accuracy and reliability [24, 25]. IZ-1D was achieved by visually identifying the IZ location for each axial column. As shown in Fig. 2(a–b), the IZ was defined by the point of symmetry from the bipolar sEMG mapping [8]. For instance, if phase reversal was observed in neighboring bipolar channels, the IZ was identified as the monopolar channel in the middle that contributes to both bipolar channels, shown in Fig. 2(b). If a bipolar channel with near-zero signal amplitude separated the signal phase reversal; the midpoint of the two monopolar channels which contribute to the attenuated bipolar channel was identified as the IZ, shown in Fig. 2(a). Therefore, a spatial resolution of 4.25 mm (half of the inter-electrode spacing) and 8.5 mm was achieved for IZ detection in the axial and mediolateral directions, respectively. One-sided MUAP propagation and symmetrical distribution of MUAPs without propagation was not considered to be a reliable indicator of an IZ [10]. More than one IZ can be identified for each column, and the IZ location was marked as empty for this specific column if no proper patterns of propagation were present. IZ-1D was performed in sEMG signals during 20%, 50% 100% levels of MVC, and supramaximal M-wave response obtained from electrical stimulation.
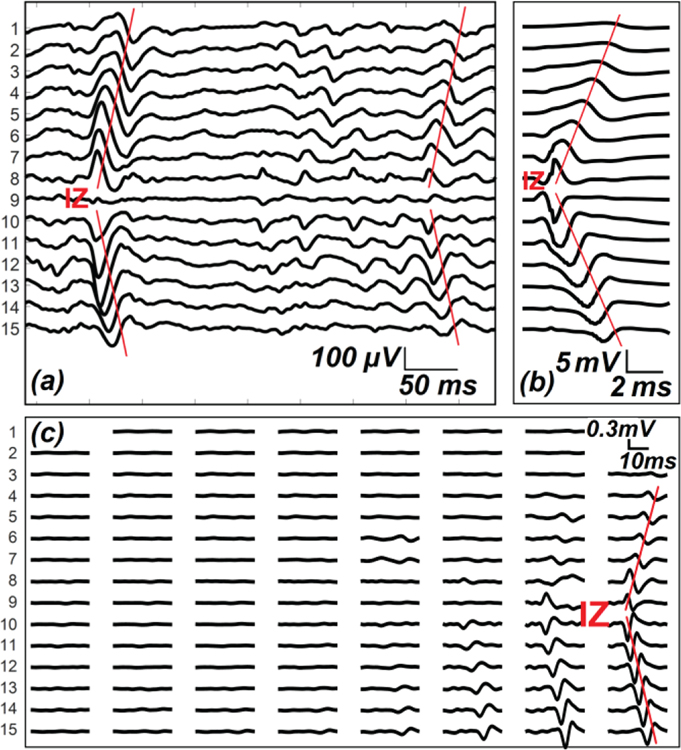
Examples of IZ identification using (a) sEMG recordings during voluntary contraction (IZ-1D); (b) sEMG recordings in response to one electrical stimulation, or M-wave (IZ-1D); (c) decomposed bipolar MUAP mapping (IZ-2D). (a) and (b) shows the 15 bipolar signals from one axial column (16 channels) of sEMG sensors. The red traces mark the signal polarity reversal and propagation. (c) shows the bipolar mappings (15 by 8) of one decomposed MUAP.
2) IZ detection based on sEMG decomposition (IZ-2D)
High-density sEMG signals acquired from voluntary contraction were decomposed into constituent MUAP trains using the K-means convolution kernel compensation (KmCKC) algorithm [4, 26]. Briefly, a K-means clustering method was employed to cluster the firing instances that belong to each specific motor unit; then conventional convolution kernel compensation (CKC) was applied to improve the decomposition accuracy iteratively [27]. Decomposed firing sequences were used to obtain the MUAP waveforms by spike-triggered averaging the sEMG signals in a channel-specific manner. IZ-2D approaches were expected to fully incorporate the spatiotemporal information from high-density sEMG recordings, and provide a representative sample of the entire MU pool [4, 28]. As the territory of a single motor unit is limited to a circular area of 5–7 mm2 [29], only one IZ was determined for each MUAP mapping (Fig. 2(c)). Similarly, each IZ was manually identified by the point of symmetry in the axial and mediolateral directions; thus, a spatial resolution of 4.25 mm was achieved in both directions. IZ-2D was only performed in sEMG signals acquired at 20% and 50% of MVC. sEMG under 100% MVC was not decomposed because of the high levels of MUAP superimposition.
3) 3D IZ Imaging (IZ-3D)
IZ-3D is performed as described in our previous work [19]. In brief, a realistic computational model of the arm was reconstructed from magnetic resonance images as shown in Fig. 1(b). The model was modified and meshed into a finite element model, consisting of 234,103 tetrahedral elements and 40,865 nodes. The conductivity of all anatomical parts was assigned according to literature, and muscle anisotropy was introduced by assigning axial conductivity to be 5 times the muscle conductivity of radial direction [30]. A total of 34,619 discrete current dipoles were positioned with an inter-dipole spacing of 2 mm, and each dipole possessed three orthogonal components. A weighted minimum norm estimation (WMNE) algorithm was employed for source imaging [7, 19, 31–33]. Briefly, the relationship between the source vector J and measurement vector Φ can be expressed as in:
where G is the lead field matrix that maps the sources space to the measurement space; n is the noise vector. The source strength J can be then obtained as:
where W is the weighting matrix that modulates the source influence at different depths; λ is the regularization parameter determined by the L-curve method [34]. Reconstructed dipoles with a current density greater than 50% of the maximal dipole intensity were considered active, and the region marked by the cluster of active dipoles was noted as the IZ region. The intersection of IZ clusters determined in three trials was selected for comparison with other approaches. IZ-3D was performed specifically with supramaximal M-wave recordings.
D. Comparison between different IZ detection approaches
IZ coordinates were determined in reference to the distal-lateral end of the electrode grid. The geometric center of the IZs defined by all three different detection approaches was determined. The Euclidean distance between the IZ centers was used to compare the detection results. IZ-3D yields clusters of discrete active dipoles that indicate the IZ distributions. To better compare IZ-3D with other approaches, the selected dipoles were then projected to the 2D plane of electrode sensors using a weighted average of the k-nearest neighbor method. In brief, the Euclidean distance between the dipoles and sensors was calculated in the 3D space, and the nearest k neighbors were determined, and their weights calculated by Shepard’s method. The projected dipole location was defined by the weighted average of the k nearest neighbors in the 2D X-Y plane. Then the boundary of the projected dipoles was selected to mark the territory of the projected IZ-3D. In this study, k was set empirically to 6. As the dipoles may be located outside the coverage of the sEMG grid, an extended 3D sensor mapping with a fixed inter-sensor spacing was used. The ratio of IZs detected by IZ-1D and IZ-2D that fell into the projected IZ-3D territory was determined.
E. Trial-to-trial repeatability of each IZ detection strategy
The average absolute Euclidean distance between IZ centers was used to assess the trial-to-trial repeatability. Specifically, for IZ-1D, the variance of the IZ location was also evaluated on a column-specific basis; for IZ-3D, the repeatability was also indicated by the similarity coefficient between IZ clusters determined, using an extended Sørensen similarity index:
Where T1, T2, T3 represents the number of dipoles reconstructed from three stimulation trials; and T1T2, T1T3, T2T3 represents the number of dipoles shared by every two trials, respectively, and T1T2T3 the number of dipoles shared by all three trials [35]. The similarity index was presented as a 0–1 index, where 1 means complete similarity.
III. RESULTS
All seven subjects yielded successful sEMG recordings. Two trials were excluded due to poor recording quality in one subject (one trial at 20%MVC and one at 50% MVC). One corrupted channel was identified from Subject 05 and removed from further analysis. Clear patterns of phase reversal and MUAP propagation were observed in 616 of 656 bipolar sEMG columns investigated. An averaged number of IZ detected with IZ-1D per trial was 12±2, 12±2, 10±3, 7±1 for 20%, 50%, 100% MVC and M-wave recordings, respectively. IZs identified using the IZ-1D were concentrated mostly around the muscle belly (Subject 02 and 03), while the IZs were located proximally in Subject 01.
sEMG decomposition was successfully performed using the KmCKC algorithm, yielding 9±3 MUs at 20% MVC, and 11±2 MUs at 50% MVC. IZs were identified in 92.5% and 91.8% of the bipolar MUAP mappings at 20% and 50% MVC, respectively. IZ-3D was performed in all subjects and provided an estimation of the IZ locations and volume in the 3D space of the biceps muscle. In three of the subjects tested, two distinct IZ clusters were reconstructed, and only one IZ cluster was reconstructed for the remaining subjects. Fig. 3a--3c3c shows three representative imaging results with spatial IZ distributions across all three trials.
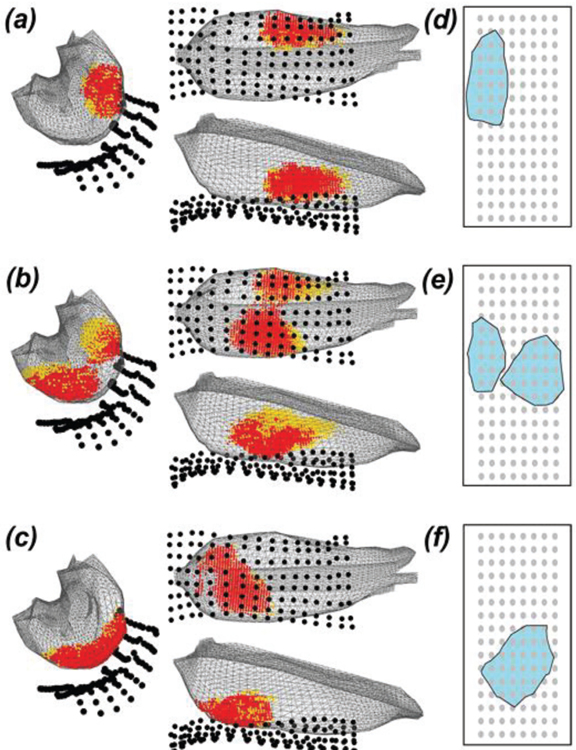
IZ-3D results in three representative participants (a–c). Red dots mark the intersection of IZ clusters defined by three repeating trials. Each orange dot marks the dipole location that was not mutually activated. The cluster of active dipoles exhibit the region of IZ reconstructed using IZ-3D approach. The corresponding IZ cluster projected to 2D X-Y surface was shown on the right (d–f). The grey dots represent the sensor location. The shaded region (cyan) shows the area of IZ projected to the 2D plane.
The geometric centers of all IZs were averaged across all trials. The longitudinal distances in reference to the medial epicondyle of the humerus were 7.11±1.69, 7.16±1.62, 7.05±1.49, 6.77±1.66 cm by IZ-1D at 20%, 50%, 100% MVC and M-wave recordings, respectively. For IZ-2D, the distance from the IZ center to the anatomical landmark was calculated as 7.24±1.56 and 6.96±1.18 cm for the decomposed sEMG recorded at 20% and 50% MVC, respectively. IZ-3D yielded a center-to-reference distance of 7.31±1.95 cm and a mean IZ depth of 1.43±0.32 cm from the skin surface.
Comparison between IZs defined by IZ-1D, IZ-2D, and IZ-3D in three representative subjects is visualized in Fig. 4. The IZ-3D territory, shown as the shaded region in Fig. 4, overlapped the majority of IZs (mean of 81.0±5.9%, from 71.0 to 87.5%) defined by other approaches. The coverage ratio was summarized in Table 1. The IZ territory defined by the IZ-3D approach exhibited the best coverage of IZ-2D results (86.1±18.8% at 20% MVC and 87.5±14.0% at 50% MVC). The comparison between different IZ centers is shown in Fig. 5. Results show an overall similarity between all IZ centers. IZ-2D defined the most distant IZ centers (> 1cm) compared to other approaches, shown by Fig. 4 and Fig. 5.
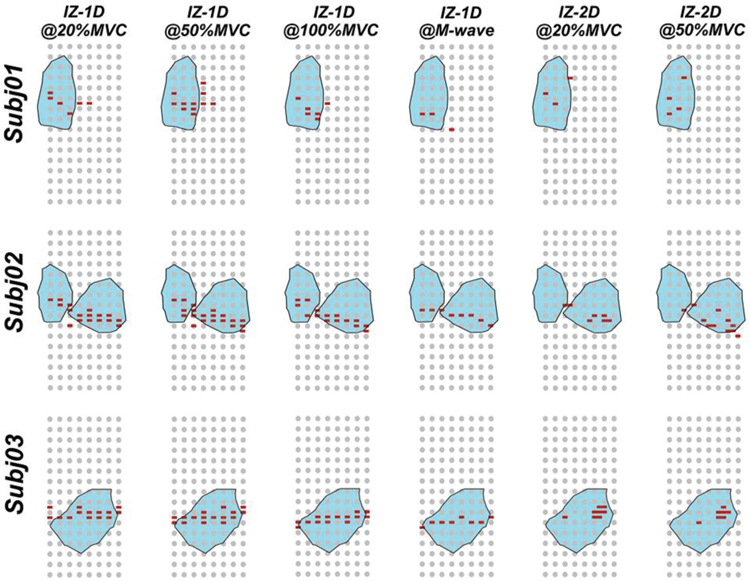
Summarization of identified IZ results using three detection strategies and at different levels of muscle activation. The grey dots represent the sensor locations and red dots the location of identified IZs. Shaded region (cyan) shows the area of corresponding IZ-3D results projected to the 2D X-Y plane.

Heat map summarizing the distance between IZ centers determined by different detection approach. The diagonal represents the trial-to-trial center variations under the same detection approach.
Table 1.
The coverage ratio of IZ-3D results to the other two approaches
| Subj# |  IZ-1D @20% IZ-1D @20% |  IZ-1D @50% IZ-1D @50% |  IZ-1D @100% IZ-1D @100% |  IZ-1D @M-wave IZ-1D @M-wave |  IZ-2D @20% IZ-2D @20% |  IZ-2D @50% IZ-2D @50% |
|---|---|---|---|---|---|---|
| 1 |   63.3% 63.3% |   64.6% 64.6% |   75.0% 75.0% |   50.0% 50.0% |   90.0% 90.0% |   87.3% 87.3% |
| 2 |   92.0% 92.0% |   86.0% 86.0% |   82.0% 82.0% |   88.0% 88.0% |   94.0% 94.0% |   84.0% 84.0% |
| 3 |   77.0% 77.0% |   83.0% 83.0% |   70.0% 70.0% |   75.0% 75.0% |   100.0% 100.0% |   100.0% 100.0% |
| 4 |   75.0% 75.0% |   81.0% 81.0% |   81.0% 81.0% |   50.0% 50.0% |   100.0% 100.0% |   100.0% 100.0% |
| 5 |   100.0% 100.0% |   100.0% 100.0% |   100.0% 100.0% |   100.0% 100.0% |   100.0% 100.0% |   100.0% 100.0% |
| 6 |   73.0% 73.0% |   81.0% 81.0% |   71.0% 71.0% |   71.0% 71.0% |   64.0% 64.0% |   63.0% 63.0% |
| 7 |   71.0% 71.0% |   82.0% 82.0% |   83.0% 83.0% |   63.0% 63.0% |   55.0% 55.0% |   78.0% 78.0% |
| Mean |   78.8% 78.8% |   82.5% 82.5% |   80.3% 80.3% |   71.0% 71.0% |   86.1% 86.1% |   87.5% 87.5% |
| SD |   12.8% 12.8% |   9.6% 9.6% |   10.2% 10.2% |   18.7% 18.7% |   18.8% 18.8% |   14.0% 14.0% |
IV. Discussion
This study compared three IZ detection approaches at different levels of muscle activation including mild (20% MVC: IZ-1D and IZ-2D), moderate (50% MVC: IZ-1D and IZ-2D) and full activation (100% MVC: IZ-1D; M-wave: IZ-1D and IZ-3D). Similar geometry IZ centers were identified using different approaches, especially in the axial direction, which confirms the detection reliability of all approaches. A relative distance of 6.77–7.31 cm to the anatomical landmark at the right elbow is very close to the prior estimation of 7.58 cm in biceps brachii [36]. The results are also consistent with a prior anatomical staining study that reported a distance of 7–10 cm from the motor endplate band of biceps brachii to the olecranon [37]. This IZ-to-reference distance is slightly lower than the 9.4 cm reported in our earlier 3D IZ study [19]. The difference may be caused by the adoption of a more representative anisotropic model, and the altered placement of electrode grids, with more sensors placed along the longitudinal direction in our current study. Therefore, better reconstruction accuracy, especially along the axial direction of the arm, is expected. Meanwhile, the high trial-to-trial repeatability observed suggests that the IZ can be reliably identified with all strategies studied. Our results agree with previous studies by exhibiting the high repeatability of IZ detection for IZ-1D [24], IZ-2D [18], and IZ-3D [19]. Variability of global IZ distribution between subjects has been observed in all three detection strategies, which can be attributed to the individual difference in muscle geometry [38]. Prior studies have demonstrated signs of IZ shift at different contraction levels during isometric voluntary contractions [16, 24]. Although changes in IZ location were observed at higher contraction levels, this study lacks adequate evidence of an IZ shift in the axial direction (Data not shown).
IZ-1D was performed by treating each individual column of sensors as an independent linear array and combining results of all columns to reveal the global distribution of the IZs. Our results have demonstrated that the IZ-1D approach revealed the most detailed information about the IZ that may be neglected by IZ-2D or IZ-3D approaches, shown in Fig. 4. However, the MUAPs of relatively large MUs can be detected by multiple columns of sensors. Thus, an erroneous approximation of the IZ distribution may result from the repeated identification of the same MUAP. Second, IZ-1D cannot distinguish MUs that share the same innervation location, and thus fails to provide the density of IZ distributions. Consequently, the center tends to appear in the midline of the recording grid in the mediolateral direction. On the other hand, EMG decomposition can provide a more representative MUAP activation pattern [39, 40]. IZ-2D distinguishes MUs with mutual IZs; therefore, the IZ distribution density can be obtained. Additionally, the MUAP amplitude was attenuated in sEMG channels located further away from the IZ column; hence the over-identification of the same IZ was unlikely. The decomposition-based IZ detection approach has previously been employed to study the innervation symmetry of pelvic muscles [4, 5, 13, 28], where compromised innervation symmetry may suggest the presence of neuromuscular dysfunctions.
IZ-1D with M-wave exhibited the best trial-to-trial repeatability of all approaches studied, which can be attributed to the consistent muscle response to nerve stimulation [41]. IZ-1D with M-wave was most consistent with IZ-1D results at 100% MVC, less consistent at 50% MVC and the least consistent at 20% MVC, which is likely due to the similar activation levels between M-wave and 100% MVC recordings. Aside from a recent study that used point of symmetry and highest slope of the rising phase of M-wave for the assessment of IZ location [42], limited effort has been made to use M-wave for IZ identification. Compared to voluntary contraction, IZ-1D based on M-wave recordings features distinct advantages. First, the full and reliable activation of the muscle can be obtained by M-wave recordings. As M-wave precedes muscle contraction, the process can also be considered ideally isometric [19]. Furthermore, M-wave signals do not require the voluntary control of the muscles and hence can still be reliably obtained in patients with impaired motor or cognitive function. Therefore, global IZ detection based on M-wave recordings maintains potential applicability in both research and clinical fields.
By incorporating a high-density M-wave recording, the 3D muscle source imaging technique provides global innervation information of a given muscle. This global information, especially the IZ depth, is uniquely valuable in the clinical guidance of BTX injection for the treatment of spasticity and myofascial pain. Aside from the depth information it yields, IZ-3D also exhibited a high center-to-center consistency with IZ-1D results in this study. The projected IZ territory was able to cover the majority of IZs detected using both the IZ-1D and IZ-2D approaches. More importantly, in cases where the IZ fell beyond the coverage of the sensor grid, IZ-3D was the only method which compensates for this grid misplacement [19], shown in Fig. 4(a) (Subject 01). All these results suggest that, although IZ-3D is the most calculation-intensive approach, it can provide the most comprehensive information regarding the global IZ distribution, without losing 2D accuracy. In addition, IZ-3D based on M-wave also features the advantages of high repeatability and broader clinical applicability.
Moreover, IZ-1D and IZ-2D rely largely on the bidirectional propagation of MUAPs; hence the accuracy of these two approaches can be compromised by short muscle fiber length [25] and/or the misalignment of the electrode grid along the muscle fiber orientation [25, 43]. Therefore, care should be taken when positioning the detecting electrodes. Misalignment can be compensated by adjusting the differential analysis of recordings, by subtracting each channel with its closest neighbor along the fiber direction (in this study, the axial direction) [25, 44]. IZ-3D is not sensitive to the relative changes of fascicle orientation, and therefore more applicable to muscles with varied fiber length and orientations. However, muscle anisotropy should be adjusted accordingly.
In this study, 20% and 50% MVC were selected for IZ identification using IZ-1D and IZ-2D strategies, as these force levels have been most commonly used in previous studies [8, 24]. Although only a portion of the motor unit pool is activated at these levels, the results are expected to provide a representative sample by locating the IZ specifically for the activated motor units. Our results also suggest a good match between overall IZ results at lower and higher force levels. It should also be noted that 3D-IZ results are performed with supramaximal M-wave recordings but not MVCs. The rationale behind this signal selection is that the potential mapping during contraction can alter rapidly over time, making repeatable imaging difficult. Second, signal cancellation may happen and the active dipoles reconstructed from surface potential mapping can involve complicated physiological meanings, and may not be considered a direct indicator of IZ location. Our previous work also employed a decomposition-based IZ-3D method to approach an accurate IZ depth [7]. However, the method relies on the prior knowledge of IZ-2D results and thus does not fit into the purpose of this study.
A previous study in which motor endplates in the human biceps were stained reported that endplate zone was a 1 cm width band located 7–11 cm away from the olecranon [37]. In our study, IZ-3D results provided the most blurred estimation of the IZ distribution with an axial spread of approximately 3–6 cm inter-electrode spacing. Although very similar to a prior study on IZ estimation [1], the axial spread is wider than both the human staining results, and IZs detected with the other two approaches. Axial spread can be suppressed by increasing the threshold of selecting active current dipoles which indicate possible IZ locations; yet it will compromise the proper estimation of innervation depth. However, the geometry centers of IZ-3D results are consistent with the other two approaches in the axial direction, suggesting this blurred estimation does not affect the axial accuracy. Clinically, an IZ detection technique may be used for guiding the placement of surface electrodes for EMG recording or injection of botulinum toxin for targeted muscle relaxation. The center of IZ-3D results can be used for the guidance, due to the consistency between different approaches.
Prior studies have demonstrated the necessity of guided BTX injection in spasticity management, evidencing that injections further than 1 cm away from the IZ can lower the treatment efficacy by approximately half [9]. Therefore, the accurate detection of the global IZ distribution is of significant clinical importance. Interestingly, we have found that the discrepancies between strategy-specific IZ centers were largely contributed by disagreements in the mediolateral, rather than axial direction. Future validation studies are needed to confirm which approach is more suggestive of the most effective injection site. A simulation study with a known IZ distribution may be indicative of such and remains our future work [45]. Furthermore, this comparative study was performed in healthy muscles, yet anatomical and neuromuscular alterations may occur after stroke or spinal cord injury, and consequently affect the innervation territory and EMG signal quality. Care should be taken while applying IZ-3D method in pathological muscles where the tissue conductivity may be altered. IZ-3D will be generally more applicable than IZ-1D or IZ-2D strategies as the ability to accomplish contraction tasks may be partly or fully compromised in patients. The small sample size in this study provides a preliminary glance at the performance consistencies of three different IZ detection strategies. Larger sample size may be required to confirm these conclusions.
V. Conclusion
In this study, three different approaches were employed to localize the global IZ distribution in healthy biceps brachii muscles. Intra-approach comparison has suggested excellent trial-to-trial repeatability for all approaches. In inter-approach comparisons, IZ location difference was noted mainly in the mediolateral direction rather than axial direction. As there lacks a direct, in vivo approach for the identification of global IZs, the method which provides the best mediolateral estimation requires further investigation. Nonetheless, IZ-3D provides the most comprehensive information, by localizing the IZ under full motor unit activation and assessing the IZ distribution in the 3D muscle space. IZ-3D is expected to provide an accurate global IZ location that can be used to guide the clinical injection of BTX for the management of spasticity or dystonia. The technique can also be further adapted other muscles that can be accessed with sEMG and nerve stimulations.
Table 2.
Repeatability for IZ-1D and IZ-3D approach
 Subj# Subj# |  IZ-1D @20% IZ-1D @20% |  IZ-1D @50% IZ-1D @50% |  IZ-1D @100% IZ-1D @100% |  1Z-1D @M-wave 1Z-1D @M-wave |  IZ-3D Similarity Index IZ-3D Similarity Index |
|---|---|---|---|---|---|
| 1 | 0.13 | 0.11 | 0.04 | 0.00 | 0.88 |
| 2 | 0.04 | 0.02 | 0.00 | 0.00 | 0.86 |
| 3 | 0.05 | 0.12 | 0.07 | 0.00 | 0.87 |
| 4 | 0.19 | 0.09 | 0.25 | 0.04 | 0.98 |
| 5 | 0.16 | 0.09 | 0.16 | 0.00 | 0.97 |
| 6 | 0.16 | 0.16 | 0.02 | 0.00 | 0.92 |
| 7 | 0.11 | 0.08 | 0.18 | 0.00 | 0.86 |
 Mean Mean | 0.12 | 0.10 | 0.10 | 0.01 | 0.91 |
| SD | 0.06 | 0.04 | 0.09 | 0.01 | 0.05 |
Acknowledgment
This work was supported in part by NIH R21HD090453, R00DK082644, R24HD050821 and the University of Houston.
Contributor Information
Chuan Zhang, Department of Biomedical Engineering, University of Houston, Houston, TX 77204 USA.
Nicholas Dias, Department of Biomedical Engineering, University of Houston, Houston, TX 77204 USA.
Jinbao He, School of Electronic and Information Engineering, Ningbo University of Technology, Ningbo, P.R. China.
Ping Zhou, Department of Physical Medicine and Rehabilitation, University of Texas Health Science Center at Houston, Houston, TX, 77030 USA.
Sheng Li, Department of Physical Medicine and Rehabilitation, University of Texas Health Science Center at Houston, Houston, TX, 77030 USA.
Yingchun Zhang, Department of Biomedical Engineering, University of Houston, Houston, TX 77204 USA.
References
Full text links
Read article at publisher's site: https://doi.org/10.1109/tbme.2019.2919906
Read article for free, from open access legal sources, via Unpaywall:
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7135959
Citations & impact
Impact metrics
Citations of article over time
Article citations
NeuroMotion: Open-source platform with neuromechanical and deep network modules to generate surface EMG signals during voluntary movement.
PLoS Comput Biol, 20(7):e1012257, 03 Jul 2024
Cited by: 2 articles | PMID: 38959262 | PMCID: PMC11251629
Muscle innervation zone estimation from monopolar high-density M-waves using principal component analysis and radon transform.
Front Physiol, 14:1137146, 15 Mar 2023
Cited by: 0 articles | PMID: 37008017 | PMCID: PMC10050562
Motor Unit Number Estimation in Spastic Biceps Brachii Muscles of Chronic Stroke Survivors Before and After BoNT Injection.
IEEE Trans Biomed Eng, 70(3):1045-1052, 17 Feb 2023
Cited by: 1 article | PMID: 36126033 | PMCID: PMC10676740
Three-dimensional mapping reveals heterochronic development of the neuromuscular system in postnatal mouse skeletal muscles.
Commun Biol, 5(1):1200, 08 Nov 2022
Cited by: 4 articles | PMID: 36347940 | PMCID: PMC9643545
Motor unit distribution and recruitment in spastic and non-spastic bilateral biceps brachii muscles of chronic stroke survivors.
J Neural Eng, 19(4), 24 Aug 2022
Cited by: 6 articles | PMID: 35926440 | PMCID: PMC9526353
Go to all (8) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Spatial characterization of innervation zones under electrically elicited M-wave.
Annu Int Conf IEEE Eng Med Biol Soc, 2016:121-124, 01 Aug 2016
Cited by: 1 article | PMID: 28268294
Innervation zone distribution of the biceps brachii muscle examined using voluntary and electrically-evoked high-density surface EMG.
J Neuroeng Rehabil, 16(1):73, 11 Jun 2019
Cited by: 9 articles | PMID: 31186009 | PMCID: PMC6560814
Investigation of innervation zone shift with continuous dynamic muscle contraction.
Comput Math Methods Med, 2013:174342, 03 Jun 2013
Cited by: 8 articles | PMID: 23762179 | PMCID: PMC3677009
Distribution of innervation zone and muscle fiber conduction velocity in the biceps brachii muscle.
J Electromyogr Kinesiol, 63:102637, 04 Feb 2022
Cited by: 1 article | PMID: 35176686 | PMCID: PMC8960364
Funding
Funders who supported this work.
NIA NIH HHS (1)
Grant ID: R56 AG053778
NICHD NIH HHS (2)
Grant ID: R21 HD090453
Grant ID: R24 HD050821
NIDDK NIH HHS (2)
Grant ID: R00 DK082644
Grant ID: R21 DK113525
National Institutes of Health (3)
Grant ID: R24HD050821
Grant ID: R00DK082644
Grant ID: R21HD090453





