Abstract
Free full text

Sampling to elucidate the dynamics of infections in reservoir hosts
Abstract
The risk of zoonotic spillover from reservoir hosts, such as wildlife or domestic livestock, to people is shaped by the spatial and temporal distribution of infection in reservoir populations. Quantifying these distributions is a key challenge in epidemiology and disease ecology that requires researchers to make trade-offs between the extent and intensity of spatial versus temporal sampling. We discuss sampling methods that strengthen the reliability and validity of inferences about the dynamics of zoonotic pathogens in wildlife hosts.
This article is part of the theme issue ‘Dynamic and integrative approaches to understanding pathogen spillover’.
1. Introduction
At any point in space and time, the risk of pathogen spillover from reservoir hosts to humans, or to other animals, is a function of the intensity of infection within reservoir host populations [1]. Spillover risk is then shaped by a series of processes including the release of infectious particles from reservoir hosts, response of pathogen survival to the environment, behaviours that affect exposure of recipient hosts, and biologically driven susceptibility of recipient hosts [1]. Here, we focus on the dynamics of infection in wildlife reservoirs that determine how pathogen intensity is distributed in space and time.
Quantification of these dynamics is necessary to predict and manage zoonotic transmission [2]. Emerging zoonoses often appear suddenly in novel recipient hosts, and sampling of reservoir hosts (hosts in which the pathogen is maintained [3]) is initiated before the dynamics of the zoonosis are fully characterized. Therefore, sampling often is opportunistic or haphazard and is guided by sparse information on, for example, the observed patterns of spillover and the natural history of the reservoir host. Moreover, information on the pathogen in reservoir hosts, which often tolerate infection with no apparent clinical symptoms or pathology [4], is difficult to obtain. Catching, restraining and sampling hosts, or testing excreta such as urine or faeces, is usually required [5,6], and can be logistically intensive, expensive and hazardous. Therefore, we address how sampling can be designed to minimize these challenges while maximizing information gain.
Design of any sampling strategy requires clear specification of objectives (table 1). The fundamental objective of sampling to inform management of spillover is to identify times and places at which the risk of spillover is elevated. If the reservoir hosts of an emerging pathogen are not well characterized, a wide variety of potential hosts must be sampled to determine whether and the extent to which they can be infected by the pathogen [7]. In other situations, the reservoir hosts are known and are subject to pathogen incursions from other locations (e.g. [8]). Here, we review sampling strategies for situations in which one or more potential reservoir species have been identified, and the pathogen may be endemic. We do not cover well-described statistical approaches such as power and sample size analyses. We also simulate a theoretical wildlife disease to illustrate how spatial and temporal variability or synchrony in infection dynamics can inform sampling decisions and inferences about disease dynamics.
Table 1.
Illustrative goals and objectives motivating studies of pathogens in reservoir hosts.
| goal | objectives | data needed | sampling approaches |
|---|---|---|---|
| identify distribution of reservoir hosts and how those hosts and populations are connected through space and time | estimate the spatial distribution and density of reservoir hosts estimate the spatial and temporal extents of connections between reservoir host units | spatially explicit presence and absence of marked or unmarked animals movements of known and instrumented individuals population-level genetics on individuals and groups | aerial or ground surveys that account for detection probability and use a robust design |
| identify times and places with high prevalence in reservoir hosts | determine coarse-resolution patterns of prevalence in reservoir hosts, variation in prevalence among reservoir host populations, and the spatial extent of infection estimate the spatial and temporal autocorrelation of infectious animals or populations | spatially and temporally replicated prevalence and seroprevalence within- and among-population prevalence (or seroprevalence if the refractory period is short relative to the host lifespan) in space and time and over life-history stages | probabilistic, spatially and temporally stratified sampling of reservoir host populations adaptive sampling of probabilistically selected, higher-prevalence sites |
| identify causes of high prevalence in reservoir hosts | estimate the infectious period, exogenous and endogenous covariates associated with infection, and shedding loads | pathogen status, load, immunity and demography of infected and uninfected hosts | probabilistic sampling of populations with high, moderate and low prevalence |
| identify patterns of transmission in the reservoir host | identify covariates associated with increased susceptibility or transmission estimate rates of change of prevalence to inform the temporal resolution of sampling | time-series of cases or seroconversions in space from same locations longitudinal sampling of individual infection status to identify change in infection state of individuals over time age-stratified prevalence or seroprevalence | longitudinal sampling of individuals and populations |
| estimate risk of spillover to recipient hosts across space and time to predict future events | investigate the pathogen's potential to persist in the environment describe when, where, and how reservoir and recipient host species interact | biotic and abiotic environmental attributes at small and large spatial extents and resolutions contacts among individuals multispecies (sero)surveys to identify high-prevalence hosts in areas with high prevalence comparative studies of exuded load per host across host species to understand variation in pathogen release among host species | probabilistic, spatially and temporally stratified sampling of reservoir host populations |
| explore interventions to reduce prevalence or magnitude of an epidemic, or eradicate infection from reservoir hosts | estimate rate of epidemic growth and reproductive number (R0) estimate rates of effective vaccination or culling design effective implementation strategies (e.g. ring vaccination or culling, treatments at the infection front) | prevalence over time and duration in infection class age-stratified prevalence or seroprevalence and demographic data | longitudinal sampling during epidemics at invasion zones |
2. Processes driving the distribution and synchrony of pathogens in reservoir hosts
(a) Spatial and temporal distribution and intensity
The distribution and intensity of infection in reservoir hosts vary among individuals and among populations in space and time. This variation is driven by many within- and between-host factors, including host demography and movement, transmission rates, infectious periods and herd immunity. Below we describe the factors that influence spatial and temporal variation. In most instances, there is little a priori information to decipher the drivers of variation, and these knowledge gaps must be addressed with sampling (table 1).
When a pathogen first invades a population of hosts, transmission dynamics may be synchronized through the invasion process [9]. Such invasion dynamics may characterize West Nile virus and avian influenza H5N1 invasion in wild birds in the USA, or Zika virus invasion in marmosets (Callithrix species) in Brazil [10–12]. During this phase, the basic reproduction number, R0, the average number of secondary infections generated over an individual's infectious period when infection is rare [13], is a powerful distillation of the efficiency of pathogen spread. Beyond the initial stage of pathogen invasion, however, R0 does not capture all fundamental elements of pathogen dynamics that affect the distribution of infection in space and time. For example, a pathogen that produces an acute (short-lived) immunizing infection with high transmission and mortality rates might spread quickly through local host populations and then fade out, to be reintroduced after the pool of susceptible hosts is replenished. Such short-lived epidemics of Yersinia pestis in rats, for example, may explain the sporadic outbreaks of bubonic plague in humans in both fourteenth to sixteenth century Europe [14] and modern urban Madagascar [15]. By contrast, another pathogen with a comparable R0, but a long infectious period and low transmission rate, may persist in the same population for long periods, eventually producing a spatially and temporally stable infection intensity as exemplified by Mycobacterium bovis in white-tailed deer (Odocoileus virginianus) in Michigan, USA [16].
Once a pathogen has established in the reservoir host populations, within-host factors (e.g. duration of infection within hosts) interact with the population dynamics, density and movement of reservoir hosts to determine the distribution of infection among hosts [17–19]. The intensity of infection within individuals is governed by immune responses and pathogen life history. Because individuals acquire immunity, they typically have higher pathogen loads during their first infection than during subsequent infections. For example, juvenile Rousettus aegyptiacus bats that excreted high levels of Marburg virus during their first infections were linked to spillover of the virus to humans in Uganda [20]. Similarly, pathogen burden and shedding rates can vary over the course of infection as a function of changes in the immune response, microbiome and pathogen distribution within the host tissues. Bank voles (Clethrionomys glareolus) infected with Puumala virus shed high titres of virus during the acute phase of infection and low titres during the chronic phase of infection [21]. Pathogen levels also can rise if host individuals are infected with multiple pathogens or are immunocompromised by physiological or environmental stress. Laboratory mice infected with both worms and bacteria, for example, shed more of both for longer than those infected with either pathogen in isolation [22], and bats (Pteropus alecto) are hypothesized to excrete zoonotic viruses during winter, when environmental stress drives reactivation of latent viruses [23–25], but not during summer, when food is abundant [26].
(b) Synchrony
The nature of the transmission process usually leads to synchrony in the distribution of infection among individuals at some spatial scale. Tobler's first law of geography states ‘near things are more related than distant things' [27]. Accordingly, the correlation of values of a variable through space (spatial autocorrelation) and time (temporal autocorrelation) is usually positive. Understanding spatial synchrony of infection [28] can help inform sampling design.
Synchrony of infections within populations can arise through myriad processes that drive pathogen transmission (electronic supplementary material, table S1). These include processes that drive synchrony of animal populations (dispersal, social organization and Moran effects (correlation between population size or density that is linearly related to the correlation between their environments), figure 1), processes that drive synchrony of population-immunity (e.g. the strong and directional autocorrelation of invasion, the influx of susceptibles through birth, and synchronization of susceptibility through stress from environmental perturbations), and processes that drive synchrony of exposure, such as pathogen survival (e.g. the response of influenza survival to humidity [29] and of Hendra virus survival to temperature [30]), or behaviour (e.g. winter consumption of date-palm sap by humans in Bangladesh [31]). Synchrony of transmission commonly is seasonal, especially in temperate zones [32]. Efficient sampling of the distribution of infection requires estimating the spatial and temporal scales at which infection dynamics in the reservoir host are synchronized and the extent to which variability or trends in those dynamics are predictable [32].
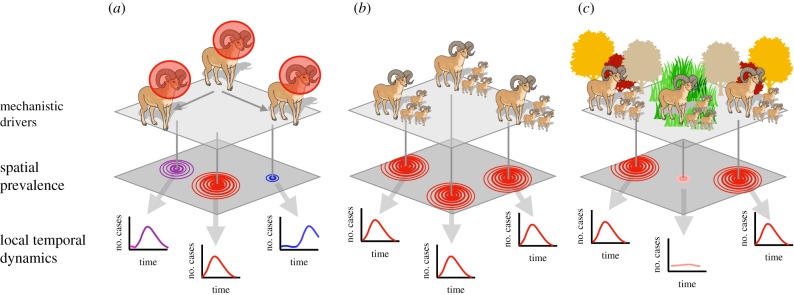
Mechanisms governing spatial and temporal patterns and structure of disease dynamics include dispersal of individuals, social organization and synchrony of host populations and Moran effects. For each mechanism, the color on the spatial prevalence panel indicates the time at which the local outbreak began, and the circles represent the extent of the pathogen in space. The prevalence curves in the local temporal dynamics panel show prevalence through time at the epicentre of each local outbreak. In (a), dispersal of infected hosts (bighorn sheep with red circles) produces spatial and temporal autocorrelation consistent with the movement patterns of the primary host. In (b), synchronous demographic or behavioural dynamics within the host species produce synchrony in spatial and temporal dynamics of prevalence within all host populations. In (c), Moran effects across populations create synchrony among populations experiencing similar environmental conditions. Here, we imagine that limited nutritional availability consistently increases host susceptibility to infection during autumn in forest populations. This leads to synchronous outbreaks in all forest populations that experience the nutrient deficit, without simultaneous outbreaks in populations in locations that are not forested. Cases are infected individuals.
The spatial extent of synchrony depends on the extent of the process driving synchrony. When host movement drives infection dynamics, spatial autocorrelation is driven by the rate of host movement relative to the infectious period of the pathogen [33]. For example, the more thoroughly mixed the contacts among populations, and the longer the infectious period, the lower the spatial variability in infection dynamics (figure 2c,d). However, acute pathogens in hosts with high connectivity may be as thoroughly mixed as chronic pathogens in hosts with low connectivity [33]. If movement rates of hosts are not high enough to ensure transmission to new subpopulations before recovery from infection, infection can become trapped in subgroups [35]. For example, the spread of measles, an acute disease, is limited in regions where walking is a more common mode of transportation than motorized vehicles [36]. By contrast, measles occurred in waves across the UK prior to vaccination [37] because great distances could be travelled by car or train within the two-week infectious period. High movement rates relative to infectious periods create synchronous dynamics across populations, maintenance of herd immunity and dampening of epidemics [38]. However, high synchrony also can lead to synchronous pathogen extinction across all infected populations. Understanding host movement relative to the pathogen's infectious period is critical to inform sampling.
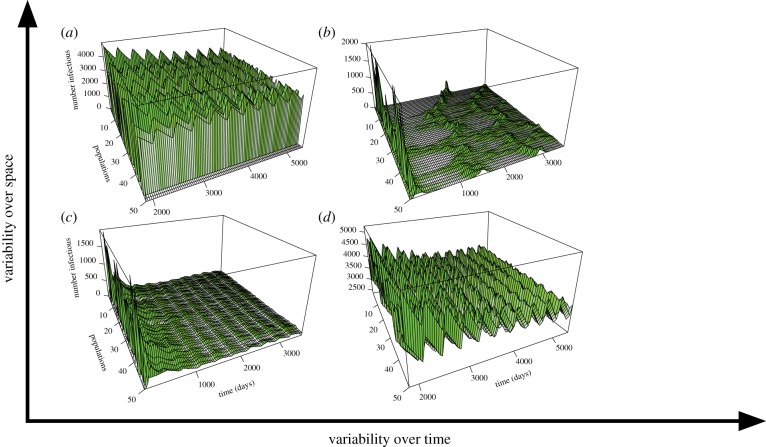
A simulation of pathogen dynamics in reservoir host populations with varying autocorrelation of prevalence in space (populations) and time (days). Prevalence falls along spatial and temporal gradients of variability. In (a), variability is high over space but low over time (e.g. chronic infections with highly variable prevalence over locations but stable prevalence over time such as hepatitis B in human populations) [34]. In (b), variability is high over space and time (e.g. acute pathogens such as canine distemper virus in carnivores at the extent of the USA). In (c), variability is low over space and time, as with chronic, endemic pathogens in highly connected populations, such as herpes simplex virus in human populations. In (d), variability is low over space but high over time, as in highly contagious infections with seasonal transmission such as influenza. Methods for the simulations are described in electronic supplementary material, Methods.
Unpredictable spatial synchrony in transmission can be generated through synchronous environmental stochasticity [39]. Stochastic perturbations in climate or extreme events such as hurricanes and fires have synchronized parasitic disease in grouse (Lagopus lagopus scoticus) [39,40] and have been hypothesized to cause pulses of viral shedding from bats (Pteropus species) [38,41]. Comparing the extent of synchronous infection dynamics with the extent of environmental variation can be useful for causal inference [42].
Truly decoupled dynamics across space or time, where dynamics vary chaotically among populations or depend on factors that are limited in space and time (figure 2b), also can occur. Isolation, for example on islands, may foster uncoupling from other populations, and reduce the likelihood of pathogen persistence, particularly if populations are small and infectious periods are short relative to host lifespans [33]. Complex transmission feedbacks within populations may drive spatial asynchrony. For example, longer infectious periods in older bighorn sheep (Ovis canadensis) may drive feedbacks that result in either high or low endemic states of pneumonia-causing Mycoplasma ovipneumoniae depending on the age-structure of the population at first infection [43]. These feedbacks could create dynamics that are relatively independent across space but have temporal trends. Thus, sampling multiple populations across space, with many sampling points through time, is essential to make inferences that can be generalized across all infected bighorn sheep populations [44,45].
3. Sampling the distribution of infection in reservoir hosts
(a) Basic sampling principles
Designing a sampling strategy that identifies how pathogens are distributed in space and time is challenging. In particular, trade-offs between the spatial extent of sampling and intensity of sampling are ubiquitous. Sampling intensity should be informed by temporal and spatial variability in prevalence (the proportion of infected individuals in a population) and by spatial and temporal autocorrelation. In general, more sampling is required in more variable and less autocorrelated systems. The observed autocorrelation depends on resolution of observation and units for sampling and analysis (e.g. individuals, populations or regions; days, months or years), which must reflect the objectives of the study (table 1). For example, canine distemper virus in wolves (Canis lupus) might appear patchily distributed at coarse resolution (e.g. counties within Montana), but synchronous at fine resolution (e.g. Yellowstone National Park [46]). If the resolution of data collection is coarse, one may infer that infection dynamics are spatially independent (figure 2a,b), whereas finer-resolution sampling within a more limited spatial extent may indicate spatial homogeneity (figure 2c,d). Neither choice is erroneous, as long as the inferences are aligned with the scale of investigation. Ultimately, however, trade-offs between spatial versus temporal sampling, and decisions on the resolution and units of analysis, are decided by the prioritization of objectives and resources available for sampling.
To draw valid statistical inferences from field data, theory generally prescribes sampling randomly in space and time [47]. However, for logistical reasons, probabilistic sampling (random selection of samples in which all units have equal probability of being selected) is rare in animal epidemiology. For example, social hosts, such as bats that roost in a common location, are not randomly distributed, and it is also challenging to randomly sample bats within these roosts [48]. Stratified random sampling or other generalized random stratified designs may be more feasible while achieving a spatially well-balanced random sample and valid inferences [49–52]. The stratification can be informed by knowledge of seasonal peaks in prevalence and concentrations of infection to focus efforts in high-risk places and times. Sampling also continues at times and in locations where risk of infection is thought to be low. Designs with unequal probability selection based on an auxiliary variable also can be considered in such cases.
Stratified random sampling is less feasible for pathogens for which prevalence responds to ephemeral environmental drivers, or to transient dynamics in the reservoir host. In these circumstances, one may wish to implement adaptive sampling, in which probabilistic sampling is complemented by more-intensive spatial and temporal sampling during an outbreak or spillover. Opportunistic sampling often is deployed following spillover in an effort to isolate pathogens or identify reservoir hosts [53]. However, if opportunistic sampling is accompanied by some probabilistic sampling, it typically provides more insight into the spatial and temporal dynamics of infection [54–58].
Although adaptive sampling designs are valuable for maximizing data collection around mortality events or spillover, or for sampling when there is little a priori information, simulations suggest that statistical power to detect temporal trends in infection dynamics is greater when populations are sampled repeatedly and consistently over a long period of time (e.g. monthly over a few years) than when a given population is sampled for a short period of time, albeit repeatedly [59] (box 1; e.g. daily or weekly over a few months). Alternative sampling designs [59,73,74] are robust to infrequent sampling, distant sites and large spatial extents. These include: rotating panels, which sample each site repeatedly but during temporal windows that do not fully overlap; augmented, serially alternating panels, which complement rotating panels with consistent sampling of one location; and partially augmented, serially alternating panels, in which infrequent sampling of a given location periodically is complemented with frequent sampling of the location (box 1 and table 2).
Table 2.
Sampling designs used in studies of pathogen dynamics in reservoir hosts.a
| sampling design | description | advantages | disadvantages |
|---|---|---|---|
| opportunistic | nearby populations are sampled following a spillover event | isolating pathogen, identify reservoir hosts, pragmatic | overestimate prevalence, cannot capture spatial or temporal variation, skew inference of prevalence |
| single longitudinal | repeated sampling of single population over time | infer some temporal dynamics | cannot capture spatial variation, regular intervals could consistently miss shedding pulses |
| replicated longitudinal | repeated sampling of multiple populations over time | infer some spatial and temporal dynamics | logistically challenging, regular intervals could consistently miss shedding pulses |
| random sample | random distribution of sampling events over space and time | reduce bias from sampling at regular intervals | may not capture spatial or temporal variation when truly random, may not be feasible for many species |
| random stratified | random sampling from predetermined regions in space and time | more likely to obtain a representative spatial and temporal sample | may require greater effort than a simple random sample |
| adaptive sampling | random sampling augmented by intensive spatio-temporal sampling near outbreaks | reduce bias while capturing benefits of opportunistic sampling (e.g. isolating pathogen) | uncertainty in final sample size |
| rotating panel | each site is sampled x number of times and then the next site is sampled x times | infer fine-resolution temporal dynamics efficiently over space | few longitudinal samples from any one population, can modify system if sampling of given sites is too frequent |
| augmented serial panel | increases the between-site interval from a rotating panel design, adds a longitudinal study for one site | higher power for trend detection, longitudinal analysis possible, less likely to modify system | may require greater effort in terms of time and funding |
| partially augmented serial | replaces the longitudinal sampling of the augmented serial panel with repeated sampling of multiple sites | higher power for trend detection, longitudinal analysis possible, minimized bias | may require greater effort in terms of time and funding |
aSee box 1 for references.
Another framework that recently has emerged from the disease ecology literature is model-guided fieldwork [75], where mathematical models of pathogen dynamics are developed a priori to guide field data collection. Modellers and biologists work together to incorporate multiple hypotheses and uncertainty about the structure of dynamics and then iterate between models and measurement. Such approaches can facilitate transdisciplinary research and lead to more robust inferences.
(b) Targeted approaches to increase information about prevalence
Prevalence is usually inferred from spatially and temporally explicit data on individual infection or exposure status. These data are usually information-weak because the outcome of every sample is binary (infected or not infected), and the outcomes may be subject to error. In addition to simply increasing the number of individuals sampled, the information content of wildlife field samples can be augmented in several ways.
Information on ages of sampled animals is useful because age–seroprevalence or age–prevalence curves can be used to estimate transmission rates [17]. Seroconversion of juveniles provides clear evidence of ongoing pathogen transmission within a population. If juveniles seroconvert each year, the pathogen is likely to be persistent and endemic in that population rather than infrequent and oscillatory. Serosurveys of juveniles are particularly useful in systems where long-lived circulating antibodies are the only measurable indication of exposure (e.g. African bat henipaviruses, in which RNA rarely is found, and virus has not yet been isolated [76,77]), as long as maternal immunity is not mistaken for juvenile exposure [78]. Sampling of isolated populations (e.g. [76]) similarly can help distinguish between pathogen persistence at the population level versus spatially and temporally patchy transmission.
Seroprevalence can be useful for monitoring spatial and temporal trends in prevalence if few individuals are infected at any point in time (e.g. with infectious periods short or transmission rates low), or if detection is difficult (e.g. lethal sampling is required to test whether lyssaviruses are present in most mammals [79]). However, if antibodies persist for long periods relative to the lifespan of individual hosts, seroprevalence can remain relatively stable over time, even if pathogen prevalence oscillates or the pathogen is extinct locally [80].
Longitudinal sampling of even a small number of known animals over the course of their infections can place preliminary constraints on disease process parameters, which in turn may prove useful for identifying the duration of infection and immunity with stratified or adaptive sampling of populations. This strategy has been used to study wildlife diseases in diverse hosts, from bighorn sheep [43] to bats [81,82]), and is essential for elucidating the within-host dynamics of poorly understood bat viruses [23].
One may identify spatial extents and resolutions for investigation of spillover risk by focusing early sampling at invasion fronts, as suggested for non-native invasive species [9,83,84]. Informal adaptive sampling often is employed following spillover events, but it would be valuable to use formal adaptive sampling [54–58]. Focused sampling at invasion fronts facilitates explicit estimation of transmission, recovery and disease-induced mortality rates before herd immunity shapes dynamics. Moreover, higher public health burdens are often observed at the invasion front because epidemic curves in the reservoir hosts peak at those fronts, exerting high pathogen pressure. Moreover, human populations at invasion fronts rarely are well prepared to reduce spillover [11]. Sampling at the invasion front can be informed by an iterative process of data assessment, dynamic modelling, spatial and temporal forecasting and model validation [60]. Adaptive sampling, which complements random or random stratified sampling across space and time with focused sampling (e.g. in the region and months following a spillover event), also could be informative, but rarely has been implemented [56,85–87].
(c) Characterization of spatial and temporal dynamics
If there is no recent outbreak epicentre, various statistical approaches can be used to estimate the spatial and temporal structure of a pathogen to inform the sampling design. At most scales of observation, infection dynamics have some level of spatial and temporal dependence that decreases with distance or time. Understanding the extent of spatial and temporal autocorrelation can inform the allocation of sampling effort [59,73,74]; this can be accomplished formally through exploratory tools such as correlograms (e.g. plotting the between-site correlation as a function of between-site distance) or semivariograms, for which semivariance is modelled as a function of spatial and temporal lags [88]. Pairs or clusters of samples within regions can be compared with samples among regions to estimate spatial autocorrelation. For example, Tobin [84] demonstrated that within a given spatial extent, sampling clusters of points estimated spatial autocorrelation more accurately than sampling evenly distributed but distant points.
The larger the extent of spatial dependence, the further the sampling units (e.g. sampled populations) can be from each other to make general inferences about risk across a landscape. For example, systems with little spatial variability—e.g. highly connected systems and those in which the infectious period is long relative to the lifespan of the host (e.g. figure 2c,d)—require sampling of a small number of spatially disparate populations. In this case, more frequent sampling of one or two locations may be more informative than infrequent sampling of many locations. By contrast, spatially asynchronous infections may require infrequent sampling of many locations across the ranges of the pathogen and host.
In theory, the lower the temporal variance, the less frequently one needs to sample. Surveillance of the temporal dynamics of infection often is systematic, with sampling at regular intervals within single or multiple populations, and this is often dictated by logistical and funding constraints. For example, the Soay sheep (Ovis aries) population of St Kilda, Scotland, UK was sampled annually to reveal long-term fluctuations in parasite prevalence [64], and vampire bats (Desmodus rotundus) were sampled annually and biannually to reveal endemic viral and bacterial pathogens [65,66]. However, systematic sampling of a population in which prevalence is either extrinsically driven and seasonal or endogenous and epidemic may not detect temporal peaks in prevalence, particularly if the interval between samples is similar to or longer than the periodicity in the pathogen cycles or the peaks in epidemics. Random or rotating sampling designs can reduce the likelihood of this type of bias (box 1 and table 2). When temporal variance is high, as in cases with seasonal oscillations or multiple-year peaks, the sampling interval should reflect the periodicity of the disease. In such cases, generalized random stratified approaches may be used to avoid the pitfalls of systematic sampling and the clumping of simple random sampling [49].
The most challenging pathogens to sample, and therefore those that require the most-intense sampling, are those with highly localized infection dynamics [38]. If only one population is sampled, one erroneously might infer that all populations have similar dynamics. Characterization of infection structure in these systems is best captured with random, rotating or augmented sampling (box 1 and figure 3).
4. Conclusion
Uncertainty in predictions of spillover risk is reduced by knowledge of the spatial and temporal distribution of infection among populations of reservoir hosts. Financial and logistical constraints often force one to make inferences on the basis of small sample sizes and wide confidence intervals, and to make trade-offs between spatial and temporal replication. Adopting wise design choices that are appropriate to the background dynamics of a particular system can extend the utility of even sparse data, and is essential to efficiently understand prevalence dynamics in reservoir host populations.
Acknowledgements
We thank Megan Higgs, Paul Cross and Kathi Irvine for comments on the manuscript, and Jamie Lloyd-Smith and Peter Hudson for conversations that inspired the manuscript.
Authors' contributions
All authors wrote the first draft and contributed to writing and editing the manuscript. D.J.B., K.R.M. and R.K.P. made the figures.
Funding
This work was funded by the Defense Advanced Research Projects Agency (Young Faculty Award D16AP00113 and the DARPA PREEMPT Cooperative Agreement no. D18AC00031), US National Science Foundation (DEB-1716698), US National Institute of General Medical Sciences of the US National Institutes of Health (P20GM103474 and P30GM110732), and the USDA National Institute of Food and Agriculture (Hatch project 1015891). D.J.B. was also supported by an appointment to the Intelligence Community Postdoctoral Research Fellowship Program at Indiana University, administered by Oak Ridge Institute for Science and Education through an interagency agreement between the US Department of Energy and the Office of the Director of National Intelligence. The content of the information does not necessarily reflect the position or the policy of the US government, and no official endorsement should be inferred.
References
Articles from Philosophical Transactions of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society
Full text links
Read article at publisher's site: https://doi.org/10.1098/rstb.2018.0336
Read article for free, from open access legal sources, via Unpaywall:
https://royalsocietypublishing.org/doi/pdf/10.1098/rstb.2018.0336
Citations & impact
Impact metrics
Citations of article over time
Smart citations by scite.ai
Explore citation contexts and check if this article has been
supported or disputed.
https://scite.ai/reports/10.1098/rstb.2018.0336
Article citations
Epidemiological modeling of SARS-CoV-2 in white-tailed deer (Odocoileus virginianus) reveals conditions for introduction and widespread transmission.
PLoS Comput Biol, 20(7):e1012263, 12 Jul 2024
Cited by: 1 article | PMID: 38995977 | PMCID: PMC11268674
Advances in understanding bat infection dynamics across biological scales.
Proc Biol Sci, 291(2018):20232823, 06 Mar 2024
Cited by: 1 article | PMID: 38444339 | PMCID: PMC10915549
Review Free full text in Europe PMC
Transboundary determinants of avian zoonotic infectious diseases: challenges for strengthening research capacity and connecting surveillance networks.
Front Microbiol, 15:1341842, 16 Feb 2024
Cited by: 0 articles | PMID: 38435695 | PMCID: PMC10907996
Review Free full text in Europe PMC
The Impact of Respiratory Function Training and Rehabilitation Nursing on the Recovery of Patients With Mycoplasma Pneumoniae Pneumonia.
Cureus, 16(2):e53461, 02 Feb 2024
Cited by: 0 articles | PMID: 38435183 | PMCID: PMC10909399
Robust evidence for bats as reservoir hosts is lacking in most African virus studies: a review and call to optimize sampling and conserve bats.
Biol Lett, 19(11):20230358, 15 Nov 2023
Cited by: 5 articles | PMID: 37964576 | PMCID: PMC10646460
Review Free full text in Europe PMC
Go to all (33) article citations
Data
Data behind the article
This data has been text mined from the article, or deposited into data resources.
BioStudies: supplemental material and supporting data
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Infection and disease in reservoir and spillover hosts: determinants of pathogen emergence.
Curr Top Microbiol Immunol, 315:113-131, 01 Jan 2007
Cited by: 8 articles | PMID: 17848063
Review
Percolation models of pathogen spillover.
Philos Trans R Soc Lond B Biol Sci, 374(1782):20180331, 12 Aug 2019
Cited by: 12 articles | PMID: 31401950 | PMCID: PMC6711313
Public health threat of new, reemerging, and neglected zoonoses in the industrialized world.
Emerg Infect Dis, 16(1):1-7, 01 Jan 2010
Cited by: 161 articles | PMID: 20031035 | PMCID: PMC2874344
Review Free full text in Europe PMC
Cross-species pathogen spillover across ecosystem boundaries: mechanisms and theory.
Philos Trans R Soc Lond B Biol Sci, 374(1782):20180344, 12 Aug 2019
Cited by: 48 articles | PMID: 31401953 | PMCID: PMC6711298
Review Free full text in Europe PMC
Funding
Funders who supported this work.
Defense Advanced Research Projects Agency (2)
Grant ID: D18AC00031
Grant ID: D16AP00113
Directorate for Biological Sciences (1)
Grant ID: DEB-1716698
NIGMS NIH HHS (2)
Grant ID: P20 GM103474
Grant ID: P30 GM110732
National Institute of General Medical Sciences (1)
Grant ID: P20GM103474 and P30GM110732
USDA National Institute of Food and Agriculture (1)
Grant ID: 1015891





