Abstract
Free full text

An averaging model for analysis and interpretation of high-order genetic interactions
Abstract
While combinatorial genetic data collection from biological systems in which quantitative phenotypes are controlled by active and inactive alleles of multiple genes (multi-gene systems) is becoming common, a standard analysis method for such data has not been established. The currently common approaches have three major drawbacks. First, although it is a long tradition in genetics, modeling the effect of an inactive allele (a null mutant allele) contrasted against that of the active allele (the wild-type allele) is not suitable for mechanistic understanding of multi-gene systems. Second, a commonly-used additive model (ANOVA with interaction) mathematically fails in estimation of interactions among more than two genes when the phenotypic response is not linear. Third, interpretation of higher-order interactions defined by an additive model is not intuitive. I derived an averaging model based on algebraic principles to solve all these problems within the framework of a general linear model. In the averaging model: the effect of the active allele is contrasted against the effect of the inactive allele for easier mechanistic interpretations; there is mathematical stability in estimation of higher-order interactions even when the phenotypic response is not linear; and interpretations of higher-order interactions are intuitive and consistent—interactions are defined as the mean effects of the last active genes added to the system. Thus, the key outcomes of this study are development of the averaging model, which is suitable for analysis of multi-gene systems, and a new, intuitive, and mathematically and interpretationally consistent definition of a genetic interaction, which is central to the averaging model.
Introduction
Accumulation of genetic knowledge in many biological systems and technological advances that made combining multiple genetic loci easier have facilitated combinatorial genetic analysis among multiple genes, each of which has active (“wild-type”) and inactive (null “mutant”) allele states, involved in single quantitative traits, e.g., [1–4], which I here call multi-gene systems. Such a multi-gene system necessarily implies a gene network, in which the gene functions are not organized in a series (i.e., not in a single pathway). This is because a series of genes, each of which can only take a active or inactive state, can only generate an on-or-off, non-quantitative output. Instead, a gene network must have a converging node(s) to generate a single trait. Converging nodes are sources of complex system behaviors [5, 6]. For a data set, I consider the measurement of the quantitative trait as the phenotype and measurements made with exhaustively combinatorial genotypes (i.e., for a n-gene system, the number of the exhaustively combinatorial genotypes is 2n) as the data.
However, conventional genetics is not well built for analysis and interpretation of high-order genetic interactions among multiple genes involved in a single quantitative trait. This is because conventional genetics is an extension of early objectives of analyzing functionally independent and/or qualitative genes. The objective of this study is to establish a general linear model approach that is suitable for mechanistic interpretations of higher order gene interactions in multi-gene systems. First, comparing multiple mutant phenotypes to the wild-type phenotype does not allow simple mechanistic interpretations. The phenotype of a particular genotype should be compared to the phenotype of the most disrupted mutant state (e.g., a quadruple null mutant in a 4-gene system) for simple mechanistic interpretations.
Second, a method to define and interpret interactions among multiple genes is not definitively integrated. The main topic of this paper concerns this second point. An additive model based on ANOVA with interaction is a simple implementation for analysis of high-order genetic interactions. However, such an additive model fails with a nonlinear system, such as a system with a saturating response, when it contains genetic interactions among more than two genes. This problem is caused by the fact that the additive model requires the conservation of the distributive law ((A + B):C = A:C + B:C, where “:” indicates the interaction defined in the additive model), whereas conservation of this law cannot be assumed in a nonlinear system. We previously proposed a network reconstitution (formerly called signaling allocation) general linear model (NR model), which does not assume conservation of the distributive law, to resolve this problem [2, 7]. This was achieved by averaging the interaction terms at each order (“averaging principle”), instead of simply adding them (e.g., ABC = A + B + C + (A:B + B:C + C:A) / 3 +A:B:C in the NR model, while ABC = A + B + C + A:B + B:C + C:A + A:B:C in the additive model; the italicized upper-case letters denote the genotype carrying wild-type alleles A, B, and C; the intercept is omitted).
I recently realized that the interaction operator in the NR model is not consistent, e.g., in the above example of the ABC description, The “:” operators in A:B and A:B:C are not defined in a consistent manner. This was caused by the fact that the 2-gene interaction was defined in the same way in both the NR and additive models, AB = A + B + A:B. To resolve this issue, the averaging principle should be extended to the 1-gene effect terms as well: e.g., ABC = (A + B + C) / 3 + (A;B + B;C + C;A) / 3 +A;B;C. I call this an averaging model. It is a general linear model with the averaging principle applied consistently. I use a “;” to denote the interaction operator defined in the averaging model (“averaging interaction”).
The averaging model can estimate high-order genetic interactions in a stable manner with nonlinear multi-gene systems because each averaging interaction can be defined using only observed values, e.g., A;B;C = ABC–(AB + AC + BC) / 3. The interpretations of averaging interactions are intuitive and consistent: a genetic interaction is the average impact of adding the last gene; note that the above definition of A;B;C is the equivalent of A;B;C = {(ABC–AB) + (ABC–AC) + (ABC–BC)} / 3. The additive and averaging models without interaction can be understood as two extreme approximations in a 2-gene system: there is no mechanistic reason to favor one of the models without additional mechanistic information. Since the averaging model is mathematically stable, provides intuitive and consistent interpretations of gene interactions, and is mechanistically tractable, I propose the averaging model as a standard general linear model for descriptions of multi-gene system behaviors.
Results and discussion
General notation rules
I assume that all the genes of interest are homozygous in diploid organisms. A single gene is denoted by a single alphabetical letter in italics, with upper-case and lower-case letters denoting the wild-type and null mutant alleles, respectively. For example, ABc represents the genotype with the wild-type alleles for genes A and B and the mutant allele for gene C. I also use the genotype notation omitting the mutant alleles, such as AB instead of ABc, for simplicity, clarity, and generalization. The notation of a genotype can represent its phenotype as well. The non-italic lower-case letters, such as a, b, and c, represent the mutant allele effects defined in comparison to the wild-type alleles. The wild-type allele effects, represented by non-italic upper-case letters, such as A, B, and C, are defined in comparison with the mutant alleles. The additive effect of A and B is denoted A + B. The additive and averaging interactions between A and B are denoted A:B and A;B, respectively. In a mechanistic network model underlying the observation, the node corresponding to gene A and its output are denoted as nA. Although I often use a 3-gene system, ABC, with the intercept term omitted for simple examples, the points discussed subsequently can be generalized to a system consisting of an arbitrary number of genes.
Comparing to the most disrupted state instead of the intact state gives better interpretability
A convention in genetics is to compare a mutant phenotype to the wild-type phenotype. Here I argue that instead, comparing a phenotype of any genotype to the phenotype of the most disrupted state, e.g., comparing to the triple mutant state in a 3-gene system, leads to much better mechanistic interpretations. For a simple example, I use a system defined by an ANOVA-based, 3-gene additive model, i.e., assuming a linear phenotypic response (although I will discuss a linear assumption issue later).
Fig 1A shows a mechanistic network underlying a system with 6 nodes, in which three nodes (nA, nB, and nC) can be manipulated by mutations and the other three (nX, nY, and nZ) cannot. Thus, for the purpose of genetic analysis, this is a 3-gene system. nA, nB, nX, and nY are input nodes, and their values are arbitrarily set at 5, -3, 4, and 2, respectively. nZ is the output node, and the output of nZ can be measured as the quantitative trait of the system. Simple additive rules at nodes nC and nZ are assumed, nC = nA + nB + nX and nZ = nC + nY, respectively. Fig 1B shows the nZ output (i.e., phenotype) of 8 exhaustively combinatorial genotypes. Fig 1C shows the effects and interactions of the mutant alleles that are calculated according to an ANOVA model with interaction. Fig 1D shows the effects and interactions of the wild-type alleles that are calculated according to an ANOVA model with interaction. With Fig 1D, it is easy to reconstitute the mechanistic network shown in Fig 1A: there is a basal activity of 2 in the absence of A, B, and C; A and B are not active by themselves, while C has its own activity of 4 regardless of A and B; the connection between A and C is positive with a value of 5, and the connection between B and C is negative with a value of -3; No A:B:C interaction means that additive effects up to two-gene interactions can explain the system behavior completely. In comparison, mechanistic interpretations based on Fig 1C are not simple: e.g., it is not easy to decipher that B is completely dependent on C from ABC = 8, b = 3, c = -6, and b:c = -3. I conclude that the behavior of a multi-gene system should be interpreted using wild-type allele effects. I will subsequently model a system with wild-type allele effects and their interactions.
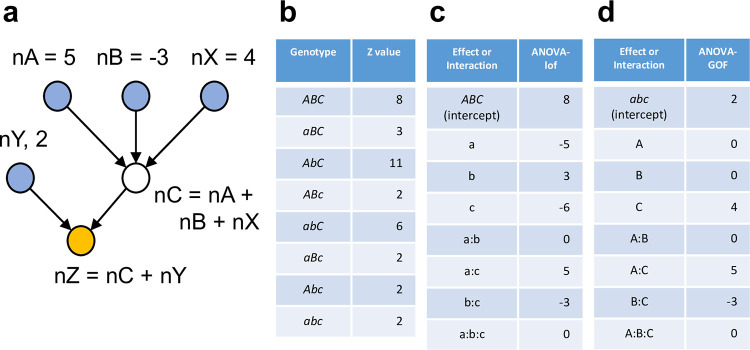
(a) A mechanistic model of a network containing 3 nodes that can be mutationally manipulated (a 3-gene system). The network consists of 6 nodes, among which nA, nB, and nC are mutationally manipulable and nX, nY, and nZ are not. The output of each node is given either as a value or an equation. The output of nZ is the quantitative phenotype of the system. (b) The phenotype values of all 8 combinatorial genotypes. (c) The values for the mutant allele effects and interactions. (d) The values for the wild-type allele effects and interactions.
Derivation of the averaging model
See S1 Text for details of this section. The additive model requires the distributive law but this law is violated when the system behavior is nonlinear. A typical biological system has a limited phenotype range. When the sizes of the effects and interactions of the genes in a multi-gene system are substantial compared to the phenotype range, the system behavior is nonlinear and the distributive law is violated—consequently the additive model fails. The NR model [2, 7] allows non-distributivity. However, the definitions of the 2-gene interaction and of the 3-or-more-genes interaction were not consistent in the NR model. The averaging model was derived by extending the definition of the 3-or-more-genes interaction in the NR model to the 2-gene interaction. Thus, the averaging model allows non-distributivity, and its interaction definition is consistent regardless of the number of genes involved. The three models and a 1-way ANOVA model for each genotype are all general linear models with different ways to decompose the fitted values. When the models are fit to data with replication as statistical models, their fitted values and residuals are identical. Therefore, subsequently I sometimes use only the mean estimates of the models for model comparisons (such as Fig 2).
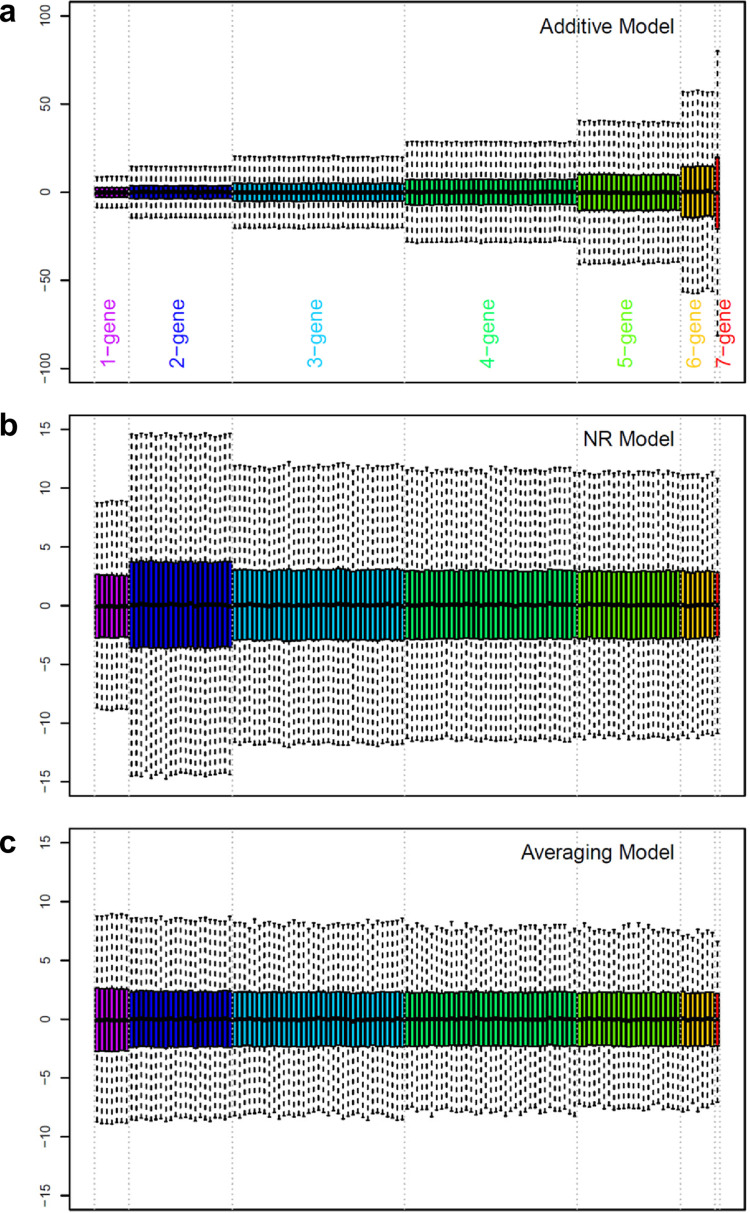
Distributions of the gene effects and interaction values when the phenotype values were randomly sampled from a uniform distribution with (a) additive, (b) NR, or (c) averaging models. Each order of interactions is color-coded separately, and the color coding is shown at the bottom of (a). Note that the scales in the y-axes are much larger in (a) than in (b) or (c).
Unlike the additive model, the averaging model stably estimates high-order genetic interactions
The situation in which the additive model fails due to a limited phenotype range was simulated using a 7-gene system. A system with many genes was used because it shows the problem more clearly. With 7 genes, the number of combinatorial genotypes is 27 = 128. A simulated mean phenotype value for each genotype was randomly sampled from a uniform distribution ranging from 1 to 10, and each model was solved using these randomly generated data values. This simulation procedure was repeated 10,000 times and the model estimate distributions, except for the model intercept (i.e., the septuple mutant value), were visualized as a box plot (Fig 2). Fig 2A shows that in the additive model, the higher the order of interactions is, the higher the representations of the interactions are. The length of the box (the difference between the 75th and 25th percentiles) of the 7-gene interaction is about 7.5 times larger than those of the 1-gene effects and about 5 times larger than the phenotype range. Therefore, if the additive model is used, the absolute values of higher order additive interactions are grossly overestimated in general. This problem was solved in the NR model, except for the 2-gene interactions, which were still additive interactions (Fig 2B). Note the y-axis scale difference between Fig 2A–2C: the distributions of the 1-gene effects are essentially the same across the models. The distributions of estimates were very consistent across all the effects and averaging interactions in the averaging model (Fig 2C). These results strongly suggest that the averaging interactions that do not assume distributivity can be stably estimated even when the system behavior is nonlinear.
To investigate a situation with actual biological data, we reanalyzed our previously published data set with a 4-gene system [2] using the additive, NR, and averaging models (Fig 3). The data set used in this figure was the quantitative phenotype of Effector-Triggered Immunity (ETI) induced by a bacterial effector AvrRpt2 in the model plant Arabidopsis (AvrRpt2-ETI) [8–11]. The inhibition of bacterial growth in the plant leaf, in log10(cfu/cm2), was the AvrRpt2-ETI phenotype measure. The hub genes of four major signaling sectors (subnetworks) in the plant immune signaling network were subjected to mutational analysis. The signaling sectors were the jasmonate, ethylene, PAD4, and salicylate sectors, which are indicated as J, E, P, and S, respectively. I also call their hub genes J, E, P, and S, in this context of analysis of the 4-gene system. Biological and experimental details are provided in [2].
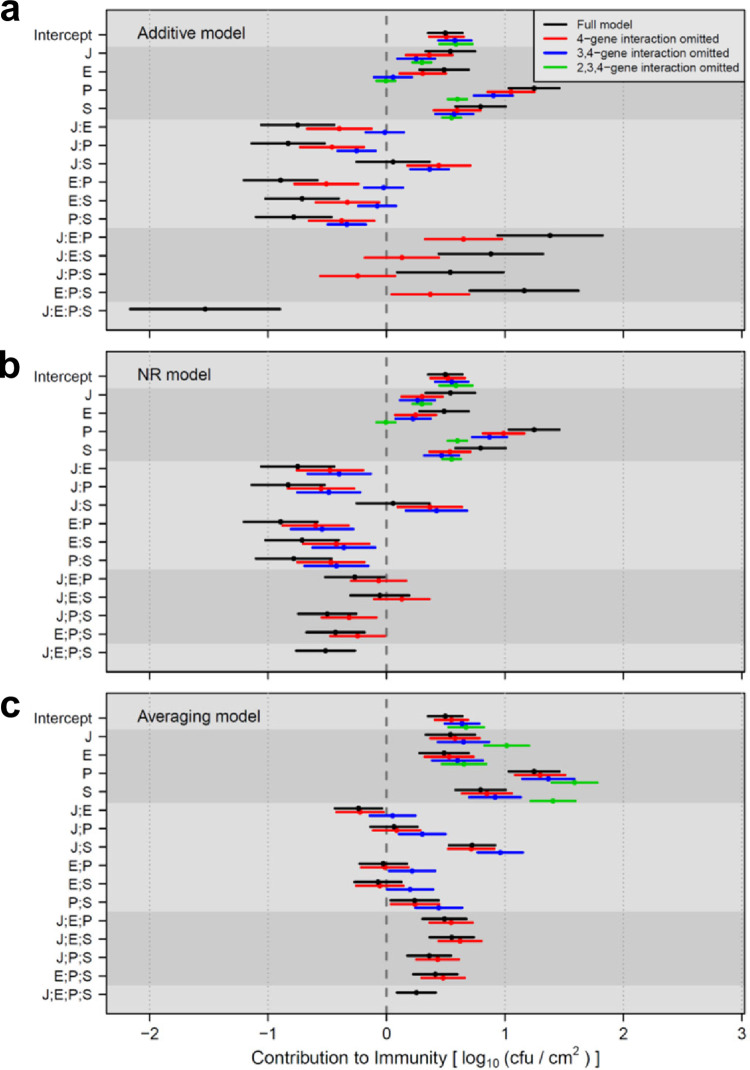
in (a) additive, (b) NR, and (c) averaging models. The 95% confidence intervals are shown as horizontal bars, with the means as points. Different levels of model reduction (omitting higher order interactions from the model) are color-coded according to the color code in (a). Different shades of gray background are used to show different orders of interactions. “:” and “;” indicate additive and averaging interactions, respectively.
Here we focus on the behaviors of the model estimates from the three models. Note that the data set had replicated observations for each combinatorial mutant, the models were fit to the data (instead of solving), and the confidence intervals of the model estimates were obtained. The 95% confidence intervals of the full additive models (which include up to the 4-gene interaction) were evidently wider with high-order interactions in the additive model (Fig 3A, black bars). This problem of uneven confidence interval sizes was moderated in the NR model (Fig 3B) and not noticeable in the averaging model (Fig 3C). Furthermore, in the additive model, since the effect sizes of higher order interactions were overestimated, the estimates for the 1-gene effects and lower order interactions were substantially affected when higher-order interactions were omitted (model reduction; Fig 3A, compare red to black and blue to red). In addition, the 95% confidence interval sizes of the same terms were affected by model reduction in the additive model. These problems in model reduction were moderated in the NR model, and almost non-existent in the averaging model (Fig 3B and 3C). In summary, the problems associated with non-distributivity in this biological data set are evident in the additive model while the averaging model appears free of these problems. These observations made with a biological data set directly corroborate the simulation results in Fig 2.
Why does the averaging model describe a multi-gene system better than the additive model?
In the 2-gene additive interaction, A:B = AB–(A + B), the 2-gene additive interaction A:B can be estimated using only observed values, i.e., estimation of A:B can be independent of other model estimates. Essentially, an error originating from the nonlinearity of data is absorbed by the 2-gene additive interaction A:B. However, estimation of a 3-gene additive interaction, A:B:C = ABC–(A + B + C)—(A:B + A:C + B:C), is not independent of other model estimates, A:B, A:C, and B:C. In a nonlinear system, there is no guarantee that the value of A:B in the 3-gene model is the same as that of A:B estimated by the 2-gene model. Thus, on average, higher-order interactions accumulate errors from lower-order interactions in the additive model with a nonlinear system, which was demonstrated in simulation and analysis of an actual data set (Figs (Figs2A2A and and3A3A).
On the other hand, any order of averaging interactions can be estimated using only observed values, e.g., A;B;C = ABC–(AB + AC + BC) / 3, so their estimations can be independent of other model estimates. Thus, nonlinearity-originated errors are confined to individual averaging interactions and do not accumulate toward higher-order interactions (Figs (Figs2C2C and and3C).3C). This is the reason the additive model including 3-or-more-gene interactions fails with nonlinear systems while the averaging model does not.
Interpretation of the averaging model outcome
It should be emphasized that the definitions of the additive and averaging interactions are different, and consequently their interpretations are different. The 2-gene additive interaction is understood as the difference from the addition of the 1-gene effects, A:B = AB–(A + B). When A, B, A:B > 0, A and B have a synergistic effect. When A, B > 0, A:B < 0, A and B have a compensating effect (Fig 4A). However, synergistic or compensating interpretations of additive interactions become unclear when A and B have opposite signs (Fig 4B) or the additive interactions are higher-order, e.g., A:B:C = ABC—(A + B + C + A:B + A:C + B:C) (Fig 4C).

Interpretations of interactions in (a-c) additive and (d-f) averaging models. (a, d) Two-gene interactions when both 1-gene effects A and B are positive. Two different cases (cases 1 and 2) of the AB phenotype values are used. (b, e) Two-gene interactions when the 1-gene effects have opposite signs. (c, f) Three-gene interactions. “:” and “;” indicate additive and averaging interactions, respectively.
In contrast, the interpretation of averaging interactions is consistent and highly interpretable at all orders of the averaging interactions, i.e., the averaging model is highly scalable to the number of genes in the system. An averaging interaction is the deviation of the corresponding genotype from the average of all involved genotypes that have one gene fewer. For example, in a 2-gene system, A;B = AB–(A + B)/2 (Fig 4D). Note that not just the values but also the signs of the interactions could be different between the additive and averaging interactions (compare AB (case 1) in Fig 4A and 4D). The interpretations of averaging interactions are consistent even when A and B have opposite signs (Fig 4E) or in the case of higher-order averaging interactions, e.g., A;B;C = ABC–(AB + AC + BC) / 3 (Fig 4F).
A 3-gene averaging interaction, A;B;C = ABC–(AB + AC + BC) / 3, (Fig 4D) could be a 3-gene interaction in a 7-gene system, A;B;C = ABCdefg–(ABcdefg + AbCdefg + aBCdefg) / 3. Thus, a genotype notation that omits the mutant alleles is a generalized notation for the averaging model.
An averaging model-based multi-gene analysis should only contain genes significantly involved in the phenotype
Since the averaging interaction is the phenotypic deviation of the corresponding genotype from the average of all genotypes with one gene fewer, it is affected if the analysis includes unnecessary genes. Such unnecessary genes can be detected by comparing all the genotypes containing the gene in question to the corresponding genotypes without the gene. For example, in a 3-gene system with genes A, B, and C, the test for whether gene C should be included is whether any of ABC–AB, AC–A, BC–B, and C–abc have values significantly different from 0. If none of them are significant, gene C should be removed from the averaging model.
Reinterpretation of previous results using the averaging model
Using the averaging model, I reinterpreted results from my laboratory of exhaustively combinatorial genotype analysis in a 4-gene system, which were originally analyzed using the NR model shown in Fig 4 of [2]. The study consisted of four cases of inducible immunity in the model plant Arabidopsis against strains of the bacterial pathogen Pseudomonas syringae, which are designated as the AvrRpt2-ETI, AvrRpm1-ETI, flg22-PTI, and elf18-PTI cases. ETI is Effector-Triggered Immunity, and AvrRpt2 and AvrRpm1 are triggering effectors [8–12]. Note that the data set for AvrRpt2-ETI is the same data set used in Fig 3. PTI is Pattern-Triggered Immunity, and flg22 and elf18 are triggering molecular patterns [13–15]. The inhibition of bacterial growth in the plant leaf, in log10(cfu/cm2), was the immunity phenotype measure. The hub genes of four major signaling sectors (subnetworks) in the plant immune signaling network were subjected to mutational analysis. The signaling sectors were the jasmonate, ethylene, PAD4, and salicylate sectors, which are indicated as J, E, P, and S, respectively. I also call their hub genes J, E, P, and S, in this context of analysis of the 4-gene system. Biological and experimental details are provided in [2].
Each of the AvrRpt2-ETI, AvrRpm1-ETI, flg22-PTI, and elf18-PTI cases was first tested to determine whether all four genes were significantly involved in the phenotype variation. Except for the elf18-PTI case, all four genes were significant, and the averaging model for the 4-gene system was used. In the elf18-PTI case, the phenotype was not significantly affected by the J gene in any genotype context, so the averaging model for the 3-gene system with the E, P, and S genes was used. The results of applying the averaging model to these four immunity cases are shown in Fig 5.
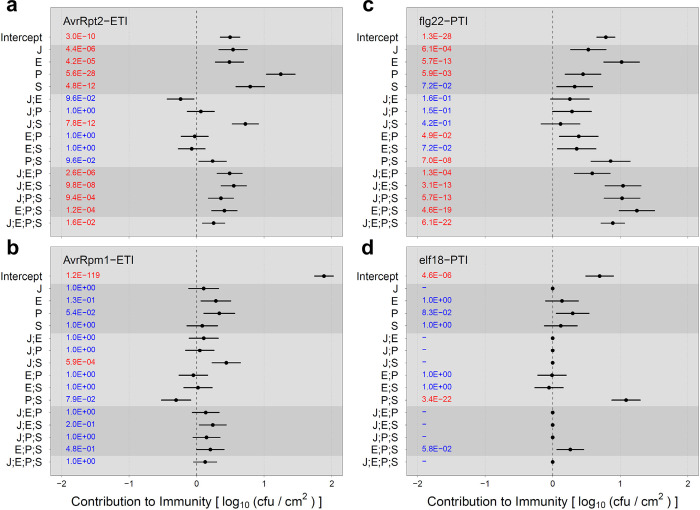
(a) AvrRpt2-ETI, (b) AvrRpm1-ETI, (c) flg22-PTI, and (d) elf18-PTI. The 95% confidence intervals are shown as horizontal bars, with the means as points. The Holm-corrected p-values are shown in the left part of each plot: red, p < 0.05; blue, p ≥ 0.05. The dataset used for AvrRpt2-ETI in Fig 5A is the same as that in used in Figs Figs33 and 5A is the same as the full model (black lines) in Fig 3C. “;” indicates the averaging interaction.
In AvrRpt2-ETI with the averaging model (Fig 5A), the values for the 1-gene effects were all positive. P had the largest effect, which was close to the wild-type level. Among the 2-gene averaging interactions, only J;S was significantly positive: while the J and S effects are both positive, combining these two genes together (JS genotype) increases the immunity from the average of the J and S genotypes, which makes the JS phenotype similar to wild type.
In AvrRpm1-ETI with the averaging model (Fig 5B), most immunity was explained by the intercept (i.e., the immunity level in the jeps genotype), showing that the quadruple mutant still maintains most of the immunity of wild-type plants. This observation can be explained by the fast kinetics of AvrRpm1-ETI signaling compared to AvrRpt2-ETI, in respect to the gating timing of the ETI-Mediated and PTI-Inhibited Sector (EMPIS) by PTI signaling [16]. Although all the 1-gene effects and the averaging interactions had lower amplitudes, their general up and down trends were similar to those of AvrRpt2-ETI, suggesting that the 4-gene network apart from EMPIS behaves similarly in AvrRpm1-ETI and AvrRpt2 ETI. J;S was the only significant averaging interaction with a positive contribution to immunity. In addition, the positive P effect was marginally significant (Holm-corrected p = 0.054).
In flg22-PTI (Fig 5C), all the 1-gene effects except S were significantly positive with E as the highest. The 2-gene averaging interactions were largely low and/or not significant, except P;S, which was significantly and strongly positive. The 3-gene and 4-gene averaging interactions were significantly and strongly positive, indicating that all the genes increase the immunity level substantially when added to the system as the 3rd or 4th genes.
In elf18-PTI (Fig 5D), only P;S was significant among all the averaging model terms, except the intercept. The P;S averaging interaction was strongly positive, indicating that a single mutation in genes P or S almost completely abolishes elf18-PTI. The difference in the importance of the E gene clearly separated flg22-PTI and elf18-PTI. Another difference between flg22-PTI and elf18-PTI was the 3-gene and 4-gene averaging interactions. All were strongly positive in flg22-PTI, and none were significant in elf18-PTI.
It is noteworthy that the roles of J;S and P;S were very different in ETI and PTI. A strongly positive P;S averaging interaction was observed in PTI (Fig 5C and 5D). Positive functional interactions between the P and S genes have been well documented in many aspects of plant immunity [17]. In contrast, this averaging interaction was insignificant in ETI, except for their contributions through higher-order averaging interactions, J;P;S, E;P;S, and J;E;P;S. On the other hand, a strongly positive J;S averaging interaction was observed in ETI while it was insignificant in PTI (Fig 5). Although negative functional interactions between the J and S genes are often described in plant immunity [17], these two genes interact positively in ETI (Fig 5A and 5B). In addition, in flg22-PTI the 3-gene and 4-gene averaging interactions were strongly positive while they were moderately positive in AvrRpt2-ETI. A disadvantage of strongly positive 3-gene and 4-gene averaging interactions is that a mutation(s) in one or two genes results in large loss of immunity. Relatively weak 3-gene and 4-gene averaging interactions in ETI indicate that ETI is more resilient against damage to one or two of these major immune signaling sectors, which could be caused by pathogen effectors [6]. In summary, the averaging model analysis highlighted that while the 4-gene system is important in both ETI and PTI (with flg22), the way they are used in ETI and PTI is quite different, and ETI is more resilient than PTI against perturbations to the signaling sectors. It also highlighted substantial differences, particularly in the roles of the J and E genes, in regulation between flg22-PTI and elf18-PTI.
Mechanistic basis of the additive and averaging models
To provide a concrete idea about what the additive and averaging models without interaction represent mechanistically, I use the following idealized 2-gene signaling network based on chemical reactions. Two genes A and B qualitatively (i.e., on or off) control two input nodes nA and nB of an output node nC (i.e., directed links from nA and nB converging on nC). The activity of each node is represented by the corresponding chemical, A, B, or C, and the chemical reactions involved are A + X → C and B + Y → C. We assume an equilibrium (or a steady state) for the reactions, and the concentration relationships, [X], [Y] >> [A], [B], [C], i.e., [X] and [Y] can be considered constant in the reactions. Under these conditions, we can describe the relationships among [A], [B], and [C] as: kA[A] = [C] and kB[B] = [C], where kA and kB are positive constants. Then the additive and averaging models without interaction can well approximate the system behavior when kA, kB >> 1 (i.e., [C] >> [A],[B]) and when kA, kB << 1 (i.e., [C] << [A],[B]), respectively (S2 Text). This discussion of an idealized system shows that the additive and averaging models without interaction could represent two opposing extreme approximations of the underlying mechanistic state. Therefore, one of the models cannot be favored over the other unless mechanistic information about the system is available in addition to the phenotypic values.
Limitation in mechanistic interpretations with a general linear model
The chemical reaction system discussion in the last section also shows that when the actual values of kA and kB are between the extreme values, both models handle the deviation with the interaction, A:B or A;B (with opposite signs). Note that the interaction is a consequence of shared [C] between two reactions: one reaction affects the other, i.e., it is truly a mechanistic interaction. However, the interaction value from a model cannot reveal the nature of the interaction–we can interpret it mechanistically in this example only because we know the underlying system mechanism. This example illustrates a limitation to describing a nonlinear system with a general linear model in terms of mechanistic interpretations based on the model. However, it should also be reemphasized that the genetic interpretations of higher-order interactions are always clear with the averaging model while this is not the case with the additive model.
Concluding remarks
I have demonstrated that multi-gene systems subjected to exhaustively combinatorial mutation analysis typically violate the distributive law due to their nonlinearity and that therefore, the additive model that requires the conservation of the distributive law is not appropriate for analysis of such systems. In contrast, an averaging model allows non-distributivity and maintains consistency from the 1-gene effects to the highest order of averaging interactions. Furthermore, averaging model results are consistently and intuitively interpretable from the 1-gene effects to the highest order of averaging interactions. I propose the averaging model as a standard general linear model for combinatorial mutation analysis of multi-gene systems.
Methods
Data sets
The biological data sets used in this study are the same data sets used in Fig 4A and 4B in Tsuda et al. (2009). Each data set consists of bacterial counts (log10(colony forming units/cm2)) for 16 exhaustively combinatorial genotypes for a 4-gene system, with or without treatment, with replication. Since the raw bacterial count data were not published previously, they are provided as Supplemental Dataset 1 in S1 File.
Random simulation with three models
The simulation was performed with a 7-gene system. The phenotype values for 27 = 128 genotypes were randomly sampled from a uniform distribution ranging from 1 to 10. The 128 phenotype values were solved for the coefficients (gene effects and interactions) in each of the additive, NR, and averaging models. To solve the 128 equations per model, the 7-gene system matrix equivalent of the 3-gene system matrix in Fig TS1.1 (S1 Text) was used (the matrices are provided in an R workspace file in Supplemental Dataset 2 in S1 File). This procedure was repeated 10,000 times for each model, and the distribution of each coefficient (except the intercept) across the repeats is shown by a box-and-whiskers in Fig 2.
Fitting averaging models to the data
A linear mixed-effect model (the lme function in the nlme R package [18]) was used. This was because (i) each data set has factors regarding the experimental design, which were included as random effects in the model and (ii) the numbers of replicates were not the same across the genotype x treatment combinations. First, a linear mixed-effect model with the genotype x treatment interactions was fit to each of the data sets for “AvrRpt2-ETI”, “AvrRpm1-ETI”, “flg22-PTI”, and “elf18-PTI”. The formula for the fixed effects was “~ genotype/treatment -1”. The random effects for the data sets were “~ 1|replicate/flat/pot”. The interaction coefficients of the linear mixed-effect model were used to test whether each gene is significant. For example, to test the significance of the J gene, the estimate differences, JEPS–EPS, JEP–EP, JPS–PS, JES–ES, JE–E, JP–P, JS–S, and J–jeps were subjected to t-tests using the associated standard errors calculated from the variance/covariance matrix and the residual degree of freedom. The p-values from all t-tests for a single data set were corrected by the Benjamini-Hochberg FDR. If none of the corrected p-values were smaller than 0.05 for the gene, the gene was designated insignificant and omitted from the following averaging model analysis. Only the J gene in “elf18-PTI” was insignificant. In this case, the data were bundled by ignoring the J gene. For example, the JEPS data were considered as part of the EPS data.
Second, the averaging model using the significant genes was fit. The 4-gene system equivalent matrix of the 3-gene system matrix in Fig TS1.1c (S1 Text) or the 3-gene system matrix was used (the matrices are provided in an R workspace file in Supplemental Dataset 2 in S1 File). The rows were replicated according to the genotypes of the observations (the design matrix for the averaging model coefficients, denoted as “m.”). Using the design matrix m., the fixed effects were, “~ m. -1 + genotype” and the random effects were, “~ 1|replicate/flat/pot” in the lme function. The averaging model coefficient estimates, their standard errors, and the p-values were extracted from the coefficient table of the lme model. The estimates, the standard errors, and the residual degree of freedom of the lme model were used to calculate the 95% confidence intervals. The p-values were subjected to the Holm multiple tests correction. The R script used to generate Fig 5 from the raw bacterial count data sets is provided as Supplemental Dataset 3 in S1 File. Supplemental Datasets are available from https://github.com/fumikatagiri/Averaging_Model.
Supporting information
S1 Text
Derivation of the averaging model and non-distributivity of the data.(DOCX)
S2 Text
Averaging and additive models without interaction are two extreme approximations of the behavior of a two-input chemical signaling system.(DOCX)
S1 File
Supplemental datasets.Supplemental Datasets are available from https://github.com/fumikatagiri/Averaging_Model.
(DOCX)
Acknowledgments
I thank Dave Mackey and Alex Turo for exposing me to their unpublished data from a 7-gene system, which led me to realization of the averaging model, Takashi Hirayama for his question, which led to the discussion regarding the additive and averaging models as approximated behaviors of a chemical signaling network, and Kenichi Tsuda for the raw data used in Figs Figs33 and and55 and for critical reading of the manuscript. I also thank Yaniv Brandvain, Ruth Shaw, and Linda Jeanguenin for critical reading of the manuscript and Jane Glazebrook for editing.
Funding Statement
This work was supported by grants to FK from National Science Foundation (MCB-1518058 and IOS-1645460; https://www.nsf.gov/) and from US Department of Agriculture-National Institute of Food and Agriculture (2020-67013-31187; http://www.nifa.usda.gov/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Data Availability
All data and R scripts essential for the averaging model are available from https://github.com/fumikatagiri/Averaging_Model.
References
Decision Letter 0
23 Oct 2023
PONE-D-23-24383An averaging model for analysis and interpretation of high-order genetic interactionsPLOS ONE
Dear Dr. Katagiri,
Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.
Please see the comments from three reviewers below. Please note that there is no requirement to cite any of the specific references suggested by any of the reviewers.
Please submit your revised manuscript by Dec 07 2023 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at gro.solp@enosolp. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.
Please include the following items when submitting your revised manuscript:
A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.
If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.
If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: https://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.
We look forward to receiving your revised manuscript.
Kind regards,
Hanna Landenmark
Staff Editor
PLOS ONE
Journal Requirements:
When submitting your revision, we need you to address these additional requirements.
1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at
https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and
2. We note that the grant information you provided in the ‘Funding Information’ and ‘Financial Disclosure’ sections do not match.
When you resubmit, please ensure that you provide the correct grant numbers for the awards you received for your study in the ‘Funding Information’ section.
3. Thank you for stating the following in the Acknowledgments Section of your manuscript:
"This work was supported by grants from National Science
454 Foundation (MCB-1518058 and IOS-1645460) and from US Department of Agriculture-National Institute
455 of Food and Agriculture (2020-67013-31187)"
We note that you have provided funding information that is not currently declared in your Funding Statement. However, funding information should not appear in the Acknowledgments section or other areas of your manuscript. We will only publish funding information present in the Funding Statement section of the online submission form.
Please remove any funding-related text from the manuscript and let us know how you would like to update your Funding Statement. Currently, your Funding Statement reads as follows:
"This work was supported by grants to FK from National Science Foundation (MCB-1518058 and IOS-1645460; https://www.nsf.gov/) and from US Department of Agriculture-National Institute of Food and Agriculture (2020-67013-31187; http://www.nifa.usda.gov/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript."
Please include your amended statements within your cover letter; we will change the online submission form on your behalf.
[Note: HTML markup is below. Please do not edit.]
Reviewers' comments:
Reviewer's Responses to Questions
Comments to the Author
1. Is the manuscript technically sound, and do the data support the conclusions?
The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.
Reviewer #1: Yes
Reviewer #2: Partly
Reviewer #3: Yes
**********
2. Has the statistical analysis been performed appropriately and rigorously?
Reviewer #1: Yes
Reviewer #2: N/A
Reviewer #3: Yes
**********
3. Have the authors made all data underlying the findings in their manuscript fully available?
The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.
Reviewer #1: No
Reviewer #2: No
Reviewer #3: Yes
**********
4. Is the manuscript presented in an intelligible fashion and written in standard English?
PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.
Reviewer #1: Yes
Reviewer #2: Yes
Reviewer #3: Yes
**********
5. Review Comments to the Author
Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)
Reviewer #1: This study focused on proposing an averaging model to explain the mechanism of multi-gene systems. Compared with other methods, it can better explain complex multi gene locus models. The paper is well-written and contributes to the solution for multi-gene interactions. However, some problems must be solved before it is considered for publication. If this paper is after major revision, I suggest it be accepted, and I believe that some contributions of this paper are important for Genome Wide Association Studies. The problems are listed in the following:
Firstly, the author points out in the abstract that the current methods are mostly linear models that cannot explain complex situations and then shows that the method proposed in this paper is also a linear model. Please explain whether the model proposed in this paper overcomes the drawbacks of traditional linear methods and provide a detailed list of innovative points.
Secondly, some recent state-of-arts of multi-gene interactions seems not to be listed in Introduction. For example, “A Secure High-Order Gene Interaction Detecting Method for Infectious Diseases,” COMPUTATIONAL AND MATHEMATICAL METHODS IN MEDICINE, 10.1155/2022/4471736; “A Secure High-Order Gene Interaction Detection Algorithm Based On Deep Neural Network”, IEEE-ACM TRANSACTIONS ON COMPUTATIONAL BIOLOGY AND BIOINFORMATICS, 10.1109/TCBB.2022.3214863. Both of these papers have designed intelligent methods for deep neural networks, and I recommend that the author cite them.
Finally, this manuscript needs careful editing and particular attention to English grammar, spelling, and sentence structure.
Reviewer #2: This paper proposes the use of averaging models to conduct combinatorial mutation analyses of multi-gene systems. The main idea consists of overcoming the weaknesses of the traditional additive model, especially when dealing with high-order gene interactions. For this purpose, the author employs as baseline a previously reported NR model, extending it to avoid inconsistencies using averaging principles. The experimental analysis is focused on showing the advantages of the refined model over other alternatives, considering different evaluation scenarios including simulated and real-world datasets with 7 and 4 genes.
My main concern with this work is related to its reproducibility. The author does not explain in detail the methodology used to conduct the evaluation and does not highlight the computational / mathematical tools employed for this purpose. To validate the consistency of the obtained results, the author must explain and provide all the resources required to reproduce the results presented in this paper (methods, software and scripts, etc.).
Secondly, the comparisons performed in this work are strongly focused on the additive model, while other interaction models are not considered primarily. To strengthen the contribution of the paper, the author must include comparisons with other models to verify the practical applicability of the averaging model in real-world scenarios.
Others comments related to the organization and presentation of the paper:
- The manuscript lacks an organization paragraph outlining the contents of the paper at the end of the introductory section. Please include it.
- The objective of study paragraphs (page 4) should be placed in the introductory section.
- A final section highlighting the main conclusions of the study and future research directions must be included.
Reviewer #3: In the study titled “An averaging model for analysis and interpretation of high-order genetic interactions,” the authors present a novel averaging model to identify high-order interactions. Given the proven evidence of high-order interactions across various model organisms, including humans, this study is essential for understanding such interactions. However, I have several comments and suggestions to enhance the clarity and impact of the manuscript:
1. Abstract: The abstract's current format needs reorganization. The predominant focus is on the limitations of existing models, particularly the additive model. As a result, it's challenging to discern the study's main findings and conclusions.
2. On page 3, the authors state, “each of which has functional (“wild-type”) and non-functional (null “mutant”) allele states.” This description warrants more nuance. For instance, in cancer research, mutations that heighten cancer risk are often termed ‘functional variants’. Depending on the model system employed, this definition may vary.
3. Also, on page 3, there's a claim: “I recently realized that the interaction operator in the NR model is not consistent...” The rationale behind this inconsistency remains unclear. Could the authors elaborate on how the model's results may vary unpredictably?
4. The study assumes that all genes of interest are homozygous in diploid organisms. In Figure 1, mutation states (e.g., B vs. b) yield starkly different values (e.g., -3 vs. +3). For diploid organisms, how can we determine whether a mutation is homozygous or heterozygous?
5. On page 7, the statement, “Biological information about the data set is described later,” disrupts the flow. This vital information should be introduced earlier to provide context for Figure 3. Without it, readers might struggle to understand the contribution to immunity and the implications of positive or negative values.
6. There are two types of high-order interactions: positive and negative. Based on Figures 2 and 3, it appears the averaging model might not detect negative interactions as effectively as the additive model. Could the authors confirm or refute this observation?
7. It would be beneficial for the authors to discuss scenarios where the additive model might be preferable to the averaging model.
8. The visual presentation in Figures 4 and 5 requires enhancement. Currently, the text and p-values are hard to discern. Specifically, for Figure 5, a conceptual model would aid comprehension. If possible, results from the additive model should be incorporated into Figure 5 for comparison.
9. While the authors delve into chemical reactions within the context of the averaging model, a discussion on its application to disease or cancer models would be invaluable. Can the authors suggest which model might be more applicable for human disease or cancer studies?
**********
6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.
If you choose “no”, your identity will remain anonymous but your review may still be made public.
Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.
Reviewer #1: No
Reviewer #2: No
Reviewer #3: No
**********
[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]
While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at gro.solp@serugif. Please note that Supporting Information files do not need this step.
Author response to Decision Letter 0
3 Dec 2023
Response to Reviewers
I thank the reviewers for their encouragement and thoughtful comments. In the following, my responses to their comments begin with [Response X.X].
Reviewer #1: This study focused on proposing an averaging model to explain the mechanism of multi-gene systems. Compared with other methods, it can better explain complex multi gene locus models. The paper is well-written and contributes to the solution for multi-gene interactions. However, some problems must be solved before it is considered for publication. If this paper is after major revision, I suggest it be accepted, and I believe that some contributions of this paper are important for Genome Wide Association Studies. The problems are listed in the following:
Firstly, the author points out in the abstract that the current methods are mostly linear models that cannot explain complex situations and then shows that the method proposed in this paper is also a linear model. Please explain whether the model proposed in this paper overcomes the drawbacks of traditional linear methods and provide a detailed list of innovative points.
[Response 1.1] Yes, this is the main point of the manuscript: the additive model does not work, but there is a general linear model solution, the averaging model. The fundamental problem of the additive model (ANOVA model with interactions) is that it mathematically fails when (1) the quantitative data in question are not completely linear and (2) the additive model has interactions with orders higher than 2-way interactions. Regarding point (1), a biological data set is typically non-linear, such as having upper and/or lower boundaries in the data value range. Unless a particular study focuses on a small data value range around the center, a data set cannot be considered as linear. In this manuscript, I am focusing on the cases in which more than two interacting genes exist in a system, so point (2) is a starting assumption in search of an appropriate model.
The following is explained in detail in Text S1. The additive model requires conservation of three laws of algebra: the commutative, associative, and distributive laws. The commutative law is conserved for the description of the genetic system. The associative law can be conserved in a non-linear data set if the averaging principle is assumed in the model. However, the distributive law cannot be conserved in a non-linear data set in general. This is the reason the additive model fails with a non-linear data set. Thus, I searched for a model that does not require the conservation of the distributive law in a data set and derived the Network Reconstitution (NR) model. Although the NR model is free of the mathematical failure the additive model suffers, interpretations of the interaction terms were not clear because the definitions of the interactions were different for 2-way interaction terms and 3 or higher order interaction terms. This inconsistency in the interaction definition was corrected in the averaging model, which gives consistent and intuitive interpretations of high-order interaction terms.
Note that I made all these corrections within the framework of linear algebra. Therefore, the additive, NR, and the averaging models are just different types of general linear model. The differences among them lie in how the fitted values are decomposed into differently defined interaction variables. Thus, the fitted values and residuals of the models fit to the same data set are the same, therefore, I focused on the algebraic differences among the models.
Secondly, some recent state-of-arts of multi-gene interactions seems not to be listed in Introduction. For example, “A Secure High-Order Gene Interaction Detecting Method for Infectious Diseases,” COMPUTATIONAL AND MATHEMATICAL METHODS IN MEDICINE, 10.1155/2022/4471736; “A Secure High-Order Gene Interaction Detection Algorithm Based On Deep Neural Network”, IEEE-ACM TRANSACTIONS ON COMPUTATIONAL BIOLOGY AND BIOINFORMATICS, 10.1109/TCBB.2022.3214863. Both of these papers have designed intelligent methods for deep neural networks, and I recommend that the author cite them.
[Response 1.2] Thanks for pointing out these papers. However, the goals of these papers and my manuscript are very different. The goal of these papers is to efficiently detect weak high-order interactions in a very large, generally open data set. I mean by an “open” data set (1) that numerous genes irrelevant to the trait of interest are included and (2) that for most genes the allelic combinations are not exhaustive. For example, considering an arbitrary number of 10 genes, the chance that all possible allelic combinations of 210 = 1024 with replication are included in the data set is very low. In short, the main point of these papers is computing efficiency and sensitivity in analysis of an open data set.
The goal of my manuscript is to consistently and comprehensively interpret the mechanistic relationships among gene effects and interactions when the exhaustive allelic combinations with replication are available in the data set, which I would call a closed data set for the multi-gene system (where the number of genes in the system is relatively limited). In short, the main point of my manuscript is mathematical and interpretational consistency in analysis of a closed data set.
Considering these very different goals, I prefer not to cite these papers to avoid confusing readers.
Finally, this manuscript needs careful editing and particular attention to English grammar, spelling, and sentence structure.
[Response 1.3] The manuscript has been edited by a biologist who is a native speaker of English.
Reviewer #2: This paper proposes the use of averaging models to conduct combinatorial mutation analyses of multi-gene systems. The main idea consists of overcoming the weaknesses of the traditional additive model, especially when dealing with high-order gene interactions. For this purpose, the author employs as baseline a previously reported NR model, extending it to avoid inconsistencies using averaging principles. The experimental analysis is focused on showing the advantages of the refined model over other alternatives, considering different evaluation scenarios including simulated and real-world datasets with 7 and 4 genes.
My main concern with this work is related to its reproducibility. The author does not explain in detail the methodology used to conduct the evaluation and does not highlight the computational / mathematical tools employed for this purpose. To validate the consistency of the obtained results, the author must explain and provide all the resources required to reproduce the results presented in this paper (methods, software and scripts, etc.).
[Response 2.1] The R script for the averaging model, including algorithms to remove insignificant genes and generate Fig. 5, was provided as Supplemental Dataset 3. All Supplemental Datasets, including the above R script and the raw data used to generate Figs. 3 and 5, are available from https://github.com/fumikatagiri/Averaging_Model, as described in the METHODS and SUPPLEMENTAL DATASETS sections. Thus, I understand that the reviewer would like the R scripts used to generate Figs. 1, 2, and 3. These scripts have been added to the above github site.
Secondly, the comparisons performed in this work are strongly focused on the additive model, while other interaction models are not considered primarily. To strengthen the contribution of the paper, the author must include comparisons with other models to verify the practical applicability of the averaging model in real-world scenarios.
[Response 2.2] I clarified the goal of my manuscript in [Response 1.2]. For this goal I am not aware of a study that doesn’t use the additive model or its modified versions other than our previous study using the NR model (Refs. 1 and 2). For example, the additive model was used in Ref 3. It is very likely that the impacts of higher-order gene interactions were grossly overestimated due to use of the additive model (e.g., Figure 3 of Ref 3 clearly shows that loss of resistance to camptothecin is almost all explained by the effect of the double mutation pdr5Δ snq2Δ. However, in Figure 4A of Ref 3, strong three-gene and five-gene interactions were shown). Ref 4 investigated three-gene interactions in many multi-gene systems in yeast. Their model defines the no interaction case multiplicatively (an equivalent of defining an additive model with no interaction for a log-scaled response) and defines the mutant gene interactions in an additive model manner (i.e., using a linear-scaled response). First, using a log-scaled response for no interaction cases moderates but does not solve the issue of the non-linearity near the upper boundary of the response range. Second, they did not mathematically justify why they used the additive interactions for multiplicatively defined no-interaction gene effects. Since the interaction was defined in an additive manner, I consider this as a modified version of the additive model. Other works by this group, including Costanzo et al. (Science 372, eabf8424 (2021)), investigating GxGxE interactions (3-way interactions), use similar models. I did not particularly discuss the models in the latter cases (Ref 4) in the manuscript because I do not recognize mathematical principles underlying the models although I could recognize influences of the additive model.
Others comments related to the organization and presentation of the paper:
- The manuscript lacks an organization paragraph outlining the contents of the paper at the end of the introductory section. Please include it.
[Response 2.3] The last paragraph of the Introduction has been revised to include a summary of the major findings of the study as follows.
“The averaging model can estimate high-order genetic interactions in a stable manner with nonlinear multi-gene systems because each averaging interaction can be defined using only observed values, e.g., A;B;C = ABC – (AB + AC + BC) / 3. The interpretations of averaging interactions are intuitive and consistent: a genetic interaction is the average impact of adding the last gene; note that the above definition of A;B;C is the equivalent of A;B;C = { (ABC – AB) + (ABC – AC) + (ABC – BC) } / 3. The additive and averaging models without interaction can be understood as two extreme approximations in a 2-gene system: there is no mechanistic reason to favor one of the models without additional mechanistic information. Since the averaging model is mathematically stable, provides intuitive and consistent interpretations of gene interactions, and is mechanistically tractable, I propose the averaging model as a standard general linear model for descriptions of multi-gene system behaviors.”
- The objective of study paragraphs (page 4) should be placed in the introductory section.
[Response 2.4] The paragraphs have been removed, and now the objective is stated in the Introduction.
- A final section highlighting the main conclusions of the study and future research directions must be included.
[Response 2.5] I am sorry that I do not understand this comment. The manuscript had a “Concluding remarks” section at the end of the Results and Discussion. In that section I propose a future direction in the research field of higher-order gene interactions: the averaging model should be used instead of the additive model.
Reviewer #3: In the study titled “An averaging model for analysis and interpretation of high-order genetic interactions,” the authors present a novel averaging model to identify high-order interactions. Given the proven evidence of high-order interactions across various model organisms, including humans, this study is essential for understanding such interactions. However, I have several comments and suggestions to enhance the clarity and impact of the manuscript:
1. Abstract: The abstract's current format needs reorganization. The predominant focus is on the limitations of existing models, particularly the additive model. As a result, it's challenging to discern the study's main findings and conclusions.
[Response 3.1] The abstract has been rewritten accordingly as follows:
“While combinatorial genetic data collection from biological systems in which quantitative phenotypes are controlled by active and inactive alleles of multiple genes (multi-gene systems) is becoming common, a standard analysis method for such data has not been established. The currently common approaches have three major drawbacks. First, although it is a long tradition in genetics, modeling the effect of an inactive allele (a null mutant allele) contrasted against that of the active allele (the wild-type allele) is not suitable for mechanistic understanding of multi-gene systems. Second, a commonlyused additive model (ANOVA with interaction) mathematically fails in estimation of interactions among more than two genes when the phenotypic response is not linear. Third, interpretation of higher-order interactions defined by an additive model is not intuitive. To solve these problems I propose an averaging model, which is a general linear model that decomposes the response into variables differently and is suitable for mechanistic understanding of multi-gene systems: the effect of the active allele is contrasted against the effect of the inactive allele for easier mechanistic interpretations; it is mathematically stable in estimation of higher-order interactions even when the phenotypic response is not linear; and the interpretations of the higher-order interactions it defines are intuitive and consistent - interactions are defined as the mean effects of the last active genes added to the system. Yet, as the averaging model is a general linear model, fitting the model is easy and accurate using common statistical tools.”
2. On page 3, the authors state, “each of which has functional (“wild-type”) and non-functional (null “mutant”) allele states.” This description warrants more nuance. For instance, in cancer research, mutations that heighten cancer risk are often termed ‘functional variants’. Depending on the model system employed, this definition may vary.
[Response 3.2] The wording has been changed to active and inactive alleles of a gene, respectively.
3. Also, on page 3, there's a claim: “I recently realized that the interaction operator in the NR model is not consistent...” The rationale behind this inconsistency remains unclear. Could the authors elaborate on how the model's results may vary unpredictably?
[Response 3.3] It is not that model results vary unpredictably (the NR model is already mathematically stable), but that the interpretations of the interaction terms in the model are not consistent or intuitive. This interpretational inconsistency arises from the fact that in the NR model, two-gene interactions are defined by the additive model and three or more-gene interactions are defined in the way the averaging model does. Note that the additive model does not mathematically fail if it only contains two-gene interactions (and the single gene effects). Thus, by using the averaging interactions for higher order interactions, the NR model is mathematically stable. However, the fact that additive and averaging interactions are mixed in a single model made the interpretations of the gene interactions in the NR model inconsistent and non-intuitive. The interpretational issues were described in the paragraph starting with the sentence, “I recently realized that the interaction operator in the NR model is not consistent.” The averaging model is the solution. In the last paragraph of the Introduction, the problem was explained as, “The interpretations of averaging interactions are intuitive and consistent: a genetic interaction is the average impact of adding the last gene; note that the above definition of A;B;C is the equivalent of A;B;C = { (ABC – AB) + (ABC – AC) + (ABC – BC) } / 3.” I think that this explains the difference between the NR model and the averaging model well.
4. The study assumes that all genes of interest are homozygous in diploid organisms. In Figure 1, mutation states (e.g., B vs. b) yield starkly different values (e.g., -3 vs. +3). For diploid organisms, how can we determine whether a mutation is homozygous or heterozygous?
[Response 3.4] As explained in [Response 1.2], the strengths of the averaging model are mathematical and interpretational consistency in analysis of a closed data set. For a closed data set, it is assumed that the genotypes of all biological samples are known.
5. On page 7, the statement, “Biological information about the data set is described later,” disrupts the flow. This vital information should be introduced earlier to provide context for Figure 3. Without it, readers might struggle to understand the contribution to immunity and the implications of positive or negative values.
[Response 3.5] The following sentences have been added to replace “Biological information about the data set is described later”:
“The data set used in this figure was the quantitative phenotype of Effector-Triggered Immunity (ETI) induced by a bacterial effector AvrRpt2 in the model plant Arabidopsis (AvrRpt2-ETI) (8-11). The inhibition of bacterial growth in the plant leaf, in log10(cfu/cm2), was the AvrRpt2-ETI phenotype measure. The hub genes of four major signaling sectors (subnetworks) in the plant immune signaling network were subjected to mutational analysis. The signaling sectors were the jasmonate, ethylene, PAD4, and salicylate sectors, which are indicated as J, E, P, and S, respectively. I also call their hub genes J, E, P, and S, in this context of analysis of the 4-gene system. Biological and experimental details are provided in (2)”
6. There are two types of high-order interactions: positive and negative. Based on Figures 2 and 3, it appears the averaging model might not detect negative interactions as effectively as the additive model. Could the authors confirm or refute this observation?
[Response 3.6] This is one of the main points of my manuscript – the additive model tends to overestimate the impact (the absolute values) of higher-order interactions when the response has a limited range, as clearly demonstrated by the simulation in Fig. 2. Such overestimations of the impact of higher-order interactions lead to the mathematical failure of the additive model.
7. It would be beneficial for the authors to discuss scenarios where the additive model might be preferable to the averaging model.
[Response 3.7] The additive model is mathematically stable only when (1) the response is approximately linear within the range of interest (e.g., the effects of each gene are relatively small compared to the entire response range) or (2) the system does not contain three or more-gene interactions. On the other hand, the averaging model does not require these conditions to be mathematically stable. Since the multi-gene systems I discuss in the manuscript do not satisfy either of the conditions, there is no case in which the additive model is preferable to the averaging model.
If the system in question satisfies condition (2), the additive model has been used in the definition of two-gene interactions in conventional genetics (or epistasis in quantitative genetics). For this historical reason, many geneticists are probably more comfortable with the additive interaction definition. However, one of the main messages my manuscript delivers is that if we, as a research field, extend our investigations into higher order gene interactions, we need to change the definition of gene interactions.
8. The visual presentation in Figures 4 and 5 requires enhancement. Currently, the text and p-values are hard to discern. Specifically, for Figure 5, a conceptual model would aid comprehension. If possible, results from the additive model should be incorporated into Figure 5 for comparison.
[Response 3.8] For Figs. 4 and 5, the overall figures have been made larger and some fonts have been made larger for easier viewing. Fig. 4 is the general conceptual model. Also, in Fig. 3, the results of the additive model and the NR model were compared to the averaging model results shown in Fig. 5a, which clearly demonstrates the problem of the additive model. Thus, I think that the information the reviewer is requesting is already in the manuscript.
9. While the authors delve into chemical reactions within the context of the averaging model, a discussion on its application to disease or cancer models would be invaluable. Can the authors suggest which model might be more applicable for human disease or cancer studies?
[Response 3.9] The purpose of this section is to demonstrate that both additive and averaging models without interaction are approximations of two separate extreme conditions, which indicates that there is no reason to prefer one model over the other for this mechanistic reason. For other reasons, i.e., mathematical stability with three or more gene interactions and with non-linear responses and intuitive and consistent interpretations of higher order gene interactions, the averaging model is the superior model. Therefore, there is no reason to prefer the additive model over the averaging model while there are multiple reasons to prefer the averaging model over the additive model. Thus, the averaging model, instead of the additive model, should be a standard model.
Attachment
Submitted filename: PLOSOne_response_to_comments_2311fs2.docx
Decision Letter 1
27 Dec 2023
PONE-D-23-24383R1An averaging model for analysis and interpretation of high-order genetic interactionsPLOS ONE
Dear Dr. Fumiaki Katagiri,
Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.
Please submit your revised manuscript by Feb 10 2024 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at gro.solp@enosolp. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.
Please include the following items when submitting your revised manuscript:
A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.
If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.
If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: https://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.
We look forward to receiving your revised manuscript.
Kind regards,
Solip Park
Guest Editor
PLOS ONE
Journal Requirements:
Please review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript. If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.
Additional Editor Comments (if provided):
Point 1 (Abstract Structure): Although the author has undergone a change in the revised version, there remains a need for substantial improvement in the abstract's structure. Notably, the abstract lacks a clear articulation of the primary findings or conclusions. Currently, it appears to comprise two principal components: (i) a discussion of the limitations of another method, and (ii) an exposition of the hypotheses and assumptions. To enhance the abstract's effectiveness, it is imperative to incorporate a succinct summary of the key outcomes or conclusions.
Point 7 (Incorporation of Changes): It is imperative that the recommended change be seamlessly integrated into the revised text. If the author has already undertaken this inclusion in the revised manuscript, kindly specify the precise location for reference and review. This is pivotal for ensuring that the recommended revisions are adequately addressed and reflected in the final manuscript.
[Note: HTML markup is below. Please do not edit.]
Reviewers' comments:
[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]
While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at gro.solp@serugif. Please note that Supporting Information files do not need this step.
Author response to Decision Letter 1
28 Jan 2024
Response to Editor
Point 1 (Abstract Structure): Although the author has undergone a change in the revised version, there remains a need for substantial improvement in the abstract's structure. Notably, the abstract lacks a clear articulation of the primary findings or conclusions. Currently, it appears to comprise two principal components: (i) a discussion of the limitations of another method, and (ii) an exposition of the hypotheses and assumptions. To enhance the abstract's effectiveness, it is imperative to incorporate a succinct summary of the key outcomes or conclusions.
[Response to Point 1] I have rewritten the second half of the abstract. I have added a sentence describing the key outcomes at the end of the abstract. The following is the revised abstract.
“While combinatorial genetic data collection from biological systems in which quantitative phenotypes are controlled by active and inactive alleles of multiple genes (multi-gene systems) is becoming common, a standard analysis method for such data has not been established. The currently common approaches have three major drawbacks. First, although it is a long tradition in genetics, modeling the effect of an inactive allele (a null mutant allele) contrasted against that of the active allele (the wild-type allele) is not suitable for mechanistic understanding of multi-gene systems. Second, a commonly-used additive model (ANOVA with interaction) mathematically fails in estimation of interactions among more than two genes when the phenotypic response is not linear. Third, interpretation of higher-order interactions defined by an additive model is not intuitive. I derived an averaging model based on algebraic principles to solve all these problems within the framework of a general linear model. In the averaging model: the effect of the active allele is contrasted against the effect of the inactive allele for easier mechanistic interpretations; there is mathematical stability in estimation of higher-order interactions even when the phenotypic response is not linear; and interpretations of higher-order interactions are intuitive and consistent - interactions are defined as the mean effects of the last active genes added to the system. Thus, the key outcomes of this study are development of the averaging model, which is suitable for analysis of multi-gene systems, and a new, intuitive, and mathematically and interpretationally consistent definition of a genetic interaction, which is central to the averaging model.”
Point 7 (Incorporation of Changes): It is imperative that the recommended change be seamlessly integrated into the revised text. If the author has already undertaken this inclusion in the revised manuscript, kindly specify the precise location for reference and review. This is pivotal for ensuring that the recommended revisions are adequately addressed and reflected in the final manuscript.
[Response to Point 7] To make the response to “Point 7 (Incorporation of Changes)” clearer, I have included the previous Response to Reviewers section below the dashed line. The line numbers in the marked-up manuscript (or “(I have not changed the manuscript.)”) have been added in red to indicate where the revisions were made. In addition, to make this point clear in the manuscript, the marked-up version of the manuscript retains changes from the first revision in colors (red or green). There were some additional minor editorial changes in
addition to those explained in the previous Response to Reviewers (marked up by red). For this second revision, the only substantive changes in the manuscript relative to the first revision are in the Abstract (see [Response to Point 1]).
--------------------
Response to Reviewers for revision 1
I thank the reviewers for their encouragement and thoughtful comments. In the following, my responses to their comments are indented and begin with [Response X.X].
Reviewer #1: This study focused on proposing an averaging model to explain the mechanism of multi-gene systems. Compared with other methods, it can better explain complex multi gene locus models. The paper is well-written and contributes to the solution for multi-gene interactions. However, some problems must be solved before it is considered for publication. If this paper is after major revision, I suggest it be accepted, and I believe that some contributions of this paper are important for Genome Wide Association Studies. The problems are listed in the following: Firstly, the author points out in the abstract that the current methods are mostly linear models that cannot explain complex situations and then shows that the method proposed in this paper is also a linear model. Please explain whether the model proposed in this paper overcomes the drawbacks of traditional linear methods and provide a detailed list of innovative points.
[Response 1.1] (I have not changed the manuscript.) Yes, this is the main point of the manuscript: the additive model does not work, but there is a general linear model solution, the averaging model. The fundamental problem of the additive model (ANOVA model with interactions) is that it mathematically fails when (1) the quantitative data in question are not completely linear and (2) the additive model has interactions with orders higher than 2-way interactions. Regarding point (1), a biological data set is typically non-linear, such as having upper and/or lower boundaries in the data value range. Unless a particular study focuses on a small data value range around the center, a data set cannot be considered as linear. In this manuscript, I am focusing on the cases in which more than two interacting genes exist in a system, so point (2) is a starting assumption in search of an appropriate model.
The following is explained in detail in Text S1. The additive model requires conservation of three laws of algebra: the commutative, associative, and distributive laws. The commutative law is conserved for the description of the genetic system. The associative law can be conserved in a non-linear data set if the averaging principle is assumed in the model. However, the distributive law cannot be conserved in a non-linear data set in general. This is the reason the additive model fails with a non-linear data set. Thus, I searched for a model that does not require the conservation of the distributive law in a data set and derived the Network Reconstitution (NR) model. Although the NR model is free of the mathematical failure the additive model suffers, interpretations of the interaction terms were not clear because the definitions of the interactions were different for 2-way interaction terms and 3 or
higher order interaction terms. This inconsistency in the interaction definition was corrected in the averaging model, which gives consistent and intuitive interpretations of high-order interaction terms.
Note that I made all these corrections within the framework of linear algebra. Therefore, the additive, NR, and the averaging models are just different types of general linear model. The differences among them lie in how the fitted values are decomposed into differently defined interaction variables. Thus, the fitted values and residuals of the models fit to the same data set are the same, therefore, I focused on the algebraic differences among the models.
Secondly, some recent state-of-arts of multi-gene interactions seems not to be listed in Introduction. For example, “A Secure High-Order Gene Interaction Detecting Method for Infectious Diseases,” COMPUTATIONAL AND MATHEMATICAL METHODS IN MEDICINE, 10.1155/2022/4471736; “A Secure High-Order Gene Interaction Detection Algorithm Based On Deep Neural Network”, IEEE-ACM TRANSACTIONS ON COMPUTATIONAL BIOLOGY AND BIOINFORMATICS, 10.1109/TCBB.2022.3214863. Both of these papers have designed intelligent methods for deep neural networks, and I recommend that the author cite them.
[Response 1.2] (I have not changed the manuscript.) Thanks for pointing out these papers. However, the goals of these papers and my manuscript are very different. The goal of these papers is to efficiently detect weak high-order interactions in a very large, generally open data set. I mean by an “open” data set (1) that numerous genes irrelevant to the trait of interest are included and (2) that for most genes the allelic combinations are not exhaustive. For example, considering an arbitrary number of 10 genes, the chance that all possible allelic combinations of 210 = 1024 with replication are included in the data set is very low. In short, the main point of these papers is computing efficiency and sensitivity in analysis of an open data set.
The goal of my manuscript is to consistently and comprehensively interpret the mechanistic relationships among gene effects and interactions when the exhaustive allelic combinations with replication are available in the data set, which I would call a closed data set for the multi-gene system (where the number of genes in the system is relatively limited). In short, the main point of my manuscript is mathematical and interpretational consistency in analysis of a closed data set.
Considering these very different goals, I prefer not to cite these papers to avoid confusing readers.
Finally, this manuscript needs careful editing and particular attention to English grammar, spelling, and sentence structure.
[Response 1.3] The manuscript has been edited by a biologist who is a native speaker of English.
Reviewer #2: This paper proposes the use of averaging models to conduct combinatorial mutation analyses of multi-gene systems. The main idea consists of overcoming the weaknesses of the traditional additive model, especially when dealing with high-order gene interactions. For this purpose, the author employs as baseline a previously reported NR model, extending it to avoid inconsistencies using averaging principles. The experimental analysis is focused on showing the advantages of the refined model over other alternatives, considering different evaluation scenarios including simulated and real-world datasets with 7 and 4 genes. My main concern with this work is related to its reproducibility. The author does not explain in detail the methodology used to conduct the evaluation and does not highlight the computational / mathematical tools employed for this purpose. To validate the consistency of the obtained results, the author must explain and provide all the resources required to reproduce the results presented in this paper (methods, software and scripts, etc.).
[Response 2.1] The R script for the averaging model, including algorithms to remove insignificant genes and generate Fig. 5, was provided as Supplemental Dataset 3. All Supplemental Datasets, including the above R script and the raw data used to generate Figs. 3 and 5, are available from https://github.com/fumikatagiri/Averaging_Model, as described in the METHODS and SUPPLEMENTAL DATASETS sections. Thus, I understand that the reviewer would like the R scripts used to generate Figs. 1, 2, and 3. These scripts have been added to the above github site.
Secondly, the comparisons performed in this work are strongly focused on the additive model, while other interaction models are not considered primarily. To strengthen the contribution of the paper, the author must include comparisons with other models to verify the practical applicability of the averaging model in real-world scenarios.
[Response 2.2] (I have not changed the manuscript.) I clarified the goal of my manuscript in [Response 1.2]. For this goal I am not aware of a study that doesn’t use the additive model or its modified versions other than our previous study using the NR model (Refs. 1 and 2). For example, the additive model was used in Ref 3. It is very likely that the impacts of higher-order gene interactions were grossly overestimated due to use of the additive model (e.g., Figure 3 of Ref 3 clearly shows that loss of resistance to camptothecin is almost all explained by the effect of the double mutation pdr5Δ snq2Δ. However, in Figure 4A of Ref 3, strong three-gene and five-gene interactions were shown). Ref 4 investigated three-gene interactions in many multi-gene systems in yeast. Their model defines the no interaction case multiplicatively (an equivalent of defining an additive model with no interaction for a log-scaled response) and defines the mutant gene interactions in an additive model manner (i.e., using a linear-scaled response). First, using a log-scaled response for no interaction cases moderates but does not solve the issue of the non-linearity near the upper boundary of the response range. Second, they did not mathematically justify why they used the additive interactions for multiplicatively defined no-interaction gene effects. Since the interaction was defined in an additive manner, I consider this as a modified version of the additive model. Other works by this group, including Costanzo et al. (Science 372, eabf8424 (2021)),
investigating GxGxE interactions (3-way interactions), use similar models. I did not particularly discuss the models in the latter cases (Ref 4) in the manuscript because I do not recognize mathematical principles underlying the models although I could recognize influences of the additive model.
Others comments related to the organization and presentation of the paper: - The manuscript lacks an organization paragraph outlining the contents of the paper at the end of the introductory section. Please include it.
[Response 2.3] The last paragraph of the Introduction has been revised to include a summary of the major findings of the study as follows. (lines 97-109)
“The averaging model can estimate high-order genetic interactions in a stable manner with nonlinear multi-gene systems because each averaging interaction can be defined using only observed values, e.g., A;B;C = ABC – (AB + AC + BC) / 3. The interpretations of averaging interactions are intuitive and consistent: a genetic interaction is the average impact of adding the last gene; note that the above definition of A;B;C is the equivalent of A;B;C = { (ABC – AB) + (ABC – AC) + (ABC – BC) } / 3. The additive and averaging models without interaction can be understood as two extreme approximations in a 2-gene system: there is no mechanistic reason to favor one of the models without additional mechanistic information. Since the averaging model is mathematically stable, provides intuitive and consistent interpretations of gene interactions, and is mechanistically tractable, I propose the averaging model as a standard general linear model for descriptions of multi-gene system behaviors.”
- The objective of study paragraphs (page 4) should be placed in the introductory section.
[Response 2.4] The paragraphs have been removed, and now the objective is stated in the Introduction. (the paragraph has been moved to lines 56-62) (the objective statement is in lines 67-68)
- A final section highlighting the main conclusions of the study and future research directions must be included.
[Response 2.5] (I have not changed the manuscript.) I am sorry that I do not understand this comment. The manuscript had a “Concluding remarks” section at the end of the Results and Discussion. In that section I propose a future direction in the research field of higher-order gene interactions: the averaging model should be used instead of the additive model.
Reviewer #3: In the study titled “An averaging model for analysis and interpretation of high-order genetic interactions,” the authors present a novel averaging model to identify high-order interactions. Given the proven evidence of high-order interactions across various model organisms, including humans, this study is essential for understanding such interactions. However, I have several comments and suggestions to enhance the clarity and impact of the
manuscript: 1. Abstract: The abstract's current format needs reorganization. The predominant focus is on the limitations of existing models, particularly the additive model. As a result, it's challenging to discern the study's main findings and conclusions.
[Response 3.1] The abstract has been rewritten accordingly as follows: (Please see the [Response to Point 1] above for the latest version of the Abstract.)
“While combinatorial genetic data collection from biological systems in which quantitative phenotypes are controlled by active and inactive alleles of multiple genes (multi-gene systems) is becoming common, a standard analysis method for such data has not been established. The currently common approaches have three major drawbacks. First, although it is a long tradition in genetics, modeling the effect of an inactive allele (a null mutant allele) contrasted against that of the active allele (the wild-type allele) is not suitable for mechanistic understanding of multi-gene systems. Second, a commonlyused additive model (ANOVA with interaction) mathematically fails in estimation of interactions among more than two genes when the phenotypic response is not linear. Third, interpretation of higher-order interactions defined by an additive model is not intuitive. To solve these problems I propose an averaging model, which is a general linear model that decomposes the response into variables differently and is suitable for mechanistic understanding of multi-gene systems: the effect of the active allele is contrasted against the effect of the inactive allele for easier mechanistic interpretations; it is mathematically stable in estimation of higher-order interactions even when the phenotypic response is not linear; and the interpretations of the higher-order interactions it defines are intuitive and consistent - interactions are defined as the mean effects of the last active genes added to the system. Yet, as the averaging model is a general linear model, fitting the model is easy and accurate using common statistical tools.”
2. On page 3, the authors state, “each of which has functional (“wild-type”) and non-functional (null “mutant”) allele states.” This description warrants more nuance. For instance, in cancer research, mutations that heighten cancer risk are often termed ‘functional variants’. Depending on the model system employed, this definition may vary.
[Response 3.2] The wording has been changed to active and inactive alleles of a gene, respectively. (lines 27, 32, 40, 41, 44, 54, 58)
3. Also, on page 3, there's a claim: “I recently realized that the interaction operator in the NR model is not consistent...” The rationale behind this inconsistency remains unclear. Could the authors elaborate on how the model's results may vary unpredictably?
[Response 3.3] It is not that model results vary unpredictably (the NR model is already mathematically stable), but that the interpretations of the interaction terms in the model are not consistent or intuitive. This interpretational inconsistency arises from the fact that in the NR model, two-gene interactions are defined by the additive model and three or more-gene interactions are defined in the way the averaging model does. Note that the additive model does not mathematically fail if it only contains two-gene interactions (and the single gene effects). Thus, by using the averaging interactions for higher order interactions, the NR model is mathematically stable. However, the fact that additive and averaging interactions are mixed in a single model made the interpretations of the gene interactions in the NR model inconsistent and non-intuitive. The interpretational issues were described in the paragraph starting with the sentence, “I recently realized that the interaction operator in the NR model is not consistent. (line 89)” The averaging model is the solution. In the last paragraph of the Introduction, the problem was explained as, “The interpretations of averaging interactions are intuitive and consistent: a genetic interaction is the average impact of adding the last gene; note that the above definition of A;B;C is the equivalent of A;B;C = { (ABC – AB) + (ABC – AC) + (ABC – BC) } / 3. (lines 100-102)” I think that this explains the difference between the NR model and the averaging model well.
4. The study assumes that all genes of interest are homozygous in diploid organisms. In Figure 1, mutation states (e.g., B vs. b) yield starkly different values (e.g., -3 vs. +3). For diploid organisms, how can we determine whether a mutation is homozygous or heterozygous?
[Response 3.4] (I have not changed the manuscript.) As explained in [Response 1.2], the strengths of the averaging model are mathematical and interpretational consistency in analysis of a closed data set. For a closed data set, it is assumed that the genotypes of all biological samples are known.
5. On page 7, the statement, “Biological information about the data set is described later,” disrupts the flow. This vital information should be introduced earlier to provide context for Figure 3. Without it, readers might struggle to understand the contribution to immunity and the implications of positive or negative values.
[Response 3.5] The following sentences have been added to replace “Biological information about the data set is described later”: (lines 221-228)
“The data set used in this figure was the quantitative phenotype of Effector-Triggered Immunity (ETI) induced by a bacterial effector AvrRpt2 in the model plant Arabidopsis (AvrRpt2-ETI) (8-11). The inhibition of bacterial growth in the plant leaf, in log10(cfu/cm2), was the AvrRpt2-ETI phenotype measure. The hub genes of four major signaling sectors (subnetworks) in the plant immune signaling network were subjected to mutational analysis. The signaling sectors were the jasmonate, ethylene, PAD4, and salicylate sectors, which are indicated as J, E, P, and S, respectively. I also call their hub genes J, E, P, and S, in this
context of analysis of the 4-gene system. Biological and experimental details are provided in (2)”
6. There are two types of high-order interactions: positive and negative. Based on Figures 2 and 3, it appears the averaging model might not detect negative interactions as effectively as the additive model. Could the authors confirm or refute this observation?
[Response 3.6] (I have not changed the manuscript.) This is one of the main points of my manuscript – the additive model tends to overestimate the impact (the absolute values) of higher-order interactions when the response has a limited range, as clearly demonstrated by the simulation in Fig. 2. Such overestimations of the impact of higher-order interactions lead to the mathematical failure of the additive model.
7. It would be beneficial for the authors to discuss scenarios where the additive model might be preferable to the averaging model.
[Response 3.7] (I have not changed the manuscript.) The additive model is mathematically stable only when (1) the response is approximately linear within the range of interest (e.g., the effects of each gene are relatively small compared to the entire response range) or (2) the system does not contain three or more-gene interactions. On the other hand, the averaging model does not require these conditions to be mathematically stable. Since the multi-gene systems I discuss in the manuscript do not satisfy either of the conditions, there is no case in which the additive model is preferable to the averaging model.
If the system in question satisfies condition (2), the additive model has been used in the definition of two-gene interactions in conventional genetics (or epistasis in quantitative genetics). For this historical reason, many geneticists are probably more comfortable with the additive interaction definition. However, one of the main messages my manuscript delivers is that if we, as a research field, extend our investigations into higher order gene interactions, we need to change the definition of gene interactions.
8. The visual presentation in Figures 4 and 5 requires enhancement. Currently, the text and p-values are hard to discern. Specifically, for Figure 5, a conceptual model would aid comprehension. If possible, results from the additive model should be incorporated into Figure 5 for comparison.
[Response 3.8] For Figs. 4 and 5, the overall figures have been made larger and some fonts have been made larger for easier viewing. Fig. 4 is the general conceptual model. Also, in Fig. 3, the results of the additive model and the NR model were compared to the averaging model results shown in Fig. 5a, which clearly demonstrates the problem of the additive
model. To make this point clear a sentence was inserted in lines 313-314: “Note that the data set for AvrRpt2-ETI is the same data set used in Fig. 3.” Thus, I think that the information the reviewer is requesting is already in the manuscript.
9. While the authors delve into chemical reactions within the context of the averaging model, a discussion on its application to disease or cancer models would be invaluable. Can the authors suggest which model might be more applicable for human disease or cancer studies?
[Response 3.9] (I have not changed the manuscript.) The purpose of this section is to demonstrate that both additive and averaging models without interaction are approximations of two separate extreme conditions, which indicates that there is no reason to prefer one model over the other for this mechanistic reason. For other reasons, i.e., mathematical stability with three or more gene interactions and with non-linear responses and intuitive and consistent interpretations of higher order gene interactions, the averaging model is the superior model. Therefore, there is no reason to prefer the additive model over the averaging model while there are multiple reasons to prefer the averaging model over the additive model. Thus, the averaging model, instead of the additive model, should be a standard model.
Attachment
Submitted filename: PLOSOne_response_to_comments_240128_f.pdf
Decision Letter 2
13 Feb 2024
An averaging model for analysis and interpretation of high-order genetic interactions
PONE-D-23-24383R2
Dear Dr. Fumiaki Katagiri,
We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.
Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.
An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at gro.solp@gnillibrohtua.
If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact gro.solp@sserpeno.
Kind regards,
Solip Park
Guest Editor
PLOS ONE
Additional Editor Comments (optional):
The author has been changed based on the reviewer's comments and explain the details about the comments.
Reviewers' comments:
Acceptance letter
26 Mar 2024
PONE-D-23-24383R2
PLOS ONE
Dear Dr. Katagiri,
I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now being handed over to our production team.
At this stage, our production department will prepare your paper for publication. This includes ensuring the following:
* All references, tables, and figures are properly cited
* All relevant supporting information is included in the manuscript submission,
* There are no issues that prevent the paper from being properly typeset
If revisions are needed, the production department will contact you directly to resolve them. If no revisions are needed, you will receive an email when the publication date has been set. At this time, we do not offer pre-publication proofs to authors during production of the accepted work. Please keep in mind that we are working through a large volume of accepted articles, so please give us a few weeks to review your paper and let you know the next and final steps.
Lastly, if your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact gro.solp@sserpeno.
If we can help with anything else, please email us at gro.solp@eracremotsuc.
Thank you for submitting your work to PLOS ONE and supporting open access.
Kind regards,
PLOS ONE Editorial Office Staff
on behalf of
Dr. Solip Park
Guest Editor
PLOS ONE
Articles from PLOS ONE are provided here courtesy of PLOS
Full text links
Read article at publisher's site: https://doi.org/10.1371/journal.pone.0299525
Read article for free, from open access legal sources, via Unpaywall:
https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0299525&type=printable
Lay summaries
Plain language description
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Folic acid supplementation and malaria susceptibility and severity among people taking antifolate antimalarial drugs in endemic areas.
Cochrane Database Syst Rev, 2(2022), 01 Feb 2022
Cited by: 12 articles | PMID: 36321557 | PMCID: PMC8805585
Review Free full text in Europe PMC
FSHB -211 G>T is a major genetic modulator of reproductive physiology and health in childbearing age women.
Hum Reprod, 33(5):954-966, 01 May 2018
Cited by: 20 articles | PMID: 29617818
Evolutionary and convergence stability for continuous phenotypes in finite populations derived from two-allele models.
J Theor Biol, 310:206-215, 07 Jul 2012
Cited by: 6 articles | PMID: 22781555
The conflict theory of genomic imprinting: how much can be explained?
Curr Top Dev Biol, 40:255-293, 01 Jan 1998
Cited by: 35 articles | PMID: 9673853
Review
Funding
Funders who supported this work.
Division of Integrative Organismal Systems (1)
Grant ID: IOS-1645460
Division of Molecular and Cellular Biosciences (1)
Grant ID: MCB-1518058
National Institute of Food and Agriculture (1)
Grant ID: 2020-67013-31187

 *
*


