Europe PMC

This website requires cookies, and the limited processing of your personal data in order to function. By using the site you are agreeing to this as outlined in our privacy notice and cookie policy.

A cortical potential imaging study from simultaneous extra- and intracranial electrical recordings by means of the finite element method.

Author information

Affiliations

  • 1. University of Minnesota, Department of Biomedical Engineering, 7-105 Hasselmo Hall, 312 Church Street SE, Minneapolis, MN 55455, USA.
      Authors
    • Zhang Y 1
    (1 author)

ORCIDs linked to this article

Neuroimage, 02 May 2006, 31(4):1513-1524
https://doi.org/10.1016/j.neuroimage.2006.02.027 PMID: 16631381 PMCID: PMC1866308

Free full text in Europe PMC

Abstract 

In the present study, we have validated the cortical potential imaging (CPI) technique for estimating cortical potentials from scalp EEG using simultaneously recorded electrocorticogram (ECoG) in the presence of strong local inhomogeneity, i.e., Silastic ECoG grid(s). The finite element method (FEM) was used to model the realistic postoperative head volume conductor, which includes the scalp, skull, cerebrospinal fluid (CSF) and brain, as well as the Silastic ECoG grid(s) implanted during the surgical evaluation in epilepsy patients, from the co-registered magnetic resonance (MR) and computer tomography (CT) images. A series of computer simulations were conducted to evaluate the present FEM-based CPI technique and to assess the effect of the Silastic ECoG grid on the scalp EEG forward solutions. The present simulation results show that the Silastic ECoG grid has substantial influence on the scalp potential forward solution due to the distortion of current pathways in the presence of the extremely low conductive materials. On the other hand, its influence on the estimated cortical potential distribution is much less than that on the scalp potential distribution. With appropriate numerical modeling and inverse estimation techniques, we have demonstrated the feasibility of estimating the cortical potentials from the scalp EEG with the implanted Silastic ECoG gird(s), in both computer simulations and in human experimentation. In an epilepsy patient undergoing surgical evaluation, the cortical potentials were reconstructed from the simultaneously recorded scalp EEG, in which main features of spatial patterns during interictal spike were preserved and over 0.75 correlation coefficient value was obtained between the recorded and estimated cortical potentials. The FEM-based CPI technique provides a means of connecting the simultaneous recorded ECoG and the scalp EEG and promises to become an effective tool to evaluate and validate CPI techniques using clinic data.

Free full text 

Logo of nihpaLink to Publisher's site
Neuroimage. Author manuscript; available in PMC 2007 Jul 15.
Published in final edited form as:
PMCID: PMC1866308
NIHMSID: NIHMS15330
PMID: 16631381

A Cortical Potential Imaging Study from Simultaneous Extra- and Intra-cranial Electrical Recordings by Means of the Finite Element Method

Yingchun Zhang,1 Lei Ding,1 Wim van Drongelen,2 Kurt Hecox,2 D Frim,2 and Bin He1,*
Author information Copyright and License information Disclaimer

Abstract

In the present study, we have validated the cortical potential imaging (CPI) technique for estimating cortical potentials from scalp EEG using simultaneously recorded electrocorticogram (ECoG) in the presence of strong local inhomogeneity, i.e. Silastic ECoG grid(s). The finite element method (FEM) was used to model the realistic post-operative head volume conductor, which includes the scalp, skull, cerebrospinal fluid (CSF) and brain, as well as the Silastic ECoG grid(s) implanted during the surgical evaluation in epilepsy patients, from the co-registered magnetic resonance (MR) and computer tomography (CT) images. A series of computer simulations were conducted to evaluate the present FEM-based CPI technique, and to assess the effect of the Silastic ECoG grid on the scalp EEG forward solutions. The present simulation results show that the Silastic ECoG grid has substantial influence on the scalp potential forward solution due to the distortion of current pathways in the presence of the extremely low conductivity materials. On the other hand, its influence on the estimated cortical potential distribution is much less than that on the scalp potential distribution. With appropriate numerical modeling and inverse estimation techniques, we have demonstrated the feasibility of estimating the cortical potentials from the scalp EEG with the implanted Silastic ECoG gird(s), in both computer simulations and in human experimentation. In an epilepsy patient undergoing surgical evaluation, the cortical potentials were reconstructed from the simultaneously recorded scalp EEG, in which main features of spatial patterns during interictal spike were preserved and over 0.75 correlation coefficient value was obtained between the recorded and estimated cortical potentials. The FEM-based CPI technique provides a means of connecting the simultaneous recorded ECoG and the scalp EEG, and promises to become an effective tool to evaluate and validate CPI techniques using clinic data.

Keywords: finite element method, cortical potential imaging, electrophysiological neuroimaging, brain mapping, EEG, ECoG, interictal spike, epilepsy

I. Introduction

Brain electrical activity is spatially distributed within the brain and evolves with time. While the scalp electroencephalogram (EEG) has the advantage of unsurpassed millisecond temporal resolution necessary for resolving dynamic neural processes, its application to mapping spatial distribution of brain electrical activity is limited by its poor spatial resolution due to the blurring effect of the head volume conductor, especially the low-conductivity skull layer (Nunez, 1981; He, 2004, 2005). Tremendous effort has been made to enhance the spatial resolution of the conventional EEG by solving the so-called EEG inverse problem, which attempts to overcome the head volume conductor effect (Scherg & Von Cramon, 1985; He et al., 1987, 1996, 1999, 2001, 2002; Cohen et al., 1990; Sidman et al., 1990; Dale & Sereno, 1993; Le & Gevins, 1993; Ebersole et al., 1994; Gevins et al., 1994; Nunez et al., 1994; Babiloni et al., 1997, 2003; Fuchs et al., 1999; Michel et al., 1999; Ollikainen et al., 2001; Zhang et al., 2003).

Of interest is the development of cortical potential imaging (CPI) approach, which maps the scalp potential distribution onto the epicortical surface (which we shall call “cortical potentials” below), thus, improving the spatial resolution of the EEG by deconvolving the spatial low-pass filtering characteristics of the skull. An early attempt to reconstruct the cortical potentials used an intermediate hemisphere equivalent dipole layer to generate an inward harmonic potential function in a homogeneous head volume conductor model (Sidman et al., 1990). The inverse procedure was used to estimate the equivalent dipole distribution from the scalp EEG, and then the cortical potentials were reconstructed by solving the forward problem from the estimated equivalent dipole layer to the cortical potential. He and co-workers (He et al., 1996; He, 1998; Wang and He, 1998) used a concentric three-spheres head model to include the significant conductivity inhomogeneity, the skull, and a closed-spherical dipole layer with higher density to improve the numerical accuracy. Babiloni et al. (1997) pursued the intermediate-dipole-layer-based cortical potential imaging to include both the skull inhomogeneity and the realistic geometry of the head by means of the boundary element method (BEM) (He et al., 1987; Hamalainen & Sarvas, 1989). He and co-workers further developed a direct CPI approach to estimate the cortical potentials from the scalp potentials without an intermediate dipole layer, in a multi-layer realistic geometry head model using the BEM (He et al., 1999). The direct BEM-based CPI technique has been validated in somatosensory evoked potentials (SEP) (He et al., 2002) by comparing the CPI results estimated from pre-operative scalp SEP data with the post-operative electrocorticogram (ECoG) during somatosensory stimulation. Gevins and co-workers (Le & Gevins, 1993; Gevins et al., 1994) developed the first finite element method (FEM) based CPI, to estimate directly the cortical potentials from the scalp potentials. While it has the potential to incorporate local conductivity inhomogeneity by means of FEM, Gevins and co-workers only included skull inhomogeneity into their FEM algorithm and evaluated it by intracranial recordings in separated recordings from two neurosurgical patients (i.e. inverse cortical potentials estimated from pre-operative recordings and compared with post-operative ECoG recordings).

Not affected by the insulating skull layer, the estimated cortical potentials offer more spatial details in assessing the underlying brain electrical activity compared to the blurred scalp potentials. Furthermore, the cortical potential distribution can be experimentally measured using ECoG grids (Le & Gevins, 1993; Gevins et al., 1994; Towle et al., 1995; Lantz et al., 1997; He et al., 2002; Tao et al., 2005). The dramatic improvement of spatial resolution achieved in the previous studies is promising and indicates that CPI may play an important role in lateralization and localization of epileptogenic foci in presurgical evaluation. However, till now, to our knowledge, all the evaluation and validation studies were reported in a set-up of two separated recording sessions with one before and one after implantation of subdural ECoG grid(s). There is no report to date on the validation of the CPI techniques using simultaneously recorded ECoG and scalp EEG. This may be due to the following two reasons. First, the implanted subdural ECoG grid(s) usually consists of Silastic base which is insulating and distorts substantially the current flow in its vicinity, thus leading to distorted scalp potential fields. Second, traditional spherical head model and boundary element (BE) models are not effective on handling such problems.

The objective of the present study is to validate CPI techniques using simultaneous extra- and intra-cranial electrical recordings. A finite element (FE) model is constructed to handle the inclusion of the extremely low conductivity Silastic ECoG gird(s). The FEM has been reported to effectively handle both conductivity inhomogeneity (Yan et al., 1991) and anisotropy (Kim et al., 2003). The feasibility and performance of this FEM-based CPI technique are evaluated by a series of computer simulations, and validated in an epilepsy patient with postoperative simultaneous scalp EEG and ECoG recordings during interictal spike.

II. Methods

1. Forward Solver

In the present study, the EEG forward problem is considered as follows: Given the positions and moments of current dipole sources and the geometry and electrical conductivity profile of the volume conductor, i.e. the head, calculate the electrical potential on the scalp. Theoretically, this problem can be stated by Poisson’s equation which is defined on the volume conductor Ω (Gulrajani, 1998) and the Neumann boundary condition on the scalp S

∇⋅(σ∇ϕ)=−∑ΩIsinΩσ(∇ϕ)⋅n=0onS
(1)

where σ is the conductivity tensor, which is the function of location, (x, y, z), within the volume conductor, n is the outward unit normal to the scalp S, and Is the volume current densities due to the presence of current sources. The unknown ϕ is the electrical potential generated by current sources. Generally, σ at each location is different from other locations with certain level of discrepancy. Such discrepancy shall be small and negligible within each of the main structures of human head, i.e. the scalp, skull, brain, and CSF, which leads to the layered volume conductor model widely adopted in the EEG forward modeling, e.g. three-concentric-spheres model (Rush & Driscoll, 1969), four-concentric-spheres model (Cuffin & Cohen, 1979), and BE models (He et al., 1987; Hamalainen & Sarvas, 1989; Babiloni et al., 1997; Mosher et al., 1999; He et al., 1999, 2002; Finke et al., 2003). On the other hand, when local inhomogeneity presents in the volume conductor, such as Silastic subdural ECoG grid(s), the forward problem cannot be easily handled by the layered BE modeling. In the present study, we constructed the realistic geometry inhomogeneous FE head model, which consists of the scalp, skull, brain, CSF, and Silastic ECoG grid(s) as described in Section II.3 and used the FEM to solve the EEG forward problem.

Poisson’s equation can be transformed into a group of linear equations defined on the FE nodes in the FE model when using the FEM. The final form of the equation can be formulated in a matrix form as follows and the detailed derivation can be found in our previous report (Zhang et al., 2004).

K⋅Φ=G
(2)

where K is the stiffness matrix which incorporates the volume conductor model information, e.g. geometry and conductivity, Φ is the potential vector on the FE nodes, and G is the load matrix due to the current sources. Equation (2) can be rewritten as follows,

[K]⋅[ΦsΦcΦr]=[G]
(3)

where Φs refers to the scalp potential, Φc the cortical potential, and Φr the potential field on the FE nodes other than nodes on the scalp and cortical surface. The linear problem stated either as equation (2) or (3) can be solved by the linear solver, i.e., preconditioned conjugate gradients method (Silvester & Ferrari, 1996).

2. FEM-CPI Inverse Solver

The FEM-based CPI (FEM-CPI) inverse solver in the present study includes two steps, which is also known as indirect CPI as reported previously in the spherical head model (Sidman et al., 1990; He et al., 1996; Wang & He, 1998) and in BE models (Babiloni et al., 1997). The first step is to estimate the current dipole strength distribution on an equivalent dipole layer (EDL), which has fixed number of dipoles with fixed locations and orientations, and has been studied to represent the current dipole distribution in a 3-dimensional (3D) volume (Sidman et al., 1990; He et al., 1996; Babiloni et al., 1997; Wang & He, 1998). The EDL located just inside of the cortical surface (8 mm below the epicortical surface) in the FE model (see Section II.3 for details) and shared the same geometric shape with the epicortical surface. Fig. 1 shows the geometry of the EDL and the dipole locations used in the present study. The inner surface spanned by triangles refers to the EDL surface, and the dots on the centers of triangles illustrate the dipole locations in the EDL. The outer gray layer shows the epicortical surface. The EDL consists of 3,272 dipoles, which were uniformly distributed over the surface and perpendicularly oriented to the local curvature of the epicortical surface. The norm of local curvature of the epicortical surface was determined by the norm of triangles, which were obtained during the surface triangulation (see Section II.3). The second step was, then, to calculate the cortical potential field from the EDL with current dipole strengths estimated in step one.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0001.jpg

Illustration of the equivalent dipole layer (the inner surface with triangles) underneath the epicortical surface (the outer gray surface). Dots refer to locations of the dipoles over the equivalent dipole layer.

Note that there are two lead fields involved in the above mentioned two-step procedure: one relates the EDL with the scalp potential field Φs in step one and another connects the EDL with the cortical potential field Φc in step two. While the forward equation (3) only implicitly states the relationship between current sources and potentials, the explicit lead field calculation is achieved by the following procedure. First, the conversion from current dipole source distribution used in the EDL to the current density source distribution used in G of equation (3) is made based on the method discussed by Yan et al. (1991) (also see Zhang et al., 2004). Then, assuming only one dipole on the EDL is active with unit strength and other dipoles are silent, the potential field corresponding to each current dipole on the EDL can be obtained by solving equation (3), iteratively. The Φs for each dipole source can be separated from the entire solution and the lead field matrix relating the dipoles on the EDL and the scalp potential field can thus be formed column by column, denoted as A. Similarly, the lead field matrix relating the dipoles on the EDL and the cortical potential field can be obtained in the similar way, denoted as B. Both are expressed as

A⋅S=ΦsandB⋅S=Φc
(4)

where S is the strength vector of dipoles on the EDL. In the present study, we computed the lead field matrix based on its definition, although recent work suggested possible means of speeding up the computation (Wolters et al., 2004).

The step one of the FEM-CPI technique requires to invert matrix A to obtain current dipole distribution S on the EDL from the scalp potential Φs. However, in general, this is an underdetermined problem because the number of measurements is less than the number of sources. Also note that the measurement of scalp potentials will only be a part of Φs in equation (3) because the potential cannot be measured practically with such high density at all FE nodes. To obtain a unique solution, the minimum-norm regularization was introduced in the step one.

minimizeΔ=∥Φs−A⋅S∥22+λ∥S∥22
(5)

where the first term of the objective function is the error term in the least squares sense and the second term is the regularization term which attempts to minimize the total energy of the solution. This is the constrained inverse solution and has been widely used in the BEM based CPI (He et al., 1999, 2002) and many other distributed source localization methods (Marin et al., 1998).

In the present study, the weighed minimum-norm regularization (Pascual-Marqui et al., 1994; Fuchs et al., 1999) is actually implemented and the objective function (5) is transformed to the following equation

minimizeΔ=∥Φs−A⋅S∥22+λ∥WS∥22
(6)

where W is a diagonal matrix, in which the values for diagonal elements are defined as column norm of the lead field matrix A. The regularization parameter λ is chosen by means of the L-curve approach (Hansen, 1992). The average potential over the scalp surface was used as reference in both simulations and experimental data analysis.

Then, the step two of the present FEM-CPI technique is simply the implementation of the second equation of equation (4), which obtains the cortical potential distribution from the estimated current dipole distribution on the EDL in step one.

3. Realistic geometry finite element head model consisting of Silastic ECoG grid

In this section, we present a new procedure, as shown in Fig. 2, to generate the 3D FE mesh from the co-registered magnetic resonance (MR) and computerized tomography (CT) datasets. The MR images were used to segment the main human head structures, i.e. the scalp, skull, CSF, and brain, while the CT images were used to determine the locations of ECoG grids.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0002.jpg

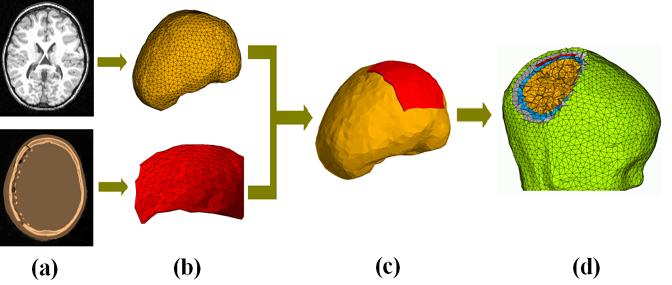
Schematic diagram illustrating the procedure to construct the finite element model. (a) MRI and CT slice; (b) the triangulated surface model of the brain built from MRI and the triangulated surface model of the Silastic strip ECoG grid built from CT images; (c) the volume model consisting of both the brain and Silastic strip ECoG grid after co-registration; (d) the finite element model consisting of the scalp (green), skull (gray), CSF (blue), brain (yellow) and Silastic strips ECoG grid (red).

A set of T1-weighted MR images was obtained in a subject preoperatively with a 1.5 Tesla scanner, which composed of 124 continuous coronal slices with 1.5 mm slice thickness. Each slice contained 256×256 pixels and the fields of vision (FOV) are 220× 220 (mm). A set of postoperative CT images was obtained from the same subject, which composed of 116 continuous axial slices with slice thickness of 1.25 mm. Each slice contained 512×512 pixels and the FOV are 250×250 (mm). The MR image dataset (Fig. 2(a), top) was segmented, edge-detected, and contoured for the scalp, skull, CSF, and brain, respectively, using CURRY 4.5 (NeuroScan Lab, TX). Nodal points representing the contours of the four surfaces were extracted from MR images and downsampled. The four surfaces were then triangulated and defined by the triangle meshes, namely the scalp, skull, CSF and brain (Fig. 2(b), top). The triangulated surface model for Silastic ECoG grid was obtained by identifying metal electrodes’ locations in the CT images. The Silastic subdural electrode pads were segmented using CURRY 4.5, from the CT images (Fig. 2(a), bottom). Because the implanted subdural ECoG grids are of rectangular shape, only four corner electrodes were needed to characterize their locations on the epicortical surface. After four corner electrodes were identified from the segmentation, the whole electrodes set on the Silastic ECoG grid was generated using surface path fitting algorithm from CURRY 4.5 with the known electrode arrangement. The triangulated surface model for Silastic ECoG grid (Fig. 2(b), bottom) was then generated using the known electrode positions and known thickness of the electrode pad. While the actual thickness of the electrode pad is 1.5-2 mm, the Silastic grids were built in the FE Model with thickness of about 3 mm. Except the dimension of thickness, the grids were meshed with the 5 mm length tetrahedron finite element. We used approximation in the thickness of the Silastic grids in order to make a balance between the mesh quality and mesh size, for the purpose of improving numerical accuracy. In the present triangulated surface models, there are 5,266, 3,954, 3,272, 3,272 and 1,290 triangular elements in the triangulated surface models for the scalp, skull, CSF, brain, and Silastic ECoG grid, respectively.

The co-registration between the different image modalities, i.e. MR and CT (Fig. 2(c)), and between structure images with electrical recording sensors, i.e. scalp electrodes (Fig. 3(a-c)), ECoG electrode pads (Fig. 3(d-f)), was achieved by the fiducial points (nasion, left, and right preauricular points) and a surface fitting algorithm (CURRY 4.5).

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0003.jpg

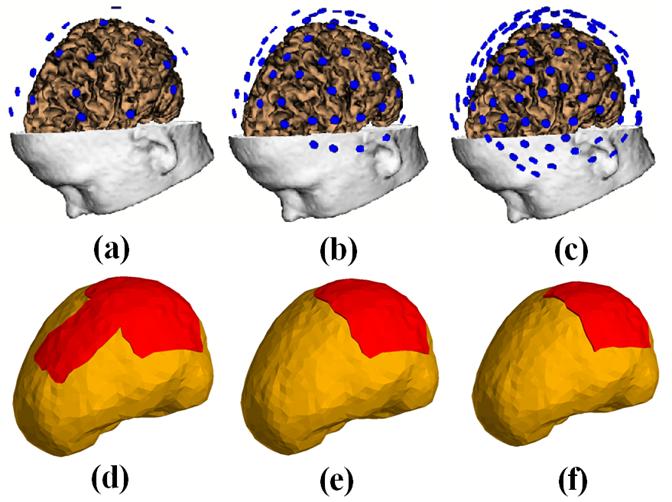
The configurations of scalp electrodes ((a): 30 electrodes; (b) 64 electrodes; and (c) 128 electrodes) after coregistration, and three kinds of Silastic ECoG grid(s) with different sizes ((d) one 80 mm by 80mm grid plus a 40 mm by 80 mm grid; (e) one 80 mm by 80 mm grid; (f) one 60 mm by 60 mm grid). The ECoG grid is illustrated by red.

The triangulated surface models were then transformed to volume definition model by Rhinoceros software (Robert McNeel & Assoc., WA) using Non-Uniform Rational B-Splines (NURBS), which is an accurate mathematical description of 3D geometry, in order to generate FE meshes. Five NURBS geometries, namely, the scalp, skull, CSF, brain and Silastic ECoG grid were generated by transforming all the triangles from the corresponding surface model into the closed NURBS geometry (Fig. 2(c)). Note that they are overlapped with each other, such as the scalp NURBS geometry covering the entire skull NURBS geometry, the skull covering the whole CSF, and etc. The Boolean operations were used to delete those overlapping and build a uniform and integrated NURBS geometry consisting of five separated parts. Note that, in this way, the boundaries between different parts are reserved and neighboring parts share the same boundary.

The FE model was thus obtained by meshing the integrated NURBS geometry, shown in Fig. 2(d) using ANSYS 7.0 (ANSYS. Inc, PA). Note that, because of the existence of boundaries, there is no element which will cross the boundaries, and because the neighboring parts share the same boundary, the distribution of finite elements along the both sides of the boundary is continuous. The global average length of the finite element was set to 5 mm and the whole FE model consists of 84,888 elements and 15,407 nodes. The conductivities of the scalp and brain were set to 0.33 S · m-1 (Stok, 1987), the conductivity of the skull was set to 1/20 of the conductivity of the brain, 0.0165 S · m-1 (Oostendorp et al., 2000; Lai et al., 2005), and the conductivity of the CSF was set to 1 S · m-1 (Stok, 1987). Because the Silastic pad is a kind of insulator, a very small conductivity value, 3.3e-11 S · m-1 was set to the Silastic ECoG grids.

4. Simulation Protocols

Computer simulations were conducted to evaluate the performance of the FEM-CPI technique in the presence of Silastic ECoG grids. The FE head model described above was used in all computer simulations. The influence of Silastic ECoG grids on the forward potential field and inverse cortical potential reconstruction was assessed with or without the Silastic ECoG grids and by varying the size of grids. The FE model A included two Silastic strips, one was 80×80 (mm) and the other one was 80×40 (mm) (Fig. 3(d)), which was consistent with the case of the epilepsy patient studied in the present study. The FE model B only has one Silastic ECoG grid, with size of 80×80 (mm) (Fig. 3(e)). The FE model C also has one Silastic ECoG grid, but, with smaller size of 60 ×60 (mm) (Fig. 3(f)).

Two groups of dipole locations were considered in the computer simulations. The 1st group consisted of 9 dipoles placed from 7 mm to 39 mm evenly below the center of the Silastic ECoG grid (the center of the 80×80 (mm) grid if there are two grids). The 2nd group consisted of 10 dipoles placed 11 mm below the Silastic ECoG grid and distributed along the cortical surface away from the center of the grid to the edge of the grid. Fig. 4 shows the locations of dipoles with relevance to the location of the Silastic ECoG grid. For each source configuration, only one current dipole was considered at a time. At each dipole position, both radial and tangential oriented dipoles were considered. The radial and tangential directions were defined by the local curvature of the point on the epicortical surface, which is closest to the simulated dipole source. Gaussian white noise (GWN) of 10%, which is defined as the ratio between the standard deviation of noise and the root mean square of the potential, was used to simulate the noise-contaminated recording environment for all performed computer simulations except those designed to investigate the noise effect as described below.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0004.jpg

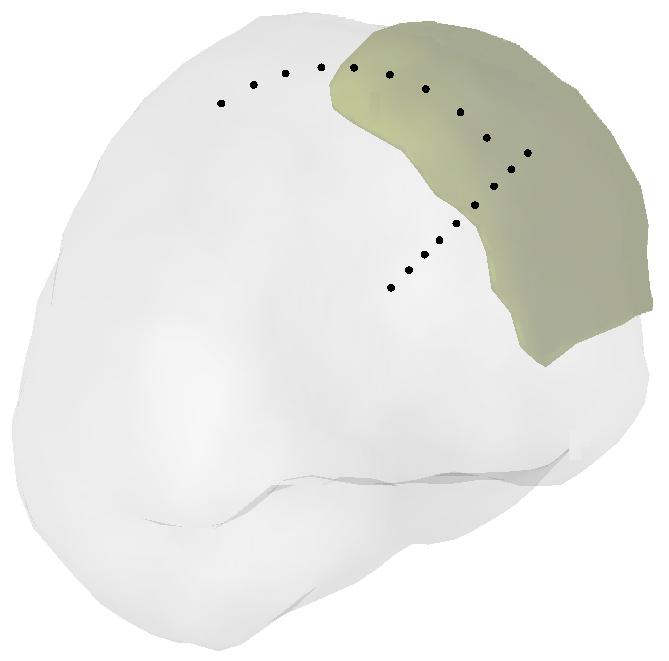
Locations of simulated dipoles. Two groups of dipole locations were considered in the computer simulations. The 1st group consisted of 9 dipoles placed from 7 mm to 39 mm evenly below the center of the Silastic ECoG grid. The 2nd group consisted of 10 dipoles placed 11 mm below the Silastic ECoG grid and distributed along the cortical surface away from the center of the grid to the edge of the grid and the 1st dipole in the 2nd dipole group shares the same position with the 2nd dipole in the 1st dipole group.

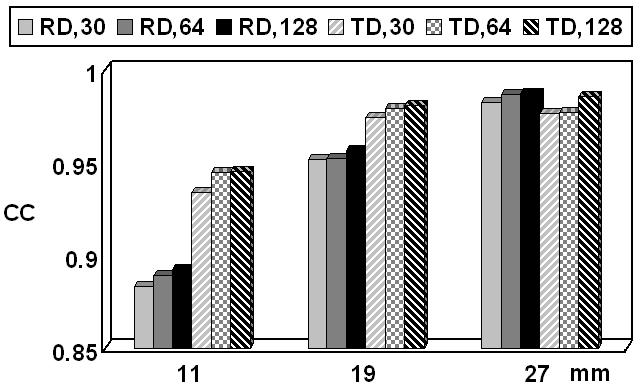
Furthermore, the effect of number of scalp electrodes on CPI results was also assessed using 30 (used in the epilepsy patient), 64, and 128 electrodes (Fig. 3(a-c)). Different levels of GWN of 0%-20% were added and noise effects assessed.

Correlation coefficient (CC) between the forward simulated cortical potential and FEM-CPI reconstructed cortical potential was calculated and used to access the performance of the FEM-CPI technique.

CC=∑i=1N(ΦiI−Φ‒I)(ΦiS−Φ‒S)∑i=1N(ΦiI−Φ‒I)2∑i=1N(ΦiS−Φ‒S)2
(7)

where N is the number of locations over the cortical surface where cortical potentials ΦIi and ΦSi were evaluated. ΦIi and ΦI are the FEM-CPI reconstructed cortical potential at ith location and it’s mean value. ΦSi and ΦS are the simulated cortical potential at ith location and it’s mean value.

5. Data Collection in Epilepsy Patient

The scalp EEG and ECoG data from a female epilepsy patient of 12 years old was collected according to a protocol approved by the Institutional Review Boards (IRBs) of the University of Minnesota and the University of Chicago. Two standard subdural electrode grids were used in this patient, one contained 64 (8×8) platinum contacts in a rectangular array with the same 10 mm center-to-center distance covering the left parietal lobe and left posterior frontal lobe and the other one consisted of 32 (4×8) platinum disks with the same 10 mm center-to-center distance and was positioned to encompass the anterior frontal lobe. The platinum disks were embedded in the Silastic base and had an exposed surface diameter of 2.3 mm. Continuous recordings on scalp channels (i.e. 30) and subdural channels (i.e. 46 out of 64 for 8×8 grids and 32 for 4×8 grids) were obtained simultaneously. Both extra- and intra-cranial electrical potentials were recorded using BMSI6000 (Nicolet Biomedical, Madison, WI). The data were measured with frequency bandwidth of 1-100 Hz and sampled at a rate of 400 Hz. The scalp electrode positions were measured with a 3D digitizer (Polhemus, Colchesterm, VT). Intra-cranial electrode positions were determined using postoperative CT image (Fig. 2(a), bottom) as described in Section II.3.

Interictal epileptiform spikes were selected from the continuous recorded scalp electrical signals and analyzed to validate the FEM-CPI technique. The reconstructed cortical potentials were qualitatively (via visual inspection) and quantitatively compared to the direct subdural recordings in term of CC, which was calculated over the ECoG electrode space.

III. Results

1. Influence of Silastic ECoG grid on the EEG forward solution

Fig. 5 depicts examples of the scalp potential distributions obtained using the FE head model without (Fig. 5(a, c)) or with (Fig. 5(b, d)) the Silastic ECoG grid (FE model A) due to the same radial dipole source (Fig. 5(a-b)) or tangential dipole source (Fig. 5(c-d)).

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0005.jpg

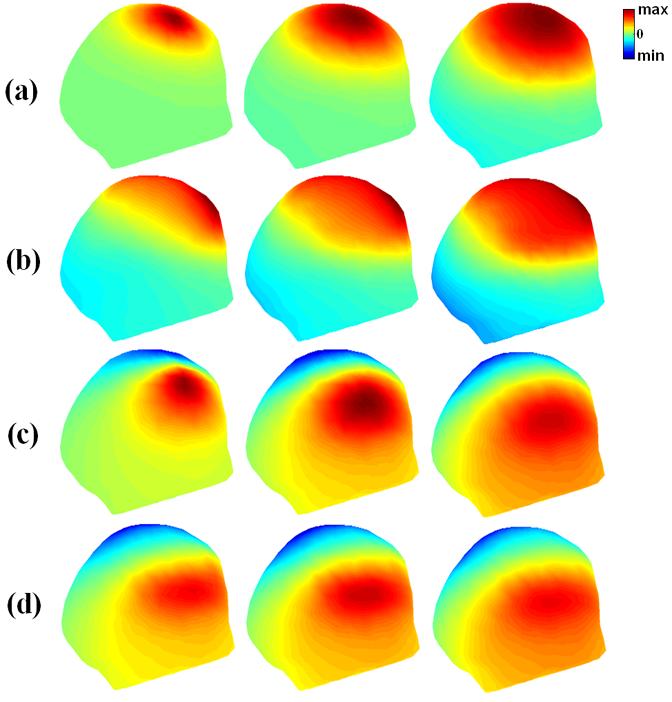
The simulated scalp potential distributions with or without Silastic ECoG grids (model shown in Fig. 3(d)). Three dipole locations in the 1st dipole group, 7mm, 23mm, and 39mm, were used and shown on the left, middle, and right column, respectively. (a)-(b) show scalp potential distributions due to a radial dipole; and (c)-(d) show scalp potential distributions due to a tangential dipole. (a) and (c) refer to scalp potential distributions without the ECoG grids; and (b) and (d) refer to the potential distributions with the ECoG grids. Note the substantial effect of the ECoG grids on the scalp potential distributions due to radial dipole.

The scalp potentials in these examples were generated by the 1st, 5th and 9th dipole in the 1st group of dipoles, which are 7 mm, 23 mm and 39 mm, respectively, below the center of the grid. From left to right, the depth of simulated dipoles increases. The strengths for both radial and tangential dipoles were set to 100 nA [center dot] m. The reduction in strength of the potentials can be observed by comparing Fig. 5(a) with Fig. 5(b) and Fig. 5(c) with Fig. 5(d) for both radial and tangential dipoles. The maximum value of the scalp potential field without the ECoG grids for radial dipole is about 52.3 μV at the location closest to the cortical surface, which is more than 12 times larger than that obtained with the ECoG grids (about 4.1 μV). About 2.3 times reduction of the maximal potential value over the scalp is observed for the tangential dipole (26.3 μV reduced to 11.4 μV). Obviously, the ECoG grids have larger influence on the radial dipole than the tangential dipole.

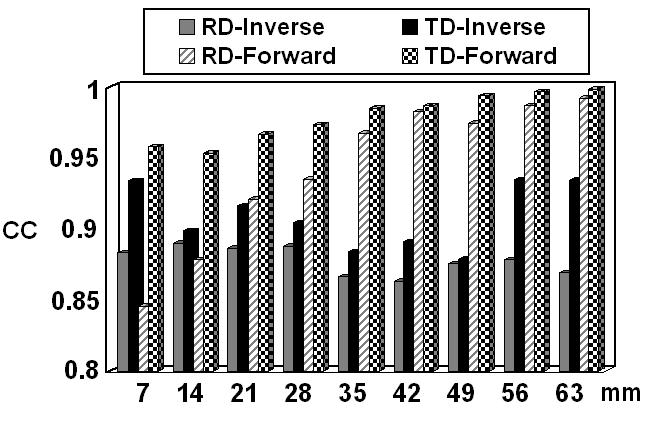
When the depth of simulated dipole increases (Fig. 5, from left to right), the strength of the scalp potentials, obtained from the FE model without the ECoG grids, reduces markedly for radial dipoles ((Fig. 5(a), more than 3 times reduction at the 3rd depth), but the strength of the scalp potentials, obtained from the FE model with the ECoG grids for radial dipoles (Fig. 5(b)) increases somehow. When the radial dipole moved away from the ECoG grids, more currents may be able to flow into the region behind the Silastic ECoG grid pads, which balanced the reduction in the scalp potentials the dipole would otherwise cause when moved away from the scalp. There are almost no changes of the strength of the scalp potentials for tangential dipoles on the FE model with and without the ECoG grids. The CC values between the potential fields with the ECoG grids and without the ECoG grids for more depths are depicted with curves in Fig. 6 (bottom). The solid line with triangles indicates the CC for radial dipole and the dashed line with triangles is for tangential dipole. It is clear that the CC decreases when the distance from the simulated dipole to the ECoG grids becomes smaller. Also, the curve for tangential dipole is quite separated from the curve for radial dipole at every simulated depth with higher CC values, which is consistent with above mentioned difference between simulated radial and tangential dipoles in term of potential field reduction.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0006.jpg

Upper panel: Correlation coefficient (CC) between the simulated cortical potentials and the FEM-CPI reconstructed cortical potentials, produced by the dipoles in the 1st dipole group located in the finite element model A, with or without ECoG grids. Lower panel: CC between the potentials at 30 scalp electrodes produced by dipoles in the 1st dipole group located in the finite element model A, with and without ECoG grids.

2. Influence of Silastic ECoG grids on the FEM-CPI inverse solution

The 1st group of dipoles was used to assess the influence of Silastic ECoG grids on the accuracy of the FEM-CPI inverse solution. Along with the CC between the scalp potentials with and without the ECoG grids (Fig. 6, lower panel), the upper panel of the Fig. 6 depicts the CC between the FEM-CPI reconstructed and forward simulated cortical potentials using the FE model A with or without the ECoG grids, which indicates the cortical potential reconstruction errors using either model. It is observed that the reconstruction error is lower in the model without the ECoG grids than the model with the ECoG grids when the simulated dipoles are close to the cortical surface. When the simulated dipoles moved away from the cortical surface, the difference of the reconstruction errors from the model with or without the ECoG grids became smaller. It can also be observed that the reconstruction error from the tangential dipoles is lower than those from the radial dipoles in either model with or without the ECoG grids when the simulated dipoles are close to the cortical surface, which shares the same feature as the curve of the CC for scalp potentials (Fig. 6, lower panel). The reconstruction errors for both models with and without the ECoG grids are keeping increasing when the simulated dipoles become closer and closer to the cortical surface. The trend is consistent with the trend observed in the CC for scalp potentials (Fig. 6, lower panel). The lowest CC is 0.76 in the model with the ECoG grids with a radial dipole placed 7 mm below the center of the big grid. Most of the CC values is higher than 0.9.

3. Influence of dipole locations

As Fig. 6 shows the cortical potential reconstruction error decreases greatly as the dipole depth increases, Fig. 7 shows the change of the reconstruction errors as the dipole location changes using other dipole locations from the 2nd group of dipoles with the FE model A. As we can see, the CC values between the scalp potentials with and without the ECoG grids changed as the dipole location changed from directly below the center to the edge, and then to the outside of the ECoG grid at the same depth level, for both radial and tangential dipole. However, the CC values between inversely reconstructed and simulated cortical potentials are relatively stable. Again, the different influences of the ECoG grids on the radial dipole and the tangential dipole could be observed for this group of simulated dipoles.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0007.jpg

Solid bars: CC between the simulated cortical potentials and the FEM-CPI reconstructed cortical potentials, produced by the dipoles in the 2nd dipole group (not including the 1st dipole because it shares the same position with the 2nd dipole in the 1st dipole group) located in the finite element model A, with ECoG grids. Shaded bars: CC between the potentials at 30 scalp electrodes produced by dipoles in the 2nd dipole group located in the finite element model A, with and without the ECoG grids.

4. Influence of size of Silastic ECoG grids on FEM-CPI inverse solution

Fig. 8 shows the CC values using the 1st group of dipoles with different size of Silastic ECoG grids, i.e. the FE model A, B, and C. The plots in the upper panel are the CC values between reconstructed and simulated cortical potentials at different conditions, while the plots in the lower panel are the CC values between scalp potentials with and without the ECoG grids. The pattern of curves shares the similar trends as observed in Fig. 6, which indicates that the effects of dipole depths and orientation dominate the results. While the difference between the three models for the scalp potentials is recognizable, the difference for the cortical potentials is almost negligible as compared with other effects for both radial and tangential dipoles on each dipole location.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0008.jpg

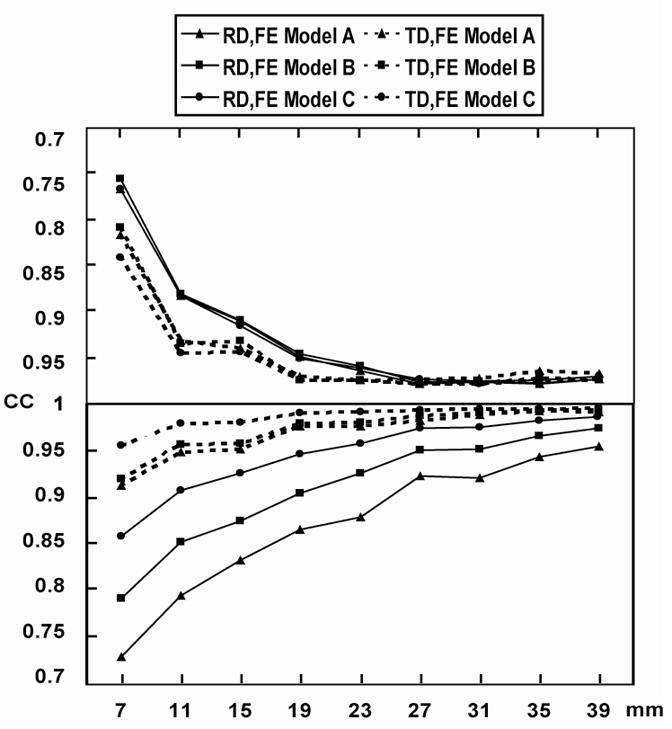
Upper panel: CC between the simulated cortical potentials and the FEM-CPI reconstructed cortical potentials produced by dipoles in the 1st dipole group located in the finite element models A, B and C (see Fig. 3(d-f)). Lower panel: CC between the potentials at 30 scalp electrodes, produced by dipoles in the 1st dipole group, located in the finite element models A, B and C (see Fig. 3(d-f)).

5. Influence of electrode number

Fig. 9 depicts the CC values with different scalp electrode numbers based on the FE model A using the 1st group of dipoles. Three electrode numbers, i.e. 30, 64 and 128, were used in this simulation. It is observed that the electrode number has little influence on the FEM-CPI inverse solution in term of CC although the slight decrease in reconstruction error can be noticed as the number of electrodes increases.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0009.jpg

CC between the simulated cortical potentials and the FEM-CPI reconstructed cortical potentials obtained from scalp EEG recordings with different electrode numbers, produced by the 2nd, 4th and 6th dipole in the 1st dipole group located in the finite element model A.

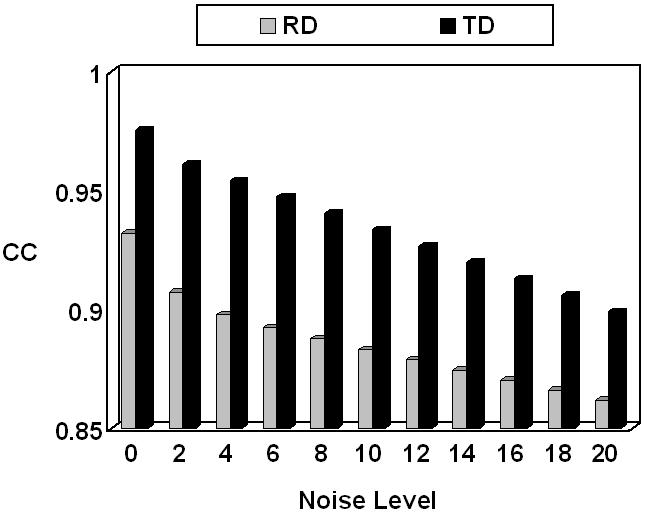
6. Influence of noise level

The 3rd dipole location in the 1st group of dipoles, which is 15 mm away from the center of ECoG grid, was selected to investigate the influence of noise levels on the accuracy of FEM-CPI inverse solution. Gaussian white noise with different noise levels was added to the simulated scalp potentials produced by the above mentioned dipole in the FE model A for both radial and tangential dipoles. The changes of the CC values caused by the changes of noise levels, from 0% to 20%, were shown in Fig. 10. Note that the reconstruction error increases when the noise level increases in all conditions.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0010.jpg

CC between the simulated cortical potential and the FEM-CPI reconstructed cortical potential at different noise levels, produced by the 3rd dipole in the 1st dipole group located in the finite element model A.

7. Validation of the FEM-CPI using simultaneous extra- and intra-cranial electrical recordings in epilepsy patient

Fig. 11 shows an example of validation results of the present FEM-CPI in an epilepsy patient using simultaneous extra- and intra-cranial electrical recordings around an interictal spike. In total, maps at five time points (two time points before and after the spike peak, and the spike peak) with time separation of 2.5 ms, are depicted. Figs. 11(a) and (b) show the potential maps over the scalp and cortical surface, respectively. Note the dramatic effect of the Silastic ECoG grids and the skull on the scalp potential distribution. Fig. 11(c) shows inversely reconstructed cortical potentials using the present FEM-CPI. The major activity with major energy concentration in the large ECoG grid was well reconstructed, although slight shift of the maximum in the reconstructed inverse maps is observed as compared with the simultaneously recorded cortical potential. Figs. 11(a), (b), and (c) are normalized with its own maximal absolute values. The CC values between the reconstructed cortical potential and measured cortical potential are listed on the right of each map in Fig. 11(c). The CC values are higher than 0.75 for this sequence surrounding the spike peak. It is also observed from the spatial pattern of the cortical potentials that the measured intracranial potential field is more focal than the reconstructed field. This is in consistence with our intuition since the present inverse solution is essentially a weighted minimum norm solution, which provides a smoothed reconstruction of the actual potential distribution. However, comparing of Fig. 11(a) and Fig. 11(c) indicates clearly that the CPI restores high frequency information which is lost during volume conduction from the cortical surface towards the scalp, especially in the presence of Silastic ECoG grids.

An external file that holds a picture, illustration, etc. Object name is nihms-15330-0011.jpg

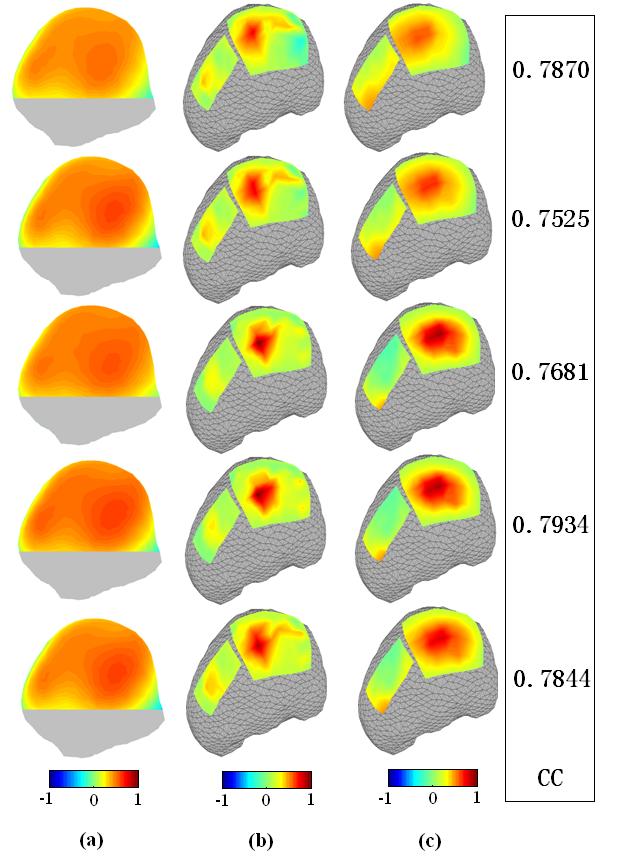
Comparison between the ECoG recordings (b) and the reconstructed cortical potentials (c) at different time points during an interictal spike of a pediatric epilepsy patient, from 5 ms before and 5 ms after the peak of the spike. (a) shows the corresponding scalp potential distributions from 30 electrode recordings. CCs between ECoG recordings and the reconstructed cortical potentials on the ECoG grids are listed on the right. Note the much smoothed spatial distribution of the scalp EEG due to the Silastic ECoG grid, and the good performance of the present FEM-CPI in reconstructing the major features of the cortical potentials.

IV. Discussion

In the present study, we used a finite element method-based cortical potential imaging approach to reconstruct the cortical potentials from the scalp EEG recordings in the presence of Silastic ECoG grids which are commonly implanted in epilepsy patients during surgical evaluation. The Silastic ECoG grids are incorporated into the volume conductor modeling and the EEG forward problem was solved by the FEM. The approach is able to establish the relationship between the extracranial EEG recordings and the intracranial ECoG recordings during a set-up of simultaneous acquisition.

The present study demonstrates the feasibility of building a finite element head model from MR and CT images of a subject including the Silastic ECoG grid(s). A complex finite element model of the head volume conductor was constructed in the present study from MR and CT images of the subject using a hybrid procedure combining surface triangulation and finite element modeling. The intermediate step of triangulated surface model reconstruction reserves the good boundary characteristics for surfaces, e.g. the cortical surface, which is important for cortical potential imaging over a smooth surface. The preoperative MR images were used to segment and identify the boundary of the scalp, skull, CSF and brain, while the postoperative CT images were used to locate the positions of the Silastic ECoG grids placed for surgical evaluation. The surface triangulation for these compartments were realized with the aid of CURRY 4.5 and exported to Rhinoceros for volume generation defined by NURBS surface. These volumes were then fused together under the description of NURBS with reserved boundaries and subjected to the finite element mesh generation performed by ANSYS 7.0.

It is known that opening the human skull may accompany sometimes brain shift (Nimsky et al., 2000). In the experimental data analysis, we compared the data either reconstructed on the ECoG grids or measured on the ECoG grids. Because the positions of ECoG grids are reconstructed from the post-operative CT and the ECoG and scalp EEG were recorded simultaneously, the possible brain shift during the operation may not cause significant location shift of interictal sources relative to the position of ECoG grids. Of course, the brain shift may lead to error in the FEM head model which is based pre-operative MRI, and maybe one of sources of the reconstruction errors of the present results.

The performance of the present FEM-CPI has been evaluated by a series of computer simulations. The influence of the Silastic ECoG grid(s) to both the forward and inverse solutions has been assessed. The effects of Silastic ECoG grids on the EEG forward solutions and inverse solutions are shown in Fig. 5 and Fig. 6, respectively. The distribution patterns and strengths of scalp potentials are changed dramatically due to the presence of Silastic ECoG grids (Fig. 5). On the other hand, the relatively small reduction in CC values for the inverse solution using models with or without the ECoG grids (Fig. 6), as compared with the CC changes for the scalp forward solution, suggests the ability of the FEM-CPI technique to reconstruct cortical potentials from the scalp potentials even with the Silastic ECoG grids consisting of extremely low conductive material. When the locations of current dipoles vary from the center to the edge and reaching outside of the ECoG grid (Fig. 7), the effect of the Silastic ECoG grid on the radial dipole source is obvious as observed from scalp potential observations, especially in case that the current dipole is located beneath the Silastic ECoG grid. On the other hand, such trend disappeared in the cortical potential inverse solution. This suggests that the FEM-CPI technique can represent well the relationship between the scalp and cortical potentials in the presence of the extremely low conductive ECoG grid, since in the inverse solution the effect of the Silastic ECoG grid is incorporated. Similar behavior can be observed from Fig. 8 when various sizes of the Silastic ECoG grids are used. The scalp EEG forward solution is distorted by the Silastic ECoG grid, thus having sensitive CC curves. On the other hand, the cortical potential inverse solution shows insensitive behavior to the size of the Silastic ECoG grid. Also of noteworthy is the different effect of the Silastic ECoG grid on the radial dipoles vs. the tangential dipoles. The cortical potential reconstruction errors are consistently lower for the tangential dipoles than those for the radial dipoles as shown in Fig. ​Fig.66-​-10.10. This phenomenon could be explained that the current flows due to dipole sources tangentially oriented in reference to the position of ECoG grids are easier to bypass the extremely low conductive Silastic ECoG grids, thus leading to less distortion of the scalp potential field. On the other hand, current flows due to the radial dipoles located beneath the extremely low conductive Silastic ECoG grids are blocked significantly if the dipole is close to the poor conductor.

An epilepsy patient was studied with simultaneously recorded postoperative scalp EEG and ECoG. The interictal epileptiform spikes were analyzed to validate the FEM-CPI technique. As shown in Fig. 11, the present FEM-CPI technique can reconstruct the major features of the cortical potential distribution which are generally consistent with the patterns recorded in ECoG. Although the reconstructed cortical potential distributions appear to be more spread than the measured cortical potential distributions, the major activity patterns coincide with each other quite well. This spread-out phenomenon is well observed in weighted minimum norm inverse solutions and may partly be due to the use of L2 norm in the present study. While reports suggest that L1 norm may provide much focal distribution in reconstructing brain current sources (Fucks et al, 1999), we chose L2 norm in the present study since the cortical potential is relatively distributed over the space instead of focused on a few discrete points.

The quantitative analysis of CC between the measured and estimated cortical potentials returned a CC value of about 77.7% (mean value). Compared with our previous work in validating the BEM based CPI approach using a somatosensory evoked potential protocol, where the CC values between the measured and estimated cortical potentials were in the range of 70-84%, the present results suggests the feasibility of reconstructing cortical potentials from scalp EEG even with extremely low conductive Silastic ECoG grid.

Note that we only tested the dipole sources located 7 mm from the grid electrodes, since the tetrahedrons in the present FE model have an average element size of 5 mm. The relative coarse FE resolution (15,407 nodes) is one reason limiting the dipole approaching to the epicortical surface. However by refining the mesh locally or use high-order tetrahedron element (Zhang et al., 2004), it is possible to treat sources closer to the ECoG grids. Such finer FE model may also further improve the numerical accuracy.

In summary, we have reconstructed the cortical potentials from the scalp EEG in the presence of the Silastic ECoG grid during a set-up of simultaneous EEG and ECoG recordings. The present cortical potential imaging (CPI) approach incorporates the FEM modeling and weighted minimum norm regularization. The present computer simulations examined the effects of the Silastic ECoG grid to the forward solution of scalp EEG, as well as the inverse solution using the FEM-CPI technique. The present promising simulation results and experimental results in an epilepsy patient with simultaneous scalp EEG and ECoG recordings demonstrate the feasibility of estimating cortical potentials from the post-operative scalp EEG recordings.

Acknowledgement

The authors would like to thank Dr. VL Towle and ZM Liu for useful discussions, Y Lai for assistance in clinical data analysis, and Y Yao for assistance in FEM modeling. This work was supported in part by NIH RO1 EB00178, NSF BES-0411898, NSF-BES-0411480, and partly supported by the Biomedical Engineering Institute and Supercomputing Institute of the University of Minnesota.

Reference

  • Babiloni F, Babiloni C, Carducci F, Fattorini L, Anello C, Onorati P, Urbano A. High resolution EEG: A new model-dependent spatial deblurring method using a realisticallyshaped MR-constructed subject’s head model. Electroenceph. Clin. Neurophysiol. 1997;102:69–80. [Abstract] [Google Scholar]
  • Babiloni F, Babiloni C, Carducci F, Romani GL, Rossini PM, Angelone LM, Cincotti F. Multimodal integration of high-resolution EEG and functional magnetic resonance imaging data: a simulation study. Neuroimage. 2003;19:1–15. [Abstract] [Google Scholar]
  • Cohen D, Cuffin BN, Yunokuchi K, Maniewski R, Purcell C, Cosgrove GR, Ives J, Kennedy JG, Schomer DL. MEG versus EEG localization test using implanted sources in the human brain. Ann Neurol. 1990;28:811–817. [Abstract] [Google Scholar]
  • Cuffin BN, Cohen D. Comparison of the magnetoencephalogram and electroencephalogram. Electroencephalogr. Clin. Neurophysiol. 1979;47:132–146. [Abstract] [Google Scholar]
  • Dale AM, Sereno MI. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: a linear approach. J. Cognit. Neurosci. 1993;5:162–176. [Abstract] [Google Scholar]
  • Ebersole JS. Non-invasive localization of the epileptogenic focus by EEG dipole modeling. Acta Neurol Scand. 1994;152:20–28. [Abstract] [Google Scholar]
  • Finke S, Gulrajani RM, Gotman J. Conventional and reciprocal approaches to the inverse dipole localization problem of electroencephalography. IEEE Trans Biomed. Eng. 2003;50:657–666. [Abstract] [Google Scholar]
  • Fuchs M, Wagner M, Kohler T, Wischmann HA. Linear and nonlinear current density reconstructions. J Clin Neurophysiol. 1999;16:267–295. [Abstract] [Google Scholar]
  • Gevins A, Le J, Martin NK, Brickett P, Desmond J, Reutter B. High resolution EEG: 124-channel recording, spatial deblurring and MRI integration method. Electroenceph clin Neurophysiol. 1994;90:337–358. [Abstract] [Google Scholar]
  • Gulrajani RM. Bioelectricity and Biomagnetism. John Wiley & Sons, Inc.; New York: 1998. [Google Scholar]
  • Hamalainen M, Sarvas J. Realistic conductor geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans. Biomed. Eng. 1989;36:165–171. [Abstract] [Google Scholar]
  • Hansen PC. Analysis of discrete ill-posed problems by means of the L-curve. SIAM Rev. 1992;34:561–580. [Google Scholar]
  • He B, Musha T, Okamoto Y, Homma S, Nakajima Y, Sato T. Electrical dipole tracing in the brain by means of the boundary element method and its accuracy. IEEE Trans. Biomed. Eng. 1987;34:406–414. [Abstract] [Google Scholar]
  • He B, Wang YH, Pak S, Ling Y. Cortical source imaging from scalp electroencephalograms. Med Biol Eng Comput. 1996;34:257–258. [Abstract] [Google Scholar]
  • He B. High resolution source imaging of brain electrical activity. IEEE Eng Med Biol Mag. 1998;17:123–129. [Abstract] [Google Scholar]
  • He B, Wang YH, Wu DS. Estimating cortical potentials from scalp EEG’s in a realistically shaped inhomogeneous head model. IEEE Trans Biomed Eng. 1999;46:1264–1268. [Abstract] [Google Scholar]
  • He B, Lian J, Spencer KM, Dien J, Donchin E. A cortical potential imaging analysis of the P300 and novelty P3 components. Hum Brain Mapp. 2001;12:120–130. [Europe PMC free article] [Abstract] [Google Scholar]
  • He B, Zhang X, Lian J, Sasaki H, Wu DS, Towle VL. Boundary element method-based cortical potential imaging of somatosensory evoked potentials using subjects’ magnetic resonance images. Neuroimage. 2002;16:564–576. [Abstract] [Google Scholar]
  • He B, editor. Modeling and imaging of bioelectrical activity: Principles and applications. Kluwer Academic/Plenum Publishers; New York: 2004. [Google Scholar]
  • He B, editor. Neural Engineering. Kluwer Academic/Plenum Publishers; New York: 2005. [Google Scholar]
  • Kim S, Kim TS, Zhou Y, Singh M. Influence of conductivity tensors on the scalp electrical potential: study with 2-D finite element models. IEEE Trans Nuclear Science. 2003;50:133–139. [Google Scholar]
  • Lai Y, van Drongelen W, Ding L, Hecox KE, Towel VL, Frim DM, He B. Estimation of in vivo brain-to-skull conductivity ration from simultaneous extra- and intra-cranial electrical potential recording. Clinical Neurophysiology. 2005;116:456–465. [Abstract] [Google Scholar]
  • Lantz G, Michel CM, Pascual-Marqui RD, Spinelli L, Seeck M, Seri S, Landis T, Rosen I. Extracranial localization of intracranial interictal epileptiform activity using LORETA (low resolution electromagnetic tomography) Electroenceph clin Neurophysiol. 1997;102:414–422. [Abstract] [Google Scholar]
  • Le J, Gevins A. Method to Reduce Blur Distortion from EEG’ Using a Realistic Head Model. IEEE Trans Biomed. Eng. 1993;40:517–528. [Abstract] [Google Scholar]
  • Marin G, Guerin C, Baillet S, Garnero L, Meunier G. Influence of skull anisotropy for the forward and inverse problem in EEG: Simulation studies using FEM on realistic head models. Human Brain Mapping. 1998;6:250–269. [Europe PMC free article] [Abstract] [Google Scholar]
  • Michel CM, de Peralta RG, Lantz G, Andino SG, Spinelli L, Blanke O, Landis T, Seeck M. Spatiotemporal EEG analysis and distributed source estimation in presurgical epilepsy evaluation. J Clin Neurophysiol. 1999;16:239–266. [Abstract] [Google Scholar]
  • Mosher JC, Leahy RM, Lewis PS. EEG and MEG: forward solutions for inverse methods. IEEE Trans. Biomed. Eng. 1999;46:245–259. [Abstract] [Google Scholar]
  • Nimsky C, Ganslandt O, Cerny S, Hastreiter P, Greiner G, Fahlbusch R. Quantification of, visualization of, and compensation for brain shift using intraoperative magnetic resonance imaging. Neurosurgery. 2000;47:1070–1080. [Abstract] [Google Scholar]
  • Nunez P. Electric Field of the Brain. Oxford University Press; London: 1981. [Google Scholar]
  • Nunez P, Silibertein RB, Cdush PJ, Wijesinghe RS, Westdrop AF, Srinivasan R. A theoretical and experimental study of high resolution EEG based on surface Laplacian and cortical imaging. Electroenceph clin Neurophysiol. 1994;90:40–57. [Abstract] [Google Scholar]
  • Ollikainen JO, Vauhkonen M, Karjalainen PA, Kaipio JP. A New Computational Approach for cortical Imaging. IEEE Trans Biomed. Eng. 2001;20:325–332. [Abstract] [Google Scholar]
  • Oostendorp TF, Delbeke J, Stegeman DF. The conductivity of the human skull: results of in vivo and in vitro measurements. IEEE Trans Biomed Eng. 2000;47:1487–1492. [Abstract] [Google Scholar]
  • Pascual-Marqui RD, Michel CM, Lehmann D. Low resolution electromagnetic tomography: a new method for localizing electrical activity in the brain. Int. J. Psychophysiol. 1994;18:49–65. [Abstract] [Google Scholar]
  • Rush S, Driscoll DA. EEG electrode sensitivity-An application of reciprocity. IEEE Trans Biomed. Eng. 1969;16:15–22. [Abstract] [Google Scholar]
  • Scherg M, Von Cramon D. Two bilateral sources of the AEP as identified by a spatio-temporal dipole model. Electroenceph. Clin. Neurophysiol. 1985;62:32–44. [Abstract] [Google Scholar]
  • Sidman R, Ford M, Ramsey G, Schlichting C. Age-related features of the resting and P300 auditory evoked responses using the dipole localization method and cortical imaging technique. J Neurosci Methods. 1990;33:23–32. [Abstract] [Google Scholar]
  • Silvester PP, Ferrari RL. Finite elements for electrical engineering. Cambridge University Press; New York: 1996. [Google Scholar]
  • Stok CJ. The influence of model parameters on EEG/MEG single dipole source estimation. IEEE Trans. Biomed. Eng. 1987;34:289–296. [Abstract] [Google Scholar]
  • Tao JX, Ray A, Hawes-Ebersole S, Ebersole JS. Intercranial EEG substrates of scalp EEG intericatal spikes. Epilepsia. 2005;46:669–676. [Abstract] [Google Scholar]
  • Towle VL, Cohen S, Alperin N, Hoffmann K, Cogen P, Milton J, Grzeszczuk R, Pelizzari C, Syed I, Spire JP. Displaying electrocorticographic findings on gyral anatomy. Electroenceph. Clin. Neurophysiol. 1995;94:221–228. [Abstract] [Google Scholar]
  • Wang YH, He B. A computer simulation study of cortical imaging from scalp potentials. IEEE Trans. Biomed. Eng. 1998;45:724–735. [Abstract] [Google Scholar]
  • Wolters CH, Grasedyck L, Hackbusch W. Efficient Computation of Lead Field Bases and Influence Matrix for the FEM-based EEG and MEG Inverse Problem, Inverse Problems. 2004;20:1099–1116. [Google Scholar]
  • Yan Y, Nunez PL, Hart RT. Finite-element model of the human head: scalp potentials due to dipole sources. Medical & Biological Engineering & Computing. 1991;29:475–481. [Abstract] [Google Scholar]
  • Zhang X, Drongelen WV, Hecox KE, Towle VL, Frim DM, McGee AB, He B. High-resolution EEG: Cortical potential imaging of interictal spikes. Clin Neurophysiol. 2003;114:1963–1973. [Abstract] [Google Scholar]
  • Zhang YC, Zhu SA, He B. A Second-Order Finite Element Algorithm for Solving the Three-Dimensional EEG Forward Problem. Phys. Med. Biol. 2004;49:2975–2987. [Abstract] [Google Scholar]

Full text links 

Read article at publisher's site: https://doi.org/10.1016/j.neuroimage.2006.02.027

Read article for free, from open access legal sources, via Unpaywall: https://europepmc.org/articles/pmc1866308?pdf=renderUnpaywall

Citations & impact 

Impact metrics

36
Citations
Jump to Citations

Citations of article over time

Smart citations by scite.ai
Smart citations by scite.ai include citation statements extracted from the full text of the citing article. The number of the statements may be higher than the number of citations provided by EuropePMC if one paper cites another multiple times or lower if scite has not yet processed some of the citing articles.
Explore citation contexts and check if this article has been supported or disputed.
https://scite.ai/reports/10.1016/j.neuroimage.2006.02.027

Supporting
Mentioning
Contrasting
0
51
0

Article citations

Go to all (36) article citations

Similar Articles 

To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.

Funding 

Funders who supported this work.

NIBIB NIH HHS (2)

National Institutes of Health (3)