Europe PMC

This website requires cookies, and the limited processing of your personal data in order to function. By using the site you are agreeing to this as outlined in our privacy notice and cookie policy.

Probing protein aggregation using discrete molecular dynamics.

Author information

Affiliations

  • 1. Department of Biochemistry and Biophysics, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599, USA.
      Authors
    • Sharma S 1
    (1 author)

ORCIDs linked to this article

Frontiers in Bioscience : a Journal and Virtual Library, 01 May 2008, 13:4795-4808
https://doi.org/10.2741/3039 PMID: 18508545 PMCID: PMC2497428

ReviewFree full text in Europe PMC

Abstract 

Understanding the role of biomolecular dynamics in cellular processes leading to human diseases and the ability to rationally manipulate these processes is of fundamental importance in scientific research. The last decade has witnessed significant progress in probing biophysical behavior of proteins. However, we are still limited in understanding how changes in protein dynamics and inter-protein interactions occurring in short length- and time-scales lead to aberrations in their biological function. Bridging this gap in biology probed using computer simulations marks a challenging frontier in computational biology. Here we examine hypothesis-driven simplified protein models in conjunction with discrete molecular dynamics in the study of protein aggregation, implicated in series of neurodegenerative diseases, such as Alzheimer's and Huntington's diseases. Discrete molecular dynamics simulations of simplified protein models have emerged as a powerful methodology with its ability to bridge the gap in time and length scales from protein dynamics to aggregation, and provide an indispensable tool for probing protein aggregation.

Free full text 

Logo of nihpaLink to Publisher's site
Front Biosci. Author manuscript; available in PMC 2008 Aug 6.
Published in final edited form as:
Front Biosci. 2008 May 1; 13: 4795–4808.
Published online 2008 May 1. https://doi.org/10.2741/3039
PMCID: PMC2497428
NIHMSID: NIHMS56907
PMID: 18508545

Probing protein aggregation using simplified models and discrete molecular dynamics

Shantanu Sharma,1 Feng Ding,1 and Nikolay V. Dokholyan1
Author information Copyright and License information Disclaimer

Abstract

Understanding the role of biomolecular dynamics in cellular processes leading to human diseases and the ability to rationally manipulate these processes is of fundamental importance in scientific research. The last decade has witnessed significant progress in probing biophysical behavior of proteins. However, we are still limited in understanding how changes in protein dynamics and inter-protein interactions occurring in short length- and time-scales lead to aberrations in their biological function. Bridging this gap in biology probed using computer simulations marks a challenging frontier in computational biology. Here we examine hypothesis-driven simplified protein models in conjunction with discrete molecular dynamics in the study of protein aggregation, implicated in series of neurodegenerative diseases, such as Alzheimer's and Huntington's diseases. Discrete molecular dynamics simulations of simplified protein models have emerged as a powerful methodology with its ability to bridge the gap in time and length scales from protein dynamics to aggregation, and provide an indispensable tool for probing protein aggregation.

Keywords: Protein Aggregation, Protein Misfolding, Simplified Modeling, Aggregation Kinetics, Folding Thermodynamics, Discrete Molecular Dynamics, Molecular Dynamics, Computational Biology, Biophysics, MD, DMD, Misfolding, Molecular Dynamics, Review

2. INTRODUCTION

Protein aggregation is known to implicate in the etiology of a range of human diseases such as the Alzheimer's disease, Creutzfeldt–Jakob disease, Parkinson's disease, Huntington's disease and Amyotropic Lateral Schelerosis (also known as Lou Gehrig's Disease, ALS) (1). Many of these diseases are prevalent in adult humans, inherited genetically, and are often fatal. The presence of fibrillar proteinaceous deposits termed “senile amyloid plaques” is characteristic of the Alzheimer's disease onset (2). Similarly mutations in the cytoplasmic Cu, Zn Superoxide Dismutase enzyme (SOD1) are the precursor in the onset of a significant fraction of familial ALS (FALS) disease. Understanding the fundamental biophysical principles and molecular-level mechanisms of protein aggregation is of immense interest in the biological and medical research community. Significant changes in protein conformational dynamics and stability are often associated with protein misfolding/aggregation. An accurate understanding of structural dynamics, kinetics and energetics of proteins and how it relates to their cellular function and aggregation-associated cytotoxicity is indispensable in order to comprehensively describe molecular-level protein conformational changes lead to aggregation and diseases.

Alterations in protein sequence leads to changes in conformational dynamics, kinetics and energetics of proteins. These changes may result in significant changes in the native state stability of proteins, often leading to aggregation-prone conformations. For instance, multiple missense mutations in the cytosolic SOD1 genes are found, each of these mutations leading to the FALS disease phenotype (3). In poly-glutamine neurodegenerative disorders, such as Huntington's disease and related cerebrospinal atrophies, insertion of poly-glutamine repeats in proteins beyond 35−45 glutamines (caused by erroneous expansion of -CAG- nucleotide sequence in corresponding genes) leads to aggregation (4). Such alterations in the primary sequence manifest as changes in protein folding kinetics and thermodynamics, thereby facilitating non-native misfolded conformations. Oligomerization of non-native conformations ultimately leads to fibrillar aggregate formation.

Molecular dynamics (MD) simulations have emerged as a potent and predictive tool to study aggregation mechanisms at molecular levels. Over the last decade, many computational tools for modeling protein dynamics have been developed to study protein aggregation using MD simulations. Discrete molecular dynamics (5, 6) (DMD) simulations explore long time scales and length scales of simulations (7) and have therefore emerged as an especially useful tool to simulate protein aggregation. Notably, physiologically-relevant protein dynamics spans multiple orders of length and time scales, often with significant conformational changes in constituent proteins, thereby necessitating the use of simplified/coarse-grained protein models with unconventional MD simulation approaches such as DMD to investigate protein aggregation. The extent of simplification used in the model is often correlated with the complexity of the protein being investigated.

Applications of simplified protein models focusing on protein folding and design have been reviewed earlier (8-10). In this article, we present some of the recent research frontiers wherein simplified protein modeling and DMD simulations of protein aggregation have lead us to a better comprehension of the changes involved in protein dynamics potentially lead to aggregation and cause cytotoxicity. Broad applications of DMD simulations in probing protein dynamics and aggregation are discussed earlier, see articles by Urbanc et al. and Hall et al. (5, 6, 11). During the last decade, several protein models of different complexities have been developed for use in DMD simulations to probe protein aggregation. Here we focus on case-studies showing the applications of simplified protein models having different complexity and how DMD simulations of simplified protein model forms an indispensable tool to investigate protein aggregation.

3. DISCRETE MOLECULAR DYNAMICS (DMD) ALGORITHM

The discrete molecular dynamics (also known as discontinuous molecular dynamics, DMD) algorithm is event-driven, i.e. increments in the simulation trajectory occurs as inter-particle collision events occur. This is opposed to conventional MD simulations, wherein periodic Verlet integration is used to update the corresponding trajectory. A fundamental difference between DMD and conventional MD simulations is the use of step-wise (square-well) potentials for two-body interactions, as opposed to continuous potentials (e.g. Lennard-Jones potential). Due to square-well nature of the interaction potentials in DMD, particles translate with constant velocities before colliding with neighboring particles. Upon collision, the particle velocities are updated instantaneously following conservation of energy and momentum of colliding particles.

Simulation advancements in the form of inter-particle collisions results in significant acceleration in computational time required for DMD simulations (7). As opposed to periodic updates in MD simulations, the principal computation in DMD is of sorting a list of collision events and finding the soonest collision. The chapter Step Potentials in the book The Art of Molecular Dynamics Simulations (12) describes the prototypical algorithm as well as the software code for performing DMD simulations. Computational sorting of numeric data is a software engineering challenge. Recent advancements in sorting algorithms and computer architectures assist in rapid sorting of collision events resulting in improvements in computational costs of DMD simulations. As a result of the simplifications in modeling protein structures, DMD simulations of simplified protein models are found to exhibit many orders of magnitude improvements in computational performance and conformational sampling efficiency as compared to conventional all-atom MD simulations (9).

Because of the ability of DMD to explore significantly longer time and length scales, DMD simulations of simplified protein models has emerged as an especially useful tool for computational analyses of protein aggregation. While the fundamental algorithm of DMD was known as early as 1959 by the work of Alder and Wainwright (13) and later applied to studying dynamics of polymer chains by Rapaport (14, 15), pioneering work in application of DMD and simplified one-bead protein models was done in the last decade by Zhou and Karplus (16), where the authors used the one-bead protein model to study the folding of a model three-helix bundle protein. Soon after, DMD with simplified protein models was widely used to study folding dynamics of model proteins (16-19).

Events in DMD simulations consist of two-body inter-particle collisions. The simulated system is often constrained in a cubical box and the constituent particles are also referred to as beads. The simulation box is further subdivided into many cubical cells having dimensions larger than the interaction range between particles, to reduce the search space for computation of subsequent collisions to adjoining cells. DMD simulations incorporate the periodic boundary condition to overcome finite dimensions of the box used to perform the simulation. A heat bath based on the Berendsen thermostat (20) or the Anderson thermostat (21) is used to control the simulation temperature. During the course of the simulation with Berendsen thermostat, periodic rescaling of particle velocities is performed at a constant rate in order to scale the existing temperature to the desired simulation temperature. In simulations with the Anderson thermostat, each particle randomizes its velocity according to the Maxwell's distribution due to random collisions with the time intervals following Poisson distribution.

The first step in the simulation process is of initializing the coordinates and velocities of particles and a collision event list to enlist the pairs of colliding particles. The second step constitutes identifying the soonest colliding particles; say pi and pj, and scheduling the collision. Upon collision, the coordinates and velocities of colliding particles pi and pj are instantaneously updated following the laws of conservation of linear momentum, angular momentum and energy before and after collision. The collision between the two particles is recorded into the collision event list and potential immediate collisions of particles pi and pj with other particles are identified and scheduled in the collision event list. Repeating these steps multiple times lead to evolution of the simulation trajectory. Thermodynamic and biophysical properties along the simulation trajectory such as particle coordinates, particle velocities, potential energy, temperature, radius of gyration are periodically stored to record the simulation progress. Besides DMD, many computational protocols have been developed to study protein aggregation. These approaches include molecular dynamics simulations in explicit (22, 23) or implicit solvent (24, 25), Monte Carlo simulations (26), activation-relaxation technique (27, 28) and parallel tempering simulations (29). Applications of these computational techniques towards protein aggregation are presented in a recent review by Ma and Nussinov (30). It is important to highlight the similarities and differences between DMD simulations and these computational protocols for probing protein aggregation. Notably, replica exchange and simulated annealing algorithms are readily implemented using DMD for conformational exploration instead of using Monte Carlo or MD based conformational sampling. Prototypical DMD simulations involve an implicit solvation approach, wherein the inter-particle interaction potentials are scaled in accordance with solvent effects. Modeling of electrostatic salt bridge interactions (31) and hydrophobic, hydrophilic and hydrogen bond interactions (32) in DMD simulations are also discussed in Section 4. The simplification of the protein model results in improved predictive power at the expense of (8-10) higher numerical precision of force-field based explicit/implicit solvent MD simulations.

4. INVESTIGATING PROTEIN AGGREGATION WITH SIMPLIFIED PROTEIN MODELS

Over the last two decades, several simplified protein models (one-bead, two-bead, four-bead and united-atom models) having differing structural resolution and complexity have been developed to study protein aggregation. Native structure-based Go model (33-36) have been extensively used to simulate protein folding and aggregation (11, 17, 19, 37, 38). Inter-particle interactions in the Go model are assigned based on the native state of the protein and are consequently biased towards the native state, thus Go models don't use an ab initio force field. Recently, explicit modeling of inter-particle interaction potentials such as the hydrophobic and electrostatic salt-bridge interactions in proteins have resulted in accurate protein models having remarkable predictive power (31, 39, 40). While high-resolution protein models provide accurate structural details, they result in a larger number of beads representing the same protein. Increased computational costs associated with high-resolution models may prohibit simulations of large protein aggregates over experimentally relevant timescales. Thus, there is a necessity to design accurate computational models of proteins having different complexity and detail. In the remainder of this section, we highlight various cases wherein these simplified protein models are used along-with DMD simulations to probe protein aggregation.

4.1. One-bead protein models with Go-like potentials

One of the simplest protein models used to study protein dynamics is the one-bead per residue model, which is based on a representation of each individual amino acid by a single sphere and the protein as a polymer with bead-on-a-string representation (16, 17) (Figure 1a). Zhou et al. (41) used DMD simulations of a one-bead model to study first order phase transitions in a homopolymers chain of 64 beads. The authors note that the first order disordered-to-ordered phase transition exhibited by this model homopolymer was analogous to simulating conformational changes in the protein folding process, despite significant differences in the final native state conformations of two species.

An external file that holds a picture, illustration, etc. Object name is nihms-56907-f0001.jpg

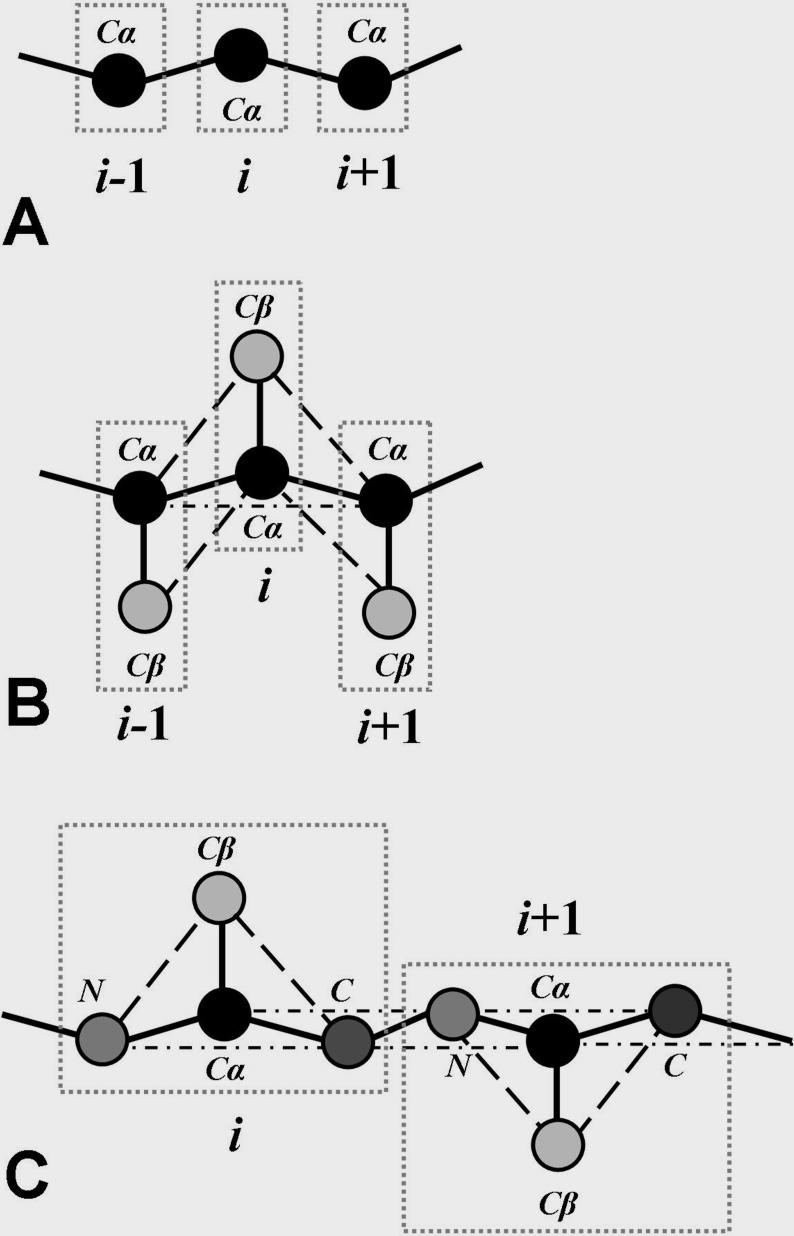
Schematic diagrams of (a) the one-bead protein model, (b) the two-bead peptide model, (c) the four bead protein model Solid thick lines represent covalent and peptide bonds. Dashed thin lines denote effective bonds assigned to mimic the tetrahedral constraint of each amino acid and the planar constraint of the peptide bond. High resolution protein structures available in the Protein DataBank(89) are used to generate coordinates of effective beads in the simplified model. As described in the main text, DMD simulations of these simplified protein models have been extensively used to study protein aggregation. Furthermore, hydrogen bonding and hydropathic interactions can be added in the residue-interactions to probe the role of electrostatic and hydrophobic interactions in protein aggregation.

Later, Zhou and Karplus (16, 42) used the one-bead model to study folding of a model three-helix bundle protein (16). Despite the inherent structural simplicity of the one-bead model, the simulations show experimentally observed transitions from a collapsed state to a native-like topology, whose folding thermodynamics was comparable to all-atom MD simulations by Bockzo and Brooks (43). These DMD simulations formed one of the early evidences of applicability of simplified models and DMD in probing protein folding and misfolding transitions.

Dokholyan et al. (17, 19) demonstrated the ability of one-bead protein models to capture the thermodynamics and kinetics of folding and misfolding transitions in model proteins. The authors also used DMD simulations having Go potential for inter-residue interactions to characterize the folding nucleus of a model 46-residue protein (19). Dokholyan et al. observed that few contacts in proteins are essential for mediating the folding kinetics and energetics of the folding transition barrier (19). The authors also suggested that proteins having similar structures but differing sequence may share common locations of folding nuclei. Biophysical observations derived from these DMD simulations regarding phase transitions upon folding are general and expected to be consistent for folding transitions in other proteins.

Clark (44) used the one-bead model to perform Langevin dynamics simulation of protein aggregation kinetics of protein G, L and their mutations, each 56 residue long. The author used a simplified off-lattice cooperative folding model (non-Go interactions), representing each protein residue as a single bead. The mutations investigated disrupt hydrophobic interactions in the protein core without significantly changing the overall structure and folding propensities of the two proteins. Moreover, the simulation conditions are chosen to have similar populations of the folded states. The authors note that for simulations with these simplified models, folding cooperativity is the most significant determinant of folding time, estimating the effective population of folding intermediate. Clark observes that aggregates observed in simulations of the one-bead model are less structured as compared to the corresponding native states (44).

Chahine and Cheung (37) used a simplified one-bead per residue protein model to study reversible domain swapping of the p13suc1 protein. MD simulations with a Go-like potential were used to study the p13suc1 dimer formation. Two transition states, the monomer transition state and the dimer transition states are observed in the domain-swapped dimerization process, suggesting a “lock-and-dock” mechanism for p13suc1 dimerization, wherein domain swapping of one strand of a monomer onto an adjoining monomer results in locking of the dimer conformation followed by docking to stabilize the domain-swapped conformation (37). The authors characterize two populated species coexisting at temperatures significantly lower than the folding transition temperature. The simulations also suggests that folding kinetics of native-like monomer formation will be significantly slower in the course of domain-swapping (37).

4.2. Two-bead model applications in protein aggregation

While the one-bead model is able to capture the salient features of protein folding kinetics (19, 45), the need to obtain structural details of the transition state ensemble (TSE) resulted in the development of the two-bead model of the protein (46), in which Calpha and Cbeta atoms were modeled as the constituent protein beads (Figure 1b). Khare et al. (38) used the two bead model with Go-type interactions to study folding of SOD1 protein monomer (discussed in section 5.2). Peng et al. (47) applied a two-bead protein model with Go-like interactions to study aggregation of Abeta40 proteins into a fibrillar structure. DMD simulations of the Abeta40 protein at temperatures exceeding alpha-helix unfolding transition temperature show a conformational transition of the Abeta40 peptides into multi-layered parallel beta sheets having an interstrand separation of 4.8 Angstroms, in agreement with the structure of the Abeta40 amyloid fibers derived using electron microscopy (48). Furthermore, the authors observe the presence of unbound beta sheet edges in the Abeta40 amyloid aggregates predicted by DMD simulations which may facilitate further aggregation into longer oligomeric species.

Simulations of amphipathic alpha-helix monomer folding demonstrated that the folding process is mediated via a competition between hydrophobicity and hydrogen-bonding interactions in the alpha-helix residues. The temperature dependence of folding kinetics was also dependent on the strength of hydrophobic interactions used in the simulation. Contributions of side-chain entropy and non-backbone hydrogen-bonding to folding kinetics was absent in this model, however, the authors suggested scaling the strength of square-well interactions based on side-chain hydrophobicities to model side chain contributions. Notably, a number of conformations are sampled in the simulations, including non-native topologies, which subsequently lead to misfolded aggregates.

Smith et al. (49) studied the conformational transitions of a polyalanine chain to an alpha-helix using DMD simulations of a simplified two-bead protein model with excluded-volume and hydrogen-bonding interactions. The authors note that the (phi, psi) values adopted by the polyalanine chain during the course of conformational transitions in DMD simulation are limited to the valid protein regions in the Ramachandran map and that the formation of is alpha-helices is mediated by backbone hydrogen bonding and is largely cooperative. As opposed to polgyglycine chains, which adopt non-helical topologies, alanine polymers are mostly helical in nature.

4.3. Four-bead model applications in protein aggregation

The four-bead protein model captures significant details of the protein structure and is extensively used for studying protein aggregation using DMD simulations. In this model, three backbone beads N, Calpha, C and one side-chain bead Cbeta are used to represent each residue (Figure 1c). Ding et al. (50) developed a four-bead protein model with hydrogen bonding interactions for DMD simulations. The authors used this protein model to study the temperature dependent conformational transformations of a 16-residue long model polyalanine chain having alpha-helical native conformation. In the DMD simulations, the authors observe that the alpha-helix native conformation changes into a partially-stable beta-hairpin conformation. The authors also note an important role of physicochemical nature of the protein environment and hydrophobicity of adjoining residues in governing the aggregation propensity of the polyalanine chain and suggest the presence of sequence-independent backbone hydrogen bonding mediates such conformational transitions. Larger entropy of the beta-hairpin conformation relative to the native alpha-helix stabilizes the beta-hairpin.

Hall and coworkers developed four-bead protein models to study ab initio DMD simulations of the assembly of 16 residue long amphipathic alpha-helices into a four-helix bundle (51). The authors performed multiple DMD simulations to accurately sample the conformational space of the monomeric alpha-helix and the tetrameric alpha-helical bundle and describe the tetramer folding landscape (51). Notably, the conformations explored by the helix monomers and the helical bundle in the DMD simulations were found to be consistent with experiments of DeGrado and coworkers (52-55). The authors also report rapid conformational sampling ability of DMD, leading to significant conformational sampling with less computational cost (49, 51) and the efficacy of the simplified protein model in understanding the dynamics of multi-protein complexes.

Lam et al. (56) used DMD simulations of a four-bead protein model with hydrogen bonds and amino-acid specific interactions to study temperature-driven conformational changes in the Amyloid-beta42 protein. The conformational changes observed in DMD simulations were found to be in good agreement with temperature dependent solution structures of Amyloid-beta protein determined by Gursky and Aleshkov (57). Under low temperature conditions, the Abeta42 protein was found to be mostly globular, however, beta-rich conformations lacking helical content are observed in simulations at elevated temperatures. While the folded Abeta42 showed dynamic conformational transitions, turns centered on the Abeta G25-S26, G37-G38 residues were found to be persistent and important for formation of amyloid fibrils.

Urbanc et al. (58) applied a four-bead protein model for the Amyloid-beta protein to investigate dimer formation in Amyloid-beta aggregation and probe the oligomerization process of two predominant amyloid-beta alloforms, Abeta40 and Abeta42 using DMD. The authors report aggregation of both proteins into oligomers of variable sizes. Dimer conformations were generated using DMD simulations at different constant temperature simulations with the simplified four-bead protein model. These simplified protein conformations were converted into corresponding all-atom representations by superposition against amino-acid structural templates, and subsequent optimization using a Monte Carlo algorithm, resulting in a multiscale model of Abeta protein dynamics.

Urbanc et al. (32) modified the four-bead protein model introducing effective hydrophobic, hydrophilic interactions in addition to the hydrogen bond interactions present in the original model lacking hydropathic interactions (58). Using this model, the authors investigated folding and oligomerization of the Amyloid-beta protein using DMD simulations. Both hydrophilic repulsion and hydrophobic attraction were found to be critical for modeling Amyloid-beta oligomer distributions consistent with experiments by Teplow and coworkers (59-61). Notably, oligomers resulting from folding and aggregation simulations of Abeta monomers displayed variable size distributions, with Abeta40 oligomers being predominantly dimeric while Abeta42 forming pentameric oligomers having globular, hydrophobic core (32). The authors suggest that the presence of Gly-37-Gly-38 turn in Abeta42, not observed in Abeta40 plays a crucial role in Abeta42 pentamer formation. These structural differences between high molecular-weight oligomers of Abeta40 and Abeta42 proteins were suggested to cause differences in oligomerization propensities of the two alloforms.

Yun et al. (31) used DMD simulation with simplified four-beads per residue protein models to study the electrostatic interactions in Amyloid beta (Abeta) protein oligomerization and the role of electrostatic interactions between charged residues in the Abeta protein. Mechanistic differences between aggregation kinetics of Abeta40 and Abeta42 were observed to be based on differences in electrostatic interactions between pairs of charged amino-acids in Abeta40 and Abeta42. Differences in protein aggregation propensities resulting from change of polypeptide length is of considerable interest in amyloid research community. The rates of aggregation for Abeta40 and Abeta42 proteins, the major components of amyloid plaques formed in Alzheimer's disease, are significantly different. However, the precise mechanisms of these differences in aggregation propensities are not completely understood. The work of Yun et al. (31) suggests that electrostatic interactions in Amyloid beta-protein favor formation of larger oligomeric species in both Abeta40 and Abeta42, thereby shifting the oligomer size distribution to larger oligomers. However, the Abeta40 size distribution remains largely unimodal, while size distribution of Abeta42 is trimodal, in agreement with experimental findings. Importantly, differences in folded structures of Abeta40 and Abeta42 monomers are unaffected by electrostatic interactions. A C-terminus turn, found in Abeta42 folded structure is absent in Abeta40, suggesting a key role of the C-terminal tail in Abeta42 oligomerization. These simulations with simplified protein models also suggest inhibitors targeting the Abeta42 C-terminal domain may prevent oligomer formation thereby reducing its cytotoxicity.

Smith et al. (51) probed the assembly of a prototypical tetrameric alpha-helical bundle using DMD simulations of a simplified four-bead per residue protein model having detailed backbone geometry (three beads modeling the backbone and one bead modeling the side chain). Starting from random coil conformations, DMD simulations of the model monomer amphipathic polypeptides undergo folding transitions resulting in alpha-helical native topologies. Equilibrium between side-chain hydrophobic interactions and backbone hydrogen-bonding mediates the stability of model peptide's alpha-helical native state. The authors observe formation of non-native hydrogen bonds in the course of simulations, resulting in exploration of non-native misfolded conformations, rich in beta-structures (beta-turn, beta-hairpin, or beta-sheet motifs). Simulations of tetramers of 16-residue chains result in parallel and anti-parallel tetrameric alpha-helical bundles with hydrophobic side-chains shielded in the bundle interior as the most stable conformation. Low temperature simulations were found to be often trapped in misfolded states because of stronger hydrogen bonding and hydrophobic interactions relative to thermal fluctuations. Notably, structures with non-native and beta-hydrogen bonds are often observed in tetramer simulations, resulting in non-ideal folding trajectories leading to misfolded states.

Nguyen et al. (62) studied the kinetics of polyalanine fibril formation using an intermediate-resolution four-bead per residue protein model, termed PRIME (49, 51, 63). The model has three beads representing the peptide backbone and one bead representing the side chain atoms. As opposed to the native conformation based Go-model, the PRIME four-bead protein model is devoid of any conformational bias towards native or non-native conformations. In addition to distance, angular and dihedral constraints modeling the protein structure, intra- and inter-molecular hydrogen bonding and hydrophobic interactions are modeled for inter-residue interactions. While DMD simulations of the 48−96 residue long polyalanine chains show that the mechanism of amyloid fibril formation is in agreement with three known models, namely: templated assembly; nucleated polymerization; and nucleated conformational conversion. However, none of these models could alone explain the kinetics of fibril formulation with significant accuracy. The authors suggested that the kinetics of polyalanine conformational conversion is manifested as progression from small amorphous aggregate state to beta-sheets, which form an ordered nucleus ultimately leading to fibrillar protofilament species. The kinetics of amyloid fibril formation increased with increasing polyalanine concentration as well as decreasing simulation temperature. Furthermore, the simulations indicate that the polyalanine oligomers growth involved beta-sheet elongation adding polyalanine peptides in the end as well as lateral appending of existing beta-sheets (62).

4.4. United-atom model applications in protein aggregation

The united-atom model represents groups of atoms as novel atom types having physical properties such as particle diameter and inter-particle interactions scaled corresponding to the constituent atoms. Borrguero et al. (39) used a detailed unified-atom model representing all atoms except hydrogens and DMD simulations to study the folding dynamics of a 10 residue segment (Ala 21-Ala 30) of the amyloid beta protein. This segment is suggested to nucleate the folding of monomeric Abeta protein. The authors report that hydrophobic interactions between constituent Val-24, Lys-28 residues and an equilibrium between electrostatic interactions of Glu-22 and Asp-23 with Lys-28 result in folding of this domain into a stable loop structure. Salt bridge interactions of Asp-23 with Lys-28 was also consistent with Abeta conformational stability analyses by Ma et al. (22) and the NMR-derived model of Abeta by Petkova et al. (64). Different conformations adopted by this 10 residue segment Abeta(21-30), as observed in the NMR solution structure of Abeta(10-35) (65), Protein DataBank accession number: 1HZ3, are shown in Figure 2. Side chains of residues Glu-22, Asp-23 and Lys-28 are highlighted for clarity. Familial mutations of Alzheimer's disease at the Glu-22 are suggested to change the interactions of Glu-22 with Lys-28, thereby altering the stability of Abeta folding nucleus (39). Subsequent long timescale all-atom MD simulations by Cruz et al. (66) also confirm the role of hydrophobic and salt bridge interactions in folding dynamics of Abeta(21-30) peptide.

An external file that holds a picture, illustration, etc. Object name is nihms-56907-f0002.jpg

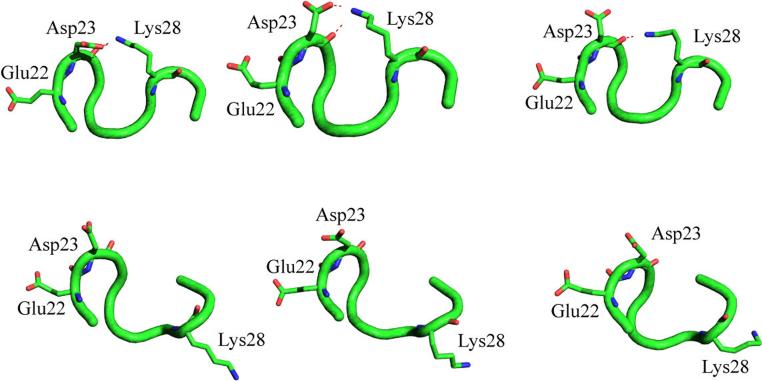
Conformational dynamics of the model Amyloid-β folding nucleus (residues 21−30, derived from Protein DataBank accession number: 1HZ3). Salt bridge interactions between residues Glu22, Asp23 and Lys28 are highlighted. These residues are suggested to mediate conformational transitions in the model folding nucleus of Amyloid-β protein, thereby mediating the Amyloid-β oligomerization process (39). Figure generated using the PyMOL molecular visualization software (90).

5. DMD SIMULATIONS AS A COMPUTATIONAL TOOL TO STUDY PROTEIN MISFOLDING

In this section we will present a few of the recent applications of DMD simulations and simplified protein models discussed in section 4, towards probing different biophysical phenomena associated with protein misfolding. We will also discuss some of the recently developed computational tools and web-services harnessing DMD simulations to characterize folding/misfolding dynamics of any protein.

5.1. Probing conformational changes in beta2 microglobulin leading to aggregation

Deposition of human beta2-microglobulin (beta2m) protein into serum amyloid fibrils is observed in hemodialysis-related amyloidosis (67) and is a serious complication in patients receiving long-term renal dialysis treatment (68). Chen et al. (69) used DMD simulations with a simplified four-bead model of beta2m protein to explore the mechanistic differences between aggregation of oxidized and reduced forms of the beta2m protein. The authors note that the beta2m aggregate morphologies were dependent on the oxidation state of beta2m protein: oxidized beta2m forming needle-like fibrils under acidic conditions (pH 2.5); whereas reduced beta2m loses the intramolecular disulfide bond under acidic conditions and rather than forming amyloid fibrils, reduced beta2m forms flexible filaments. DMD simulations of a beta2m dimer highlighted an important mechanistic role of a highly conserved disulfide bond between residues Cys25 and Cys80 of beta2m (Protein DataBank accession number: 1LDS; Figure 3) in beta2m aggregation. The authors show that oxidized beta2m protein forms domain-swapped dimers whereas reduced beta2m protein forms dimers and trimers consisting of parallel beta-sheets stabilized by a network of backbone hydrogen bonds. The oligomers are capable for further aggregation yielding high molecular-weight aggregates. Notably, these DMD simulations suggest that formation of Cys25-Cys80 disulfide bonds mediate the aggregation pathway of oxidized and reduced beta2m, and suggest that the mechanism of aggregate expansion in oxidized beta2m is via domain swapping while aggregate expansion in reduced beta2m occurs via parallel stacking of partially folded beta2m (67).

An external file that holds a picture, illustration, etc. Object name is nihms-56907-f0003.jpg

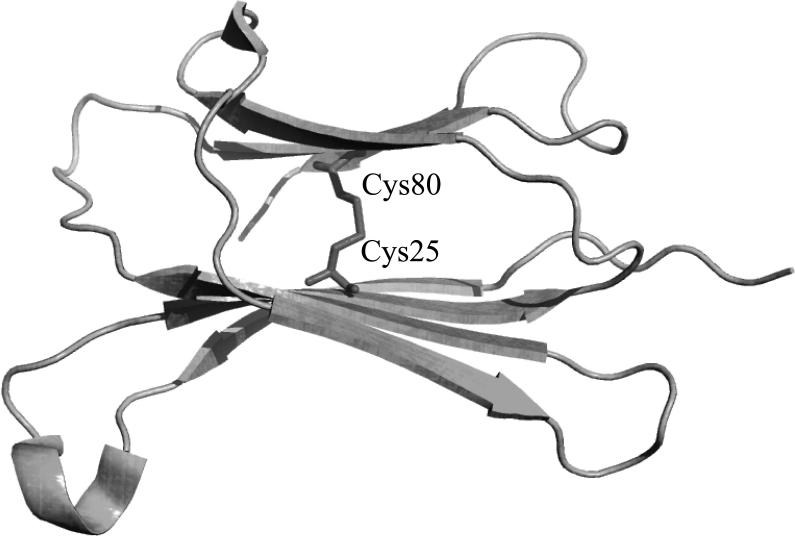
Seven β strands present in the β2 microglobulin protein monomer (Protein DataBank accession number: 1LDS). Disruption of the single β2 microglobulin disulfide bond interaction between residues Cys80 and Cys25 results in domain swapping conformational transition and is a suggested to be the precursor in β2 microglobulin amyloidogenesis (69). Figure generated using the PyMOL molecular visualization software (90).

5.2. Superoxide Dismutase misfolding mechanism

Khare et al. (38) performed DMD simulations to study the folding and misfolding of SOD1 protein (Protein DataBank accession number: 1SPD). The authors characterized residues in SOD1 protein important for the two-state folding kinetics using DMD simulations. The authors also used DALI (70) structural alignment software to compare kinetically important SOD1 residues with a structurally similar protein Tnf3 (Protein DataBank accession number: 1TEN) belonging to the same immunoglobin super-family, whose folding kinetics was well understood (71) (Figure 4). Notably, SOD1 residue positions identified by DMD simulations to play a functional role in SOD1 folding kinetics correlate with residues identified by structural comparison with Tnf3 (38). Furthermore, Khare et al. postulate that disruption of key interactions at these residues caused by mutations may expose the edges of SOD1 beta-strands, and this change in native state conformational stability leads to non-native interactions, ultimately causing SOD1 misfolding. Interactions at the edges of beta-sheets mediate SOD1 folding, loop-crossing and salt bridge interactions at the kinetically important residues regulate SOD1 folding. The authors also report that residues mediating SOD1 folding kinetics are interspersed on SOD1 surface and are absent in the hydrophobic core (38) (Figure 4).

An external file that holds a picture, illustration, etc. Object name is nihms-56907-f0004.jpg

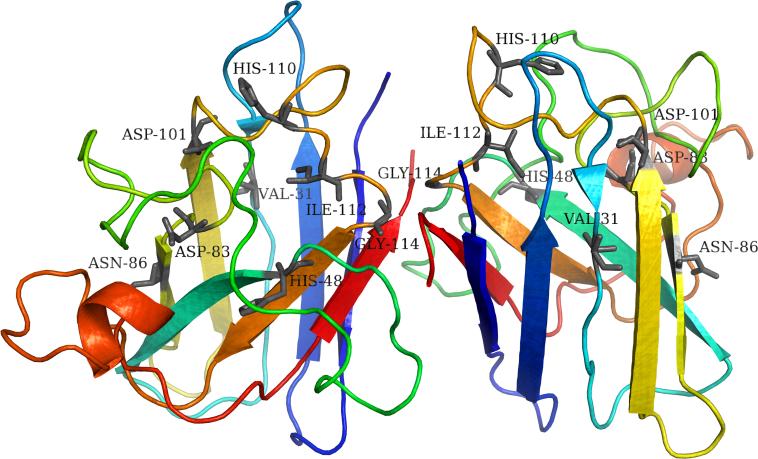
Kinetically important residues in the core of Cu-Zn superoxide-dismutase (SOD1) dimer protein (38) (Protein DataBank accession number: 1SPD). The residues Val31, His48, Asp83, Asn86, Asp101 His110, Ile112 and Gly114 of both dimers are labeled and shown in black. These SOD1 residues were identified by structural comparison against nuclear residues of the immunoglobin-like protein super-family sibling Tnf3 (Protein DataBank accession number: 1TEN) whose folding kinetics is characterized using [var phi]-value analysis (71). These residues are suggested to function as the SOD1 folding nucleus and mutations in the putative folding nucleus are suggested to mediate the protein's folding kinetics, potentially leading to SOD1 aggregation (38). Note that the kinetically important residues are dispersed throughout the surface of SOD1. Figure generated using the PyMOL molecular visualization software (90).

5.3. Length-dependent aggregation of poly-glutamine repeats

Poly-glutamine (PolyQ) or CAG repeat disorders are implicated in several neurodegenerative diseases, including Huntington's disease (72), six forms of spinocerebellar ataxia (73) and Kennedy disease (74). Insertion of PolyQ peptides longer than 35−45 residues into proteins is associated with protein aggregation and cytotoxicity (75). Barton et al. (76) used DMD simulations with the four-bead protein model to study the length dependence of PolyQ-mediated aggregation of the Chymotrypsin Inhibitor-2 (CI2) protein. The authors generate chimeric CI2 and CI2-PolyQ insert proteins having insert lengths spanning the critical pathogenicity threshold (77). The authors report that CI2 monomer folding kinetics in DMD simulations was highly cooperative, in agreement with previous experimental findings. However, CI2-PolyQ chimeras having PolyQ insert length greater than the pathogenicity threshold exhibit significantly less cooperative monomer folding kinetics, with inter-glutamine hydrogen bonding as a predominant mode of dimerization (76). The authors also proposed a general mechanism for PolyQ-mediated aggregation where PolyQ inserts mediate formation of unfolded intermediate states by destabilizing the interactions in the corresponding protein. Subsequent formation of inter-glutamine hydrogen bonds stabilizes the unfolded PolyQ-protein intermediates, leading to formation of aggregate fibrils (76).

5.4. Prion-like conformational conversion exposing hydrophobic surfaces

Conformational conversion of alpha-helices to beta-sheet topologies is often manifested in prion diseases and other aggregation disorders such as Alzheimer's disease and Lou Gehrig's disease (78-80). Ding et al.(81) used DMD simulations to probe this prion-like conformational conversion in a de novo engineered peptide ccbeta found to undergo temperature dependent conformational conversion into amyloid fibrils (82). The authors report presence of a critical temperature below which the peptide folds into a native-like alpha-helical coiled-coil topology, whereas, above the critical folding temperature, the protein misfolds into aggregation-prone amyloid like fibrils rich in anti-parallel beta-sheet. Notably, this conformational conversion is mediated by exposure of hydrophobic surfaces in ccbeta and unsaturated hydrogen bonds, which may function as templates for further aggregation. These observations are also consistent with a template-based mechanism of prion infectivity originally proposed by Prusiner (78).

5.5. Hinge region predictor probing protein domain swapping

An important biophysical phenomena associated with some proteins is the presence of hinge regions. Hinge regions are those loci which function as a pivot/hinge axis around which the protein undergoes significant conformational changes often leading to domain swapped. Domain swapping was first noticed in proteins by the pioneering work of Eisenberg and coworkers (83). Ding et al. (84) used two-bead protein model to study the domain-swapped dimmer formation for a set of proteins and proposed that hinge regions of domain swapping is governed by monomeric protein topologies, and developed a hinge region prediction server, H-predictor (http://dokhlab.unc.edu/tools/h-predictor), to identify potential hinge regions in arbitrary proteins. The H-predictor estimates the enthalpy change upon hinge formation, del(EH), by measuring the changes in the number of native-contacts, native disulfide bonds and hydrogen bonds (84). The authors also devise a metric measuring the change in conformational entropy upon hinge formation, del(SH) based on changes in average minimal path between two protein residues (84), and use del(EH)/del(SH) as a measure of hinge conformational transition temperature. Residues corresponding to minimum values of the hinge transition temperature, and therefore del(EH)/del(SH), are predicted as the hinge loci. Notably, using the H-predictor, the authors predicted multiple hinge regions and two domain swapped dimers in RNase A and FAT domain proteins.

5.6. iFold webserver as a tool to study protein aggregation

The iFold server (85) (http://iFold.dokhlab.org) is a general purpose tool for studying protein dynamics using simplified protein models. The iFold server was created to enable a general purpose web-interface for simulation and exploration of protein dynamics. The back-end of iFold server integrates a distributed high performance computing resources with efficient DMD simulations of simplistic two-bead protein models and the front-end presents a convenient interface to the research community for using the DMD algorithm and exploring the conformational transitions in the aggregation pathways of arbitrary proteins. The operational diagram of the iFold server is shown in Figure 5. A Beowulf Linux cluster resource provided by the UNC Information Technology services furnishes the high performance computation requirements for many DMD simulations submitted to the iFold portal. Recently, the Open Science Grid computational infrastructure (86) is added to the iFold portal's accessible computational resource, thereby facilitating longer time-scale DMD simulations of protein aggregation utilizing the world-wide computational infrastructure.

An external file that holds a picture, illustration, etc. Object name is nihms-56907-f0005.jpg

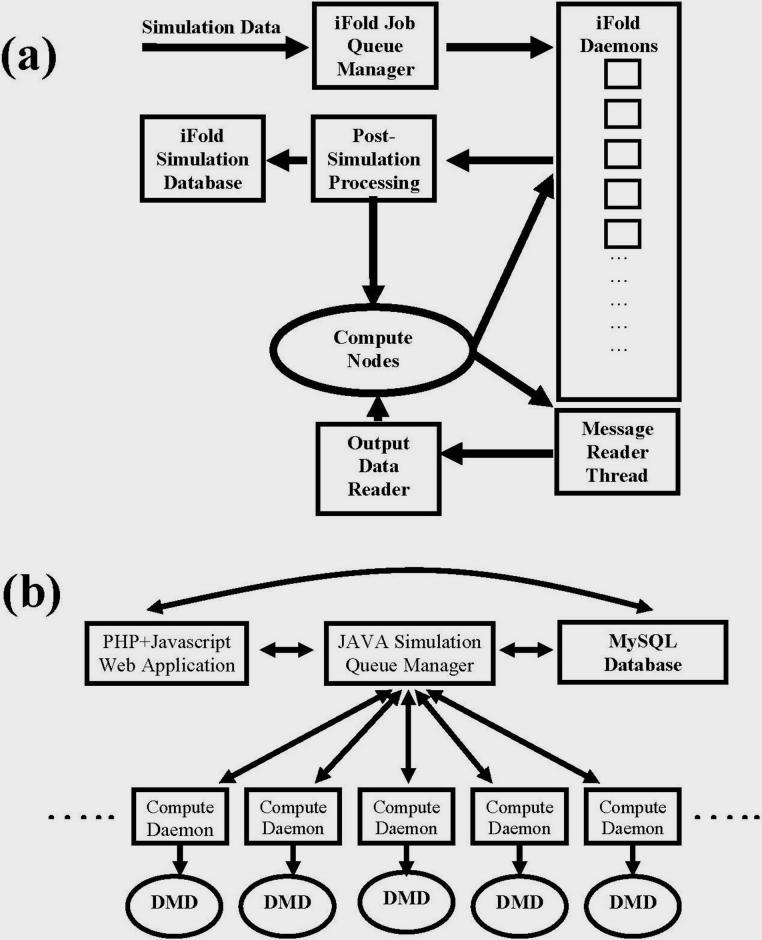
Control flow diagram of the iFold server (http://iFold.dokhlab.org). The iFold portal provides a globally accessible computational resource for exploring aggregation mechanisms and oligomerization/folding dynamics of arbitrary proteins using DMD simulations of simplified protein models. (a) Communication between different segments of the server are shown, with emphasis on scheduling of simulation jobs. (b) Flow of data from the web-application, via the simulation scheduler to submitted simulation database. iFold compute nodes run DMD simulations (indicated by oval boxes) of simplified two-bead protein models and are highly computational scalable.

6 LIMITATIONS OF SIMPLIFIED PROTEIN MODELS AND DMD SIMULATIONS

We have presented numerous case studies and applications of simplified protein models and DMD simulations for investigating protein aggregation. Nevertheless, it is important to highlight the limitations of simplified protein modeling and their impact on the predictive power of simplified modeling. Urbanc et al. (5) highlight several important limitations of DMD simulations of simplified models, which must be appreciated in order to effectively use simplified models in studying protein aggregation and other biophysical phenomena. Despite significant improvements in accurate yet simplified models of proteins in recent years (7), a large extent of conformational freedom of proteins is often lost owing to the structural coarse-graining. Subtle changes in protein dynamics may be undetected in simplified protein models, while clearly evident in high-resolution atomic models. The interaction model used in simulations is often phenomenologically-derived (5), and may be biased and/or inaccurate because of limitations in availability or resolution of experimentally-derived structural parameters. With increasing structural genomics efforts, novel protein structures are derived leading to better statistical analyses of native-like protein structures.

Approximations in the interaction potential due to unbiased treatment of simplified beads of different residues also lead to inaccuracies in the protein model, thereby limiting the predictive accuracy of DMD simulations of simplified models. However, such limitations may be eliminated by introducing novel types of peptide side-chain-dependent backbone beads having different interaction behaviors. Also, the strength of hydrogen bond and hydropathic interactions used in ab initio simplified models are often independent of the amino acid sequence context (5). While directional dependence of acceptor and donor atoms in hydrogen bonding is implemented in DMD simulations, it is not specific of the underlying sequence context. The cumulative effect of sequence-specific hydrogen bonds may be of mechanistic relevance in protein aggregation.

The solvent is implicitly modeled in DMD simulations, thus reducing the complexity of computing interactions of protein beads with the solvent. Physicochemical properties of the solvent, counterion density and biophysical properties of the simulation environment including temperature, pressure, molecular concentration, etc. may cause substantial changes in effective local interactions. Due to implicit solvation, such local variations in electrostatic interactions are ignored in the simulations. Improvements in the protein interaction model such as environment-dependent dynamic scaling of local interactions may overcome such limitations of simplified models.

The work of Zhou and Karplus (16, 42) was among the foremost evidence demonstrating the efficacy of constant-temperature DMD simulations for exploring the folding kinetics and thermodynamics of a model three-helix bundle protein. Later, the work of Ding et al. (46) suggests that DMD simulations using simplified protein models also faithfully recapitulates the thermodynamics as well as kinetics of folding-unfolding transition in C-Src SH3 protein as observed in experiments (46). This protein model was also useful in predicting the amyloidogenesis mechanism of the C-Src SH3 domain (87). Furthermore, applications and limitations of DMD-based methods in probing kinetics and thermodynamics of protein aggregation are also discussed in the recent review articles by Hall et al. (6) and Urbanc et al. (5).

7. SUMMARY AND PERSPECTIVES

Simplified protein models have provided an important tool for computational studies of protein aggregation. In this article we present several case studies demonstrating that DMD simulations of simplified protein models are particularly useful in probing the slow time-scales and large length-scales of protein aggregation. Despite the simplicity of one-bead to four-bead protein models, numerous important biophysical insights and testable hypotheses regarding three-dimensional protein domain swapping, length-dependent mechanistic differences in formation of Amyloid beta aggregates are attained using simplified protein models. With increasing computational speeds, we expect further applications of simplified models in studying amyloid oligomerization and for probing the structure and dynamics of higher-order oligomeric species.

The iFold server (http://iFold.dokhlab.org) facilitates probing aggregation of arbitrary proteins at long time and length scales using DMD simulations of two-bead protein models. The hinge region predictor server (http://dokhlab.unc.edu/tools/h-predictor) enables the exploration of domain swapping based on DMD simulations of two-bead protein models. Recent applications of multiscale modeling and DMD simulations to study dynamics of large complexes such as the nucleosome core particle (88) (>200 kDa) also suggests DMD simulations of simplified models may also be suitable for probing dynamics and conformational transitions in oligomeric aggregates at unprecedented length and time scales. Significant improvements in structural details and predictability of simplified protein models are attainable via accurately modeling hydrogen bonding and hydrophobic/hydrophilic interactions. DMD simulations of multiscale protein models can be performed by iteratively performing simulations using high and low-resolution protein models. Multiscale modeling has emerged as a useful tool to study high resolution mechanistic details of inter-particle interaction without losing the predictive power by adequate conformational sampling. Utilizing simplified protein models to sample the conformations of large-scale processes and systems, and using higher-resolution models are used for improving the accuracy of simulation predictions is the hallmark of multiscale modeling. With increasing computational power, we foresee significant applications of simplified protein modeling and DMD simulations towards understanding the fundamental principles of protein aggregation.

8. ACKNOWLEDGEMENTS

This work was supported in part by American Heart Association grant 0665361U, and North Carolina Biotechnology Center grant 2006-MRG-1107. Shantanu Sharma is supported by UNC Integrated Biomedical Research Training Program (5T90DA022857-02). The authors thankfully acknowledge the support from Ruth Marinshaw and Steven Fishback from the UNC Informational Technology Services for providing high performance computing resources for the iFold server.

Abbreviations

DMDDiscrete Molecular Dynamics
MDMolecular Dynamics
SOD1Cu, Zn superoxide dismutase
AbetaAmyloid beta-protein
beta2mbeta2-microglobulin
PolyQPoly-glutamine
CI2Chymotrypsin Inhibitor-2

REFERENCES

1. Koo EH, Lansbury PT, Jr., Kelly JW. Amyloid diseases: abnormal protein aggregation in neurodegeneration. Proc. Natl. Acad. Sci. U. S. A. 1999;96:9989–9990. [Europe PMC free article] [Abstract] [Google Scholar]
2. Alzheimer A, Stelzmann RA, Schnitzlein HN, Murtagh FR. An English translation of Alzheimer's 1907 paper, “Uber eine eigenartige Erkankung der Hirnrinde”. Clin. Anat. 1995;8:429–431. [Abstract] [Google Scholar]
3. Rosen DR, Siddique T, Patterson D, Figlewicz DA, Sapp P, Hentati A, Donaldson D, Goto J, O'Regan JP, Deng HX. Mutations in Cu/Zn superoxide dismutase gene are associated with familial amyotrophic lateral sclerosis. Nature. 1993;362:59–62. [Abstract] [Google Scholar]
4. Riley BE, Orr HT. Polyglutamine neurodegenerative diseases and regulation of transcription: assembling the puzzle. Genes Dev. 2006;20:2183–2192. [Abstract] [Google Scholar]
5. Urbanc B, Borreguero JM, Cruz L, Stanley HE. Ab initio discrete molecular dynamics approach to protein folding and aggregation. Methods Enzymol. 2006;412:314–338. [Abstract] [Google Scholar]
6. Hall CK, Wagoner VA. Computational approaches to fibril structure and formation. Methods Enzymol. 2006;412:338–365. [Abstract] [Google Scholar]
7. Ding F, Dokholyan NV. Simple but predictive protein models. Trends Biotechnol. 2005;23:450–455. [Abstract] [Google Scholar]
8. Dinner AR, Sali A, Smith LJ, Dobson CM, Karplus M. Understanding protein folding via free-energy surfaces from theory and experiment. Trends Biochem. Sci. 2000;25:331–339. [Abstract] [Google Scholar]
9. Dokholyan NV. Studies of folding and misfolding using simplified models. Curr. Opin. Struct. Biol. 2006 [Abstract] [Google Scholar]
10. Head-Gordon T, Brown S. Minimalist models for protein folding and design. Curr. Opin. Struct. Biol. 2003;13:160–167. [Abstract] [Google Scholar]
11. Hall CK, Nguyen HD, Marchut AJ, Wagoner V. Misbehaving Proteins. Springer; New York: 2006. Simulations of Protein Aggregation. [Google Scholar]
12. Rapaport DC. The Art of Molecular Dynamics Simulation. Cambridge University Press; 2004. [Google Scholar]
13. Alder BJ, Wainwright TE. Studies in Molecular Dynamics. I. General Method. The Journal of Chemical Physics. 1959;31:459–466. [Google Scholar]
14. Rapaport DC. Molecular dynamics simulation of polymer chains with excluded volume. J. Phys. A: Math. Gen. 1978;11:L213–L217. [Google Scholar]
15. Rapaport DC. Molecular dynamics simulation of polymer chains in solution. J. Chem. Phys. 1979;71:3299–3303. [Google Scholar]
16. Zhou Y, Karplus M. Folding thermodynamics of a model three-helix-bundle protein. Proc. Natl. Acad. Sci. U. S. A. 1997;94:14429–14432. [Europe PMC free article] [Abstract] [Google Scholar]
17. Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Discrete molecular dynamics studies of the folding of a protein-like model. Fold. Des. 1998;3:577–587. [Abstract] [Google Scholar]
18. Zhou Y, Karplus M. Folding of a model three-helix bundle protein: a thermodynamic and kinetic analysis. J. Mol. Biol. 1999;293:917–951. [Abstract] [Google Scholar]
19. Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Identifying the protein folding nucleus using molecular dynamics. J. Mol. Biol. 2000;296:1183–1188. [Abstract] [Google Scholar]
20. Berendsen HJC, Postma JPM, Van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics. 1984;81:3684. [Google Scholar]
21. Andersen HC. Molecular-Dynamics Simulations at Constant Pressure And-Or Temperature. Journal of Chemical Physics. 1980;72:2384–2393. [Google Scholar]
22. Ma B, Nussinov R. Stabilities and conformations of Alzheimer's beta -amyloid peptide oligomers (Abeta 16−22, Abeta 16−35, and Abeta 10−35): Sequence effects. Proc. Natl. Acad. Sci. U. S. A. 2002;99:14126–14131. [Europe PMC free article] [Abstract] [Google Scholar]
23. Ma B, Nussinov R. Molecular dynamics simulations of alanine rich beta-sheet oligomers: Insight into amyloid formation. Protein Sci. 2002;11:2335–2350. [Europe PMC free article] [Abstract] [Google Scholar]
24. Fernandez A, de las Mercedes Boland M. Solvent environment conducive to protein aggregation. FEBS Lett. 2002;529:298–301. [Abstract] [Google Scholar]
25. Cellmer T, Bratko D, Prausnitz JM, Blanch HW. Protein aggregation in silico. Trends Biotechnol. 2007;25:254–261. [Europe PMC free article] [Abstract] [Google Scholar]
26. Leonhard K, Prausnitz JM, Radke CJ. Solvent-amino acid interaction energies in three-dimensional-lattice Monte Carlo simulations of a model 27-mer protein: Folding thermodynamics and kinetics. Protein Sci. 2004;13:358–369. [Europe PMC free article] [Abstract] [Google Scholar]
27. Barkema GT, Mousseau N. Event-Based Relaxation of Continuous Disordered Systems. Physical Review Letters. 1996;77:4358–4361. [Abstract] [Google Scholar]
28. Santini S, Wei G, Mousseau N, Derreumaux P. Pathway complexity of Alzheimer's beta-amyloid Abeta16−22 peptide assembly. Structure. 2004;12:1245–1255. [Abstract] [Google Scholar]
29. Tsai HH, Reches M, Tsai CJ, Gunasekaran K, Gazit E, Nussinov R. Energy landscape of amyloidogenic peptide oligomerization by parallel-tempering molecular dynamics simulation: significant role of Asn ladder. Proc. Natl. Acad. Sci. U. S. A. 2005;102:8174–8179. [Europe PMC free article] [Abstract] [Google Scholar]
30. Ma B, Nussinov R. Simulations as analytical tools to understand protein aggregation and predict amyloid conformation. Curr. Opin. Chem Biol. 2006;10:445–452. [Abstract] [Google Scholar]
31. Yun S, Urbanc B, Cruz L, Bitan G, Teplow DB, Stanley HE. Role of electrostatic interactions in amyloid beta-protein (A beta) oligomer formation: a discrete molecular dynamics study. Biophys. J. 2007;92:4064–4077. [Europe PMC free article] [Abstract] [Google Scholar]
32. Urbanc B, Cruz L, Yun S, Buldyrev SV, Bitan G, Teplow DB, Stanley HE. In silico study of amyloid beta-protein folding and oligomerization. Proc. Natl. Acad. Sci. U. S. A. 2004;101:17345–17350. [Europe PMC free article] [Abstract] [Google Scholar]
33. Abe H, Go N. Noninteracting local-structure model of folding and unfolding transition in globular proteins. II. Application to two-dimensional lattice proteins. Biopolymers. 1981;20:1013–1031. [Abstract] [Google Scholar]
34. Taketomi H, Ueda Y, Go N. Studies on protein folding, unfolding and fluctuations by computer simulation. I. The effect of specific amino acid sequence represented by specific inter-unit interactions. Int J Pept Protein Res. 1975;7:445–459. [Abstract] [Google Scholar]
35. Ueda Y, Taketomi H, Go N. Studies on protein folding, unfolding, and fluctuations by computer simulation. II. A. Three-dimensional lattice model of lysozyme. Biopolymers. 1978;17:1531–1548. [Google Scholar]
36. Go N, Taketomi H. Respective roles of short- and long-range interactions in protein folding. Proc. Natl. Acad. Sci. U. S. A. 1978;75:559–563. [Europe PMC free article] [Abstract] [Google Scholar]
37. Chahine J, Cheung MS. Computational studies of the reversible domain swapping of p13suc1. Biophys. J. 2005;89:2693–2700. [Europe PMC free article] [Abstract] [Google Scholar]
38. Khare SD, Ding F, Dokholyan NV. Folding of Cu, Zn superoxide dismutase and familial amyotrophic lateral sclerosis. J. Mol. Biol. 2003;334:515–525. [Abstract] [Google Scholar]
39. Borreguero JM, Urbanc B, Lazo ND, Buldyrev SV, Teplow DB, Stanley HE. Folding events in the 21−30 region of amyloid beta-protein (Abeta) studied in silico. Proc. Natl. Acad. Sci. U. S. A. 2005;102:6015–6020. [Europe PMC free article] [Abstract] [Google Scholar]
40. Khare SD, Ding F, Gwanmesia KN, Dokholyan NV. Molecular origin of polyglutamine aggregation in neurodegenerative diseases. PLoS. Comput. Biol. 2005;1:230–235. [Europe PMC free article] [Abstract] [Google Scholar]
41. Zhou Y, Hall CK, Karplus M. First-Order Disorder-to-Order Transition in an Isolated Homopolymer Model. Physical Review Letters. 1996;77:2822–2825. [Abstract] [Google Scholar]
42. Zhou Y, Karplus M. Interpreting the folding kinetics of helical proteins. Nature. 1999;401:400–403. [Abstract] [Google Scholar]
43. Boczko EM, Brooks CL., III First-principles calculation of the folding free energy of a three-helix bundle protein. Science. 1995;269:393–396. [Abstract] [Google Scholar]
44. Clark LA. Protein aggregation determinants from a simplified model: cooperative folders resist aggregation. Protein Sci. 2005;14:653–662. [Europe PMC free article] [Abstract] [Google Scholar]
45. Borreguero JM, Dokholyan NV, Buldyrev SV, Shakhnovich EI, Stanley HE. Thermodynamics and folding kinetics analysis of the SH3 domain from discrete molecular dynamics. Journal of Molecular Biology. 2002;318:863–876. [Abstract] [Google Scholar]
46. Ding F, Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Direct molecular dynamics observation of protein folding transition state ensemble. Biophys. J. 2002;83:3525–3532. [Europe PMC free article] [Abstract] [Google Scholar]
47. Peng S, Ding F, Urbanc B, Buldyrev SV, Cruz L, Stanley HE, Dokholyan NV. Discrete molecular dynamics simulations of peptide aggregation. Phys. Rev. E. Stat. Nonlin. Soft. Matter Phys. 2004;69:041908. [Abstract] [Google Scholar]
48. Malinchik SB, Inouye H, Szumowski KE, Kirschner DA. Structural analysis of Alzheimer's beta(1−40) amyloid: protofilament assembly of tubular fibrils. Biophys. J. 1998;74:537–545. [Europe PMC free article] [Abstract] [Google Scholar]
49. Voegler Smith A., Hall CK. alpha-helix formation: discontinuous molecular dynamics on an intermediate-resolution protein model. Proteins. 2001;44:344–360. [Abstract] [Google Scholar]
50. Ding F, Borreguero JM, Buldyrey SV, Stanley HE, Dokholyan NV. Mechanism for the alpha-helix to beta-hairpin transition. Proteins-Structure Function and Genetics. 2003;53:220–228. [Abstract] [Google Scholar]
51. Smith AV, Hall CK. Assembly of a tetrameric alpha-helical bundle: computer simulations on an intermediate-resolution protein model. Proteins. 2001;44:376–391. [Abstract] [Google Scholar]
52. Hill CP, Anderson DH, Wesson L, DeGrado WF, Eisenberg D. Crystal structure of alpha 1: implications for protein design. Science. 1990;249:543–546. [Abstract] [Google Scholar]
53. Betz SF, Bryson JW, DeGrado WF. Native-like and structurally characterized designed alpha-helical bundles. Curr. Opin. Struct. Biol. 1995;5:457–463. [Abstract] [Google Scholar]
54. Raleigh DP, Betz SF, DeGrado WF. A de Novo Designed Protein Mimics the Native State of Natural Proteins. Journal of the American Chemical Society. 1995;117:7558–7559. [Google Scholar]
55. Ho SP, DeGrado WF. Design of a 4-helix bundle protein: synthesis of peptides which self-associate into a helical protein. Journal of the American Chemical Society. 1987;109:6751–6758. [Google Scholar]
56. Lam A, Urbanc B, Borreguero JM, Lazo ND, Teplow DB, Stanley HE. Discrete Molecular Dynamics Study of Alzheimer Amyloid beta-protein (Abeta) Folding.. Proceedings of the 2006 international conference on bioinformatics and computational biology322−328; (2006). [Google Scholar]
57. Gursky O, Aleshkov S. Temperature-dependent beta-sheet formation in beta-amyloid Abeta(1−40) peptide in water: uncoupling beta-structure folding from aggregation. Biochim. Biophys. Acta. 2000;1476:93–102. [Abstract] [Google Scholar]
58. Urbanc B, Cruz L, Ding F, Sammond D, Khare S, Buldyrev SV, Stanley HE, Dokholyan NV. Molecular dynamics simulation of amyloid beta dimer formation. Biophys. J. 2004;87:2310–2321. [Europe PMC free article] [Abstract] [Google Scholar]
59. Bitan G, Tarus B, Vollers SS, Lashuel HA, Condron MM, Straub JE, Teplow DB. A molecular switch in amyloid assembly: Met35 and amyloid beta-protein oligomerization. J. Am. Chem Soc. 2003;125:15359–15365. [Abstract] [Google Scholar]
60. Bitan G, Vollers SS, Teplow DB. Elucidation of primary structure elements controlling early amyloid beta-protein oligomerization. J. Biol Chem. 2003;278:34882–34889. [Abstract] [Google Scholar]
61. Bitan G, Kirkitadze MD, Lomakin A, Vollers SS, Benedek GB, Teplow DB. Amyloid beta -protein (Abeta) assembly: Abeta 40 and Abeta 42 oligomerize through distinct pathways. Proc. Natl. Acad. Sci. U. S. A. 2003;100:330–335. [Europe PMC free article] [Abstract] [Google Scholar]
62. Nguyen HD, Hall CK. Kinetics of fibril formation by polyalanine peptides. J. Biol Chem. 2005;280:9074–9082. [Abstract] [Google Scholar]
63. Nguyen HD, Marchut AJ, Hall CK. Solvent effects on the conformational transition of a model polyalanine peptide. Protein Sci. 2004;13:2909–2924. [Europe PMC free article] [Abstract] [Google Scholar]
64. Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. A structural model for Alzheimer's beta -amyloid fibrils based on experimental constraints from solid state NMR. Proc. Natl. Acad. Sci. U. S. A. 2002;99:16742–16747. [Europe PMC free article] [Abstract] [Google Scholar]
65. Zhang S, Iwata K, Lachenmann MJ, Peng JW, Li S, Stimson ER, Lu Y, Felix AM, Maggio JE, Lee JP. The Alzheimer's peptide a beta adopts a collapsed coil structure in water. J. Struct. Biol. 2000;130:130–141. [Abstract] [Google Scholar]
66. Cruz L, Urbanc B, Borreguero JM, Lazo ND, Teplow DB, Stanley HE. Solvent and mutation effects on the nucleation of amyloid beta-protein folding. Proc. Natl. Acad. Sci. U. S. A. 2005;102:18258–18263. [Europe PMC free article] [Abstract] [Google Scholar]
67. Floege J, Ketteler M. beta2-microglobulin-derived amyloidosis: an update. Kidney Int Suppl. 2001;78:S164–S171. [Abstract] [Google Scholar]
68. Gejyo F, Homma N, Suzuki Y, Arakawa M. Serum levels of beta 2-microglobulin as a new form of amyloid protein in patients undergoing long-term hemodialysis. N. Engl. J Med. 1986;314:585–586. [Abstract] [Google Scholar]
69. Chen Y, Dokholyan NV. A single disulfide bond differentiates aggregation pathways of ss2-microglobulin. J. Mol. Biol. 2005;354:473–482. [Abstract] [Google Scholar]
70. Holm L, Sander C. Protein structure comparison by alignment of distance matrices. J. Mol. Biol. 1993;233:123–138. [Abstract] [Google Scholar]
71. Hamill SJ, Steward A, Clarke J. The folding of an immunoglobulin-like Greek key protein is defined by a common-core nucleus and regions constrained by topology. J. Mol. Biol. 2000;297:165–178. [Abstract] [Google Scholar]
72. Andrew SE, Goldberg YP, Kremer B, Telenius H, Theilmann J, Adam S, Starr E, Squitieri F, Lin B, Kalchman MA. The relationship between trinucleotide (CAG) repeat length and clinical features of Huntington's disease. Nat. Genet. 1993;4:398–403. [Abstract] [Google Scholar]
73. Pulst SM, Nechiporuk A, Nechiporuk T, Gispert S, Chen XN, Lopes-Cendes I, Pearlman S, Starkman S, Orozco-Diaz G, Lunkes A, DeJong P, Rouleau GA, Auburger G, Korenberg JR, Figueroa C, Sahba S. Moderate expansion of a normally biallelic trinucleotide repeat in spinocerebellar ataxia type 2. Nat. Genet. 1996;14:269–276. [Abstract] [Google Scholar]
74. Amato AA, Prior TW, Barohn RJ, Snyder P, Papp A, Mendell JR. Kennedy's disease: a clinicopathologic correlation with mutations in the androgen receptor gene. Neurology. 1993;43:791–794. [Abstract] [Google Scholar]
75. Krobitsch S, Lindquist S. Aggregation of huntingtin in yeast varies with the length of the polyglutamine expansion and the expression of chaperone proteins. Proc. Natl. Acad. Sci. U. S. A. 2000;97:1589–1594. [Europe PMC free article] [Abstract] [Google Scholar]
76. Barton S, Jacak R, Khare SD, Ding F, Dokholyan NV. The length dependence of the polyQ-mediated protein aggregation. J. Biol. Chem. 2007 [Abstract] [Google Scholar]
77. Ross CA, Poirier MA, Wanker EE, Amzel M. Polyglutamine fibrillogenesis: the pathway unfolds. Proc. Natl. Acad. Sci. U. S. A. 2003;100:1–3. [Europe PMC free article] [Abstract] [Google Scholar]
78. Prusiner SB. Prions. Proc. Natl. Acad. Sci. U. S. A. 1998;95:13363–13383. [Europe PMC free article] [Abstract] [Google Scholar]
79. Nguyen J, Baldwin MA, Cohen FE, Prusiner SB. Prion protein peptides induce alpha-helix to beta-sheet conformational transitions. Biochemistry. 1995;34:4186–4192. [Abstract] [Google Scholar]
80. Hardy J, Selkoe DJ. The amyloid hypothesis of Alzheimer's disease: progress and problems on the road to therapeutics. Science. 2002;297:353–356. [Abstract] [Google Scholar]
81. Ding F, LaRocque JJ, Dokholyan NV. Direct observation of protein folding, aggregation, and a prion-like conformational conversion. J. Biol. Chem. 2005;280:40235–40240. [Abstract] [Google Scholar]
82. Kammerer RA, Kostrewa D, Zurdo J, Detken A, Garcia-Echeverria C, Green JD, Muller SA, Meier BH, Winkler FK, Dobson CM, Steinmetz MO. Exploring amyloid formation by a de novo design. Proc. Natl. Acad. Sci. U. S. A. 2004;101:4435–4440. [Europe PMC free article] [Abstract] [Google Scholar]
83. Bennett MJ, Choe S, Eisenberg D. Domain swapping: entangling alliances between proteins. Proc. Natl. Acad. Sci. U. S. A. 1994;91:3127–3131. [Europe PMC free article] [Abstract] [Google Scholar]
84. Ding F, Prutzman KC, Campbell SL, Dokholyan NV. Topological determinants of protein domain swapping. Structure. 2006;14:5–14. [Abstract] [Google Scholar]
85. Sharma S, Ding F, Nie HF, Watson D, Unnithan A, Lopp J, Pozefsky D, Dokholyan NV. iFold: a platform for interactive folding simulations of proteins. Bioinformatics. 2006;22:2693–2694. [Abstract] [Google Scholar]
86. Pordes R, Petravick D, Kramer B, Olson D, Livny M, Roy A, Avery P, Blackburn K, Wenaus T, Wnrthwein F, Foster I, Gardner R, Blatecky A, McGee J, Quick R. The open science grid. Journal of Physics: Conference Series. 2007;78:012057–012072. [Google Scholar]
87. Ding F, Dokholyan NV, Buldyrev SV, Stanley HE, Shakhnovich EI. Molecular dynamics simulation of the SH3 domain aggregation suggests a generic amyloidogenesis mechanism. J Mol. Biol. 2002;324:851–857. [Abstract] [Google Scholar]
88. Sharma S, Ding F, Dokholyan NV. Multiscale modeling of nucleosome dynamics. Biophys. J. 2007;92:1457–1470. [Europe PMC free article] [Abstract] [Google Scholar]
89. Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000;28:235–242. [Europe PMC free article] [Abstract] [Google Scholar]
90. DeLano WL. The PyMOL Molecular Graphics System. DeLano Scientific; San Carlos, CA: 2002. [Google Scholar]

Full text links 

Read article at publisher's site: https://doi.org/10.2741/3039

Read article for free, from open access legal sources, via Unpaywall: https://article.imrpress.com/bri/Landmark/articles/pdf/Landmark3039.pdfUnpaywall

Citations & impact 

Impact metrics

10
Citations
Jump to Citations

Citations of article over time

Article citations

Go to all (10) article citations

Data 

Data behind the article

This data has been text mined from the article, or deposited into data resources.

BioStudies: supplemental material and supporting data

Protein structures in PDBe (4)

Similar Articles 

To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.

Funding 

Funders who supported this work.

NIDA NIH HHS (2)

NIGMS NIH HHS (3)