Abstract
Free full text

White Matter Injury Susceptibility via Fiber Strain Evaluation Using Whole-Brain Tractography
Abstract
Microscale brain injury studies suggest axonal elongation as a potential mechanism for diffuse axonal injury (DAI). Recent studies have begun to incorporate white matter (WM) structural anisotropy in injury analysis, with initial evidence suggesting improved injury prediction performance. In this study, we further develop a tractography-based approach to analyze fiber strains along the entire lengths of fibers from voxel- or anatomically constrained whole-brain tractography. This technique potentially extends previous element- or voxel-based methods that instead utilize WM fiber orientations averaged from typically coarse elements or voxels. Perhaps more importantly, incorporating tractography-based axonal structural information enables assessment of the overall injury risks to functionally important neural pathways and the anatomical regions they connect, which is not possible with previous methods. A DAI susceptibility index was also established to quantify voxel-wise WM local structural integrity and tract-wise damage of individual neural pathways. This “graded” injury susceptibility potentially extends the commonly employed treatment of injury as a simple binary condition. As an illustration, we evaluate the DAI susceptibilities of WM voxels and transcallosal fiber tracts in three idealized head impacts. Findings suggest the potential importance of the tractography-based approach for injury prediction. These efforts may enable future studies to correlate WM mechanical responses with neuroimaging, cognitive alteration, and concussion, and to reveal the relative vulnerabilities of neural pathways and identify the most vulnerable ones in real-world head impacts.
 : Dartmouth Head Injury Model, fiber strain, neural pathway, tractography, traumatic brain injury, white matter injury
: Dartmouth Head Injury Model, fiber strain, neural pathway, tractography, traumatic brain injury, white matter injuryIntroduction
Traumatic brain injury (TBI) is a leading cause of morbidity and mortality in the United States.1 To better understand the mechanisms of brain injury at the macroscale level, numerous kinematic injury metrics have been proposed (e.g., peak linear [

Most of the model-based injury studies use isotropic response variables, such as the maximum principal strain (



Ji and colleagues22 used subject-specific head FE models to evaluate and compare 





While these studies suggest the importance of WM structural anisotropy,25 continued development along this line of research by incorporating whole-brain tractography derived from diffusion tensor imaging (DTI) for 
 mm along fibers or “streamlines”) than those “averaged” at coarse FE elements or voxels (e.g., element size up to 7.73
mm along fibers or “streamlines”) than those “averaged” at coarse FE elements or voxels (e.g., element size up to 7.73 mm,26 or DTI voxel size of 2
mm,26 or DTI voxel size of 2 mm ×2
mm ×2 mm ×3.6
mm ×3.6 mm27).
mm27).
For example, Chatelin and associates18 used weighted directions averaged from 70–4096 DTI voxels for each element. Both Cloots and coworkers17 and Wright and Ramesh19 employed a multiscale approach to couple a macroscale three dimensional (3D) or two dimensional (2D) head model, respectively, with a microscale element embedding a single axon. Work from Wright and colleagues,21 Kraft and associates,20 Sahoo and coworkers,26, and Giordano and Kleiven27 assigned average FA values and fiber directions to each element from coregistered DTI for strain evaluation. Instead of averaging on elements, Ji and associates22 evaluated fiber strain at each DTI voxel transformed into the corresponding FE model space using strain tensors from the closest FE element on a subject-specific basis.
Assessing tractography-based fiber strains is of particular interest in WM regions with crossing fibers or other complex fiber configurations. In addition, the ability to evaluate 
The goal of this study was to develop a technique to evaluate 
As an illustration, we investigated the injury susceptibilities of the whole-brain WM voxels as well as transcallosal fiber tracts traversing the corpus callosum (CC). Finally, these efforts allowed us to investigate the 


Methods
The Dartmouth Head Injury Model
All brain strain responses were obtained using the Dartmouth Head Injury Model (DHIM; Fig. 1). The DHIM is a subject-specific model created with high mesh quality and geometrical accuracy based on high-resolution magnetic resonance imaging (MRI) of an athlete. Details of the model description, material properties, and validation performances were reported previously.22,35,36
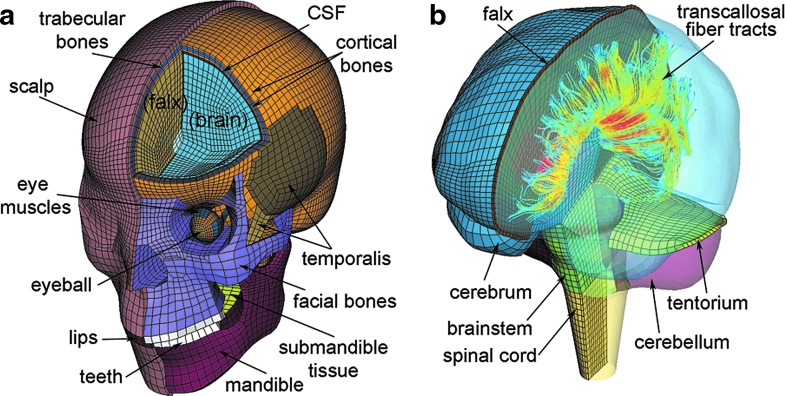
The Dartmouth Head Injury Model (DHIM) showing the head exterior (a) and the brain components (b). The model incorporates whole-brain tractography from the same individual used for the baseline DHIM creation. A subset of fractional anisotropy-encoded transcallosal fibers is shown (b). CSF, cerebrospinal fluid. Color image is available online at www.liebertpub.com/neu
Briefly, the DHIM is composed of solid hexahedral and surface quadrilateral elements with a total of 101.4 k nodes and 115.2 k elements and a combined mass of 4.562 kg for the whole head. The brain has a total of 56.6 k nodes and 55.1 k elements, with a combined mass of 1.558
kg for the whole head. The brain has a total of 56.6 k nodes and 55.1 k elements, with a combined mass of 1.558 kg. The average element sizes for the whole head and the brain are 3.2
kg. The average element sizes for the whole head and the brain are 3.2 ±
± 0.94
0.94 mm and 3.3
mm and 3.3 ±
± 0.79
0.79 mm, respectively.
mm, respectively.
The entire brain is modeled with the C3D8R type of hexahedral elements37 using a homogenous, second-order Ogden hyperelastic material model with rate effects incorporated through linear viscoelasticity. A layer of soft elements representing the cerebrospinal fluid between the brain and its neighboring structures (skull, falx, and tentorium) is incorporated by node sharing to enable brain interfacial sliding.
The DHIM has successfully passed the numerical convergence test and is of high mesh quality in terms of warpage, aspect ratio, skew, Jacobian, minimum length, and minimum/maximum angle.22 In addition, the model has been successfully validated against relative brain-skull displacement38,39 and intracranial pressure responses40,41 from cadaveric experiments, as well as full-field strain responses in a live human volunteer.42 The overall “good” to “excellent” validation at the low (~250–300 rad/s2 for the volunteer), mid (~1.9–2.3 krad/s2 for impact tests C755-T2 and C383-T1), and high (~11.9 krad/s2 for test C393-T4) levels of
rad/s2 for the volunteer), mid (~1.9–2.3 krad/s2 for impact tests C755-T2 and C383-T1), and high (~11.9 krad/s2 for test C393-T4) levels of 
Neuroimage acquisition
T1-weighted MRI (Magnetization Prepared Rapid Gradient Echo, MPRAGE; voxel resolution of 1.2 mm ×1
mm ×1 mm ×1
mm ×1 mm) and DTI (isotropic resolution of 2
mm) and DTI (isotropic resolution of 2 mm) scans were acquired in the Dartmouth Advanced Imaging Center. DTIs had 46 diffusion directions (collected with b
mm) scans were acquired in the Dartmouth Advanced Imaging Center. DTIs had 46 diffusion directions (collected with b =
= 1000
1000 s/mm2, NEX
s/mm2, NEX =
= 1) plus an additional volume without diffusion gradients (b
1) plus an additional volume without diffusion gradients (b =
= 0) serving as a reference image. Diffusion tensors, eigenvectors, and scalar diffusion parameters were computed using a well-established tractography software package, ExploreDTI,43 with corrections for eddy currents and motion before fitting a tensor model.
0) serving as a reference image. Diffusion tensors, eigenvectors, and scalar diffusion parameters were computed using a well-established tractography software package, ExploreDTI,43 with corrections for eddy currents and motion before fitting a tensor model.
In this study, we used the pre-season DTI scans of the selected person to generate whole-brain tractography via ExploreDTI using the default set of parameters for a deterministic streamline approach, which were selected for optimized performance.43 Tracts were propagated from all brain voxels as seed points following the direction of the principal diffusion orientation at each seed point and subsequent voxel with a 1 mm step size and linear interpolation. Tracts were terminated if FA fell below a specified threshold (0.2) or if the tract angle changed by more than 30 degrees. All tracts with lengths of 50 to 500
mm step size and linear interpolation. Tracts were terminated if FA fell below a specified threshold (0.2) or if the tract angle changed by more than 30 degrees. All tracts with lengths of 50 to 500 mm were retained, resulting in ~35 k fibers for the selected individual.
mm were retained, resulting in ~35 k fibers for the selected individual.
Voxel- and anatomically constrained fiber tract clustering
Intravoxel fibers traversing a given voxel were identified from the whole-brain tractography by testing whether any fiber sampling point fell inside the boundary of the corresponding hexahedral element converted from the voxel. Automatic clustering of fiber tracts/bundles based on anatomical ROIs is still an active, ongoing research topic. Here, we adopted an existing method44 to identify transcallosal fibers using the ICBM DTI-81 WM atlas45 as an anatomical constraint. This atlas is a stereotaxic probabilistic map averaged from 81 normal subjects with hand-segmented WM parcellation of 50 deep WM structures. The atlas is provided within a standard anatomical template (ICBM-152, isotropic image resolution of 1 mm45), which allows for transformation of a given individual's MRI and WM atlas into the same coordinates via affine registration. The registration was performed between the MPRAGE MRI of the individual selected for DHIM creation and the ICBM-152 template, using the ITK Segmentation and Registration Toolkit (Version 4.7; Fig. 2).
mm45), which allows for transformation of a given individual's MRI and WM atlas into the same coordinates via affine registration. The registration was performed between the MPRAGE MRI of the individual selected for DHIM creation and the ICBM-152 template, using the ITK Segmentation and Registration Toolkit (Version 4.7; Fig. 2).

Checkerboard images overlaying the individual's magnetic resonance image (appears lighter) with the coregistered ICBM-152 template (background; appears darker) on two axial planes (a,b). The alignment (arrows) suggests a satisfactory registration. A 10% randomly selected subset of the individual's fractional anisotropy-encoded, whole-brain tractography is shown in the ICBM-152 space (c). Color image is available online at www.liebertpub.com/neu
Transcallosal fibers from the whole-brain tractography were identified by testing whether they traversed the genu, splenium, or main body of the CC based on the ICBM DTI-81 WM atlas. This could be determined by first transforming the fiber sampling points into the WM atlas space and then rounding their coordinates to their closest voxels to perform a voxel-wise overlapping test.44 Alternatively, we converted CC voxels into hexahedral elements instead and directly tested whether real-valued coordinates of fiber sampling points fell inside the outer boundary of the aggregated hexahedral mesh. This avoided rounding errors and reduced the number of spuriously intersecting fibers.
To further minimize “outlier” fibers spuriously intersecting the target region, thresholding was performed based on the number of intersection points.44 Additional filtering based on geometry and tract self-consistency was also performed (e.g., by fitting each fiber into a plane to test its orientation, or by assessing the average distance from fiber sampling point relative to the tract centroid). For each CC subregion, less than 3% of the total number of fibers were considered spurious and were thus removed. This led to 1740, 2866, and 2661 fibers retained for the genu, splenium, and main body of the CC, respectively. The clustering process is illustrated in Figure 3.
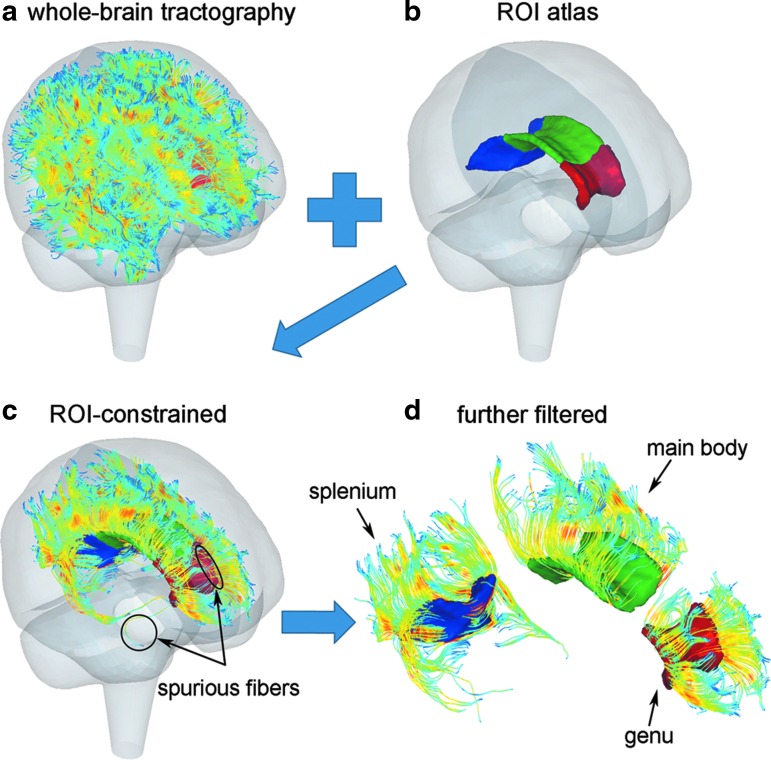
Illustration of anatomically or region of interest (ROI) constrained fiber tract clustering. (a) Fractional anisotropy-encoded whole-brain tractography overlaid within the Dartmouth Head Injury Model brain mesh boundary; (b) anatomical boundaries of the three corpus callosum subregions; (c) the resulting ROI-constrained transcallosal fiber tracts; (d) spurious fibers further filtered. A 10% randomly selected fiber sample is shown. Color image is available online at www.liebertpub.com/neu
Idealized head impacts
Brain responses corresponding to axial, coronal, and sagittal (anterior-to-posterior) rotations (Fig. 4a) were selected from an existing pre-computed brain response atlas (pcBRA32,46). The pcBRA employs triangulated 

Illustration of the three idealized head rotations (a) and the acceleration/velocity profile used for impact simulation (b).
For the selected brain responses, the 




 ms “hold” with zero
ms “hold” with zero 
The choice of this particular acceleration-only profile without deceleration was made to mimic actual on-field head impact data available, where a single largest acceleration peak dominates.50,51 Linear acceleration, 



Injury susceptibility index
For each WM DTI voxel, the accumulated peak 





The value of 
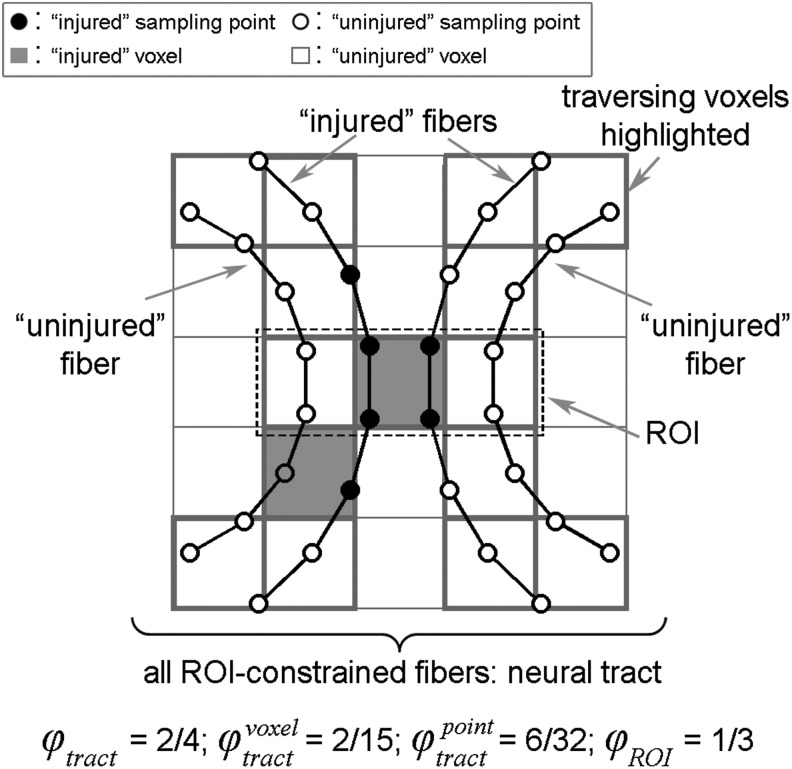
Quantifying WM structural integrity or the “likelihood” of injury locally at each voxel is important to correlate brain mechanical responses with neuroimaging at the voxel level. Nonetheless, it does not capture the degree of functional impairment of a neural pathway, which could be of interest for clinical symptomatic measures. Here, we considered an anatomically constrained fiber (i.e., a single streamline in tractography passing through a given ROI) as injured when at least one sampling point, regardless of the location — either within or outside the ROI boundary—has 



The injury susceptibility indices depend on a pre-defined injury threshold. For illustration purposes, here we selected two representative 


Strategies to assess tract-wise injury susceptibility
Effectively, 


and

The different WM injury susceptibility indices are illustrated in Figure 5.
Data analysis
Voxel-wise binary injury maps were created by considering voxels with 





For the three transcallosal fiber tracts, distributions of 









The computational time to obtain 
 =
= 64.3 k) for a 28 msec impact simulation using the voxel- and tractography-based approach was ~12
64.3 k) for a 28 msec impact simulation using the voxel- and tractography-based approach was ~12 min and ~66
min and ~66 min, respectively. The time to obtain
min, respectively. The time to obtain 
 min, which scaled approximately linearly when compared with running on a 10% subset. All data analyses were performed with in-house programs (not yet optimized) in MATLAB (R2014a; MathWorks, Natick, MA) on a 12-core Linux machine (Intel Xeon X5560, 2.80 GHz, 126 GB memory).
min, which scaled approximately linearly when compared with running on a 10% subset. All data analyses were performed with in-house programs (not yet optimized) in MATLAB (R2014a; MathWorks, Natick, MA) on a 12-core Linux machine (Intel Xeon X5560, 2.80 GHz, 126 GB memory).
Results
The voxel- and tractography-based approaches produced largely similar distribution patterns for real-valued 
 =
= 0; Fig. 6). Not surprisingly, the latter produced smoother distributions because more sampling points were used to compute an average
0; Fig. 6). Not surprisingly, the latter produced smoother distributions because more sampling points were used to compute an average 

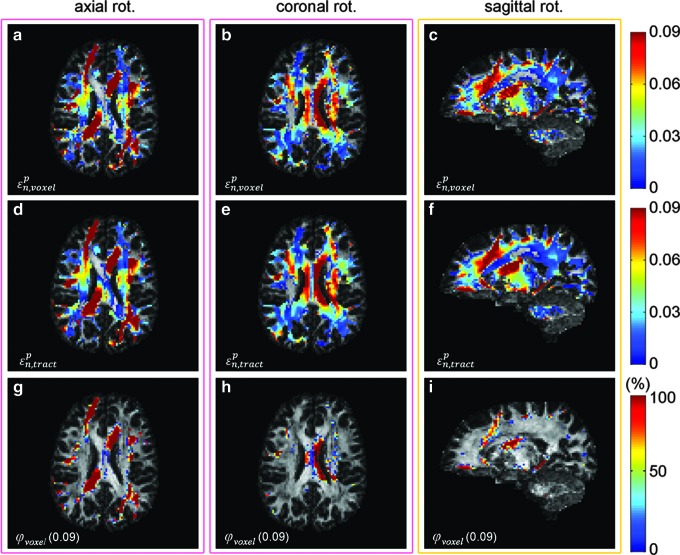
Maps of 
The tractography-based binary or dichotomous injury maps (thresholded from real-valued 




 <
< 0.01; Table 1). Interestingly, both approaches predicted a comparable extent of potential injury for the whole-brain WM voxels, or proportion of CC subregions affected, regardless of
0.01; Table 1). Interestingly, both approaches predicted a comparable extent of potential injury for the whole-brain WM voxels, or proportion of CC subregions affected, regardless of 
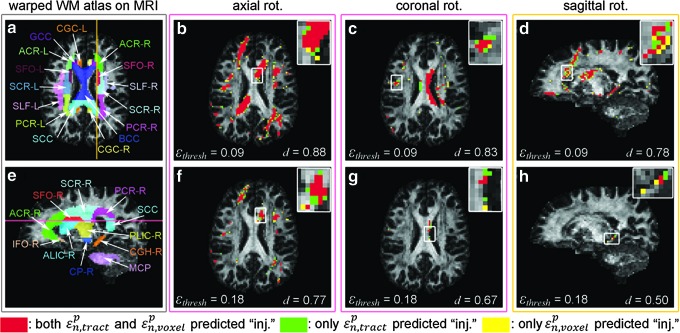
The ICBM-81 white matter (WM) atlas warped onto the individual's anatomical magnetic resonance image (MRI) (a and e; on axial and sagittal MRI, respectively). Binary injury maps overlaid on an axial (for axial (b and f) and coronal (c and g) rotations) and a sagittal (for sagittal rotation; d and h) MRI. “Injured” voxels (i.e., corresponding to 




Table 1.
Comparison of Predicted Distributions of Potential “Injury” Locations in Terms of Dice Coefficient, d, between the Voxel- and Tractography-Based Approaches at Two 
 | Axial | Coronal | Sagittal | Avg. | ||
|---|---|---|---|---|---|---|
| 0.09 | Dice coefficient, d | 0.86 | 0.81 | 0.76 | 0.81 | |
| FA | Both predicted “injury” | 0.51 ± ± 0.16 (8.6 k) 0.16 (8.6 k) | 0.51 ± ± 0.18 (3.0 k) 0.18 (3.0 k) | 0.48 ± ± 0.15 (3.2 k) 0.15 (3.2 k) | 0.50 | |
| Only one predicted “injury” | 0.34 ± ± 0.16 (2.7 k) 0.16 (2.7 k) | 0.40 ± ± 0.16 (1.4 k) 0.16 (1.4 k) | 0.41 ± ± 0.15 (2.0 k) 0.15 (2.0 k) | 0.38 | ||
| 0.18 | Dice coefficient, d | 0.74 | 0.62 | 0.63 | 0.66 | |
| FA | Both predicted “injury” | 0.51 ± ± 0.16 (1.7 k) 0.16 (1.7 k) | 0.44 ± ± 0.22 (126) 0.22 (126) | 0.40 ± ± 0.13 (83) 0.13 (83) | 0.45 | |
| Only one predicted “injury” | 0.42 ± ± 0.16 (1.2 k) 0.16 (1.2 k) | 0.37 ± ± 0.16 (152) 0.16 (152) | 0.33 ± ± 0.15 (96) 0.15 (96) | 0.37 |
FA, fractional anisotropy.
Voxels consistently predicted as “injured” by the two approaches had a mean FA value significantly higher than those predicted by one but not the other. The numbers of identified voxels for each case are shown in parentheses.
Table 2.
Summary of the Predicted Extent of Injury (as Percentages) for the Whole-Brain White Matter Voxels and the Three Corpus Callosum Subregions Using the Voxel- and Tractography-Based (in Parenthesis) Approaches at Two 
 | Axial % | Coronal % | Sagittal % | |
|---|---|---|---|---|
| Whole-brain | 14.84 (16.05) | 5.71 (5.99) | 6.19 (6.61) | |
| Genu | 35.53 (37.06) | 1.53 (2.01) | 2.20 (1.81) | |
| 0.09 | Main body | 15.61 (16.85) | 14.48 (15.31) | 0.95 (0.59) |
| Splenium | 27.04 (28.72) | 7.23 (7.48) | 3.18 (2.55) | |
| Whole-brain | 2.95 (4.12) | 0.29 (0.34) | 0.15 (0.25) | |
| Genu | 20.06 (23.30) | 0 (0) | 0 (0) | |
| 0.18 | Main body | 3.56 (4.57) | 0.83 (1.31) | 0 (0) |
| sSlenium | 0.12 (0.37) | 0 (0) | 0 (0) |
To further compare the two strain evaluation approaches, three representative voxels in the axial rotation were selected that were either consistently predicted as potentially injured by both techniques or by one but not the other (Fig. 8). Their 

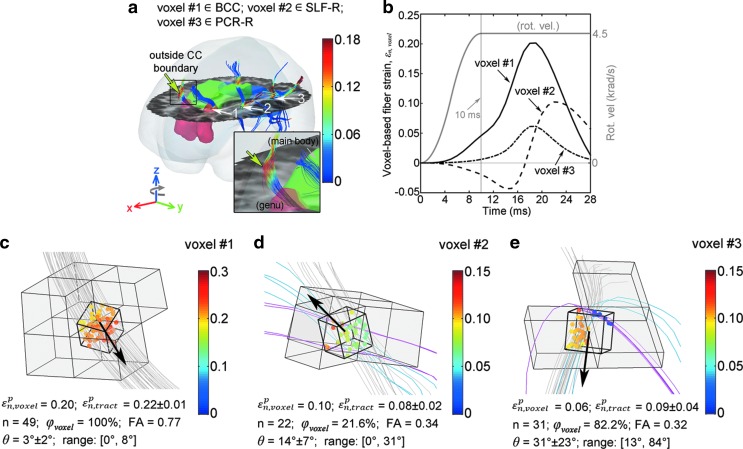
Illustration of 


 ±
± 35 on average (range 0–269) for whole-brain white matter voxels;
35 on average (range 0–269) for whole-brain white matter voxels; 


For the range of 






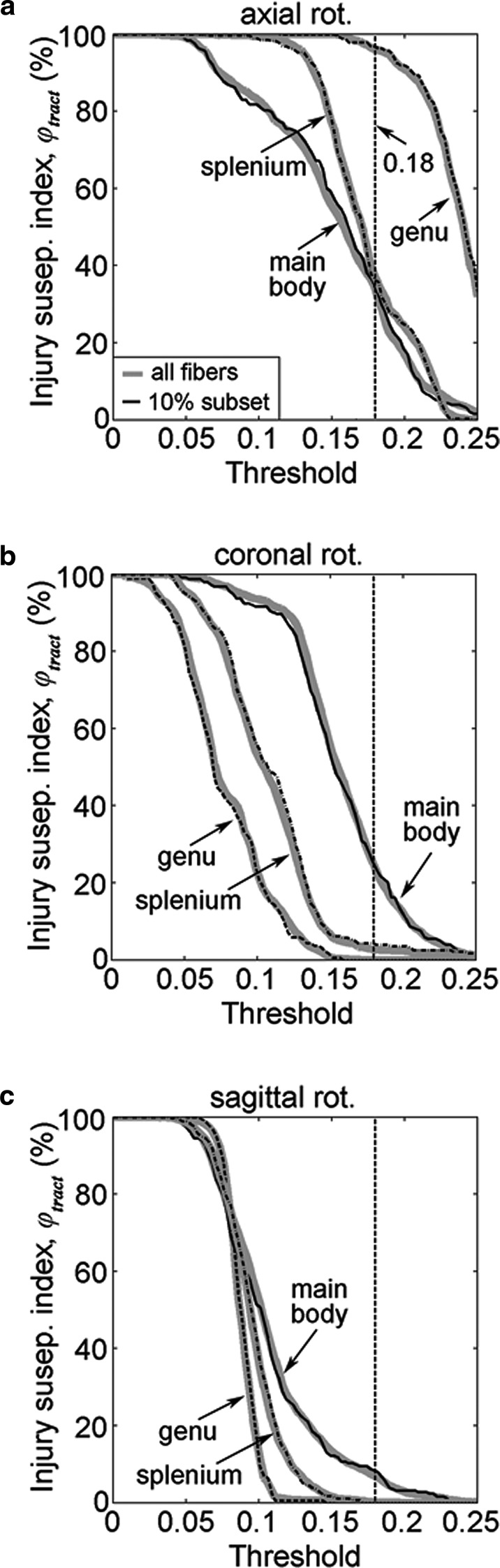
Tract-wise injury susceptibility index, 



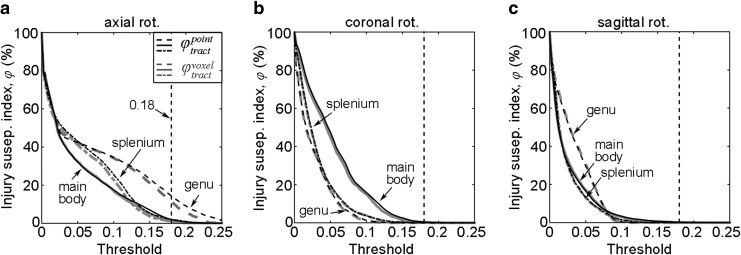
Injury susceptibility indices, 








Discussion
Recent brain injury studies suggest the importance of incorporating WM structural anisotropy for improved injury prediction performance.25 Here, we extended previous work that used average orientations on coarse elements18,20,21,27 or voxels22 to analyze accumulated peak fiber strain, 
 mm) sampling points, improving on the native DTI voxel resolution (2
mm) sampling points, improving on the native DTI voxel resolution (2 mm). More importantly, a tractography-based analysis allowed assessment of injury vulnerabilities of entire WM neural pathways, which is not possible with previous ROI-based methods.
mm). More importantly, a tractography-based analysis allowed assessment of injury vulnerabilities of entire WM neural pathways, which is not possible with previous ROI-based methods.
Assessing the mechanical responses of functionally important WM neural pathways may be of particular interest for future studies that correlate them with subtle changes in cognition for brains with or even without clinically diagnosed concussion.33,55 As an initial illustration, we have demonstrated this tractography-based technique using idealized head impacts in the context of sports-related concussion for all WM voxels as well as three transcallosal fiber tracts, with results compared with those from a voxel-based approach.
At the voxel level, a unique capability of our tractography-based technique that appears unachievable with an element/voxel-based analogue was to enable assessment of the “degree” (vs. dichotomy) of WM structural damage. This was quantified in terms of a voxel-wise injury susceptibility index (
This “graded” susceptibility (vs. a binary injury status) may provide a confidence measure in injury definition. For example, it could serve as a voxel selection criterion when comparing brain mechanical responses with longitudinal neuroimaging alterations (e.g., larger 

Interestingly, with an empirical injury susceptibility threshold of 50% to define a binary injury, the tractography-based approach predicted an extent of WM injury (i.e., volume fraction or number of injured voxels) comparable to that from the voxel-based technique for all cases evaluated (Table 2). This finding suggests a certain fundamental concordance between the two approaches. For a “binary” injury prediction based on the volume or number of injured WM voxels for the whole-brain, a DTI voxel-based method appears sufficient and may be preferred because of its relatively modest computation relative to the tractography-based analogue (~12 min vs. ~66
min vs. ~66 min in this work).
min in this work).
The two approaches can differ significantly, however, in terms of binary injury distribution after thresholding (despite the similar pattern of real-valued 

Regardless, another unique capability of our tractography-based technique is to assess injury susceptibilities for functionally important WM neural pathways, which does not appear feasible with a voxel-based approach. Because fibers serve as communication connections between functionally important cortical areas, injury assessment along their entire lengths (vs. confined within an ROI boundary) is likely critical to capturing the overall vulnerability of a given neural pathway. This is illustrated in Figure 8a (arrow), where potential injury locations with high 
The degree of damage to neural tracts can be similarly assessed with a tract-wise injury susceptibility index, which is essentially the proportion of potentially injured fibers, a measure intended to approximate that of “injured” axons.57 As an illustration, we computed 



The feasibility to down-sample while preserving 

The 




The current definition of 




WM injury directional dependency
Numerous model-based30,32,58 and animal59–61 injury studies have reported injury directional dependency. Our results were largely consistent with previous findings based on 



In the coronal rotation, the main body had the largest injury susceptibility. Contrary to earlier reports based on 
 cm3 and lateral width of 34
cm3 and lateral width of 34 mm vs. 10.5
mm vs. 10.5 cm3 and 12
cm3 and 12 mm, respectively).
mm, respectively).
While no injury was predicted in the CC anatomy in the sagittal rotation at the optimal 

Unlike a previous study that reported no injury in this rotation at the optimal threshold,21 we also identified a small amount (0.2–0.3%) as potentially injured (Table 2). The discrepancy may have been the result of differences in simulated head impacts. In addition, the simplified 2D head models of 21, coupled with fiber direction projections that were unable to capture intrinsic 3D brain deformations (vs. a realistic 3D model with actual 3D fiber directions in our study), may also be responsible.
Finally, the directional dependency found with 
WM injury susceptibility
An important purpose of our study was to propose WM injury susceptibility indices to assess local structural integrity and functional damage to individual neural pathways (

Further, the tract-wise susceptibility index may also serve as a quantitative indicator for the relative vulnerabilities of WM neural pathways. For example, because injury is assumed whenever high fiber strain occurred anywhere along an entire fiber length, regardless of the location, the tract-specific 

Limitations
Several limitations must be noted. First, while we have focused our effort here on developing a tractography-based fiber strain evaluation technique and compared it with a previous voxel-based counterpart, we did not use real-world injury cases to discern their potential differences in injury prediction performance. On the voxel-level, the two approaches appear to differ primarily in predicting WM injury location and spatial distribution (Fig. 7 and Table 1), rather than the extent or binary injury status of the whole brain, according to results from the three idealized head impacts (Table 2). Therefore, real-world injury/noninjury cases with neuroimaging available (as opposed to injured vs. noninjured status only)11,68 may be necessary to serve as an independent source of voxel-wise injury markers to correlate injuries with biomechanical findings.
Further investigations are needed to confirm the importance of a tractography-based approach and to verify the clinical significance of the WM injury susceptibility measures we established. These points will be the focus of future studies.
Second, there are limitations related to the neuroimaging data and tractography techniques currently available. Our tractography-based strain evaluation was based on ExploreDTI-generated tractography; however, it has been shown that different software packages can produce discordant results.69 Therefore, there is some uncertainty about the accuracy of tractography-based results, and there is a need to better understand the impact of tractography software packages and/or techniques/parameters on 
In addition, fibers from tractography are still much larger in dimension than axons, and they do not incorporate features such as neuronal plasticity or dynamic “rewiring” on injury29 that could be important to brain function as well. Regardless, we anticipate that our technique could be easily adapted when more advanced neuroimaging and/or more accurate tractography becomes available in the future.
Third, although our fiber sampling points were of high resolution (1 mm; generated from isotropic 2
mm; generated from isotropic 2 mm DTI voxels), the DHIM mesh is still relatively coarse (average element size of 3.3
mm DTI voxels), the DHIM mesh is still relatively coarse (average element size of 3.3 ±
± 0.79
0.79 mm; total number of 55.1 k). Because a nearest neighbor interpolation was adopted,22 the same strain tensor was used for all fiber sampling points within an element. Some resolution loss in
mm; total number of 55.1 k). Because a nearest neighbor interpolation was adopted,22 the same strain tensor was used for all fiber sampling points within an element. Some resolution loss in 
Conceptually, the same limitation applies equally to other studies that incorporate averaged fiber orientations derived from uniformly sized DTI voxels into (even coarser) FE elements that typically have a range of sizes across the brain with differing local orientations. For example, Sahoo and associates26 used isotropic 1 mm DTI voxels and 5320 brain elements of size 1.14–7.73
mm DTI voxels and 5320 brain elements of size 1.14–7.73 mm. In comparison, the KTH model coupled voxels of size 2
mm. In comparison, the KTH model coupled voxels of size 2 mm
mm ×
× 2
2 mm
mm ×
× 3.6
3.6 mm with 7128 brain elements, whose information on FE element size appears not available (albeit, anticipated to be comparable to the earlier example).27
mm with 7128 brain elements, whose information on FE element size appears not available (albeit, anticipated to be comparable to the earlier example).27
To mitigate this issue, a multiscale simulation approach—already performed in brain injury analysis17,19—can be employed. This is analogous to the “multiresolution” strategy widely adopted in medical image registration. In this case, our relatively coarse FE mesh (compared with the 1 mm fiber sampling points) could serve as an initial estimation of whole-brain responses, from which more targeted, potentially injured, regions can be localized. A second level simulation with locally refined mesh resolution can then be employed to potentially improve accuracy.11 Such a multiscale simulation strategy may offer an excellent compromise between accuracy and runtime. In addition, WM material anisotropy can also be incorporated at the microscale using explicit mesh representations, thereby avoiding the limitations in current studies that use rather coarse elements, as similarly envisioned.11
mm fiber sampling points) could serve as an initial estimation of whole-brain responses, from which more targeted, potentially injured, regions can be localized. A second level simulation with locally refined mesh resolution can then be employed to potentially improve accuracy.11 Such a multiscale simulation strategy may offer an excellent compromise between accuracy and runtime. In addition, WM material anisotropy can also be incorporated at the microscale using explicit mesh representations, thereby avoiding the limitations in current studies that use rather coarse elements, as similarly envisioned.11
A fourth limitation is that the injury susceptibility only incorporates strain and not strain rate, which could also be important.70 In addition, there may be regional differences in injury tolerance71 that were not considered. We anticipate, however, that our injury susceptibility indices could be extended to combine both strain and strain rate (i.e., resulting in a function dependent on both variables) and further incorporate regional injury thresholds when they become available for injury definition.
Fifth, our tract-specific injury analysis was only applied to three CC subregions as an illustration. Nevertheless, we anticipate that the technique could be extended to other neural pathways (as many as 130 according to some investigators72). The significant additional computational time (~28 min for the three transcallosal tracts, which is expected to scale with the number of tracts considered) could be a concern. This may be mitigated by tract down-sampling (e.g., using a 10% subset) to greatly reduce calculation time without significantly altering the results (Fig. 9). In addition, a pre-computation strategy may also be effective in the context of contact sports,32,46 because the head's impact temporal characteristics appear largely similar within or across subjects.50,51 On the other hand, when using realistic head impacts as model inputs, tract-specific injury susceptibility indices could allow assessment of the relative injury vulnerabilities of neural pathways to identify the most vulnerable ones in real-world injury scenarios. These will be the subjects of future investigations.
min for the three transcallosal tracts, which is expected to scale with the number of tracts considered) could be a concern. This may be mitigated by tract down-sampling (e.g., using a 10% subset) to greatly reduce calculation time without significantly altering the results (Fig. 9). In addition, a pre-computation strategy may also be effective in the context of contact sports,32,46 because the head's impact temporal characteristics appear largely similar within or across subjects.50,51 On the other hand, when using realistic head impacts as model inputs, tract-specific injury susceptibility indices could allow assessment of the relative injury vulnerabilities of neural pathways to identify the most vulnerable ones in real-world injury scenarios. These will be the subjects of future investigations.
Last, similarly to other works evaluating fiber strain,19,73 the DHIM uses a homogenous, isotropic material model for the entire brain. It does not yet incorporate material property heterogeneity74 or WM material anisotropy (vs. structural anisotropy) resulting from fiber reinforcement.26,27 While more sophisticated material properties for the brain may further enhance the model predictive power, we chose not to incorporate them in our current work for several practical reasons.
First, the fiber strain magnitude appears to be dominated by WM structural anisotropy rather than material anisotropy,54 suggesting that focusing on the former via tractography is appropriate for our current “technique development” study. Second, although the baseline DHIM is subject-specific, we intend to use it for population-based studies as well—e.g., via the pre-computed brain response atlas (pcBRA32,46,76). Unfortunately, a detailed population-based, “average” DTI or tractography atlas appears unavailable, and it is not feasible to create a subject-specific pcBRA for each athlete (e.g., hundreds), at least at present.
If material anisotropy is incorporated using DTI from a single specific person (e.g., as in the baseline DHIM) while incorporating structural anisotropy from different athletes' respective DTI/tractography, there could be unwanted challenges in result interpretation because of the mismatch between the baseline model material anisotropy and individualized structural anisotropy. Employing a homogeneous material for the brain, although it may not be ideal, avoids such difficulties, and appears appropriate. On the other hand, for individualized injury analyses (vs. population-based studies), incorporating WM material anisotropy may indeed be desirable. This appears relatively straightforward (e.g., via an existing Holzapfel-Gasser-Ogden model75 in Abaqus37); nevertheless, it requires fresh model validations.26,27 Given these considerations, it seems appropriate to incorporate DHIM with material anisotropy in a separate study in the future when suitable.
Regardless, incorporating transversely isotropic behavior for the WM may lower 
Conclusion
We have developed a tractography-based approach for fiber strain evaluation using voxel- or anatomically constrained whole-brain tractography. The technique potentially improves previous element-/voxel-based techniques because it evaluates strains along the entire lengths of fibers (as opposed to averages on coarse elements/voxels). In addition, this technique enables quantifying the “degree” of local WM structural integrity and injury susceptibilities of functionally important neural pathways, which are not possible with previous methods. Therefore, the tractography-based approach may be important to enable new brain injury analyses in the future.
Voxel- and tract-wise injury susceptibility indices were also established to assess local WM structural integrity and functional damage in neural pathways. Implications from the tract-wise injury susceptibility measure were consistent with previous neuropathological and DTI studies of TBI across a spectrum of injury severities. Potentially, therefore, our study may lay important foundations for follow-on investigations using real-world head impacts and actual brain injury/noninjury cases to explore the multifaceted mechanisms of DAI.
Future investigations will: (1) analyze real-world impacts to confirm the importance of the tractography-based approach and to verify the clinical significance of the WM injury susceptibility measures; (2) apply the technique to other WM neural pathways; and (3) use realistic head impacts to assess the relative injury susceptibilities of WM neural pathways and identify the most vulnerable ones in real-world injury scenarios.
Acknowledgments
Funding is provided by the NIH grants R01 NS092853, R21 NS088781 and R21 NS078607, and the Dartmouth Hitchcock Foundation (SJ). JF was supported, in part, by The Dartmouth Clinical and Translational Science Institute, under award number UL1TR001086 from the National Center for Advancing Translational Sciences (NCATS) of the NIH. The content is solely the responsibility of the author(s) and does not necessarily represent the official views of the NIH.
SJ conceived and designed the study, drafted the manuscript; WZ carried out the work, created the contents, and participated in article drafting; JF generated tractography; JF, LF, and TM offered critical insight on neuroimaging and neuropathology; TM provided neuroimaging necessary for the work. All authors discussed the study, revised the article, and gave final approval for its publication.
Author Disclosure Statement
No competing financial interests exist.
References
Articles from Journal of Neurotrauma are provided here courtesy of Mary Ann Liebert, Inc.
Full text links
Read article at publisher's site: https://doi.org/10.1089/neu.2015.4239
Read article for free, from open access legal sources, via Unpaywall:
https://europepmc.org/articles/pmc5079419?pdf=render
Citations & impact
Impact metrics
Citations of article over time
Alternative metrics
Smart citations by scite.ai
Explore citation contexts and check if this article has been
supported or disputed.
https://scite.ai/reports/10.1089/neu.2015.4239
Article citations
Diffusion Tensor Imaging Reveals Elevated Diffusivity of White Matter Microstructure that Is Independently Associated with Long-Term Outcome after Mild Traumatic Brain Injury: A TRACK-TBI Study.
J Neurotrauma, 39(19-20):1318-1328, 18 Jul 2022
Cited by: 17 articles | PMID: 35579949 | PMCID: PMC9529303
Real-time dynamic simulation for highly accurate spatiotemporal brain deformation from impact.
Comput Methods Appl Mech Eng, 394:114913, 09 Apr 2022
Cited by: 6 articles | PMID: 35572209 | PMCID: PMC9097909
Integrating material properties from magnetic resonance elastography into subject-specific computational models for the human brain.
Brain Multiphys, 2:100038, 09 Oct 2021
Cited by: 5 articles | PMID: 37168236 | PMCID: PMC10168673
Displacement voxelization to resolve mesh-image mismatch: Application in deriving dense white matter fiber strains.
Comput Methods Programs Biomed, 213:106528, 13 Nov 2021
Cited by: 3 articles | PMID: 34808529 | PMCID: PMC8665149
An anatomically detailed and personalizable head injury model: Significance of brain and white matter tract morphological variability on strain.
Biomech Model Mechanobiol, 20(2):403-431, 10 Oct 2020
Cited by: 40 articles | PMID: 33037509 | PMCID: PMC7979680
Go to all (26) article citations
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
White Matter Anisotropy for Impact Simulation and Response Sampling in Traumatic Brain Injury.
J Neurotrauma, 36(2):250-263, 10 Aug 2018
Cited by: 22 articles | PMID: 29681212 | PMCID: PMC6338585
Comparing a diffusion tensor and non-tensor approach to white matter fiber tractography in chronic stroke.
Neuroimage Clin, 7:771-781, 14 Mar 2015
Cited by: 42 articles | PMID: 25844329 | PMCID: PMC4375634
Group-wise evaluation and comparison of white matter fiber strain and maximum principal strain in sports-related concussion.
J Neurotrauma, 32(7):441-454, 06 Feb 2015
Cited by: 71 articles | PMID: 24735430 | PMCID: PMC4376290
Detection of white matter injury in concussion using high-definition fiber tractography.
Prog Neurol Surg, 28:86-93, 06 Jun 2014
Cited by: 15 articles | PMID: 24923395
Review
Funding
Funders who supported this work.
NINDS NIH HHS (3)
Grant ID: R21 NS078607
Grant ID: R01 NS092853
Grant ID: R21 NS088781
 1,,4
1,,4