Robust skull stripping using multiple MR image contrasts insensitive to pathology.

Roy S; Butman JA; Pham DL; undefined

doi:10.1016/j.neuroimage.2016.11.017

Robust skull stripping using multiple MR image contrasts insensitive to pathology.

Roy S ¹,

Butman JA ²,

Pham DL ¹,

Alzheimers Disease Neuroimaging Initiative

Affiliations

1. Center for Neuroscience and Regenerative Medicine, Henry M. Jackson Foundation, United States.
Authors
Roy S¹
Pham DL¹
(2 authors)
2. Center for Neuroscience and Regenerative Medicine, Henry M. Jackson Foundation, United States; Diagnostic Radiology Department, National Institute of Health, United States.
Authors
Butman JA²
(1 author)

ORCIDs linked to this article

Roy S | 0000-0002-7997-3993

Neuroimage, 15 Nov 2016, 146:132-147
https://doi.org/10.1016/j.neuroimage.2016.11.017 PMID: 27864083 PMCID: PMC5321800

Free full text in Europe PMC

Abstract

Automatic skull-stripping or brain extraction of magnetic resonance (MR) images is often a fundamental step in many neuroimage processing pipelines. The accuracy of subsequent image processing relies on the accuracy of the skull-stripping. Although many automated stripping methods have been proposed in the past, it is still an active area of research particularly in the context of brain pathology. Most stripping methods are validated on T₁-w MR images of normal brains, especially because high resolution T₁-w sequences are widely acquired and ground truth manual brain mask segmentations are publicly available for normal brains. However, different MR acquisition protocols can provide complementary information about the brain tissues, which can be exploited for better distinction between brain, cerebrospinal fluid, and unwanted tissues such as skull, dura, marrow, or fat. This is especially true in the presence of pathology, where hemorrhages or other types of lesions can have similar intensities as skull in a T₁-w image. In this paper, we propose a sparse patch based Multi-cONtrast brain STRipping method (MONSTR),² where non-local patch information from one or more atlases, which contain multiple MR sequences and reference delineations of brain masks, are combined to generate a target brain mask. We compared MONSTR with four state-of-the-art, publicly available methods: BEaST, SPECTRE, ROBEX, and OptiBET. We evaluated the performance of these methods on 6 datasets consisting of both healthy subjects and patients with various pathologies. Three datasets (ADNI, MRBrainS, NAMIC) are publicly available, consisting of 44 healthy volunteers and 10 patients with schizophrenia. Other three in-house datasets, comprising 87 subjects in total, consisted of patients with mild to severe traumatic brain injury, brain tumors, and various movement disorders. A combination of T₁-w, T₂-w were used to skull-strip these datasets. We show significant improvement in stripping over the competing methods on both healthy and pathological brains. We also show that our multi-contrast framework is robust and maintains accurate performance across different types of acquisitions and scanners, even when using normal brains as atlases to strip pathological brains, demonstrating that our algorithm is applicable even when reference segmentations of pathological brains are not available to be used as atlases.

Free full text

Neuroimage. Author manuscript; available in PMC 2018 Feb 1.

Published in final edited form as:

Neuroimage. 2017 Feb 1; 146: 132–147.

Published online 2016 Nov 15. https://doi.org/10.1016/j.neuroimage.2016.11.017

PMCID: PMC5321800

NIHMSID: NIHMS832658

PMID: 27864083

Robust Skull Stripping Using Multiple MR Image Contrasts Insensitive to Pathology

Snehashis Roy,^a,^* John A. Butman,^a,^b Dzung L. Pham,^a and for The Alzheimers Disease Neuroimaging Initiative¹

Author information Copyright and License information Disclaimer

The publisher's final edited version of this article is available at Neuroimage

See other articles in PMC that cite the published article.

Go to:

Associated Data

Supplementary Materials: NIHMS832658-supplement.pdf (256K)

Go to:

Abstract

We compared MONSTR with four state-of-the-art, publicly available methods: BEaST, SPECTRE, ROBEX, and OptiBET. We evaluated the performance of these methods on 6 datasets consisting of both healthy subjects and patients with various pathologies. Three datasets (ADNI, MRBrainS, NAMIC) are publicly available, consisting of 44 healthy volunteers and 10 patients with schizophrenia. Other three in-house datasets, comprising 87 subjects in total, consisted of patients with mild to severe traumatic brain injury, brain tumors, and various movement disorders. A combination of T₁-w, T₂-w were used to skull-strip these datasets. We show significant improvement in stripping over the competing methods on both healthy and pathological brains. We also show that our multi-contrast framework is robust and maintains accurate performance across different types of acquisitions and scanners, even when using normal brains as atlases to strip pathological brains, demonstrating that our algorithm is applicable even when reference segmentations of pathological brains are not available to be used as atlases.

Keywords: skull stripping, brain extraction, patches, atlas, segmentation, non-local, sparsity

Go to:

1. Introduction

Skull-stripping of magnetic resonance (MR) images is an important pre-processing step for most neuroimaging pipelines. Skull-stripping (or brain extraction) usually results in a binary brain mask of an MR image after removal of non-brain structures, such as eyes, fat, bone, marrow, and dura. Most skull-stripping methods are optimized and validated on T₁-w images, since high resolution T₁-w structural images are prevalent in clinical studies. Furthermore, T₁-w images provide excellent contrast between brain tissues, making it the leading imaging sequence for volumetric measurements. Subsequent post-processing steps, such as tissue segmentation, cortical labeling and thickness computations, are usually performed on stripped T₁-w images. The accuracy of the post-processing steps depends on the accuracy of skull-stripping. Incorrect inclusion of dura, sinus, or meninges, which have gray matter (GM) like intensities on T₁-w images, may result in systematic overestimation of gray matter or cortical thicknesses (van der Kouwe et al., 2008). Therefore accurate, automated estimation of brain masks is desirable, since manual delineations of brain masks, although considered gold standards, are time-consuming and prone to intra- and inter-rater variability.

There are two main categories of stripping methods that have been proposed in the past, edge based and template based. The first type of methods try to find an edge between brain and non-brain structures, since both brain and fat are isointense in T₁-w MRI, but the skull is dark. The Brain Extraction Tool (BET) (Smith, 2002) uses a deformable surface model which is initialized as a sphere at the center of gravity of the brain, and deformed until it reaches the brain boundary. Brain surface extraction (BSE) (Shattuck et al., 2001) employs series of image processing steps such as anisotropic diffusion, edge detection, and morphological filtering to detect the boundary. Another popular stripping tool in the AFNI^² package is 3dSkullStrip, which is a modified version of BET where robust measures are undertaken to distinguish between brain and skull. GCUT (Sadananthan et al., 2010) is a graph cut based tool that finds an initial brain mask by a threshold that is chosen as an intensity between GM and cerebro-spinal fluid (CSF) intensities via histogram analysis. Then narrow connections between brain and non-brain tissues, which consists primarily of CSF and skull, are removed to get the brain mask. Freesurfer (Dale et al., 1999) uses a hybrid combination of watershed and deformable surface evolution to robustly initialize the brain mask and subsequently improving it by local intensity correction using a probabilistic atlas. Other methods employ convolutional neural networks (Kleesiek et al., 2016), morphological filtering (Lemieux et al., 1999), region growing (Roura et al., 2014; Park and Lee, 2009), edge detection (Mikheev et al., 2008), watershed (Hahn and Peitgen, 2000), histogram threshold (Galdames et al., 2012; Shan et al., 2002), and level sets (Zhuang et al., 2006). Note that most of these algorithms are optimized for T₁-w images, although BET (Smith, 2002) and MARGA (Roura et al., 2014) can also work with T₂-w images.

While these methods are shown to be widely successful on healthy subjects, they tend to be less accurate when presented with pathology. Furthermore, their performance can vary significantly when applied to images from different sites, scanners, and imaging acquisition protocols (Iglesias et al., 2011; Boesen et al., 2004). To improve the robustness, the second type of stripping methods involve affine or deformable registrations with templates. ROBEX^³ (Iglesias et al., 2011) uses a random forest classifier to segment a brain mask after registering the subject to a template via affine registration, and then a point distribution model is fitted to the segmentation result to make sure the shape of the mask is reasonable. It is devoid of any tunable parameters and is robust on multiple inhomogeneous datasets. SPECTRE (Carass et al., 2007, 2011) uses a combination of registration and tissue segmentation. Multiple atlases, having manually drawn brain masks, are linearly registered to the subject image to create an initial estimate of the subject brain mask. Then the image is segmented into objects like GM, WM, CSF, bone, and background, and the segmentation is combined with the initial brain mask to compute the final mask. OptiBET (Lutkenhoff et al., 2014) is a modified version of BET, which was shown to be robust on pathological brains. Another modification of BET uses registration to an atlas to drive the deformable surface to the brain boundary (Wang et al., 2011).

Using the more recent label fusion techniques (Heckemann et al., 2006; Wang et al., 2013), multi-atlas deformable registration based stripping methods have been also been proposed. These methods, such as MASS (Doshi et al., 2013), MAPS (Leung et al., 2011), BEMA (Rex et al., 2004), Pincram (Heckemann et al., 2015), ANTs (Avants et al., 2011), and others (Serag et al., 2016; Shi et al., 2012), involve deformable registrations of multiple atlases to a target image. The atlases contain accurate, often manually or semi-automatically drawn brain masks. After registration, the brain masks are deformed to the subject space and fused together using joint label fusion (Wang et al., 2013), or STAPLE (Warfield et al., 2004). The accuracy of stripping depends on the accuracy of registrations. Therefore large number of atlases are usually needed to capture the wide variability in brain anatomy. As a result, these methods are time-consuming and computationally intensive (Eskildsen et al., 2012).

Multi-atlas label fusion based methods generally outperform the edge based methods both in terms of accuracy and robustness (Rehm et al., 2004). However, all of them are optimized for T₁-w images and validated on normal brains. In the presence of traumatic brain injury (TBI) and other pathologies such as tumors, there are two problems with multi-atlas label fusion. First, T₁-w images may not be optimal to detect brain boundary, since hemorrhages, tumors or lesions can have similar intensities as non-brain tissues; second, deformable registration may not be accurate enough or can be trapped in a local minima if atlases do not have similar lesions as the subject at a similar location of the brain.

Recently, non-local patch (Buades et al., 2005) based methods have been successful in many neuroimaging applications, such as tissue segmentations (Coupé et al., 2012; Hu et al., 2014; Roy et al., 2015b; Rousseau et al., 2011; Wang et al., 2014), classification (van Tulder and de Bruijne, 2015), lesion segmentation (Roy et al., 2014b, 2010b; Guizard et al., 2015), registration (Roy et al., 2014a; Iglesias et al., 2013), super resolution (Roy et al., 2010a; Manjon et al., 2010), intensity normalization (Jog et al., 2013, 2015; Roy et al., 2013b) and image synthesis (Roy et al., 2013a; Rousseau, 2008; Burgos et al., 2014; Roy et al., 2014c). A recent skull-stripping method, BEaST (Eskildsen et al., 2012) is based on non-local patch matching using multiple atlases. An atlas is composed of a T₁-w image and the brain mask. Atlases are transformed to the subject space via affine registration and an initial subject brain mask is estimated. Then for every patch within a narrow band around the initial estimated brain boundary on the subject T₁-w image, a search neighborhood is defined. Relevant patches from the registered atlases within that neighborhood are then collected and similarity weights are computed between each of those atlas MR patches and the subject MR patch. Corresponding atlas brain mask patches are combined by the same weights to generate a brain mask.

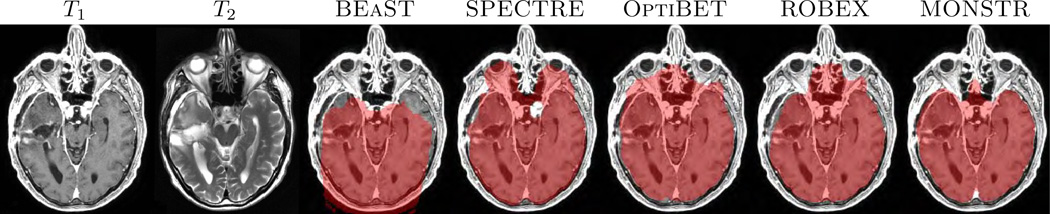
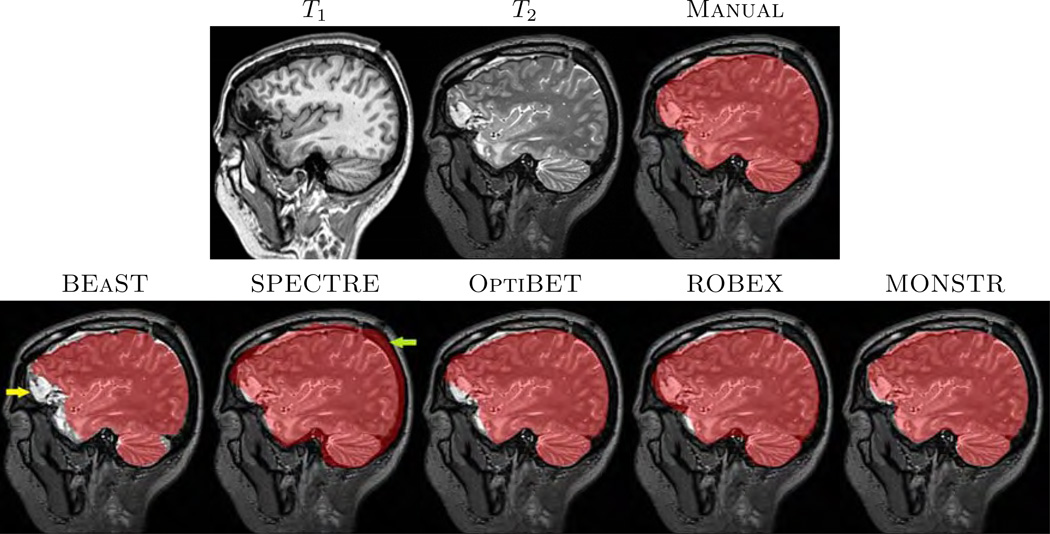
In most applications, it is imperative that brain masks include all lesions, so that subsequent tumor, hemorrhage segmentations, or even tissue segmentation methods (Ledig et al., 2015), perform optimally. An example is given in Fig. 1, where T₁-w and T₂-w images of one normal subject (Fig. 1(a)–(b)) and two patients with severe TBI and congenital malformations (Fig. 1(c)–(d)) are shown, along with brain masks obtained from 5 different methods, BEaST (Eskildsen et al., 2012), SPECTRE (Carass et al., 2011), OptiBET (Lutkenhoff et al., 2014), ROBEX (Iglesias et al., 2011), and our proposed Multi-cONtrast brain STRipping (MONSTR). Significant amount of skull and marrow is present on the normal subject for 4 methods, except the proposed one, because T₂ provides excellent contrast to distinguish skull from brain. For patients with TBI, T₂-w images provide better contrast for the blood and brain vs skull, while T₁-w images provide desired contrast for only one patient (Fig. 1(d)). Therefore inclusion of multiple contrasts or imaging sequences can provide better brain vs skull delineation. While BEaST underestimates the brain masks by removing all of the lesions, SPECTRE and ROBEX can overestimate the masks by including some skull and marrow, shown in Fig. 1(c)–(d), yellow arrow. T₂-w images can also provide better contrast to distinguish between brain and other non-brain tissues such as dura, marrow, meninges, and sinuses, which are dark in T₂ but have GM like intensities in T₁. Consequently, MONSTR generates a more accurate estimate of the brain masks by including the lesion and excluding the skull. A recent neural network based method (Kleesiek et al., 2016) addresses the stripping of images with tumors using multi-contrast data. However, the ventricular system, subarachnoid CSF and the tumors were excluded from the brain mask, keeping only GM and WM, which may not be suitable for further image processing tasks, such as the segmentation of tumors or quantification of the intracranial volume.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f1.jpg

Figure 1

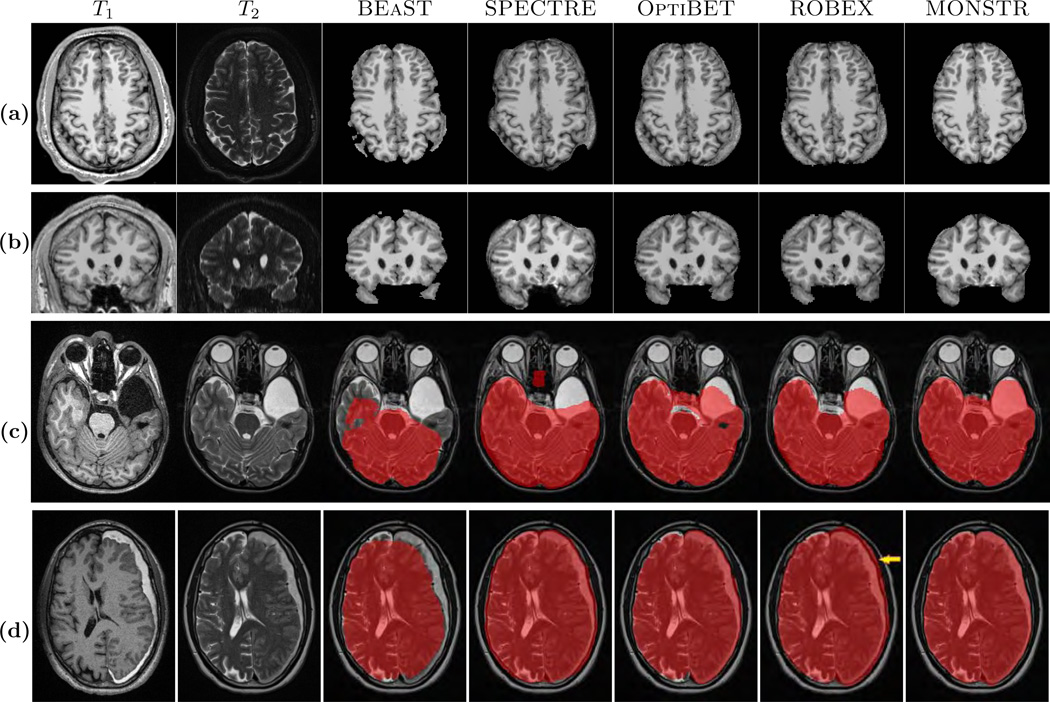
(a) and (b) show axial and coronal orientations of a healthy subject, where brainmasks from 5 different skullstripping methods, BEaST (Eskildsen et al., 2012), SPECTRE (Carass et al., 2011), OptiBET (Lutkenhoff et al., 2014), ROBEX (Iglesias et al., 2011), and our multi-contrast approach called MONSTR, are compared. MONSTR, which use both T₁ and T₂-w images, minimizes inclusion of extracranial tissues. Other methods include parts of skull and marrow. (c) shows a patient with congenital malformation and (d) with severe TBI. Note that lesions can be hypointense (c) or hyperintense (d) on T1-w images. BEaST removes both types of lesions from the mask, and other T1-w image based methods include parts of the skull (yellow arrow). MONSTR retains the lesions within the brain mask while including most of the intracranial tissues. The first two rows used T₁ images to demonstrate cases where segmentations erroneously included tissues outside of the brain (e.g. bone marrow). The bottom rows used T₂ images to better illustrate segmentation errors that did not include the entire intracranial vault (eg. CSF was outside the mask).

The proposed method MONSTR is a patch based method involving atlas registrations. An atlas consists of multiple image sequences, like T₁-w, T₂-w etc, and its binary brain mask. The brain mask includes CSF, GM, WM, and excludes skull, fat, eyes, dura, meninges, and sinuses. The atlases are first deformably registered to the subject. Then the corresponding atlas brain masks are transformed to the subject space to form an initial estimate of the subject brain mask. Then for every subject patch within a narrow band around the initial brain boundary, a neighborhood is found, and a sparse weight is computed for the atlas patches within that neighborhood based on the similarity between the subject patch and the atlas patches of the multiple MR sequences. Corresponding atlas brain mask patches are combined using the sparse weights to generate a probability function, which is thresholded at 0.5 to form a binary mask.

There are three main differences between our method and BEaST. First, BEaST only uses T₁-w images, while MONSTR can use multiple MR sequences, or other modalities e.g. CT. Second, for a particular subject patch, instead of choosing relevant patches based on local mean and standard deviations, we choose a sparse collection of patches based on an elastic net formulation (Zou and Hastie, 2005), which automatically selects a few relevant matching patches. Third, instead of using affine registration, the atlases are registered to the subject via a coarse deformable registration using ANTS (Avants et al., 2011); details are given in Sec. 2.3. The advantage of using an approximate deformable registration over affine is it provides a better initial brain mask while taking approximately the same amount of time.

Go to:

2. Materials and Method

2.1. Datasets

We used 6 datasets to validate our method, of which three are publicly available. The first dataset, referred to as ADNI-29, consists of 29 normal subjects obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (Mueller et al., 2005). They have T₁-w MPRAGE (GE 1.5T, T_R = 8.9 ms, T_E = 3.9 ms, T_I = 1 s, flip angle 8°, resolution 1.01 × 1.01 × 1.20 mm³) and T₂ (T_R = 3 s, T_E = 96 ms, flip angle 90°, resolution 0.94 × 0.94 × 3 mm³) images. Whole brain segmentations of these images were manually drawn on T₁-w images and provided by Neuromorphometrics^⁴. We used all non-zero voxels in the segmentations to generate the brain masks. Although 30 subjects were in the Neuromorphometrics database, we excluded one because it was a repeat scan.

The second dataset, referred to as NAMIC-20, obtained from NAMIC multimodality project^⁵, consists of 10 normal controls and 10 patients with schizophrenia. They have T₁-w spoiled gradient-recalled acquisition (SPGR) images (GE 3T, T_R = 7.4 ms, T_E = 3 ms, T_I = 600 ms, 10° flip angle, resolution 1 × 1 ×1 mm³), T₂-w (T_R = 2500 ms, T_E = 80 ms, resolution 1 × 1 × 1 mm³), and binary brain masks based on T₂-w images.

The third dataset, referred to as MRBrainS-5, obtained from the 2013 MRBrainS MICCAI grand challenge^⁶ (Mendrik et al., 2015), consists of 5 normal controls. They have T₁-w MPRAGE (Philips 3T, T_R = 7.9 ms, T_E = 4.5 ms, resolution 1 × 1 × 1 mm³) and T₂ FLAIR (T_R = 11 s, T_E = 125 ms, T_I = 2.8 s, resolution 0.96 × 0.96 × 3 mm³) images. 3-class segmentations (CSF, GM, WM) were provided, and we used non-zero voxels from the segmentations to generate brain masks.

The fourth dataset, referred to as TBI-19), is in-house and consists of 19 patients with mild to severe TBI. They have T₁ MPRAGE, both precontrast and postcontrast, (Siemens 3T, T_R = 2.53 s, T_E = 3.03 ms, T_I = 1.1 s, flip angle 7°, resolution 1 × 1 × 1 mm³), and T₂-w (T_R = 3.2 s, T_E = 409 ms, flip angle 120°, resolution 0.49 × 0.49 × 1 mm³) images. T₂ and postcontrast T₁ images were rigidly registered (Avants et al., 2008) to the MPRAGE, and binary brain masks were drawn on the registered T₂-w images.

The fifth dataset contains 32 patients with various movement disorders (called MOV-32). The scans consist of T₁-w MPRAGE (Philips 3T, T_R = 8.1 ms, T_E = 3.7 ms, flip angle 8°, resolution 0.94 × 0.94 × 1 mm³), T₂-w (T_R = 2.5 s, T_E = 235 ms, flip angle 90°, resolution 0.98 × 0.98 × 1.1 mm³), and CT (Siemens, 120kVp, dimensions 512 × 512 × 247, resolution 0.5 × 0.5 × 1 mm³). These images do not contain any focal lesions or tumors. There are no manual brain masks available for this dataset. We chose this dataset so as to compare the different stripping methods independently via CT, as CT provides excellent contrast between brain and bone.

The sixth dataset, referred to as TUMOR-36, consists of 36 patients with tumors. Instead of using pre-contrast images as before, this dataset contains postcontrast T₁-w images (Philips 3T, T_R = 4.9 ms, T_E = 2.2 ms, flip angle 15°, resolution 0.94 × 0.94 × 1 mm³), T₂-w (T_R = 3375 ms, T_E = 100 ms, flip angle 90°, resolution 0.43 × 0.43 × 5 mm³), and CT (Siemens Biograph128 PET/CT, 120kVp, dimensions 512 × 512 × 149, resolution 0.59 × 0.59 × 1.5 mm³). We show that our method is robust and can be generalized across different MR acquisition protocols when other methods can have gross failures and inaccuracies, because they are not optimized for postcontrast images.

For visual demonstration, 6 patients with severe TBI and congenital malformations from an acute study are chosen to show the comparison of MONSTR with competing methods. For this dataset, called Acute, there is no manual ground truth available. The images are shown in Fig. 1(c)–(d) and Fig. 10 for visual comparisons only. There are MPRAGE (1 × 0.94 × 0.94 mm³) and T₂-w (0.5 × 0.5 × 4 mm³) images available for this dataset.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f10.jpg

Figure 10

The figure shows comparison of skull stripping performance in the presence of large arachnoid cysts and extraxial fluid collections/hematomas in various locations. Four cases from the Acute dataset (see Sec. 2.1 for details) are presented, where original MPRAGE and T₂-w images are shown. (a) shows a large infarct and an overlying extraaxial fluid collection. Only MONSTR completely segments the intracranial contents. (b) shows two extraaxial collections, a chronic subdural hematoma on the right and a subacute epidural hematoma on the left. (c) shows a large posterior fossa arachnoid cyst/mega cisterna magna. (d) shows a large middle cranial fossa arachnoid cyst. MONSTR virtually completely segments the intracranial contents in (a)–(c), and nearly completerly segments in (d), where the performance of MONSTR is still superior in comparison to the other methods.

For all datasets, both T₁-w and T₂-w images (postcontrast T₁ for TUMOR-36) are used to generate the brain masks. Some postcontrast T₁ images from TBI-19 dataset are used as atlases here. See Sec. 3.7 for details. If available, other image sequences such as PD or FLAIR, can also be used in the algorithm. In our use, the combination of T₁-w and T₂-w images provided excellent results without the need for additional contrasts.

There is usually no unifying definition of what should be included or excluded in the stripping protocol. For example, BET (Smith, 2002) and BSE (Shattuck et al., 2001) include some part of the brainstem, SPECTRE (Carass et al., 2011) includes the transverse and sagittal sinuses in the brainmask, while BEaST (Eskildsen et al., 2012) excludes them. ROBEX and SPECTRE include the subarachnoid CSF in the brainmasks, but BEaST is generally more aggressive in removing CSF, especially near the parietal lobe. In this paper, while delineating the brainmasks of TBI-19 data, we included subarachnoid CSF, GM, WM, ventricles (lateral, 3rd, 4th), and cerebellum in the brainmask, but excluded the sinuses, eye, fat, skull, dura, and bones. The brainmasks of NAMIC-20 and MRBrainS-5 data already conform to this definition. This definition is consistent with what many would consider to be the intracranial volume, a useful measure for normalization in volumetric analyses (Malone et al., 2015).

2.2. Preprocessing

The brain masks are generated in the space of the T₁-w images. T₂-w images are rigidly registered (Avants et al., 2011) to the T₁-w images. For robustness in registration, necks were removed from the images using FSL robustfov. All MR images are corrected for intensity inhomogeneities by N4 (Tustison et al., 2010). Since the scaling of MR image intensities is not standardized, the images were scaled linearly so that the modes of the WM intensities of T₁ and T₂ images were set to the values of 1 and 2, respectively. The modes were automatically detected using a kernel density estimator (Pham and Prince, 1999). T₂-w images set to a higher intensity scale than T₁-w images to give them a higher weight in the subsequent patch matching, since they usually provide superior contrast to distinguish brain and CSF from skull and dura.

2.3. Method

The proposed method uses a combination of registration and patch matching. Following a coarse registration, patches from the subject are matched to similar patches from atlases. A patch is defined as a p×q×r 3D sub-image around a voxel. Typically p = q = r, and we used 3 × 3× 3 patches in our experiments. A subject is defined as a collection of images {s₁, …, s_M}, where M is the number of image contrasts. In our case, we used T₁-w and T₂-w contrasts, therefore M = 2. All s_k, k = 1, …, M, are assumed to be coregistered. A subject patch at the i^th voxel is denoted by s(i). We define s(i) to be a concatenation of the i^th patches from each of the M contrasts, hence s(i) [set membership] ^{Md × 1}, where d = pqr. An atlas is a collection of M + 1 images, ${a_{1}^{(t)}, \dots, a_{M}^{(t)}, a_{M + 1}^{(t)}}$ , Where $a_{k}^{(t)}$ , k = 1, …, M are the MR images for the t^th atlas, and $a_{M + 1}^{(t)}$ denotes the binary brain mask, t = 1, …, T, T being total number of atlases. The atlas MR patch at the j^th voxel, denoted by $a_{1}^{(t)} (j)$ , is the concatenation of M patches at voxel j from each of $a_{k}^{(t)}$ , k = 1, …, M, $a_{1}^{(t)} (j) \in ℝ^{M d \times 1}$ . The j^th patch of the brain mask $a_{M + 1}^{(t)}$ is denoted by $a_{2}^{(t)} (j) \in ℝ^{d \times 1}$ . The elements of $a_{2}^{(t)} (j)$ are 0 and 1. Without loss of generality, we assume that s₁ and $a_{1}^{(t)}$ are T₁-w images.

As mentioned earlier in Sec. 1, $a_{1}^{(t)}$ is registered to s₁ via “approximate ANTS”. The parameters used are shown in Table 1. Essentially, after the affine step, the deformable registration SyN is applied on the subsampled (by 4) $a_{1}^{(t)}$ with 100 iterations. The rest of the parameters are set as default. This approximate ANTS takes about 2 minutes between two 256 × 256 × 160 images having 1 mm³ resolution on Intel Xeon 2.80GHz 20-core processors. On the same setting, FLIRT (Jenkinson and Smith, 2001) takes about 1.5 minutes, MINC bestlinreg s (Collins et al., 1994) takes about 2.5 minutes, ANTS with affine setting (antsaffine.sh) takes about 30 seconds, and IRTK^⁷ areg2 takes about 1.5 minutes. Note that only ANTS takes advantage of parallel processing, while other registration methods use a single core. We chose to use a coarse deformable registration because it provides better matching than affine, while taking similar computation time as other popular affine registration tools. Also, by using SyN with only a few iterations on subsampled images, local minima can be avoided, especially when images have significant pathology as shown in Fig. 1.

Table 1

Approximate ANTS parameters are shown in this table.

Transform `-t`	Metric `-m`	Iterations `-m`	Smoothing Sigma `-s`	Shrink Factor `-f`
Rigid	Mattes	100 × 50 × 25	4 × 2 × 1	3 × 2 × 1
Affine	Mattes	100 × 50 × 25	4 × 2 × 1	3× 2 × 1
SyN	CC	100 × 1 × 0	1 × 0.5 × 1	4 × 2 × 1

Once the atlases $a_{1}^{(t)} s$ are registered to s₁, the corresponding atlas images and brain masks $a_{2}^{(t)}, \dots, a_{M + 1}^{(t)}$ are also transformed to the subject space using the same deformation. For simplicity of notation, from now on, we denote the registered atlases by ${a_{1}^{(1)}, \dots, a_{M + 1}^{(t)}, t = 1, \dots, T}$ . A thresholded version of the average of the registered atlas brain masks ${a_{M + 1}^{(1)}, \dots, a_{M + 1}^{(T)}}$ at 0.5 provides an initial estimate of the subject brain mask. To reduce computational overhead, voxels within a narrow band of the initial estimated brain boundary are considered. An example is shown in Fig. 2, where 4 atlases are registered to a subject, and the average of the transformed atlas brain masks are overlaid on the subject. The average is thresholded at 0.5 to generate the initial subject brain boundary. A narrow band size parameter of w, defined in voxel units, controls the amount of dilation and erosion of the subject brain mask are matched to atlas patches. The size of the narrow band is estimated using a cross-validation strategy, as described later in Sec. 3.1.2.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f2.jpg

Figure 2

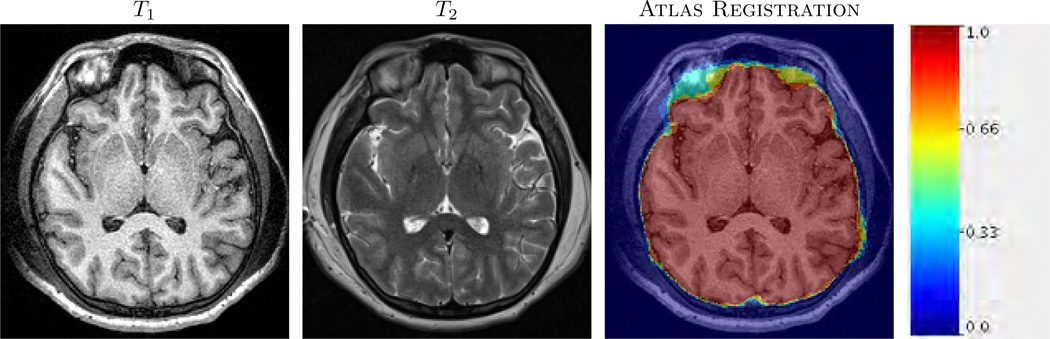
An example of T₁-w, T₂-w and registered atlases are shown. 4 atlases are registered via approximate ANTS (see Sec. 2.3) to a subject T₁-w image. The average of the transformed atlas brain masks are overlaid on the subject. The color indicates initial fuzzy brainmask.

For a patch at voxel i within that narrow band, a neighborhood N_i of radius s is first defined, where N_i is a 3D neighborhood of size (2s + 1) × (2s + 1) × (2s + 1) with the center voxel being i. Next, for the subject patch s(i), a few relevant atlas patches are chosen from the set ${a_{1}^{(t)} (j), j \in N_{i}, t = 1, \dots, T}$ using a sparse matching criteria that we now define mathematically. For every subject patch s(i), an atlas MR patch collection A₁ (i) and brain mask patch collection A₂ (i) can be defined as the collection of all atlas MR and brain mask patches in the neighborhood N_i as follows,

A_{1} (i) = [[a_{1}^{(1)} (j)], \dots, [a_{1}^{(T)} (j)]],

A_{2} (i) = [[a_{2}^{(1)} (j)], \dots, [a_{2}^{(T)} (j)]], j \in N_{i}, A_{1} (i) \in ℝ^{M d \times | N_{i} | T}, A_{2} (i) \in ℝ^{M \times | N_{i} | T}

(1)

where |N_i| = (2s + 1)³ is the total number of voxels within the neighborhood. Each $[a_{1}^{(t)} (j)]$ is a M d × |N_i| matrix of all MR patches within N_i from the t^th atlas. Similarly $[a_{2}^{(t)} (j)]$ are brain mask patches. Therefore A₁(i) contains all MR atlas patches within N_i from T atlases. Since the subject and atlases are registered, we assume that given a sufficient number of atlases and a large enough neighborhood size s, it is likely a few atlas patches from A₁(i) can be found that are similar to s(i), and their convex combination produces the subject patch s(i). The sparse patch matching criteria (Roy et al., 2015a) is written as,

s (i) \approx A_{1} (i) x (i), x (i) \geq 0, x (i) \in ℝ^{| N_{i} | T \times 1}, {‖ x (i) ‖}_{0} ≪ | N_{i} | T,

(2)

where x(i) is a sparse vector containing positive weights for a few similar patches, and is zero otherwise, indicated by the small [ell] ₀ norm, i.e., number of non-zero elements. The non-negativity constraint on x(i) enforces similarity between textures of s(i) and the contributing atlas patches.

Since a direct solution of Eqn. 2 requires combinatorial complexity (Donoho, 2006), we use elastic net regularization (Zou and Hastie, 2005) to solve Eqn. 2 by minimizing both [ell] ₁ and [ell] ₂ norm of x(i),

x (i) = {argmin}_{α} {‖ s (i) - A_{1} (i) α ‖}_{2}^{2} + λ_{1} {‖ α ‖}_{1} + λ_{2} {‖ α ‖}_{2}^{2}, α \geq 0 .

(3)

The first term ensures that the subject patch matches to the convex combination of atlas patches. The second term allows only a few atlas patches to be selected, while the third term is a ridge regression penalty. Penalizing both the [ell] ₁ and [ell] ₂ norm enforces grouping of several similar looking atlas patches (Zou and Hastie, 2005), while keeping the total number of chosen patches (i.e. having non-zero weight) low. Eqn. 3 is solved using the SPASM^⁸ toolbox (Mairal et al., 2014). To get a meaningful estimate of x(i) from Eqn. 3, the vector s(i) and columns of A₁(i) are normalized to have unit [ell] ₂ norm (Roy et al., 2013a). The parameters λ₁ and λ₂ were both fixed at 0.01, which empirically provided a stable solution for a wide variety of experiments.

For every patch within the narrow band, once the sparse weight x(i) is computed, corresponding brain mask patches were combined using the same weight as,

\hat{s} (i) = A_{2} (i) x (i),

(4)

where ŝ(i) is a membership value between 0 and 1 representing the bain mask at the i^th voxel. After the brain mask membership is computed, it is thresholded at 0.5. As a brain-skull boundary is biologically expected to be smooth, the boundary of the mask is smoothed (Desbrun et al., 1999) so that the maximum curvature of the boundary does not exceed 0.3. Smoothing has little impact on numerical performance, but produces qualitatively more realistic boundaries.

2.4. Optimization of competing methods

OptiBET uses FSL atlases for registration purposes but not for training data, hence we did not change it on every dataset for OptiBET. The ROBEX package includes its own atlas, which is not easy to modify. We were not able to determine how to use an external atlas with ROBEX. Nonetheless, ROBEX with its default atlases has been shown to be robust and accurate across datasets with variable scanners. The other methods were tested under the same training data conditions. For every dataset (except TBI-19, see Sec. 3.5 for details), we randomly chose 4 subjects within that dataset as atlases in SPECTRE, BEaST, and MONSTR, and skullstripped the remaining using those atlases. For BEaST, since left-right flipped atlases are used in conjunction with the originally provided atlases, the effective number of atlases is 8. Although BEaST and MONSTR use actual image intensities from atlases for computing the final mask, SPECTRE uses them only for registration and initial brain mask generation.

2.5. Evaluation Criteria

For the ADNI-29, NAMIC-20, and TBI-19 datasets, the manual ground truth masks are available. Therefore we used two metrics, Dice and average symmetric surface distance (d_S). Dice coefficient between two binary images A and B is defined as $\frac{2 | A \cap B |}{| A | + | B |}$ , where |·| indicates number of non-zero voxels. The average symmetric surface distance d_S (Geremia et al., 2011) between two masks M₁ and M₂ is defined as

\frac{\sum_{x \in \partial (M_{1})} min_{y \in \partial (M_{2})} d (x, y) + \sum_{x \in \partial (M_{2})} min_{y \in \partial (M_{1})} d (x, y)}{| M_{1} \cup M_{2} |},

(5)

where ∂(M₁) and ∂(M₂) indicate boundaries of M₁ and M₂, d(·, ·) indicates Euclidean distance. This is a robust and symmetric modification of the Hausdorff distance.

For the TUMOR-36 and MOV-32 datasets, manual brain masks are not available. Therefore we used CT to independently validate the masks. CT is not actually used in the computation of the brainmasks, rather it is only used for validation. CT images of each subject were rigidly (Avants et al., 2008) registered to the corresponding T₁. Note that any systematic registration errors from rigid registration would affect the performance of all methods equally. Hounsfield units (HU) at a voxel indicates if the voxel is soft tissue (< 150) or bone (> 300). Based on CT, we define a metric based on the percentage of boundary voxels that are erroneous, i.e., the ratio between the boundary voxels that are completely within bone or brain and the total number of boundary voxels. Fig. 3(a)–(c) shows T₁-w, T₂-w and CT scans of a patient from the MOV-32 dataset. A brain mask from BEaST is overlaid on the CT image (Fig. 3(c)). For every voxel on the boundary (black boxes in Fig. 3(d)), we define a 3 × 3 × 3 neighborhood (Fig. 3(e)). The ratio between the median CT HU of the “outside voxels” (red boxes) and inside voxels (yellow boxes) is computed for the center voxel (black boxes), which lies on the brain mask boundary. For an accurate boundary, the computed number is the ratio between average bone HU and average soft tissue HU, such as voxel #1 in Fig. 3(d). For under-estimation (e.g., voxel #2), both the median HU numbers are from brain, while for over-estimation both numbers will be from bone. For both under and over-estimations, the ratio is ≈ 1. Therefore if it is [dbl greater-than sign] 1, then that brain mask boundary voxel (voxel #1 in Fig. 3(d)) should be accurate and should lie on the true brain-skull boundary. We compute the percentage of boundary voxels that have a ratio ≤ 1.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f3.jpg

Figure 3

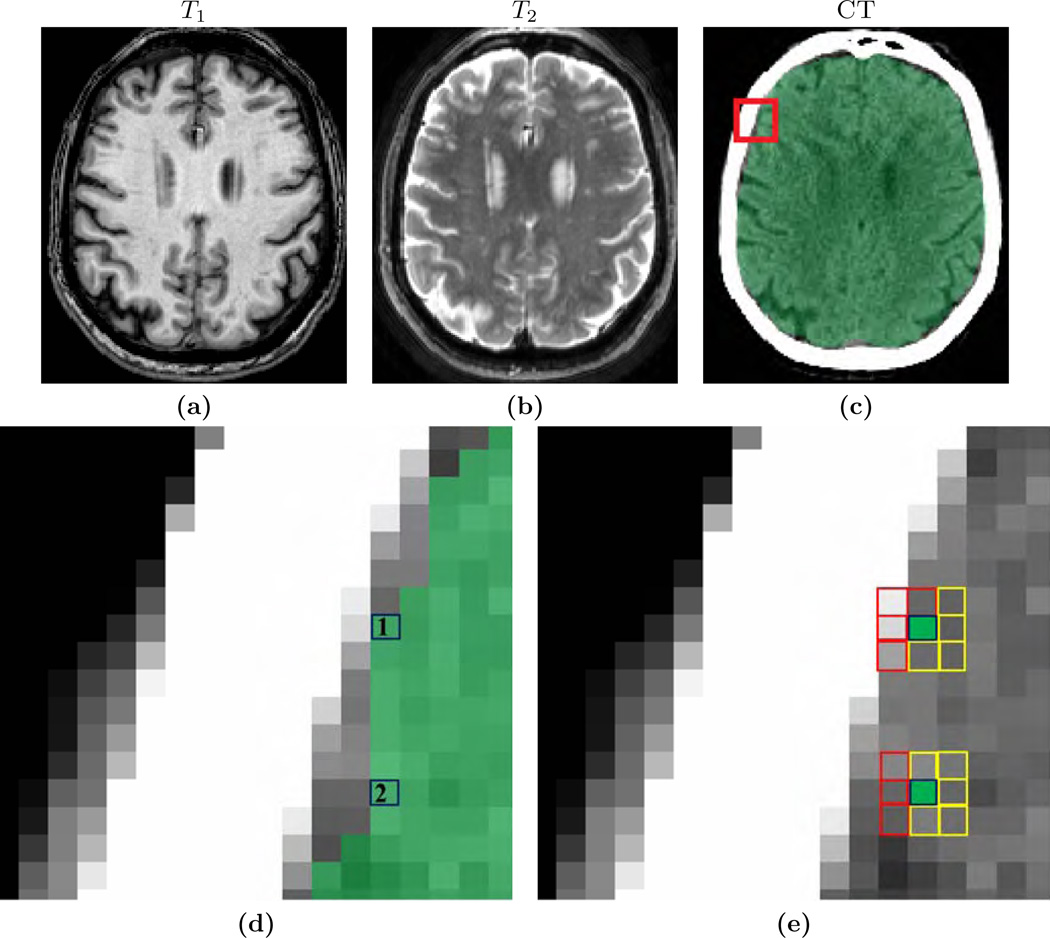
The figure shows an independent evaluation scheme of brain masks via CT images. (a)–(b) show T₁-w and T₂-w images of one patient from MOV-32 dataset, where the brain mask from BEaST is overlaid on (c) the CT. A zoomed view of the CT is shown in (d), where two voxels on the brain mask boundary are considered (black boxes). A 3 × 3 × 3 neighborhood is chosen for each boundary voxel. In that neighborhood, “inside” and “outside” voxels (yellow and red boxes, respectively), are considered, as obtained from the binary mask,. The ratio of median CT intensities of “outside voxels” (red boxes) and “inside voxels” (yellow boxes) is computed for every boundary voxel. If the ratio [dbl greater-than sign] 1 (e.g., upper voxel #1), then that voxel (#1) is on brain-skull boundary. If the ratio ≈ 1 (e.g., lower voxel #2), then it is completely within brain or within bone. A high ratio is desired for a good stripping mask. See Sec. 2.5 for details.

Go to:

3. Results

In our experiments, the run-times of BEaST, SPECTRE, OptiBET and MONSTR are similar, averaging 15 – 20 minutes for 1 mm³ resolution images on a server with two Intel Xeon 2.80GHz 10-core processors. ROBEX takes only 3 – 4 minutes, mostly because the generative model is pre-computed unlike the other methods, which compute their own models on-the-fly. For MONSTR, 4 registrations take about 8 minutes, and 8 – 10 minutes are spent on patch-matching. MONSTR and ROBEX are optimized to use multiple cores, while BEaST, OptiBET, and SPECTRE are not.

Some parameter tuning was also performed for SPECTRE and BEaST to achieve optimal results. ROBEX does not offer any free parameters and we were unable to determine how to modify its atlas. We varied the number of atlases for SPECTRE but its performance did not vary greatly because the atlases are only for obtaining initial brain masks. We also optimized parameters for BEaST and found that the default parameters were most robust. Although our experiments used 4 atlases with BEaST, in the supplemental material we evaluate its performance with additional atlases. OptiBET was run with default atlases and parameters. All statistical comparisons were performed with paired Wilcoxon signed rank test.

This section is organized as follows. First, we evaluate the number of atlases and the search radius in Sec. 3.1. Then we compare MONSTR with the other 4 methods, BEaST, SPECTRE, OptiBET, and ROBEX, in Sec. 3.2–3.7 on the 6 datasets as described in Sec. 2.1. Next, we evaluate the differences in performance of MONSTR between using only the T₁ contrast and the addition of multiple contrasts in Sec. 3.8. The effect of resolution on the stripping result is then explored in Sec. 3.9. Finally, the effect of choosing atlases from different scanners, acquisition protocols, or resolutions, other than ones from the same dataset, is described in Sec. 3.10.

3.1. Parameter Optimization

The algorithm has 4 important parameters: patch size, the number of atlases T, the size of the narrow band around the initial brain boundary, and the radius (s) of the search neighborhood N_i. In practice, we chose the width of narrow band to also be s to reduce number of parameters. The patch size is kept fixed at 3 × 3 × 3, because we have experimentally found that increasing patch size to 5³ or higher exponentially increases the required memory and computation time, while not significantly improving the stripping results. In this section, we describe a cross validation strategy to estimate these parameters T and s. We used the ADNI-29 dataset because it has the highest number of subjects with manual brain masks. To estimate each parameter, we keep the other ones fixed. Approximate ANTS parameters (Table 1) are empirically chosen so as to keep the runtime similar to an affine registration, as described in Sec. 2.3.

3.1.1. Number of Atlases

The number of atlases is an important parameter in most skull-stripping methods. As mentioned earlier, label fusion based methods (Doshi et al., 2013; Heckemann et al., 2015; Leung et al., 2011) need significantly larger number of atlases compared to patch based methods. For example, the suggested number of atlases is 60 in Pincram (Heckemann et al., 2015). This is because registration algorithms are not always able to obtain accurate results due to anatomical variability, and more atlases are needed to compensate. In comparison, we show that MONSTR needs only a few atlases, partly because the patch matching step reduces the dependency on accurate registrations for voxel based fusion. We arbitrarily chose 6 subjects as atlases, and generated the brain masks for the remaining 23 using 1 – 6 atlases. The narrow band width around the initial boundary and the patch search window size was fixed at s = 5 voxels (11 × 11 × 11 search window).

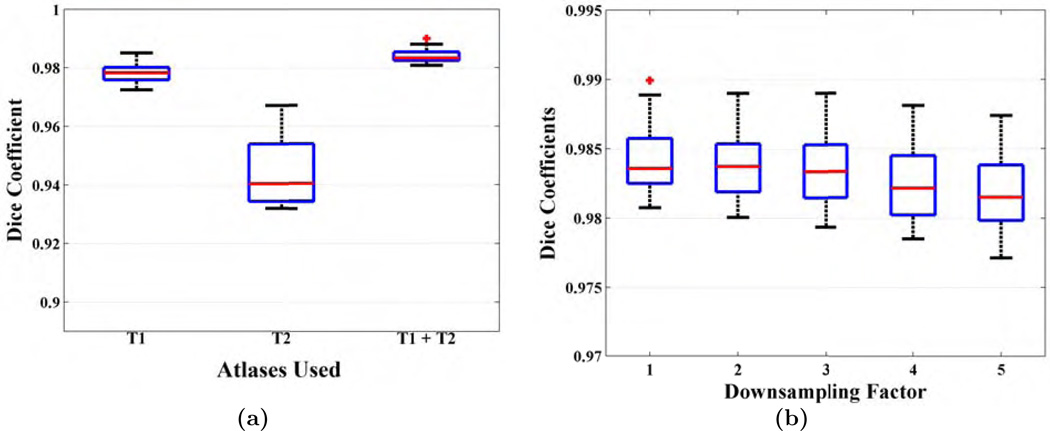
Fig. 4(a) shows Dice coefficients from 23 subjects when MONSTR brain masks are compared with the manual ones. Median Dice coefficients are 0.9588, 0.9665, 0.9693, 0.9712, 0.9718, and 0.9709 for 1 – 6 atlases. The median Dice coefficient for 4 or more atlases are not significantly different (p > 0.05 between each pairs), while 3 or less atlases produce significantly lower Dice (p < 0.001, Wilcoxon sign-rank test) than 4 or more atlases. Hence, we use the same 4 atlases for the remaining experiments for BEaST, SPECTRE, and MONSTR.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f4.jpg

Figure 4

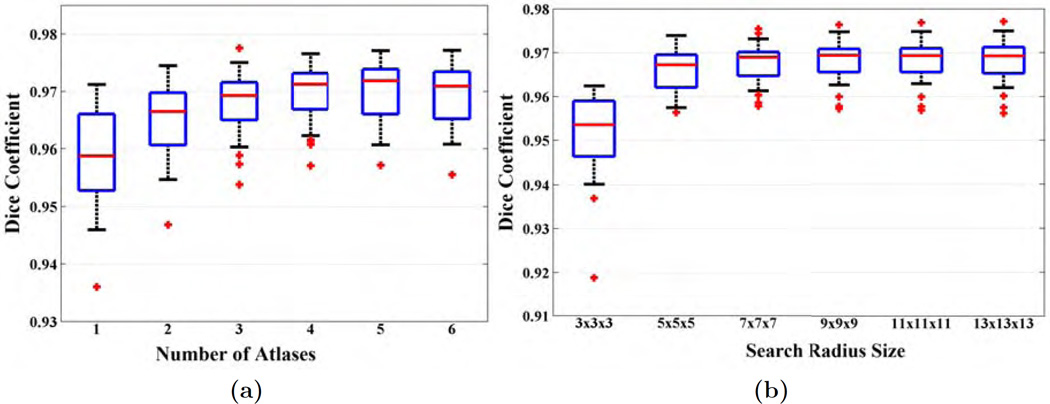
(a) Dice coefficients between brain masks generated by MONSTR and manual masks are plotted for the ADNI-29 dataset. 6 subjects are chosen as atlases and the remaining 23 subjects are stripped using 1 – 6 atlases. (b) Dice coefficients of 25 subjects are plotted for various search window sizes from s = 1 (3 × 3 × 3) to s = 6 (13 × 13 × 13). Number of atlases used is 4.

3.1.2. Search Window Size

If the registrations are accurate, then smaller search windows are sufficient. Generally higher window size requires more computation time and memory. For every subject patch, a window s = 4 (i.e., searching within a 9×9×9 neighborhood) indicates that Eqn. 3 is solved for A₁(i) using |N_i|T = 2916 atlas patches. Therefore more accurate registrations are preferred so as to reduce the computational overhead of solving Eqn. 3. For images with TBI or tumor, we expect that higher window sizes may facilitate stripping, as registrations may be sub-optimal due to presence of pathologies. However, instead of optimizing the parameter on every dataset separately, we optimize the radius once and use it for rest of the experiments.

Fig. 4(b) shows the Dice coefficients for 25 subjects from the ADNI-29 dataset between automated and manual masks for window sizes from s = 1 to s = 6. Statistically significant improvement (p < 0.05) is observed for s = 4, 5, 6 compared to s = 1, 2, 3. Although s = 4 provides the best result, the Dice improvement from s = 3 to s = 4 is small (median Dices 0.9690 to 0.9694). The standard deviations are similar for s = 2 or higher (0.0048 for s = 2), while it is large for s = 1 (0.0100). Also there was one outlier in s = 1 with Dice < 0.92, which improved after increasing the window size. We use s = 4 for rest of the experiments.

3.2. `ADNI-29` Dataset

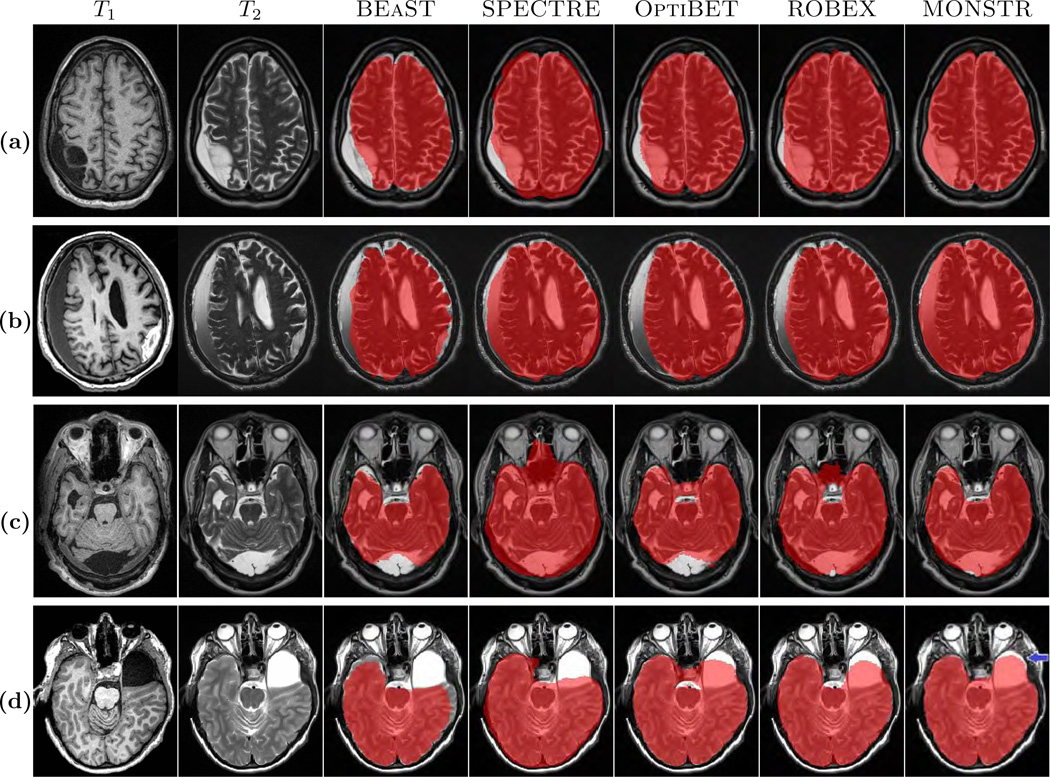
We compared the performance of MONSTR against the other methods on healthy brains from the ADNI-29 dataset. Fig. 5 shows two subjects from the ADNI-29 dataset along with brain masks obtained from the 5 methods and the manual one. It is sometimes difficult to distinguish between marrow and GM solely based on T₁-w images. Similarly both CSF and skull have similar intensities. This is illustrated in Fig. 5, where the first 4 methods, using only the MPRAGE, can overestimate the mask either by including skull and marrow (yellow arrows) or underestimate by excluding CSF. T₂ provides better contrast between CSF and skull. Hence MONSTR produces comparatively better stripping by using multi-contrast information and visually matches closest to the manual one.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f5.jpg

Figure 5

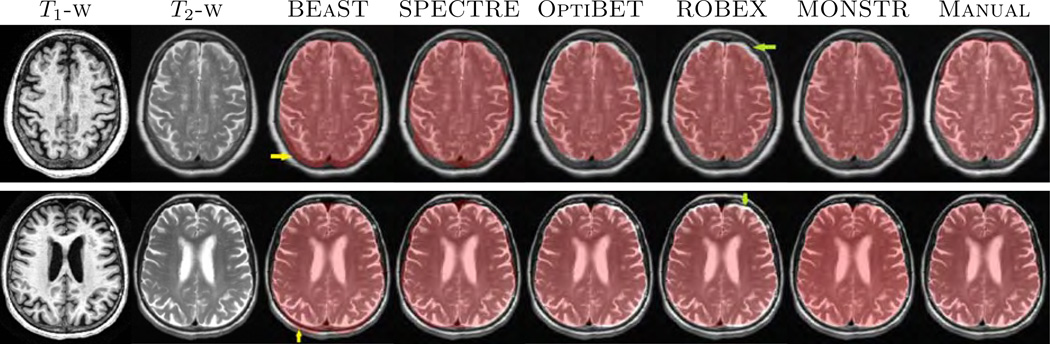
Figure shows MPRAGE and T₂ images of two subjects from ADNI-29 dataset along with the stripping masks from 5 algorithms overlaid on T₂. While BEaST and SPECTRE overestimate by including some skull and fat in the mask (yellow arrows), OptiBET and ROBEX underestimate by removing some CSF (green arrows). MONSTR generates a comparatively better mask by considering multiple contrasts.

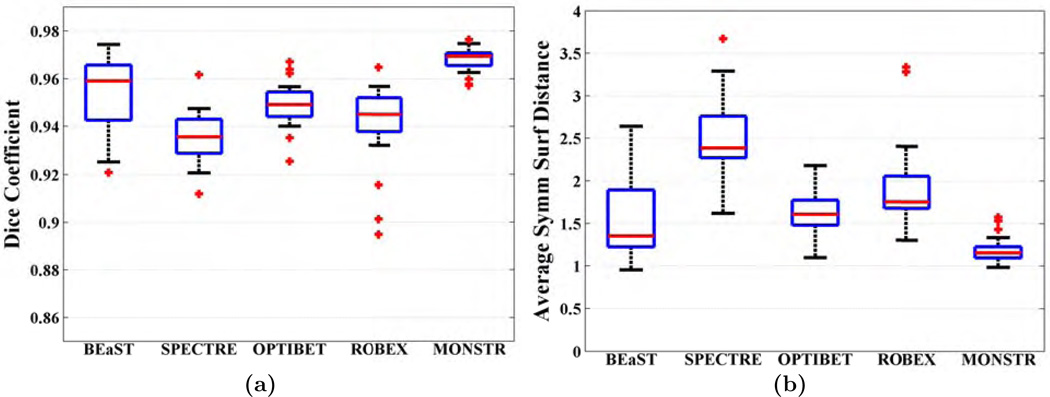
Fig. 6(a)–(b) shows quantitative improvement, where Dice coefficients and d_S (see Sec. 2.5 for definitions) are plotted. The median Dice coefficients for BEaST, SPECTRE, OptiBET, ROBEX and MONSTR are 0.9590, 0.9356, 0.9491, 0.9450, and 0.9694, respectively. Median d_S are 1.35, 2.38, 1.61, 1.75, and 1.15 mm, respectively. Dice coefficients of MONSTR are significantly higher and d_S are significantly lower (p < 10⁻⁴ for both) than other methods, indicating superior performance. Note that while other methods have wide variations in d_S, MONSTR generates a very low variation. Standard deviations of the surface distances are 0.49, 0.43, 0.25, 0.49, and 0.15, indicating that the MONSTR brain masks are the most consistent and robust. The standard deviations of Dice coefficients and d_S from MONSTR are significantly lower (F-test, p < 0.001) than all other methods. See supplemental material for comparison of MONSTR and BEaST with more than 4 atlases.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f6.jpg

Figure 6

(a) Dice coefficients and (b) average symmetric surface distances (d_S) between automated and manual brain masks are plotted for 25 subjects from ADNI-29 dataset. MONSTR produces significantly higher Dice (p < 0.001) and lower d_S (p < 0.001) compared to the other 4 methods.

3.3. `NAMIC-20` Dataset

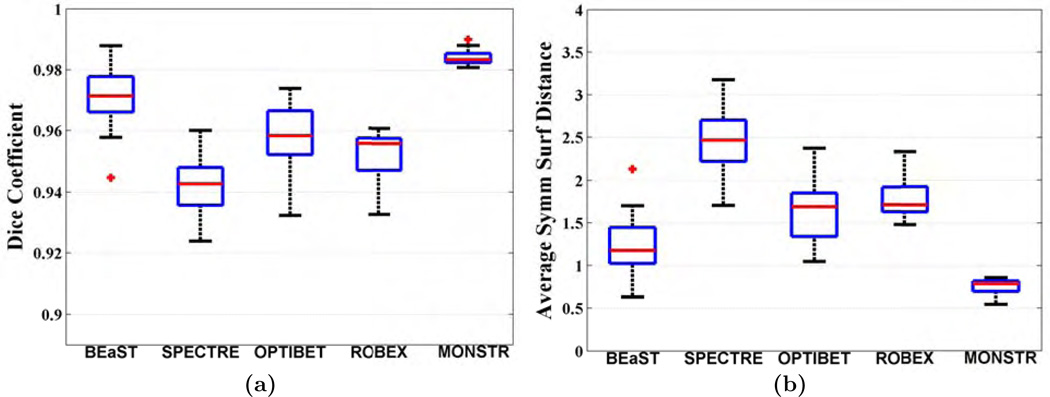
Fig. 7 shows MR images and brain masks from the NAMIC-20 dataset obtained from the 5 methods, along with the manual mask, overlaid on the T₂-w image. Similar to the ADNI-29 dataset, BEaST and SPECTRE include some skull and marrow in the mask (yellow arrow), while OptiBET and ROBEX remove some CSF (green arrow). We have found that generally BEaST and SPECTRE include some dura and skull, especially near the parietal lobe. Also ROBEX and OptiBET often exclude CSF. OptiBET, being a robust modification of BET, tries to find an edge between brain and skull, therefore mislabeling some CSF on MPRAGE as part of skull. MONSTR provides a better mask by excluding dura and skull and including most intracranial CSF. Quantitative improvement is shown for 16 subjects in Fig. 8, where MONSTR has the significantly higher Dice coefficient 0.9833 (p < 10⁻⁴) compared to the other methods, which are 0.9713, 0.9427, 0.9583, 0.9558 for BEaST, SPECTRE, OptiBET and ROBEX, respectively, Similarly, MONSTR has the lowest d_S (p < 10⁻⁴), 0.78 vs 1.17, 2.47, 1.67, 1.71. The standard deviations of Dice coefficients and d_S from MONSTR are significantly lower (F-test, p < 10⁻⁵) than all other methods. Note that the median Dice (0.9833) and d_S (0.78) for MONSTR are better than those from the ADNI-29 dataset (0.9694 and 1.15). There are two reasons for this. (a) The NAMIC-20 dataset has 1 mm³ isotropic T₂ images, while ADNI-29 has T₂ images with 3 mm thick slices. Masks computed with isotropic atlas images generally produced more accurate performance. (b) ADNI-29 brainmasks were delineated on T₁ images, while NAMIC-20 brainmasks were delineated on T₂. For stripping purpose, the T₂ images are advantageous. So we believe the masks are of better quality for the NAMIC-20 data than the ADNI-29 data.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f7.jpg

Figure 7

Figure shows MPRAGE and T₂ images of a patient with schizophrenia from NAMIC-20 dataset along with the stripping masks from 5 algorithms overlaid on T₂. Similar to the ADNI-29 dataset, BEaST and SPECTRE include some skull and marrow (yellow arrow), while ROBEX and OptiBET exclude some subarachnoid CSF (green arrow).

An external file that holds a picture, illustration, etc.
Object name is nihms832658f8.jpg

Figure 8

(a) Dice coefficients and (b) average symmetric surface distances (d_S) between automated and manual brain masks are plotted for 16 subjects from NAMIC-20 dataset. MONSTR produces significantly higher Dice (p < 0.001) and lower d_S (p < 0.001) compared to the other 4 methods.

3.4. `MRBrainS-5` Dataset

Since the MRBrainS-5 dataset has only 5 subjects, we did a leave one out cross validation. The quantitative results are shown in Table 2, where Dice coefficients and d_S for each subject are listed. MONSTR outperforms SPECTRE, OptiBET, and ROBEX on all 5 subjects in terms of both Dice and d_S, while BEaST produces higher Dice and lower d_S on one subject than MONSTR. Nevertheless, MONSTR has the highest average Dice and lowest average d_S. Since there are only 5 subjects, any statistical test will have insufficient power to claim significance.

Table 2

Leave one out cross validation of 5 subjects from MRBrainS-5 data is shown. Bold indicates maximum Dice or minimum surface distances (d_S) among the 5 methods.

		Subject #

		1	2	3	4	5	Mean
Dice	BEaST	0.9705	0.9496	0.9579	0.9574	0.9687	0.9608
	SPECTRE	0.9318	0.9250	0.9334	0.9301	0.9282	0.9297
	OptiBET	0.9490	0.9488	0.9388	0.9315	0.9266	0.9409
	ROBEX	0.9431	0.9425	0.9375	0.9274	0.9353	0.9372
	MONSTR	0.9653	0.9717	0.9659	0.9712	0.9731	0.9695

d_S	BEaST	1.11	1.66	1.32	1.26	1.24	1.32
	SPECTRE	1.89	2.24	1.97	2.03	2.14	2.06
	OptiBET	1.59	1.56	1.84	1.68	1.78	1.69
	ROBEX	1.62	1.61	1.69	1.70	1.67	1.66
	MONSTR	1.17	1.11	1.13	1.01	1.13	1.11

3.5. `TBI-19` Dataset

The effect of T₂ in stripping is most prominent in the presence of TBI, where hemorrhages and lesions can be hypointense like the skull in MPRAGE. Therefore, the T₂ image provides sufficient contrast to distinguish blood from skull. For this dataset, 4 patients were carefully chosen as atlases using the following criteria, (1) they have mild TBI, (2) there is very little or no visual presence of hemorrhages or lesions. The reason is that there is no publicly available dataset with TBI, where multi-contrast images as well as manually drawn brain masks are available. Therefore we want MONSTR to work well with available normal atlases (like ADNI-29) so that it is useful to the community when optimal atlases may not be available. More details about the effect of different atlases from different datasets can be found in Sec. 3.10.

Examples are shown in Fig. 9, where images of one patient with severe TBI from the TBI-19 dataset are shown. As before, BEaST underestimates the mask by stripping the hemorrhage (yellow arrow), while SPECTRE includes some skull (green arrow). OptiBET and ROBEX generally perform better than BEaST and SPECTRE, while MONSTR is consistently better than all four methods. Four other patients from the Acute dataset (see Sec. 2.1 for details) are shown in Fig. 10, for which manual brain masks are not available. Visually, it is clear that in these extreme cases, MONSTR produces the best brain mask by excluding skull and including most of the intracranial contents. Some errors are still noticeable, e.g. Fig. 10(d), blue arrow. A possible reason is that the parameters such as number of atlases and search radius are chosen based on normal subjects (Sec. 3.1), which may not be optimal for these extreme cases. Nevertheless, MONSTR clearly outperforms the other methods by including the lesions and excluding dura and skull.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f9.jpg

Figure 9

The figure shows T₁ and T₂-w images of a patient with severe TBI from the TBI-19. The manual brainmask is overlaid on the T₂. The stripping masks from 5 different stripping methods are compared.

Quantitative comparisons are shown in Fig. 11(a), where the median Dice coefficient from 15 patients is 0.9811 for MONSTR, compared to 0.9425, 0.9316, 0.9602, 0.9563 for BEaST, SPECTRE, OptiBET, and ROBEX, respectively. Median d_Ss (Fig. 11(b)) are 2.03, 2.71, 1.45, 1.49, and 0.84. Using a paired Wilcoxon signed rank test, both Dice and d_S of MONSTR are significantly better (p = 4 × 10⁻⁴) than the other 4 methods. Also the standard deviations of Dice coefficients from MONSTR are significantly lower (F-test, p < 10⁻⁴) than all other methods. Note that median Dice of BEaST is lower than that of ADNI-29 (0.9605) and NAMIC-20 (0.9713) datasets, because BEaST usually removes most of the hemorrhages. OptiBET and ROBEX are comparable on this dataset (p > 0.05 for both Dice and d_S). Dice and d_S from all methods for these three datasets are shown in Table 3.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f11.jpg

Figure 11

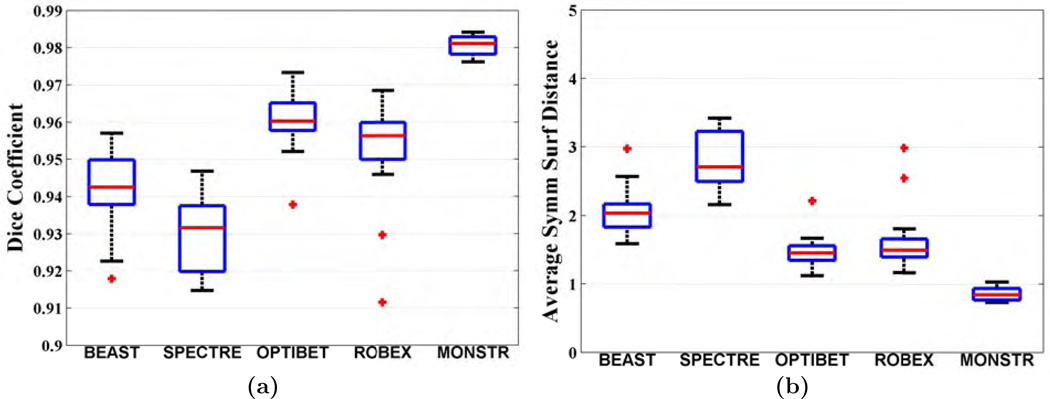
(a) Dice coefficients and (b) average symmetric surface distances (d_S) between automated and manual brain masks are plotted for 16 subjects from TBI-19 dataset. MONSTR produces significantly higher Dice (p < 0.001) and lower d_S (p < 0.001) compared to the other 4 methods.

Table 3

Dice coefficients and surface distances (d_S) obtained from the 5 different methods are shown for ADNI-29, TBI-19 and NAMIC-20 datasets. An asterisk indicates statistical significance (p < 0.001) using paired Wilcoxon signed rank test over all the other competing methods.

Dataset	Dice	d_S	Dice	d_S	Dice	d_S	Dice	d_S	Dice	d_S
	BEaST		SPECTRE		OptiBET		ROBEX		MONSTR

`ADNI-29`	0.9590	1.35	0.9356	2.38	0.9491	1.61	0.9450	1.75	0.9694*	1.15*
`NAMIC-20`	0.9713	1.17	0.9427	2.47	0.9583	1.67	0.9558	1.71	0.9833*	0.78*
`TBI-19`	0.9425	2.03	0.9316	2.71	0.9602	1.45	0.9563	1.49	0.9811*	0.84*

3.6. `MOV-32` Dataset

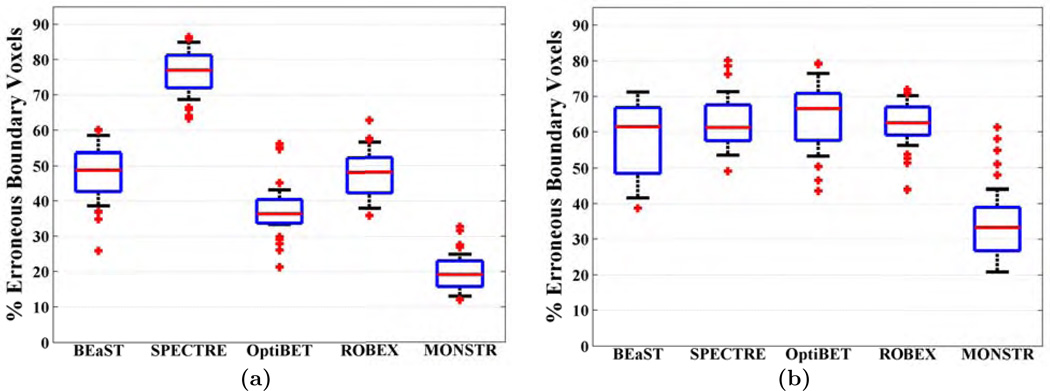
As mentioned in the Sec. 2.1, there is no manually segmented brain mask for this dataset. Hence CT images are used to independently compare different methods. We use the same atlases from TBI-19, as both sets have high resolution T₂. As described in Sec. 2.5, the percentage of erroneous boundary voxels is computed for each method, where an erroneous boundary voxel is one for which the ratio of median “outside voxels” HU and median “inside voxels” HU in a 3 × 3 × 3 patch around it is ≤ 1. Fig. 12(a) shows a boxplot of % erroneous voxels. MONSTR produces significantly lower (p = 10⁻⁶) percentage of erroneous voxels (median 19.17%), compared to the other four, 48.77%, 77.01%, 36.34%, and 48.03%, for BEaST, SPECTRE, OptiBET and ROBEX, respectively.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f12.jpg

Figure 12

Percent of erroneous boundary voxels (Sec. 2.5) are shown for (a) MOV-32 and (b) TUMOR-36 datasets.

3.7. `TUMOR-36` Dataset

This experiment shows the robustness of MONSTR with post-contrast T₁-weighted images. We chose the same 4 images that were used as atlases in the TBI-19 dataset, but used their post-contrast T₁ and T₂ images. These 4 atlases were also used for BEaST and SPECTRE. ROBEX and OptiBET were run with default atlases. Each brain mask from each method was visually checked for gross failures. The segmentation was considered to be a failure when either 1) the brain mask was completely blank or 2) the mask encompassed the whole head, including skull,fat, and eyes, indicating that minimal tissue had been removed. BEaST failed on 25 subjects, and OptiBET failed on 1. There were no failures for ROBEX and MONSTR.

Fig. 12(b) shows the % of erroneous boundary voxels for the 5 methods, of which MONSTR produces the least error (p < 10⁻⁵ with Wilcoxon rank-sum test). Since the number of valid brain masks for each method are different, we did not use a paired test. There were 33.34% erroneous boundary voxels in MONSTR compared to only 19.17% in MOV-32 dataset. This is attributed to the fact that postcontrast T₁ is not optimal for stripping purposes because the brain-skull boundary do not have enough contrast. However, the use of the T₂-w images helps MONSTR to achieve lower errors than other T₁ based methods. Fig. 13 shows images of one subject. Although, all 5 methods have visible errors of various degrees, the MONSTR brain mask respects the T₁ boundary more compared to others.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f13.jpg

Figure 13

Postcontrast T₁ and T₂ images of a patient from TUMOR-36 are shown, along with brain masks obtained from 5 methods.

3.8. Effect of Multi-contrast Images vs Only T₁

In this section, we evaluate the contribution of different contrasts by stripping with only the T₁ or T₂ images. We use NAMIC-20 dataset for this purpose because both isotropic T₁ and T₂ images available. Although there were 10 subjects with schizophrenia, their images do not contain any cortical lesions, tumors, or hemorrhages, like the TBI-19 or TUMOR-36 data. We chose M = 1, and set $a_{1}^{(t)}$ as T₁-w and T₂-w, respectively. Fig. 14(a) shows the Dice coefficients for each case. Median Dice coefficients are 0.9783, 0.9587, and 0.9833 for T₁-w, T₂-w, and the multi-contrast T₁ + T₂-w images. A paired sign-rank test shows multicontrast skull-stripping outperforms both single channel results (p = 4 × 10⁻⁴ for both). Lower performance using only T₂-w images is attributed to our observation that sometimes T₂-T₂ atlas registrations were worse than T₁-T₁ registrations. Nevertheless, the addition of a separate T₂ channel improves the Dice (0.9783 to 0.9833) even for these lesion-free brains. Also MONSTR using only a T₁ image can still outperform other methods, which are also only T₁ based. See supplemental material for more results.

An external file that holds a picture, illustration, etc.
Object name is nihms832658f14.jpg

Figure 14

(a) Dice coefficients for NAMIC-20 dataset are shown when only T₁ and only T₂ images are used for skull-stripping in the MONSTR framework, as compared to the complete multi-channel T₁ and T₂ images. (b) The effect of resolution is shown on the NAMIC-20 dataset, when the images are downsampled in the inferior-superior direction by a factor of 2 – 5.

3.9. Effect of Resolution

In this section, we explore the effect of resolution in the patch matching framework and show the necessity of high resolution atlases. We again used the NAMIC-20 dataset for this experiment. Although high resolution 3D T₁-w images are common in clinical scans, often T₂ images are acquired using 2D sequences and with lower resolution out of plane. To simulate a 2D T₂ acquisition, we averaged and downsampled the 1 mm³ isotropic T₂ images in the inferior-superior (I-S) direction to 2 – 5 mm and then used the downsampled images (1 × 1 × r mm³, r=2, …, 5) along with the original isotropic T₁ in the MONSTR framework. As described in Sec. 2.2, downsampled T₂ images were first interpolated by cubic b-spline interpolation to the dimension of corresponding T₁.

Fig. 14(b) shows Dice coefficients of 16 subjects with varying downsampling factors. Median Dice coefficients were 0.9833, 0.9829, 0.9819, 0.9810, for downsampling factors of 2 – 5. Using a Wilcoxon signed rank test, Dice coefficients from r mm images are lower (p < 0.05) than the downsampled images for r − 1 mm, r = 3, 4, 5, while there is no significant difference in Dice between 1 mm³ and 1 × 1 × 2 mm³ images. Note that these numbers are not directly comparable to the ADNI-29 data because (1) the brain masks were delineated on T₁-w images on ADNI-29 data while they were drawn on T₂ images in this data, (2) the atlases used in ADNI-29 data had 3 mm I-S resolution interpolated to 1 mm³ isotropic, while the atlases in this experiment have native 1 mm³ resolution. However, the numbers are comparable to the results in TBI-19 data (median Dice 0.9811), which also had high resolution T₂. The Dice with 5 mm I-S resolution (0.9810) is still significantly (p = 0.004) better than BEaST (0.9713), which had the best performance among the other 4 T₁ based methods. Therefore this result highlights both the importance of having high resolution atlases as well as a second contrast.

3.10. Effect of Atlases from Different Datasets

In all of the previous experiments, we have chosen atlases from within the datasets, so that the intensity based patch-matching is based on identical contrasts. In practice, however, it is sometimes difficult to obtain atlases acquired with identical sequences to the data under study, primarily because manual delineations of brain masks are tedious and time-consuming. Therefore ideally the performance of a good stripping algorithm should not degrade much when atlases from different datasets are used. In this section, we explore how the choice of atlases from different sites and scanners affect the performance of MONSTR. Three datasets, ADNI-29, TBI-19, and NAMIC-20 are used for these experiments. For every dataset, we use the same 4 atlases from the other two datasets, which were chosen in the original experiments, i.e. Sec. 3.2, 3.3, 3.5. Note that while ADNI-29 and TBI-19 have MPRAGE, NAMIC-20 has SPGR T₁-w images.

Fig. 15(a)–(c) shows Dice coefficients of three datasets, ADNI-29, TBI-19, and NAMIC-20, respectively. As expected, for every dataset, the atlases chosen from the same dataset produces the highest Dice. Median Dice coefficients and corresponding p-values when compared with results from other atlas sets are shown in Table 4. For ADNI-29 (Fig. 15(a)), the median Dice coefficients are 0.9646, 0.9563, and 0.9694 for TBI-19, NAMIC-20, and ADNI-29 atlases. ADNI-29 atlases produce the highest (p < 10⁻⁴) Dice among the three. Also since NAMIC-20 has SPGR, it produces smaller Dice than TBI-19 (p = 0.09), although the difference is not statistically significant. Similarly for the NAMIC-20 dataset, the median Dices are 0.9746, 0.9811, and 0.9833. In this case, NAMIC-20 atlases produces significantly higher Dice than the other two (p = 0.002 and p = 4 × 10⁻⁴), because the images are SPGR compared to MPRAGE atlases in the other two datasets. Finally, for the TBI-19 data, the median Dice coefficients are 0.9763, 0.9765, 0.9811. In this case also, using TBI-19 atlases results in significantly higher Dice that the other two (p = 4 × 10⁻⁴). NAMIC-20 atlases produces more variation than both the TBI-19 and ADNI-29 atlases (F-test, p < 10⁻⁹), indicating lower robustness. Interestingly, for every dataset, the worst Dice is still better or comparable to the best Dice among the other 4 competing methods. For example, on the ADNI-29 dataset, both the NAMIC-20 and TBI-19 atlases produce comparable Dice (0.9563 and 0.9646) to BEaST (0.9590), p = 0.71 and 0.38 respectively. On the NAMIC-20 dataset, TBI-19 atlases produce comparable Dice (0.9746) to BEaST (0.9713) (p = 0.50), but the ADNI-29 atlases produce higher Dice (0.9811) than BEaST (p = 0.003). On the TBI-19 dataset, the NAMIC-20 atlases produce comparable Dice (0.9763) to OptiBET (0.9602) (p = 0.19), but the ADNI-29 atlases produce higher Dice (0.9765) than OptiBET (p = 4 × 10⁻⁴).

An external file that holds a picture, illustration, etc.
Object name is nihms832658f15.jpg

Figure 15

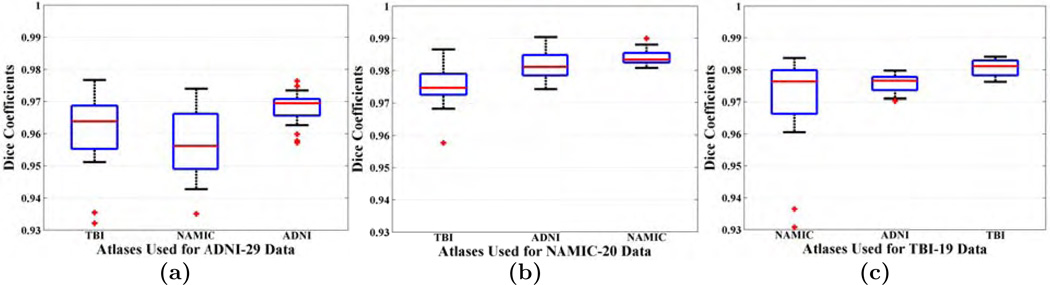
Each of (a) ADNI-29, (a) NAMIC-20, and (c) TBI-19 datasets are stripped with atlases chosen from the other two. See Sec. 3.10 for details.

Table 4

Dice coefficients obtained from MONSTR on 3 different datasets are shown, when the atlases are drawn from other datasets. Asterisks indicates statistical significance over using the other two atlases. The p-values are shown for pairwise comparison between results with the atlas set from the same database vs the chosen atlas set.

Atlas		`ADNI-29`		`NAMIC-20`		`TBI-19`

		Dice	p	Dice	p	Dice	p
Subject	`ADNI-29`	0.9694**	1	0.9563	< 10⁻⁴	0.9646	< 10⁻⁴
	`NAMIC-20`	0.9746	0.0004	0.9833**	1	0.9811	0.0020
	`TBI-19`	0.9763	0.0004	0.9765	0.0004	0.9811**	1

Go to:

4. Discussion

We have proposed a fully automatic patch-based multi-contrast skull-stripping algorithm called MONSTR, and have evaluated it against 4 leading stripping algorithms BEaST, SPECTRE, OptiBET, and ROBEX. We have shown that by using multiple contrasts, MONSTR produces more accurate results than the competing methods on both healthy subjects, as well as subjects with pathologies such as TBI and tumor. The software is available in http://www.nitrc.org/projects/monstr. We have also proposed a novel independent way of comparing stripping methods via CT in Sec. 3.6–3.7. In acute clinical studies, CT images are often acquired and can provide a relative comparison of multiple stripping methods in the absence of a ground truth. By using this approach, we avoid the necessity of generating a ”gold standard” brain mask from the CT.

MONSTR uses a sparse, convex combination of atlas patches to reproduce a given subject patch. There are alternative ways to combine atlas patches, such as the non-local weighting done in BEaST (Coupé et al., 2012; Eskildsen et al., 2012). While both ways approaches have merits, sparsity is advantageous when both subject and atlases have pathologies, and are anatomically quite different. In regions corresponding to tumors or other types of lesions, sparsity requires contribution from only a few patches within the training data, whereas non-local approaches will compute weights from a large patch set even though many of those patches will likely be from healthy tissue. This potentially enables the size of the training data to be smaller and still yield good performance, as we showed in Sec. 3.1.1.

To validate our method, we chose 4 atlases from each dataset, and stripped the remaining subjects with them. We found that the particular choice of atlases had little effect on the performance of MONSTR. This is shown in the supplemental material, where we evaluated the variability of the performance using a two-fold cross validation on the TBI-19 dataset. Choosing atlases from the same dataset is crucial, as shown in Sec. 3.10. In our experiments, we have found that compared to 4 atlases chosen from the same dataset, BEaST results were worse with default atlases^⁹, partly because the default atlases were SPGR, while most of our experimental data is MPRAGE. Therefore we did not show comparisons with default atlases. Also note that BEaST was reported as not being optimized for brain images with pathology (Eskildsen et al., 2012).

The number of atlases T is an important parameter in most atlas based stripping methods. BEaST results may be suboptimal since the recommended number of atlases is 20 (Eskildsen et al., 2012). See supplemental material for comparison of MONSTR and BEaST with more than 4 atlases. However in practice, manually delineating 20 brain masks for every dataset is costly. In contrast, we have shown that only 4 atlases suffice (Sec. 3.1.1) for MONSTR, and even using 3 atlases, the change in Dice coefficient is small from 0.9712 to 0.9693 on ADNI-29 data. Also we have shown in Sec. 3.10 that MONSTR is robust such that atlases from different datasets with different acquisitions, scanners, and resolutions still produce better results than the competing methods, especially on pathological brains. Therefore MONSTR can be applied relatively easily for a variety of datasets.

Although many patch based methods have been proposed in the past that can be straightforwardly extended to multi-contrast images (Wang et al., 2014), one of the important aspect in our framework is the combination of an approximate deformable registration, rather than an affine registration to the patch-based framework. We did not observe any failure of “approximate ANTS” even with severely pathological brains, e.g. Fig. 10. This is due to the fact that fewer iterations are used on a subsampled image. The “approximate” deformable registration has two additional advantages. First, it helps to decrease the runtime, as opposed to full ANTS (antsRegistrationSyN.sh), which uses 100 × 70 × 50 × 20 iterations for 4 levels by default. Second, due to a better initialization, only a 9 × 9 × 9 search neighborhood suffices in our experiments.

Only T₁-w atlas images are registered to T₁-w subject images and the corresponding transformations are applied to the T₂-w atlas images, which were already coregistered to T₁. This is preferred because clinically acquired T₂-w or FLAIR images may have thick slices, which when combined with isotropic T₁-w images in a multi-channel registration framework, can produce sub-optimal registrations (Zhao et al., 2016). Although the incorporation of T₂ images improves stripping, especially for pathological brains, this also limits applicability if T₂ images are not available, because many publicly available datasets do not usually include T₂. In absence or with low resolution T₂ images, MONSTR can also use FLAIR images for stripping. Although it is possible to use both the T₂ and FLAIR images, we found little improvement with this approach. Future work will consist of validation with FLAIR or PD images. With the recent improvement of image synthesis methods (Rousseau, 2008; Roy et al., 2013a; Jog et al., 2015; Iglesias et al., 2013), we will explore the possibility of synthesizing T₂ from T₁ and using that as a substitute for original T₂ scans.

The large number of failures when applying BEaST to the TUMOR-36 data set could be partially attributed to poor registrations (based on visual inspection) for 15 cases. However, even when registrations were accurate, failures still occurred on 10 cases. This is likely because BEaST was designed for standard T₁-w images, rather than post contrast images, which exhibit enhancement of the meninges and vessels that bridge the subarachnoid gap between brain and the skull. The presence of tumors and edema may have also played a role in the failures. Thus, while improving the registration in BEaST may reduce the number of failures, it would not eliminate them.

A drawback of our study is the relatively limited number of subjects with pathology. These numbers can not represent an entire disease population, and we would be hesitant to claim that any specific number would be sufficient to do so. This is especially true for TBI, a highly heterogeneous disease for which where there are currently no publicly available data with manual segmentations. Our TBI-19 set contains a mixture of mild, moderate, severe cases, and we were able to obtain significant improvements with MONSTR over some competing approaches on 19 subjects. Similarly the populations of tumor and movement disorders are in no way fully represented by our choice of 36 and 32 patients, but it is a sufficient number of subjects for which we can obtain statistical significance between methods. 5.

Go to:

Supplementary Material

Click here to view.^{(256K, pdf)}

Go to:

Acknowledgments

Support for this work included funding from the Department of Defense in the Center for Neuroscience and Regenerative Medicine and intramural research program at NIH. This work was also partially supported by grants NIH/NINDS R01NS070906 and National MS Society RG-1507-05243.

We gratefully acknowledge Dr. Mark Gilbert for providing access to the imaging data which comprises the TUMOR-36 dataset, obtained by the Neuro Oncology Branch of the National Cancer Institute. We gratefully acknowledge Dr. Kareem Zaghloul for providing access to the imaging data for the MOV-32 dataset, obtained by the Surgical Neurology Branch of the National Institute for Neurologic Disorders and Stroke.

For the ADNI-29 dataset, data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimers Association; Alzheimers Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.

Go to:

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

¹http://www.nitrc.org/projects/monstr

²https://afni.nimh.nih.gov/afni/

³https://www.nitrc.org/projects/robex

⁴http://www.neuromorphometrics.com/

⁵http://insight-journal.org/midas/collection/view/190

⁶http://mrbrains13.isi.uu.nl/

⁷https://github.com/BioMedIA/IRTK

⁸http://spams-devel.gforge.inria.fr/

⁹http://packages.bic.mni.mcgill.ca/tgz/beast-library-1.1.tar.gz

Go to:

References

Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med. Image Anal. 2008;12(1):26–41. [Europe PMC free article] [Abstract] [Google Scholar]
Avants BB, Tustison NJ, Song G, Cook PA, Klein A, Gee JC. A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage. 2011;54(3):2033–2044. [Europe PMC free article] [Abstract] [Google Scholar]
Boesen K, Rehm K, Schaper K, Stoltzner S, Woods R, Lüders E, Rottenberg D. Quantitative comparison of four brain extraction algorithms. NeuroImage. 2004;22(3):1255–1261. [Abstract] [Google Scholar]
Buades A, Coll B, Morel JM. A Non-Local Algorithm for Image Denoising. Intl. Conf. on Comp. Vision. and Patt. Recog. (CVPR) 2005;2:60–65. [Google Scholar]
Burgos N, Cardoso MJ, Thielemans K, Modat M, Pedemonte S, Dickson J, Barnes A, Ahmed R, Mahoney CJ, Schott JM, Duncan JS, Atkinson D, Arridge SR, Hutton BF, Ourselin S. Attenuation correction synthesis for hybrid PET-MR scanners: Application to brain studies. IEEE Trans. Med. Imag. 2014;33(12):2332–2341. [Abstract] [Google Scholar]
Carass A, Cuzzocreo J, Wheeler MB, Bazin PL, Resnick SM, Prince JL. Simple paradigm for extra-cerebral tissue removal: Algorithm and analysis. NeuroImage. 2011;56(4):1982–1992. [Europe PMC free article] [Abstract] [Google Scholar]
Carass A, Wheeler MB, Cuzzocreo J, Bazin P-L, Bassett SS, Prince JL. A Joint Registration and Segmentation Approach to Skull Stripping; Intl. Symp. on Biomed. Imag. (ISBI); 2007. Apr, pp. 656–659. [Google Scholar]
Collins DL, Neelin P, Peters TM, Evans AC. Automatic 3D intersubject registration of MR volumetric data in standardized talairach space. Journal of Comput. Assist. Tomogr. 1994;18(2):192–205. [Abstract] [Google Scholar]
Coupé P, Eskildsen SF, Manjn JV, Fonov VS, Collins DL the Alzheimer’s disease Neuroimaging Initiative. Simultaneous segmentation and grading of anatomical structures for patient’s classification: application to Alzheimer’s disease. NeuroImage. 2012;59(4):3736–3747. [Abstract] [Google Scholar]
Dale AM, Fischl B, Sereno MI. Cortical Surface-Based Analysis I: Segmentation and Surface Reconstruction. NeuroImage. 1999;9(2):179–194. [Abstract] [Google Scholar]
Desbrun M, Meyer M, Schroder P, Barr AH. Implicit fairing of irregular meshes using diffusion and curvature flow. SIGGRAPH. 1999:317–324. [Google Scholar]
Donoho DL. For most large underdetermined systems of linear equations, the minimal ₁-norm near-solution approximates the sparsest near-solution. Communications on Pure and Applied Mathematics. 2006;59(7):907–934. [Google Scholar]
Doshi J, Erus G, Ou Y, Gaonkar B, Davatzikos C. Multi-atlas skull-stripping. Academic Radiology. 2013;20(12):1566–1576. [Europe PMC free article] [Abstract] [Google Scholar]
Eskildsen SF, Coupe P, Fonov V, Manjon JV, Leung KK, Guizard N, Wassef SN, Ostergaard LR, Collins DL The Alzheimer’s Disease Neuroimaging Initiative. BEaST: Brain extraction based on nonlocal segmentation technique. NeuroImage. 2012;59(3):2362–2373. [Abstract] [Google Scholar]
Galdames FJ, Jaillet F, Perez CA. An accurate skull stripping method based on simplex meshes and histogram analysis for magnetic resonance images. Journal of Neurosci. Methods. 2012;206(2):103–119. [Abstract] [Google Scholar]
Geremia E, Clatz O, Menze BH, Konukoglu E, Criminisi A, Ayache N. Spatial decision forests for ms lesion segmentation in multi-channel magnetic resonance images. NeuroImage. 2011;57(2):378–390. [Abstract] [Google Scholar]
Guizard N, Coupe P, Fonov VS, Manjon JV, Arnold DL, Collins DL. Rotation-invariant multi-contrast non-local means for MS lesion segmentation. NeuroImage: Clinical. 2015;8:376–389. [Europe PMC free article] [Abstract] [Google Scholar]
Hahn HK, Peitgen H-O. The skull stripping problem in MRI solved by a single 3d watershed transform. Med. Image Comp. and Comp. Asst. Intervention (MICCAI) 2000;1935:134–143. [Google Scholar]
Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33(1):115–126. [Abstract] [Google Scholar]
Heckemann RA, Ledig C, Gray KR, Aljabar P, Rueckert D, Hajnal JV, Hammers A. Brain extraction using label propagation and group agreement: Pincram. PLoS One. 2015;10(7):e0129211. [Europe PMC free article] [Abstract] [Google Scholar]
Hu S, Coupé P, Pruessner JC, Collins DL. Nonlocal regularization for active appearance model: Application to medial temporal lobe segmentation. Human Brain Mapping. 2014;35(2):377–395. [Europe PMC free article] [Abstract] [Google Scholar]
Iglesias JE, Konukoglu E, Zikic D, Glocker B, Leemput KV, Fischl B. Is synthesizing MRI contrast useful for inter-modality analysis? Med. Image Comp. and Comp. Asst. Intervention (MICCAI) 2013;16:631–638. [Europe PMC free article] [Abstract] [Google Scholar]
Iglesias JE, Liu CY, Thompson P, Tu Z. Robust brain extraction across datasets and comparison with publicly available methods. IEEE Trans. Med. Imag. 2011;30(9):1617–1634. [Abstract] [Google Scholar]
Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Med. Image Anal. 2001;5(2):143–156. [Abstract] [Google Scholar]
Jog A, Carass A, Roy S, Pham DL, Prince JL. MR image synthesis by contrast learning on neighborhood ensembles. Med. Image Anal. 2015;24(1):63–76. [Europe PMC free article] [Abstract] [Google Scholar]
Jog A, Roy S, Carass A, Prince JL. Pulse sequence based multi-acquisition MR intensity normalization. Proceedings of SPIE Medical Imaging (SPIE) 2013;8669:86692H. [Europe PMC free article] [Abstract] [Google Scholar]
Kleesiek J, Urban G, Hubert A, Schwarz D, Maier-Hein K, Bendszus M, Biller A. Deep MRI brain extraction: A 3D convolutional neural network for skull stripping. NeuroImage. 2016;129:460–469. [Abstract] [Google Scholar]
Ledig C, Heckemann RA, Hammers A, Lopez JC, Newcombe VFJ, Makropoulos A, Lotjonen J, Menon DK, Rueckert D. Robust whole-brain segmentation: Application to traumatic brain injury. Med. Image Anal. 2015;21(1):40–58. [Abstract] [Google Scholar]
Lemieux L, Hagemann G, Krakow K, Woermann FG. Fast, accurate, and reproducible automatic segmentation of the brain in T1-weighted volume MRI data. Mag. Reson. Med. 1999;42(1):127–135. [Abstract] [Google Scholar]
Leung KK, Barnes J, Modat M, Ridgway GR, Bartlett JW, Fox NC, Ourselin S Alzheimer’s Disease Neuroimaging Initiative. Brain MAPS: An automated, accurate and robust brain extraction technique using a template library. NeuroImage. 2011;55(3):1091–1108. [Europe PMC free article] [Abstract] [Google Scholar]
Lutkenhoff ES, Rosenberg M, Chiang J, Zhang K, Pickard JD, Owen AM, Monti MM. Optimized Brain Extraction for Pathological Brains (optiBET) PLoS One. 2014;9(12):e115551. [Europe PMC free article] [Abstract] [Google Scholar]
Mairal J, Bach F, Ponce J. Sparse modeling for image and vision processing. Foundations and Trends in Computer Graphics and Vision. 2014;8(2–3):85–283. [Google Scholar]
Malone IB, Leung KK, Clegg S, Barnes J, Whitwell JL, Ashburner J, Foxa NC, Ridgway GR. Accurate automatic estimation of total intracranial volume: A nuisance variable with less nuisance. NeuroImage. 2015;104(2):366–372. [Europe PMC free article] [Abstract] [Google Scholar]
Manjon JV, Coupe P, Buades A, Collins DL, Robles M. Mri superresolution using self-similarity and image priors. Intl. Journal of Biomedical Imaging. 2010;2010:425891. [Europe PMC free article] [Abstract] [Google Scholar]
Mendrik AM, Vincken KL, Kuijf HJ, Breeuwer M, Bouvy WH, de Bresser J, Alansary A, de Bruijne M, Carass A, El-Baz A, Jog A, Katyal R, Khan AR, van der Lijn F, Mahmood Q, Mukherjee R, van Opbroek A, Paneri S, Pereira S, Persson M, Rajch M, Sarikaya D, Smedby O, Silva CA, Vrooman HA, Vyas S, Wang C, Zhao L, Biessels GJ, Viergever MA. MRBrainS challenge: Online evaluation framework for brain image segmentation in 3T MRI scans. Computational Intelligence and Neuroscience. 2015;2015(813696) [Europe PMC free article] [Abstract] [Google Scholar]
Mikheev A, Nevsky G, Govindan S, Grossman R, Rusinek H. Fully automatic segmentation of the brain from t1-weighted MRI using bridge burner algorithm. Journal of Magn. Reson. Imaging. 2008;27(6):1235–1241. [Europe PMC free article] [Abstract] [Google Scholar]
Mueller SG, Weiner MW, Thal LJ, Petersen RC, Jack C, Jagust W, Trojanowski JQ, Toga AW, Beckett L. The Alzheimer’s disease neuroimaging initiative. Neuroimaging Clin. N. Am. 2005 Nov;15(4):869–877. [Europe PMC free article] [Abstract] [Google Scholar]
Park JG, Lee C. Skull stripping based on region growing for magnetic resonance brain images. NeuroImage. 2009;47(4):1394–1407. [Abstract] [Google Scholar]
Pham DL, Prince JL. Adaptive Fuzzy Segmentation of Magnetic Resonance Images. IEEE Trans. Med. Imag. 1999;18(9):737–752. [Abstract] [Google Scholar]
Rehm K, Schaper K, Anderson J, Woods R, Stoltzner S, Rottenberg D. Putting our heads together: a consensus approach to brain/non-brain segmentation in T1-weighted MR volumes. NeuroImage. 2004;22(3):1262–1270. [Abstract] [Google Scholar]
Rex DE, Shattuck DW, Woods RP, Narr KL, Luders E, Rehm K, Stolzner SE, Rottenberg DA, Toga AW. A meta-algorithm for brain extraction in MRI. NeuroImage. 2004;23(2):625–637. [Abstract] [Google Scholar]
Roura E, Oliver A, Cabezas M, Vilanova JC, Rovira A, Ramio-Torrenta L, Llado X. MARGA: Multispectral adaptive region growing algorithm for brain extraction on axial MRI. Computer Methods and Programs in Biomedicine. 2014;113(2):655–673. [Abstract] [Google Scholar]
Rousseau F. Brain hallucination. European Conf. on Comp. Vision. 2008;5302:497–508. [Google Scholar]
Rousseau F, Habas PA, Studholme C. A supervised patch-based approach for human brain labeling. IEEE Trans. Med. Imag. 2011;30(10):1852–1862. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, Carass A, Jog A, Prince JL, Lee J. MR to CT registration of brains using image synthesis. Proceedings of SPIE Medical Imaging (SPIE) 2014a;9034:903419. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, Carass A, Prince JL. Synthesizing MR contrast and resolution through a patch matching technique. Proceedings of SPIE Medical Imaging (SPIE) 2010a;7263:76230j. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, Carass A, Prince JL. Magnetic resonance image example based contrast synthesis. IEEE Trans. Med. Imag. 2013a;32(12):2348–2363. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, Carass A, Prince JL, Pham DL. Longitudinal patch-based segmentation of multiple sclerosis white matter lesions. Machine Learning in Medical Imaging. 2015a;9352:194–202. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, Carass A, Shiee N, Pham DL, Calabresi P, Reich D, Prince JL. Longitudinal intensity normalization in the presence of multiple sclerosis lesions; Intl. Symp. on Biomed. Imag. (ISBI); 2013b. pp. 1384–1387. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, Carass A, Shiee N, Pham DL, Prince JL. MR Contrast Synthesis for Lesion Segmentation; Intl. Symp. on Biomed. Imag. (ISBI); 2010b. pp. 932–935. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, He Q, Carass A, Jog A, Cuzzocreo JL, Reich DS, Prince JL, Pham DL. Example based lesion segmentation. Proceedings of SPIE Medical Imaging (SPIE) 2014b;9034:90341Y. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, He Q, Sweeney E, Carass A, Reich DS, Prince JL, Pham DL. Subject specific sparse dictionary learning for atlas based brain MRI segmentation. IEEE Journal of Biomedical and Health Informatics. 2015b;19(5):1598–1609. [Europe PMC free article] [Abstract] [Google Scholar]
Roy S, Wang WT, Carass A, Prince JL, Butman JA, Pham DL. PET attenuation correction using synthetic CT from ultrashort echo-time MR imaging. Journal of Nuclear Medicine. 2014c;55(12):2071–2077. [Europe PMC free article] [Abstract] [Google Scholar]
Sadananthan SA, Zheng W, Chee MWL, Zagorodnov V. Skull stripping using graph cuts. NeuroImage. 2010;49(1):225–239. [Abstract] [Google Scholar]
Serag A, Blesa M, Moore EJ, Pataky R, Sparrow SA, Wilkinson AG, Macnaught G, Semple SI, Boardman JP. Accurate learning with few atlases (ALFA): an algorithm for MRI neonatal brain extraction and comparison with 11 publicly available methods. Scientific Reports. 2016;6:23470. [Europe PMC free article] [Abstract] [Google Scholar]
Shan ZY, Yue GH, Liu JZ. Automated histogram-based brain segmentation in T1-weighted three-dimensional magnetic resonance head images. NeuroImage. 2002;17(3):1587–1598. [Abstract] [Google Scholar]
Shattuck D, Sandor-Leahy S, Schaper K, Rottenberg D, Leahy R. Magnetic resonance image tissue classification using a partial volume model. NeuroImage. 2001;13(5):856–876. [Abstract] [Google Scholar]
Shi F, Wang L, Dai Y, Gilmore JH, Lin W, Shen D. LABEL: Pediatric brain extraction using learning-based meta-algorithm. NeuroImage. 2012;62(3):1975–1986. [Europe PMC free article] [Abstract] [Google Scholar]
Smith SM. Fast robust automated brain extraction. Human Brain Mapping. 2002;17(3):143–155. [Europe PMC free article] [Abstract] [Google Scholar]
Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC. N4ITK: improved N3 bias correction. IEEE Trans. Med. Imag. 2010;29(6):1310–1320. [Europe PMC free article] [Abstract] [Google Scholar]
van der Kouwe AJW, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho mprage. NeuroImage. 2008;40(2):559–569. [Europe PMC free article] [Abstract] [Google Scholar]
van Tulder G, de Bruijne M. Why does synthesized data improve multi-sequence classification? Med. Image Comp. and Comp. Asst. Intervention (MICCAI) 2015;9349:531–538. [Google Scholar]
Wang H, Suh JW, Das SR, Pluta JB, Craige C, Yushkevich PA. Multi-atlas segmentation with joint label fusion. IEEE Trans. Med. Imag. 2013;35(3):611–623. [Europe PMC free article] [Abstract] [Google Scholar]
Wang L, Shi F, Gao Y, Li G, Gilmore JH, Lin W, Shen D. Integration of sparse multi-modality representation and anatomical constraint for isointense infant brain MR image segmentation. NeuroImage. 2014;16(1):152–164. [Europe PMC free article] [Abstract] [Google Scholar]
Wang Y, Nie J, Yap P-T, Shi F, Guo L, Shen D. Robust deformable-surface-based skull-stripping for large-scale studies. Med. Image Comp. and Comp. Asst. Intervention (MICCAI) 2011;6893:635–642. [Abstract] [Google Scholar]
Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans. Med. Imag. 2004;23(7):903–921. [Europe PMC free article] [Abstract] [Google Scholar]
Zhao C, Carass A, Jog A, Prince JL. Effects of spatial resolution on image registration. Proceedings of SPIE Medical Imaging (SPIE) 2016:97840. [Europe PMC free article] [Abstract] [Google Scholar]
Zhuang AH, Valentino DJ, Toga AW. Skull-stripping magnetic resonance brain images using a model-based level set. NeuroImage. 2006;32(1):79–92. [Abstract] [Google Scholar]
Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society. Series B. 2005;67(2):301–320. [Google Scholar]

Full text links

Read article at publisher's site: https://doi.org/10.1016/j.neuroimage.2016.11.017

Read article for free, from open access legal sources, via Unpaywall: http://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_Acknowledgement_List.pdf

Citations & impact

Impact metrics

Citations

Jump to Citations

Citations of article over time

Alternative metrics

Altmetric item for https://www.altmetric.com/details/13813932

Altmetric
Discover the attention surrounding your research
https://www.altmetric.com/details/13813932

Article citations

Biologically informed deep neural networks provide quantitative assessment of intratumoral heterogeneity in post treatment glioblastoma.
Wang H, Argenziano MG, Yoon H, Boyett D, Save A, Petridis P, Savage W, Jackson P, Hawkins-Daarud A, Tran N, Hu L, Singleton KW, Paulson L, Dalahmah OA, Bruce JN, Grinband J, Swanson KR, Canoll P, Li J
NPJ Digit Med, 7(1):292, 19 Oct 2024
Cited by: 0 articles | PMID: 39427044 | PMCID: PMC11490546
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
Effect of Human Head Shape on the Risk of Traumatic Brain Injury: A Gaussian Process Regression-Based Machine Learning Approach.
Upadhyay K, Jagani R, Giovanis DG, Alshareef A, Knutsen AK, Johnson CL, Carass A, Bayly PV, Shields MD, Ramesh KT
Mil Med, 189(suppl 3):608-617, 01 Aug 2024
Cited by: 0 articles | PMID: 38739497
Hippocampal volume changes after (R,S)-ketamine administration in patients with major depressive disorder and healthy volunteers.
Evans JW, Graves MC, Nugent AC, Zarate CA
Sci Rep, 14(1):4538, 24 Feb 2024
Cited by: 0 articles | PMID: 38402253 | PMCID: PMC10894199
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC
Neuroimaging Findings in US Government Personnel and Their Family Members Involved in Anomalous Health Incidents.
Pierpaoli C, Nayak A, Hafiz R, Irfanoglu MO, Chen G, Taylor P, Hallett M, Hoa M, Pham D, Chou YY, Moses AD, van der Merwe AJ, Lippa SM, Brewer CC, Zalewski CK, Zampieri C, Turtzo LC, Shahim P, Chan L, [...] Lai C
JAMA, 331(13):1122-1134, 01 Apr 2024
Cited by: 1 article | PMID: 38497822 | PMCID: PMC10949155
Free full text in Europe PMC
Stroke Lesion Segmentation and Deep Learning: A Comprehensive Review.
Malik M, Chong B, Fernandez J, Shim V, Kasabov NK, Wang A
Bioengineering (Basel), 11(1):86, 17 Jan 2024
Cited by: 2 articles | PMID: 38247963 | PMCID: PMC10813717
Review
This article is in the Europe PMC Open access subset. Refer to the copyright information in the article for licensing details.
Free full text in Europe PMC

Go to all (49) article citations

Data

Data behind the article

This data has been text mined from the article, or deposited into data resources.

BioStudies: supplemental material and supporting data

http://www.ebi.ac.uk/biostudies/studies/S-EPMC5321800?xr=true

Funding

Funders who supported this work.

Center for Neuroscience and Regenerative Medicine

Intramural NIH HHS (1)

Grant ID: Z99 CL999999
1130 publications

NIA NIH HHS (1)

Grant ID: U01 AG024904
3784 publications

NINDS NIH HHS (1)

Grant ID: R01 NS070906
50 publications

National Institute of Neurological Disorders and Stroke (1)

Grant ID: R01NS070906
3 publications

National Institutes of Health

National Multiple Sclerosis Society (1)

Grant ID: RG-1507-05243
9 publications

Search life-sciences literature (45,103,589 articles, preprints and more)

Robust skull stripping using multiple MR image contrasts insensitive to pathology.

Author information

Affiliations

Authors

Authors

ORCIDs linked to this article

Abstract

Free full text

Robust Skull Stripping Using Multiple MR Image Contrasts Insensitive to Pathology

Snehashis Roy

John A. Butman

Dzung L. Pham

Associated Data

Abstract

1. Introduction

2. Materials and Method

2.1. Datasets

2.2. Preprocessing

2.3. Method

Table 1

2.4. Optimization of competing methods

2.5. Evaluation Criteria

3. Results

3.1. Parameter Optimization

3.1.1. Number of Atlases

3.1.2. Search Window Size

3.2. ADNI-29 Dataset

3.3. NAMIC-20 Dataset

3.4. MRBrainS-5 Dataset

Table 2

3.5. TBI-19 Dataset

Table 3

3.6. MOV-32 Dataset

3.7. TUMOR-36 Dataset

3.8. Effect of Multi-contrast Images vs Only T1

3.9. Effect of Resolution

3.10. Effect of Atlases from Different Datasets

Table 4

4. Discussion

Supplementary Material

Acknowledgments

Footnotes

References

Full text links

Citations & impact

Impact metrics

Citations of article over time

Alternative metrics

Article citations

Data

Data behind the article

BioStudies: supplemental material and supporting data

Similar Articles

Funding

Center for Neuroscience and Regenerative Medicine

Intramural NIH HHS (1)﻿

NIA NIH HHS (1)﻿

NINDS NIH HHS (1)﻿

National Institute of Neurological Disorders and Stroke (1)﻿

National Institutes of Health

National Multiple Sclerosis Society (1)﻿

Partnerships & funding

3.2. `ADNI-29` Dataset

3.3. `NAMIC-20` Dataset

3.4. `MRBrainS-5` Dataset

3.5. `TBI-19` Dataset

3.6. `MOV-32` Dataset

3.7. `TUMOR-36` Dataset

3.8. Effect of Multi-contrast Images vs Only T₁

Intramural NIH HHS (1)

NIA NIH HHS (1)

NINDS NIH HHS (1)

National Institute of Neurological Disorders and Stroke (1)

National Multiple Sclerosis Society (1)