Europe PMC

This website requires cookies, and the limited processing of your personal data in order to function. By using the site you are agreeing to this as outlined in our privacy notice and cookie policy.

Reduction of Pressure Gradient and Turbulence Using Vortex Generators in Prosthetic Heart Valves.

Author information

Affiliations

  • 1. Department of Biomedical Engineering, The Ohio State University, 473W 12th Ave., Columbus, OH, 43210, USA.
      Authors
    • Hatoum H 1
    • Dasi LP 1
    (2 authors)

Annals of Biomedical Engineering, 12 Sep 2018, 47(1):85-96
https://doi.org/10.1007/s10439-018-02128-6 PMID: 30209706 PMCID: PMC6408289

Free full text in Europe PMC

Abstract 

Blood damage and platelet activation are inherent problems with present day bi-leaflet mechanical heart valve designs. Passive flow control through different arrangements of vortex generators (VG) as means of improving pressure gradients and reducing turbulence are investigated. Rectangular VG arrays were mounted on the downstream surfaces of a 23 mm 3D printed mechanical valve. The effect of VGs on the resulting flow structures were assessed under pulsatile physiological flow conditions where high resolution particle image velocimetry measurement was performed. The co-rotating VGs showed lower Reynolds shear stresses and improved pressure gradients (PG) compared with the counter-rotating ones and the no-VG control one (that showed higher turbulence). RSS was found 38.13 ± 0.89, 12.95 ± 0.32, 15.75 ± 0.71, 24.54 ± 0.84 and 16.33 ± 0.58 Pa for the control, co-rotating VGs, 8 counter-rotating VGs, 4 far-spaced VGs and 4 closely-spaced VGs, respectively. PG of 10.45 ± 0.94 mmHg was obtained with co-rotating VGs and the difference was significant compared with the other configurations (control 14.88 ± 0.4 mmHg; 8 counter-rotating VGs 13.76 ± 0.51 mmHg; 4 far-spaced VGs 13.84 ± 0.09 mmHg; and 4 closely-spaced VGs 15.37 ± 0.16 mmHg). Co-rotating VGs for this application induce a more delayed flow separation and a more homogenized and streamlined transition of flow compared with the counter-rotating VGs. Passive flow control techniques deployed on BHMVs is potentially beneficial as significant control of flow at small length scales without inducing large-scale design modifications of the valve.

Free full text 

Logo of nihpaLink to Publisher's site
Ann Biomed Eng. Author manuscript; available in PMC 2020 Jan 1.
Published in final edited form as:
PMCID: PMC6408289
NIHMSID: NIHMS1506616
PMID: 30209706

Reduction of pressure gradient and turbulence using vortex generators in prosthetic heart valves

Hoda Hatoum, PhD and Lakshmi P. Dasi, PhD
Author information Copyright and License information Disclaimer

Associated Data

Supplementary Materials

Abstract

Blood damage and platelet activation are inherent problems with present day bi-leaflet mechanical heart valve (BMHV) designs. Passive flow control through different arrangements of vortex generators (VG) as means of improving pressure gradients and reducing turbulence are investigated. Rectangular VG arrays were mounted on the downstream surfaces of a 23mm 3D printed mechanical valve. The effect of VGs on the resulting flow structures were assessed under pulsatile physiological flow conditions where high resolution particle image velocimetry measurement was performed. The co-rotating VGs showed lower Reynolds shear stresses and improved pressure gradients (PG) compared with the counter-rotating ones and the no-VG control one (that showed higher turbulence). RSS was found 38.13±0.89Pa, 12.95±0.32Pa, 15.75±0.71Pa, 24.54±0.84Pa and 16.33±0.58Pa for the control, co-rotating VGs, 8 counter-rotating VGs, 4 far-spaced VGs and 4 closely-spaced VGs, respectively. PG of 10.45±0.94 mmHg was obtained with co-rotating VGs and the difference was significant compared with the other configurations (control 14.88±0.4mmHg; 8 counter-rotating VGs 13.76±0.51mmHg; 4 far-spaced VGs 13.84±0.09mmHg; and 4 closely-spaced VGs 15.37±0.16mmHg). Co-rotating VGs for this application induce a more delayed flow separation and a more homogenized and streamlined transition of flow compared with the counter-rotating VGs. Passive flow control techniques deployed on BHMVs is potentially beneficial as significant control of flow at small length scales without inducing large-scale design modifications of the valve.

Keywords: bi-leaflet mechanical valves, Reynold’s shear stress, vortex generators, co-rotating, counter-rotating, flow separation, anti-coagulant, blood damage

Introduction

Bi-leaflet mechanical heart valves (BMHVs) became the gold standard in mechanical heart valve implantation and are still widely used specifically in younger patients needing valve replacement. While mechanical valve designs evolved to improve hemodynamic performance, blood damage expressed in platelet activation and hemolysis remains a seemingly non-avoidable risk. Thromboembolism is the most common complication associated with mechanical valves affecting around 0.1% to 5.7% per patient year despite strong anti-coagulation therapy[1]. Anticoagulation therapy puts patients at several risks such as hemorrhage [2-4]. Clinical studies have shown that patients with mechanical valves have shortened platelet and red blood cell half-lives[5, 6]. St. Jude Medical (SJM) valves, despite being known for their superior hemodynamic performance and low relative thrombogenicity, still can cause patient mortality due to valvular thrombosis [7-10]. Even though tremendous design improvements in cardiovascular devices over the last 50 years and the development of new drug therapies have taken place, the problems of platelet activation, hemolysis, and thromboembolism in BMHVs still persist.

Turbulent stresses are well established factors contributing to valve related hemolysis and platelet activation[11, 12]. Therefore, minimizing the risk for platelet activation and hemolysis through reduction of turbulent stresses is the objective of every new mechanical valve design[11, 13]. Towards this goal, previous studies utilized passive flow control surface features such as vortex generators on the leaflet surface [1, 14, 15] to minimize turbulence, through delaying boundary layer separation, and platelet activation associated with the regurgitant jet. Briefly, vortex generators are passive devices placed at the surface of the valve leaflets in order to manipulate the flow to restrict detrimental effects or promote the beneficial ones[1]. The impact of vortex generators on passively controlling the flow has been studied extensively in mechanical and aerospace applications [16-18]. The main effect of vortex generators is to delay and even suppress flow separation through bringing momentum from the free stream into the boundary layer in order to allow it to sustain the strong local streamwise adverse pressure gradient[16].

Because of the “drag penalty” induced by these passive devices, many optimization studies have led, in 20 years, to a significant reduction of the vortex generator height from the order of the boundary layer thickness to only a fraction of it[16, 18]. Nevertheless, the impact of vortex generators on BMHV forward flow or the knowledge of how to choose an appropriate vortex generator configuration is still unknown, specifically for heart valve applications. Configurations of vortex generators can vary between co-rotating to counter-rotating types, with equal spaces between them or not.

The objective of this study is to investigate the impact of different vortex generator (VG) configurations and arrangements for a BMHV on pressure gradient (PG), and turbulent Reynolds shear stresses (RSS).

Materials and Methods

The effects of the VG arrangements on the downstream side of mechanical valve leaflets were quantified under pulsatile flow conditions using high resolution particle image velocimetry (PIV) technique.

Vortex generators

Five different 23mm BMHVs (Figure 1) were 3D printed and designed as follows: one BMHV was designed without VGs and considered the control case while the four others had different VG configurations mounted on the downstream side of the BMHV: (1) with 4 co-rotating equally distant VGs, (2) with counter-rotating 8 closely spaced VGs, (3) with counter-rotating 4 far spaced VGs, and (5) with counter-rotating 4 closely spaced VGs. VG heights were chosen to be 1mm, length 2.8mm, the spacing 5mm and set at an angle of incidence of 23° based on Bradbury et al[15]. Lealfets length is 20mm. VGs and valve leaflets were manufactured using high resolution stereolithography. The leaflets were 3D printed using the high resolution Stratasys Objet 30 Pro Desktop 3D Printer (Edina, Minnesota). The material utilized was VeroClear rigid transparent material. The material modulus of elasticity was reported to be 2000-3000 MPa. These 4 VG configurations and arrangements were particularly chosen as a continuation of previous studies [1, 14, 17].

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0001.jpg

Schematic of the 4 types of vortex generators used in this study: (a) co-rotating, (b) 8 equally spaced counter-rotating VGs, (c) 4 far spaced counter-rotating VGs and (d) 4 closely spaced counter-rotating VGs.

Hemodynamic assessment

Hemodynamic parameters were evaluated under pulsatile flow conditions created by a left heart simulator yielding physiological flow and pressure curves as previously described[12, 19] and as shown in (Figure 2). The cardiac output was set to be 5 L/min, the heart rate 60 beats per minutes and pressures of 120/80 mmHg. The peak flow rate reached was 25 L/min. The peak Reynolds number was 7667.4. The working fluid in this study was a blood-analogue mixture of water-glycerine (99% pure glycerine) producing a density of 1060Kg/m3 and a kinematic viscosity of 3.5cSt. One Hundred consecutive cardiac cycles of aortic pressure, ventricular pressure and flow rate data were recorded at a sampling rate of 100Hz. Flow data were acquired using ultrasonic flow probes (HXL, Transonic Inc., Ithaca, NY, USA), and pressures upstream and downstream of the valve were measured with Validyne pressure transducers (DP, Validyne Engineering Corp., Northridge, CA, USA). The mean transvalvular pressure gradient (PG) - that we will refer to as pressure gradient as adopted clinically - is defined as the average of positive pressure difference between the ventricular and aortic pressure curves during forward flow.

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0002.jpg

Schematic of the pulse duplicating left heart simulator flow loop.

The effective orifice area (EOA) is an important parameter to evaluate valve orifice opening as it is a measure of the vena contracta area. It is also an indicator of prosthetic valve efficiency[20]. EOA was computed using the Gorlin’s equation:

EOA=Q51.6PG
(1)

Where Q represents the root mean square aortic valve flow in cm3/s over the same averaging interval of the PG (in mmHg).

Particle Image Velocimetry (PIV)

For PIV, the flow was seeded with fluorescent PMMA-Rhodamine B particles with diameters ranging from 1 to 20 μm. For all cases, the velocity field within the distal flow region were measured using high spatial and temporal resolution PIV. Briefly, this involved illuminating the flow region using a laser sheet created by pulsed Nd:YLF single cavity diode pumped solid state laser coupled with external spherical and cylindrical lenses while acquiring high-speed images of the fluorescent particles within the region. The plane of measurement was aligned along the center plane of the chamber and was perpendicular to the leaflet axis. Figure 3 shows the PIV plane orientation with respect to the valve. Time-resolved PIV images were acquired with a resulting spatial and temporal resolutions of 0.035mm/pixel and 500Hz respectively. Phase locked measurements were recorded for 4 phases of the cardiac cycle (acceleration, peak, deceleration and diastole) repetitively with 250 ensembles each with a spatial resolution of 0.035mm/pixel. Refraction was corrected using a calibration in DaVis particle image velocimetry software (DaVis 7.2, LaVision Germany). Velocity vectors were calculated using adaptive cross-correlation algorithms. The thickness of the shear layers was measured from the PIV data of the vorticity and velocity fields figure. Further details of PIV measurements can be found in Hatoum et al [21-27].

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0003.jpg

Schematic of the flow through the bi-leaflet mechanical valve along with the measurement and PIV plane.

Vorticity Dynamics

Using the velocity measurements from PIV, vorticity dynamics were also evaluated distal to the valve. Vorticity is the curl of the velocity field and therefore captures rotational components of the blood flow shearing as well as visualizing turbulent eddies[12, 23]. Regions of high vorticity along the axis perpendicular to the plane indicate both shear and rotation of the fluid particles. Vorticity was computed using the following equation:

ωz=−(dVxdy−dVydx)
(2)

Where ωz is the vorticity component with units of s−1; Vx and Vy are the x and y components of the velocity vector with units of m/s respectively. The x and y directions are axial and lateral respectively with the z direction being out of plane measurement.

Reynolds shear stress (RSS)

Reynolds shear stress has been widely correlated to turbulence and platelet activation[12, 28]. It is a statistical quantity that measures the shear stress between fluid layers when fluid particles decelerate or accelerate while changing direction[12, 19]. 250 instantaneous measurements of velocity field for every phase (acceleration, peak, deceleration and diastole) were recorded. From these ensembles, the average velocity field was calculated for each phase. This average was then subtracted from the instantaneous to yield 250 fluctuating velocity fields at each phase. From the fluctuating velocity ensembles, the RSS was computed using:

RSS=ρ(u′u′¯−v′v′¯2)2+(u′v′¯)2
(3)

Equation (3) yields the principal RSS, where ρ is the blood density, and are the instantaneous velocity fluctuations in the x and y directions respectively.

Statistics

All data are presented as mean ± standard deviation. ANOVA and Bonferroni post-hoc test were used to compare the means and p < 0.05 was considered statistically significant. Analyses were performed over 100 replicates.

Results

Hemodynamic parameters

Table 1 summarizes the hemodynamic parameters of the 5 different valves. The hemodynamic assessment of the different valves showed that the Co-rotating VGs yielded the lowest pressure gradient of 10.45±0.94 mmHg. The difference between this PG value and the rest obtained with the different VG arrangements is significant with p < 0.01. The 4 far-spaced and 8 counter-rotating VG valves yielded 13.84±0.09 and 13.76±0.51 mmHg respectively, while the 4 counter-rotating closely spaced VGs yielded a pressure gradient of 15.37±0.16 mmHg. The control valve’s pressure gradient obtained was 14.88±0.40 mmHg.

Table 1:

Summary of the hemodynamic data of the 5 different valves.

Control
Valve		Co-rotating
VGs		8 Counter-
rotating equally
spaced VGs		4 Far spaced
counter-rotating
VGs		4 Closely
spaced counter-
rotating VGs
Pressure Gradient (mmHg)14.88±0.4010.45±0.9413.76±0.5113.84±0.0915.37±0.16
Effective Orifice Area (cm2)1.43±0.042.26±0.171.58±0.051.53±0.021.42±0.01

The effective orifice area values follow the trend of the pressure gradient with the Co-rotating VG valves yielding the highest EOA of 2.26±0.17 cm2. The EOA obtained with the 4 and 8 counter-rotating far spaced and closely spaced VG valves respectively were 1.53±0.02 cm2 and 1.58±0.05 cm2, and that obtained with the 4 counter-rotating closely spaced VG valves was 1.42±0.01 cm2. The EOA obtained with the control valve was 1.43±0.04 cm2.

Flow velocity fields and profiles

Figure 4 represents a schematic describing the flow through a bi-leaflet mechanical valve with vortex generators. The flow features are elucidated in this sketch and serve as a guidance for the flow field figures along with the velocity profile Vx versus y. The red and blue traces represent shear layers with red and blue being CCW and CW vorticity generated from the inner and outer surface boundary layers of each leaflet.

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0004.jpg

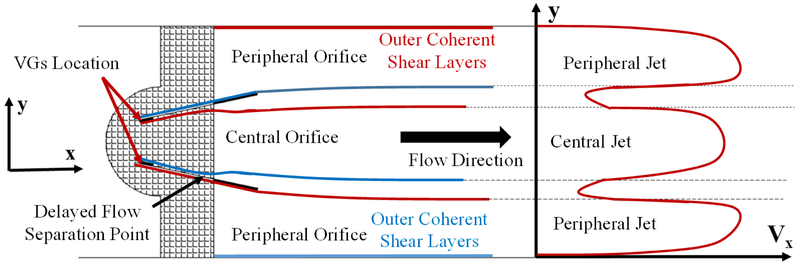
Schematic of the flow through the bi-leaflet mechanical valve with vortex generators along with the fluid structures and the velocity profile (Vx) as a function of y. The red and blue traces represent shear layers with red and blue being CCW and CW vorticity generated from the inner and outer surface boundary layers of each leaflet.

Flow velocity field is an important indicator of the velocity and vorticity state of the flow. Figure 5 shows the phase averaged velocity vectors and vorticity contours at the four different phases in the cardiac cycle for the different VG arrangement valves. Video 1 shows the fluid particles streaks for every valve case in every model over the cardiac cycle. The video explicitly shows the main differences in flow features between the 5 different valve cases. For example, the 4 far spaced counter-rotating VG valve was the last to fully open, in addition to displaying a flow pattern that looks exponentially increasing from the bottom side of the chamber to the top (at t = 2 s). The closure of the valves on the other hand takes place in the same time.

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0005.jpg

Phase averaged velocity vectors and vorticity contours at the four different phases in the cardiac cycle for the different VG arrangement valves.

Qualitatively examining the velocity and vorticity fields starting from early systole, the close counter-rotating VGs whether 4 or 8, cause streamwise decay of the central shear layers evident at acceleration, peak, and deceleration phases. They are characterized by coherent outer shear layers at the peripheral jets compared to the central shear layers which diffuse almost immediately at the valve outlet. Excluding these 2 VG cases, the fastest streamwise decay occurs with the control case without any VGs where at peak systole, vorticity in the shear layers dissipate almost immediately after detaching from the leaflet surfaces. The control case is followed by the 4 counter-rotating far spaced VG valve. The shear layer thickness at peak systole of both cases is almost equal (2.130±0.015 mm for the control case and 2.080±0.022 mm of the 4 counter-rotating far spaced VGs). The co-rotating VG case on the other hand is characterized by thinner shear layer thicknesses (1.13±0.010 mm) and a slower decay of the main jet shear layers. The observation of the slow decay is clear in deceleration where the central shear layers for the co-rotating VGs are the last to decay.

Quantitatively, the centerline velocity magnitude right at peak systole was maximal with the 4 far spaced counter-rotating VGs (1.19±0.02 m/s), followed by the co-rotating VGs (1.17±0.05m/s). The lowest centerline velocity magnitudes 0.76±0.03 m/s and 0.79±0.04 m/s were obtained for the 4 and 8 closely spaced counter-rotating VGs respectively. The valve without VGs yielded a peak velocity at peak systole of 1.14±0.03 m/s. The velocity magnitude variations during early systole (acceleration) followed the same order however, the slowest was observed with the no-VG control valve with a velocity of 0.75±0.02 m/s. During deceleration, the variation in velocity magnitudes followed that of systole.

To better visualize the variation in velocity for every case, Figures 6, ​,77 and ​and88 show the velocity profiles in the longitudinal direction (Vx) versus X (mm) along the centerline between the leaflets; and versus Y (mm) at X = 0 (right after the flow exit the leaflets) and at X = 20 mm to quantify the evolution of velocity profiles.

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0006.jpg

Vx profile at the horizontal centerline (Y=0) between the leaflets during (a) acceleration, (b) peak systole and (c) deceleration respectively.

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0007.jpg

Vx profile right after the leaflets are open (X=0) versus y during (a) acceleration, (b) peak systole and (c) deceleration respectively.

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0008.jpg

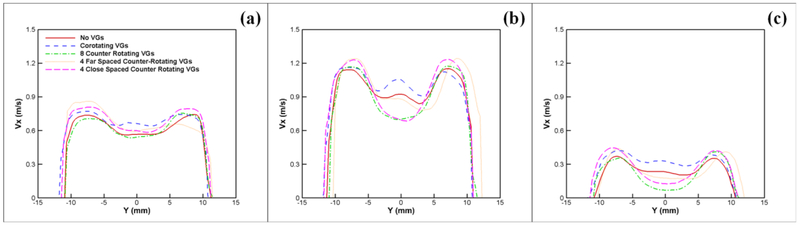
Vx profile versus y at X = 20 mm during (a) acceleration, (b) peak systole and (c) deceleration respectively.

Figures 6a, ​,6b6b and ​and6c6c shows Vx profile at the horizontal centerline (Y=0) between the leaflets during acceleration, peak systole and deceleration respectively. During acceleration, the counter-rotating VGs experience the most drastic change from the leaflets exit (X=0) throughout the region to the end of the domain centerline while the co-rotating and the no-VG control valve velocities decay in parallel, slower for the co-rotating VGs than the control case. At peak systole, the highest velocity and slowest decay in magnitude longitudinally in x was found in the co-rotating VGs case reaching 1.26m/s and ending at 1.03m/s (0.23m/s difference). Without VGs, the peak velocity was found to be 1.16m/s, decaying to reach 0.92m/s (0.24 m/s difference). The lowest peak magnitudes of Vx were found in the 4 and 8 counter-rotating closely spaced VGs reaching a maximum of 0.85m/s and ending at 0.73m/s (0.12m/s). The 4 far closely spaced VGs reached a peak of 1.86m/s and ends at 0.84m/s (1.02 m/s difference). The same profile trends were observed in deceleration.

Figures 7a, ​,7b7b and ​and7c7c show the Vx profile right after the leaflets are open versus Y. During acceleration, the co-rotating VG valve yields the highest centerline velocity with the centerline and the peripheral jet velocities being the closest (0.05 m/s) compared to the other VGs. During peak systole, the lowest Vx magnitudes at the center jet were obtained with the 4 and 8 counter-rotating VG cases reaching 0.77m/s while the peripheral jets reach a velocity of 1.27m/s (0.5m/s difference). The 4 far-spaced counter-rotating VGs Vx varied from 1.22m/s in the central jet to 1.31m/s in the peripheral jets (0.09m/s). 0.03m/s velocity difference was obtained with the co-rotating VGs (the smallest difference), and 0.08m/s difference was obtained with the control case without any VGs. The same profile trends were observed in deceleration.

Figures 8a, ​,8b8b and ​and8c8c show the Vx profile versus y at x = 20 mm. The most interesting feature in this figure is the relative reduction in Vx for the no-VG control valve case compared with Figure 7a during acceleration (0.56 m/s from 0.69 m/s). The centerline velocity profile is flatter than that observed at the outlet of the leaflets and is “catching up” to the peripheral velocity profiles.

Reynolds shear stress (RSS) field

Figure 9 displays the Reynolds shear stress contours of the different valve cases at different time points throughout the cardiac cycle.

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0009.jpg

Reynolds shear stress contours of the different valve cases at different time point throughout the cardiac cycle.

Qualitatively during acceleration, when VGs are far spaced, the distribution of RSS looks different compared to all the other cases irrespective of the magnitude. During mid-systole, more dispersion due to turbulent advection is noted with the 4 far and closely spaced counter-rotating VGs along with the control case without any VG. Decay in RSS is observed in all the cases with increasing distance from the valve.

Quantitatively, RSS magnitudes decreased significantly with VGs compared to the control case. During acceleration, RSS varied as follows: 19.3±0.72Pa, 9.76±0.13Pa, 9.16±0.54Pa, 15.14±0.42Pa, and 7.76±0.34Pa for control, co-rotating VGs, 8 counter-rotating VGs, 4 far-spaced VGs and 4 closely-spaced VGs respectively. At peak systole, RSS magnitudes calculated for the VG cases were also lower than those calculated without VGs. RSS was found to be 38.13±0.89Pa, 12.95±0.32Pa, 15.75±0.71Pa, 24.54±0.84Pa and 16.33±0.58Pa for control, co-rotating VGs, 8 counter-rotating VGs, 4 far-spaced VGs and 4 closely-spaced VGs respectively. The co-rotating VGs yielded the lowest RSS magnitudes with statistically significant differences compared with all the other cases (p < 0.001).

Discussion

In this manuscript, to evaluate the reduction in turbulence and its effect on valve performance, several parameters were assessed namely, (a) pressure gradient and effective orifice area, (b) Reynolds shear stress fields, and (c) flow velocity fields, for all five valve cases with and without VGs. While PG and EOA are net measures of energy losses and therefore valve performance, RSS and flow velocity fields help identify the spatio-temporal locations of flow instabilities and quantify overall turbulence characteristics. With such a broad set of parameters to evaluate the reduction in turbulence, it is possible to simultaneously assess the mechanisms of turbulence reduction along with assessing clinical impact in terms of valve performance as well as potential for blood damage and platelet activation. In this study, the differences engendered as a result of having 4 different arrangement of VGs on the downstream side of the mechanical valve leaflet versus no VGs on the leaflet were assessed through looking at (a) the relevant hemodynamic performance parameters and (b) the turbulent Reynolds shear stresses. Flow through a bi-leaflet mechanical heart valve can be highly turbulent with Reynolds numbers exceeding 5000 and reaching 8000 [29, 30]. The importance of studying turbulence post implantation stems from its effect on platelet activation, hemolysis, and effects on pressure drop and recovery. In addition, the most optimal VG arrangement for the mechanical valve application has not been completely established yet specifically for this type of applications and this study constitutes a first step towards that goal. The inherent simplicity of VGs along with their low drag are demonstrated to be critical and highly important for many applications and in particular to heart valve engineering[17].

Hemodynamic parameters

Previous studies have shown that the presence of vortex generators eliminates the inflection point in the streamwise pressure distribution curve that indicates the location of separation of the boundary layer[17]. This indicates that the separation has significantly reduced. Not only separation is reduced, but also a significant improvement in downstream pressure recovery was also observed and obtained[17]. The data presented in this manuscript concord the results of these previous studies with the pressure gradients being less or equal to the no-VG control case [1, 14, 17] and the EOA significantly improved compared to the control case. Undeniably the addition of VGs has induced a reduction in transvalvular pressure gradients and improved the EOA. EOA improvement signifies a great improvement in the efficiency of the prosthetic heart valve [20].

The co-rotating VGs showed improved reduction in pressure gradients compared with the counter-rotating ones. Previous studies have shown that the choice between co-rotating and counter-rotating VGs depends strongly on the type of flow separation[17]. However, to investigate this aspect, the turbulent flow field needs to be investigated as explained in the section below.

In addition, the difference between the counter-rotating VG valves will be further investigated through looking at the turbulent flow field characteristics.

Flow velocity fields and profiles and relationship with turbulence

The flow velocity fields and shear layers are different among the different valves. The drastic difference in velocity throughout the x direction in the far-spaced VGs case partially explains the diffusion and the higher RSS values obtained compared to the other VGs. Meanwhile the minimum losses in velocity (and therefore mean shear) in the x and y direction along with the smooth decay were found with the co-rotating VGs case. This result highlights the lower turbulence and thus the lower RSS obtained (shown in Figures 5 and ​and9).9). The intensity of the vorticity concentrations are clearly lowest for the co-rotating VGs case, which indicates that the vorticity generated from the VGs not only disperses and disintegrates the coherent flow structure but also diminishes the local shear and rotation indicating a counter balancing effect of the introduced/shed vorticity from the VGs[14]. The overall effect of this disintegration and diminution of the mean shear translates to lower turbulent production (and consequently lowered energy dissipation) with lower Reynolds stresses as opposed to a strong coherent flow structure of high stress and large scale instability.

To verify this point, the root mean square of the fluctuations in velocity (Vx’ and Vy’) for the different valve cases are shown in Figure 10. Velocity fluctuations are characteristics of turbulent flow. These fluctuations give an indication about how turbulent the blood flow is thus providing an assessment of the valve performance[12].

An external file that holds a picture, illustration, etc. Object name is nihms-1506616-f0010.jpg

Root mean square of the fluctuations in velocity (Vx’ and Vy’) at peak systole for the different valve cases.

Comparing the co-rotating VGs valve with the control case, the contour plots of Vx’ RMS show the overlap in shear layers at the exit from the leaflets while the shear layers are widely spread out for the Co-rotating VGs case. This observation strengthens the fact that separation without VGs has started earlier (characterized by a growth in shear layers[31, 32]) while with the co-rotating ones it was delayed. This delay contributed to lower turbulence, which in turn explains the decrease in pressure gradient along with RSS. The fluctuations in the y-direction are tightly related to the unsteadiness explained in the streamwise component of velocity, and vorticity fields above showing a more stable behavior for the Co-rotating VGs.

It is clear, based on the above discussion that the co-rotating VGs for this application induce a more delayed flow separation compared with the counter-rotating VGs, and a more homogenized and streamlined transition of flow. Lin et al have also highlighted the streamlined flow transition with the use of co-rotating VGs[17].

Looking closely at the velocity fluctuations of the counter-rotating VGs, it is clear that the far-spaced ones cause the most of the observed instabilities in Vx and Vy which explains the high RSS values obtained. It seems that allowing a space between the counter-rotating VGs on the surface of the leaflet geometrically altered the efficient momentum transfer between vortices [14, 16, 17]. The most optimal counter-rotating VG arrangement seems to be the closely spaced equally distributed 8 VGs. Not only the close arrangement allows the efficient moment transfer of vortices, but also it ensures that there is no discontinuity. Because separation in flow across mechanical valves occurs in the mid-section [29, 33, 34], the effect of spacing between the counter-rotating VGs (far spaced) was more drastic on the engendered turbulence than the spacing at the 2 top sides (4 closely spaced counter-rotating VGs). And because of the same reason, the 8 counter-rotating closely spaced VG arrangement yielded – though insignificantly - less turbulence than the 4 closely spaced counter-rotating VG one (Figure 9).

The more drastic the differences in Vx between the middle jet and those at the periphery are, the more they validate the occurrence of flow shearing. Thus, the turbulent diffusion and dissipation that show in the middle of the RSS plots particularly in the cases of the 4 and 8 closely spaced co-rotating VGs, are explained and confirmed by the velocity contour plots. In addition to this, geometry of the closely spaced VGs in the counter-rotating cases plays an important role. The closely spaced counter-rotating VGs seem to be blocking the propagation of the vorticity layers in the middle jet. The velocity values obtained in the middle jet for both cases were lowest and the differences between the velocity of the middle jet and that of the peripheral jets was shown to be highest. However, longitudinally the losses are not as tremendous thus the RSS obtained were not expected to be highest as confirmed by the results. The far spaced counter-rotating VGs allow the shear layers to propagate through the middle. However, the constriction of the VGs comes into play generating a more turbulent flow thus causing higher RSS in that region.

Counter-rotating VGs (owing to the geometry) may have enhanced turbulence compared to the co-rotating ones. This may be due to interaction of opposite signed axial vortices. While co-rotating VGs generated same sign axial vortices that helped streamline the flow and maintain a high velocity and a more gradual decay from leaflet tips at x=0mm to x=20mm (Fig.7). Without any VGs, the early separation not only leads to stronger turbulence, but also to more energy dissipation characterized by a drastic and fast drop in velocity until the end. This observation has also been highlighted on swept wings of aircrafts where boundary layer separation was delayed more efficiently with co-rotating VGs compared with counter-rotating ones[35].

However and as explained in Dasi et al[14], the remarkable turbulence reduction in the presence of VGs compared to the control case, is in fact due to the dispersion of the jet due to added instabilities. Nevertheless, in their study, the co-rotating arrangement of VGs on the downstream side of the leaflets was not studied. The local convective acceleration noted from the velocity magnitude differences occurs due to the partial blockage from the VG particular geometry. The dispersion on the other hand occurs due to vorticity generated from the tips of the VGs. The convective acceleration and the dispersion of the jet are two simultaneous mechanisms that work together by stabilizing the flow thus reducing the generation of fine scale structure (turbulence), and diminishing mean shear (thus turbulence production).

Previous in-vitro studies investigated and assessed the risk of blood damage and attempted to set some thresholds that mark the onset of platelet activation. However, thresholds are not well-established, and indeed the characterization of turbulent stress is still controversial. Hung et al. reported platelet damage at 100–165 dynes/cm2 with an exposure time of 102 s[36]. Williams et al established the onset of platelet activation at 130 dynes/cm2 under an exposure time of 1023 s[37]. Ramstack et al. reported platelet activation at 300–1000 dynes/cm2 at an exposure time of 10s[38]. It was also shown in a study by Kameneva et al that turbulent flow increase the level of hemolysis compared with laminar flow[39] at the same exposure time. Even further, a study by Quinlan et al [40] explains that in laminar flow, the maximum stress on a cell is approximately equal to the macroscopic viscous shear stress. In turbulent flow through a prosthetic heart valve, the flow-induced stress on a cell is estimated to be at least an order of magnitude less than the Reynolds stress[40]. In addition to this study, another study by Hund et al [41] elucidates that RSS may not be fully representative of the effects of turbulent flow on blood trauma and in fact introduces an error. Antiga and Steinman [42] highlighted the importance of cell-to-cell interaction in blood damage during turbulent flow and how turbulent velocity fluctuations can give rise to viscous shear stress however they don’t rule out the importance of RSS as a potential indicator of blood damage. Yin et al reported for bi-leaflet mechanical valves a particle shear stress history of 2 Pa.s [43]. The RSS values obtained in this study under a prolonged exposure time fall within this limit. Instantaneous vorticity dynamics illustrate that VGs lead to a delay in flow separation and a reduction in free shear instabilities. This contributes to lower pressure drop and lower turbulence and RSS compared to not having any VGs[1].

In summary, in this paper the effectiveness of passive flow control concepts applied to prosthetic bi-leaflet heart valve flows was evaluated and the most optimal arrangement among the 4 different ones studied in this work was identified. Co-rotating VG and counter-rotating VG arrays were distributed on the downstream side of the valve leaflets. The addition of vortex generators enhances lower transvalvular pressure gradients and yield Reynolds shear stress values that are lower than those obtained without any vortex generators. Co-rotating equally-spaced VGs on the downstream side of the leaflet present the most optimal case for a better pressure gradient, an improved EOA and minimal turbulence. Vortex generators represent a passive flow control and design addition that would help mitigate the hemodynamic factors leading to platelet activation and potential thrombus formation risk for a better and more optimal mechanical valve design.

Limitations

There are a few limitations in this study. Only 4 different VG configurations were studied including only one co-rotating configuration. Further studies are needed to investigate different VG arrangements, in addition to optimize the best geometry, dimensions and distribution. Also, 2D fluid mechanics analysis may not be sufficient to comprehensively evaluate the flow features across the valve and further studies are required to investigate these flow features in more details. The results in this study are provided for only one plane. Vortex generators will skew energy onto other planes in the form of longitudinal vortices, making the results valid only for the plane studied. We also acknowledge the potential complex manufacturability of the bi-leaflet mechanical valves with vortex generators as these are small structures of particular spacing and sizing. Our study resolves all the scales above the Taylor microscale where the energy containing eddies exist.

Supplementary Material

Video 1:

Fluid particles streaks for every valve case in every model over the cardiac cycle.

Acknowledgment

The research done was partly supported by National Institutes of Health (NIH) under Award Number R01HL119824 and R01HL135505.

Abbreviations, symbols and terminology

VGVortex Generators
PGPressure Gradient
RSSReynolds shear stress
PIVParticle Image Velocimetry
EOAEffective Orifice Area
BMHVBi-leaflet Mechanical Heart Valve

Footnotes

Conflict of Interest: Dr. Dasi reports having two patent applications on novel surgical and transcatheter valves. He also has a patent issued on vortex generators on heart valves and a patent application on super hydrophobic vortex generator enhanced mechanical heart valves. No other conflicts were reported.

References

1. Murphy DW, et al., Reduction of procoagulant potential of b-datum leakage jet flow in bileaflet mechanical heart valves via application of vortex generator arrays. Journal of biomechanical engineering, 2010. 132(7): p. 071011. [Abstract] [Google Scholar]
2. Poller L, et al., Managing oral anticoagulant therapy. Chest, 2001. 119: p. 22S–38S. [Abstract] [Google Scholar]
3. Cannegieter SC, et al., Optimal oral anticoagulant therapy in patients with mechanical heart valves. New England Journal of Medicine, 1995. 333(1): p. 11–17. [Abstract] [Google Scholar]
4. Vandenmeer F, et al. Bleeding complications in patients treated with oral anticoagulants in a routine situation. in Thrombosis and Haemostasis. 1993. FK SCHATTAUER VERLAG GMBH PO BOX 10 45 45, LENZHALDE 3, D-70040 STUTTGART, GERMANY. [Google Scholar]
5. Dale J and Myhre E, Intravascular hemolysis in the late course of aortic valve replacement. Relation to valve type, size, and function. American heart journal, 1978. 96(1): p. 24–30. [Abstract] [Google Scholar]
6. Harker LA and Slichter SJ, Studies of platelet and fibrinogen kinetics in patients with prosthetic heart valves. New England Journal of Medicine, 1970. 283(24): p. 1302–1305. [Abstract] [Google Scholar]
7. Baudet EM, et al., A 5 1/2 year experience with the St. Jude Medical cardiac valve prosthesis. Early and late results of 737 valve replacements in 671 patients. The Journal of thoracic and cardiovascular surgery, 1985. 90(1): p. 137–144. [Abstract] [Google Scholar]
8. Chang B, et al., Long-term results with St. Jude Medical and CarboMedics prosthetic heart valves. The Journal of heart valve disease, 2001. 10(2): p. 185–194; discussion195. [Abstract] [Google Scholar]
9. Ibrahim M, et al., The St. Jude Medical prosthesis: a thirteen-year experience. The Journal of thoracic and cardiovascular surgery, 1994. 108(2): p. 221–230. [Abstract] [Google Scholar]
10. Masters R, et al., Comparative results with the St. Jude Medical and Medtronic Hall mechanical valves. The Journal of thoracic and cardiovascular surgery, 1995. 110(3): p. 663–671. [Abstract] [Google Scholar]
11. Dasi LP, et al., Fluid mechanics of artificial heart valves. Clinical and experimental pharmacology and physiology, 2009. 36(2): p. 225–237. [Europe PMC free article] [Abstract] [Google Scholar]
12. Hatoum H, et al., An In-Vitro Evaluation of Turbulence after Transcatheter Aortic Valve Implantation. The Journal of Thoracic and Cardiovascular Surgery, 2018. [Europe PMC free article] [Abstract] [Google Scholar]
13. Vongpatanasin W, Hillis LD, and Lange RA, Prosthetic heart valves. New England Journal of Medicine, 1996. 335(6): p. 407–416. [Abstract] [Google Scholar]
14. Dasi LP, et al., Passive flow control of bileaflet mechanical heart valve leakage flow. Journal of Biomechanics, 2008. 41(6): p. 1166–1173. [Abstract] [Google Scholar]
15. Bradbury L and Khadem A, The distortion of a jet by tabs. Journal of Fluid Mechanics, 1975. 70(4): p. 801–813. [Google Scholar]
16. Godard G and Stanislas M, Control of a decelerating boundary layer. Part 1: Optimization of passive vortex generators. Aerospace Science and Technology, 2006. 10(3): p. 181–191. [Google Scholar]
17. Lin JC, Review of research on low-profile vortex generators to control boundary-layer separation. Progress in Aerospace Sciences, 2002. 38(4-5): p. 389–420. [Google Scholar]
18. Lin J Control of turbulent boundary-layer separation using micro-vortex generators. in 30th Fluid Dynamics Conference 1999. [Google Scholar]
19. Hatoum H, et al., Impact of Patient Morphologies on Sinus Flow Stasis in Transcatheter Aortic Valve Replacement: An in-vitro study. The Journal of Thoracic and Cardiovascular Surgery, 2018. [Europe PMC free article] [Abstract] [Google Scholar]
20. Yoganathan AP, He Z, and Casey Jones S, Fluid mechanics of heart valves. Annu. Rev. Biomed. Eng, 2004. 6: p. 331–362. [Abstract] [Google Scholar]
21. Hatoum H, et al., Aortic sinus flow stasis likely in valve-in-valve transcatheter aortic valve implantation. The Journal of thoracic and cardiovascular surgery, 2017. 154(1): p. 32–43. e1. [Europe PMC free article] [Abstract] [Google Scholar]
22. Hatoum H, et al., Implantation Depth and Rotational Orientation Effect on Valve-in-Valve Hemodynamics and Sinus Flow. The Annals of thoracic surgery, 2018. [Europe PMC free article] [Abstract] [Google Scholar]
23. Hatoum H, et al., Effect of severe bioprosthetic valve tissue ingrowth and inflow calcification on valve-in-valve performance. Journal of biomechanics, 2018. 74: p. 171–179. [Europe PMC free article] [Abstract] [Google Scholar]
24. Hatoum H, Heim F, and Dasi LP, Stented valve dynamic behavior induced by polyester fiber leaflet material in transcatheter aortic valve devices. Journal of the mechanical behavior of biomedical materials, 2018. 86: p. 232–239. [Europe PMC free article] [Abstract] [Google Scholar]
25. Hatoum H, Moore BL, and Dasi LP, On the Significance of Systolic Flow Waveform on Aortic Valve Energy Loss. Annals of biomedical engineering, 2018: p. 1–10. [Europe PMC free article] [Abstract] [Google Scholar]
26. Hatoum H and Dasi LP, Sinus Hemodynamics in Representative Stenotic Native Bicuspid and Tricuspid Aortic Valves: An In-Vitro Study. Fluids, 2018. 3(3): p. 56. [Google Scholar]
27. Hatoum H, et al., Sinus Hemodynamics Variation with Tilted Transcatheter Aortic Valve Deployments. Annals of biomedical engineering, 2018: p. 1–10. [Europe PMC free article] [Abstract] [Google Scholar]
28. Giersiepen M, et al., Estimation of shear stress-related blood damage in heart valve prostheses-in vitro comparison of 25 aortic valves. The International journal of artificial organs, 1990. 13(5): p. 300–306. [Abstract] [Google Scholar]
29. Chandran KB, Rittgers SE, and Yoganathan AP, Biofluid mechanics: the human circulation. 2006: CRC press. [Google Scholar]
30. Khalili F, Gamage P, and Mansy HA, Hemodynamics of a Bileaflet Mechanical Heart Valve with Different Levels of Dysfunction. arXiv preprint arXiv:1711.11153, 2017. [Google Scholar]
31. Simpson RL, Turbulent boundary-layer separation. Annual Review of Fluid Mechanics, 1989. 21(1): p. 205–232. [Google Scholar]
32. Dovgal A, Kozlov V, and Michalke A, Laminar boundary layer separation: instability and associated phenomena. Progress in Aerospace Sciences, 1994. 30(1): p. 61–94. [Google Scholar]
33. David T and Hsu C, The integrated design of mechanical bi-leaflet prosthetic heart valves. Medical engineering & physics, 1996. 18(6): p. 452–462. [Abstract] [Google Scholar]
34. Govindarajan V, et al., Impact of design parameters on bi-leaflet mechanical heart valve flow dynamics. The Journal of heart valve disease, 2009. 18(5): p. 535. [Europe PMC free article] [Abstract] [Google Scholar]
35. KJ L and S. JJ Experimental investigation of maneuver performance enhancements on an advanced fighter/attack aircraft. in AIAA 33rd Aerospace Sciences Meeting 1995. Reno, NV. [Google Scholar]
36. Hung T, et al., Shear-induced aggregation and lysis of platelets. ASAIO Journal, 1976. 22(1): p. 285–290. [Google Scholar]
37. Williams A, Release of serotonin from human platelets by acoustic microstreaming. The Journal of the Acoustical Society of America, 1974. 56(5): p. 1640–1643. [Abstract] [Google Scholar]
38. Ramstack J, Zuckerman L, and Mockros L, Shear-induced activation of platelets. Journal of biomechanics, 1979. 12(2): p. 113–125. [Abstract] [Google Scholar]
39. Kameneva MV, et al., Effects of turbulent stresses upon mechanical hemolysis: experimental and computational analysis. ASAIO journal, 2004. 50(5): p. 418–423. [Europe PMC free article] [Abstract] [Google Scholar]
40. Quinlan NJ and Dooley PN, Models of flow-induced loading on blood cells in laminar and turbulent flow, with application to cardiovascular device flow. Annals of biomedical engineering, 2007. 35(8): p. 1347–1356. [Abstract] [Google Scholar]
41. Hund SJ, Antaki JF, and Massoudi M, On the representation of turbulent stresses for computing blood damage. International journal of engineering science, 2010. 48(11): p. 1325–1331. [Europe PMC free article] [Abstract] [Google Scholar]
42. Antiga L and Steinman DA, Rethinking turbulence in blood. Biorheology, 2009. 46(2): p. 77–81. [Abstract] [Google Scholar]
43. Yin W, et al., Flow-induced platelet activation in bileaflet and monoleaflet mechanical heart valves. Annals of biomedical engineering, 2004. 32(8): p. 1058–1066. [Abstract] [Google Scholar]

Full text links 

Read article at publisher's site: https://doi.org/10.1007/s10439-018-02128-6

Read article for free, from open access legal sources, via Unpaywall: https://europepmc.org/articles/pmc6408289?pdf=renderUnpaywall

Citations & impact 

Impact metrics

11
Citations
Jump to Citations

Citations of article over time

Alternative metrics

Altmetric item for https://www.altmetric.com/details/53424383
Altmetric
Discover the attention surrounding your research
https://www.altmetric.com/details/53424383

Article citations

Go to all (11) article citations

Data 

Data behind the article

This data has been text mined from the article, or deposited into data resources.

BioStudies: supplemental material and supporting data

Similar Articles 

To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.

Funding 

Funders who supported this work.

NHLBI NIH HHS (3)

National Institutes of Health (2)