Abstract
Free full text

Confronting models with data: the challenges of estimating disease spillover
Abstract
For pathogens known to transmit across host species, strategic investment in disease control requires knowledge about where and when spillover transmission is likely. One approach to estimating spillover is to directly correlate observed spillover events with covariates. An alternative is to mechanistically combine information on host density, distribution and pathogen prevalence to predict where and when spillover events are expected to occur. We use several case studies at the wildlife–livestock disease interface to highlight the challenges, and potential solutions, to estimating spatio-temporal variation in spillover risk. Datasets on multiple host species often do not align in space, time or resolution, and may have no estimates of observation error. Linking these datasets requires they be related to a common spatial and temporal resolution and appropriately propagating errors in predictions can be difficult. Hierarchical models are one potential solution, but for fine-resolution predictions at broad spatial scales, many models become computationally challenging. Despite these limitations, the confrontation of mechanistic predictions with observed events is an important avenue for developing a better understanding of pathogen spillover. Systems where data have been collected at all levels in the spillover process are rare, or non-existent, and require investment and sustained effort across disciplines.
This article is part of the theme issue ‘Dynamic and integrative approaches to understanding pathogen spillover’.
1. Introduction
Predicting where and when a pathogen will transmit, or spillover, from a reservoir host to another species is a key issue for managing health risks to humans, livestock and wildlife [1–3]. Developing a better understanding of this transmission process would allow for more strategic investment of resources to disease prevention, by optimizing the allocation of assets to areas, populations and times of highest spillover risk. Models of disease spillover come in many different forms—from models of viral evolution within a host, to Kermack–McKendrick models of disease dynamics over time in a population, to phenomenological statistical models of disease emergence events [4,5]. Here, we focus on estimating the spillover dynamics of pathogens known to transmit across the wildlife–livestock interface. We describe research challenges and opportunities for mechanistic models to improve our understanding and prediction of pathogen spillover, and highlight lessons learned from case studies of brucellosis and avian influenza.
Lloyd-Smith et al. [6] noted how the force of infection from one host species to another is a function of prevalence in the reservoir (donor host (h1)), contact rate between donor and recipient host species (h2) and probability of infection given contact. Plowright et al. [7] elaborated on this idea, noting how the contact rates among host species depend on spatial distribution and host density as well as the persistence and movement of the pathogen in the environment or vectors. These factors can be modelled as a series of conditional probabilities [7]. Conceptually, this process is straightforward; however, when trying to apply this framework to specific systems and datasets, we have encountered numerous challenges.
Disease models typically focus on the dynamics in either the donor or recipient host species [6]. More comprehensive spillover risk assessments will require a synthesis of many datasets across host species and will vary along a spectrum of mechanistic and phenomenological approaches. By phenomenological, we mean approaches that relate the observed spillover events, z, as the dependent variable to some linear or nonlinear function of predictor variables, X, and coefficients β (e.g. [5,8,9]). Alternatively, one could combine information on host species density, prevalence, contact rate and infection rates to predict the number of spillovers,
In figure 1, mechanistic approaches attempt to move from data to inference about spillovers by first going left to right across each layer (rows) to create spatio-temporal distributions of host density, pathogen prevalence, transmission and shedding. Those spatio-temporal maps can then be combined to predict spillover events. Phenomenological models move directly across the bottom row of figure 1, using direct observations of spillovers to estimate risk using covariates (e.g. temperature, precipitation, habitat type and land-use) that are correlated with host and pathogen distributions but may not include direct information on those components. By choosing covariates that align well with the spatial and temporal resolution of interest, phenomenological models may avoid some of the difficulty noted below when direct estimates of host density and pathogen shedding patterns are required. A mechanistic approach may be possible when spillover events are rare or are hard to differentiate from subsequent transmission in the recipient host. When spillover events are common, they can be investigated directly using either mechanistic or phenomenological models. Mechanistic models are likely to be constructed at finer spatio-temporal resolutions, making them more useful to local landowners and agencies compared to the coarser resolutions in phenomenological models that are informative at the regional, or national, level. Both approaches are important and useful, particularly when they can be compared to one another, and they are challenged by similar empirical issues. We focus below on the empirical issues that we have encountered in several well-studied wildlife–livestock systems. We briefly describe the elements of a mechanistic approach to spillover and then relate this to our case studies. We end with a discussion of the challenges and potential ways forward in the empirical estimation of disease spillover.
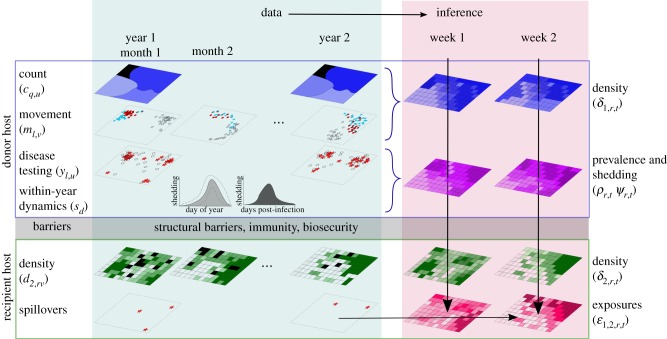
Observational data are collected at a variety of spatial and temporal resolutions (e.g. v = month, u = year, d = day of year, q = management units and l = point locations) that must be related to the regions, r, and times, t, of interest. A mechanistic approach estimates the underlying layers and combines them together to predict spillover (across rows and then down), while a phenomenological approach uses the spillover data themselves to predict exposures (bottom row) and relates that to covariates. Black regions represent missing count and density data, while white regions reflect recipient host densities that are zero. Movement data (here depicted as from three individuals) may be missing from some regions and years. Disease testing data may be collected as point locations but need to be smoothed over space or time. Pathogen shedding may vary seasonally either owing to the population dynamics of vectors or owing to within-year variation in disease prevalence.
2. Building in mechanisms to models of spillover
As an example of a ‘mechanistic’ model of spillovers, let δ1,r,t represent the density of host species 1 (the donor) in region r at time t. The disease prevalence is ρ1,r,t and the rate of shedding given an individual is positive is ψ. The total amount of pathogen shed into a region at a point in time would be δ1(r, t)ρ1(r, t)ψ. Then the predicted number of spillovers
Figure 1 highlights some of the issues associated with going from the observed data on each layer (left side) to statistical inference (right side) and then predictions of spillover (bottom right). Data come from different sampling designs and spatio-temporal resolutions. For example, host movement information may come from tracking devices that collect data at high spatial and temporal resolution (e.g. daily or hourly). However, the data may be only available for a few known individuals which may not be representative of all regions or donor species. In figure 1, the movement data are summarized by month, while the donor host population counts are only available annually at a management unit scale. Individual disease tests may be sparse and collected at point locations during one season even though pathogen shedding, vector abundances and disease prevalence may vary within and across years. Finally, the recipient host density, δ2, may also vary in space and time, and be collected at a different spatial and temporal resolution. The first challenge in combining these datasets is to place them on a common spatial and temporal resolution.
The choice of spatio-temporal resolution affects both the methodology and the utility of the resulting predictions. Coarse resolutions allow the aggregation of data, decreasing the number of regions with missing data and may be appropriate for national-level policy and allocation of resources to states or provinces at highest risk. However, livestock producers or local governments need finer scale information prior to investing in preventive measures. Fine-scale predictions will also require more estimation of unsampled areas, probably have higher uncertainty, and incur more computational demands. In addition, movement of hosts across boundaries is likely to become a more important issue for finer spatial resolutions.
Data aggregation creates both scale and zoning effects [12]. The smoothing effect caused by averaging over larger areas or timespans tends to reduce the heterogeneity among units. For pathogens or hosts that are highly variable in space or time, aggregation will result in information loss. The zoning effect refers to how the location of the regional boundaries can also affect statistical estimates and conclusions. Gerrymandering, or the redrawing of boundaries to concentrate some types of voters, is an example of the importance of the zoning effect. In the spatial statistical literature, this is often referred to as a modifiable areal unit problem, or more generally, as a change of support problem [12]. Changing the scale and support of a variable, say by aggregating point-level data to annual summaries for a region, creates a new variable with different uncertainty properties. Correlations between variables, or in this case between spillover events and donor host and disease distributions, will vary depending on how data are aggregated. This issue is not easily resolved, but has important consequences for understanding underlying mechanisms [13]. One approach to analysis of data at mismatched scales or supports is to model the process of interest (i.e. risk) at a resolution fine enough that the support of all data streams can be approximated by aggregating the fine resolution. As some data sources are only available at coarser resolutions, a hierarchical model could be constructed [13] in which missing data at the fine resolution are seen as latent variables to be estimated. In this approach, data collected at a coarser resolution constrain the latent variables at the fine resolution, as the sum of the latent process over the region observed at a coarser resolution must equal the total observation at the coarser resolution.
Many datasets of population counts, movement or disease tests will lack information for some regions or times, or have areas of limited overlap. In figure 1, there are regions with movement, but not count data and vice versa. To fill in the missing estimates, one could insert the global mean, interpolate the mean of its neighbours in space or time, or predict the missing values based on covariates. Movement information may help predicting changes in wildlife distributions, particularly for species that seasonally migrate. In addition, movement data can be used in habitat selection models to ‘downscale’ regional information on host abundance to more local estimates that account for wildlife hosts concentrating in better habitats within the region. Most habitat selection models or species distribution models, however, are based on presence-only information, either from movement or sighting data, and provide only relative, rather than absolute, measures of selection, occurrence or abundance [14]. This makes it difficult to estimate δ directly from either occurrence or movement data alone [15]. Integrating host count and movement information may allow for the estimation of the latent host density, δ1,r,t at a finer spatial and temporal resolution than the count data. However, this would make for a relatively complicated statistical model even prior to incorporating the other layers in the spillover process. As example, electronic supplementary material, figure S1 shows a directed acyclic graph that illustrates the various dependencies between the observed movement and count data and the inferred host density. This model can then be fitted with standard Markov chain Monte Carlo approaches that would allow us to assess our uncertainty in the density estimates and account for the different scales of observation. One might wonder whether this level of statistical detail is necessary. At some spatial and temporal scales, it may be reasonable to ignore movements across regions. However, a statistical model will almost certainly be required to predict unsampled areas, convert from one scale to another, and generate estimates of uncertainty.
We can construct additional statistical models for estimates of disease prevalence, pathogen shedding, vector abundance and movement, and recipient host densities. Any one of the layers in the spillover process can quickly become complicated. One of the key challenges in this mechanistic approach is to identify those processes which may be simplified or ignored while still providing biologically meaningful inference. The mechanistic approach here potentially has several different submodels for the different layers, which are then combined. Deciding which statistical models to fit jointly, and which can be fitted one at a time, has important implications for estimating the uncertainty of our predictions. Fitting models separately and using parameter estimates from one model as fixed parameters in another model, ignoring the uncertainty in these estimates, is referred to as an empirical Bayesian approach [16]. More complicated approaches include propagating the uncertainty in the posterior distribution of parameters in one model by integrating over that uncertainty, as is done in multiple imputation, e.g. [17]. A full Bayesian approach would specify a hierarchical model and obtain joint inference on all latent variables simultaneously. An empirical Bayesian approach is likely to produce estimates with less uncertainty than a full Bayesian approach, while multiple imputation is likely to produce estimates with more uncertainty than a full Bayesian approach. Thus, inference based on multiple imputation is likely to be slightly conservative, while inference based on empirical Bayesian is likely to be slightly anti-conservative. Recent work has introduced approaches for approximating fully Bayesian inference from output from individual models fitted separately [18], but these approaches have not been applied to systems as complex as disease risk prediction.
There is little theoretical guidance on the relationship between empirical Bayesian multiple imputation, and full Bayesian approaches to inference. Hierarchical Bayesian inference is often a defensible choice, but we do not view them as a panacea. Combining multiple models requires significant time to understand how the different pieces influence one another, whether parameters are identifiable, and the relative importance of prior distributions and data. In addition, the computational cost can be extreme. Researchers are time-limited, so time spent on a more complex statistical model may come at the cost of overlooking some other important component or assumption. Finally, the appropriate weighting of different datasets may not be obvious and is not necessarily proportional to the number of observations (e.g. global positioning system (GPS) movement datasets may include millions of locations on only a few individuals). Developing better methods to understand the uncertainty in our spillover estimates is an important avenue of future development—it determines whether regional differences in risk are significant, given our uncertainty, and where additional investment could be more optimally allocated to reduce that uncertainty.
3. Case study: brucellosis in elk, bison and livestock in Montana and Wyoming
In the 1930s, brucellosis was widespread in livestock across the USA and a significant human health concern [19]. Test-and-cull and vaccination programmes in livestock largely eradicated the disease from domestic animals, but not before this European pathogen spilled-over from livestock to wildlife multiple times [20]. Currently, elk (Cervus canadensis) and bison (Bison bison) in the Greater Yellowstone Ecosystem of Montana, Wyoming and Idaho are the last reservoirs of Brucella abortus, one of the causative agents of brucellosis, in the USA. Several cattle herds are infected by elk in each of these states per year [21] resulting in quarantines and slaughter to maintain the disease-free status of the rest of the US livestock population. As the name suggests, B. abortus is transmitted via abortion events that primarily occur in the spring [22].
From 2002 to 2014, only 21 livestock herds were affected in the region, limiting the amount of information that could be gleaned from the spillovers directly [23]. However, Brennan et al. [23] concluded that the rate of spillover was weakly associated with the density of seropositive elk at the coarse management unit scale and was increasing over time. This analysis, however, is of limited use to individual livestock producers for assessing relative risk on federal grazing allotments versus private properties because of its coarse spatial scale.
Merkle et al. [24] took a more mechanistic and fine-scale approach around the supplemental feeding grounds of Wyoming. These supplemental feeding grounds segregate elk and bison spatially from livestock during the late winter and early spring, but also create dense aggregations that probably facilitate brucellosis transmission within elk. The feeding grounds also facilitate data collection such that annual elk population counts, disease testing and movement information were collected from all feeding grounds. These datasets were at the same spatial resolution with no missing information, although some of the datasets were sparse in particular sites or years. Using movement data, we simulated the diffusion of elk away from the supplemental feeding grounds as a function of the receding snowpack and other habitat covariates (table 1). This movement model provided a predicted probability density function, which was multiplied by the elk counts, disease seroprevalence and the seasonal timing of abortion events, ψ, to estimate spillover risk. The explicit modelling of elk movement from known point locations facilitated the integration of multiple datasets. However, the movement model incurred a computation cost of calculating the probability of movement between every pair of pixels per day (millions of pairs for each of 23 feeding grounds), which required us to ignore some long-distance movement and meant that assessing our uncertainty by running many simulations was time prohibitive even on supercomputing facilities.
Table 1.
Summary of the data, methods and challenges faced by three case studies estimating disease spillover at the wildlife–livestock interface.
| data layers | brucellosis—USA [23]a | brucellosis—USA [24,25]b | HPAIV China [26–28]c | challenge | solutions (potential/used) |
|---|---|---|---|---|---|
| donor host population size | annual counts at a regional scale, missing years were statistically interpolated | most recent annual count from regional management units. Rayl et al. pooled some sampling units to avoid missing information | developed distributions for >30 species using habitat [27] and applied two levels of population data to create donor species-level distributions [28] | missing information, unquantified uncertainty associated with sightability and identification biases | aggregate regions to limit missing data. Statistically model population size to interpolate regions and years. Use expert opinion and data from other regions to simulate potential uncertainty |
| donor host movement | not accounted for either within or between regions | Rayl et al. [25] simulated migration from GPS data, Merkle et al. [24] accounted for habitat selection with resource selection models and adjusted elk counts using available movement data | seasonal models (breeding, wintering) created for each donor species [27]. Habitat models restricted by known species-level ranges | extrapolation to regions without movement information. Many approaches provide relative rather than absolute probability of use | use cross-validation approaches to assess how predictable movement and habitat selection patterns are from one area to another. Create seasonal distribution models if movement data are not available |
| donor host disease prevalence | seroprevalence from regional management units, statistically interpolated missing years and regions | seroprevalence collected from feeding grounds [24] or from regional management units, statistically interpolated for missing years and regions [25] | based on influenza surveillance within geographical model extent | difficult to collect enough data for pathogens with high spatial and temporal variability | develop mechanistic disease models that use the available host density and prevalence data |
| timing of pathogen shedding within a year | not incorporated | concentrated in March–May based on timing of abortion events | based on literature and laboratory trials, not specific to China | not known for many directly transmitted pathogens but vector-borne diseases will be highly seasonal in some regions | use day of year, temperature, precipitation and other environmental covariates to predict seasonal dynamics |
| recipient population size | NA | NA | provincial-level census data. Modelling required to produce consistent estimates from multiple parameter inputs | privacy concerns may limit access to data | statistically downscale county or province level data using environmental covariates |
| recipient movement | NA | accounted for the seasonal timing of when public grazing allotments were available to cattle | NA | privacy concerns may limit access to data | cellphone and transportation networks for human systems. For domestic species, agency records of movement across state or provincial lines or online records of sellers and buyers |
| spillover events | 21 events, location of affected livestock herds only available at the regional scale | not used | not used | infrequent in many systems or can be difficult to differentiate from subsequent transmission events in the recipient host | genomic analyses may help identify spillover events. When spillovers are frequent they may be analysed directly, otherwise mechanistic models may provide a null hypothesis |
| other covariates | predators, spring snowpack, normalized difference vegetation index (NDVI, 250 m in May) | slope, aspect, tree cover, roads (30 m), NDVI (250 m daily interpolation), snow (interpolated 1 km daily) | biosecurity information for poultry recipients/donors. Shedding and uptake rates for both recipients and donors | limited information on biosecurity; no uncertainty incorporated with these model variables | make assumptions about parameter development transparent in model description |
aPhenomenological model using 21 spillover events from 2002 to 2014 at the management unit scale (roughly 1600 km2 units) and an annual temporal resolution.
bMechanistic models of risk simulated for each day during the transmission season at a 250 × 250 m spatial resolution across approximately 40 000 km2.
cMechanistic models of risk simulated across for four seasons deterministically at the 1 × 1 km resolution and at the 30 × 30 km resolution for assess uncertainty.
Rayl et al. [25] conducted a similar risk assessment in Montana, but was presented with several additional, and probably common, challenges. First, Montana does not have supplemental feeding grounds. As a result, monitoring disease in elk either requires helicopter captures or hunter killed samples, and so not all areas had disease prevalence, or movement data. In addition, the movement, count and prevalence data were collected at different scales and elk often move across management unit boundaries. Our previous movement modelling approaches were not as effective in this region, so we used a more traditional resource selection approach that allowed us to downscale the population counts and account for habitat selection within a management unit. However, this methodology did not account for movement across regional boundaries, which is an important part of comparing risks among regions if a significant fraction of the population moves among units within a year. In addition, for regions where no movement data are available, one would have to infer movement using data from other regions. Rayl et al. [25] did not model this movement across regions, but instead assumed no movement where the data were lacking. In this study, uncertainties were not integrated and errors were not propagated comprehensively. In part, this was because some layers (e.g. population counts) did not have any assessment of their measurement error or a rigorous sampling design, but computational limitations also played a role.
Despite the limitations, this process provided both biological and methodological insight. In this system, host population size, disease prevalence and movements were all highly variable in space and time. As a result, none could be easily ignored in the risk assessment process. While doing the Montana study, we also realized that accounting for seasonal changes in where livestock are located during the transmission season is critical, which was partially accomplished by including information on when public properties were available for cattle grazing. This additional information changed our conclusions about spillover risk, highlighting that most spillovers were predicted to occur on private properties rather than federal grazing allotments. More complete information on livestock density and movements is often limited by privacy concerns within the USA (table 1).
Only 30 spillover events have been observed in the region from 2001 to 2018 (electronic supplementary material, figure S2), which limits opportunities for more direct statistical modelling of the spillover events themselves. However, mechanistic risk estimates of where elk may be transmitting B. abortus were crudely correlated with reported spillover events (electronic supplementary material, figure S2). Outliers in the electronic supplementary material, figure S2 demonstrate the need for further model refinements. In one management unit, predicted risks were almost two times higher than other areas, but no livestock herds have been infected there. This discrepancy may be because few livestock were present in that unit even though the land was zoned for agricultural use, a weakness with using data on ‘potential’ areas of livestock occupancy rather than actual density estimates.
4. Case study: goose/guangdong lineage highly pathogenic avian influenza in waterfowl and poultry in China and North America
In 1996, a novel goose/guangdong (GsGD) lineage of highly pathogenic avian influenza virus (HPAIV) emerged in China [29]. Unlike previous HPAIVs that evolved and remained in domestic poultry (recipient host) populations following spillover, GsGD HPAIVs have periodically spilled back into wild birds where they have continued to spread, evolve and been associated with mortality events [30]. GsGD HPAIV has now been disseminated throughout countries in Asia, Africa, Europe and North America [31] where it has caused considerable economic losses. A potentially important mechanism of spread of GsGD HPAIV is repeated spillover and spillback of GsGD HPAIV between wild birds and domestic poultry. The challenges of estimating spillover and spillback of GsGD HPAIV in China and North America were greater than the brucellosis examples above because of the larger spatial scale covered by the reservoir host species and the fact that there are many different competent reservoir host species.
To identify H5N1 transmission risk at the interface between wild and domestic birds within China, Prosser et al. [26] developed large-scale nationwide mechanistic models of spillover and spillback. The largest challenge was the lack of spatial and temporal information on wild waterfowl (donor) and poultry (recipient) densities (δ1, δ2). As H5N1 prevalence, susceptibility and pathogenicity differed among species within the recipient and donor populations [32,33], density distributions needed to be considered across a suite of susceptible species; for China, this included three recipient species and more than 30 donor species. The approach for achieving spatial layers for δ2 included disaggregating species-level poultry census data using agricultural and environmental covariates to produce 1 km resolution gridded density predictions [34]. A substantial challenge to this approach was the variation in spatial scale of census data, which ranged from county to province level. In addition, poultry metrics (e.g. population numbers, total sold, etc.) were not consistently available across all regions, thus additional analyses were needed to identify relationships among the available metrics and model these to produce the final population estimates. Input data (c, m) for the donor hosts (wild waterfowl) were less available than for poultry, forcing a different iterative modelling approach. First steps defined suitable habitats for each species and across subannual seasons, as migratory behaviour results in very different seasonal distributions [27]. To create geospatial layers of δ1, abundance estimates [35,36] were distributed across the predicted habitat ranges [28]. Given the large number of donor species potentially associated with HPAIV, it is unlikely that comprehensive challenge studies or surveillance efforts could cover all species equally. We took the approach of binning species into applicable guilds and applied ψ and ρ estimates to these guilds using available data (e.g. [35,37,38]). Inclusion of uncertainty estimates was important, given the multitude of modelling steps that integrated inputs having very different levels of confidence, both between layers and geospatially within layers. Probability density functions ranged from normal (δ2) to triangular (δ1, biosecurity), to uniform (ψ, virus uptake). Propagating the uncertainty across all variables and models required high levels of computing power and reducing the model resolution from 1 to 30 km. A strong match exists between our transmission risk models and existing outbreaks; however, the available surveillance and phylogenetic data were not able to identify spillover and spillback events versus farm-to-farm transmission. This restricts our ability to do more formal validations of our mechanistic approaches or correlational models of the spillover events themselves. Advances in phylogenetic approaches to identify spillover events versus subsequent transmission in the recipient are an important avenue for continued development.
In North America, Clade v. 2.3.4.4 GsGD lineage HPAIV was first introduced in late 2014 [31,39,40], resulting in widespread poultry outbreaks, and phylodynamic analyses supported numerous instances of spillover and spillback across the wild bird–poultry interface [41]. Modelling efforts suggested that HPAIV could be maintained in both wild bird and poultry host populations [42], but, to our knowledge, quantitative risk assessments similar to those described above have not yet been conducted. In addition, there is currently no routine wildlife surveillance for spillover of avian influenza at the wildlife–livestock interface. Future risk modelling in North America is likely to encounter similar challenges to those described above. Donor host population distributions, densities (δ1) and movement (m) over time have been estimated at coarse spatial scales (200 × 200 km) from waterfowl banding and recovery data (e.g. [43]), but producer-level risk would require finer spatial resolution. Like our cattle example, poultry farm locations are not publicly available in the USA for privacy reasons and must be estimated from survey data. Additionally, limited data exist on backyard poultry production, which has lower biosecurity relative to commercial operations, but can interact with the commercial and live-bird markets. Therefore, it is an important component in overall spillover risk [44]. Surveillance at the wildlife–livestock interface is critical to observe spillover and spillback mechanisms in real time, and ultimately to develop risk assessment frameworks for North America.
5. Discussion
Identifying the regions and times of high transmission risk across wildlife, livestock and humans will allow for more efficient surveillance, control and prevention efforts. Here, we focused on mechanistic approaches for estimating spillover risk between wildlife and domestic animals, which are especially useful in systems where spillover events are infrequent, rarely observed, or hard to differentiate from within-species transmission events. The mechanistic approach can provide an a priori hypothesis about how the different layers contribute to spillover risk and predict the effectiveness of different interventions. Phenomenological models that directly correlate spillover events to covariates provide an alternative approach that requires more spillover events but does not necessarily require host density or pathogen shedding information as covariates. The combination and confrontation of these two approaches will help refine our mechanistic understanding (electronic supplementary material, figure S2). For example, in the brucellosis system, we have predicted high levels of livestock risk in some regions with no observed cattle cases. This discrepancy is probably owing to our lack of information on where cattle are located owing to privacy issues. In addition, we often assume host susceptibility and pathogen shedding rates do not vary spatially. Observing more spillovers in areas of predicted lower risk based on host disease distributions may indicate when these assumptions should be re-evaluated.
The ability to differentiate spillover events from secondary transmission within a given host species will vary by system. In systems where the recipient host is a dead-end [45], all recipient host infections are spillovers. However, as the transmission rate in the recipient host species increases, the ability to identify primary spillover events versus secondary within-species transmission will become more difficult. In the brucellosis example, most, if not all, livestock outbreaks were independent spillovers from elk [20]. In the GsGD HPAIV example, spillovers were less obvious in China and the USA owing to transmission back to wildlife and differentiating primary versus secondary cases, which may have been owing to poultry-to-poultry transmission. Pathogen genomics plays an increasingly important role in identifying spillover events, but inference can still be limited by spillover frequency, sampling designs, availability of metadata, substitution rate and genome size [46].
We have focused on case studies of avian influenza and brucellosis at the wildlife–livestock interface, but the challenges we encountered are likely to be similar to many human systems. First, datasets may not align in space and time, which requires a statistical model to predict the unsampled areas and times across the multiple datasets using the available information. For avian influenza, this problem can be exacerbated by the fact that there are many potential donor host species that can move long distances in short periods of time such that it can be difficult to obtain samples from all relevant hosts in the same place at the same time. Thus, disease dynamics and spillover risk are highly variable in space and time. Second, data on wildlife distributions tend to be sparse and sampled at a coarse spatial and temporal scale, while we would often like to know risk to agricultural producers or people at a much finer scale. This issue was even more difficult in the GsGD HPAIV case study where the full scope of competent reservoir species remains poorly understood, and species-level differences in transmission potential and contact rates of reservoir species with poultry are not well known. Third, one might expect that the distribution and density of agricultural species is more well known than their wildlife counterparts; however, this information is often protected owing to privacy concerns. Finally, inconsistencies in data reporting (e.g. omission of species-level information, lack of clarity in measurement error) are another common challenge.
Hierarchical Bayesian approaches are an obvious way to synthesize multiple datasets and propagate uncertainties, and have been extended to dynamical spatio-temporal models [47]. However, the inclusion of many different likelihoods and datasets can be challenging to implement and fit depending on system-specific data features. Often, we will desire risk assessments at the finest resolution and broadest scale possible, but this will be limited by both the available data and computational demands. Even with improvements in computing speeds, researchers may still need to make compromises on spatio-temporal resolution, extent and how uncertainty is characterized. Statistical inference on high-resolution spatio-temporal systems is challenging, especially when mechanistic, science-based models are used. Multi-resolution approaches have shown promise in some fields, with, for example, homogenization (harmonic averaging over multiple scales) providing a computationally efficient approach to ecological diffusion [48,49]. Another approach to approximate inference is to replace a computationally challenging likelihood (i.e. the likelihood of observed seroprevalence data which depends on a mechanistic spatial SIR model which must be solved numerically) with an emulated likelihood, where the true process is approximated by a nonlinear, flexible statistical or machine learning model for the process [50].
The challenges listed above lead us to several suggestions for future work. Restif et al. [51] nicely outline how models can be used to guide data collection, hone hypotheses and provide a nexus for multidisciplinary collaboration. Model predictions are only as good as the data we collect. In our case studies, data collection largely preceded the mathematical model specification. However, our initial mechanistic models can now highlight data gaps and we can iteratively improve both the field data collection and the model design. Modelling results may suggest where resources could be allocated to more efficiently reduce our prediction uncertainty and target layers of the spillover process that are most influential in prediction and less costly to sample. Improving predictions of disease spillover will require an iterative approach; however, model-guided fieldwork has not been implemented very often [52]. Consistent relationships across disciplines, agencies and stakeholders, and long-term funding of team efforts are needed to provide relevant data for modelling spillover risk. Mechanistic modelling approaches can determine more efficient and feasible data collection of the most important parameters.
Acknowledgements
We thank E. Gurley, B. Nikolay, the Bozeman disease ecology laboratory and two anonymous reviewers for their suggestions.
Authors' contributions
P.C.C. initiated and led the writing and figure development. K.M.P., D.J.P., E.M.H. and A.M.R. contributed to the ideas, design and drafting of the article. All the authors assisted in the writing and revision and gave final approval of the manuscript.
Disclaimer
Any use of trade, firm or product names is for descriptive purposes only and does not imply endorsement by the US Government.
References
Articles from Philosophical Transactions of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society
Full text links
Read article at publisher's site: https://doi.org/10.1098/rstb.2018.0435
Read article for free, from open access legal sources, via Unpaywall:
https://royalsocietypublishing.org/doi/pdf/10.1098/rstb.2018.0435
Citations & impact
Impact metrics
Citations of article over time
Alternative metrics
Smart citations by scite.ai
Explore citation contexts and check if this article has been
supported or disputed.
https://scite.ai/reports/10.1098/rstb.2018.0435
Article citations
Modeling spillover dynamics: understanding emerging pathogens of public health concern.
Sci Rep, 14(1):9823, 29 Apr 2024
Cited by: 0 articles | PMID: 38684927 | PMCID: PMC11058258
Risk of African swine fever virus transmission among wild boar and domestic pigs in Poland.
Front Vet Sci, 10:1295127, 06 Nov 2023
Cited by: 1 article | PMID: 38026636 | PMCID: PMC10657852
Mathematical modeling at the livestock-wildlife interface: scoping review of drivers of disease transmission between species.
Front Vet Sci, 10:1225446, 06 Sep 2023
Cited by: 0 articles | PMID: 37745209 | PMCID: PMC10511766
Review Free full text in Europe PMC
Human disturbance increases coronavirus prevalence in bats.
Sci Adv, 9(13):eadd0688, 31 Mar 2023
Cited by: 2 articles | PMID: 37000877 | PMCID: PMC10065436
The role of invasive alien species in the emergence and spread of zoonoses.
Biol Invasions, 25(4):1249-1264, 20 Dec 2022
Cited by: 2 articles | PMID: 36570096 | PMCID: PMC9763809
Go to all (19) article citations
Data
Data behind the article
This data has been text mined from the article, or deposited into data resources.
BioStudies: supplemental material and supporting data
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
Percolation models of pathogen spillover.
Philos Trans R Soc Lond B Biol Sci, 374(1782):20180331, 12 Aug 2019
Cited by: 12 articles | PMID: 31401950 | PMCID: PMC6711313
The problem of scale in the prediction and management of pathogen spillover.
Philos Trans R Soc Lond B Biol Sci, 374(1782):20190224, 12 Aug 2019
Cited by: 19 articles | PMID: 31401958 | PMCID: PMC6711304
Review Free full text in Europe PMC
Ecological interventions to prevent and manage zoonotic pathogen spillover.
Philos Trans R Soc Lond B Biol Sci, 374(1782):20180342, 12 Aug 2019
Cited by: 54 articles | PMID: 31401951 | PMCID: PMC6711299
Review Free full text in Europe PMC
Sampling to elucidate the dynamics of infections in reservoir hosts.
Philos Trans R Soc Lond B Biol Sci, 374(1782):20180336, 12 Aug 2019
Cited by: 34 articles | PMID: 31401966 | PMCID: PMC6711310
Review Free full text in Europe PMC
Funding
Funders who supported this work.
Animal and Plant Health Inspection Service
U.S. Geological Survey (2)
Grant ID: Environmental Health RR00.GQN30
Grant ID: RR00.99L21





