Abstract

Significance

Cytotoxic T lymphocytes (CTLs) are key players of the adaptive immune system and eliminate tumor cells or pathogen-infected cells. To fulfill their functions in the body, they migrate in complex biological microenvironments, which is shaped by the extracellular matrix. The mechanisms underlying their navigation and search strategy are not well understood. To better understand CTL migration in the extracellular matrix, we analyze their trajectories in three-dimensional collagen networks. Our main observation is that CTLs tear the collagen fibers forming channels, which facilitate movement of other T cells in the collagen network. We describe the underlying slow, fast, and mixed motilities and observed persistences by a two-state random walk model, which reproduces the behavior of CTLs without additional free parameters.

Introduction

Cytotoxic T lymphocytes (CTLs) are fully activated CD8⁺ T cells, which are key players of the adaptive immune system to eliminate tumorigenic or pathogen-infected cells (1). CTLs need to find the cognate antigens presented by target cells, for example pathogen-infected or tumorigenic cells, to eliminate those aberrant cells in the immunosurveillance process. These target cells are often low in number in the early stages of disease development (2, 3, 4). Thus, the ability of CTLs to efficiently navigate and search is crucial for an efficient immune response. Migration behavior of immune cells in the body and the search strategies they might follow is currently of great interest in physics and biology (5, 6, 7). Migration of naive T cells in lymph nodes reportedly follows a Brownian or even subdiffusive dynamics (8, 9, 10), but switchings between fast and slow motility modes have also been observed (11). Outside the lymph node, activated T cells are destined to find their targets in peripheral tissues, most of which are characterized by a dense extracellular matrix (ECM) (12). Here, a faster migration, e.g., via longer phases of superdiffusive dynamics or less switchings to the slow diffusive mode, is advantageous to scan a larger tissue efficiently. For instance, it was reported that the dynamics of CD8⁺ T cells in infected brain tissue resembles a Levy walk (13).

The ECM—the major component of peripheral tissues—mainly consists of collagens and has essential regulatory roles in nearly all cellular functions. Some collagens have inhibitory effects on the function of different immune cells (14,15). In various types of cancer, the collagen network becomes dense, stiff, and linearized in the vicinity of tumors, facilitating the transport of cancerous cells and making the ECM an important player in cancer metastasis, intravasion, and prognosis (16, 17, 18, 19, 20, 21). Additionally, the proliferation of CTLs is impaired in a high-density collagen matrix (22). Recently, different immune cells have been investigated in immunotherapy studies as potential drug delivery vehicles into tumors (23,24). Understanding the migration and interactions of immune cells in collagen networks is crucial to unravel the underlying details of the immune response and design effective treatment strategies.

Collagen-based assays have been used to investigate the migration of lymphocytes in ECM and study the possible underlying mechanisms of immune interactions with ECM (14,25, 26, 27, 28, 29). In a recent study, collagen hydrogels were employed to compare migration patterns of human CD8⁺ T cells in aligned and nonaligned collagen fibers microenvironments, resembling tumor cells and normal tissues, respectively (30).

In this study, we use bovine collagen to construct a three-dimensional (3D) environment in vitro as a model for the ECM. The trajectories of primary human CTLs in collagen matrices with different concentrations are analyzed for two blood donors. We find three different types of motion in both donors; the migration of CTLs can be categorized into slow, fast, and mixed subgroups and show that a persistent random walk model with two different motility states, a slow one and a fast one, and transitions between describes the experimental data accurately. Finally, we provide a biophysical interpretation of the two motility modes of T cells in collagen matrix related to channel formation and movement within channels.

Materials and Methods

Results

To investigate migration patterns of CTLs in a 3D environment, we embedded primary human CTLs into collagen matrices and visualized their movements using light-sheet microscopy (Fig. 1). Different concentrations of collagen mimic the ECM of normal tissue (2 mg/mL), soft solid tumor (4 mg/mL), and hard solid tumor (5 mg/mL), respectively (35, 36, 37). The resulting parameters are summarized in Table 1. The cross correlation between velocity and persistence, $C{C}_{v,\mathcal{R}}=\left(\langle v\mathcal{R}\rangle -\langle v\rangle \langle \mathcal{R}\rangle \right)/{\sigma }_v{\sigma }_{\mathcal{R}}$, which shows how these two parameters are related, also shows no systematic dependence on the collagen density. We find that $C{C}_{v,\mathcal{R}}$ is always positive, which means that faster T cells move more persistently than slower ones. The distributions of velocity, turning angle, and persistence are shown in Fig. 2. The average velocity is higher at lower densities of collagen as expected. The distributions of ${\mathcal{R}}_n$ and ϕ show a tendency to turn with an angle around 0.4–0.5 radian (corresponding to a persistence around $\mathcal{R}\simeq 0.9$).

Open in a separate window

Figure 1

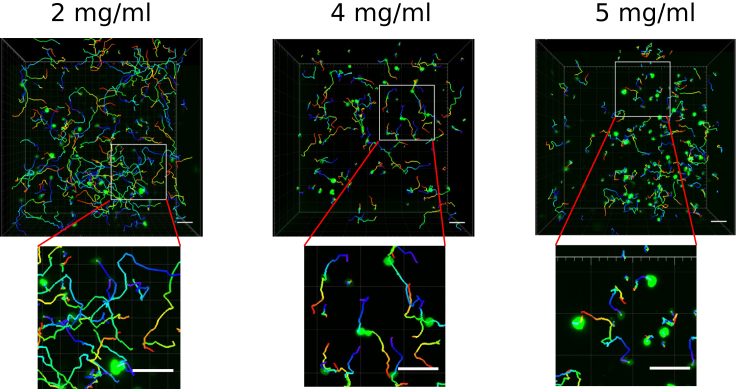
Trajectories of CTLs in 3D collagen matrices. CTL migration was visualized by light-sheet microscopy (20× objective) at 37°C for 30 min with an interval of 30 s in 3D collagen matrices with different concentrations. The nuclei of human primary CTLs were labeled with overexpressed Histone 2B-GFP (green). CTL migration trajectories were tracked automatically using Imaris 8.1.2. Scale bars, 40 μm. In the lower panels, magnified images of the area marked by the solid squares are shown. To see this figure in color, go online.

Open in a separate window

Figure 2

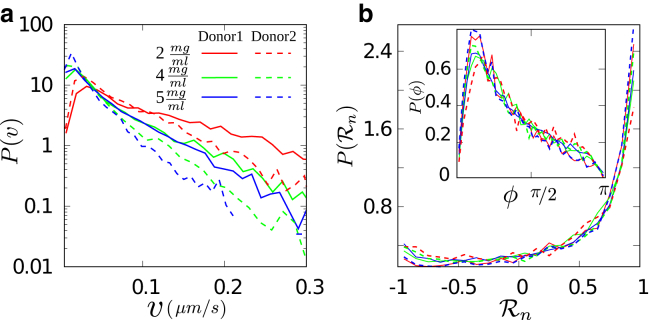
Distributions of (a) velocity and (b) persistence of T cells in collagen networks with different concentrations. Turning angle distributions are shown in the inset. To see this figure in color, go online.

T cell dynamics

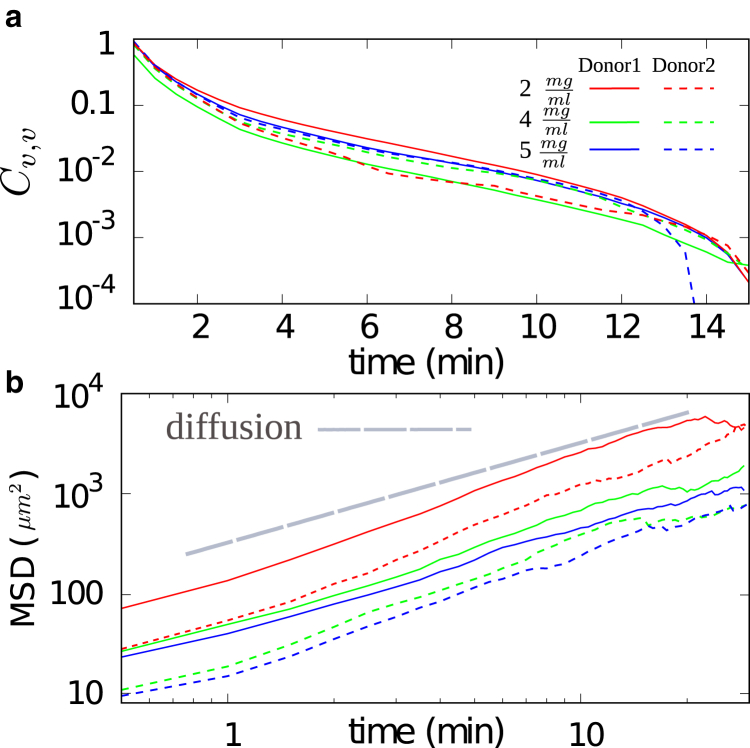
To better understand the dynamics of T cells in matrices with different collagen concentrations, we analyze the velocity autocorrelation C_ν,ν as well as the mean-square displacement (MSD) separately for each experimental condition in Fig. 3. The gray dashed line in Fig. 3 b corresponds to Brownian diffusion. The smaller slope of the MSD curves under all conditions shows that the cell motion is slower than normal diffusion and eventually crosses over to diffusive dynamics at long times. Both the decay of C_ν,ν and the crossover of the MSD to asymptotic diffusion show that the cell orientation is randomized after a while.

Open in a separate window

Figure 3

(a) Velocity autocorrelation of CTLs for different donors and collagen concentrations. (b) Time evolution of the MSD of CTLs is shown. The colors and types of the lines are the same as in (a). To see this figure in color, go online.

Three motility groups can be distinguished in CTL dynamics

Single track analysis of CTL trajectories reveals that there are three different types of CTL trajectories: 1) slow T cells that perform a subdiffusive motion with velocities that always remain below a threshold value, 2) a faster group with velocities always above a threshold value, and 3) the third group with velocities that switch between fast and slow modes. In our analysis, we noticed that CTLs from both donors have all motility types, although the corresponding fractions are not exactly the same in both donors (shown in Table 2). This difference could owe to variations between donors because the CTLs were primary CD8⁺ T cells. The velocity evolution of typical tracks and a few trajectories for each cell motility type are shown in Fig. 4.

Table 2

Percentage of Different Motility Types of CTLs and the Threshold Velocities ν_c1 and ν_c2 to Categorize T Cell Migration Patterns for Each Experiment with a Different Donor or Collagen Density

	Donor 1			Donor 2
Density $\left(\frac{\mathrm{m}\text{g}}{\text{mL}}\right)$	2	4	5	2	4	5
Slow (%)	33	43	48	15	27	26
Fast (%)	35	14	19	30	25	24
Mixed (%)	26	37	25	48	40	43
νc1 (μm/s)	0.075	0.055	0.04	0.05	0.02	0.02
νc2 (μm/s)	0.11	0.09	0.10	0.08	0.04	0.04

Open in a separate window

Open in a separate window

Figure 4

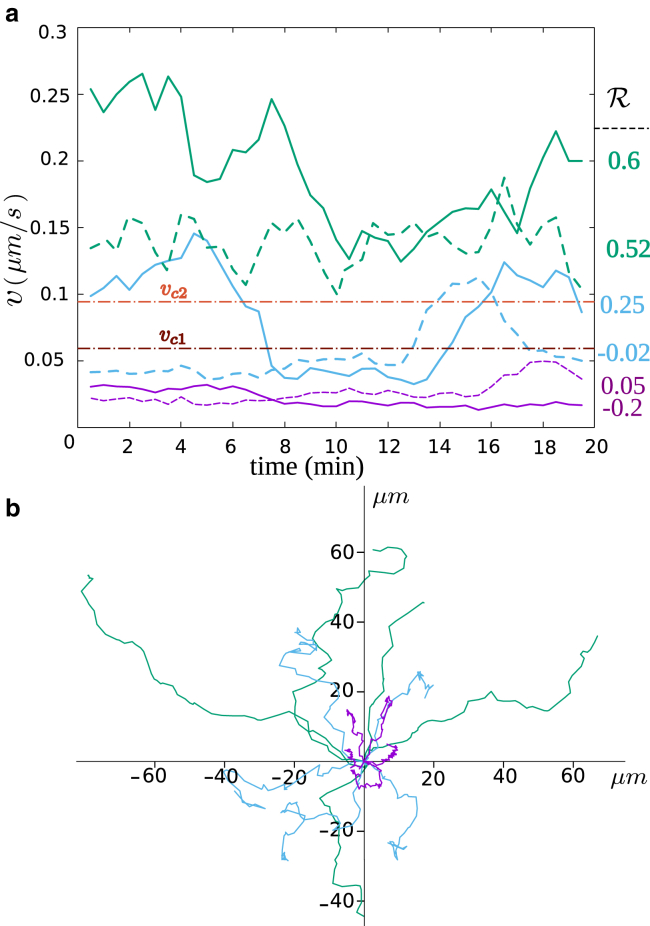
(a) Typical velocities of CTL trajectories. Green, purple, and blue colors correspond to a few examplary trajectories of fast, slow, and mixed types of motility, respectively. The corresponding persistence value $\mathcal{R}$ for each trajectory is given on the right y axis. The horizontal lines represent the threshold velocities ν_c1 and ν_c2 to categorize T cell migration patterns. (b) Typical trajectories of different motility types are shown. The trajectories belong to donor 1 in the collagen matrix with 2 mg/mL concentration. To see this figure in color, go online.

We define the three classes of trajectory types—fast, slow, and mixed—by introducing two threshold velocities ν_c1 and ν_c2 (ν_c2 > ν_c1 > 0). A trajectory is classified into the “fast” type if the velocity is at all time t larger than ν_c2, i.e., ν(t) > ν_c2 for all t. It is of the “slow” type if its velocity is always smaller than ν_c1, i.e., ν(t) < ν_c1 for all t and of the “mixed” type if ν(t) > ν_c2 for some t and ν(t′) < ν_c1 for some other t′. For each experimental data set, distinguished by donor and collagen density, we adapt (ν_c1, ν_c2) such that the number of trajectories that does not belong into one of the defined classes (e.g., those with ν(t) > ν_c1 for all t but not ν(t) > ν_c2 for all t) becomes minimal. We checked that in all experiments, the trajectories that do not belong to any of the three identified migration categories remain below 6–8% of all trajectories when adopting an optimal set of (ν_c1, ν_c2). The relative populations of the cells in three migration types moderately change upon varying the threshold velocities ν_c1 and ν_c2 around their optimal choices. Throughout the article, we refer to the fast and slow migration types with F and S subscripts and represent the slow and fast substates of the mixed type of migration with subscripts I and II, respectively.

To further confirm that the three populations are not donor dependent, we pooled data from two donors and analyzed the average velocities and persistence of all populations. Fig. 5, a and b summarizes the average velocities and persistences of different types in different collagen concentrations for both donors. One observes a moderate increase of the average persistence, and a moderate decrease of the average velocity is observed with increasing collagen density. The scatter plots of instantaneous persistence versus velocity, which are shown in Fig. 5 c in different collagen densities, indicate once again that the faster T cells are more persistent than the slow ones. The MSD of different types of motion are clearly distinguishable (see e.g., Fig. 5 d). The similarities in the overall time evolution of the MSD curves indicate that the underlying structures guiding the cells are similar. The differences in the level of MSD curves reflect the differences in the average velocity of CTLs in various migration types. In the next section, we compare the MSD T cell trajectories with the prediction of a two-state random velocity model.

Open in a separate window

Figure 5

(a) $\mathcal{R}$ and (b) velocity and their standard derivations for different motility types in two donors represented by open and full symbols. (c) Shown are scatter plots of ${\mathcal{R}}_n$ versus v in different collagen densities in donor 1; different colors correspond to different migration types as indicated in the legend of part (b). (d) Shown is the MSD of different motility types of donor 2 in collagen concentration 5 mg/mL. The error bars represent the standard error. The solid line represents the MSD of all T cells. To see this figure in color, go online.

The two-state motility type

In the following, we study the mixed-velocity trajectories of T cells in more details.

MSD

The MSD of the mixed type coincides with the total MSD in nearly all cases (see the solid line in Fig. 5 d). This shows that the mean velocity of all T cells is nearly the same as the mean velocity of the mixed type when the resident times in the substates of the mixed type are taken into account.

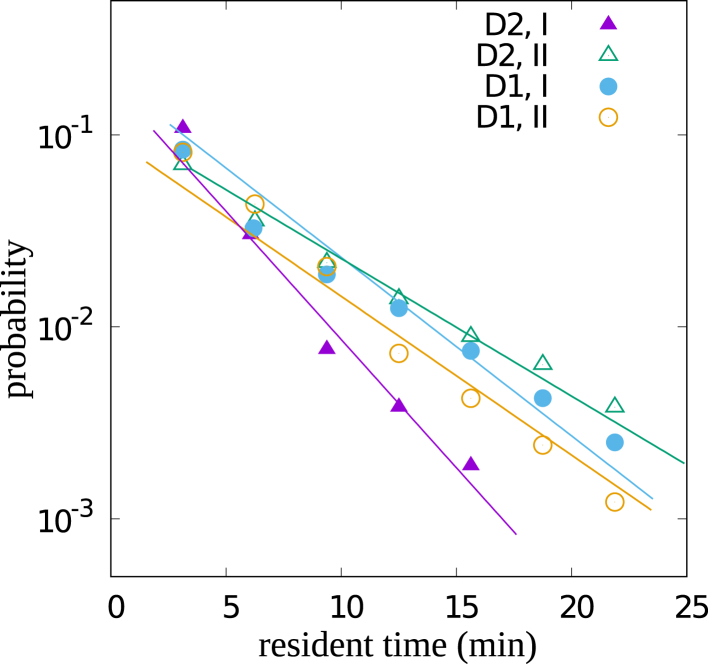
Exponential distribution of sojourn time in each state

The distribution of the times that the T cells remain in one state before they switch, the so-called sojourn times, follow an exponential decay as shown in Fig. 6. In this example, the sojourn time distribution of T cells in the different states of the mixed T cell migration type of two donors is plotted. The exponential decay of these distributions indicates that the transition probabilities are time independent.

Open in a separate window

Figure 6

Sojourn time distributions in states I and II of mixed type of T cells in collagen with 4 mg/mL concentration. The lines are the corresponding theoretical estimate for each case (same color). D stands for donor. To see this figure in color, go online.

Probability distribution of persistence in different migration types

Fig. 7 shows the probability distribution of the instantaneous persistence of the three different cell types. Whereas the distributions for fast and mixed types show a persistent motion for all collagen concentrations, slow T cells perform antipersistent motion in 2 mg/mL collagen and become persistent in denser ones. A possible explanation is that the average pore size increases with decreasing collagen density (38), which implies that for low collagen densities, T cells can more easily find some pores around them that are large enough to get into them; this might allow slow T cells to change their direction when they face a constriction while creating a channel. This is, however, less probable in denser collagens as most pores are smaller than T cells and need equal effort to pass.

Open in a separate window

Figure 7

(a) Probability distributions of persistence $\mathcal{R}$ at different collagen concentrations for the slow cell type. (b) Shown is the mean persistence $\mathcal{R}$ for slow cells (p < 0.001, t-test). The error bars represent the standard error. (c) Shown is similar to (a) for fast and mixed cell types. To see this figure in color, go online.

CTLs enter channels in the collagen matrix

Next, we explored in detail how CTLs migrate in collagen matrices. We fluorescently stained collagen and visualized the movements of CTLs using light-sheet microscopy. We found that during migration, CTLs could enter channels in the collagen matrix. Inside the channel, they had a high speed that was significantly slowed down when leaving the channel (Fig. 8, a and c; Video S1). Slow CTLs appeared to be trapped in some channels and moved slowly (Fig. 8, b and c; Video S2). In addition, we observed that in some cases, after one CTL migrated through the matrix, a second CTL followed the same path, indicating that CTLs use channels created by other cells (see Fig. 8 d; Video S3). When the trajectories of two CTLs overlap, the following cell probably moves within the channel created by the leading cell, resulting in a substantial velocity increase of the following cells as shown in Fig. 8 e.

Open in a separate window

Figure 8

Visualization of CTL migration in 3D collagen matrices. Primary Human CTLs were transiently transfected with mCherry (red). Collagen (5 mg/mL) was stained with Atto 488 NHS ester (green or gray as indicated). CTL migration was visualized at 37°C using light-sheet microscopy. Exemplary cells for mixed and slow migration are shown in (a and b), respectively (Videos S1 and S2). One layer of z-stack is presented. (c) Quantification of migration velocity at all time points were examined. CTL migration trajectories were tracked and analyzed by Imaris. Scale bars, 10 μm. (d) Shown is an exemplary migrating CTL following another cell in the same trace. CTLs were visualized with Cell Observer. Nuclei were labeled with Hoechst 33342 and tracked with Imaris. The trajectory of the preceding and the succeeding cell is in red and purple, respectively. Scale bars, 7 μm (Video S3). (e) The velocity of the preceding cell is similar with the succeeding cell before the overlapping part of the traces. When the traces overlap, the velocity of the succeeding cell increases. Each dot presents one time point for the same cell. (f) The correlation of cell body volume and velocity during cell migration is shown. Each dot represents one cell. All results were from at least three independent experiments. The error bars represent the standard error. To see this figure in color, go online.

Video S1. Migration of an Exemplary Cell from the Mixed Cell Type:

CTLs (bead-stimulated primary human CD8+ T cells) were transiently transfected with mCherry (red). Collagen (5 mg/ml) was stained with Atto 488 NHS (left: in green, right: in grey). CTL migration was visualized using lightsheet microscopy with a 20X objective at 37^oC with an interval of 30 sec. A z-stack was acquired with a step size of 1 μm. One layer is shown here. Time stamp is HH:MM:SS. Scale bar is 10 μm.

Click here to view.^{(1.5M, mp4)}

Video S2. Migration of an Exemplary Cell from the Slow Cell Type:

CTLs (bead-stimulated primary human CD8+ T cells) were transiently transfected with mCherry (red). Collagen (5 mg/ml) was stained with Atto 488 NHS (left: in green, right: in grey). CTL migration was visualized using lightsheet microscopy with a 20X objective at 37^oC with an interval of 30 sec. A z-stack was acquired with a step size of 1 μm. One layer is shown here. Time stamp is HH:MM:SS. Scale bar is 10 μm.

Click here to view.^{(1.4M, mp4)}

Video S3. An Example of Two CTLs Shared Partially Overlapped Tracks:

CTLs (bead-stimulated primary human CD8+ T cells) were stained with Hoechst 33342 (blue) and then embedded in collagen matrix (2 mg/ml). Cell migration was visualized using Cell Observer (20X objective) at 37^oC with an interval of 30 sec. The migration trajectories were tracked with Imaris8.1.2. The trajectory of the preceding and the succeeding cell are in red and purple, respectively. Time stamp is HH:MM:SS. Scale bar is 7 μm.

Click here to view.^{(6.4M, mp4)}

Two-state persistent random walk model

In the following, we show that the experimentally measured T cell trajectories are well described by a stochastic process that involves a persistent random walk with two different motility states (39). Similar stochastic two-state models have been widely used to describe altering phases of motion in other systems (40,52, 53, 54).

We adopt a discrete time approach because it is best adapted to our experimental data, which consists of the positions of the CTLs at equidistant times. First, we focus on the trajectories of the mixed type, which involves the slow and the fast motility mode and transitions between them. Later, we show that the trajectories of the fast type and those of the slow type are described by the same stochastic process as the mixed type but without transitions from the fast to the slow mode or from low to fast, respectively. This observation complies with the physical interpretation that the slow motility mode is caused by CTLs creating new channels in the collagen matrix and the fast motility mode by CTLs using already existing channels. A persistent random walk in discrete time is a stochastic process for the position of a particle that moves during a time interval Δt with a certain velocity v in a certain direction ϕ. At the end of the time interval, a transition takes place to a new velocity and a new direction. These transitions are characterized by a velocity distribution F(ν) and a turning angle distribution R(ϕ). A persistent random walk with two motility states involves two velocity distributions F_I(ν) and F_II(ν) and two turning angle distribution R_I(ϕ) and R_II(ϕ) for the slow (I) and fast (II) motility mode and transitions between the two motility states characterized by transition probabilities κ_I→II and κ_II→I for switching from state I to II and vice versa. These probabilities are estimated by the inverse of the sojourn time in the two states of mixed trajectories, e.g., ${\kappa }_{\text{I}\to \text{II}}\sim {\langle \tau \rangle }_{\text{I}}^{-1}$. Constant probability transitions κ_I→II (κ_II→I) lead to an exponential distribution of the sojourn time ${\mathcal{F}}_{\text{I}}\left(\tau \right)\sim {\text{e}}^{\text{ln}\left(1-{\kappa }_{\text{I}\to \text{II}}\right)\tau }$ $\left({\mathcal{F}}_{\text{II}}\left(\tau \right)\sim {\text{e}}^{\text{ln}\left(1-{\kappa }_{\text{II}\to \text{I}}\right)\tau }\right)$. As a first approximation, ${\mathcal{F}}_{\text{I}}\left(\tau \right)\sim e^{-\tau /{\langle \tau \rangle }_I}$ and ${\mathcal{F}}_{\text{II}}\left(\tau \right)\sim e^{-\tau /{\langle \tau \rangle }_{II}}$ are plotted in Fig. 6, which show a very good agreement with the experimental resident time distribution in each state of the mixed motion. Introducing the probability density functions $P_t^{\text{I}}\left(x,y|\theta \right)$ and $P_t^{\text{II}}\left(x,y|\theta \right)$ for the probability to find the walker at position (x, y) along the direction θ at time t in each of the motility states; the temporal evolution of the stochastic process can be described by the following set of coupled master equations:

$$\begin{array}{c}{P}_{t+\text{Δ}t}^{\text{I}}\left(x,y|\theta \right)=\left(1-{\kappa }_{\text{I}\to \text{II}}\right)\int dv{F}_{\text{I}}\left(v\right)\underset{-\pi }{\overset{\pi }{\int }}d\gamma R_{\text{I}}\left(\theta -\gamma \right)P_t^{\text{I}}\left(x^{\prime },y^{\text{′}}|\gamma \right)+{\kappa }_{\text{II}\to \text{I}}\int dv{F}_{\text{I}}\left(v\right)\underset{-\pi }{\overset{\pi }{\int }}d\gamma R_{\text{II}}\left(\theta -\gamma \right)P_t^{\text{II}}\left(x^{\prime },y^{\text{′}}|\gamma \right),\\ P_{t+\text{Δ}t}^{\text{II}}\left(x,y|\theta \right)=\left(1-{\kappa }_{\text{II}\to \text{I}}\right)\int dv{F}_{\text{II}}\left(v\right)\underset{-\pi }{\overset{\pi }{\int }}d\gamma R_{\text{II}}\left(\theta -\gamma \right)P_t^{\text{II}}\left(x^{\prime },y^{\text{′}}|\gamma \right)+{\kappa }_{\text{I}\to \text{II}}\int dv{F}_{\text{II}}\left(v\right)\underset{-\pi }{\overset{\pi }{\int }}d\gamma R_{\text{I}}\left(\theta -\gamma \right)P_t^{\text{I}}\left(x^{\prime },y^{\text{′}}|\gamma \right),\end{array}$$

(1)

with x′ = x − νΔtcosθ and y′ = y − νΔtsinθ. By solving these sets of master equations, one can evaluate arbitrary moments of the position of the walker, such as the MSD. The analytical details to calculate the MSD are presented in the Appendix. It should be emphasized that the derived formula for the MSD, i.e., the second moment of the position, depends only on the first two moments of the velocity distributions F_I(ν) and F_II(ν) and the first moment of the turning angle distribution.

We extracted the model parameters from the experimental data analysis; thus, there remains no free parameter to be tuned. In the case of the mixed type, moments of velocity (${\langle v\rangle }_{\text{I}}$, ${\langle v\rangle }_{\text{II}}$, ${\langle v^2\rangle }_{\text{I}}$, and ${\langle v^2\rangle }_{\text{II}}$) in each state are calculated by averaging over local velocities of trajectories. The persistences ${\mathcal{R}}_{\text{I}}$ and ${\mathcal{R}}_{\text{II}}$ are measured by averaging over cosines of turning angles (see Eq. 3). The transition probabilities κ_I→II and κ_II→I are the inverse of average sojourn time in states I and II, respectively. In the case of the fast and slow types, as explained in the Appendix, the model shrinks to a one-state model. All extracted model parameters are summarized in Tables 3 and ​and44 for mixed state and fast/slow states, respectively. Note that according to our initial hypothesis, the model parameters for the stochastic process describing the trajectories of the slow type (S) should be identical to the model parameters with index I of the mixed type and for the fast type identical to the ones with index II. By comparing the corresponding values in Tables 3 and ​and4,4, one observes that they do approximately agree, except for the slow motility type where significant differences between the (S) and the (I) parameters occur. We attribute this difference to variations in the local environment in which CTLs move; CTLs displaying trajectories of the mixed type move in an environment where pre-existing channels and therefore deformed collagen matrix exist, leading plausibly to an easier and consequently faster migration even outside the channels, whereas “slow” CTLs move in a local environment where no pre-existing channels exist and average velocity is lower.

Table 3

Parameters Extracted from the Experimental Data of Mixed Type of Motility and Used in the Two-State Model

	Donor 1			Donor 2
Density $\left(\frac{\mathrm{m}\text{g}}{\text{mL}}\right)$	2	4	5	2	4	5
${\langle v\rangle }_I\left(\mu \mathrm{m}/\mathrm{s}\right)$	0.066	0.047	0.048	0.047	0.023	0.020
${\langle v\rangle }_{II}\left(\mu \mathrm{m}/\mathrm{s}\right)$	0.138	0.120	0.111	0.099	0.061	0.055
${\langle v^2\rangle }_I\left(\mu {\mathrm{m}}^2/{\mathrm{s}}^2\right)$	0.0189	0.0038	0.0037	0.0149	0.0009	0.0006
${\langle v^2\rangle }_{II}\left(\mu {\mathrm{m}}^2/{\mathrm{s}}^2\right)$	0.0510	0.0198	0.0165	0.038	0.0055	0.0040
RI	0.15	0.35	0.38	0.19	0.26	0.35
RII	0.62	0.59	0.59	0.33	0.56	0.69
Δt (min)	0.5	0.5	0.5	0.5	0.5	0.5
κI→II	0.20	0.08	0.09	0.11	0.10	0.07
κII→I	0.06	0.14	0.17	0.14	0.11	0.13
${\langle \tau \rangle }_{\text{I}}$ (min)	2.5	6.2	5.5	4.5	5	7.1
${\langle \tau \rangle }_{\text{II}}$ (min)	8.3	3.5	2.9	3.6	4.6	3.8

Open in a separate window

Table 4

Parameters Extracted from the Experimental Data of Fast (Up) and Slow (Down) Types of Motility

	Donor 1			Donor 2
Density $\left(\frac{\mathrm{m}\text{g}}{\text{mL}}\right)$	2	4	5	2	4	5
${\langle v\rangle }_F\left(\mu \mathrm{m}/\mathrm{s}\right)$	0.17	0.12	0.09	0.11	0.07	0.07
${\langle v^2\rangle }_F\left(\mu {\mathrm{m}}^2/{\mathrm{s}}^2\right)$	0.033	0.019	0.013	0.018	0.008	0.006
RF	0.54	0.41	0.45	0.53	0.40	0.56
Δt (min)	0.5	0.5	0.5	0.5	0.5	0.5
${\langle v\rangle }_S\left(\mu \mathrm{m}/\mathrm{s}\right)$	0.032	0.019	0.017	0.027	0.011	0.010
${\langle v^2\rangle }_S\left(\mu {\mathrm{m}}^2/{\mathrm{s}}^2\right)$	0.0014	0.0006	0.0005	0.0010	0.0002	0.0001
RS	−0.12	0.18	0.19	0.05	0.21	0.37
Δt (min)	0.5	0.5	0.5	0.5	0.5	0.5

Open in a separate window

The time evolution of the MSD obtained from the model is in good agreement with the data (exemplary match is shown in Fig. 9). Although the model describes the dynamics of T cells very well, the MSD does not contain further distinctive information to differentiate between various migration types of T cells.

Open in a separate window

Figure 9

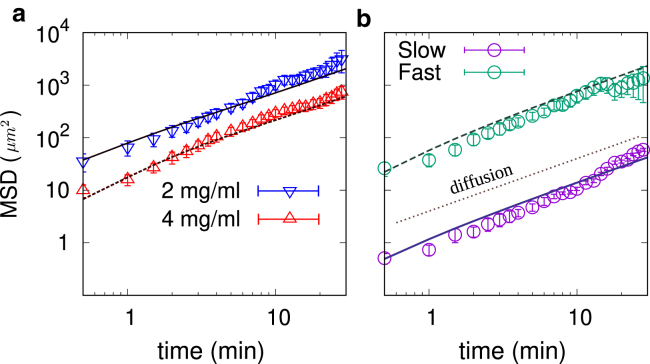
(a) The MSD of mixed motility type in various collagen concentrations obtained from the experiments (symbols) and analytical approach (Eq. 2 with parameters extracted from experimental data summarized in Table 3) (solid lines) for donor 2. (b) Shown is the MSD of slow and fast motility types in collagen concentration 4 mg/mL. The solid lines represent the theoretical estimate of Eq. 5 with parameters extracted from the experiments (Table 4). The error bars represent the standard error. To see this figure in color, go online.

Discussion

We analyzed the trajectories of CTLs within 3D collagen matrices with different concentrations. We found three motility types in all experiments: slow, fast, and mixed. Similar motility types have been reported for natural killer cells in hydrogel collagen with a concentration of 3 mg/mL in the presence of target cells (29). The similarity of the characteristics of CTLs and natural killer cell trajectories points toward a common mechanism for migration of both cell types through collagen networks.

A plausible scenario to explain our findings is that the cells that arrive first in the collagen network perform a persistent random walk unless they move into denser areas of the network, where they become slower but eventually find a way to move again, which leads to two-state motility. When the cells move through the collagen network, they leave a channel by displacing or stretching collagen fibers. These channels facilitate the movement of other T cells, such that cells entering already existing channels move faster and tend to remain in the existing channel network. They do not switch to slow movement and thus establish the fast type. The slow cells mainly remain in one part of the network and only “wiggle” around and seem to be nearly immobile.

In principle, more and more channels can be built by migrating T cells with time, therefore leading to an increase in overall migration speed over time. For our experiments, however, the visualization period was about an hour, and we can estimate the number of new channels that are produced by the T cells. The cell density is 10⁷ cells/mL, which gives an average cell to cell distance of 50 μm. The average velocity of the slow cells—which are those that drill new channels and are nearly one third of all T cells—is 0.02 μm/s. If the motion would be totally persistent $\left({\mathcal{R}}_n=1\right)$, a slow T cell drills within the observation time of 1 h a 72-μm long new channel, which is not long enough to allow a significantly more number of channels to be built. Assuming a cylindrical shape of the channels with a radius of roughly the radius of a T cell, around 5 μm, one can estimate the total volume of new channels created during the observation period in 1 mL to be 0.019 mL, i.e., 2% of the total volume. This is only a small portion and is the reason why the average velocity does not increase during the observation period. We should also note that before the observation period starts, the T cells were already present for 2 h in the collagen matrix. This is the reason why right from the beginning of the observation period, one observes fast T cells; they move in pre-existing channels (which are rather sparse, though: 11% vol). We would like to stress that the low channel production rate is the reason why in the theoretical model we use, one can neglect the production of new channels in the observation period; for short observation times, the statistics of the cell movement is well reproduced by assuming a static network of channels. Our model includes another simplification: instead of generating and fixing this static network before the observation starts, we assume that it is generated “on the fly” when the cells are in the “fast” mode. This simplification is similar to using the annealed approximation (41,42) for quenched disorder, which is known to be good for sufficiently high dilution, which is the case for a sparse channel network. Long-term visualizations will be of great help to verify these points. However, as in the current experimental settings, the collagen matrix falls apart within 8–12 h, depending on the density. Nevertheless, our conclusion is supported by a recent study, which shows that in vivo in salivary gland, T cells follow trajectories established by macrophages, allowing T cells to migrate faster (43).

Compelling evidence shows that when immune cells, including T cells, go through a constricted space, the nucleus, as the stiffest organelle in the cells, is the rate-limiting factor (44,45). Therefore, when the width of the channels in ECM is smaller than the diameter of nucleus, it would become a speed limiting factor for CTL migration in 3D matrix. If the channels are too narrow for the nucleus to pass, the T cells would appear to halt at the position until the matrix breaks loose or until they manage to squeeze themselves out. According to the experimentally determined pore size distribution in collagen matrices with various concentrations (38), one can estimate that the average pore diameter is around 7.5 μm for collagen density 2 mg/mL. The diameter distribution is broad enough to have some pores with a diameter around 9 μm, where T cells with a diameter of 10 μm can squeeze through without deforming the surrounding collagen fibers. On the other hand, in collagen concentrations 4 and 5 mg/mL, the average pore diameter is less than 5 μm with a very narrow distribution, and T cells hardly find pores large enough to squeeze through. This is likely the reason of the different $P\left({\mathcal{R}}_n\right)$ in Fig. 7 a. As a consequence, the channel formation of CTLs during the preparation period is even more essential to explain the observed fast migration in denser collagen matrices.

The morphology of the “channel” visible in Fig. 8 is incompatible with a randomly generated filament network (see background). The latter has of course randomly distributed regions with higher and lower filament density, but elongated cylindrical tunnels as visible in Fig. 8 with a diameter of approximately equal to the diameter of a T cell and completely void of filaments cannot occur by chance with a significant probability. The cylindrical tunnels could be produced by T cells, as observed in Video S4, as they pass through and, if some collagen fibers do not completely spring back to their original position, leaving a broadened channel behind. Another possibility is that these channels have been produced by either T cells degrading the local matrix by secretion of matrix metalloproteases (MMP) or by T cells tearing matrix apart by the exertion of mechanical forces during the 2 h before the observation, and tracking was started, leaving behind elongated, cylindrical tunnels of approximately the same diameter as T cells. Concerning the former option, it is reported that treatment of MMP inhibitors in human CD4⁺ T cell blasts does not affect T cell speed (46). In CD4⁺ T cells, MMP2 and MMP9 are expressed (47), which do not degrade collagen type I (48), which was used in our experiments. The collagen type I-degrading MMPs (MMP1, MMP8, MMP12, and MMP14) are not expressed in bead-stimulated primary human CD8⁺ T cells (unpublished data). Because of lack of MMPs, channel formation most probably proceeds via collagen filament deformation or destruction rather than degradation.

In summary, the aim of this study was to analyze the migration dynamics of CTLs in collagen matrices with different densities to understand potential differences in T cell migration patterns and to elucidate the role of collagen density. The investigation of the effects of the migration patterns that we reveal for the search efficiency of CTLs remains for future studies. Based on our observations, we expect that the search efficiency of T cells decreases in dense collagen matrices because even though the migration pattern per se does not differ, the velocity of CTLs decreases in dense ECM. Interestingly, T cells “dig” into the collagen network and create channels that are later used by other T cells. This is beneficial for faster movement but not necessarily for a more efficient search; channels are only there, where other CTLs have been before. When searching for scattered immobile targets, it is generally not a good strategy to follow the trail of other searchers; as long as those did not find the target, CTLs should avoid the channels because they do not lead toward the target. This is different when CTLs follow a chemotactic signal toward an area of infection; then, channels help subsequent cells to reach this area faster by faster movement. Also, when searching a mobile target, it could be beneficial to follow channels because a mobile target could have moved toward a channel after it was created. Obviously, the effect of channels on the search efficiency of CTLs in collagen matrices is complex but an interesting issue that should be addressed in future studies.

Author Contributions

Z.S., B.Q., M.H., and H.R. designed the research. R.Z. performed the experiments, tracked the trajectories, extracted the corresponding 3D coordinates, and did the analyses in Fig. 8, c, e, and f. Z.S. analyzed the experimental data and employed the analytical model. All authors contributed to the interpretation of the results. Z.S., B.Q., and H.R. wrote the manuscript, which was edited by all authors.

Acknowledgments

Notes

Editor: Jennifer Curtis.

Footnotes

References