Abstract
Free full text

POTATO: Automated pipeline for batch analysis of optical tweezers data
Abstract
Optical tweezers are a single-molecule technique that allows probing of intra- and intermolecular interactions that govern complex biological processes involving molecular motors, protein-nucleic acid interactions, and protein/RNA folding. Recent developments in instrumentation eased and accelerated optical tweezers data acquisition, but analysis of the data remains challenging. Here, to enable high-throughput data analysis, we developed an automated python-based analysis pipeline called POTATO (practical optical tweezers analysis tool). POTATO automatically processes the high-frequency raw data generated by force-ramp experiments and identifies (un)folding events using predefined parameters. After segmentation of the force-distance trajectories at the identified (un)folding events, sections of the curve can be fitted independently to a worm-like chain and freely jointed chain models, and the work applied on the molecule can be calculated by numerical integration. Furthermore, the tool allows plotting of constant force data and fitting of the Gaussian distance distribution over time. All these features are wrapped in a user-friendly graphical interface, which allows researchers without programming knowledge to perform sophisticated data analysis.
Significance
Studying (un)folding of biopolymer structures with optical tweezers under different conditions generates very large data sets for statistical data analysis. Recent technical improvements accelerated data acquisition by coupling modern instruments with microfluidic systems, at the same time creating the need for a high-throughput and unbiased data analysis. We developed practical optical tweezers analysis tool (POTATO), an open-source python-based tool that can process data gathered by any optical tweezers force-ramp experiment in an automated fashion. POTATO is principally designed for data preprocessing, identification of (un)folding events, and the fitting of force-distance curves. In addition, all parameters for preprocessing, statistical analysis, and fitting of the curves can be adapted to suit the data set under analysis in an easy-to-use graphical user interface.
Introduction
Arthur Ashkin received the Nobel Prize in 2018 for his research on trapping dielectric particles with laser light in optical tweezers (OTs) (1). OTs enable probing of structural dynamics of individual molecules by monitoring internal forces and short-lived intermediate states in real time (2, 3, 4, 5). This technique has been widely used to study structures of nucleic acids and dynamics of RNA/protein folding (6, 7, 8, 9, 10). In addition, OTs can also be used to probe the molecular interactions between small molecules, proteins, and nucleic acids (11, 12, 13). Recently, the combination of OTs with confocal microscopy enabled simultaneous measurements of force and fluorescence that provided unprecedented insights into molecular mechanisms such as timing and order of events during transcription or translation (12,14, 15, 16). Basically, in a typical OT experiment, a biopolymer, such as a protein, DNA, or RNA molecule, is tethered between two dielectric beads via labeled handles. The beads are then trapped by focused laser beams, so-called optical traps. Following this, several modes of operation are possible. In force-ramp mode, the beads are precisely displaced in a monotonous manner, which applies increasing forces onto the biopolymer (Fig. 1 A). Since trapped beads behave as if they were attached to mechanical springs, the applied force can be calculated from the measured displacement of the beads out of the trap focus according to Hooke’s law (Fig. 1 B) (17). This mode is commonly used to determine the elastic properties of the molecule and/or to determine the rupture forces at which transitions in folding and unfolding occur.
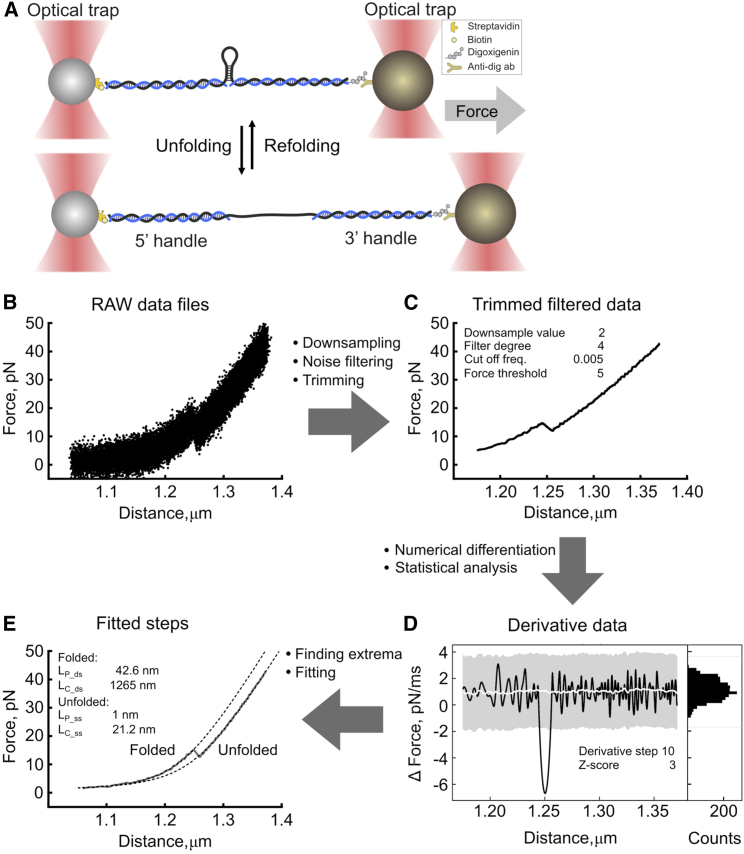
Schematic of the pipeline. (A) Diagram illustrating the optical tweezers experiments. RNA is hybridized to single-stranded DNA handles and immobilized on beads. These are used to exert a pulling force on the RNA with a focused laser beam. In force-ramp operation mode, the force is gradually increased until the structure in the middle is unfolded (bottom). Release of the force allows the structure to refold (top). (B and C) RAW data files (B) are downsampled, the noise is filtered using a Butterworth signal filter, and the data are trimmed at a minimum force threshold to yield the trimmed filtered data (C). (D) Then, the time derivative is calculated numerically to yield the derivative data; a histogram of the derivative value distribution (right) shows two populations—normal-like distribution represents the experimental noise, while the other population of outliers represents the (un)folding steps. The derivative data are then statistically analyzed—the standard deviation and moving median are calculated. Peaks in derivative data that exceed median (white line) ± Z score (gray region) are classified as (un)folding events. The beginning and end of each event are derived. (E) The coordinates of the events are then used to define the region for fitting, yielding the fitted steps. Finally, the output data files are exported according to the selected settings. The FD curve shown here was simulated (see supporting material). To see this figure in color, go online.
On the other hand, a constant-force operation mode allows tracking the molecule of interest in real time as it transitions between different conformational states, yielding kinetic parameters of folding-unfolding of molecules or progressive movements of molecular motors (5). Accordingly, OT experiments also allow precise calculation of the work done on the system of interest (18,19). Previously, OT instruments were self-built by researchers, and thus application required substantial physics and engineering background. Furthermore, such experiments were highly time demanding and labor intensive because a large amount of data needed to be collected for a quantitative analysis. Recently, commercial instruments became available on the market. Another breakthrough was the integration of OT instruments with microfluidic systems, which accelerated both experimental setup and data acquisition (14,15). Nowadays, high-frequency data acquisition allows the generation of large data sets in a relatively short time. Subsequent data analysis, however, still requires custom written scripts to perform data preprocessing, identification of (un)folding events or different folding states, mathematical modeling, and statistical analysis. There are few algorithms developed for the analysis of single-molecule force spectroscopy data, which can perform alignment and pattern-recognition functions (20, 21, 22, 23). Such algorithms are mostly tailored for atomic force spectroscopy data analysis and thus are not directly applicable for OT data (20, 21, 22, 23, 24, 25). In addition, device manufacturers would provide basic solutions for the analysis of force spectroscopy data, yet processing of the data still require bioinformatics and statistics skills, and this therefore remains a major bottleneck.
Here, we present an automated python-based pipeline for the analysis of OT force-ramp and constant-force data (POTATO). Using statistical analysis of the time derivative of force and distance data, both unfolding as well as refolding steps are deduced automatically, and values such as (un)folding force and step length are derived. These values are then directly employed for fitting of force-distance (FD) curves. Additionally, we provide a basic constant-force analysis function. In order to allow the users to modify the analysis parameters to suit their needs, we integrated an easy-to-use graphical user interface (GUI) in POTATO. Since the pipeline allows automated processing of multiple raw data files, our tool reduces the analysis time substantially, and the automated analysis ensures reproducibility and eliminates inconsistencies of manual analysis (26). Next, applicability of the tool is demonstrated on an artificially generated data set, which covers a broad range of possible parameter combinations for force-ramp data, and also on real experimental data (27,28). Finally, we also evaluated the performance of POTATO on a published data set independently generated using a self-built OT system (29). Our results indicate that POTATO exhibits a robust performance in identifying (un)folding events with high accuracy, precision, and recall.
Materials and methods
Algorithm implementation
The algorithm is written in python 3. We designed a GUI and wrapped the code into a Windows standalone executable with pyinstaller to open this tool to a broader audience without a bioinformatics background. The code is freely available on GitHub (https://github.com/REMI-HIRI/POTATO), and the architecture of the python files and GUI is further explained in the supporting material.
Artificial data generation
Artificial force spectroscopy data were generated using a custom-written python script (supporting material). The fully folded part of FD curves was modeled using an equation for extensible worm-like chain (WLC) models (Eq. 4). The partially unfolded region was modeled using a combination of WLC and freely jointed chain (FJC) models (Eqs. 5 and 6). For a more detailed description, see the supporting material.
Results and discussion
Data preprocessing
Raw data (Fig. 1 B) from various input file formats (.h5 or .csv files containing force and distance information) can be loaded and preprocessed before marking the (un)folding events (supporting material). Depending on the data collection frequency, downsampling can be performed, which accelerates the analysis and saves storage space. Downsampling is especially crucial when data are collected at high frequencies. The instrument we used automatically collects data in the high-frequency mode (78,000 Hz), and the raw data need to be downsampled for ease of analysis. On the other hand, self-built systems allow collecting the data at lower frequencies. In principle, if the data frequency is sufficiently high to detect the molecule while transitioning from folded to unfolded states, and vice versa, POTATO can perform the analysis. Therefore, the downsampling rate should be defined by the user empirically. We also note that data sets of very low data-gathering frequency may not be suitable for direct analysis by POTATO. In that case, further preprocessing steps can be implemented (see data augmentation in supporting material). At the next step, a low pass Butterworth filter is employed to reduce the noise out of the signal (Eq. 1) (31). This filter allows efficient noise removal while keeping the actual (un)folding events intact and is therefore commonly used (Fig. 1 C). The algorithm then trims the data at a minimum force threshold set by the user (Table S1). Similar to downsampling, the noise filtering can also be disabled in the GUI if the loaded data is already preprocessed.
Butterworth filter:
G is gain, ω is frequency, ωc is cut-off frequency, and n is filter degree.
Force-ramp data analysis
For the identification of (un)folding events, we employed a derivative-based approach, which has been previously demonstrated to allow efficient step recognition (23). There are also other algorithms available that are based on probabilistic approaches, such as FEATHER (22). However, it must be noted that these tools are mostly developed for the analysis of atomic-force-microscopy-generated data (20, 21, 22, 23, 24, 25). Here, we aimed to combine step recognition with downstream data fitting and determination of work, based solely on recorded force and distance values. Furthermore, we aimed to keep the pipeline intuitive and adjustable to user requirements. Although this tool was initially developed for the analysis of Lumicks FD data in H5 format, in principle, POTATO can be employed to analyze any data set format independent of the type of OT instrument.
Statistical analysis
In force-ramp trajectories, an unfolding event is characterized by a simultaneous drop in force and a quick increase in distance as the secondary structure of the polymer undergoes a sudden transition from the folded to the unfolded state (Fig. 1 C). Refolding events have opposite characteristics, in which the distance decreases and the force increases upon refolding. When flipped, the refolding data cannot be distinguished from the unfolding data and the processing, therefore step identification can be performed in an identical manner. Ultimately, these (un)folding events can be identified as a local maximum in the derivative of the distance and a local minimum in the derivative of the force (Eq. 2). When plotted, the numerical derivative data of both distance and force show two populations of values. The first is a normal-like distribution representing the measurement noise, while outliers from the normal distribution represent the second population—the actual (un)folding events. To distinguish real (un)folding events from background noise, we calculate the moving median and the standard deviation (SD). These are then used to separate the normally distributed data from the extreme values outside a given Z score (i.e., number of SDs = 3 by default) (Fig. 1 D). This should include 99.73% of the normally distributed data points. As the initially calculated SD is affected by the outliers, a second SD is calculated from the data points inside the threshold, and the data are sorted again. The cycle is repeated until the difference between initial and secondary SD is <x (with x default = 5%). After the force and distance derivatives are sorted, our algorithm finds the local extrema of the derivatives, representing the saddle points of the (un)folding events in the FD curve. Then, it finds the adjacent crossing points of the derivative with the moving median, representing the start or end of the corresponding unfolding events.
Numerical approximation of the derivatives:
F is force, D is distance, t is time, x is position, and step d is a change in position.
Data fitting
Once the respective (un)folding steps are identified, this information is employed for data fitting. Data fitting is performed on the untrimmed data to model the trajectories more precisely. For the characterization of the mechanical properties of the (bio)polymer under tension, the extensible WLC model is commonly used, relating the applied force and molecular extension (Eq. 3) (32). For that, the FD curve is split into multiple parts. The fully folded part (until the first detectable unfolding step) is fitted with a WLC (32) to calculate the persistence length (dsLP) of the tethered molecule, while the contour length (dsLC) is fixed. In addition, baseline and offsets in both force and distance are included in the model to compensate for the experimental variability in the FD curves.
The partially and fully unfolded parts of the FD curves are subsequently fitted using a combined model comprising WLC (describing the folded double-stranded handles) and FJC (Eqs. 4 and 5) or another WLC model (representing the unfolded single-stranded parts) (Eq. 6) (Fig. 1 E) (32,33). To mathematically fit the models, we applied model polymer stretching functions from the free python package pylake (Lumicks).
Extensible WLC model:
X is an extension, LC is contour length, F is force, LP is persistence length, kB is Boltzmann constant, T is thermodynamic temperature, K0 is stretch modulus, Foffset is force offset, and doffset is distance offset.
FJC:
Work calculations
Unfolding and refolding FD trajectories also yield crucial information on the thermodynamic properties of the molecule under study. Accordingly, the work applied by the OT instrument onto the system can be calculated from the area under the FD curve (AUC), here using composite Simpson’s rule (Eq. 7). First, we determine the work applied to the whole construct, including the handles (Fig. 2 A). The total work on the construct is the sum of the AUC of the folded model until the starting point of the step (Wds) and work performed during the step transition (Wstep), represented by the rectangular area of the step length times force average ((Fstart + Fend)/2) (Fig. 2 A). In order to extract the amount of work applied only to the structure of interest (Wstructure; Fig. 2 C), the work applied to the handles, represented by the AUC of the combined model (Wss), is subtracted from the sum of the work on the whole construct (Eq. 8; Fig. 2 B and C). It shall be noted that the work derived from these calculations equals the Gibbs free energy of the studied structure provided the system is in thermodynamic equilibrium. However, if the (un)folding trajectories do not coincide, it indicates that the molecule is out of equilibrium. In non-equilibrium scenario, Gibbs free energy can be extracted from the work values (5,18,19,29,34, 35, 36) (Fig. S3). It should be noted that while POTATO performs work calculations, the estimations of free-energy values have to be derived by the user separately.

Work determination of a simple hairpin. (A–C) FD curve obtained during force-ramp experiment of a short stem loop of 30 nucleotides. Inlets: the optical tweezers construct stretched between the beads with gray regions indicating to what parts of the construct the calculated work relates. (A) Marked region (gray) corresponding to the work necessary for stretching of the whole construct including the structure of interest. (B) Marked region (gray) corresponding to the work necessary for stretching of the handles and the unfolded single-stranded RNA. (C) Marked region (gray) corresponding to the work necessary for stretching of the RNA structure of interest. See the subsequent analysis in Fig. S3. To see this figure in color, go online.
Numerical integration using composite Simpson’s rule:
where xj = a + jh for j = 0, 1, …, n-1 with h=(b-a)/n; x0 = a and xn = b.
Non-equilibrium work calculation:
Wstructure is work needed to unfold the structure of interest. Wds is numerical integration of the fully folded model, Wss is numerical integration of the unfolded model, and Wstep is numerical integration of the step region between the two models.
Constant-force data analysis
In addition to force-ramp experiments, the algorithm we provide can also analyze constant-force data (Fig. S1). In this way, the dynamics of the structure at a given force can be investigated. This way, the equilibrium force at which the chance of the structure to be folded or unfolded are equal can be derived.
The constant-force analysis accepts the same input formats as the force-ramp batch analysis, and data preprocessing is performed similarly by downsampling and filtering of the data without trimming. First, it is necessary to display the constant-force data in order to optimize the preprocessing parameters and the plot’s axis (Fig. S1 B). At this step, two plots are generated for visualization. In the first plot, distance is plotted against time. Here, the difference in distance corresponds to the change in the contour length of the tethered molecule. The second plot is a histogram of the distance distribution (Fig. S1 C). From this histogram, the number of different folding states can be deduced. Afterward, the histogram is fitted with multiple Gaussian functions. According to the position distribution histograms, the user can interactively provide initial estimates for various parameters including the number, localization, width (SD, Z score), and amplitude of the fits. After the optimization, the model parameters are exported together with the percentage of each folding state as a table in csv format (comma separated values).
Artificial data sets to test the limits of detection
To test the limits of (un)folding events detectable by the POTATO pipeline, an artificial data set was generated (supporting material). In this data set, some curves can show a negative step length that would not be observed in real unfolding events. We considered these steps as non-identifiable and used them as negative controls. The phenomenon of negative steps can mainly be observed for small contour-length changes (ΔLC) between the models, combined with high force drop (ΔF) values. To test the performance of the algorithm, we defined identifiable steps as events with a drop in force and a simultaneous increase in distance (supporting material). To evaluate if a specific parameter combination results in an identifiable curve, Eq. 9 with x = 0 was solved for all sets of parameters. Each time two parameters were fixed, and the third parameter was optimized.
Minimal step calculation:
where WLC corresponds to expression from Eq. 3, ss refers to the model corresponding to single-strand values, and ds describes the double-stranded region.
A hyperplane showing the interface of theoretically identifiable and non-identifiable steps was generated from these optimized values (Fig. 3 A). This allowed us to classify the generated data set based on a combination of parameters: one with curves where POTATO is expected to find an unfolding step (x > 0) and the other one where POTATO should not identify the steps (x ≤ 0). After analyzing the artificial data set (comprising 2520 curves) with different Z scores, the expected results, based on the input parameters when the data were generated, were compared with the steps identified by POTATO. For the default Z score of 3, the expected parameters were then plotted into the three-dimensional plot and colored based on the identification by POTATO (Fig. 3 A). For an unfolding force of 25 pN, the ΔF and ΔLC values are shown in a two-dimensional plot, making it easier to identify and compare single unfolding events analyzed with different Z scores. It can be seen that all identified steps at this specific unfolding force are above the theoretical threshold and that more unfolding events are identified at Z score 2.5 than at 3 (Fig. 3 B). Accordingly, the effect of the Z score on the derivative of force (Fig. 3 C) and distance (Fig. 3 D) can be investigated for an individual FD trajectory. In the representative trajectory, the local maximum in the derivatives of distance is above the Z score threshold for both cases. In the derivative of force, the local minimum at the same position is only detected for the lower Z score (Fig. 3 C and D).
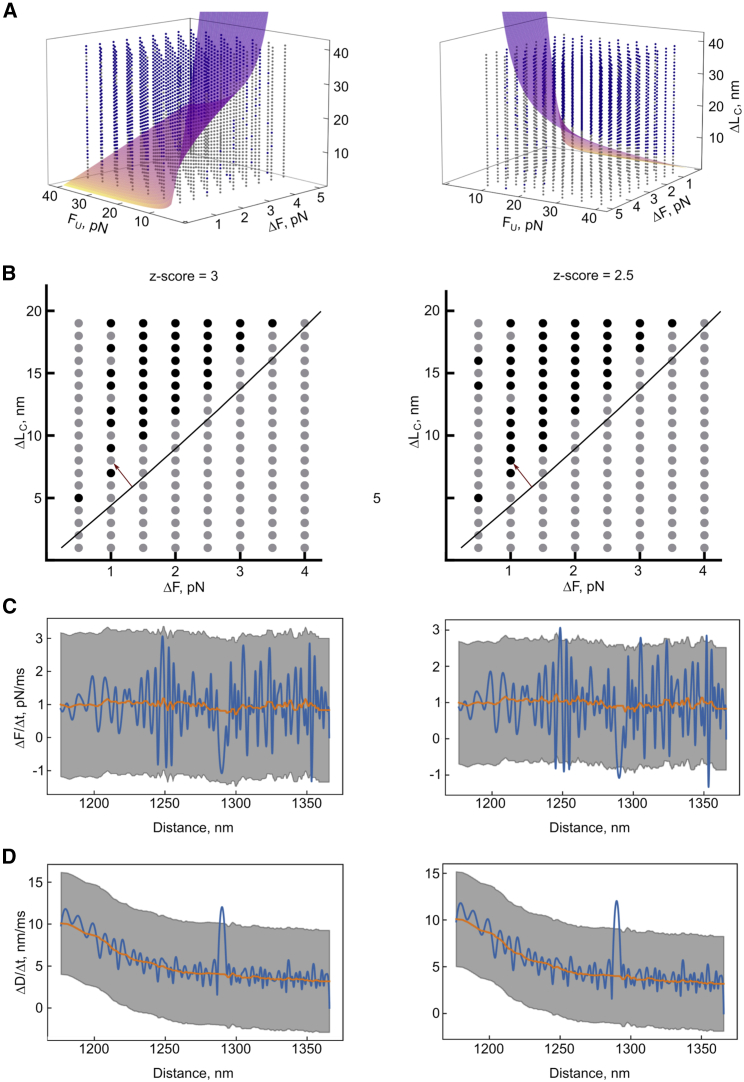
Testing the limits of POTATO. For each combination of the parameters unfolding force (FU), force drop (ΔF), and contour-length change (LC), two parameters were fixed, and the third one was optimized so that the Eq. 9 (supporting material) evaluates to zero. (A) A hyperplane was generated from the optimized values that separate the resolvable space above the hyperplane (parameter combinations that result in identifiable steps) from the unresolvable space below the hyperplane (parameter combinations that result in unidentifiable steps). Each analyzed curve is plotted in blue if its step was identified by POTATO or in gray if it was not recognized. (B) Slices of the three-dimensional plot at FU = 25 pN were analyzed with different Z scores. The black line corresponds to the theoretical limit of resolvable/unresolvable parameter combinations. The black dots represent curves with identified steps, whereas the gray dots represent curves where POTATO could not identify the step. (C and D) The derivatives of force (C) and distance (D) of the curve that is marked with a red arrow in (B) are displayed at different Z scores.
Next, we calculated performance measures such as accuracy, precision, sensitivity, specificity, and F1 score to validate the performance of POTATO. For a Z score of 3.2, a precision score of 0.974 indicates that most of the positive classified steps were actual steps, and even for a Z score of 2.5, the precision was still above 0.944 (Table S2). As expected, higher precision comes with the trade-off to miss certain positive events (recall 0.870–0.939), and the optimal Z score has to be chosen depending on the application. For smaller unfolding events that are difficult to detect, lower Z score should be employed, as for distinct unfolding events, the Z score can be set to higher values. This way, the number of false-positive events detected can be minimized. Since the present data set was generated using artificial parameter combinations, those might not be found in actual OT measurements. Therefore, it is important to keep in mind that we were exploring the limits of the tool by using these strict parameter constraints. Performance measures would also vary depending on where a specific data set is located in the parameter space and which Z scores were employed.
Furthermore, we investigated how accurately POTATO estimates step parameters (FU, ΔLC, ΔF). For that, we compared the expected and measured values of these parameters for all curves analyzed (Fig. 4). We then calculated the linear regression of the true positive values to estimate possible biases of POTATO-estimated FU and ΔLC values. Our analysis shows that in the case of FU (Fig. 4 A), the values determined by POTATO are in perfect agreement with the expected values (slope of the linear regression = 0.9912). For ΔLC (Fig. 4 B), the comparison shows a broader distribution of the measured values, with an overall trend suggesting a minor overestimation (slope of the linear regression = 1.0282) of around 3%. Lastly, in the case of ΔF (Fig. 4 C), the trend shows a slight underestimation of the measured values (slope of the linear regression = 0.8517), resulting in a bias of 12%–15%. Taken together, our performance-measures analysis suggests that the presented tool successfully identifies most (un)folding events correctly with only few false classifications (false positives/false negatives). Accordingly, in most of the cases, performance measures were above 0.9 (Table S2). Moreover, we show that POTATO can precisely estimate the parameter values describing the (un)folding events (FU, ΔLC, ΔF; Fig. 4). Overall, the performance measures and the accuracy of the estimates show that POTATO represents a reliable tool for optical tweezer data analysis.
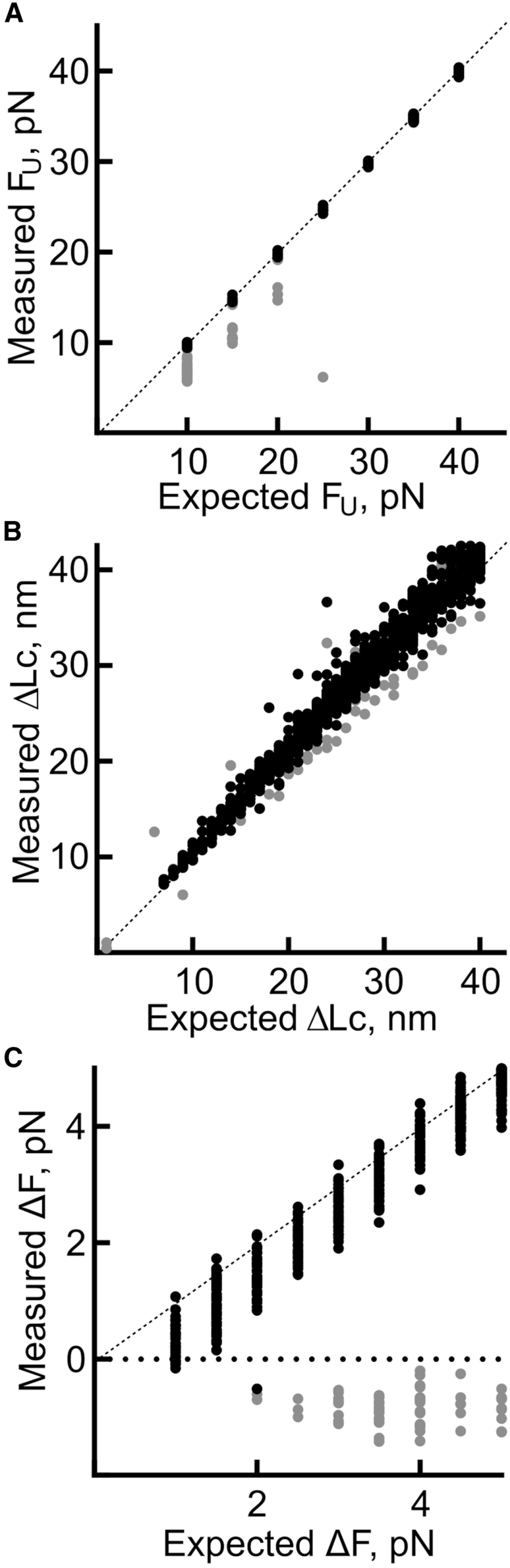
Evaluation of the performance of POTATO. The parameters used for the generation of the data set compared with the parameters identified by POTATO are plotted against each other. All three parameters used for the data generation are evaluated with a Z score of 3. (A–C) The values of the true positive steps (black) and the values of the false-positive steps (gray) are visualized for (A) the unfolding force (FU), (B) the contour length change (ΔLC), and (C) the force drop (ΔF). A dashed line represents the theoretical perfect correlation between measured and expected value.
Applicability of POTATO on real experimental data
Next, we employed POTATO to test its performance on real experimental data generated from FD measurements of the programmed ribosomal frameshifting element of the encephalomyocarditis virus and severe acute respiratory syndrome coronavirus 2 (27,28). We compared the POTATO results with manually annotated steps of a subset of our data set. The results obtained with manual step identification and data fitting were in good agreement with the automated analysis using the pipeline (Fig. S2 A). Harnessing POTATO in the data processing allowed us to speed up the analysis significantly compared with previous manual analysis. Furthermore, we saw that POTATO is not only suitable for curves with a single (un)folding event like in the artificial data set, but we successfully fit FD curves with as many as five unfolding steps, and we were able to identify even short-lived intermediate states of the unfolding process (Fig. S2 B and C). In addition to the contour-length change obtained by curve fitting, the Gibbs free energy is also an important variable to conclude on the nature of the (un)folded structure as it is dependent on the base pairing of the RNA. We were able to use the work calculated by the POTATO to estimate the Gibbs free energy of the structures and thereby distinguish between different secondary structures (27). Here, to demonstrate the energy calculation, we used a stem-loop mRNA of 30 nucleotides in length (Fig. S3) (28). First, we used mfold (37) to predict the secondary structure and its Gibbs free energy (Fig. S3 A). Then, we plotted the unfolding as well as refolding work distributions calculated by POTATO (Fig. S3 B). We then employed the results of POTATO analysis to estimate the Gibbs free energies by applying 1) Crooks fluctuation theorem and 2) Jarzynski equality with bias correction (Fig. S3 C) as described in (18,34, 35, 36).
To evaluate the performance of POTATO on other published data sets generated using a self-built OT instrument, we analyzed the severe acute respiratory syndrome coronavirus 2 pseudoknot RNA FD data by Neupane et al. (29). Since the data set provided had a lower data frequency, resulting in less than 250 data points per FD curve, we first had to artificially augment the datapoints (see supporting material). Despite that, we could still successfully assign the steps and reproduce the unfolding force distribution (Fig S2) as well as the contour-length estimate (Table S3). We were also able to detect the refolding steps’ force distribution and detected steps as low as 6 pN (Fig. S2). In conclusion, regardless of the system used, we demonstrate that the pipeline output matched well with manual data analysis on real-experiment data sets and that POTATO performed analysis of FD trajectories with multiple steps or even short-live intermediates in a reliable way. Therefore, POTATO represents a versatile tool for high-throughput OT data analysis for many upcoming studies.
Limitations of the study
Processing automation comes with trade-offs (38,39). First, the statistical analysis applied in the pipeline might be prone to false-positive event discoveries due to external causes, such as vibration that might induce step-like events in the FD profile of gathered data. We split the FD data and analyze the derivatives of force and distance separately to minimize this effect. Only the events found by both approaches are considered real (un)folding events. Therefore, the robustness of the analysis is increased.
Second, the pipeline output strongly depends on parameters and threshold values that are applied throughout the analysis. The default values were set empirically to suit our needs. Therefore, it might require optimization to fit specific needs and reach an analysis output consistent with the manual data analysis. User input is required despite the user-friendly GUI environment, and an understanding of the analysis workflow is necessary to adjust the parameters rationally.
The current algorithm does not annotate the repeated folding and unfolding of a structure during force-ramp measurements and identifies this oscillation as independent steps. Nevertheless, this mainly occurs at slow loading rates and does not affect the contour-length estimates. To overcome any unexpected issues with the automated analysis, POTATO also includes a tab that allows full manual analysis of the force-ram data files. This should help to eliminate bias caused by omission of certain files from the analysis during the automated analysis.
Summary
Here, we present a publicly available pipeline for batch analysis of OT data. Our pipeline allows OT raw or preprocessed data processing from force-ramp or equilibrium measurements (constant force/position). These are widely employed experimental approaches in the OT field, applied to nucleic acid structure probing, protein folding, RNA-protein interactions, or even to analyze events as complex as translation. Here, by wrapping our algorithm in a standalone application and designing an intuitive GUI, we aim to open the data analysis to a broader audience without the need for a bioinformatics background. The user can adjust all parameters directly in the GUI without diving into the code to tailor the pipeline to their exact needs. With the parameters optimized for the here-presented data sets, POTATO showed high precision and accuracy in the identification of (un)folding events. Moreover, compared with manual data analysis, the pipeline is faster and, most importantly, consistent throughout the analysis, thus yielding reproducible results.
Author contributions
N.C., L.P., and S.B. designed the pipeline. L.P. and S.B. wrote the python scripts. L.P. generated the artificial data. S.B. analyzed the artificial data. L.P. and S.B. performed the OT experiments. L.P. analyzed experimental data. L.P. and S.B. prepared the figures with input from N.C. N.C., L.P., and S.B. wrote the manuscript.
Acknowledgments
We thank Vojtech Vrba for helpful python discussions. We thank Dr. Anke Sparmann for critically reviewing the manuscript. The work in our laboratory is supported by the Helmholtz Association and European Research Council (ERC) grant no. 948636.
Declaration of interests
The authors declare no competing interests.
Footnotes
Stefan Buck and Lukas Pekarek contributed equally to this work.
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2022.06.030.
Supporting material
References
Articles from Biophysical Journal are provided here courtesy of The Biophysical Society
Full text links
Read article at publisher's site: https://doi.org/10.1016/j.bpj.2022.06.030
Read article for free, from open access legal sources, via Unpaywall:
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC9388390
Citations & impact
Impact metrics
Alternative metrics

Discover the attention surrounding your research
https://www.altmetric.com/details/130517993
Article citations
Cis-mediated interactions of the SARS-CoV-2 frameshift RNA alter its conformations and affect function.
Nucleic Acids Res, 51(2):728-743, 01 Jan 2023
Cited by: 13 articles | PMID: 36537211 | PMCID: PMC9881162
The short isoform of the host antiviral protein ZAP acts as an inhibitor of SARS-CoV-2 programmed ribosomal frameshifting.
Nat Commun, 12(1):7193, 10 Dec 2021
Cited by: 47 articles | PMID: 34893599 | PMCID: PMC8664833
Similar Articles
To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.
High-resolution optical tweezers for single-molecule manipulation.
Yale J Biol Med, 86(3):367-383, 20 Sep 2013
Cited by: 27 articles | PMID: 24058311 | PMCID: PMC3767221
Review Free full text in Europe PMC
Introduction to Optical Tweezers: Background, System Designs, and Commercial Solutions.
Methods Mol Biol, 1665:3-23, 01 Jan 2018
Cited by: 1 article | PMID: 28940061
High-Precision Single-Molecule Characterization of the Folding of an HIV RNA Hairpin by Atomic Force Microscopy.
Nano Lett, 18(10):6318-6325, 24 Sep 2018
Cited by: 12 articles | PMID: 30234311
Single-Molecule Protein Folding Experiments Using High-Precision Optical Tweezers.
Methods Mol Biol, 1486:357-390, 01 Jan 2017
Cited by: 20 articles | PMID: 27844436 | PMCID: PMC5508109
Funding
Funders who supported this work.
European Research Council (1)
Grant ID: 948636





