Abstract

1. Introduction

Rhythmic motor behavior, such as walking, swimming, flying, breathing, and chewing, are important for vertebrates and invertebrates (Marder and Calabrese, 1996; Marder and Bucher, 2001; Katz, 2016; Kiehn, 2016; Sakurai and Katz, 2016; Lu et al., 2022). Motor behaviors are modulated by the rhythmic patterns generated in the central pattern generators (CPGs) or neuronal circuits with inhibitory coupling, such as the stomatogastric ganglion (STG) in Cancer borealis or Panulirus interruptus. The triphasic rhythm generated by three neurons of the pyloric network of the STG controls the digestive function (Selverston, 2005; Szücs et al., 2009; Zhu et al., 2016). The bursting period, burst duration, duty cycle, spike frequency, spikes per burst of rhythmic bursting activity are essential factors to modulate rhythmic behaviors (Daun et al., 2009; Coleman et al., 2013; Kueh et al., 2016). For instance, shortened period of bursting in the leech heart interneurons speeds up the heartbeat (Tobin and Calabrese, 2005). Especially, rhythmic patterns have been widely used to control the motion of robot (Ijspeert, 2008; Habu et al., 2019; Fukuoka et al., 2022). Then, identification of modulations such as inhibitory currents of synapses and ionic currents of neurons to the rhythmic motion is an important issue (Marder and Bucher, 2007; Grashow et al., 2009; O’Leary et al., 2014; Kueh et al., 2016).

Inhibitory synaptic current (I_syn) modulates the dynamical behaviors of two neurons with reciprocal inhibition coupling (Alaçam and Shilnikov, 2015; Sakurai and Katz, 2016; Baruzzi et al., 2020; Onasch and Gjorgjieva, 2020), such as the antiphase rhythm composed of firing (active) phase and silence (inhibited) phase. For example, changes in durations of the two phases underlie various rhythmic behaviors, such as breathing fast or slow (Peña et al., 2004; Baertsch et al., 2018). The antiphase rhythmic patterns can be roughly classified into two typical mechanisms: escape and release (Wang and Rinzel, 1992; Skinner et al., 1994). In this paper, they are called escape mode and release mode, which correspond to the low and high voltage thresholds (V_th) of the inhibitory synapse, respectively. For the escape mode, the low membrane potential during the silence phase of neuron 1 can depolarize to go beyond V_th and become firing, which terminates the firing phase of neuron 2 (Skinner et al., 1994). For the release mode, the membrane potential of the firing phase of neuron 1 falls below V_th to reduce the inhibitory synaptic current (I_syn) outputted to the silence phase of neuron 2, then, the silence phase of neuron 2 transits to the firing phase. The firing phase in Wang and Rinzel (1992) is not burst but a spike due to the relatively simple ionic currents of the neuron model. For the bursting neuron model such as the Hindmarsh–Rose model, inhibitory coupling can induce antiphase bursting (Yao et al., 2013). Other currents such as the calcium current and pump current play important roles to modulate the rhythmic patterns containing the antiphase bursting (Olsen et al., 1995; Olypher et al., 2006; Simoni and DeWeerth, 2006; Doloc-Mihu and Calabrese, 2011; Doloc-Mihu Anca and Calabrese, 2014; Li et al., 2018). More interestingly, for the spiking neuron with hyperpolarization-activated cation current (I_h), inhibitory coupling can induce antiphase bursting (Sharp et al., 1996).

The I_h, which has been identified in many different types of neurons (Robinson and Siegelbaum, 2003; He et al., 2014; Xu et al., 2017; Dashevskiy and Cymbalyuk, 2018), is known to regulate rhythmic behavior and excitability (Lüthi and McCormick, 1998; Sorensen et al., 2004; Biel et al., 2009; Wahl-Schott and Biel, 2009; Datunashvili et al., 2018). Especially, as a neuron is subjected to negative, hyperpolarization, or inhibitory stimulation, the membrane potential becomes lower, which can activate the positive I_h to promote the neuronal excitability and evoke action potentials. Then, the I_h and the co-regulations of the inhibitory synaptic current I_syn and the I_h play important roles in modulating the antiphase bursting in many different types of neurons (Sorensen et al., 2004; Grashow et al., 2009; Ellingson et al., 2021; Morozova et al., 2022). For example, in pairs of the leech heart interneurons with mutually inhibitory coupling, increase of the I_h current induces the bursting period of the antiphase bursting decreased to speed up the heartbeat (Tobin and Calabrese, 2005). Especially, in the mutually inhibitory circuit containing two gastric mill (GM) neurons of the STG of the crab, many rhythm patterns that does not contain the antiphase bursting appear in the absence of the I_h, whereas introduction of the I_h induces stable antiphase bursting (Sharp et al., 1996; Morozova et al., 2022). Unfortunately, the parameter regions of the I_h and I_syn for the antiphase bursting and other rhythm patterns, and the changes of the parameter region with respect to changes of V_th (the synaptic threshold voltage), are still unclear, which are studied in the present paper.

Then, complex dynamics of two mechanisms of the antiphase bursting modulated by the I_h are studied (Sharp et al., 1996; Clewley, 2011; Morozova et al., 2022). With increasing the conductance (g_h) of the I_h, the bursting period decreases and increases, respectively, for the escape mode and release mode, exhibiting opposite changes (Sharp et al., 1996; Morozova et al., 2022). More complex, a mixture mechanism locating between the escape mode and release mode is observed in a recent study (Morozova et al., 2022), and the robustness of the two manners is studied. Especially, the opposite changes of the bursting period with respect to the I_h also provide a convenient and feasible measure to generate rhythmic bursting patterns with various periods, which may be used as a potential candidate to control motion of the robot. Although experimental investigations, there are lack of theoretical studies. In addition, although the alternation between the burst and the silence of the antiphase bursting for the escape mode and release mode is presented (Sharp et al., 1996; Morozova et al., 2022), the co-regulations of the I_h and I_syn in modulating the opposite changes of the bursting period for the two manners have not been explained very well. Then, reproduction of the antiphase bursting for the escape, release, and mixture modes in the simulations, and identification of the roles of the I_h and I_syn in the opposite changes of bursting period for the escape mode and release mode, are important questions, which are answered in the present paper.

In addition, according to the fast-slow dynamics of the bursting (Izhikevich, 2000; Li Y. et al., 2021; Ma et al., 2021), a neuron model with bursting behavior contains a fast subsystem and slow variables (Wang et al., 2021; Yuan et al., 2021), and the fast-slow analysis is effective to analyze the dynamics of the bursting and spiking modulated by one slow variable (Lü et al., 2019). After obtaining the bifurcations of the fast subsystem with the slow variable taken as a bifurcation parameter, the burst phase and quiescent (silence) phase of the bursting pattern are, respectively, related to the stable limit cycle behavior (spiking) and stable equilibrium point of the fast subsystem (Belykh and Shilnikov, 2008). However, a spiking is only related to the stale limit cycle instead of the stable equilibrium point. Recently, fast-slow analysis with two slow variables is proposed. Up to now, fast-slow analysis has seldom been used to analyze the bursting from the coupled neurons. In the experimental study (Sharp et al., 1996), for the isolated neurons with a slow I_h generating the spiking instead of the antiphase bursting, the antiphase bursting appears after the inhibitory coupling. Unfortunately, the mechanism for the transition from the spiking to the antiphase bursting and the fast-slow dynamics of the antiphase bursting, which are modulated by the I_syn and I_h, are still unclear. Then, the fast-slow dynamics of the antiphase bursting, the roles of the I_syn and I_h in the alternation between the silence and burst phases, and the roles of the two currents within the burst and silence phases are studied in the present paper.

In the present paper, the questions mentioned above for the dynamics of the antiphase bursting are answered in a theoretical model of two neurons with mutually inhibitory coupling. Firstly, the roles of the slow I_h to ensure the formation of the antiphase bursting, and the different influences of the I_h and I_syn on the antiphase bursting at different values of V_th, are obtained. The I_h is identified to be the necessary condition for the antiphase bursting, closely matching the experimental observation (Sharp et al., 1996). At different levels of V_th, the dependence of the antiphase bursting and other rhythm patterns on the I_h and I_syn is different, which presents the parameter region of the antiphase bursting. Secondly, the opposite changes of the antiphase bursting for the escape mode and release mode, respectively, corresponding to low and high V_th, and a mixture mode for a middle V_th, are reproduced in the simulations, closely matching the experimental observations (Morozova et al., 2022). Furthermore, the roles of the I_h and I_syn in modulating the opposite changes of bursting period for the escape mode and release mode are obtained. For the escape mode, increase of the I_h induces elevated membrane potential of the silence inhibited by a strong I_syn, which reduces the silence duration to go beyond V_th, resulting in reduced bursting period. For the release mode, with increasing I_h, the tough value of the burst elevates, then, the burst duration with tough value higher than V_th is lengthened, meanwhile, enhanced I_syn is outputted to the partner neuron to prolong the silence period, resulting in prolonged bursting period. Finally, the fast-slow dynamics of antiphase bursting modulated by the I_h and I_syn are acquired. Using the one-parameter and two-parameter bifurcations of the fast subsystem of a single neuron, the burst of the antiphase bursting is related to the stable limit cycle modulated by a weak I_syn, and the silence modulated by a strong I_syn to the stable equilibrium point to a certain extent. The I_h mainly modulates the dynamics within the burst and silence. Furthermore, using the fast subsystem of the coupled neurons, the silence is related to the unstable equilibrium point. The results present theoretical explanations to the variations in the bursting period and fast-slow dynamics of the antiphase bursting modulated by the I_syn and I_h, which is helpful for understanding the antiphase bursting. Especially, a potential and feasible measure to modulate the rhythmic motion via modulations to only two factors (the I_h and I_syn) to obtain different bursting patterns with various periods.

2. Models and methods

3. Results

3.1. Antiphase bursting of the coupled neurons with the I_h

3.1.1. Four rhythm patterns in the absence of the I_h current

In the absence of the I_h, the two neurons with the inhibitory coupling produce four patterns of electrical activity, as shown in Figure 1. Unfortunately, antiphase bursting does not appear. The solid black and solid red curves represent the voltage of the neuron 1 and neuron 2, respectively, and the dashed curve denotes the inhibitory synaptic current I_syn. For a small coupling strength such as g_syn=0.5 nS, either neuron exhibits spiking similar to that of the isolated neuron, as shown in Figure 1A, which is called double-spiking pattern in this article. For g_syn=2 nS, the two neurons inhibit each other at first due to the increase of the synaptic current, then the behavior of the two neurons changes to silence state, as depicted in Figure 1B, called double-silence pattern. With further increasing g_syn to 5 nS, antiphase spiking appears, induced by the mutual inhibitions between the two neurons, as shown in Figure 1C. As g_syn becomes strong such as 10 nS, the inhibitory current from the neuron 1 to the neuron 2 is strong enough, resulting in that spiking appears for neuron 1 and subthreshold oscillation for neuron 2, as illustrated in Figure 1D, which is called pattern of spiking and subthreshold oscillation. Such a symmetrical behavior is caused by different initial values of the two neurons.

Open in a separate window

Figure 1

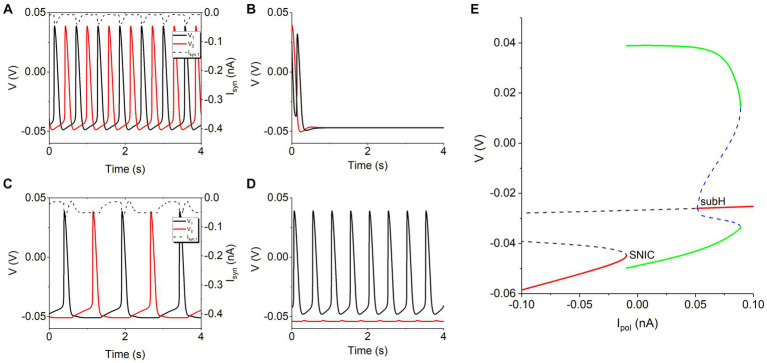
The four rhythm patterns of model without I_h current at different g_syn values. (A) Double-spiking pattern for g_syn=0.5 nS. (B) Double-silence pattern for g_syn=2 nS. (C) Antiphase spiking for g_syn=5 nS. (D) Pattern of spiking and subthreshold oscillation for g_syn=10 nS. Synaptic threshold V_th=−0.047V. (E) Bifurcations of an isolated neuron to explain the rhythm patterns in panels (A,C).

The rhythm patterns in panels (A,C) are different, which can be explained with the inhibitory coupling current and the bifurcations of the isolated neuron. For the panel (A), the inhibitory synaptic current (dashed curve for neuron 1) between two continuous spikes is small, weaker than −0.009485nA, as shown in Figure 1A, which can play a weak role and then can seldom influence the spiking behavior. For the panel (C), the inhibitory synaptic current (dashed curve for neuron 1) between two continuous spikes is strong, stronger than −0.009485nA for a relatively long time, which can inhibit a spike to from a relatively long interspike interval (ISI). As shown in Figure 1E, there is a saddle-node bifurcation on an invariant cycle (SNIC) at I_pol=−0.009485nA for the isolated neuron. Via the SNIC bifurcation, the resting state (left red, stable node) changes to the spiking (green curves). The resting state appears for I_pol<−0.009485nA. Then, I_syn weaker than −0.009485nA in panel (A) cannot go beyond the bifurcation, forming the silence, whereas I_syn stronger than −0.009485nA for a relatively long time in the panel (C) can induce silence corresponding to the resting state and appearing between two continuous spikes, resulting in a long ISI. Other bifurcations are not related to the results of the present paper (not addressed here).

3.1.2. Antiphase bursting pattern in the presence of the slow I_h

In the presence of the slow I_h, in addition to the four electrical activity patterns mentioned above, the antiphase bursting activity appears, as shown in Figure 2A, black representing the neuron 1 and red denoting the neuron 2, which is consistent with the experimental results in Sharp et al. (1996). It is well-known that the bursting behavior is modulated by slow variables (Berry et al., 2022; Xing et al., 2022). The gating variable m_h of the I_h is a slow variable, as shown by the magenta curve in Figure 2B. The variables h_Na (green) and m_K (orange) of the neuron 1 are shown in Figure 2B, and the I_h of the neuron 1 is shown in Figure 2C. Obviously, during the burst, variables h_Na (green) and m_K (orange) oscillate fast, similarly to V, whereas m_h (magenta) changes slowly and gradually, showing that m_h is the slow variable to ensure the bursting activity.

Open in a separate window

Figure 2

The slow I_h for the antiphase bursting with g_syn=15 nS, g_h=5 nS, and V_th=−0.047V. (A) Spike trains with black curve for neuron 1 and red curve for neuron 2. (B) Variables h_Na (green), m_K (orange), and m_h (magenta) with slow dynamics for the neuron 1 (black). (C) I_h for the neuron 1 (black).

3.1.3. The dependence of the antiphase bursting on g_h and g_syn for different values of V_th

The distribution of the five rhythm patterns at different values of V_th in the plane (g_h, g_syn) are shown in Figures 3A–F. The lower cyan area (①), black area (②), upper cyan area (③), red area (④), and blue area (⑤) represent the double-spiking pattern, double-silence pattern, antiphase spiking pattern, antiphase bursting pattern, and pattern of spiking and subthreshold oscillation, respectively. In Ellingson et al. (2021), V_th determines the escape mode and release mode for the antiphase bursting. The value of V_th determines the level of inhibitory synaptic current (please refer to Supplementary Figure S1). With increasing V_th, the inhibitory synaptic current becomes weak. Therefore, the distribution of the rhythm patterns on plane (g_h, g_syn) at different values of V_th are different, as shown in Figure 3. The results present more detailed relationships between the different rhythm patterns (Sharp et al., 1996) show as follows:

1. When g_h is zero or small, no antiphase bursting (red) appears. Antiphase bursting (red area) occurs for positive g_h values, which is consistent with the experimental results in Wahl-Schott and Biel (2009).

2. The red region for the antiphase bursting exhibits large g_syn and g_h, showing that the antiphase bursting appears for strong I_h and strong I_syn.

3. The red region for the antiphase bursting exhibits different characteristics for lower V_th [panels (A–D) for −0.05V, −0.047V, −0.045V, and V_th=−0.043V, respectively] and higher V_th [panels (E,F) for −0.04V and −0.035V, respectively]. As V_th increases, the red parameter region for the antiphase bursting becomes large for a lower V_th, and becomes small for a higher V_th. The borders of red region (the antiphase bursting) for low V_th exhibit shapes different from those of high V_th. Then, different dynamics for a lower V_th (−0.047V as representative) and a higher V_th (−0.04V as representative) are studied in the following paragraphs.

Open in a separate window

Figure 3

Distribution of different rhythm patterns in plane (g_h, g_syn) at different V_th values. (A) V_th=−0.05V; (B) V_th=−0.047V; (C) V_th=−0.045V; (D) V_th=−0.043V; (E) V_th=−0.04V; (F) V_th=−0.035V. The areas marked with ①, ②, ③, ④, and ⑤ represent the double-spiking pattern, double-silence pattern, antiphase spiking pattern, antiphase bursting pattern, and pattern of spiking and subthreshold oscillation.

3.2. The roles of the I_syn and I_h for the escape mode and release mode of the antiphase bursting

The antiphase bursting for escape mode (V_th=−0.047V as representative) and release mode (V_th= −0.04V as representative) is studied in the present subsection. As mentioned above, the neuron 1 and neuron 2 exhibit symmetrical behaviors. Then, the inhibited (silence) phase of the neuron 1 (black) corresponds to the active (burst) phase of the neuron 2 (red), and the burst duration of the neuron 1 equals the duration of the silence phase of the neuron 2, and vice verse, as shown in Supplementary Figure S2.

3.2.1. Distributions of the bursting period in plane (g_h, g_syn) for the three manners

The period of the antiphase bursting shows opposite changes at different synaptic thresholds, as shown in Supplementary Figure S2. The distributions of the bursting period on two-parameter plane (g_h, g_syn) at different V_th values are shown in Figure 4. The antiphase bursting appears in the colorful region and the color scale represents the value of the bursting period, and the blank area represents other rhythm patterns. For different V_th values, the bursting period exhibits different changes with respect to g_h.

Open in a separate window

Figure 4

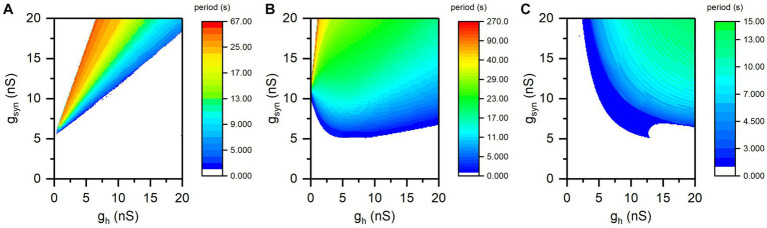
The distribution of period of antiphase bursting in plane (g_h, g_syn). (A) V_th=−0.047V for the escape mode; (B) V_th=−0.043V for the mixture mode; (C) V_th=−0.040V for the release mode. Color scale represents the value of bursting period.

For V_th=−0.047V (escape mode), as illustrated in Figure 4A, the bursting period decreases with the increase of g_h for all values of g_syn, which presents the simulation results to the experimental observations in Sharp et al. (1996) and Morozova et al. (2022). And the maximum bursting period exceeds 60s.

When V_th=−0.043V, the change of bursting period with increasing g_h is complex, as shown in Figure 4B. As g_syn is approximately less than 11 nS, the bursting period increases at first and then decreases. When g_syn is approximately greater than 11 nS, the bursting period decreases. Such a manner does not correspond to the typical escape mode or release mode, but to the mixture mode observed in the experiment (Morozova et al., 2022).

For V_th=−0.04V (release mode), the period of bursting increases with increasing g_h for all g_syn values, as depicted in Figure 4C, presenting simulation results to the experimental observations reported in Sharp et al. (1996) and Morozova et al. (2022). In addition, the maximum burst period at V_th=−0.04V is less than 15s, which is significantly lower than the bursting period for V_th=−0.047V.

In addition, the bursting period increases with increasing g_syn for different V_th and g_h values, which is easy to be understand. The larger the g_syn is, the stronger the I_syn is, and the longer the silence duration is. Then, burst duration and bursting period increases with increasing g_syn, which is not studied in the present paper.

3.2.2. Co-regulations of the two currents for the escape mode

The roles of the two current in the decreased bursting period with increasing g_h are addressed in Figure 5, with g_syn=15 nS as representative. Here, the neuron 1 is plotted and the neuron 2 is ignored, since the symmetrical behaviors for the two neurons. The behavior for time t<82,134ms is the bursting with g_h=5 nS. Then, g_h is increased to 8 nS at t=82,134ms (green dashed vertical line, i.e., the ending point of the burst) and g_h remains unchanged after t=82,134ms. The formation process of the antiphase bursting for g_h=8 nS begins from t=82,134ms. Olive curves represent g_h=5 nS, and pink curves denote g_h=8 nS. The four panels from top to bottom show the membrane voltage V₁, the I_h,1, the I_syn,1, and the total current I_total,1 (i.e., CdV₁/dt) in turn.

Open in a separate window

Figure 5

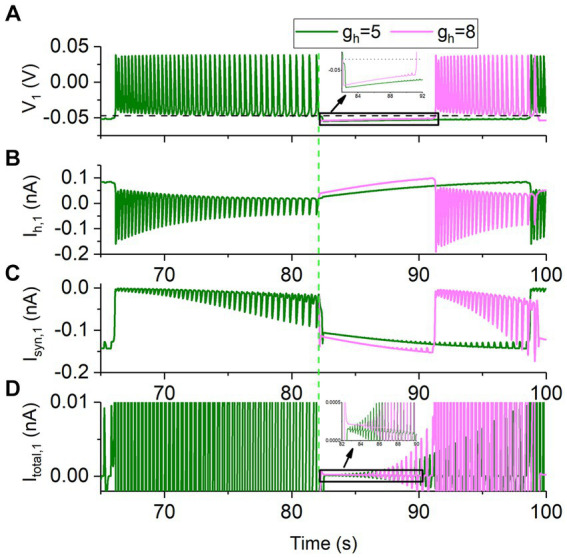
Changes of the membrane potential and ionic currents of the neuron 1 for g_syn=15 nS and V_th=−0.047V. The bursting at g_h=5 nS (olive), and formation process of bursting at g_h=8 nS (pink) for time t≥82,134ms. (A) Membrane potential V₁. The black horizontal dashed line represents the synaptic threshold voltage V_th=−0.047V. (B) I_h,1current. (C) Inhibitory synaptic current I_syn,1. (D) Total current I_total,1. The green dashed vertical line represents t=82,134ms at which g_h is changed from 5 to 8 nS.

As shown in Figure 5A, the rise rate of the membrane voltage in the silence phase is larger for the stronger g_h. During the silence phase, the larger the g_h, the larger the Ih current (Figure 5B) and thus the larger the total current. Larger total current induces faster increase of the membrane voltage V₁ (Figure 5A and the insert panel) to be higher than the synaptic threshold V_th=−0.047V (the black dashed line in Figure 5A and the insert panel). Then, the inhibitory current from the neuron 1 to the neuron 2 generates, inhibiting the neuron 2 to form the silence and resulting in the earlier appearance of the burst of the neuron 1. Thus, the larger the g_h is, the shorter the inhibited phase is, showing that the duration of the inhibited phase decreases with increasing g_h, since the period of the bursting is doubled to the duration of the inhibited phase. Then, the period of the bursting decreases with increasing g_h. The result presents a detailed co-regulation process of the I_syn and I_h for the escape mode.

Although I_syn,1 received by the neuron 1 becomes stronger with increasing g_h, as shown in Figure 5C, the total current I_total,1 becomes more positive (Figure 5D), induced by more positive I_h,1 (Figure 5B). The results show that the I_h plays a dominant role, compared with I_syn.

3.2.3. Roles of the two currents for the release mode

Compared with V_th=−0.047V, the I_syn for V_th=−0.040V becomes small. Then, different from V_th=−0.047V, the co-regulations of the I_syn and I_h for V_th=−0.040V can be explained with the burst phase of one neuron and the silence phase of the other neuron. Then, the behaviors of the neurons 1 and 2 are shown in Figure 6. The behavior of the neuron 1 is shown in Figure 6A. The behavior for t<32,430ms is the antiphase bursting for g_h=10 nS and g_syn=15 nS. Then, g_h increases to 20 nS at t=32,430ms (green dashed vertical line, i.e., the starting point of burst) and g_h remains unchanged after t=32,430ms. The behavior of the neuron 2 is shown in Figure 6B. Olive and pink curves appearing after t=32,430ms represent g_h=10 nS and 20 nS, respectively, and the four panels from top to bottom show the membrane voltage V, I_h, I_syn, and the total current in turn.

Open in a separate window

Figure 6

Changes of membrane potential and ionic currents for g_syn=15 nS and V_th=−0.04V. The bursting at g_h=10 nS (olive), and formation process of bursting at g_h=20 nS (pink) for t>32,430ms for neuron 1 shown in (A) and for neuron 2 depicted in (B). The panels from top to bottom show the membrane voltage, I_h current, inhibitory synaptic current I_syn, total current. The black horizontal dashed line represents the synaptic threshold voltage V_th=−0.04V. The green dashed vertical line represents t=32,430ms at which g_h is changed from 10 nS to 20 nS.

Obviously, the membrane potential, the I_h, and I_syn, and the total current during the silence phase shown in Figure 6A are different from those of V_th=−0.047V (Figure 5, the escape mode). Then, the burst of the neuron 1 is chosen as the starting point to explain the co-regulations of the two currents, as shown in Figure 6A. The larger the g_h is, the larger the I_h,1 current for the neuron 1 is. Then, the larger I_h,1 elevates the valley voltage within the burst (Figure 6A), resulting in a larger synaptic current, I_syn,2, as shown by the pink curve in Figure 6B. The larger I_syn,2 causes the lower membrane voltage in neuron 2, which in turn causes neuron 1 to receive the smaller I_syn,1. Therefore, the time duration in which the valley voltage of the burst is higher than the synaptic threshold V_th (the black dashed line in Figure 6A) prolongs, resulting in a prolonged burst duration. As the valley voltage within the burst of the neuron 1 falls below V_th to a certain extent, the inhibitory synaptic current outputted to the neuron 2 (I_syn,2) becomes weak, as shown in Figure 6B, i.e., the maximal negative peak value of the I_syn,2 (pink) after 35s elevates. As the I_syn,2 becomes small enough to not maintain the silence phase of the neuron 2, the neuron 2 becomes burst and the burst can induce silence of neuron 1 via the inhibitory current I_syn,1, as shown in Figure 6. In a word, the time duration of the valley voltage of the burst of the neuron 1 higher than V_th increases with increasing g_h, resulting in a prolonged burst duration and bursting period, as shown in Supplementary Figure S3.

3.3. Fast-slow dynamics modulated by the I_h and I_syn of the antiphase bursting

In the present subsection, the behaviors before and after coupling are analyzed with fast-slow analysis. Firstly, with the one-parameter bifurcations of the fast subsystem of a single neuron, a single neuron is identified to exhibit a spiking behavior, the burst of the antiphase bursting after coupling is related to the stable limit cycle of the fast subsystem, whereas no correspondence to the silence is found. Then, with the two-parameter bifurcations of the fast subsystem of a single neuron, the silence is related to the stable equilibrium point of the fast subsystem to a certain extent. Furthermore, with one-parameter bifurcations of the fast subsystem of the coupled neurons, the silence is related to the unstable equilibrium point. Especially, the roles of the two currents I_h and I_syn within the burst and silence phase are discussed.

3.3.1. Fast-slow analysis with one-parameter bifurcations of the fast subsystem of a single neuron

For the single neuron model with the I_h, m_h that described by Equation 4 is the slow variable and Eqs. 1–3 are the fast subsystem. Figure 7 shows the bifurcations of the fast subsystem and trajectory of the spiking for different g_h. In each panel, the unstable equilibrium point (horizontal dashed black line) changes to a stable one (solid red line) via a subcritical Hopf (subH) bifurcation. Meanwhile, an unstable limit cycle (blue curves) emerges, contacting with a stable one (green curves) to form a saddle node bifurcation of the limit cycles (SNLC). Obviously, the spiking (vertical black line in Figure 7) runs along the stable limit cycle and is not related to the stable focus. More details please refer to the Supplementary material and Supplementary Figure S4.

Open in a separate window

Figure 7

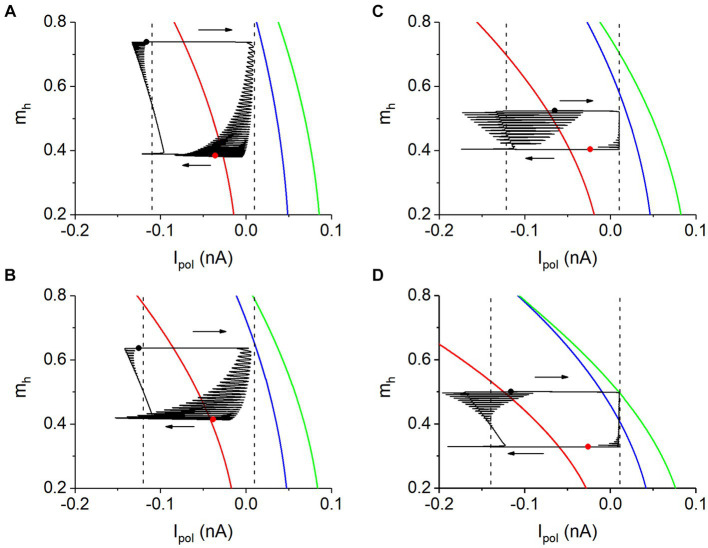
Spikes of burst of the antiphase bursting run along the stable limit cycle of the fast subsystem of the isolated neuron. (A) V_th=−0.047V and g_h=5 nS; (B) V_th=−0.047V and g_h=8 nS; (C) V_th=−0.040V and g_h=10 nS; (D) V_th=−0.040V and g_h=20 nS. Other parameter values: g_syn=15 nS and I_pol=0.01nA. Arrow in each panel represents the running direction.

3.3.1.1. Burst of the antiphase bursting is associated with the stable limit cycle

In some previous studies (Gu and Zhao, 2015; Qi et al., 2023), the dynamics of the fast subsystem of an isolated neuron can also characterize the bursting modulated by the synaptic (autaptic) current. Then, the dynamics of the fast subsystem of a single neuron instead of the coupling model is used here. Bifurcations shown in Supplementary Figure S4 are used to characterize the antiphase bursting modulated by the synaptic current, as illustrated in Figure 7. The phase trajectory of the antiphase bursting of the neuron 1 with I_pol=0.01nA is superimposed on Supplementary Figure S4 to form Figure 7, with V_th=−0.047V for Figures 7A,​,BB and V_th=−0.04V for Figures 7C,​,D.D. Obviously, the spikes (orange) of the burst run along the stable limit cycle (green). Within the burst duration of the neuron 1, the inhibitory synaptic current I_syn from neuron 2 during the silence phase is small or nearly zero, showing that the neuron 1 during the burst resembles an isolated neuron, which is the cause that the burst of the coupled neurons can be explained with the stable limit cycle of the isolated neuron model. Unfortunately, the termination phase of the burst has not been related to a bifurcation, awaiting further studies in future.

3.3.1.2. The I_syn induces the membrane potential decreased to enhance m_h

Obviously, the bursting appears at m_h higher than that of the spiking (gray). At the beginning point of the silence phase of the antiphase bursting, the membrane potential is smaller than that of the spiking, induced by the negative I_syn. Then, m_h at the beginning point becomes larger than that of the spiking, as shown in each panel of Figure 7, since the hyperpolarization activation of the I_h. Then, m_h during the silence phase increases with respect to time, i.e., from left to right, since m_h < $m_{\mathrm{h}:\infty }\left(m_{\mathrm{h}:\infty }=1/\left(1+2e^{180\left(V+{\theta }_{\mathrm{h}}\right)}+e^{500\left(V+{\theta }_{\mathrm{h}}\right)}\right)\right)\text{.}$ Then, $\frac{\mathrm{d}{m}_{\mathrm{h}}}{\mathrm{d}t}=\frac{m_{\mathrm{h}:\infty }-m_{\mathrm{h}}}{{\tau }_{\mathrm{h}}}>0$ during the silence phase, resulting in the increase of m_h.

3.3.2. Fast-slow analysis with two-parameter bifurcations of the fast subsystem of a single neuron

As shown in each panel of Figure 7, silence phase shows no relationship to the equilibrium point (red) of the fast subsystem. During the silence phase, the neuron receiving strong I_syn. Then, compared with the isolated neuron, the model of coupling neurons during the silence phase contains a negative I_syn. However, the neuronal model for the bifurcations shown in Figure 7 does not contain an inhibitory coupled current. Then, I_pol corresponding to I_syn should be considered. Then, the bifurcations in two-parameter (I_pol, m_h) plane of the fast subsystem of a single neuron are acquired to characterize the antiphase bursting. Here, the bifurcations with respect to m_h at I_pol=0.01nA (corresponding to zero I_syn) can be used to analyze the burst of the antiphase bursting, as depicted in Figure 8. And the bifurcations with respect to m_h at a negative I_pol, corresponding to the negative I_syn during the silence phase, can be used to analyze the dynamics of the silence phase, which are addressed in the following paragraphs.

Open in a separate window

Figure 8

The two-parameter bifurcations and phase trajectory (black curve) in plane (I_pol, m_h). (A) V_th=−0.047V and g_h=5 nS; (B) V_th=−0.047V and g_h=8 nS; (C) V_th=−0.040V and g_h=10 nS; (D) V_th=−0.040V and g_h=20 nS. Parameter: g_syn=15 nS. Arrows represent the running direction of bursting. In each panel, phase trajectory from black to red solid circles represents burst, and from red to black solid circles denotes silence phase. Right vertical dashed lines in each panel represents I_pol=0.01nA. Left vertical dashed lines in panels (A–C) and (D) represent I_pol=−0.11, −0.12, −0.122, and −0.14nA, respectively.

3.3.2.1. Phase trajectory of the antiphase bursting in the two-parameter plane

Figure 8 show the two-parameter (I_pol and m_h) bifurcations of the fast subsystem. The green, blue, and red curves represent the saddle-node bifurcation of the limit cycle (SNLC), Hopf bifurcation of the equilibrium point, and saddle-node bifurcation on an invariant circle (SNIC), respectively. With the increase of I_pol or m_h, the SNIC bifurcation, Hopf bifurcation, and SNLC bifurcation appear. More detailed bifurcations are shown in the Supplementary material and Supplementary Figure S5.

The phase trajectory (I_syn+0.01, m_h) of the bursting shown by the black curve and the bifurcations in the plane (I_pol, m_h) are plotted together in each panel of Figure 8. Here, the value “0.01” in “I_syn+0.01” is the value of I_pol for the antiphase bursting. Figures 8A,​,BB correspond to g_h=5 nS and g_h=8 nS for V_th=−0.047V, respectively. Figures 8C,​,DD correspond to g_h=10 nS and g_h=20 nS for V_th=−0.04V, respectively. The bursting trajectory in (I_pol, m_h) plane runs in a clockwise direction, as shown by the arrows in Figure 8, from the black to the red solid circles representing the burst phase, and from the red to the black solid circles denoting the silence phase. The I_syn changes drastically from the burst to the silence and from the silence to the burst, showing that the I_syn is related to the alternation between the burst and silence, and m_h changes drastically within the burst or silence phases, showing that the I_h current is associated with the dynamics within the two phases.

The silence and burst phases of the antiphase bursting correspond to the low (around left dashed line) and high (close to right dashed line) I_syn values, respectively. Therefore, the bifurcation of the fast subsystem of the single neuron model with respect to m_h at a high I_pol value (I_pol=0.01nA) can be used to explain the burst of the antiphase bursting, which has been addressed in Figure 8. The bifurcations of the fast subsystem with respect to m_h at a low I_pol value can be used to explain the silence phase of the antiphase bursting.

3.3.2.2. Silence of the antiphase bursting is related to the stable equilibrium point to a certain extent

For g_h=5 nS and V_th=−0.047V, the bifurcations of the fast subsystem with respect to m_h at I_pol=−0.11nA are shown in Figure 9A, corresponding to those along the left vertical dashed line of Figure 8A. Figures 9B–D show the bifurcations along the left vertical dashed lines of Figures 8B–D respectively. The bifurcations are similar to Supplementary Figure S5D and the parts for larger m_h are not shown here, due to far away from the bursting trajectory. The phase trajectories of the antiphase bursting of the neuron 1 in the (m_h, V) plane for different values of g_h and V_th are illustrated by the solid black curves in Figure 9. Each panel shows the silence phase runs near the stable equilibrium point (red curve) of the fast subsystem, showing that the silence phase is associated with the stable equilibrium point to a certain extent. In other words, the silence phase of the antiphase bursting runs around the equilibrium point of the fast subsystem of single neuron, modulated by the changes of I_h current and negative I_syn current. The difference between the silence phase and stable equilibrium point (red curve) is induced by the difference between the I_syn and I_pol.

Open in a separate window

Figure 9

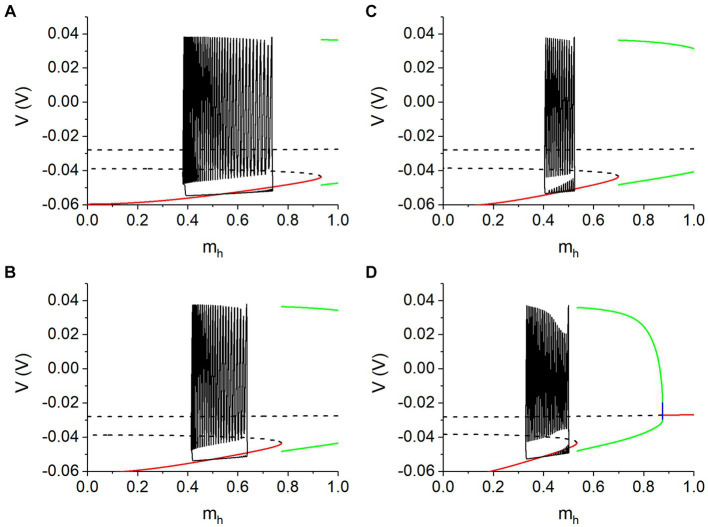
Bursting trajectory (black curve) plotted with bifurcations with respect to m_h at lower I_pol values. (A) V_th=−0.047V, g_h=5 nS, and I_pol=−0.11nA; (B) V_th=−0.047V, g_h=8 nS, and I_pol=−0.12nA; (C) V_th=−0.040V, g_h=10 nS and I_pol=−0.122nA; (D) V_th=−0.040V, g_h=20 nS and I_pol=−0.14nA. Parameter g_syn=15 nS for antiphase bursting.

3.3.3. Fast-slow analysis with bifurcations of the fast subsystem of the coupled neurons

Since the silence behavior of antiphase bursting is not well explained with the single neuron model, fast-slow analysis with bifurcations of the fast subsystem of the coupled neurons are used to analyze the dynamics of the silence behavior in the following paragraphs. For the coupled neurons, the fast subsystem is an eight-dimensional model including Eqs. 5–7, 9 with i=1 and 2. The variables are V1, V2, h_Na,1, h_Na,2, m_K,1, m_K,2, S1 and S2, with m_h,1 and m_h,2 taken as bifurcation parameters. Because the exchange of i and j does not change the model, the fast subsystem also exhibits symmetry. Therefore, m_h=m_h,1=m_h,2 is set in the fast subsystem of the coupled neurons. Then, the bifurcations of the fast subsystem in the plane (m_h, V) are obtained, which can be used to analyze the dynamics of the antiphase bursting.

3.3.3.1. Bifurcations of the fast subsystem of the coupled neurons

The bifurcations of the fast subsystem in the plane (m_h, V) are obtained, as shown in the left column of Figure 10. Different rows of Figure 10 represent different combinations of V_th and g_h. Except for the bursting trajectory (solid black curve), other curves represent the bifurcation curves of the equilibrium points and limit cycles. The solid red curves and dashed black curves represent the stable and unstable equilibrium points, respectively. The dashed blue curves and solid green curves denote the unstable and stable limit cycles, respectively. For V_th=−0.047V, the unstable equilibrium point changes into the stable equilibrium point via a subcritical Hopf bifurcation point (label as subH1) at m_h≈2.53169nA, and meanwhile an unstable limit cycle appears. At m_h≈1.55443nA, the system exhibits a saddle-node bifurcation. At m_h≈1.06626nA, there is a branch point (BP), via which the system changes from a stable equilibrium point to two stable equilibrium points and one unstable equilibrium point. The bifurcations for g_h=8 nS are similar to the bifurcation for g_h=5 nS, which are not described here. The bifurcations for V_th=−0.04V are more complex than those for V_th=−0.047V, as shown in Figures 10C,​,D.D. For V_th=−0.04V and g_h=10 nS, there are five subcritical Hopf bifurcations at m_h≈1.79022 (subH1), 1.02003 (subH2), 0.58297 (subH3), 0.70699 (subH4), and 1.01931 (subH5), respectively. An unstable limit cycle bifurcated from the subcritical Hopf bifurcation point is transformed into a stable limit cycle via a saddle-node bifurcation of limit cycles (SNLC) or period-doubling bifurcation (PD), as shown in Figure 10C. Figure 10D shows the bifurcations for g_h = 20 nS, which are similar to the bifurcations depicted in Figure 10C and will not be repeated here. As shown in Figure 10, there are multiple equilibrium points at a same m_h value. Furthermore, the bursting trajectory (solid black curve) is plotted with the bifurcations in the plane (m_h, V) to present comprehensive and accurate relationships between the antiphase bursting and dynamics of the fast subsystem.

Open in a separate window

Figure 10

Bursting trajectory (black solid curve) plotted with bifurcations with respect to m_h of the fast subsystem of the coupled neurons. (A) V_th=−0.047V and g_h=5 nS; (B) V_th=−0.047V and g_h=8 nS; (C) V_th=−0.040V and g_h=10 nS; (D) V_th=−0.040V and g_h=20 nS. Right panels are the partial enlargement of left panels. Other parameter values: g_syn=15 nS and I_pol=0.01nA.

3.3.3.2. Silence of the antiphase bursting is related to the unstable equilibrium point

In order to more clearly show the correspondence between the silence of the antiphase bursting and the equilibrium point of the fast subsystem of the coupled neurons, we omit some irrelevant equilibrium point curves in the bifurcation diagram, leaving only the key equilibrium point curves and limit cycle curves, as shown in the right column of Figure 10. Obviously, in all four panels, the silence of the antiphase bursting runs along the unstable equilibrium point of the fast subsystem, i.e., the silence of the antiphase bursting is related to the unstable equilibrium point. The result indicates that the neuron is at the unstable equilibrium point during the silence phase suppressed by the inhibitory synaptic current. Supplementary Figure S6 shows a comparison of the stable equilibrium point of the fast subsystem of a single neuron and the unstable equilibrium point of the fast subsystem of the coupled neurons.

In addition, other complex dynamics can be found from Figure 10. For example, for V_th=−0.040V, the silence of the antiphase bursting runs along the unstable equilibrium point of the fast subsystem, and the burst runs along the stable limit cycle, as shown in Figures 10C,​,D.D. For V_th=−0.040V and g_h=10 nS, the subcritical Hopf (subH1) bifurcation occurs at m_h≈0.58297. For V_th=−0.040V and g_h=20 nS, the subcritical Hopf (subH1) bifurcation appears at m_h≈0.41215, i.e., the Hopf bifurcation point shift to the left with the increase of g_h. For V_th=−0.047V, the Hopf bifurcation disappears, as shown in Figures 10A,​,B.B. These complex bifurcations will be studied in details in future.

4. Discussion and conclusion

The rhythmic patterns of two-neuron circuit with reciprocal inhibition coupling, such as the antiphase bursting, are associated with complex nonlinear dynamics and motor patterns (Daun et al., 2009; Nagornov et al., 2016; Elices and Varona, 2017; Ausborn et al., 2018). Especially, the rhythmic patterns have been widely used to control motion of the robot in recent studies (Habu et al., 2019; Li J. et al., 2021; Fukuoka et al., 2022). Identifying modulations to the rhythmic patterns of two-neuron circuit with reciprocal inhibition coupling is a very important issue for the nonlinear dynamics, neuroscience, and motion control of the robot. In the present paper, relationships among the antiphase bursting and multiple other rhythm patterns, and the dependence of the antiphase bursting on the I_h and I_syn at different values of V_th, the dependence of the escape, release, and mixture modes of the antiphase bursting on the I_h and I_syn, co-regulations of the I_h and I_syn in modulating the opposite changes of the bursting period of the escape mode and release mode, and fast-slow dynamics modulated by the I_h and I_syn of the antiphase bursting, are investigated via different processes of fast-slow dissection methods in a two-neuron model (conductance-based leech neuronal model). The results exhibit significances in the following aspects.

Firstly, the I_syn and the slow I_h with strong strength are the necessary conditions for the antiphase bursting, and the dependence of the antiphase bursting on the two currents is different for low (escape mode) and high (releases mode) threshold voltages of the inhibitory synapse. Multiple rhythmic patterns are reproduced in the model with or without the I_h current, and the relationships between different patterns are acquired. The antiphase bursting pattern, which locates between the antiphase spiking and the pattern of spiking and subthreshold oscillation, are induced by the I_h. The slow activation of the I_h is identified to be the factor to ensure the generation of bursting, which presents explanation to the experimental observation that the antiphase bursting appears in the presence of I_h current (Sharp et al., 1996). Meanwhile, as the synaptic threshold voltage shifts from low level to high level, the dependence of the antiphase bursting on the I_syn and I_h is different, suggesting that the interaction of the strong I_h and I_syn induces the antiphase bursting.

Secondly, with increasing I_h, the bursting period decreases and increases, respectively, for the escape mode and release mode, which are reproduced in the simulations, closely matching the experimental observation (Sharp et al., 1996; Morozova et al., 2022). In addition, the mixture mode observed in Morozova et al. (2022) is also reproduced at a medium synaptic threshold voltage. Furthermore, the co-regulations of the I_h and I_syn to modulate the opposite changes of the bursting period for the escape mode and release mode are obtained. For the escape mode, increase of the I_h induces elevated membrane potential of the silence inhibited by a strong I_syn, which reduces the silence duration to go beyond V_th, resulting in reduced bursting period. For the release mode, the I_h elevates the tough value of the former part of the burst of the neuron 1 modulated by a nearly zero I_syn,1, meanwhile, an enhanced I_syn,2 is outputted to the silence of the neuron 2 to prolong the silence duration. As the tough value of the burst of the neuron 1 falls below V_th, the I_syn,2 outputted to the neuron 2 decrease to nearly zero and then the neuron 2 changes to burst. The burst of the neuron 2 induces strong I_syn,1 to the neuron 1 to terminate the burst to become the silence. Then, the co-regulations of the two currents for the release mode are more complex than those the escape mode in the present paper and previous study. In addition, the co-regulations of the two currents for the release mode seems much clearer than those in Sharp et al. (1996), wherein the tough value of the burst does not fall below V_th. In this paper, the detailed dependence of the bursting period on two key factors (the I_h and I_syn) for the escape mode and release mode is obtained in a two-parameter plane. Then, through modulations to the two physiological factors, antiphase bursting patterns with various periods can be obtained, which may be applied as potential and practical measures to modulate the motion of robot.

Finally, the fast-slow dynamics of the antiphase bursting modulated by the I_h and I_syn are acquired. Using one-parameter bifurcations of the fast subsystem of a single neuron, the burst of the antiphase bursting is related to the stable limit cycle modulated by a weak I_syn, and the silence is not associated the dynamics of the fast subsystem. Considering that the antiphase bursting is modulated by the inhibitory synaptic current (nearly zero during the burst and negative during the silence phase) and the slow I_h, fast-slow analysis considering two bifurcation parameters related to the two currents are used in the present paper. Such a novel analysis process is verified to be effective to analyze the dynamics of the antiphase bursting and roles of the I_syn and I_h in the antiphase bursting. The bifurcations of the fast subsystem at a high depolarization current show that the burst is related to the stable limit cycle corresponding to a weak inhibitory synaptic current, while the silence is associated with the stable equilibrium point to a strong inhibitory synaptic current to a certain extent. Although the silence is close to the stable equilibrium, the silence exhibits difference to the stable equilibrium. Furthermore, the dynamics of the fast subsystem of the coupled neurons is used, then, the silence is associated with the unstable equilibrium point. The I_syn induces the alternation between the burst and the silence, and the I_h mainly modulates the dynamics within the burst and quiescent state. The fast-slow analysis considering two-parameter bifurcations or coupled system are novel progresses used in recent years (Li Y. et al., 2021; Ma et al., 2021). The results present theoretical explanations to the fast-slow dynamics of the antiphase bursting modulated by the I_syn and I_h, which is helpful for understanding the antiphase bursting and modulating the rhythmic motor behavior.

Although the progresses in the three aspects mentioned above, there are multiple questions related to the mechanism and co-regulations of the I_h and I_syn to be answered in future. For example, the co-regulations of the two currents in the formation of the mixture mode of antiphase bursting await further investigations. Moreover, the dynamical mechanisms by which other currents interact with the I_h and I_syn to regulate the antiphase bursting are also questions to be answered in the future. More importantly, the generality of the results of the present paper should be verified with multiple theoretical models and the heterogeneous parameter values, closely matching the real neurons or systems. Especially, the bifurcations undying the alternation between burst and silence have not been acquired with fast-slow analysis considering one or two bifurcation parameters, implying that some novel analysis process may be needed. The study to these problems can enable us to further understand the mechanisms of different rhythm patterns more deeply and comprehensively, which is helpful for the application the antiphase bursting in motion control of robot and so on. In addition, the I_h is a special current which can modulate the threshold (Guan et al., 2019) and resonances (Guan et al., 2020, 2021) and is associated with the dendritic integration, synaptic transmission, motor learning, pacemaker function, and pathologies (Robinson and Siegelbaum, 2003; Biel et al., 2009; Wahl-Schott and Biel, 2009), which should be further studied in future.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

Ethical approval was not required for the study involving animals in accordance with the local legislation and institutional requirements because no real animals were involved in this study. This study presents the simulation and analysis results of a theoretical model.

Author contributions

LG: Data curation, Investigation, Software, Writing – original draft, Validation, Visualization, Writing – review & editing. HG: Conceptualization, Methodology, Supervision, Writing – review & editing, Visualization, Writing – original draft. XZ: Formal analysis, Methodology, Writing – review & editing, Validation.

Funding Statement

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research was supported by National Natural Science Foundation of China (12202146, 12072236, and 12202147) and Foundation of He’nan Educational Committee (23A110011).

References