Abstract

1. Introduction

Cross-species spillover of pathogens occurs when a pathogen that is released by a member of a reservoir host species goes on to establish and replicate in a different (recipient) host species [1–3]. While mitigating pathogen spillover and associated disease risk at the wildlife–livestock interface is a major goal for both human and animal health agencies [4], spillover management decisions are often context-specific and based on expert opinion [5]. In particular, there is limited scientific knowledge to guide management of spillover risk in understudied systems. Here, we propose a modelling framework designed to fill that gap by providing evidence-based guidance about optimal management over a wide range of ecological contexts.

A pathogen's spatial extent, and the spatial connectivity of the host populations, are critical drivers of disease management efficacy for many important wildlife–livestock [6] and wildlife–human spillover systems [7–9], and management of reservoir versus recipient hosts has been compared in some contexts [10]. However, spatially explicit two-host disease models have received less attention, with most published models describing management efficacy within a single-host species [11]. Moreover, these single-host models are often not intended to address spillover risk per se, but rather, to characterize dynamics leading up to or trailing after a spillover event.

Another group of models builds on the idea that spillover disease burdens depend on both the frequency and the consequences of individual spillover events. These ‘multi-host’ models often compare within- and between-species transmission rates to identify pathogens with a high risk of generating problematic spillover events [12–14]. Multi-host models have proven useful for characterising spillover rates, especially when merged with phylogenetic information specifically identifying the source of a given spillover event [15]. However, they are rarely extended to account for changing spillover risk as local reservoir prevalences vary through space and time (but see [16]).

Here, we explore how best to manage pathogen spillover and transmission in wildlife–livestock systems, using actions that are spatially explicit and could be applied to either the reservoir or the recipient host. Our model takes ideas previously employed for forecasting management performance in specific systems [17], but scales the approach up to apply across a wider range of host movement and epidemic growth rates. We start by justifying why a management-centred framework for wildlife–livestock spillover should explicitly incorporate movement. We then go on to describe a simple disease propagation model to characterise spillover risk and onward transmission across a wide range of hosts and pathogens. We next use the model to explore spillover management efficacies, and describe the patterns that the model produced. We end by discussing the limitations of this approach, and outlining features that could be added in the future.

2. Characterizing disease propagation in terms of epidemic growth rates and host movements

Our model is structured around three initial conjectures. First, we anticipate that the most efficient means of controlling pathogen spillover often rests on the spatial dynamics of the hosts. Hosts with high movement propensities can produce widespread spatial synchrony in spillover risk, making the precise location of future spillover events hard to predict [18]. In these cases, the best management option may be to target cross-species (i.e. interspecific) contacts by applying biosecurity measures or phytosanitary controls across a broad spatial extent [19]. When reservoir hosts move shorter distances, however, spatial containment in either the reservoir or the recipient host species (or both) may be possible.

Second, we anticipate that the relative efficacies of various management actions will depend on how quickly an epidemic grows. If epidemic growth is rapid in the recipient host population, then depopulation or targeted vaccination at the time of the outbreak (here referred to as retroactive vaccination) may effectively limit post-spillover epidemic size. If epidemics grow slowly, actions like prophylactic vaccination or selective removal within the reservoir population may lower reservoir prevalence to the point where any cross-species spillover event becomes vanishingly rare (figure 1). Lastly, we expect that in some cases, many management actions will perform comparably. In these situations, relative economic and social costs of each action should factor heavily into management decision-making.

Open in a separate window

Figure 1.

Hypothesized management efficacies across the pathogen propagation space. We partition pathogen propagation along two axes: epidemic growth rate and movement propensity of the reservoir host (here, quantified as typical number of kilometres moved during the infectious period). Relative performance of various management strategies is indicated with arrows outside the illustration's margins. Management actions that might fall into the upper left quadrant include local depopulation of either host at infected premises. Management in the upper right might include biosecurity measures targeting premises of either host, or prophylactic vaccination of the reservoir host. Management in the lower right could include a wide range of actions. Many actions might perform well in the relatively easily managed lower left-hand quadrant. System-specific values derived from a search of the empirical literature are indicated within the illustration. Values were left intentionally vague, and the values corresponding with the quadrant lines are arbitrarily chosen, since they will vary with ecological context, and with the particular organisms involved. Spatial extents indicated here are based on one important, current reservoir host listed beside each point. The upper bound of movement for avian influenza has been curtailed. See electronic supplementary material, table S1 for system-specific estimates. CDV references canine distemper virus.

Testing these conjectures requires us to explicitly incorporate epidemic growth rates and host movement propensities into a model of epidemic spread. Like many single-host models [7], our model considers management in the context of a dynamic disease transmission process, but we make that process spatially explicit and allow new spillovers to emerge autonomously owing to underlying infection dynamics in the reservoir host. Like many multi-host models [13,14], magnitude of spillover risk is central to our model structure. However, where those models focus on the magnitude of risk in terms of force of infection from the reservoir host, we additionally focus on the spatial extent over which those events occur. Spatially linking both hosts in one model allows us to compare a wider range of management actions that span both host species.

3. Spillover simulation model

Our model includes three elements: transmission of the pathogen within a host species, transmission of the disease between species and movement of hosts across space. The model operates on a 50 × 50 grid of spatial cells. We assume that host population sizes are fixed and identical in all occupied cells. The model uses a deterministic SIR (susceptible--infected--recovered) disease process model with stochastic cell-to-cell host movements and between-species interactions to capture the effects of both host movement and epidemic growth.

Epidemic dynamics within a spatial cell follow the classic disease model of Kermack & McKendrick [20] without demography, which assumes that each individual's infection status transitions from susceptible (S) to infectious (I) to recovered (R). By keeping population sizes constant in all grid cells, we circumvent questions about whether within- and between-host-species transmission should be frequency- or density-dependent. During an epidemic's early exponential growth phase, the epidemic growth rate is equal to the difference between the transmission coefficient (β) and the recovery rate (γ) (electronic supplementary material, S2). We held recovery rate constant across all simulations and systematically altered epidemic growth rates by manipulating β alone (electronic supplementary material, figure S1A).

The model's spatial process starts with construction of an occupancy map for each host species, based on a stochastic selection of cells. The probability that a cell is occupied by a particular host species is determined with a draw from a symmetric, bivariate Gaussian kernel centred on that host's activity centre (i.e. surrounding a spatial centroid) and with a variance equal to 50 (figure 2a). If a previously drawn cell is chosen a second time for the same species, we redraw from the same distribution until a set of 1000 unique cells is identified for each host (though both hosts can occupy the same cell). Spatial alignment between the host species is determined by the distance between host activity centres. This structure allows us to capture a gradient of spatial overlap between host species, from complete segregation to extensive spatial overlap throughout their ranges (electronic supplementary material, S4 and figure S2).

Open in a separate window

Figure 2.

Simulation protocol. (a) Simulations begin by defining the spatial extent of the reservoir (light grey) and recipient (dark grey) hosts. A single infected individual is introduced into two reservoir host cells (b), with the structure of the subsequent epidemic determined by epidemic growth rate and host movement propensities. (c) The pathogen can then stochastically spill over to the recipient host in cells occupied by both host species (reservoir shown in grey; recipient in colour), at a rate determined by the interspecific contact rate and the pathogen's prevalence in the local reservoir host population. Management (here, retroactive vaccination of the recipient host) can alter the epidemic's progression in both host species (d,e). Management actions are compared in terms of their ability to minimize the epidemic's spatial extent in the recipient or reservoir host, and minimize the total number of recipient or reservoir host cases. Variation generated by manipulating spatial structure, local epidemic dynamics and management efficacy are shown in electronic supplementary material, figures S2–S4, respectively.

Individual reservoir and recipient hosts move stochastically between occupied grid cells at discrete time steps according to a tau-leap algorithm (electronic supplementary materials, S2.1). We assume that these movements have a negligible effect on cell population densities and hold population sizes constant within each occupied cell throughout the simulation. We only track the size of each disease compartment (namely, proportion of susceptible, infected and recovered individuals of each host species) within cells, not the disease status of particular individuals. Stochastic movement events by ‘individual’ infected animals spark dynamics within newly contacted cells, without altering cell densities. Movement rates are normalized so that the same number of cell-to-cell movements is expected in all simulations, but the structure of these movements varies controllably: movements are drawn from a monotonically decreasing function of Euclidean distance between cell centroids (i.e. a movement kernel; electronic supplementary material, S2.2) and we control host movement patterns by manipulating the distribution of movement distances (which we refer to as the host's ‘movement propensity’). The probability that a dispersing host is infected is proportional to the local prevalence in that host's population. Movement kernels with heavy tails correspond to high-dispersal systems (high movement propensity), while movement kernels with light tails correspond to low-dispersal (low movement propensity) systems (electronic supplementary material, figure S1B). Note that larger values of c, the parameter controlling tail weight, correspond to lighter tails (electronic supplementary material, figure S1B). Epidemics simulated under high movement propensities seed more new infections at a distance than epidemics arising under lower movement propensities [21], facilitating faster spatial spread. For simplicity, we apply the same dispersal kernel to both host species in all simulations presented here, and we do not allow colonization of unoccupied cells. Arrival of a single infected host in an uninfected host cell always and instantly sparks a local epidemic in the newly contacted cell (figure 2b).

Contacts between reservoir and recipient hosts are also treated as stochastic. The number of interspecific contacts is based on a pre-specified interspecific contact rate, which is held constant across all simulations. Contacts are then randomly assigned across all cells occupied by both reservoir and recipient hosts. The probability that an interspecific contact involves an infected reservoir host is proportional to the current infection prevalence in that cell's reservoir host population. Though reservoir-to-recipient contacts are required to initiate epidemic dynamics in the recipient host population, we assume that recipient host populations experience no additional force of infection from reservoir hosts in local or neighbouring cells following the initial spillover event (figure 2c). Stochastic movements between cells populated with recipient hosts can then allow the epidemic to propagate throughout the entire recipient host population.

(a) Management actions

Our investigation focused on six forms of management: prophylactic vaccination applied across an entire population regardless of current disease status, retroactive vaccination applied to infected cells and their neighbours following detection of disease, contact biosecurity, depopulation, spatial containment and selective removal of infected reservoir hosts (figure 2d,e). Details on the implementation of all management actions within the model are contained in table 1 and electronic supplementary material, S2.3. In all cases except for prophylactic vaccination, management was applied only to cells exceeding a specified threshold prevalence in the reservoir host (and to the direct neighbours of those cells for retroactive vaccination and depopulation; table 1).

Table 1.

Management implementation within the model. The user-specified prevalence at which management began was varied systematically to take on values 0.001, 0.010, 0.100 and 1.00. S_Reserv and S_Recip reference the proportion of susceptible reservoir and recipient hosts, respectively; and I_Reserv and I_Recip refer to the proportion of infected reservoir hosts and recipient hosts, respectively. β is the transmission coefficient. N is the number of reservoir hosts per occupied cell and e_ij denotes the movement rate between the ith and jth cells. Throughout our simulations, we took a cell's neighbourhood to consist of all cells whose centroids were within three cell lengths of the target cell.

action	prevalence at which action begins	effect of action on system dynamics	action's spatial extent
biosecurity	user-specified	βIReservSRecip becomes δβIReservSRecip where δ(0, 1) is a multiplicative factor reducing β	neighbourhood of target cell
containment	user-specified	eij = 1/10 000 when i and j are not on the same side of the containment boundary	all cells
depopulation	user-specified	I reset to 0 when depopulation occurs	neighbourhood of target cell
prophylactic vaccination	n.a.	S reset to S(1 − ν), where ν N/cell, the host's density within a cell	all cells
retroactive vaccination	user-specified	S reset to S(1 − ν), where ν = 1/R0, the herd immunity rate	neighbourhood of target cell
selective removal	user-specified	IReserv is reset to 0, and SReserv is proportionally increased	neighbourhood of target cell

Open in a separate window

This management structure leaves ample room for further development, including exploration of cost constraints and more complex management schemes. However, adding more detail would require tailoring the model to a specific system, so here we simply present the overarching structure and leave further specification to future work.

4. Identifying the most effective management strategies

In order to identify which management action produced the best results under particular conditions of host movement propensities and epidemic growth, we ran simulations across a gridded version of the parameter space (electronic supplementary material, S3 and table S1). Parameters varied along the following six dimensions: (i) epidemic growth rate; (ii) variance and kurtosis of the hosts' dispersal function (‘movement propensity’); (iii) prevalence at which management began; (iv) host density within each cell; (v) distance between reservoir and recipient host activity centres; and (vi) management objective of interest. The objectives we considered were minimizing spatial extent of the epidemic in the recipient host; minimizing total number of recipient host cases; minimizing spatial extent of the epidemic in the reservoir host; or minimizing total number of reservoir host cases. We focus primarily on spillover management in the recipient host population, but include results from objectives focused on the reservoir host in electronic supplementary material, S5.4.

We first explored raw output values over the disease propagation space (figure 3) and then tabulated which management action performed ‘best’ (i.e. minimized epidemic size or epidemic spatial extent in the reservoir or recipient host) at every parameter combination (figure 4a–d). We then used logistic regression to correlate when a management action was ranked as the best (yes or no), with epidemic growth rate and tail weight in the host's dispersal kernel. All simulations contributed to model fits, so that inferences were balanced over a range of values for reservoir population density, spatial divide between host activity centres and prevalence at which management began. Finally, we grouped management actions according to their coefficient estimates from the logistic regression (figure 4) and compared conditions of strong relative performance for each group to our expectations in figure 1.

Open in a separate window

Figure 3.

Simulation output. Heat maps (a–c) show the aggregate recipient host prevalence under three different management actions along the dimensions of epidemic growth rate (cases per timestep) and movement distance (movement propensity increases to the right): (a) depopulation of the reservoir host; (b) prophylactic vaccination of the reservoir host; and (c) selective removal of the reservoir host. In cases where unmanaged epidemics were large, outcomes varied dramatically among management actions and a clear ‘best action’ was identifiable (this is the case among the three sets of actions shown here, in which prophylactic vaccination of the reservoir clearly outperforms the other two actions for the fastest-growing, fastest-spreading epidemics). However, in cases where unmanaged epidemics were small, many actions performed comparably and the variance in recipient prevalence among actions was low (d). Variance among management outcomes increased with both movement and the number of cases per timestep. Simulations in (a–c) partition both epidemic growth rate and host movement propensity into 20 blocks, fix management initiation prevalence to 0.01 and set the spatial divide between host centroids to 30 cells. (Online version in colour.)

Open in a separate window

Figure 4.

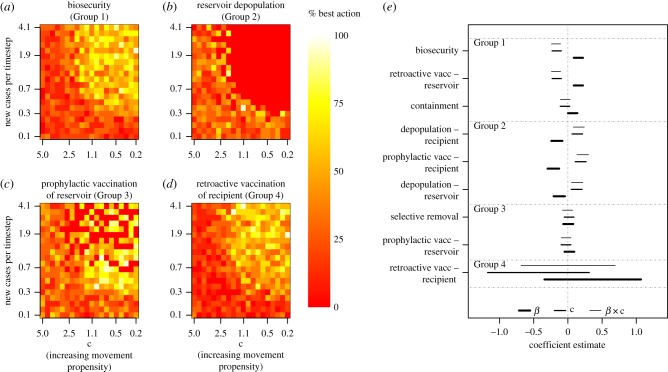
Comparison of management actions over the disease propagation space. (a–d) Relative performances of four representative management actions at controlling spillover (measured here in terms of the total number of recipient host patches infected) across the parameter space. Pixel colours represent the raw proportion of times that the action performed better than all other actions at that particular combination of epidemic growth rate and movement propensity. (e) Coefficient estimates for the relationship between epidemic growth rate (β; thickest lines), movement propensity (c; medium-width lines) and the β-by-c interaction (finest lines) from logistic regression models describing when each management action performed best. Positive coefficient estimates for β indicate that the action's performance improved relative to other actions as epidemic growth rate increased. Positive coefficient estimates for (c) indicate that the action's performance improved relative to other actions as host movement propensity declined. Positive coefficient estimates for the β-by-c interaction indicate that the action's relative performance improved when epidemic growth rates were high, but host movement propensities were low. Lines show 95% confidence intervals around each point estimate. Parallel results for the other three objectives are shown in electronic supplementary material, figures S6–S8, and additional details on the underlying simulations are included in electronic supplementary material, S5.1 and S5.3. (Online version in colour.)

5. Results

Our simulator produced a wide range of spatio-temporal spillover and transmission dynamics (figure 3; electronic supplementary material, figures S3 and S4) and these dynamics generally responded as expected to the various management interventions (figure 3; electronic supplementary material, figure S5). While the results presented here focus on one objective, limiting the total number of infected cells in the recipient host population, similar patterns were observed for limiting the total number of recipient hosts infected (electronic supplementary material, S5.3). Unsurprisingly, we saw some deviations from these patterns when objectives were centred on the reservoir host. For instance, we allowed biosecurity to only target interspecific contacts, so it had no bearing on disease dynamics in the reservoir host. Most of the observed deviations between the reservoir and recipient host objectives could be readily explained with similar logic.

Action performances typically fell into two groups when aggregated across the entire parameter space, but which actions fell into which group depended on objective (electronic supplementary material, table S3). When the objective was minimizing the epidemic's spatial extent in the recipient host population, the better-performing group consisted of biosecurity, prophylactic vaccination of the reservoir host, and retroactive vaccination of either host (electronic supplementary material, table S3). Epidemics tended to be easily controlled by many management strategies when movements were mostly local and epidemic growth rates were low (figure 3; see electronic supplementary material, S5.2 and S5.3 for statistical results, and S5.4 for results under other objectives).

Actions could be grouped according to how their relative performance related to epidemic growth rate and host movement propensities (figure 4). Biosecurity, containment and retroactive vaccination of the local reservoir host (Group 1), which all aim to limit spillover effects by controlling interspecific contact or spatial propagation, performed best for fast-growing epidemics in hosts with high movement propensities (the upper right-hand corner of figure 1). Depopulation of both hosts, along with prophylactic vaccination of the recipient host (Group 2) had the strongest relative performance in scenarios where epidemics grew quickly, but host movement propensities were low. The relative performance of selective removal and prophylactic vaccination of the reservoir (Group 3), both of which target prevalence and epidemic growth rates in the reservoir population, did not change substantially with changes in epidemic growth rate or host movement propensities. The groupings of management actions that performed similarly depended on the objective function, and this was particularly true when the measured objective focused on a different host. For instance, when the objective was to minimize infected reservoir (as opposed to recipient) patches, selective removal performed best when epidemics grew slowly, whereas prophylactic vaccination of the reservoir was best when epidemic growth rates were high, even though these actions were grouped together when the objective was to minimize epidemic size or extent in the recipient host (electronic supplementary material, figure S7).

6. Discussion

Pathogen spillover at the wildlife–livestock interface is a persistent and expensive problem for food security and wildlife conservation alike. While pathogen spillover dynamics have been explicitly studied in many wildlife–livestock systems, disease ecologists lack a general framework for considering the context in which each management action should perform best. Here, we presented a framework for forecasting management performance of spatiotemporally explicit spillover events.

Our simulation results usually agreed with our a priori intuition about how management would interact with spatially explicit epidemic propagation. Epidemic growth rate and host movement propensity interacted to generate variation in epidemic size and spatial extent (figure 4; electronic supplementary material, figures S6–S8) and epidemic growth rate was generally the most powerful determinant of which management action performed ‘best’ (figure 4e; see electronic supplementary material, S5.4 for additional results). While our findings are likely sensitive to the range of parameter values explored (epidemics sometimes failed to propagate in one or both hosts in a substantial region of the parameter space), they were nevertheless consistent with the basic categorization proposed in figure 1. In fast-growing, high-movement-propensity systems, limiting and localizing recipient host interactions with infected reservoir hosts—whether by reducing reservoir prevalence through vaccination, or by reducing interspecific contact rates through biosecurity—was the best strategy for recipient-focused objectives. Containment of the reservoir host also performed relatively well in these scenarios, except in cases where host movements consistently exceeded the size of the containment region (though the implications of varying containment region size were not explored here). Actions like depopulation of either host species or prophylactic vaccination of the recipient host, which limit epidemic growth by controlling the size of the susceptible pool without targeting movement, performed relatively better when epidemic growth rates were high and movement propensities were low. These actions might be favoured for fast-growing, low-movement-propensity epidemics, and may be competitive in higher-movement-propensity scenarios, depending on cost. Performance of actions that controlled local prevalence in reservoir host populations through prophylactic vaccination or selective removal within the reservoir population did not exhibit strong patterns with epidemic growth rate or host movement propensities. However, retroactive vaccination of the reservoir host performed comparably in the same ecological scenarios, and may be more politically and socially palatable when feasible (electronic supplementary material, table S3; [23]).

All management actions were competitive with one another when epidemic growth rates were slow, clearing a path for cost to play a larger role in decision-making (figure 3d). This partially held for fast-growing epidemics with low host movement propensities as well, and has been demonstrated in detail in several wildlife–livestock spillover systems. For instance, management models of foot-and-mouth disease (which we might categorize as a fast-growing disease with a lower host movement propensity) have investigated a wide range of different management strategies and found that a variety of actions might be deemed appropriate, depending on the specific objective, the action's cost and the prevalence at which management begins [24,25].

Contrary to our initial expectations, the tail weight of the dispersal kernel did not play a particularly powerful role in shaping management efficacy throughout our simulations (figure 4e). This could be because we held the total number of cell-to-cell movements constant throughout the simulations. In reality, host species vary in both the number and the distance of moves they make, as well as their local densities, and this has been shown to have substantial impacts on local epidemic growth in some cases (e.g. [26]). We anticipate that movement may thus play a more powerful role than these results suggest, but this question merits additional follow-up.

We elected to emphasize epidemic growth rate instead of the pathogen's basic reproductive ratio (R₀) because disease management depends on calendar time rather than the pathogen's generational timespan. Management requiring construction of fencing for biosecurity, or depopulation of infected premises, would be much more effective in a system with a slow epidemic growth rate than a rapid one, even if the epidemics were identical in terms of R₀. This could play out empirically, for example, in bovine tuberculosis (bTB) management in Michigan, USA, where models suggest that a relatively constant, but low level of spillover pressure from wildlife could be successfully mitigated through fencing [27]. It is the slow growth rate, and not that the basic reproductive ratio, that renders fencing feasible for Michigan bTB. Similarly, slow measures would be less effective for a pathogen with a comparable R₀ (estimated to be around 1.5 for Michigan bTB), but a shorter infectious period.

7. Conclusion

The risk and burden of pathogen spillover depends on a spatially explicit disease propagation process that operates in both reservoir and recipient host populations. Our model provides a useful starting point for planning management of disease at the wildlife–livestock interface based on general epidemiological traits of the system. It underscores the critical role that epidemic growth rate and spatial context play in determining management efficacy, and could be tailored to the specifics of a wide variety of pathogen spillover systems.

Supplementary Material

Supplementary Material

Disclaimer

References