Brief Review of the Mixed-Effects GTAM Method of Abney et al.

We restrict attention to a special case of the GTAM method⁴ in which one tests for an additive effect of the variant of interest (1-df test), in the presence of covariates, with additive polygenic effects and independent normal error in the model. For computational convenience, we use an asymptotic assessment of significance instead of the more robust, covariance-preserving permutation test described by Abney et al.⁴

The GTAM method uses only the set of individuals, S = N ∩ R, who have complete data on phenotype, covariates, and genotype at the variant of interest. Let s = |S| be the number of such individuals. We let Y_S and X_S represent the length s subvectors of Y and X, respectively, obtained by considering only the individuals in S. Similarly, we let W_S denote the s × (w + 1) submatrix of W obtained by extracting the s rows of W that correspond to individuals in S.

In GTAM, the analysis is prospective, not retrospective. In other words, we condition on (W_S, X_S), the covariates and genotypes, and treat the quantitative trait vector, Y_S, as random. This approach is clearly justified for individuals randomly sampled from a population, though the justification is less obvious when ascertainment is based on phenotype. The quantitative trait (possibly after suitable transformation of phenotypes and/or covariates) is modeled as

where β is the (w + 1) × 1 vector of covariate effects, including intercept, γ is the (scalar) association parameter, measuring the effect of genotype on phenotype, and ε_S is a random vector of length s, satisfying

i.e., ε_S has the s-dimensional multivariate normal distribution with mean vector 0 and variance matrix ${\sigma }_a^2{\mathbf{\Phi }}_{SS}+{\sigma }_e^2{\mathbf{I}}_s$, where ${\sigma }_a^2$ represents additive genetic variance, ${\sigma }_e^2$ represents variance due to measurement error or environmental effects assumed to be acting independently on individuals, I_s is the s × s identity matrix, and Φ_SS is the s × s kinship matrix for the individuals in S, given by

where ϕ_ij is the kinship coefficient between the i^th and j^th individuals of S, and h_i is the inbreeding coefficient of the i^th individual of S. Note that the identity 2ϕ_ii = 1 + h_i holds for all i, so the diagonal entries can be equivalently expressed as twice the self-kinship coefficients. Here, as in the original GTAM method, Φ_SS is taken to be the pedigree-based kinship matrix, though an estimated kinship matrix based on genotype data, such as that of Han and Abney,¹⁴ has also been used in GTAM.

We find it convenient to reparameterize the VCs, $\left({\sigma }_a^2,{\sigma }_e^2\right)$, in terms of $\left({\sigma }_T^2,\xi \right)$, where ${\sigma }_T^2={\sigma }_a^2+{\sigma }_e^2$ represents the total variance of the trait and $\xi ={\sigma }_a^2/\left({\sigma }_a^2+{\sigma }_e^2\right)$ is the (narrow-sense) heritability of the trait. With this parameterization, we can rewrite Equation 2 as

The null hypothesis of no association is H₀ : γ = 0, and the alternative hypothesis is H_A : γ ≠ 0. The GTAM statistic is asymptotically equivalent to the score statistic for this null hypothesis, assuming the model given in Equations 1, 2, 3, and 4. To calculate the GTAM statistic, we first estimate the heritability, ξ, by its null maximum likelihood estimate (MLE), i.e., its MLE in the submodel of Equations 1, 2, 3, and 4 in which γ = 0. We call this null MLE ${\hat{\xi }}_{0S}$, and we compute it only once per genome screen (at least at the initial stage of analysis). Let ${\hat{\mathbf{\Sigma }}}_S$ denote Σ_S evaluated at $\xi ={\hat{\xi }}_{0S}$. Then, for each marker, the calculation of the GTAM statistic can be expressed in terms of a generalized regression based on Equation 1, where we take ${\mathbf{ϵ}}_S\sim N_s\left(\mathbf{0},{\sigma }_T^2{\hat{\mathbf{\Sigma }}}_S\right)$, with ${\hat{\mathbf{\Sigma }}}_S$ treated as fixed and known and β, γ, and ${\sigma }_T^2$ treated as unknown. Then the parameter estimates, $\hat{\mathit{\beta }}$, $\hat{\gamma }$, and ${\hat{\sigma }}_T^2$, can be obtained by generalized regression under this model, and the GTAM statistic is equal to the generalized-regression t statistic for testing H₀ : γ = 0 in this model. The statistic is given by

where ${\mathbf{P}}_S={\hat{\mathbf{\Sigma }}}_S^{-1}-{\hat{\mathbf{\Sigma }}}_S^{-1}{\mathbf{W}}_S{\left({\mathbf{W}}_S^T{\hat{\mathbf{\Sigma }}}_S^{-1}{\mathbf{W}}_S\right)}^{-1}{\mathbf{W}}_S^T{\hat{\mathbf{\Sigma }}}_S^{-1}$ and ${\mathbf{Q}}_S={\mathbf{P}}_S-{\mathbf{P}}_S{\mathbf{X}}_S{\left({\mathbf{X}}_S^T{\mathbf{P}}_S{\mathbf{X}}_S\right)}^{-1}{\mathbf{X}}_S^T{\mathbf{P}}_S$ are both symmetric s × s matrices (see Abney et al.⁴ for further details). We consider (GTAM)² and assess its p value by using a ${\chi }_1^2$ asymptotic distribution under the null hypothesis.

A technical point is that the set S typically differs from marker to marker, but we would like to avoid re-estimating the null MLE of the heritability, ${\hat{\xi }}_{0S}$, at every marker, at least in the initial analysis. Instead, we try to use some representative set of individuals to obtain ${\hat{\xi }}_{0S}$, e.g., we might use the set of individuals who have nonmissing phenotype and covariate information and who have genotype data for some minimum number of markers. Then, once a subset of interesting markers has been identified by the initial analysis, one could fit the full model in Equation 1 for each of those markers, including MLE estimation of ξ based on the individuals genotyped at each marker in the subset. This approach⁴ reduces the computational burden of the method by not requiring numerical maximum likelihood estimation of ξ at every marker in the entire screen.

MASTOR

MASTOR can be viewed as an extension, to quantitative traits, of the MQLS method³ for binary traits. In contrast to GTAM, MASTOR is based on a retrospective approach, rather than a prospective approach, and it uses the larger set of individuals N R, rather than S = N ∩ R. One advantage of the retrospective approach is that it provides a natural way to incorporate information on individuals with missing genotype by using the known dependence among relatives’ genotypes under the null hypothesis. This allows MASTOR to use extra information not used by GTAM. Another advantage is that the retrospective analysis is less dependent on correct specification of the phenotypic covariance matrix under the null hypothesis. (This is because the correct calibration of MASTOR depends only on the null conditional mean and variance of the genotype data, not on the phenotype model. See Appendix C for mathematical details and subsection Assessment of Type 1 Error and the Impact of Variance Components and subsection Power Studies for empirical confirmation.) We first present the calculation of the MASTOR statistic and then provide the justification for it.

The MASTOR statistic takes the form

where V, which will be defined in the next paragraph, is a vector of length n that is a function of W, Y, and the pedigree information. We assume that under the null hypothesis of no association between genotype and phenotype, we have E₀(V^TX | W, Y) = 0 and ${\text{Var}}_0\left(\mathbf{X}|\mathbf{W},\mathbf{Y}\right)={\sigma }_X^2{\mathbf{\Phi }}_{NN}$, where Φ_NN is the n × n kinship matrix for the individuals in N (similar to Equation 3) and ${\sigma }_X^2$ is an unknown scalar. In that case, we have ${\text{Var}}_0\left({\mathbf{V}}^T\mathbf{X}|\mathbf{W},\mathbf{Y}\right)={\sigma }_X^2{\mathbf{V}}^T{\mathbf{\Phi }}_{NN}\mathbf{V}$. A previous work¹⁵ suggests estimation of ${\sigma }_X^2$ by

where 1 denotes a vector of length n with every element equal to 1. An alternative estimator that accounts for possible dependence between genotype and covariates is derived by replacing U in Equation 7 with

and replacing (n − 1) in Equation 7 by (q − w − 1), where Q is defined to be the set of individuals with both genotype and covariate information, but who may or may not have known phenotype (S Q N), with q = |Q|, Φ_QQ is the q × q kinship matrix for individuals in Q, and W_Q is the q × (w + 1) submatrix of W that is obtained by extracting the q rows of W that correspond to individuals in Q. Given the choice of ${\hat{\sigma }}_X^2$ based on either Equation 7 or 8, we use ${\widehat{\text{Var}}}_0\left({\mathbf{V}}^T\mathbf{X}|\mathbf{W},\mathbf{Y}\right)={\hat{\sigma }}_X^2{\mathbf{V}}^T{\mathbf{\Phi }}_{NN}\mathbf{V}$. Note that if N contains both members of a monozygotic (MZ) twin pair, Φ_NN is not invertible and a similar problem arises for Φ_QQ. This difficulty can be easily overcome (see Appendix B).

To define the vector V of Equation 6, we first obtain a null MLE of the heritability, call it ${\hat{\xi }}_0$, which is similar to the ${\hat{\xi }}_{0S}$ obtained for GTAM, except that it is based on the larger set of individuals, R, rather than on S R. Specifically, we let ${\hat{\xi }}_0$ denote the MLE of ξ in the model

(possibly after suitable transformation of phenotypes and/or covariates), where $\mathbf{ϵ}\sim N_r\left(\mathbf{0},{\sigma }_T^2\mathbf{\Sigma }\right)$, with Σ ≡ ξΦ_RR + (1 − ξ)I_r, where ${\sigma }_T^2$ is the sum of the additive and environmental trait variances as before, Φ_RR is the r × r kinship matrix for individuals in R (similar to Equation 3), and I_r is the r × r identity matrix. Because it is based on a different subset of individuals, the null MLE ${\hat{\xi }}_0$ for MASTOR will generally differ from the ${\hat{\xi }}_{0S}$ of GTAM. We let $\hat{\mathbf{\Sigma }}$ denote Σ evaluated at $\xi ={\hat{\xi }}_0$. Next we calculate the transformed phenotypic residuals from the generalized regression based on Equation 9, where we take $\mathbf{ϵ}\sim N_r\left(\mathbf{0},{\sigma }_T^2\hat{\mathbf{\Sigma }}\right)$, with $\hat{\mathbf{\Sigma }}$ treated as fixed and known and β and ${\sigma }_T^2$ as unknown. In this generalized regression, $\hat{\mathit{\beta }}$ is obtained as $\hat{\mathit{\beta }}={\left({\mathbf{W}}^T{\hat{\mathbf{\Sigma }}}^{-1}\mathbf{W}\right)}^{-1}{\mathbf{W}}^T{\hat{\mathbf{\Sigma }}}^{-1}\mathbf{Y}$, and we define the transformed phenotypic residual to be ${\hat{\mathbf{\Sigma }}}^{-1}\left(\mathbf{Y}-\mathbf{W}\hat{\mathit{\beta }}\right)=\mathbf{P}\mathbf{Y}$, where $\mathbf{P}={\hat{\mathbf{\Sigma }}}^{-1}-{\hat{\mathbf{\Sigma }}}^{-1}\mathbf{W}{\left({\mathbf{W}}^T{\hat{\mathbf{\Sigma }}}^{-1}\mathbf{W}\right)}^{-1}{\mathbf{W}}^T{\hat{\mathbf{\Sigma }}}^{-1}$. Then, we define the vector V by V = UΦ_NRPY, where Φ_NR is the n × r cross-kinship matrix having (i, j)^th entry equal to twice the kinship coefficient between the i^th individual in set N and the j^th individual in set R. The resulting MASTOR statistic is

where ${\mathbf{\Phi }}_{RN}={\mathbf{\Phi }}_{NR}^T$. The following two subsections give various ways of understanding this statistic.

Special Case: Complete Data

In the special case when there are complete data on all sampled individuals, we have R = N = S. In that case, it is easily verified that UΦ_NR P = P, so the numerators of the (GTAM)² and MASTOR statistics are both equal to (X^TPY)². Their denominators represent different estimators of the variance of X^TPY, with the denominator of (GTAM)² representing an estimator of Var(X^TPY | W, X) under a prospective model, and the denominator of MASTOR representing an estimator of Var₀(X^TPY | W, Y) under a retrospective model.

In the complete data case, the assumptions required for MASTOR to be a correctly calibrated statistic include the following. (1) E₀(X | W, Y) = Wα, where α is an unknown (w + 1) vector of coefficients. In other words, under the null hypothesis of no association between genotype and phenotype, the genotype is permitted to be linearly related to the covariates, or it can be unrelated to the covariates. (2) ${\text{Var}}_0\left(\mathbf{X}|\mathbf{W},\mathbf{Y}\right)={\sigma }_X^2{\mathbf{\Phi }}_{NN}$, where ${\sigma }_X^2$ is an unknown scalar. This is a version of the standard variance relationship that holds, for example, under Mendelian inheritance in a single population. Here, however, we do not require ${\sigma }_X^2=1/2p\left(1-p\right)$, where p is allele frequency, which would hold under Hardy-Weinberg equilibrium. Instead, we use the more robust estimator, ${\hat{\sigma }}_X^2$, given in the previous subsection.

Justification for the MASTOR Statistic

We briefly present two different ways of understanding and justifying the MASTOR statistic. First, an intuitively clear interpretation of the MASTOR statistic is obtained by noting that it can be rewritten (see Appendix C) as

where $\hat{\mathbf{X}}$ is defined to be a vector of length r whose entry for individual i R is X_i if i’s genotype is observed (i.e., if i is in N) and is ${\hat{X}}_i$ if i’s genotype is not observed, where ${\hat{X}}_i$ is the best linear unbiased predictor (BLUP) of the missing genotype of individual i, based on the remaining genotype data at the marker.¹⁶ The BLUP is given by

where

is the best linear unbiased estimator (BLUE) of allele frequency.¹⁷ When individual i N (i.e., i is genotyped), the formula for ${\hat{X}}_i$ reduces to X_i, the observed genotype for i. The version of the MASTOR statistic given in Equation 11 is analogous to the MASTOR statistic given for complete data, except with X replaced by $\hat{\mathbf{X}}$ (and with the variance suitably adjusted for the additional uncertainty). In the case of incomplete data, the main assumptions needed for the MASTOR statistic to be a correctly calibrated statistic can be written as (1) $E_0\left(\hat{\mathbf{X}}|\mathbf{W},\mathbf{Y}\right)=\mathbf{W}\mathit{\alpha }$, where α is an unknown length (w + 1) vector of coefficients, and (2) ${\text{Var}}_0\left(\mathbf{X}|\mathbf{W},\mathbf{Y}\right)={\sigma }_X^2{\mathbf{\Phi }}_{NN}$, where ${\sigma }_X^2$ is an unknown scalar (see Appendix C for details). These are identical to the assumptions for the complete-data case described in subsection Special Case: Complete Data above, except that in assumption (1), X is replaced by $\hat{\mathbf{X}}$.

The interpretation of MASTOR in terms of BLUP imputation of genotypes is useful in understanding the role played by missing data in MASTOR. Suppose individual i has phenotype and covariate information but is missing genotype data. Then, in the MASTOR method, the greatest potential contribution i could make to the association analysis would occur if he or she had genotyped relatives whose information could then be used in the BLUP imputation of i’s genotype. A somewhat less-substantial contribution that i could make to the association analysis would occur if i had no genotyped relatives but was in the same pedigree with an individual j such that ${\left({\hat{\mathbf{\Sigma }}}^{-1}\right)}_{ij}\ne 0$, where j has phenotype and covariate information available and is either genotyped or has a genotyped relative. In that case, ${\left({\hat{\mathbf{\Sigma }}}^{-1}\right)}_{ij}\ne 0$ means that i could contribute information to the transformed phenotypic residual of j, and j would have either an observed genotype or a BLUP and so would contribute to the analysis. Conversely, suppose individual i has genotype information, but is missing phenotype or covariate information. In that case, i will contribute to the analysis if there is at least one individual, j, who has nonmissing phenotype and covariate information, missing genotype information, and a genotyped relative. In that case, if i is not related to j, then the contribution of i will be in improved estimation of the nuisance parameter $\hat{p}$, which is used in the BLUP imputation for j, whereas if i is related to j, then i also provides more direct information about j’s genotype and will contribute to the BLUP, ${\hat{X}}_j$, through both the first and second terms of Equation 12.

A second interpretation of MASTOR is that it is a quasilikelihood score test of the null hypothesis H₀ : δ = 0, versus H_A : δ ≠ 0 in the retrospective mean model

(See Bourgain et al.¹³ and Wang and McPeek¹⁸ for more details on quasilikelihood score tests in this setting.) For a genotyped individual i, the conditional expectation in Equation 14 can be rewritten as

so the summation can be viewed as a weighted sum of the transformed phenotypic residuals, i.e., elements of ${\hat{\mathbf{\Sigma }}}^{-1}\left(\mathbf{Y}-\mathbf{W}\hat{\mathit{\beta }}\right)$, with weights proportional to the kinship coefficient between each individual and individual i. This represents the quantitative trait version of the enrichment effect,³ which basically says that phenotypic values of an individual’s relatives provide additional information, beyond that provided by the individual’s own phenotypic value, about the probability that the individual carries an allele affecting the trait.

For outbred individuals, the mean model given in Equations 14 and 15 holds up to terms of order o(δ) as δ → 0 assuming a general, 2-allele, prospective model of the form E(Y_i|W, X) = W_iβ + γ₁1_Xi=.5 + γ₂1_Xi=1 + ϵ_i, with $\mathbf{ϵ}\sim N_r\left(\mathbf{0},{\sigma }_T^2\mathbf{\Sigma }\right)$ and Σ = ξΦ_RR + (1 − ξ)I_r, where γ₁ and γ₂ are both tending to 0, combined with the assumptions E₀(X | W) = p1 and ${\text{Var}}_0\left(\mathbf{X}|\mathbf{W}\right)={\sigma }_X^2{\mathbf{\Phi }}_{NN}$. The connection between δ of Equations 14 and 15 and (γ₁, γ₂) is that $\delta ={\sigma }_T^{-2}p\left(1-p\right)\left({\gamma }_1\left(1-2p\right)+{\gamma }_{2}p\right)$, where the model of Equations 14 and 15 holds as this tends to zero. (For inbred individuals, the mean model given in Equations 14 and 15 is derived under the further assumption that the genetic effect is additive or multiplicative.)

Despite the fact that the mean model of Equations 14 and 15 does not allow X to depend linearly on W under the null hypothesis, MASTOR is still correctly calibrated when E₀(X | W, Y) = Wα (see Appendix C). To also obtain optimality for this case, we can change the mean model, replacing p1 by Wα in Equation 14, which results in a modified MASTOR statistic obtained by replacing U by U′ in Equation 10.

The T^SCORE Test

The T^SCORE test⁹ is very similar to GTAM in that it is also a prospective mixed-model analysis that incorporates covariates and uses estimated VCs for additive and environmental variance. A major difference between T^SCORE and GTAM is that T^SCORE first imputes values for missing genotypes, so that a larger subset of individuals can be analyzed. Thus, the numerator of T^SCORE resembles that of MASTOR in Equation 11 but with a different imputation approach. The denominator of T^SCORE represents a prospective variance calculation, so it is similar to GTAM in that regard, but with some differences. In the GTAM denominator, the generalized genotypic sum of squares has covariates regressed out, but they are not regressed out in the generalized genotypic sum of squares appearing in the T^SCORE denominator. In the GTAM denominator, the term $\left({\mathbf{Y}}_S^T{\mathbf{Q}}_S{\mathbf{Y}}_S\right){\left(s-w-2\right)}^{-1}$ represents a generalized regression estimate of the trait variance, based on residual sum of squares under the alternative model, using only individuals with nonmissing phenotype, covariate, and genotype. In T^SCORE, that estimated trait variance is effectively replaced with an MLE of the trait variance under the null hypothesis, using everyone with available phenotype and covariates, regardless of how much information is available on their genotypes. In contrast, the denominator of the MASTOR statistic has a phenotypic variance term that varies depending on the amount of genotype information available for the individuals having phenotype and covariate information. If all or almost all individuals who have phenotype and covariate information also have genotype data at the marker being tested, then GTAM, T^SCORE, and MASTOR should give very similar results. The main differences are in their handling of missing data. We include T^SCORE in our simulations and data analysis. Because both our simulations and data analysis involve pedigrees with >15 individuals, we use the Ghost software,⁹ in which the genotype imputation uses the Elston-Stewart algorithm to calculate T^SCORE.

ASTOR: Is the Heritability Parameter Really Needed?

MASTOR involves estimation of the heritability. This is done only once per genome screen, at least initially, for computational reasons (see subsection Computational Approach and Software). Still, one could ask whether accurate heritability is really needed for MASTOR, because, in the retrospective framework, the statistic would still be correctly calibrated if heritability were ignored. We propose a simplified approach, ASTOR, that is a version of MASTOR in which the heritability is assumed to be 0, so that Σ = I_r. The formula for ASTOR is given by Equation 10 with P replaced by P_I = I_r − W(W^TW)⁻¹ W^T, eliminating the heritability estimation step. However, note that ASTOR still correctly accounts for relatedness in the sample. (This is because the correct calibration of ASTOR depends only on the null conditional mean and variance of the genotype data, not on the phenotype model; see Appendix C.) In Results we compare ASTOR to MASTOR in terms of power and type 1 error.

Choice of Statistics to Compare by Simulation

MASTOR is designed for association analysis of quantitative traits with related individuals, taking into account covariates. The previously proposed GTAM and T^SCORE also address this problem, so it is useful to compare them to MASTOR. EMMAX is designed for samples of individuals not known to be related, rather than for family data, and when EMMAX is applied, the authors⁵ exclude individuals whose empirical kinship coefficient is greater than .10 (which corresponds to excluding first- and second-degree relatives). If EMMAX were modified to use the known pedigree information, it would be the same as GTAM in our simulation context. Therefore, within the context of our simulation, GTAM could be thought of as representing an upper bound on the power of a potential extension of EMMAX to family data. Previous work¹⁵ has shown that FBAT has very low power in simulation settings like those we consider, because it does not incorporate the data on the unrelated individuals and because many of the families do not meet the FBAT criteria for “informative families.” Thus, FBAT is not well suited to analyzing the type of data in our simulations and we do not consider this approach further. Similarly, GQLS does not allow covariates, so it is also not able to handle the type of data we consider. Of these methods, only GTAM and T^SCORE are designed to address the problem addressed by MASTOR, namely, quantitative trait association analysis in family data with general pedigree types, taking into account covariates. We also consider the simplified method ASTOR, which addresses the same problems but does not require heritability estimation.

Computational Approach and Software

We have developed software, called MASTOR, which is coded in C and implements the MASTOR, ASTOR, and GTAM methods. To calculate the MASTOR statistic, our software performs two main steps. The first step involves estimation of heritability and covariate effects under the null model, from which we can calculate the transformed phenotypic residual vector, PY. The second step is calculation of the statistic of Equation 10. The first step involves singular value decomposition (SVD) of a kinship matrix, Φ_RR, as well as numerical maximization of a likelihood to get the MLEs of the VCs. Note, however, that the computational burden is reduced in two ways. First, the block-diagonal structure of Φ_RR, with blocks corresponding to families, allows the SVD to be done independently on each block. Thus, for example, if set R were divided into f equal-size families, the computational cost of the SVD would be O(r³f⁻²) when the block-diagonal structure is exploited. Depending on f, this could be much faster than the naive SVD, which would have cost O(r³). Second, in our implementation, we use a well-known algebraic trick^4,5,19 to rewrite our likelihood as a function of just a single parameter, ${\sigma }_a^2/{\sigma }_e^2$, which eliminates the need to perform the SVD in every iteration of the numerical maximization of the likelihood.

In a genome scan, the first step of MASTOR would need to be performed only once under certain conditions. For example, this would hold if each person who is phenotyped is either genotyped or has a genotyped relative at every marker in the scan. In that case, the set R would be the same for every marker. For computational reasons, we choose to perform step 1 only once at the initial stage of the genome scan, even though R may differ slightly from marker to marker. To do this, we fix R at the beginning of the analysis. For example, one could include, in R, individuals who are phenotyped and who have at least some minimum number of markers at which they are either genotyped or have a genotyped relative. Then, once a subset of interesting markers has been identified in the initial analysis, one could perform a separate step 1 for each marker in the subset.

The second step, in which the statistic for each marker is calculated, scales linearly in the number of markers m, and for each marker there is an inversion of Φ_NN. As in the first step, the block-diagonal structure of Φ_NN greatly reduces the computational burden.

The MASTOR software also allows the option of fitting a linear mixed model to the data without performing a genome scan. This option, which we refer to below as mixedMLE, serves two purposes. First, it is useful for preliminary analyses of the phenotype and covariate data in order to formulate the null model (Equation 9). For example, the mixedMLE option could be used to fit the data under versions of the null model having different sets of covariates included and different choices of transformations of phenotype and/or covariates, in order to decide which choices should be used in the association tests. Once the null model is chosen, MASTOR can be run in the default mode to perform the association analysis. After genetic variants of interest have been identified by an initial analysis with MASTOR, the mixedMLE option of MASTOR can then serve a second purpose, namely, it can be applied, with one or more variants included as covariates, to estimate the parameters of the alternative model (Equations 1, 2, 3, and 4), including effect size(s) of variants or even interactions among them.

Simulation Studies

We perform simulation studies in order to (1) compare type 1 error and power of the tests; (2) determine whether it is possible to retain the high power of MASTOR without going to the trouble of estimating heritability (i.e., compare power of ASTOR and MASTOR); and (3) assess sensitivity of MASTOR and GTAM to misspecified VCs and to estimation of the heritability from a subset of individuals that is not exactly the same subset used in the test. To address these questions, we simulate data that include related individuals, under a variety of trait models and assumptions about missing genotype and phenotype, as we now describe.

Trait Models

We simulate five trait models, denoted I, II, III, IV, and V, all of which have sex as a covariate. Model I has a single major gene acting additively with additional additive polygenic effects. It is given by

where 1 is the vector with all elements equal to 1, 1_female is the vector with i^th element equal to 1 if i is female and 0 if i is male, $\mathbf{ϵ}\sim N\left(\mathbf{0},{\sigma }_a^2\mathbf{\Phi }+{\sigma }_e^2\mathit{I}\right)$, with ${\sigma }_a^2=4$ and ${\sigma }_e^2=7$, and X is the genotype vector with i^th element X_i = 0, .5, or 1, according to whether individual i has 0, 1, or 2 copies of allele 1 at the major gene, where the frequency of allele 1 is .1. Model II has four unlinked causal loci, three of which interact, with additional additive polygenic effects. It is given by

where $\mathbf{ϵ}\sim N\left(\mathbf{0},{\sigma }_a^2\mathbf{\Phi }+{\sigma }_e^2\mathit{I}\right)$, with ${\sigma }_a^2=4$ and ${\sigma }_e^2=7$. Here, f(X₁, X₂, X₃) is a vector with i^th element equal to f(X_1i, X_2i, X_3i) and g(X₄) is a vector with i^th element equal to g(X_4i), where X_1i, X_2i, X_3i, and X_4i are the genotype values of individual i at causal loci 1, 2, 3, and 4, respectively. Table 1 gives the values of f(x₁, x₂, x₃), for (x₁, x₂, x₃) {0,.5,1}³, and we set g(x₄) = .1, 1.25, or 1.5, according to whether x₄ = 0, .5, or 1. The frequency of allele 1 at loci 1, 2, 3, and 4 is .1, .2, .3, and .2, respectively. Model III is an additive polygenic model with no major genes. It is given by

where $\mathbf{ϵ}\sim N\left(\mathbf{0},{\sigma }_a^2\mathbf{\Phi }+{\sigma }_e^2\mathit{I}\right)$, with ${\sigma }_a^2=4$ and ${\sigma }_e^2=25$. Model IV is a heavy-tailed polygenic model with no major genes. It is given by

where $\mathbf{ϵ}\sim N\left(\mathbf{0},{\sigma }_a^2\mathbf{\Phi }+{\sigma }_e^2\mathit{I}\right)$, with ${\sigma }_a^2=4$ and ${\sigma }_e^2=25$ and the η_i’s are i.i.d. draws from the Laplace distribution with location parameter 0 and scale parameter 10. Model V is a polygenic model with both additive and dominance components of variance and no major genes. It is given by Equation 18 where $\mathbf{ϵ}\sim N\left(\mathbf{0},{\sigma }_a^2\mathbf{\Phi }+{\sigma }_d^2{\mathbf{\Delta }}_7+{\sigma }_e^2\mathit{I}\right)$, with ${\sigma }_a^2=4$, ${\sigma }_d^2=20$, and ${\sigma }_e^2=25$, where Δ₇ is the matrix with (i, j)^th entry equal to Δ₇ [i, j], the seventh condensed identity coefficient between individuals i and j, which is the probability that, at any given locus, i and j share two alleles identical by descent (IBD), with neither one homozygous by descent. If the individuals are outbred, then Δ₇ [i, i] = 1 and, for i ≠ j, Δ₇ [i, j] is the probability that i and j share two alleles IBD.

Models I and II have major genes and are used in simulations to assess both type 1 error and power. Models III, IV, and V have no major genes and are therefore used to assess only type 1 error. For each model, we consider three different phenotype configuration settings, A, B, and C. In phenotype configuration A, the sample consists of 65 ascertained families, each of which consists of 16 individuals in a three-generation outbred pedigree, with one grandparent couple in the first generation and three parent couples in the second generation, two of whom have three offspring and one of whom has two offspring. To simulate null markers and/or major genes, founder genotypes or haplotypes are drawn at random based on their assumed population frequencies. Genotypes for other individuals are then generated by a standard “gene-dropping” approach. For models I and II, phenotypes are generated conditional on the simulated genotypes for the major genes, using the conditional distributions given in the previous paragraph. For the models without major genes (III–V), phenotypes are sampled according to the distributions given in the previous paragraph. For each simulation experiment, a genotype sampling scheme is chosen (described in the next subsection), and in phenotype configuration A, a family is ascertained conditional on having at least six genotyped individuals, i.e., at least six individuals who meet the criteria for the chosen genotype sampling scheme. (Computationally, this is carried out by rejection sampling.) Phenotypes for all individuals in an ascertained family are assumed to be observed in configuration A. In phenotype configuration B, the sample consists of 20 ascertained families who satisfy all the same conditions as in A, 500 ascertained unrelated individuals who are both phenotyped and genotyped and who are sampled conditional on meeting the criteria for the chosen genotype sampling scheme (see next subsection), and 500 unrelated, unphenotyped controls who are genotyped and who are randomly sampled from the population. In phenotype configuration C, the sample consists of 65 ascertained families, each of which consists of 16 individuals in a three-generation pedigree. Initially, some individuals’ phenotypes are set missing independently at random, with individuals in the oldest, second-oldest, and youngest generations having probabilities .1, .2, and .4, respectively, of having missing phenotype. In four of the genotype sampling schemes (all, even tails, skewed tails, and upper tail, which are described in the next subsection), all individuals with missing phenotype are assumed to be genotyped, and individuals with nonmissing phenotype are selected for genotyping according to the genotype sampling scheme. (In the random genotype sampling scheme, however, individuals are chosen at random for genotyping, as described in the next subsection, regardless of whether or not they are phenotyped.) Finally, the family is ascertained conditional on having at least three individuals who are both phenotyped and genotyped, at least three who are phenotyped and not genotyped, and at least three who are genotyped and not phenotyped. Note that, as a consequence, in each family in configuration C, there will be at least six individuals genotyped and at least six individuals phenotyped, and only in the random sampling scheme can an individual be missing both genotype and phenotype.

Sampled Genotypes

We consider five different genotype sampling schemes. These genotype sampling schemes do not apply to the 500 unrelated, unphenotyped controls in phenotype configuration B, who are genotyped and are randomly sampled from the population, but they do apply to all other sampled individuals. In the “all” sampling scheme, all sampled individuals are genotyped regardless of their phenotype. As a consequence, ascertainment is random or population based when the all sampling scheme is used. In the “even tails” sampling scheme, an individual is genotyped if and only if his or her phenotype value is ≤μ − 1.5σ or ≥μ + 1.5σ, where μ and σ are the population mean and standard deviation of the trait. In the “skewed tails” sampling scheme, an individual is genotyped if and only if his or her phenotype value is ≤μ − .5σ or ≥μ + 2.5σ. In the “upper tail” sampling scheme, an individual is genotyped if and only if his or her phenotype value is ≥μ + 1σ. In the “random” sampling scheme, individuals are chosen for genotyping independently at random, with individuals in the oldest, second-oldest, and youngest generations having probabilities .4, .7, and .9, respectively, of being genotyped, regardless of phenotype.

Impact of the Variance Components

One goal of our simulation studies is to assess sensitivity of MASTOR and GTAM to (1) misspecified VCs and (2) estimation of the heritability from a subset of individuals that is not exactly the same subset used in the test. To address (1), for both MASTOR and GTAM, we perform a procedure we call “misspecified VCs” in which we first set ${\sigma }_a^2$ and ${\sigma }_e^2$ to be the values used in the corresponding simulation model (I, II, III, IV, or V above). Then, instead of using the null MLE for ξ in the analysis, we set ξ to be ${\sigma }_a^2/\left({\sigma }_a^2+{\sigma }_e^2\right)$. Furthermore, instead of using the generalized regression estimate of ${\sigma }_T^2$ under the alternative model, we plug ${\sigma }_a^2+{\sigma }_e^2$ in for ${\sigma }_T^2$. Note that because of model misspecification and ascertainment, these VCs would be the correctly specified components of variance only for model III with the all sampling scheme; otherwise, they are misspecified. The resulting statistics are referred to in the Results section as “MASTOR misspecified VCs” and “GTAM misspecified VCs.”

To address (2), we calculate MASTOR and GTAM with the heritability estimated from a slightly different sample than the one used in the association test. Ordinarily, the heritability for MASTOR is estimated based on the individuals in group R, and the heritability for GTAM is estimated based on the individuals in group S = N ∩ R. In simulations, we also consider the results when the heritability for MASTOR is estimated based only on the individuals in group S (the GTAM sample), but the individuals in the larger group R N are included in the association analysis, and when the heritability for GTAM is estimated based on the larger set of individuals in R (the MASTOR phenotype sample), but only the individuals in S are included in the association analysis. We refer to the MASTOR and GTAM statistics calculated in this way as MASTOR_G and GTAM_M, respectively, where “G” refers to the estimation of heritability from the GTAM sample and “M” refers to the estimation of heritability from the MASTOR phenotype sample.

Power Studies

To compare the power of the tests, we simulate under models I and II, which have major genes. We simulate a total of 60 scenarios, where 40 of these are obtained by choosing all possible combinations from among two models (I and II), two phenotype configurations (A and B), four genotype sampling schemes (all, even tails, skewed tails, and upper tail), and for model II, testing each of the four different causal SNPs (whereas model I has only one causal SNP). An additional 20 scenarios were obtained by simulating model II with phenotype configuration C with each of five genotype sampling schemes (the four listed above plus random) and testing each of four different causal SNPs. For each of the 60 scenarios, power was evaluated at four different significance levels, .05, .01, .005, and .001. Results from all 240 settings are represented in Figure 1, and a subset of the results appears in Table 4. Because T^SCORE was not correctly calibrated in many of the simulation settings, we did not include it in the power comparison.

Open in a separate window

Figure 1

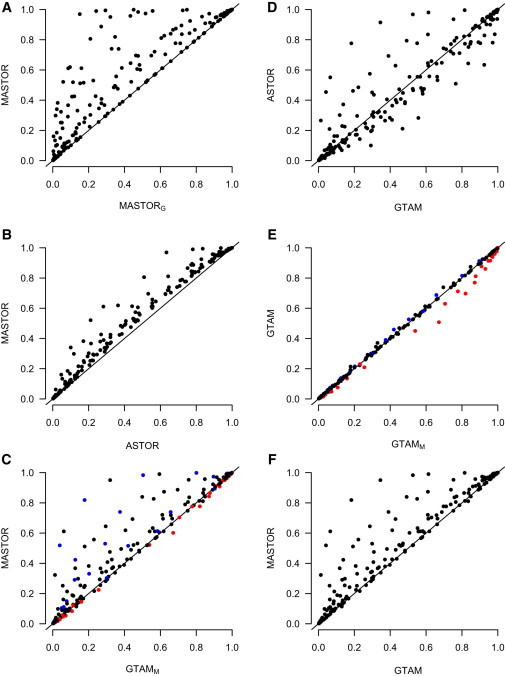
Power Comparisons between Statistics

For each of 60 stimulated scenarios, power was evaluated at four different significance levels: .05, .01, .005, and .001. Results from all 240 settings are represented. Empirical power is based on 25,000 replicates. MASTOR_G is a version of MASTOR with heritability estimated from group S (the GTAM sample) and GTAM_M is a version of GTAM with heritability estimated from R (the MASTOR phenotype sample). For each of the 240 settings, graphs plot (A) the power of MASTOR versus the power of MASTOR_G, (B) the power of MASTOR versus ASTOR; (C) the power of MASTOR versus GTAM_M; (D) the power of ASTOR versus GTAM; (E) the power of GTAM versus GTAM_M; and (F) the power of MASTOR versus GTAM. In (C) and (E), a point is blue if the type 1 error of GTAM_M was significantly deflated (.05 level) in the corresponding scenario, the point is red if the type 1 error of GTAM_M was significantly inflated (.05 level) in the corresponding scenario, and the point is black if the type 1 error of GTAM_M was not significantly different from nominal.

From Table 4 and Figure 1F, it is clear that MASTOR has power that is either approximately equal to or higher than that of GTAM in all of our simulations, and in some cases it is much higher. From rows 1 and 3 of Table 4, we can see that when there are no missing data, the power of MASTOR and GTAM is equivalent. However, in most of the missing data scenarios, MASTOR outperforms GTAM. This is expected because MASTOR uses information on dependence among relatives to allow family members with some missing data to contribute to the analysis.

One goal of our simulation studies was to determine whether we could retain the high power of MASTOR without going to the trouble of estimating heritability. Specifically, we considered whether we could do almost as well as MASTOR by setting the heritability to 0 instead of estimating it. (We called the resulting statistic ASTOR.) From Table 4 and Figure 1B, it is clear that MASTOR dominates ASTOR in terms of power, so the heritability estimation step seems important for power. From Table 4 and Figure 1D, we can see that ASTOR sometimes does much better but often does worse than GTAM. ASTOR tends to do better than GTAM in phenotype configurations A and C with missing data and worse in phenotype configuration B or in the absence of missing data. It makes sense that ASTOR would perform well in strongly family-based samples with missing data because, like MASTOR, ASTOR is able to improve power by using information on dependence among relatives to allow family members with some missing data to contribute to the analysis.

Another goal of our simulation studies was to determine whether, to estimate heritability for the MASTOR and GTAM statistics, one should use only that subset, S, of individuals who have both phenotype and genotype data, or whether one should use the larger subset, R, of phenotyped individuals who do not necessarily have genotype data (but who meet additional conditions detailed above). From Figure 1A, it is clear that for the MASTOR analysis, higher power is achieved by estimating heritability from the full subset, R, (results labeled “MASTOR” in Figure 1A) rather than from the subset having both phenotype and genotype data (results labeled “MASTOR_G” in Figure 1A). In contrast, for the GTAM analysis, there is no gain in power from including the full subset of individuals in R when some of them have missing genotype data (results labeled “GTAM_M” in Figure 1E) as opposed to including only the subset of individuals who are both genotyped and phenotyped (results labeled “GTAM” in Figure 1E). In fact, use of the larger subset of individuals to estimate heritability for GTAM can lead to either an inflation or deflation of type 1 error (Table 2 and the red and blue dots in Figures 1C and 1E).

Analysis of HDL-C Data from the Framingham Heart Study

Table 5 reports the parameter estimates for the null model of log(HDL-C), fitted in cohort 3. We estimated the heritability to be .50 (95% confidence interval of .44–.56), which is consistent with previously reported^20,21 estimates of 0.40–0.69. The Q-Q plot for the MASTOR genome scan (see Figure S1 available online) does not show evidence of inflation, and the genomic control inflation factor is λ_GC = 1.01. In the initial association analysis (before masking of genotypes), the results by GTAM and T^SCORE (not shown) are almost the same as those for MASTOR, which is to be expected because of the low proportion of individuals with phenotype and covariate information who also have missing genotype. In the initial association analysis (before masking of genotypes), one SNP, rs9989419, shows significant association with HDL-C after Bonferroni correction, with a nominal p value of 1.0 × 10⁻⁸ by MASTOR. SNP rs99894919 is located in cholesterol ester transfer protein (CETP [MIM 118470]) and has been previously reported as associated with HDL-C level.^22,23 A previous analysis of a much larger subset of the Framingham data²⁴ also identified this association, using a method that accounts only for sibling correlations, with genomic control used to make a further correction. In Table 6 we report all SNPs with p value ≤10⁻⁵ in the MASTOR analysis. These SNPs are within or in close proximity to eight gene regions, three of which (CETP, LPL [MIM 609708], and LIPG [MIM 603684]) have been reported and replicated before.^22,25–27

After masking some individuals’ genotypes (as described in the HDL-C Data from the Framingham Heart Study subsection of Material and Methods), we again tested for association with each of the 20 SNPs in Table 6 by using MASTOR, GTAM, and T^SCORE, and the results are given in the last three columns of Table 6. The GTAM p values are consistently the largest because GTAM uses only the individuals having complete data. The T^SCORE p values are generally larger than those of MASTOR in this analysis, probably because the T^SCORE variance calculation is appropriate only if either (1) the imputation procedure recovers close to complete genotype information or (2) the phenotype distribution is the same for genotyped and ungenotyped individuals. In addition, the Ghost implementation of T^SCORE does not allow loops, which occurred in six of the Framingham pedigrees.

This study was supported by the National Institutes of Health grant R01 HG001645 (to M.S.M.). The Framingham Heart Study is conducted and supported by the National Heart, Lung, and Blood Institute (NHLBI) in collaboration with Boston University (Contract No. N01-HC-25195). This manuscript was not prepared in collaboration with investigators of the Framingham Heart Study and does not necessarily reflect the opinions or views of the Framingham Heart Study, Boston University, or NHLBI. Funding for SHARe Affymetrix genotyping was provided by NHLBI Contract N02-HL-64278. SHARe Illumina genotyping was provided under an agreement between Illumina and Boston University.