Europe PMC

This website requires cookies, and the limited processing of your personal data in order to function. By using the site you are agreeing to this as outlined in our privacy notice and cookie policy.

In vivo estimates of axonal stretch and 3D brain deformation during mild head impact.

Author information

Affiliations

  • 1. Center for Neuroscience and Regenerative Medicine, The Henry M. Jackson Foundation for the Advancement of Military Medicine, Bethesda, Maryland, USA.
      Authors
    • Knutsen AK 1
    • Gangolli M 1
    • Wang WT 1
    • Pham DL 1
    (4 authors)
  • 2. Department of Neurology, Johns Hopkins University School of Medicine, Baltimore, Maryland, USA.
      Authors
    • Gomez AD 2
    (1 author)
  • 3. Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, New York, USA.
      Authors
    • Chan D 3
    (1 author)
  • 4. Center for the Developing Brain, Children's National Hospital, Washington, D.C., USA.
      Authors
    • Lu YC 4
    (1 author)
  • 5. Department of Mechanical and Manufacturing Engineering, University of Cyprus, Cyprus.
      Authors
    • Christoforou E 5
    (1 author)
    • Show all (8)

ORCIDs linked to this article

Brain Multiphysics, 03 Sep 2020, 1:100015
https://doi.org/10.1016/j.brain.2020.100015 PMID: 33870238 PMCID: PMC8049176

Free full text in Europe PMC

Abstract 

The rapid deformation of brain tissue in response to head impact can lead to traumatic brain injury. In vivo measurements of brain deformation during non-injurious head impacts are necessary to understand the underlying mechanisms of traumatic brain injury and compare to computational models of brain biomechanics. Using tagged magnetic resonance imaging (MRI), we obtained measurements of three-dimensional strain tensors that resulted from a mild head impact after neck rotation or neck extension. Measurements of maximum principal strain (MPS) peaked shortly after impact, with maximal values of 0.019-0.053 that correlated strongly with peak angular velocity. Subject-specific patterns of MPS were spatially heterogeneous and consistent across subjects for the same motion, though regions of high deformation differed between motions. The largest MPS values were seen in the cortical gray matter and cerebral white matter for neck rotation and the brainstem and cerebellum for neck extension. Axonal fiber strain (Ef) was estimated by combining the strain tensor with diffusion tensor imaging data. As with MPS, patterns of Ef varied spatially within subjects, were similar across subjects within each motion, and showed group differences between motions. Values were highest and most strongly correlated with peak angular velocity in the corpus callosum for neck rotation and in the brainstem for neck extension. The different patterns of brain deformation between head motions highlight potential areas of greater risk of injury between motions at higher loading conditions. Additionally, these experimental measurements can be directly compared to predictions of generic or subject-specific computational models of traumatic brain injury.

Free full text 

Logo of nihpaLink to Publisher's site
Brain Multiphys. Author manuscript; available in PMC 2021 Apr 15.
Published in final edited form as:
PMCID: PMC8049176
NIHMSID: NIHMS1660401
PMID: 33870238

In vivo estimates of axonal stretch and 3D brain deformation during mild head impact

Andrew K Knutsen,a,1 Arnold D. Gomez,b Mihika Gangolli,a Wen-Tung Wang,a Deva Chan,c Yuan-Chiao Lu,d Eftychios Christoforou,e Jerry L. Prince,f Philip V. Bayly,g John A. Butman,h and Dzung L. Phama
Author information Copyright and License information Disclaimer

Associated Data

Supplementary Materials
Data Availability Statement

Abstract

The rapid deformation of brain tissue in response to head impact can lead to traumatic brain injury. In vivo measurements of brain deformation during non-injurious head impacts are necessary to understand the underlying mechanisms of traumatic brain injury and compare to computational models of brain biomechanics. Using tagged magnetic resonance imaging (MRI), we obtained measurements of three-dimensional strain tensors that resulted from a mild head impact after neck rotation or neck extension. Measurements of maximum principal strain (MPS) peaked shortly after impact, with maximal values of 0.019–0.053 that correlated strongly with peak angular velocity. Subject-specific patterns of MPS were spatially heterogeneous and consistent across subjects for the same motion, though regions of high deformation differed between motions. The largest MPS values were seen in the cortical gray matter and cerebral white matter for neck rotation and the brainstem and cerebellum for neck extension. Axonal fiber strain (Ef) was estimated by combining the strain tensor with diffusion tensor imaging data. As with MPS, patterns of Ef varied spatially within subjects, were similar across subjects within each motion, and showed group differences between motions. Values were highest and most strongly correlated with peak angular velocity in the corpus callosum for neck rotation and in the brainstem for neck extension. The different patterns of brain deformation between head motions highlight potential areas of greater risk of injury between motions at higher loading conditions. Additionally, these experimental measurements can be directly compared to predictions of generic or subject-specific computational models of traumatic brain injury.

Keywords: traumatic brain injury, tagged MRI, brain biomechanics, axonal strain

1. Introduction

Traumatic brain injury (TBI) is a prominent health problem that affects people across all age groups and throughout the world. In the United States, approximately 1.7 million emergency department visits, hospitalizations, and deaths occurred due to TBI in 2010 [1]. The term TBI encompasses a wide array of injuries of varying severity. Most reported TBIs are classified as mild [2], which is typically defined as a non-penetrating injury that may lead to loss of consciousness (less than 30 minutes), post-traumatic amnesia (less than 24 hours), confusion, disorientation, and/or intracranial lesions not requiring surgery [3]. The rate of mild TBIs per year worldwide is estimated to be 600 per 100,000 people [4]—or approximately 46 million mild TBIs per year. The rapid deformation of brain tissue and elongation of axonal fibers that occurs due to head acceleration or impact can lead to injurious shearing of cerebral vasculature [5] and focal or diffuse axonal injury [6, 7]. Altered imaging findings have been detected using magnetic resonance imaging (MRI) in specific white matter regions, such as the brainstem and corpus callosum, post-injury [8-10]. The relationships between the frequency, magnitude, and orientation of head impacts and the resulting neurodegeneration in the human brain remain largely unknown. The poor correlations between imaging findings and long-term disability in mild TBI indicate that injury is occurring that current technology cannot detect [11].

Computational models of TBI offer a promising approach to predict how the human brain will deform in response to a wide variety of head impacts and impact severities; see Madhukar and Ostoja-Starzewski [12] for a comprehensive review. Computational models can, in principle, be used to predict axonal injury [13-16], estimate brain deformation from impacts during sporting events such as American football [17, 18], and to design or evaluate protective equipment such as helmets [19-21]. Such models must be based on accurate information about the geometry and structure of the human head and material properties of relevant brain structures, and should be evaluated by comparison to experimental measurements of displacement and deformation of the live human brain in response to known loading conditions.

Experiments to determine how the in vivo human brain deforms during injury-level head impacts cannot be performed. To address this limitation, different physical model systems based on surrogates or postmortem human specimens have been used to gain insight into human brain biomechanics and to validate or calibrate computational models. Physical models of the skull-brain structure, created by filling human and baboon skulls with silicone gel, have been used to examine the brain’s response to impact [6, 22]. Additionally, experiments using cadaveric human specimens have been performed using biplanar x-ray [23, 24] and sonomicrometry [25] to track implanted markers in response to head impacts across a wide range of loading conditions. These data have been analyzed to assess relative displacement of the brain with respect to the skull [23-26] and strain [26, 27], providing important measurements of how the brain displaces and deforms at levels at or near what is reasonably likely to cause injury. However, the material properties of the postmortem brain differ from the in vivo brain [28], and they do not provide dense, three-dimensional (3D) measurements spanning the whole brain.

Measurements of brain motion performed in healthy volunteers under loading that is well below injurious levels provide information that is complementary to data from studies of physical models and cadaveric specimens. Tagged magnetic resonance imaging (MRI) has been used to estimate the two-dimensional (2D) brain response during rotation within the axial plane [29-31] and sagittal plane [32, 33] during non-injurious impacts. The angular velocities and accelerations in these studies are quite low—approximately 3 rad/s and 200 rad/s2 for neck rotation [29] and 2 rad/s and 330 rad/s2 for neck extension[34]. To provide perspective on the head motion experienced by the participant, this is approximately 10–15 percent of the angular acceleration experienced during heading a soccer ball [35]. Additionally, head accelerations up to 31 g and 2888 rad/s2 were measured in 20 healthy volunteers (men and women age 26–58 years) engaged in non-injurious everyday and more vigorous activities, such as a soccer ball impact to the forehead, voluntary head shaking, plopping down on a chair, and jumping off of a step [36]. The accelerations in the current study are an order of magnitude less than those seen commonly in contact sports [36] and are similar to those experienced during a cough or sneeze [37] or jogging [38]. Thresholds for angular accelerations leading to mild traumatic brain injury were studied in Zhang et al. [39]; the smallest accelerations considered in that study (approximately 2000 rad/s2) were found to have a very low risk of injury, and even those are much larger than those experienced during the current study. Even though the loading conditions are very mild in nature, we have previously demonstrated reliable measurements of in vivo brain deformations using tagged MRI [29-34].

A limitation of the previous MRI studies of in vivo brain motion is that the computed strain fields were restricted to 2D within the acquisition plane and were provided for a limited number of slices within the brain [30-33]. However, recent methodological advancements allow for estimates of 3D displacement and strain over time from a series of 2D-tagged MR images acquired in multiple orientations [34, 40]. In this study, we applied this method to acquire tagged MRI data during either mild neck rotation or neck extension. Strains were then computed throughout the brain and along white matter tracts identified using diffusion tensor imaging (DTI). To our knowledge, this work represents the first measurements of axonal strain during human head acceleration in vivo.

2. Materials and Methods

Twenty MRI data sets were acquired in 19 healthy volunteers during either neck rotation (N=10) or neck extension (N=10), with one subject scanned using both devices 7 months apart. Eleven subjects were male and 8 were female; the average age of the volunteers was 31.0 +/− 6.1 years (range of 21–42 years). Subjects provided informed consent under a protocol approved by the National Institutes of Health CNS Institutional Review Board. All experiments were conducted in the Clinical Center at the National Institutes of Health.

2.1. Head Rotation Devices

Two MRI-compatible devices were used to generate repeatable, mild head rotations in either the axial plane (neck rotation) [29-31, 34] or the sagittal plane (neck extension) [34, 41]. The devices allow repeatable motion along consistent trajectories, which is needed to accumulate a set of tagged MR images that cover the majority of the brain with adequate spatial resolution. Both the neck rotation device and neck extension device have been described in detail previously [29, 30, 32, 34], though we provide a brief description here for completeness.

For neck rotation, the subject lies in the supine position with his/her head secured to the cradle of the device with side restraint bars and a strap. The subject voluntarily initiates the motion by manually releasing a latch. The subject then actively rotates his/her head approximately 32 degrees toward the left shoulder, at which point the shaft of the device impacts a padded stop, imparting an accelerative load to the brain. The center of rotation is located approximately 6.5 cm anterior from the back of the head and at the midsagittal plane. The head remains in this position for a few seconds, and then the subject uses a pulley to return the head back to the original position.

For neck extension, the subject lies in the supine position with his/her head secured to the device cradle using a strap. The subject voluntarily initiates the motion by manually releasing a latch. The cradle then rotates 5 degrees in the anterior to posterior direction of the head about an axis located near the base of the neck before reaching a padded stop. The center of rotation is located approximately 22 cm inferior from the top of the head and 3 cm anterior from the back of the neck. For this small angle of rotation, the motion of the head is nearly linear with a drop of 2.5 cm at the superior extreme. The subject’s head remains in this position for a few seconds before returning to the original position using a pulley system. For both devices, an MRI-compatible angular position encoder (MICRONOR, Camarillo, CA, USA) is rigidly connected to the device shaft to record angular position, velocity, and acceleration for each motion.

2.2. MRI Acquisition

All MRI scans were acquired using a Siemens 3 T Biograph mMR (Erlangen, Germany). Anatomical images were acquired using either a 32-channel or 16-channel receive-only head coil. The acquisition included a 3D T1-weighted Magnetization-Prepared Rapid Acquisition Gradient Echo (MPRAGE) with the following parameters: echo time (TE) = 3.03 ms, repetition time (TR) = 2530 ms, inversion time (TI) = 1100 ms, field of view (FOV) = 256×256×176 mm, matrix = 256×256×176. A 3D T2-weighted image was also acquired using the following parameters: TR/TE = 3200/410 ms, FOV = 250×250×176 mm, matrix = 256×256×176. The total scan time for both the motion and anatomical MRI scans was less than two hours per imaging session.

For DTI, a total of 40 diffusion weighted image (DWI) volumes were acquired using a 2D echo planar imaging (EPI) sequence with the following parameters: TR/TE = 16400/93 ms, FOV = 256×256 mm, matrix = 128×128, 75 slices, slice thickness = 2 mm, 6 DWIs at b = 0 s/mm2, 4 non-colinear DWIs at b = 300 s/mm2, and 30 non-colinear DWIs at b = 1100 s/mm2. To improve the correction of spatial distortions introduced by the EPI acquisition, an additional DWI volume (b = 0 s/mm2) was acquired with the same acquisition parameters with the reverse phase encode direction.

For the tagged MRI portion of the study, one of two MRI-compatible devices was used to generate a repeatable mild head acceleration—either during neck rotation or neck extension. A combination of one or two (depending upon slice position) three-channel, receive-only, spine coils built into the scanner bed and a six-channel, receive-only, flexible body array coil were used for the acquisition. An optically gated trigger initiated the application of a 1–1 Spatial Modulation of Magnetization (SPAMM) tagging pulse followed by a 2D-segmented cine gradient-echo acquisition with the following parameters: TR/TE = 3.01/1.67 ms, tag spacing = 8 mm, segments = 6, FOV = 240×240 mm, matrix = 24×160 (reconstructed to 160×60), slice thickness = 8 mm with a 2 mm gap between slices, temporal resolution = 18 ms, number of image frames = 10–12. For the neck rotation device, the gradient-echo acquisition was triggered by the angular position sensor when the device shaft rotated through 28.5 degrees. Additionally, the tag lines were applied at an angle of 30 degrees away from the center line of k-space so that they were located approximately along the center line of k-space at the point of impact [30].

To measure deformation over the majority of the brain, multiple slices were acquired with tag lines oriented along three orthogonal axes [34]. For the neck rotation, 11–13 axial slices were acquired first with tag lines along the y-axis and then repeated with tag lines along the x-axis. Then, six slices were acquired with tag lines along the z-axis; these slices were orthogonal to the axial plane and oriented every 30 degrees, like spokes on a wheel, about the approximate brain center. For the neck extension, 11–14 sagittal slices were acquired first with tag lines along the y-axis and then repeated with tag lines along the z-axis. An additional 8–13 axial slices were acquired with tag lines along the x-axis. Note that the x-, y-, and z-axes correspond to right-left, anterior-posterior, and inferior-superior with the subject at rest in the supine position.

2.3. Image Processing

Brain extraction was applied to the MPRAGE and T2-weighted images using the MONSTR method [42]. Segmentation of the brain-masked MPRAGE was then performed using the S3DL algorithm [43]. Segmented regions included the cortical gray matter, cerebral white matter, deep gray matter, cerebellar gray matter, cerebellar white matter, and brainstem. The DWIs were processed using the TORTOISE3 software package [44], which included motion and eddy current distortion correction [45]. EPI-induced geometric distortions were then corrected by the DRBUDDI module [46] of TORTOISE3 using the DWIs with the reversed phase encode gradients and the T2-weighted image. The diffusion tensor was fitted using a nonlinear least squares robust fitting algorithm [47] followed by computation of diffusion properties. The corpus callosum was automatically segmented from the estimated diffusion tensor using the DOTS method [48]. For this study, only fractional anisotropy [49] and the principal eigenvector of the diffusion tensor were used in subsequent analyses.

Three-dimensional displacements over time were obtained from the tagged MRI data using the Harmonic-Phase Analysis with Finite Elements (HARP-FE) method [34]. The HARP-FE algorithm combines harmonic phase (HARP) analysis [50] and the finite element method to compute mechanically regularized measurements of deformation and displacement from tagged MRI data.

Before HARP-FE, the following pre-processing steps were performed: For each tagged image slice and tag direction, frames 2 through 10 were rigidly registered to frame 1 using the command antsRegistration, which is part of the Advanced Normalization Toolkit V2 [47]. This was done to remove any potential small differences in how the subjects rotated between neighboring slices. The 3 tagged image sets—i.e., the combination of slices with the same tag line orientation—were then resampled to a 1.5 mm isotropic grid using cubic b-spline interpolation in Matlab R2016a (Mathworks, MA, USA). HARP images were created for each tag orientation and image frame by applying a spherical filter with a radius of 9 voxels in k-space.

The anatomical and tagged images were acquired using a different receive coil with the subject’s head in a different position. They therefore did not intrinsically have any spatial correspondence between them. To obtain correspondence, the MPRAGE was rigidly registered to an image volume created by summing the three tagged image sets using the antsRegistration command; the same registration parameters were used as above, except that a 3D rigid registration was performed instead of 2D. The brain segmentation, T2-weighted image, and DTI metrics were transformed to the tagged image space using nearest neighbor or cubic b-spline interpolation (as appropriate).

2.4. Calculation of Strain Metrics

HARP-FE was implemented as a plug-in for the FEBio finite element analysis software [51]. The output from HARP-FE consists of 3D displacement vector field (u) over time. Next, the computed displacement field was projected from the finite elements to each voxel. Strain fields were estimated from the displacements using a local fitting approach. For each frame, displacement (u = [u v w]) was estimated as a function of space (X, Y, Z) for a given voxel (x0, y0, z0) using the N voxels within a radius of 5 voxels and a linear, least-squares fit.

u(x0,y0,z0)=a0+a1X1,..,i,..,N+a2Y1,..,i,..,N+a3Z1,..,i,..,Nv(x0,y0,z0)=b0+b1X1,..,i,..,N+b2Y1,..,i,..,N+b3Z1,..,i,..,Nw(x0,y0,z0)=c0+c1X1,..,i,..,N+c2Y1,..,i,..,N+c3Z1,..,i,..,N
(1)

where ai, bi, and ci are the coefficients to be estimated. Only voxels labeled as brain tissue by the segmentation were used in the fit. Lagrangian strain tensors were estimated by

E=12(∇u+(∇u)T+∇u⋅(∇u)T)
(2)

where [nabla] is the gradient operator. The computed coefficients directly provide the spatial derivative of displacement. Eigenvalues and eigenvectors were computed, and the maximum principal strain (MPS) was assigned to the first eigenvalue. White matter fiber strain (Ef) was calculated using the Lagrangian strain tensor and the principal eigenvector of the diffusion tensor (n) estimated at each voxel:

Ef=n⋅E⋅n
(3)

For fiber strain, only voxels located in either the cerebral white matter, cerebellar white matter, or brainstem with a fractional anisotropy value greater than or equal to 0.2 were analyzed. This is a standard criterion for excluding regions of isotropic diffusion, such as gray matter and cerebrospinal fluid [52].

The volume fraction of strain, which is the percentage of voxels where the measured strain is above a threshold value, was computed for thresholds of 0.01, 0.02, 0.03, and 0.04. The 95th percentile value of the distribution was used (in place of the maximum value) to assess peak strain values. Pearson’s correlation coefficients were computed to assess the linear relationship between strain metrics and angular deceleration during impact and angular velocity just prior to impact.

3. Results

To acquire a data set with full brain coverage at the desired 18 ms, the subjects repeated the head motion 112–128 times for neck rotation data set and 132–156 times for neck extension. The angular position sensor recorded position, velocity, and angular acceleration for each repetition. In Figure 1, traces of angular position, velocity, and acceleration versus time are plotted for each head repetition performed during a single neck rotation and neck extension experiment. Additionally, the vertical gridlines starting at t = 0 ms in Figure 1 identify the corresponding timing of the image frames from the tagged MRI acquisition. For each repetition, the largest value was identified and the average was computed across repetitions for each subject. Note that the largest acceleration is negative in magnitude, corresponding to a rapid deceleration about the inferior-superior axis during neck rotation and the left-right axis during neck extension. For the peak of angular deceleration (α), which occurred during impact, the mean ± SEM was 212.8 ± 32.1 rad/s2 (range of 156.4–247.1 rad/s2) for neck rotation (N=10) and 282.8 ± 47.4 rad/s2 (range of 213.4–347.5 rad/s2) for neck extension (N=10). For peak angular velocity (ω), which occurred just prior to impact, the mean was 3.21 ± 0.52 rad/s (range of 2.42–3.73 rad/s) for neck rotation and 1.75 ± 0.16 rad/s (range of 1.53–2.02 rad/s) for neck extension.

An external file that holds a picture, illustration, etc. Object name is nihms-1660401-f0001.jpg

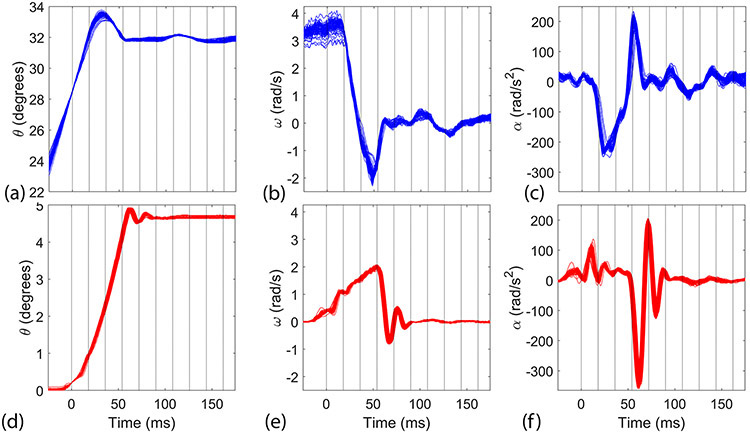
Plots of (a, d) angular position (θ), (b, e) angular velocity (ω), and (c, f) angular acceleration (α) vs time for each repetition during (a–c) neck rotation and (d–f) neck extension. The vertical lines indicate the temporal boundaries of the image frames.

Figure 2 and Supplemental Figures 1 and 2 show axial, coronal, and sagittal views of voxel-wise estimates of MPS for each image frame for a single neck rotation and neck extension data set. The spatial patterns of the MPS are complex and vary over time. The MPS values are plotted as an overlay on the subject’s MPRAGE image, which allows for visualization of the anatomy. Qualitatively, the MPS values for both head motions increased to a maximum shortly after impact and then decreased afterwards, oscillating towards a minimum value. For neck rotation, the largest MPS values appear in the cortical gray matter and cerebral white matter. For neck extension, the largest MPS values are seen in the cortical gray matter, though they are mostly limited to the midsagittal plane, and in the cerebellum and brainstem. Additionally, MPS at peak deformation appears more symmetric for neck extension than neck rotation.

An external file that holds a picture, illustration, etc. Object name is nihms-1660401-f0002.jpg

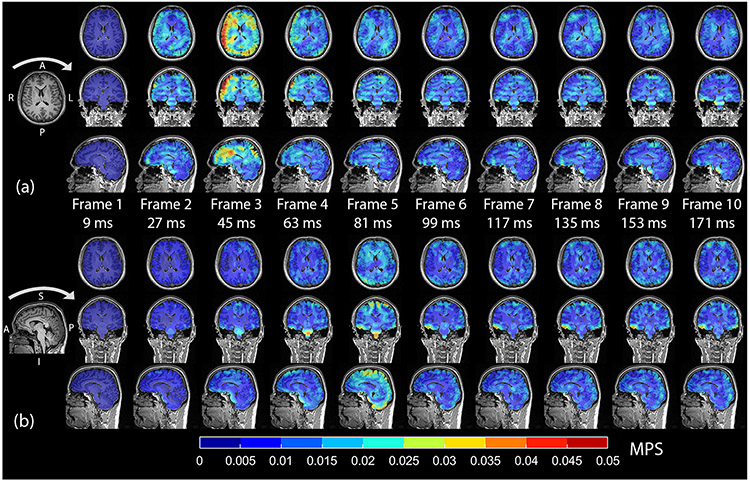
Axial, coronal, and sagittal views of MPS (color) and MPRAGE (grayscale) for each frame/time as measured during (a) one neck rotation experiment and (b) one neck extension experiment. Impact occurred during the second frame for neck rotation and the fourth frame for neck extension. Peak angular deceleration occurred during frame 2 for neck rotation and frame 4 for neck extension. The arrows above the MPRAGE on the left-most portion of the figure indicate the direction of head motion prior to impact. L=left, R=right, A=anterior, P=posterior, I=inferior, S=superior.

The volume fraction of strain provides an estimate of the volume of brain tissue with strain above a given threshold. Figure 3 shows the average volume fraction (+/− standard error) of MPS and Ef across subjects for each image frame and both head motions. This shows quantitatively that the qualitative assessment from Figure 2 holds across subjects: the largest MPS and axonal fiber strains occurred in the first frame after the peak angular acceleration and then generally decreased in subsequent frames. The neck rotation experiment produced larger volume fractions than neck extension under the range of loading conditions. MPS is useful to analyze because it provides a single metric of the maximum deformation. Additionally, Supplemental Table 1 lists values of MPS, Ef, brain volume, and ω2 for each subject. The Lagrangian strain tensor contains six unique components, and examination of each is informative. Supplemental Figures 3 and 4 show the volume fraction of strain for each strain component. These figures show the strain components within the plane of rotation (the axial plane for neck rotation and the sagittal plane for neck extension) account for the majority of deformation—though some out-of-plane shearing is observed for both motions.

An external file that holds a picture, illustration, etc. Object name is nihms-1660401-f0003.jpg

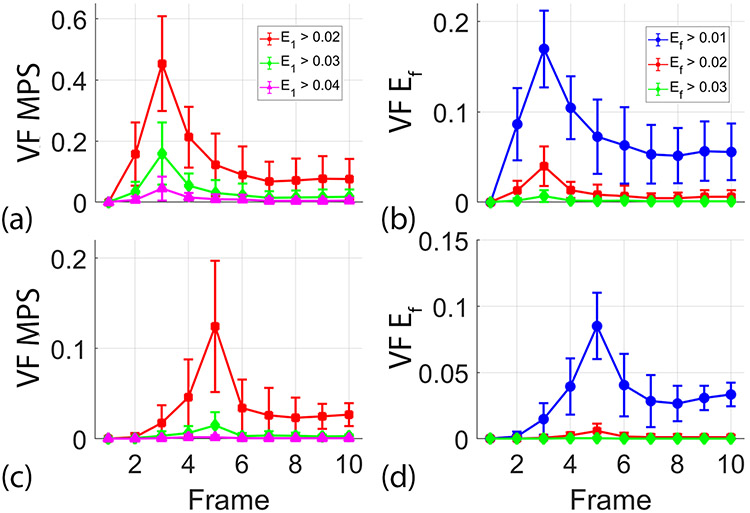
Average (+/− standard error) of volume fraction (VF) of (a, c) maximum principal strain (MPS) and (b, d) axonal fiber strain (Ef) at multiple thresholds for each acquired image frame during (a–b) neck rotation and (c–d) neck extension. The temporal resolution between image frames is 18 ms.

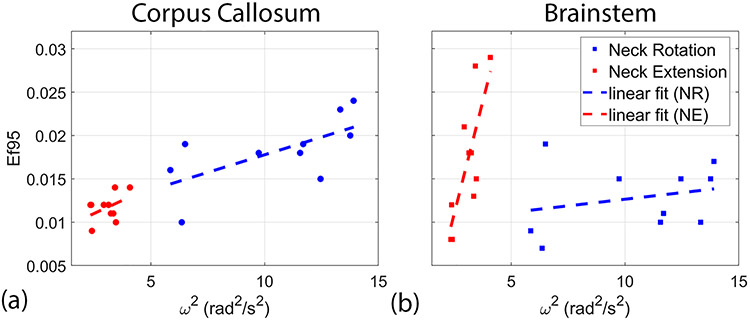
Figure 4 shows a plot of the 95th percentile of the MPS distribution (MPS95) as a function of ω2 for each subject. We focused on the image frame with the largest amount of deformation—frame 3 for neck rotation and frame 5 for neck extension. Values of MPS95 ranged from 0.026 to 0.053 for neck rotation and 0.019 to 0.029 for neck extension. For correlation, we chose to use ω2 in place of ω because it is proportional to energy at impact. A line was fitted to the data for each head motion using a linear least squares fitting algorithm (mldivide, Matlab, The Mathworks, Natick, MA) to illustrate the trend. Pearson’s correlation coefficients and p-values were computed and are listed in Table 1. Both motions showed strong correlation between MPS95 and ω2: r = 0.85 for neck rotation and r = 0.64 for neck extension.

An external file that holds a picture, illustration, etc. Object name is nihms-1660401-f0004.jpg

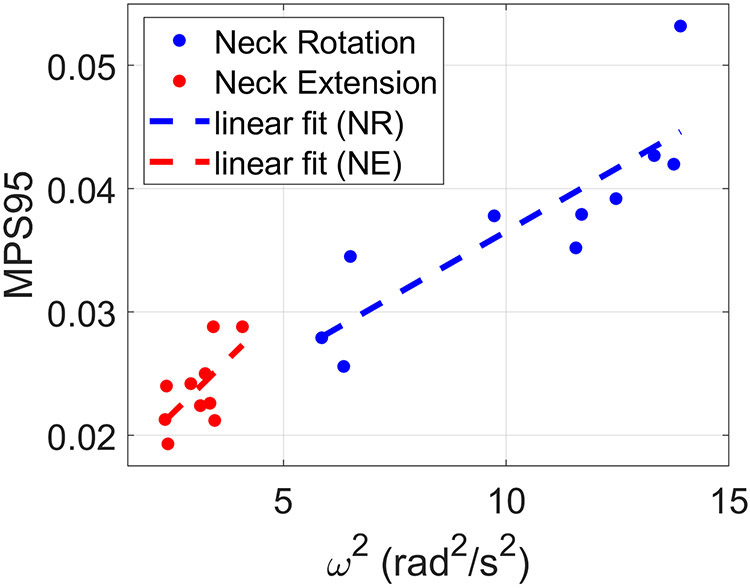
Relationship between 95th percentile of maximum principal strain (MPS95) at the time of peak deformation and angular velocity squared (ω2) during neck rotation and neck extension. Each data point shows the result for a single subject. The dashed lines show linear fits of the data.

Table 1:

Pearson’s correlation coefficients (r) and p-values for the 95th percentile of the distribution of maximum principal strain (MPS95) or axonal fiber strain (Ef95) compared to peak angular velocity squared (ω2) across various brain regions.

Strain
Metric		RegionNeck Rotation (N=10)Neck Extension (N=10)
rprp
MPS95Whole Brain0.850.00190.640.0467
Cortical Gray Matter0.840.00230.530.1115
Cerebellar Gray Matter0.620.05820.680.0300
Deep Gray Matter0.450.19160.320.3597
Cerebral White Matter0.850.00200.530.1171
Cerebellar White Matter0.350.32550.660.0383
Brainstem−0.040.91810.600.0696
Ef95Corpus Callosum0.650.04130.440.2048
Brainstem0.250.48730.790.0063

Using each subject’s tissue segmentation, separate distributions of MPS were computed within the cortical gray matter, cerebral white matter, deep gray matter, cerebellar gray matter, cerebellar white matter, and brain stems structures. Analogous to Figure 4, Figure 5 plots MPS95 as a function of ω2 for each of the segmented brain regions. Correlation coefficients and p-values were computed and are listed in Table 1. For neck rotation, the strongest correlations are seen in the cortical gray matter (r = 0.84) and cerebral white matter (r = 0.85), with a moderate correlation in the cerebellar gray matter (r = 0.62). For the neck extension experiment, moderate correlations are seen in the cerebellar gray matter (r = 0.68), cerebellar white matter (r = 0.66), and brainstem (r = 0.60).

An external file that holds a picture, illustration, etc. Object name is nihms-1660401-f0005.jpg

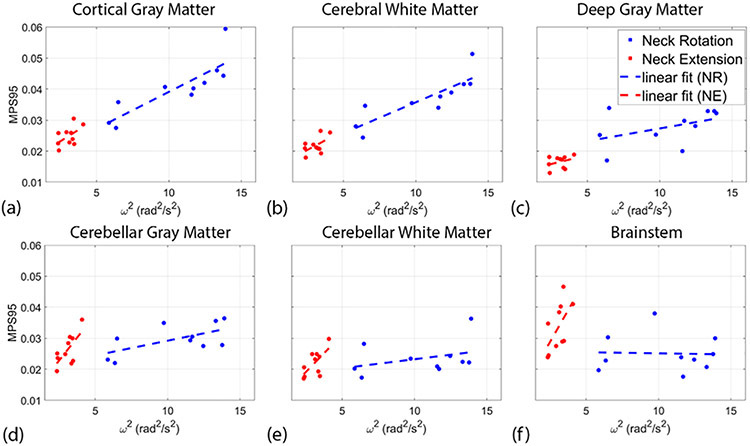
Relationship between 95th percentile of maximum principal strain (MPS95) at the time of peak deformation and angular velocity squared (ω2) in the (a) cortical gray matter, (b) cerebellar gray matter, (c) deep gray matter, (d) cerebral white matter, (e) cerebellar white matter, and (f) brainstem. Each data point shows the result for the single subject. The dashed lines show a linear fit of the data.

Figure 6 shows images of positive axonal fiber strain (elongation) from the image frame with the largest strain values; axonal fiber strains are mapped onto 3D ellipsoids that indicate the direction of axonal fibers within the white matter. Axial and sagittal views are shown in three subjects for each head motion. These images depict a heterogeneous pattern of axonal fiber strain within the brain, with similar patterns of deformation between subjects within motion and different area of high strain between the two motions. The neck rotation data shows a contre-coup pattern with high elongation in the left-frontal and right-posterior white matter, whereas the neck extension data is more symmetric with greater elongation of the brainstem. For a more quantitative assessment, we examined the 95th percentile value of the distribution of axonal fiber strains (Ef95) specifically within the brainstem and corpus callosum. Figure 7 contains a plot of Ef95 as a function of ω2 for these regions. Correlation coefficients and p-values were computed and are listed in Table 1. In the corpus callosum, stronger correlation is seen during neck rotation (r = 0.65) than neck extension (r = 0.44). Conversely, in the brainstem, stronger correlation is observed in neck extension (r = 0.79) than neck rotation (r = 0.25).

An external file that holds a picture, illustration, etc. Object name is nihms-1660401-f0006.jpg

Axial and sagittal views of fiber strain (Ef) (color) and MPRAGE (grayscale) during (a–c) neck rotation and (d–f) neck extension in six subjects at the time of peak deformation (frame 3 for neck rotation and frame 5 for neck extension). Values of Ef were mapped to 3D ellipsoids that indicate the principal direction and degree of anisotropy from the diffusion tensors. Arrows above the images in the top row indicate the direction of head motion prior to impact. L=left, R=right, A=anterior, P=posterior, I=inferior, S=superior.

An external file that holds a picture, illustration, etc. Object name is nihms-1660401-f0007.jpg

Relationships between the 95th percentile of axonal fiber strain (Ef95) and angular velocity squared (ω2) in the (a) corpus callosum and (b) brainstem. The dashed lines show linear fit of the data.

4. Discussion

Mild head deceleration during impact produces spatially heterogeneous patterns of deformation in the in vivo human brain. The MPS was presented to provide a single, invariant measure of deformation throughout the brain, which is more compact than presenting all six components of the full strain tensor. To further simplify the data for analysis, both the peak (95th percentile) and volume fractions of strain were analyzed over the entire brain and in various segmented regions. Estimates of MPS were largest shortly after impact and then decreased, though not quite to zero. We attribute this partly to the limited number of image frames analyzed—the head has not returned to rest by the last frame—and partly to decreased signal-to-noise ratio as tag lines fade. Estimates of viscoelastic time constants vary widely, but some studies, e.g. [53], suggest that time constants are larger than 1 second, which implies that viscoelastic relaxation may not be complete at the end of each data acquisition.

Coefficients of correlation between brain deformation—MPS95 and Ef95—and ω2 highlighted regional differences that depended on the type of head motion. For MPS95, higher correlations were seen in the cortical gray matter and white matter during neck rotation compared to the cerebellar white matter and brainstem during neck extension. Similarly, a regional effect was seen in strains along axonal fibers for both head motions. Ef95 was more strongly correlated with ω2 in the corpus callosum during neck rotation and in the brainstem during neck extension. For both head motions, the largest strain components correspond to the plane of rotation (Supplemental Figures 3 and 4). The largest deformations occurred in slices with the most brain tissue/mass present, such as near the mid-sagittal plane (including the cerebellum and brainstem) for neck extension and axial planes passing through the lateral ventricles for neck rotation. The current tagged MRI studies are consistent with observations from in vivo MRE. Recent MRE studies suggest brain tissue has an average dynamic shear modulus near 2 kPa under harmonic excitation at 50–60 Hz [54]. Simulations of brain deformation using an average shear modulus of 2.2 kPa predict strain amplitudes similar to those in the current study, in response to similar angular accelerations [55]. Strain levels in the current study are also similar to those seen in simulations, analyses, and experiments with a gel phantom of shear modulus 1.7 kPa under similar angular accelerations [56]. MRE can also uncover spatial variations in tissue properties. In vivo MRE data suggest decreased shear stiffness in the cerebellum compared to the cerebral gray and white matter [57]. This could account for the sharper increase in MPS95 and Ef95 versus ω2 in the cerebellum for neck extension compared to neck rotation. Additionally, it is possible that the bending of the neck during neck extension could lead directly to greater elongation of axonal fibers in the brainstem. These results highlight certain brain regions that might be more likely to be injured due to different head motions during trauma. Injury to these regions has been highly implicated in studies of chronic dysfunction following TBI [8-10], with the brainstem additionally being associated with loss of consciousness [58, 59].

To compute the preferred orientation for axonal fibers at each voxel, we used a standard model of a single diffusion tensor. The principal eigenvector of the diffusion tensor provides the preferred direction of diffusion within that voxel. We then projected the strain tensor onto the diffusion principal eigenvector, which provides a voxel-wise estimate of axonal strain. This assumes that the fiber orientation approximately uniform within each voxel. Other studies have applied a model of fiber dispersion developed for arterial vessels [60] to axonal fibers in the brain [15, 61]. Including fiber dispersion applies an approximately linear scaling to the axonal fiber strain estimates based on the FA. Under this model, the estimates provided here would represent the case of FA equals 1, yielding a maximum estimate of axonal fiber strain within each voxel. However, interpreting FA as fiber dispersion is a simplification of actual brain microstructure since it is estimated from a single tensor model for diffusion that does not account for crossing fiber bundles. The single tensor diffusion model was used because our DTI acquisition involves only 30 unique gradient directions with a single diffusion-weighting parameter (b-value). More advanced diffusion acquisitions on high performance MRI scanners can be used to acquire data with increased spatial and angular resolution. For example, the WU-Minn Human Connectome Project diffusion acquisition protocol specifies 270 diffusion weighted images with three non-zero b-values [62]. Such data allows for the use of more complex models of diffusion within each voxel that can better describe crossing fibers using multi-tensor models or orientation distribution functions. In the future, improved data acquisition will enable more advanced models of diffusion and axonal strain.

The full 3D strain fields obtained in this study confirm some features of previously-reported 2D strain fields obtained using tagged MRI. This is largely because the majority of the deformation occurs within the axial plane for neck rotation and the sagittal plane for neck extension. For example, by estimating 2D strains in a single image slice during neck extension, Bayly et al. [32] observed concentrations of high first principal strain in the cortex and cerebellum (e.g., Figure 6 from Bayly et al. [32]). That study applied peak linear accelerations of 2–3 g over a 40 ms period with a different head acceleration device than the one used here. Despite the lower peak accelerations in the previous 2D study, strain magnitudes were similar; differences between studies may be partially explained by the different acceleration profiles produced by different devices, the limited number of slices and incomplete motion data in the 2D studies, and subject-to-subject variations in anatomy and physiology. We note that head accelerations in both studies were measured from sensors on the motion-constraining device; the amount of acceleration experienced by the subject’s head is slightly different (this caveat also applies to field data from sensors mounted in mouth-guards or helmets). The relationships between brain deformation, impact velocity, peak acceleration, and the duration of the applied acceleration are critically important and targets of future research. Chan et al. [29] characterized the 2D deformation response in 34 subjects for neck rotation using same motion-constraining device used in this study. Strain patterns were similar between the studies (see Figures 3-​-55 from Chan et al. [29]). The largest values of MPS were observed shortly after the time of peak angular deceleration and occurred in the cortical gray matter.

In general, higher values of MPS were observed during neck rotation than neck extension. This is likely due largely to an increase in ω in the neck rotation experiments. Ideally, we would have observed some overlap in ω between the motions. ω is primarily determined by the range of motion of each head motion device and of how each subject accelerates his/her head prior to impact; head motion prior to impact is an active process driven by the subject. Given this, varying ω systematically and over a larger range is not feasible in healthy volunteers. However, it is possible to vary the magnitude and duration of the acceleration pulse for a given ω by changing the stiffness of the impact pad. This would allow us to assess the effectiveness of reducing acceleration, i.e., by using different types of padding, in reducing in vivo brain deformation.

The data from the current study, comprising 3D dynamic strain fields together with high-resolution anatomy and white matter fiber orientation, represent a substantial and valuable resource for the evaluation of computational models. The primary limitation of this study is that the applied loading conditions were well below the threshold for injury; this limitation is necessary for human volunteers to participate in the study. While a recent study [63] asserted that measurements of brain deformation on this order are “not relevant for studying traumatic brain injury,” we disagree. Both human and cadaver studies have strengths and limitations. While in vivo measurements of brain deformation occur in response to loading conditions well below injury thresholds, these data provide dense, high-resolution measurements of strain over time in the live, human brain. Conversely, although cadaveric specimens retain human geometry and anatomical structure, and can be tested under a larger loading regime, including at thresholds for injury, the measured displacements are sparse and provide only coarse estimates of strain [23, 24, 27]. Additionally, the material properties of cadaveric brain tissue undergo physical changes that can alter the biomechanical response of the brain [28]. Therefore, computational models should generally be evaluated by comparison to experimental data over a large range of loading conditions [64] including mild impacts studied here, particularly given the increasing interest in the chronic effects of mild and sub-concussive head impact.

Similar to cadaveric specimens, animal models can also be used to measure brain deformation over a range of loading conditions, but unlike cadavers, the biological response can be studied using histopathology. Tagged MRI has previously been used to measure in vivo strain fields in the rat brain during head impact [65, 66], and high-speed video was used to track marker position and estimate brain deformation for a hemi-section pig model of injury [7, 67, 68]. Future work will examine the use of tagged MRI in an animal model to investigate how brain deformation scales over a range of loading conditions, from non-injurious to injurious. Although tagged MRI allows sampling up to approximately 2.5 ms per image frame, loading conditions should not cause acute injury because the motion must be repeated multiple times to create an image set.

An additional challenge of using tagged MRI to investigate brain motion is that the subject must repeat the head rotation multiple times to acquire each slice of the image volume. The specific number of repetitions is proportional to the spatial and temporal resolution—more repetitions provide higher spatial and temporal resolution. The strain resolution is a function of the spatial frequencies included in the bandpass filter used for HARP, so it is approximately on the order of the tag spacing [69]. The parameters for this study (4 repetitions per image set, 24 phase encode lines, 18 ms temporal resolution, tag spacing of 8 mm) were selected based on a previous optimization study [30]. In the prior study, these parameters were shown to provide accurate estimates of deformation compared to schemes with more repetitions, and they allowed for the acquisition of a sufficient number of slices to cover the brain with tag lines along all three axes. Given that the majority of brain deformation occurs within the plane of rotation, it could be reasonable to perform some targeted tagged MRI studies in 2D. Two examples where this could be of interest are to examine specific brain regions at increased spatiotemporal resolution with a smaller tag spacing and to investigate how changing the acceleration profile for a given impact energy affects the deformation response of the brain.

In the future, results from these or similar 3D studies may be used to identify regions of interest for more detailed exploration of higher spatial and/or temporal resolution in a smaller number of 2D slices. While tagged MRI is best-suited to track motion in tissues, phase contrast MRI could be used to quantify fluid motion within the brain, e.g. [70]. The present 3D data could also be analyzed to assess the frequency response of the brain to impact, a property which has been hypothesized to play a role in concussion [50]. For developers of computer models, results from tagged MRI may be supplemented with subject-specific, spatially varying material properties measured in vivo using magnetic resonance elastography (MRE) [71, 72]. These data together can be used to estimate viscoelastic [73] and anisotropic [74, 75] material properties of the brain and to characterize frequency-dependent interactions between the scalp, brain, and skull [76].

5. Conclusions

In this study, we used tagged MRI in healthy volunteers to estimate dense 3D strain fields throughout the brain in response to a mild head impact during either neck rotation or neck extension. In general, the amount of brain deformation increased as the severity of the head impact increased, though this varied by brain region and also depended on the type of head motion. We also show that the majority of the brain deformation occurred within the plane of rotation and noted the similarity between these 3D strain measurements and previously performed 2D experiments. While obtaining full-field 3D strain fields is critical to understanding TBI, future tagged MRI experiments of brain deformation could take advantage of a more rapid 2D acquisition to investigate different features or assess varying loading conditions. Finally, this study also provides the first in vivo estimates of axonal fiber strain due to head acceleration, which were obtained by combining the computed strain tensors with axonal fiber orientations inferred from diffusion tensor imaging. We observed similar patterns of axonal fiber strain across subjects within motion that differed between motions. Notably, the brainstem had larger axonal fiber strains and was more sensitive to increased loading during neck extension than neck rotation. While axonal fiber strains were larger in the corpus callosum during neck rotation, the sensitivity to ω was similar between the motions. The combination of in vivo experimental measurements of brain deformation under two loading conditions with high resolution neuroimaging data provides an invaluable resource for development and evaluation of computational models of TBI.

​

Highlights:

  • 3D strain fields obtained from in vivo tagged MRI during non-injurious head impact

  • Peak strains of 0.02–0.05 were measured and correlated with peak angular velocity

  • First study to report in vivo estimates of impact-induced strain along axonal fibers

  • Regional differences in axonal fiber strains observed between head motions

Supplementary Material

Supplemental Figure 1

Supplemental Figure 1: Axial, coronal, and sagittal views of MPS (color) and MPRAGE (grayscale) for each frame/time as measured during two neck rotation experiments. Impact occurred during frame 2. The arrows above the MPRAGE on the left-most portion of the figure indicate the direction of head motion prior to impact. L=left, R=right, A=anterior, P=posterior, I=inferior, S=superior.

Supplemental Figure 2

Supplemental Figure 2: Axial, coronal, and sagittal views of MPS (color) and MPRAGE (grayscale) for each frame/time as measured during two neck extension experiments. Impact occurred during frame 4. The arrows above the MPRAGE on the left-most portion of the figure indicate the direction of head motion prior to impact. L=left, R=right, A=anterior, P=posterior, I=inferior, S=superior.

Supplemental Figure 3

Supplemental Figure 3: Average (+/− standard error) of volume fractions of the (a–c) normal and (d–f) shear strain components at multiple thresholds for each acquired image frame during neck rotation. L is the left/right axis, P is the posterior/anterior axis, S is the superior/inferior axis. The temporal resolution between image frames is 18 ms.

Supplemental Figure 4

Supplemental Figure 4: Average (+/− standard error) of volume fractions of the (a–c) normal and (d–f) shear strain components at multiple thresholds for each acquired image frame during neck extension. L is the left/right axis, P is the posterior/anterior axis, S is the superior/inferior axis. The temporal resolution between image frames is 18 ms.

Acknowledgements

We acknowledge funding from the National Institute of Neurological Disorders and Stroke (R01/R56 NS055951 and U01 NS112120), the Department of Defense in the Center for Neuroscience and Regenerative Medicine, and the Intramural Research Program of the National Institutes of the Health. We would like to thank all of the participants in this study for their time and effort. We also acknowledge the technical expertise of Dr. Snehashis Roy, Mr. Yi-Yu Chou, Ms. Elizabeth McGrath, Ms. Sarah Yan, Ms. Jennifer Kraszewski, Dr. Ahmed Alshareef, Mr. Aaron Carass, and Ms. Michelle Albert.

Footnotes

Competing interests

The authors declare no competing interests.

Data availability

Six data sets (3 neck extension, 3 neck rotation) are publicly available for download at https://www.nitrc.org/projects/bbir/. Additional data sets are available from the corresponding author upon request.

References

1. Faul M and Coronado V, Epidemiology of traumatic brain injury. Handb Clin Neurol, 2015. 127: p. 3–13. [Abstract] [Google Scholar]
2. Gardner RC and Yaffe K, Epidemiology of mild traumatic brain injury and neurodegenerative disease. Mol Cell Neurosci, 2015. 66(Pt B): p. 75–80. [Europe PMC free article] [Abstract] [Google Scholar]
3. Carroll LJ, et al., Methodological issues and research recommendations for mild traumatic brain injury: the WHO Collaborating Centre Task Force on Mild Traumatic Brain Injury. J Rehabil Med, 2004(43 Suppl): p. 113–25. [Abstract] [Google Scholar]
4. Cassidy JD, et al., Incidence, risk factors and prevention of mild traumatic brain injury: results of the WHO Collaborating Centre Task Force on Mild Traumatic Brain Injury. J Rehabil Med, 2004(43 Suppl): p. 28–60. [Abstract] [Google Scholar]
5. Bell ED, Donato AJ, and Monson KL, Cerebrovascular dysfunction following subfailure axial stretch. J Mech Behav Biomed Mater, 2017. 65: p. 627–633. [Europe PMC free article] [Abstract] [Google Scholar]
6. Meaney DF, et al., Biomechanical analysis of experimental diffuse axonal injury. J Neurotrauma, 1995. 12(4): p. 689–94. [Abstract] [Google Scholar]
7. Sullivan S, et al., White matter tract-oriented deformation predicts traumatic axonal brain injury and reveals rotational direction-specific vulnerabilities. Biomech Model Mechanobiol, 2015. 14(4): p. 877–96. [Europe PMC free article] [Abstract] [Google Scholar]
8. Castano-Leon AM, et al., Longitudinal Analysis of Corpus Callosum Diffusion Tensor Imaging Metrics and Its Association with Neurological Outcome. J Neurotrauma, 2019. 36(19): p. 2785–2802. [Abstract] [Google Scholar]
9. Hilario A, et al., Severe traumatic head injury: prognostic value of brain stem injuries detected at MRI. AJNR Am J Neuroradiol, 2012. 33(10): p. 1925–31. [Europe PMC free article] [Abstract] [Google Scholar]
10. Arenth PM, et al., Corpus callosum integrity and neuropsychological performance after traumatic brain injury: a diffusion tensor imaging study. J Head Trauma Rehabil, 2014. 29(2): p. E1–E10. [Europe PMC free article] [Abstract] [Google Scholar]
11. Shenton ME, et al., A review of magnetic resonance imaging and diffusion tensor imaging findings in mild traumatic brain injury. Brain Imaging Behav, 2012. 6(2): p. 137–92. [Europe PMC free article] [Abstract] [Google Scholar]
12. Madhukar A and Ostoja-Starzewski M, Finite Element Methods in Human Head Impact Simulations: A Review. Ann Biomed Eng, 2019. [Abstract] [Google Scholar]
13. Giordano C, Zappala S, and Kleiven S, Anisotropic finite element models for brain injury prediction: the sensitivity of axonal strain to white matter tract inter-subject variability. Biomech Model Mechanobiol, 2017. 16(4): p. 1269–1293. [Europe PMC free article] [Abstract] [Google Scholar]
14. Montanino A and Kleiven S, Utilizing a Structural Mechanics Approach to Assess the Primary Effects of Injury Loads Onto the Axon and Its Components. Front Neurol, 2018. 9: p. 643. [Europe PMC free article] [Abstract] [Google Scholar]
15. Wright RM, et al., A multiscale computational approach to estimating axonal damage under inertial loading of the head. J Neurotrauma, 2013. 30(2): p. 102–18. [Abstract] [Google Scholar]
16. Hajiaghamemar M, et al., Embedded axonal fiber tracts improve finite element model predictions of traumatic brain injury. Biomech Model Mechanobiol, 2019. [Europe PMC free article] [Abstract] [Google Scholar]
17. Miller LE, et al., Evaluation of Brain Response during Head Impact in Youth Athletes Using an Anatomically Accurate Finite Element Model. J Neurotrauma, 2019. [Europe PMC free article] [Abstract] [Google Scholar]
18. Post A, et al., Brain tissue analysis of impacts to American football helmets. Comput Methods Biomech Biomed Engin, 2018. 21(3): p. 264–277. [Abstract] [Google Scholar]
19. Fahlstedt M, Halldin P, and Kleiven S, The protective effect of a helmet in three bicycle accidents--A finite element study. Accid Anal Prev, 2016. 91: p. 135–43. [Abstract] [Google Scholar]
20. Giudice JS, et al., Development of Open-Source Dummy and Impactor Models for the Assessment of American Football Helmet Finite Element Models. Ann Biomed Eng, 2019. 47(2): p. 464–474. [Abstract] [Google Scholar]
21. Mosleh Y, et al., Designing safer composite helmets to reduce rotational accelerations during oblique impacts. Proc Inst Mech Eng H, 2018. 232(5): p. 479–491. [Abstract] [Google Scholar]
22. Margulies SS, Thibault LE, and Gennarelli TA, Physical model simulations of brain injury in the primate. J Biomech, 1990. 23(8): p. 823–36. [Abstract] [Google Scholar]
23. Hardy WN, et al., Investigation of Head Injury Mechanisms Using Neutral Density Technology and High-Speed Biplanar X-ray. Stapp Car Crash J, 2001. 45: p. 337–68. [Abstract] [Google Scholar]
24. Hardy WN, et al., A study of the response of the human cadaver head to impact. Stapp Car Crash J, 2007. 51: p. 17–80. [Europe PMC free article] [Abstract] [Google Scholar]
25. Alshareef A, et al., A Novel Method for Quantifying Human In Situ Whole Brain Deformation under Rotational Loading Using Sonomicrometry. J Neurotrauma, 2018. 35(5): p. 780–789. [Abstract] [Google Scholar]
26. Zou H, Schmiedeler JP, and Hardy WN, Separating brain motion into rigid body displacement and deformation under low-severity impacts. J Biomech, 2007. 40(6): p. 1183–91. [Abstract] [Google Scholar]
27. Zhou Z, et al., A Reanalysis of Experimental Brain Strain Data: Implication for Finite Element Head Model Validation. Stapp Car Crash J, 2018. 62: p. 293–318. [Abstract] [Google Scholar]
28. Weickenmeier J, et al., Brain stiffens post mortem. J Mech Behav Biomed Mater, 2018. 84: p. 88–98. [Europe PMC free article] [Abstract] [Google Scholar]
29. Chan DD, et al., Statistical Characterization of Human Brain Deformation During Mild Angular Acceleration Measured In Vivo by Tagged Magnetic Resonance Imaging. J Biomech Eng, 2018. 140(10). [Europe PMC free article] [Abstract] [Google Scholar]
30. Knutsen AK, et al., Improved measurement of brain deformation during mild head acceleration using a novel tagged MRI sequence. J Biomech, 2014. 47(14): p. 3475–81. [Europe PMC free article] [Abstract] [Google Scholar]
31. Sabet AA, et al., Deformation of the human brain induced by mild angular head acceleration. J Biomech, 2008. 41(2): p. 307–15. [Europe PMC free article] [Abstract] [Google Scholar]
32. Bayly PV, et al., Deformation of the human brain induced by mild acceleration. J Neurotrauma, 2005. 22(8): p. 845–56. [Europe PMC free article] [Abstract] [Google Scholar]
33. Feng Y, et al., Relative brain displacement and deformation during constrained mild frontal head impact. J R Soc Interface, 2010. 7(53): p. 1677–88. [Europe PMC free article] [Abstract] [Google Scholar]
34. Gomez AD, et al., 3-D Measurements of Acceleration-Induced Brain Deformation via Harmonic Phase Analysis and Finite-Element Models. IEEE Trans Biomed Eng, 2019. 66(5): p. 1456–1467. [Europe PMC free article] [Abstract] [Google Scholar]
35. Naunheim RS, et al., Linear and angular head accelerations during heading of a soccer ball. Med Sci Sports Exerc, 2003. 35(8): p. 1406–12. [Abstract] [Google Scholar]
36. Funk JR, et al., Head and neck loading in everyday and vigorous activities. Ann Biomed Eng, 2011. 39(2): p. 766–76. [Abstract] [Google Scholar]
37. Allen ME, et al., Acceleration perturbations of daily living. A comparison to 'whiplash'. Spine (Phila Pa 1976), 1994. 19(11): p. 1285–90. [Abstract] [Google Scholar]
38. Long JT, et al., Biomechanics of cranial dynamics during daily living activities. Conf Proc IEEE Eng Med Biol Soc, 2004. 2004: p. 2417–9. [Abstract] [Google Scholar]
39. Zhang L, Yang KH, and King AI, A proposed injury threshold for mild traumatic brain injury. J Biomech Eng, 2004. 126(2): p. 226–36. [Abstract] [Google Scholar]
40. Xing F, et al., Phase Vector Incompressible Registration Algorithm for Motion Estimation From Tagged Magnetic Resonance Images. IEEE Trans Med Imaging, 2017. 36(10): p. 2116–2128. [Europe PMC free article] [Abstract] [Google Scholar]
41. Lu YC, et al., A 3D Computational Head Model Under Dynamic Head Rotation and Head Extension Validated Using Live Human Brain Data, Including the Falx and the Tentorium. Ann Biomed Eng, 2019. 47(9): p. 1923–1940. [Europe PMC free article] [Abstract] [Google Scholar]
42. Roy S, et al., Robust skull stripping using multiple MR image contrasts insensitive to pathology. Neuroimage, 2017. 146: p. 132–147. [Europe PMC free article] [Abstract] [Google Scholar]
43. Roy S, et al., Subject Specific Sparse Dictionary Learning for Atlas based Brain MRI Segmentation. Mach Learn Med Imaging, 2014. 8679: p. 248–255. [Europe PMC free article] [Abstract] [Google Scholar]
44. Pierpaoli C, et al. TORTOISE: an integrated software package for processing of diffusion MRI data. in ISMRM. 2010. Stockholm, Sweeden. [Google Scholar]
45. Rohde GK, et al., Comprehensive approach for correction of motion and distortion in diffusion-weighted MRI. Magn Reson Med, 2004. 51(1): p. 103–14. [Abstract] [Google Scholar]
46. Irfanoglu MO, et al., DR-BUDDI (Diffeomorphic Registration for Blip-Up blip-Down Diffusion Imaging) method for correcting echo planar imaging distortions. Neuroimage, 2015. 106: p. 284–99. [Europe PMC free article] [Abstract] [Google Scholar]
47. Chang LC, Jones DK, and Pierpaoli C, RESTORE: robust estimation of tensors by outlier rejection. Magn Reson Med, 2005. 53(5): p. 1088–95. [Abstract] [Google Scholar]
48. Bazin PL, et al., Direct segmentation of the major white matter tracts in diffusion tensor images. Neuroimage, 2011. 58(2): p. 458–68. [Europe PMC free article] [Abstract] [Google Scholar]
49. Basser PJ and Pierpaoli C, Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J Magn Reson B, 1996. 111(3): p. 209–19. [Abstract] [Google Scholar]
50. Osman NF, McVeigh ER, and Prince JL, Imaging heart motion using harmonic phase MRI. IEEE Trans Med Imaging, 2000. 19(3): p. 186–202. [Abstract] [Google Scholar]
51. Maas SA, et al., FEBio: finite elements for biomechanics. J Biomech Eng, 2012. 134(1): p. 011005. [Europe PMC free article] [Abstract] [Google Scholar]
52. Wakana S, et al., Macroscopic orientation component analysis of brain white matter and thalamus based on diffusion tensor imaging. Magn Reson Med, 2005. 53(3): p. 649–57. [Abstract] [Google Scholar]
53. Budday S, et al., Viscoelastic parameter identification of human brain tissue. J Mech Behav Biomed Mater, 2017. 74: p. 463–476. [Abstract] [Google Scholar]
54. Hiscox LV, et al., Magnetic resonance elastography (MRE) of the human brain: technique, findings and clinical applications. Phys Med Biol, 2016. 61(24): p. R401–R437. [Abstract] [Google Scholar]
55. Ganpule S, et al., A Three-Dimensional Computational Human Head Model That Captures Live Human Brain Dynamics. J Neurotrauma, 2017. 34(13): p. 2154–2166. [Europe PMC free article] [Abstract] [Google Scholar]
56. Bayly PV, et al., Magnetic Resonance Measurement of Transient Shear Wave Propagation in a Viscoelastic Gel Cylinder. J Mech Phys Solids, 2008. 56(5): p. 2036–2049. [Europe PMC free article] [Abstract] [Google Scholar]
57. Murphy MC, et al., Measuring the characteristic topography of brain stiffness with magnetic resonance elastography. PLoS One, 2013. 8(12): p. e81668. [Europe PMC free article] [Abstract] [Google Scholar]
58. Blyth BJ and Bazarian JJ, Traumatic alterations in consciousness: traumatic brain injury. Emerg Med Clin North Am, 2010. 28(3): p. 571–94. [Europe PMC free article] [Abstract] [Google Scholar]
59. Sandhu S, et al., Brainstem Diffuse Axonal Injury and Consciousness. J Clin Imaging Sci, 2019. 9: p. 32. [Europe PMC free article] [Abstract] [Google Scholar]
60. Gasser TC, Ogden RW, and Holzapfel GA, Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface, 2006. 3(6): p. 15–35. [Europe PMC free article] [Abstract] [Google Scholar]
61. Garcia-Gonzalez D, et al., Cognition based bTBI mechanistic criteria; a tool for preventive and therapeutic innovations. Sci Rep, 2018. 8(1): p. 10273. [Europe PMC free article] [Abstract] [Google Scholar]
62. Van Essen DC, et al., The WU-Minn Human Connectome Project: an overview. Neuroimage, 2013. 80: p. 62–79. [Europe PMC free article] [Abstract] [Google Scholar]
63. Giordano C and Kleiven S, Development of an Unbiased Validation Protocol to Assess the Biofidelity of Finite Element Head Models used in Prediction of Traumatic Brain Injury. Stapp Car Crash J, 2016. 60: p. 363–471. [Abstract] [Google Scholar]
64. Zhao W and Ji S, Mesh Convergence Behavior and the Effect of Element Integration of a Human Head Injury Model. Ann Biomed Eng, 2019. 47(2): p. 475–486. [Europe PMC free article] [Abstract] [Google Scholar]
65. Bayly PV, et al., Measurement of strain in physical models of brain injury: a method based on HARP analysis of tagged magnetic resonance images (MRI). J Biomech Eng, 2004. 126(4): p. 523–8. [Europe PMC free article] [Abstract] [Google Scholar]
66. Bayly PV, et al., In vivo imaging of rapid deformation and strain in an animal model of traumatic brain injury. J Biomech, 2006. 39(6): p. 1086–95. [Europe PMC free article] [Abstract] [Google Scholar]
67. Eucker SA, et al., Physiological and histopathological responses following closed rotational head injury depend on direction of head motion. Exp Neurol, 2011. 227(1): p. 79–88. [Europe PMC free article] [Abstract] [Google Scholar]
68. Margulies SS, et al., Establishing a Clinically Relevant Large Animal Model Platform for TBI Therapy Development: Using Cyclosporin A as a Case Study. Brain Pathol, 2015. 25(3): p. 289–303. [Europe PMC free article] [Abstract] [Google Scholar]
69. Parthasarathy V and Prince JL. Strain resolution from HARP-MRI. in Proceedings of the 12th Annual Meeting of ISMRM. 2004. Kyoto, Japan. [Google Scholar]
70. Battal B, et al., Cerebrospinal fluid flow imaging by using phase-contrast MR technique. Br J Radiol, 2011. 84(1004): p. 758–65. [Europe PMC free article] [Abstract] [Google Scholar]
71. Kruse SA, et al., Magnetic resonance elastography of the brain. Neuroimage, 2008. 39(1): p. 231–7. [Europe PMC free article] [Abstract] [Google Scholar]
72. McGarry M, et al., Including spatial information in nonlinear inversion MR elastography using soft prior regularization. IEEE Trans Med Imaging, 2013. 32(10): p. 1901–9. [Europe PMC free article] [Abstract] [Google Scholar]
73. Johnson CL, et al., Viscoelasticity of subcortical gray matter structures. Hum Brain Mapp, 2016. 37(12): p. 4221–4233. [Europe PMC free article] [Abstract] [Google Scholar]
74. Anderson AT, et al., Observation of direction-dependent mechanical properties in the human brain with multi-excitation MR elastography. J Mech Behav Biomed Mater, 2016. 59: p. 538–546. [Europe PMC free article] [Abstract] [Google Scholar]
75. Schmidt JL, et al., Measurement of anisotropic mechanical properties in porcine brain white matter ex vivo using magnetic resonance elastography. J Mech Behav Biomed Mater, 2018. 79: p. 30–37. [Europe PMC free article] [Abstract] [Google Scholar]
76. Badachhape AA, et al., Relationships between scalp, brain, and skull motion estimated using magnetic resonance elastography. J Biomech, 2018. 73: p. 40–49. [Europe PMC free article] [Abstract] [Google Scholar]

Full text links 

Read article at publisher's site: https://doi.org/10.1016/j.brain.2020.100015

Citations & impact 

Impact metrics

21
Citations
Jump to Citations

Citations of article over time

Alternative metrics

Altmetric item for https://www.altmetric.com/details/92520090
Altmetric
Discover the attention surrounding your research
https://www.altmetric.com/details/92520090

Article citations

Go to all (21) article citations

Data 

Data behind the article

This data has been text mined from the article, or deposited into data resources.

BioStudies: supplemental material and supporting data

Similar Articles 

To arrive at the top five similar articles we use a word-weighted algorithm to compare words from the Title and Abstract of each citation.

Funding 

Funders who supported this work.

NINDS NIH HHS (3)

National Institute of Neurological Disorders and Stroke